二次函数的图象和性质备课素材 (2)
26.2二次函数的图象与性质(第2课时)课件(共12张PPT)

为0 。
3.函数y=3x2+5与y=3x2的图象的不同之处是( C
)
A.对称轴
B.开口方向
C.顶点
D.形状
4.已知抛物线y=2x2-<1上有两点(x1,y1 ) ,(x1,y1 ) 且x1<x2<0,则y1 y2(填“<”或“>”)
5.已知一个二次函数图像的顶点在y轴上,并 且离原点1个单位,图像经过点(–1,0),求该 二次函数解析式。
1.5
1
0.5
y3x2 1
1
2
-0.5
-1
在同一直角坐标系中
画出函数 y 1 x2 y 1x2 2 3
5 4
y
3 y 1 x2 2
3
3 2
的图像
1
x
–5 –4 –3 –2 –1O –1
–2
y 1x2 2
–3
3
–4
–5
12345
y 1 x2 2 3
y 1 x2 3
试说出函数y=ax2+k(a、k是常数,a≠0)的图 象的开口方向、对称轴和顶点坐标,并填写下 表.
1
-6 -4 -2
2
4
6
x y=3x2 y=3x2–1
… –1 –0.6
…3
1.08
…2
0.08
(2)二次函数 y=3x²-1 的图 象与二次函数
y=3x²的图象有 什么关系?
-2
-1
–0.3
0
0.3
0.27
0
0.27
–0.73 – 1 –0.73
y 3x2
2
0.6 1 … 1.08 3 … 0.08 2 …
谢谢观赏
You made my day!
二次函数的图象和性质课件

解决实际问题
实际应用场景
二次函数在许多实际问题中都有应用,如物体运动、经济 活动等。通过建立数学模型,我们可以利用二次函数来描 述和解决这些实际问题。
实际问题的求解策略
对于实际问题,我们通常需要结合二次函数的性质和实际 问题的特点来制定求解策略。这可能包括分析函数的单调 性、最值、零点等。
二次函数的顶点
总结词
二次函数的顶点坐标为(-b/2a, c-b^2/4a)。
详细描述
二次函数的最值点即为顶点。对于一般形式的二次函数y=ax^2+bx+c,其顶点的x坐标为-b/2a,y坐 标为c-b^2/4a。Biblioteka 二次函数的对称轴总结词
二次函数的对称轴为x=-b/2a。
详细描述
二次函数的对称轴是一条垂直于x轴的直线,其方程为x=-b/2a。这是由二次函数的最值性质决定的,对称轴上 方的函数值与对称轴下方的函数值相等。
二次函数图象的绘制
01
02
03
步骤一
确定二次函数的表达式, 例如 $f(x) = ax^2 + bx + c$。
步骤二
选择一个或多个点,代入 二次函数表达式中,计算 出对应的y值。
步骤三
在坐标系上标出这些点, 通过这些点绘制出二次函 数的图象。
二次函数图象的形状
形状特征一
二次函数图象是一个抛物 线。根据a的值(正或负) ,抛物线开口向上或向下 。
二次函数的图象和性质课 件
• 二次函数的基本概念 • 二次函数的图象 • 二次函数的性质 • 二次函数的解析式 • 二次函数的应用
01
二次函数的基本概念
二次函数定义
总结词
二次函数是形如$f(x) = ax^2 + bx + c$的函数,其中$a neq 0$。
261二次函数图象和性质(2)

抛物线y=x2+1,y=x2-1与抛物线y=x2的关系:
抛物线y=x2
向上平移 1个单位
抛物线
y=x2+1
抛物线y=x2
向下平移 1个单位
抛物线
y=x2-1
y
10
把抛物线y=2x2+1向上平
9 8
移5个单位,会得到那条抛物线?
7
向下平移3.4个单位呢?
6 5
4
y=x2+1 y=x2
(1)得到抛物线y=2x2+6 (2)得到抛物线y=2x2-2.4
;在对称
轴的右侧,y随着x的
,当x=____时,函数y的
值最___,最小值是
.
做一做:
1、按下列要求求出二次函数的解析式: (1)已知抛物线y=ax2+c经过点(-3,2) (0,-1)求该抛物线的解析式。
(2)形状与y=-2x2+3的图象形状相同, 但开口方向不同,顶点坐标是(0,1) 的抛物线解析式。
(3)对称轴是y轴,顶点纵坐标是-3, 且经过(1,2)的点的解析式,
2、在同一直角坐标系中,一次函数y=ax+c和 二次函数y=ax2+c的图象大致是如图中的( )
y
y
y
y
o
x
o
x
o
x
o
x
A
B
C
D
(1)抛物线y= −2x2+3的顶点坐标是
,对称轴
是
,在___
侧,y随着x的增大而
增大;在 侧,y随着x的增大而减小,当x= _____
时,函数y的值最大,最大值是 ,它是由抛物线y=
−2x2线怎样平移得到的__________.
6.2二次函数的图象和性质(2)课件

x=0时,y最大=k
抛物线y=ax2 +k(a≠0)的图象可由y=ax2的图象通过上 下平移得到。(抓住顶点 坐标的变化)
-8
上加下减
(4)函数y=4x2+5的图象可由y=4x2的图象 向上 平移 5 个单位得到;y=4x2-11的图象 下 可由 y=4x2的图象向 平移 11个单位得到。 (5)将函数y=-3x2+4的图象向 下 平移 4 个单位可得 y=-3x2的图象;将y=2x2-7的图象向 上平移 7 个 单位得到y=2x2的图象。将y=x2-7的图象 向上 平移 9 个单位可得到 y=x2+2的图象。 (6)将抛物线y=4x2向上平移3个单位,所得的 抛物线的函数式是 y=4x2+3 。 将抛物线y=-5x2+1向下平移5个单位,所得的 抛物线的函数式是 y=-5x2-4 。
知识象一艘船 让它载着我们 驶向理想的 ……
y=ax2 (a≠0)
a>0
a<0 y
O
图 象
O
y
向上 (0 ,0) y轴
当x<0时, y随着x的增大而减小。 当x>0时, y随着x的增大而增大。
x
x
开口方向 顶点坐标 对称轴 增 减 性 最值
向下 (0 ,0) y轴
当x<0时, y随着x的增大而增大。 当x>0时, y随着x的增大而减小。
5 10
x y=x2 y=x2-2
….. …… ……
-2 4
-1 1
0 0
1 1
2 4
…… ……
2
-1
y
8
0
-1
2
6
函数y=x2-2的图象 可由y=x2的图象 沿y轴向下平移2 个单位长度得到.
二次函数 的图象和性质 (PPT) (2)

7.如图,直线AB过x轴上的点B(4,0),且与
抛物线y=ax2交于A、C两点,已知A(2,2).
(1)求直线AB的函数解析式; y=ax+b
D
(2)求抛物线的函数解析式;
(3)如果抛物线上有点D,使S△OBD=S△OAC, 求点D的坐标.
D (2,2) (4,0)
解:(1)设直线表达式为y=ax+b,
∵A(2,2),B(4,0)都在y=ax+b的图象上,
2 0
2a 4a
b, b
a b
-1, 4
∴直线AB的函数解析式为:y=-x+4.
(2,2)
(2)∵点A(2,2)在y=ax2的图象上,
∴代入可得 a 1 ,
2
∴抛物线的函数解析式为 y 1 x2.
2
(4,0)
当x = 0时,最大值为0.
课后作业
1.从课后习题中选取; 2.完成练习册本课时的习题。
教学反思
本课时教学重点在于培养学生的比较能力,旨在 希望学生通过对比发现函数图象的性质,从而进一步 增强学生的数形结合意识,体会通过探究获得知识的 乐趣.
y=2x2
y 1 x2 2
2 4x
函数 y= 1 x2,y=2x2 的图象与函数y=x2 的图象相比,有什么共同点和不 同点? 2
开口都向上; 对称轴都是y轴;
增减性相同:当x<0时,y 随x增大而减小;当x>0时, y随x增大而增大.
y y=2x2 y 1 x2
8
2
6
4
a值越大,抛物线的
2
开口越小.
顶点都是原点(0,0),顶-4 -2 O 点是抛物线的最低点;
§6.2二次函数的图象和性质(2)

§6.2二次函数的图象和性质(2)学习目标:1.会用列表描点法画二次函数(a≠0)的图象。
2.会用平移变换解释二次函数(a≠0)与二次函数(a≠0)的图象的位置关系。
3.通过对二次函数图象的观察,进一步感受在同一直角坐标系中,图形运动变化与图形上点的坐标变化之间的关系。
学习重点:描点法画二次函数(a≠0)的图象学习难点:用“坐标的数值变化”与“图形的位置变化”的关系,探索二次函数(a≠0)的图象与二次函数(a≠0)的图象的关系.【知识扫描】1、已知函数,当x=1时y=3,则a= , 对称轴是,顶点是 , 抛物线的开口,在对称轴的左侧,y随x增大而,当x= 时,函数y有最值,是 .2、当x<0时,函数与在同一直角坐标系中的大致图象是----------------()A B C D3、若抛物线经过点( l,-2 ),则它也经过------------------------------------------------------------()A (-1,-2 )B (-l,2 )C ( l,2) D(2,1)★4、已知a≠0,b<0,一次函数是y=ax+b,二次函数是y=ax2则右面图中,可以成立的是------------------------()【基础练习】在同一直角坐标系中,画出函数、与的图象.列表描点、连线,画出这三个函数的图象【例题精讲】例1、仔细观察基础练习中所画图形后回答:(1)函数的图象可以由函数的图象沿_______轴向_______平移____个单位长度得到,所以它是抛物线。
这条抛物线的对称轴是,顶点坐标是________(2)函数的图象可以由函数的图象沿_______轴向_______平移____个单位长度得到,所以它是抛物线。
这条抛物线的对称轴是,顶点坐标是________.(3)如果函数的二次项系数为负数,上述结论还成立吗?归纳当k>0时,函数(a≠0)的图象可以由函数的图象沿_______轴向_____平移____ 个单位长度得到,所以它是抛物线。
《二次函数的图象和性质(2)》教学设计
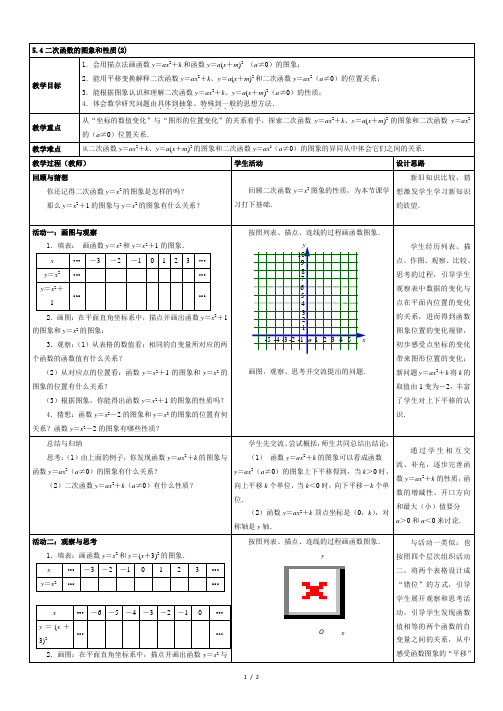
5.4二次函数的图象和性质(2)教学目标1.会用描点法画函数y=ax2+k和函数y=a(x+m)2(a≠0)的图象;2.能用平移变换解释二次函数y=ax2+k、y=a(x+m)2和二次函数y=ax2(a≠0)的位置关系;3.能根据图象认识和理解二次函数y=ax2+k、y=a(x+m)2(a≠0)的性质;4.体会数学研究问题由具体到抽象.....、特殊到一般.....的思想方法.教学重点从“坐标的数值变化”与“图形的位置变化”的关系着手,探索二次函数y=ax2+k、y=a(x+m)2的图象和二次函数y=ax2的(a≠0)位置关系.教学难点从二次函数y=ax2+k、y=a(x+m)2的图象和二次函数y=ax2(a≠0)的图象的异同从中体会它们之间的关系.教学过程(教师)学生活动设计思路回顾与猜想你还记得二次函数y=x2的图象是怎样的吗?那么y=x2+1的图象与y=x2的图象有什么关系?回顾二次函数y=x2图象的性质,为本节课学习打下基础.新旧知识比较,猜想激发学生学习新知识的欲望.活动一:画图与观察1.填表:画函数y=x2和y=x2+1的图象.x …-3 -2 -1 0 1 2 3 …y=x2……y=x2+1……2.画图:在平面直角坐标系中,描点并画出函数y=x2+1的图象和y=x2的图象;3.观察:(1)从表格的数值看:相同的自变量所对应的两个函数的函数值有什么关系?(2)从对应点的位置看:函数y=x2+1的图象和y=x2的图象的位置有什么关系?(3)根据图象,你能得出函数y=x2+1的图象的性质吗?4.猜想:函数y=x2-2的图象和y=x2的图象的位置有何关系?函数y=x2-2的图象有哪些性质?按照列表、描点、连线的过程画函数图象.画图,观察、思考并交流提出的问题.学生经历列表、描点、作图、观察、比较、思考的过程,引导学生观察表中数据的变化与点在平面内位置的变化的关系,进而得到函数图象位置的变化规律,初步感受点坐标的变化带来图形位置的变化;新问题y=ax2+k将k的取值由1变为-2,丰富了学生对上下平移的认识.总结与归纳思考:(1)由上面的例子,你发现函数y=ax2+k的图象与函数y=ax2(a≠0)的图象有什么关系?(2)二次函数y=ax2+k(a≠0)有什么性质?学生先交流、尝试概括,师生共同总结出结论:(1)函数y=ax2+k的图象可以看成函数y=ax2(a≠0)的图象上下平移得到,当k>0时,向上平移k个单位,当k<0时,向下平移-k个单位.(2)函数y=ax2+k顶点坐标是(0,k),对称轴是y轴.通过学生相互交流、补充,逐步完善函数y=ax2+k的性质,函数的增减性、开口方向和最大(小)值要分a>0和a<0来讨论.活动二:观察与思考1.填表:画函数y=x2和y=(x+3)2的图象.x …-3 -2 -1 0 1 2 3 …y=x2……x …-6 -5 -4 -3 -2 -1 0 …y=(x+3)2……2.画图:在平面直角坐标系中,描点并画出函数y=x2与按照列表、描点、连线的过程画函数图象.与活动一类似:也按照四个层次组织活动二,将两个表格设计成“错位”的方式,引导学生展开观察和思考活动,引导学生发现函数值相等的两个函数的自变量之间的关系,从中感受函数图象的“平移”xyO1 2 3 4 5 x12345678910yo-1-2-3-4-51 / 22 / 2。
6.2二次函数的图像和性质(2)

6.2 二次函数的图象和性质(2)课 型:新授课 主 备:姜晓岗 审 核:王爱忠 时 间:101216一、学习目标:1、能利用表格..和.图象..研究二次函数2ax y =的性质(如开口方向、对称轴、顶点、增减性等); 2、掌握待定系数法,学会研究函数性质的途径和方法。
二、学习重点与难点:理解二次函数2ax y =的性质和待定系数法是学习的重点;难点是对性质和待定系数法确定二次函数关系式的实质的理解。
三、自学质疑:1.自学指导:本节课主要研究P 11-P 12的内容,请注意图、表相互结合来研究问题,注重“理解”....2.思考题:1.填表并观察思考2.思:通过1中的表和图,你能否概括出函数2x y =、2x y =和25.0x y -=、2x y =的共同点和不同点?记录下来(注意记录的条理性)3.类比:对于二次函数2ax y =具有什么性质呢?你是怎样理解和记忆这些性质的呢?4.试一试:认真完成课本P 11练习(注意第3题的每一步的算理)我自学时的疑难、困惑 或 发现是:巩固案A 组:⒈根据函数关系式y=243x -填空:(1)图像开口向 ,,顶点坐标 , 对称轴 ;(2)当x ≥0时,y 随x 的增大而 ;当x= 时,y 的最 值是 .2.二次函数y=ax 2的图像如图,该函数的关系式是 .如果另一个函数的图像与该函数关于x 轴对称,那么这个函数的关系式是 .3.已知二次函数y=ax 2的图像经过点P(2,3),你能确定它的开口方向吗?你能确定a 的值吗4.根据图(1)、(2)的函数图像填空:(1)二次函数y=-7x 2的图像不可能是 , 二次函数y=232x 的图像不可能是 ; (2)有最大值的函数图像是 ,它的最大值是 ;(3)如果二次函数y=(m-1)x 2的图像是图(1),那么m 的取值范围是 .5.对于函数y=x 2,由其图像可知,下列判断中,正确的是( )A 、若m 、n 互为相反数,则x=m 与x=n 对应的函数值相等;B 、对于同一自变量x ,有两个函数值与之对应;C 、对于任意一个实数y ,有两个x 值与之对应;D 、对于任何实数x ,都有y>0. 6.在同一坐标系中,函数y=x 2,y=221x ,y=3x 2的图像如图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二十二章二次函数
22.1 二次函数的图象和性质
22.1.2 二次函数y=a x2的图象和性质
如图22-1-6,你知道打篮球
投篮时篮球运动的路线是什么吗?你知道姚明投篮为什么
那么准吗?用红色的篮球做投篮动作,观察篮球的运动路
线,思考分析投篮时篮球的运动路线有何规律,怎样用数学
规律来描述?
[说明与建议] 说明:通过对抛物线实际问题的导入,激
发学生的学习兴趣和探究新知的欲望,增加对抛物线初步的
了解和认识.建议:教师做模拟试验直观展示投篮路径,更
能激发学生对其路径的数学探究,让学生养成观察思考的好
习惯.
(1)在二次函数y=x2中,y
随x的变化而变化的规律是什么?你想直观地了解它的性质吗?
(2)请你在图22-1-7中用描点法画二次函数y =x 2的图象.
观察y =x 2的解析式,选择x 的适当值,并计算相应的y 值,完成下表:
x … -3 -2 -1 0 1 2 3 … y =x 2
在图22-1-7所示的平面直角坐标系中描点并用光滑曲线连接各点.
[说明与建议] 说明:学生已经有画函数图象的经验和水平,掌握了画函数图象的一般步骤.本节通过画二次函数y =x 2的图象,引入本节新课,进而类比二次项系数不是1的情形及它们的性质.建议:先留给学生动手画图的时间,然后教师要引导学生分析二次函数y =x 2的性质,为进一步的学习积累数学活动经验.
[命题角度1] 二次函数y =ax 2
的图象和性质
二次函数y =ax 2的图象是一条过原点的抛物线,通常两种考法:(1)给定二次函数的解析式,画二次函数的图象,或者说出二次函数图象的开口方向、对称轴、顶点坐标、增减性、最大值或最小值等;(2)给定函数图象,判断函数的未知系数.如教材P30例1,P41习题22.1 T3.
[命题角度2] 二次函数y =ax 2的图象及其性质与几何综合 此类问题一般要综合利用抛物线上的点的坐标特点及对称性,结合几何图形的性质解决问题.
例 [菏泽中考] 如图22-1-8,平行于x 轴的直线AC 分别交函数y 1=x 2
(x ≥0)与y 2=x 2
3
(x ≥0)的图象于B ,C 两点,过
点C 作y 轴的平行线交函数y 1的图象于点D ,直线DE ∥AC ,交函数y 2的图象于点E ,则
DE
AB
= 3-3 W.
P32
说出下列抛物线的开口方向、对称轴和顶点: (1)y =3x 2; (2)y =-3x 2; (3)y =31
x 2; (4)y =-31
x 2.
解:(1)抛物线y =3x 2的开口方向向上,对称轴是y 轴,顶点坐标为(0,0). (2)抛物线y =-3x 2的开口方向向下,对称轴是y 轴,顶点坐标为(0,0).
(3)抛物线y =31
x 2的开口方向向上,对称轴是y 轴,顶点坐标为(0,0). (4)抛物线y =-31
x 2的开口方向向下,对称轴是y 轴,顶点坐标为(0,0).
1. 关于函数y =2x 2的图象的描述:(1)图象有最低点,(2)图象为轴对称图形,(3)图象与y 轴的交点为原点,(4)图象的开口向上,其中正确的有( ) A .1个 B .2个 C .3个 D .4个
2.(2013丽水)若二次函数y=ax 2
的图象过点P (-2, 4),则该图象必经过点( ) A .(2, 4)
B .(-2, -4)
C .(2, -4)
D .(4, -2)
3. 在抛物线
,y =-3x 2,y =x 2中,开口最大的是( )
A .
B .y =-3x 2
C .y =x 2
D .无法确定
4. (1)若抛物线y =a x 2 与y =-2x 2
的形状相同,开口方向相同,则a = _____ .
(2)把抛物线绕原点旋转180°后的抛物线是____.
5.跳伞运动员在打开降落伞之前,下落的路程s (米)与所经过的时间t (秒)之间的关系
为s =at 2
. t (秒) 0 1 2 3 4 …
s (米)
0 45 … (1)根据表中的数据,写出s 关于t 的函数解析式; (2)完成上面自变量t 与函数s 的对应值表;
(3)如果跳伞运动员从5100米的高空跳伞,为确保安全,必须在离地面600米之前打开降落伞.问运动员在空中不打开降落伞的时间至多有几秒?
参考答案 1.D 2.A 3.A
4.(1)-2 (2)y =x²
5.解:(1)s=5t2
(2)
t(秒) 0 1 2 3 4 …
s(米) 0 5 20 45 80 …
(3)由题意得s=5t2 =5100-600,∴t2 =900,∵t>0, ∴t=30.
∴运动员在空中不打开降落伞的时间至多有30秒.
函数小史
数学史表明,重要的数学概念的产生和发展,对数学发展起着不可估量的作用.有些重要的数学概念对数学分支的产生起着奠定性的作用.我们刚学过的函数就是这样的重要概念.在笛卡尔引入变量以后,变量和函数等概念日益渗透到科学技术的各个领域.纵览宇宙,运算天体,探索热的传导,揭示电磁秘密,这些都和函数概念息息相关.正是在这些实践过程中,人们对函数的概念不断深化.
回顾一下函数概念的发展史,对于刚接触到函数的初中同学来说,虽然不可能有较深的理解,但无疑对加深理解课堂知识、激发学习兴趣将是有益的.
最早提出函数(function)概念的,是17世纪德国数学家莱布尼茨.最初莱布尼茨用“函数”一词表示幂,如都叫函数.以后,他又用函数表示在直角坐标系中曲线上一点
的横坐标、纵坐标.1718年,莱布尼茨的学生、瑞士数学家贝努利把函数定义为:“由某个变量及任意的一个常数结合而成的数量.”意思是凡变量x和常量构成的式子都叫做x的函数.贝努利所强调的是函数要用公式来表示.
后来数学家觉得不应该把函数概念局限在只能用公式来表达上.只要一些变量变化,另一些变量能随之而变化就可以,至于这两个变量的关系是否要用公式来表示,就不作为判别函数的标准.
1755年,瑞士数学家欧拉把函数定义为:“如果某些变量,以某一种方式依赖于另一些变量,即当后面这些变量变化时,前面这些变量也随着变化,我们把前面的变量称为后面变量的函数.”在欧拉的定义中,就不强调函数要用公式表示了.由于函数不一定要用公式来表示,欧拉曾把画在坐标系的曲线也叫函数.他认为:“函数是随意画出的一条曲线.”
当时有些数学家对于不用公式来表示函数感到很不习惯,有的数学家甚至抱怀疑态度.他们把能用公式表示的函数叫“真函数”,把不能用公式表示的函数叫“假函数”.1821年,法国数学家柯西给出了类似现在中学课本的函数定义:“在某些变数间存在着一定的关系,当一经给定其中某一变数的值,其他变数的值可随着而确定时,则将最初的变数叫自变量,其他各变数叫做函数.”在柯西的定义中,首先出现了自变量一词.
1834年,俄国数学家罗巴契夫斯基进一步提出函数的定义:“x的函数是这样的一个数,它对于每一个x都有确定的值,并且随着x一起变化.函数值可以由解析式给出,也可以由一个条件给出,这个条件提供了一种寻求全部对应值的方法.函数的这种依赖关系可以存在,但仍然是未知的.”这个定义指出了对应关系(条件)的必要性,利用这个关系,可以来求出每一个x的对应值.
1837年,德国数学家狄里克雷认为怎样去建立x与y之间的对应关系是无关紧要的,所以他的定义是:“如果对于x的每一个值,y总有一个完全确定的值与之对应,则y是x的函数.”这个定义抓住了概念的本质属性,变量y称为x的函数,只需有一个法则存在,使得这个函数取值范围中的每一个值,有一个确定的y值和它对应就行了,不管这个法则是公式或图象或表格或其他形式.这个定义比前面的定义带有普遍性,为理论研究和实际应用提供了方便.因此,这个定义曾被比较长期的使用着.
自从德国数学家康托尔的集合论被大家接受后,用集合对应关系来定义函数概念就是现在中学课本里用的了.
中文数学书上使用的“函数”一词是转译词.是我国清代数学家李善兰在翻译《代数学》(1895年)一书时,把“function”译成“函数”的.中国古代“函”字与“含”字通用,都有着“包含”的意思.李善兰给出的定义是:“凡式中含天,为天之函数.”中国古代用天、地、人、物4个字来表示4个不同的未知数或变量.这个定义的含义是:“凡是公式中含有变量x,则该式子叫做x的函数.”所以“函数”是指公式里含有变量的意思.
在可预见的未来,关于函数的争论、研究、发展、拓广将不会完结,也正是这些影响着数学及其相邻学科的发展.。
