2012届北京市朝阳区高三期中数学理科试题(WORD精校版)
2012届北京市海淀区高三期末数学理科试题(WORD精校版)

北京市海淀区2012届高三上学期期末考试试题数学(理)2012.01一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)复数52i=+ ( )(A )2i-(B )21i 55+(C )105i-(D )105i33-(2)如图,正方形ABCD 中,点E 是DC 的中点,点F 是BC 的一个三等分点.那么=EF (A )1123AB AD -(B )1142AB AD+(C )1132AB DA+(D )1223AB AD-(3)若数列n a 满足:119a =,13(*)nn a a nN ,则数列n a 的前n 项和数值最大时,n 的值是(A )6(B )7(C )8(D )9(4)已知平面,,直线l ,若^,l =,则(A )垂直于平面的平面一定平行于平面(B )垂直于直线l 的直线一定垂直于平面(C )垂直于平面的平面一定平行于直线l(D )垂直于直线l 的平面一定与平面,都垂直(5)函数()sin(2)(,)f x A x A =+R 的部分图象如图所示,那么(0)f =()(A )12-(B )32-FEDC BA(C )1-(D )3-(6)执行如图所示的程序框图,输出的i 值为()(A )5 (B )6 (C )7 (D )8(7)已知函数2()cos sin f x xx ,那么下列命题中假命题...是()(A )()f x 既不是奇函数也不是偶函数(B )()f x 在[,0]-上恰有一个零点(C )()f x 是周期函数(D )()f x 在(,2上是增函数(8)点P 到图形C 上每一个点的距离的最小值称为点P 到图形C 的距离,那么平面内到定圆C 的距离与到定点A 的距离相等的点的轨迹不可能...是()(A )圆(B )椭圆(C )双曲线的一支(D )直线二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上.(9)5(1)x +的展开式中2x 的系数是. (用数字作答)(10)若实数,x y 满足40,20,250,x y x y x y ì+-???--í??+-??则2z x y =+的最大值为.(11)抛物线2x ay =过点1(1,)4A ,则点A 到此抛物线的焦点的距离为.甲城市乙城市开始i=1,s=0 s=s+2i -1is ≤100i= i +1 输出i 结束是否(12)甲和乙两个城市去年上半年每月的平均气温(单位:C °)用茎叶图记录如下,根据茎叶图可知,两城市中平均温度较高的城市是____________,气温波动较大的城市是____________.(13)已知圆C:22(1)2xy,过点(1,0)A 的直线l 将圆C 分成弧长之比为1:3的两段圆弧,则直线l 的方程为.(14)已知正三棱柱'''ABC A B C -的正(主)视图和侧(左)视图如图所示. 设,'''ABC A B C 的中心分别是,'O O ,现将此三棱柱绕直线'OO 旋转,射线OA 旋转所成的角为x 弧度(x 可以取到任意一个实数),对应的俯视图的面积为()S x ,则函数()S x 的最大值为;最小正周期为 .8,3说明:“三棱柱绕直线'OO 旋转”包括逆时针方向和顺时针方向,逆时针方向旋转时,OA旋转所成的角为正角,顺时针方向旋转时,OA 旋转所成的角为负角.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.(15)(本小题满分13分)在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,2A B ,3sin 3B.(Ⅰ)求cos A 及sin C 的值;(Ⅱ)若2b =,求ABC 的面积.908773 12472247侧(左)视图正(主)视图43(16)(本小题满分13分)为加强大学生实践、创新能力和团队精神的培养,促进高等教育教学改革,教育部门主办了全国大学生智能汽车竞赛. 该竞赛分为预赛和决赛两个阶段,参加决赛的队伍按照抽签方式决定出场顺序.通过预赛,选拔出甲、乙等五支队伍参加决赛.(Ⅰ)求决赛中甲、乙两支队伍恰好排在前两位的概率;(Ⅱ)若决赛中甲队和乙队之间间隔的队伍数记为X ,求X 的分布列和数学期望.(17)(本小题满分14分)在四棱锥P ABCD -中,底面ABCD 是直角梯形,AB ∥CD ,90ABC ?,2AB PB PC BC CD ====,平面PBC ^平面ABCD .(Ⅰ)求证:AB ^平面PBC ;(Ⅱ)求平面PAD 和平面BCP 所成二面角(小于90°)的大小;(Ⅲ)在棱PB 上是否存在点M 使得CM ∥平面PAD ?若存在,求PM PB的值;若不存在,请说明理由.(18)(本小题满分13分)已知函数2()e ()xf x xaxa ,其中a 是常数.PABCD(Ⅰ)当1a 时,求曲线()y f x 在点(1,(1))f 处的切线方程;(Ⅱ)若存在实数k ,使得关于x 的方程()f x k 在[0,)上有两个不相等的实数根,求k 的取值范围.(19)(本小题满分14分)已知焦点在x 轴上的椭圆C 过点(0,1),且离心率为32,Q 为椭圆C 的左顶点.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)已知过点6(,0)5的直线l 与椭圆C 交于A ,B 两点.(ⅰ)若直线l 垂直于x 轴,求AQB 的大小;(ⅱ)若直线l 与x 轴不垂直,是否存在直线l 使得QAB 为等腰三角形?如果存在,求出直线l 的方程;如果不存在,请说明理由.(20)(本小题满分14分)已知集合{1,2,3,,}(*)M n n=N ,若集合12{,,,}(*)m A a a a M m=臀N ,且对任意的b M ?,存在,(1)i j a a A i j m 危#,使得12ij b a a =+(其中12,{1,0,1}?),则称集合A 为集合M 的一个m 元基底. (Ⅰ)分别判断下列集合A 是否为集合M 的一个二元基底,并说明理由;①{1,5}A =,{1,2,3,4,5}M =;②{2,3}A =,{1,2,3,4,5,6}M =.(Ⅱ)若集合A 是集合M 的一个m 元基底,证明:(1)m m n +;(Ⅲ)若集合A 为集合{1,2,3,,19}M =的一个m 元基底,求出m 的最小可能值,并写出当m 取最小值时M 的一个基底A .参考答案及评分标准2012.01一. 选择题:本大题共8小题,每小题5分,共40分.题号(1)(2)(3)(4)(5)(6)(7)(8)答案ADBDCABD二.填空题:本大题共6小题,每小题5分,共30分.(9)5(10)7(11)54(12)乙,乙(13)3(1)3y x =+或3(1)3y x =-+(14)8;3注:(13)题正确答出一种情况给3分,全对给5分;(12)、(14)题第一空3分;第二空2分.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.(15)(本小题满分13分)解:(Ⅰ)因为2A B ,所以2cos cos212sin A B B ==-.,,,,,,,,,,,,,,,2分因为3sin 3B,所以11cos 1233A =-?. ,,,,,,,,,,,,,,,3分由题意可知,(0,)2B ?.所以26cos 1sin 3B B =-=. ,,,,,,,,,,,,,,,5分因为22sin sin 22sin cos 3A B B B ===.,,,,,,,,,,,,,,,6分所以sin sin[()]sin()C A B A B =-+=+53sin cos cos sin 9A B A B =+=. ,,,,,,,,,,,,,,,8分(Ⅱ)因为sin sin b a B A=,2b =,,,,,,,,,,,,,,,,10分所以232233a =.所以463a =. ,,,,,,,,,,,,,,,11分所以1202sin 29ABCSab C ==. ,,,,,,,,,,,,,,,13分(16)(本小题满分13分)解:(Ⅰ)设“甲、乙两支队伍恰好排在前两位”为事件A ,则23!15!10P A. ,,,,,,,,,,,,,,,4分所以甲、乙两支队伍恰好排在前两位的概率为110.,,,,,,,,,,,,,,,5分(Ⅱ)随机变量X 的可能取值为0, 1, 2, 3. ,,,,,,,,,,,,,,,6分24!205!5P X ,323!315!10P X ,22!32!125!5P X ,23!135!10P X.,,,,,,,,,,,,,,,10分随机变量X 的分布列为:X 0123P2531015110因为231101231510510EX ,所以随机变量X 的数学期望为1.,,,,,,,,,,,,,,,13分(17)(本小题满分14分)(Ⅰ)证明:因为90ABC ?,所以AB BC .,,,,,,,,,,,,,,,1分因为平面PBC ^平面ABCD ,平面PBC 平面ABCD BC =,AB ì平面ABCD ,所以AB^平面PBC .,,,,,,,,,,,,,,,3分(Ⅱ)解:取BC 的中点O ,连接PO .因为PB PC =,所以PO BC .因为平面PBC ^平面ABCD ,平面PBC平面ABCD BC =,PO ì平面PBC ,所以PO ^平面ABCD .,,,,,,,,,,,,,,,4分如图,以O 为原点,OB 所在的直线为x 轴,在平面ABCD 内过O 垂直于BC 的直线为y 轴,OP 所在的直线为z 轴建立空间直角坐标系O xyz .不妨设2BC =.由直角梯形ABCD 中2AB PB PC BC CD ====可得(0,0,3)P ,(1,1,0)D -,(1,2,0)A .所以(1,1,3)DP =-,(2,1,0)DA =.设平面PAD 的法向量(,,)=x y z m .因为0,0.DP DAì???í????m m 所以(,,)(1,1,3)0,(,,)(2,1,0)0,x y z x y z ì??=?í???即30,20.x y z x y ì?-+=?í?+=?令1x =,则2,3y z =-=-.所以(1,2,3)=--m .,,,,,,,,,,,,,,,7分取平面BCP 的一个法向量n0,1,0. 所以2cos ,2m n m nm n.所以平面ADP 和平面BCP 所成的二面角(小于90°)的大小为4.,,,,,,,,,,,,,,,9分(Ⅲ)解:在棱PB 上存在点M 使得CM ∥平面PAD ,此时12PM PB=. 理由如下:,,,,,,,,,,,,,,,10分取AB 的中点N ,连接CM ,CN ,MN .则MN ∥PA ,12AN AB =.因为2AB CD =,OzyxPA B C DNMPABCD所以AN CD =.因为AB ∥CD ,所以四边形ANCD 是平行四边形. 所以CN ∥AD . 因为,MNCN N PAAD A ==,所以平面MNC ∥平面PAD .,,,,,,,,,,,,,,,13分因为CM ì平面MNC ,所以CM ∥平面PAD .,,,,,,,,,,,,,,,14分(18)(本小题满分13分)解:(Ⅰ)由2()e ()x f x xax a 可得2'()e [(2)]xf x x a x . ,,,,,,,,,,,,,,,2分当1a时,(1)e f ,'(1)4e f .,,,,,,,,,,,,,,,4分所以曲线()y f x 在点(1,(1))f 处的切线方程为e 4e 1y x ,即4e 3e yx .,,,,,,,,,,,,,,,5分(Ⅱ)令2'()e ((2))0xf x xa x ,解得(2)x a 或0x . ,,,,,,,,,,,,,,,6分当(2)0a ,即2a时,在区间[0,)上,'()0f x ,所以()f x 是[0,)上的增函数.所以方程()f x k 在[0,)上不可能有两个不相等的实数根.,,,,,,,,,,,,,,,8分当(2)0a ,即2a时,'(),f x f x 随x 的变化情况如下表x(0,(2))a (2)a((2),)a'()f x 0-0+()f x a↘24ea a ↗由上表可知函数()f x 在[0,)上的最小值为24((2))ea a f a .,,,,,,,,,,,,,,,10分因为函数()f x 是(0,(2))a 上的减函数,是((2),)a 上的增函数,且当x a 时,有()f x e ()aa a . ,,,,,,,,,,,,,,,11分所以要使方程()f x k 在[0,)上有两个不相等的实数根,k 的取值范围必须是24(,]ea a a .,,,,,,,,,,,,,,13分(19)(本小题满分13分)解:(Ⅰ)设椭圆C 的标准方程为22221(0)x y a b ab,且222a b c =+.由题意可知:1b =,32c a=. ,,,,,,,,,,,,,,,2分所以24a =.所以,椭圆C 的标准方程为2214xy.,,,,,,,,,,,,,,3分(Ⅱ)由(Ⅰ)得(2,0)Q .设1122(,),(,)A x y B x y .(ⅰ)当直线l 垂直于x 轴时,直线l 的方程为65x.由226,514xxy解得:6,545xy或6,54.5x y即6464(,),(,)5555A B (不妨设点A 在x 轴上方).,,,,,,,,,,,,,,,5分则直线AQ 的斜率1AQ k ,直线BQ 的斜率1BQk .因为1AQ BQ k k ,所以AQ BQ ^. 所以2AQB. ,,,,,,,,,,,,,,,6分(ⅱ)当直线l 与x 轴不垂直时,由题意可设直线AB 的方程为6()(0)5yk xk .由226(),514yk xxy消去y得:2222(25100)2401441000k xk x k.因为点6(,0)5-在椭圆C 的内部,显然0.21222122240,25100144100.25100kx x k kx x k ,,,,,,,,,,,,,,,8分因为1122(2,),(2,)QAx y QB x y ,116()5y k x ,226()5y k x ,所以1212(2)(2)QA QBx x y y 121266(2)(2)()()55x x k x k x 2221212636(1)(2)()4525k x x k x x k2222222144100624036(1)(2)()402510052510025kkk k kkk.所以QAQB .所以QAB 为直角三角形.,,,,,,,,,,,,,,,11分假设存在直线l 使得QAB 为等腰三角形,则QA QB .取AB 的中点M ,连接QM ,则QM AB ^.NQ BAOyx记点6(,0)5-为N .另一方面,点M 的横坐标22122212024225100520M x x kkx k k+==-=-++,所以点M 的纵坐标266()5520M M ky k x k=+=+.所以222221016666(,)(,)520520520520k k k QM NM kk kk+?++++222601320(520)kk +=+.所以QM 与NM 不垂直,矛盾.所以当直线l 与x 轴不垂直时,不存在直线l 使得QAB 为等腰三角形.,,,,,,,,,,,,,,,13分(20)(本小题满分14分)解:(Ⅰ)①{1,5}A =不是{1,2,3,4,5}M =的一个二元基底. 理由是1212315(,{1,0,1})棺+孜-;②{2,3}A =是{1,2,3,4,5,6}M =的一个二元基底.理由是11213,21203,30213=-?????,41212,51213,61313=?????.,,,,,,,,,,,,,,,3分(Ⅱ)不妨设12m a a a <<<,则形如10i j a a ?(1)i jm #的正整数共有m 个;形如11ii a a ?(1)im #的正整数共有m 个;形如11i j a a ?(1)ij m ?的正整数至多有2mC 个;形如(1)1i j a a -?(1)ijm ?的正整数至多有2mC 个.又集合{1,2,3,,}M n =含n 个不同的正整数,A 为集合M 的一个m 元基底.故22m mm m C C n +++,即(1)m m n +. ,,,,,,,,,,,,,,,8分(Ⅲ)由(Ⅱ)可知(1)19m m +,所以4m3.当4m =时,(1)191m m+-=,即用基底中元素表示出的数最多重复一个. *假设1234{,,,}A a a a a =为{1,2,3,,19}M =的一个4元基底,不妨设1234a a a a <<<,则410a 3. 当410a =时,有39a =,这时28a =或7.如果28a =,则由1109,198,1899,18108=-=-=+=+,与结论*矛盾. 如果27a =,则16a =或5.易知{6,7,9,10A =和{5,7,9,10}A =都不是{1,2,3,,19M =的4元基底,矛盾. 当411a =时,有38a =,这时27a =,16a =,易知{6,7,8,11}A =不是{1,2,3,,19M =的4元基底,矛盾.当412a =时,有37a =,这时26a =,15a =,易知{5,6,7,12}A =不是{1,2,3,,19M =的4元基底,矛盾.当413a =时,有36a =,25a =,14a =,易知{4,5,6,1A =不是{1,2,3,,1M =的4元基底,矛盾. 当414a =时,有35a =,24a =,13a =,易知{3,4,5,1A =不是{1,2,3,,M =的4元基底,矛盾.当415a =时,有34a =,23a =,12a =,易知{2,3,4,1A =不是{1,2,3,,1M =的4元基底,矛盾.当416a =时,有33a =,22a =,11a =,易知{1,2,3,16}A =不是{1,2,3,,M =的4元基底,矛盾.当417a 3时,A 均不可能是M 的4元基底.当5m =时,M 的一个基底{1,3,5,9,16}A =;或{3,7,8,9,10};或{4,7,8,9,10}等,只要写出一个即可. 综上,m 的最小可能值为 5.,,,,,,,,,,,,,,,14分。
2023-2024学年北京朝阳区高三(上)期中数学试题和答案

2023北京朝阳高三(上)期中数 学2023.11(考试时间120分钟 满分150分)本试卷分为选择题40分和非选择题110分第一部分(选择题 共40分)一、选择题共10小题,每小题4分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知全集U =Z ,集合{22}A x x =∈-<<Z |,{1,0,1,2}B =-,则()U A B = ð(A ){1,2}-(B ){1}(C ){0,1}(D ){2}(2)下列函数中,既是奇函数又在区间(0+)∞,上单调递增的是(A )lg y x =(B )3y x =(C )1y x x=+(D )22x xy -=+(3)若sin θθ=,则tan 2θ=(A)(B(C)(D(4)已知5log 0.5a =,0.55b =,0.60.5c =,则(A )a c b<<(B )a b c<<(C )c a b<<(D )b c a<<(5)函数π2sin(26y x =+的图象的一条对称轴是(A )6πx =-(B )0x =(C )π6x =(D )π2x =(6)设x ∈R ,则“(1)0x x +>”是“01x <<”的(A )充分而不必要条件(B )必要而不充分条件(C )充分必要条件(D )既不充分也不必要条件(7)已知平面内四个不同的点,,,A B C D 满足22BA DB DC =-,则||||AC BC = (A )23(B )32(C )2(D )3(8)已知一个圆锥的高与其底面圆的半径相等,且体积为8π3.在该圆锥内有一个正方体,其下底面的四个顶点在圆锥的底面内,上底面的四个顶点在圆锥的侧面上,则该正方体的棱长为(A )23(B )1(C)2(D)4-(9)已知函数|1|1,(,0),()ln(1),[0,),x x f x x x +-∈-∞⎧=⎨+∈+∞⎩2()44g x x x =--.设b ∈R ,若存在a ∈R ,使得()()0f a g b +=,则实数b 的取值范围是(A )[1,5]-(B )(,1][5,)-∞-+∞ (C )[1,)-+∞(D )(,5]-∞(10)已知点集{(,)|,}x y x y Λ=∈∈Z Z ,{(,)|1}5,15S a b a b ∈Λ=≤≤≤≤.设非空点集T ⊆Λ,若对S中任意一点P ,在T 中存在一点Q (Q 与P 不重合),使得线段PQ 上除了点,P Q 外没有Λ中的点,则T 中的元素个数最小值是(A )1(B )2(C )3(D )4第二部分(非选择题 共110分)二、填空题共5小题,每小题5分,共25分。
2012年北京市高考数学试卷(理科)(含解析版)
第 5页(共 27页)
20.(13 分)设 A 是由 m×n 个实数组成的 m 行 n 列的数表,满足:每个数的绝 对值不大于 1,且所有数的和为零,记 s(m,n)为所有这样的数表构成的集 合.对于 A∈S(m,n),记 ri(A)为 A 的第ⅰ行各数之和(1≤ⅰ≤m),Cj(A) 为 A 的第 j 列各数之和(1≤j≤n);记 K(A)为|r1(A)|,|R2(A)|,…, |Rm(A)|,|C1(A)|,|C2(A)|,…,|Cn(A)|中的最小值.
(1)如表 A,求 K(A)的值;
1
1
﹣0.8
0.1
﹣0.3
﹣1
(2)设数表 A∈S(2,3)形如
(1)求证:A1C⊥平面 BCDE; (2)若 M 是 A1D 的中点,求 CM 与平面 A1BE 所成角的大小; (3)线段 BC 上是否存在点 P,使平面 A1DP 与平面 A1BE 垂直?说明理由.
17.(13 分)近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃 圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生
A.28+6
B.30+6
C.56+12
D.60+12
8.(5 分)某棵果树前 n 年的总产量 Sn 与 n 之间的关系如图所示.从目前记录的
结果看,前 m 年的年平均产量最高,则 m 的值为( )
A.5
B.7
C.9
第 2页(共 27页)
D.11
二.填空题共 6 小题.每小题 5 分.共 30 分.
点 E.则( )
A.CE•CB=AD•DB
高三上学期考试数学理试题分类汇编导数及其应用 Word版含答案

北京市部分区届高三上学期考试数学理试题分类汇编导数及其应用、(昌平区届高三上学期期末)设函数,.(Ⅰ)若,求函数的单调区间;(Ⅱ)若曲线在点处的切线与直线平行.() 求的值;()求实数的取值范围,使得对恒成立.、(朝阳区届高三上学期期末)设函数,,.(Ⅰ)当时,求函数在点处的切线方程;(Ⅱ)若函数有两个零点,试求的取值范围;(Ⅲ)证明.、(朝阳区届高三上学期期中)已知函数,.(Ⅰ)当时,求曲线在点处的切线方程;(Ⅱ)若函数在上单调递减,试求的取值范围;(Ⅲ)若函数的最小值为,试求的值.、(东城区届高三上学期期末)设函数.(Ⅰ)若为的极小值,求的值;(Ⅱ)若对恒成立,求的最大值.、(丰台区届高三上学期期末)已知函数与函数的图象在点处有相同的切线.(Ⅰ)求的值;(Ⅱ)设,求函数在上的最小值.、(海淀区届高三上学期期末)已知函数.(Ⅰ)若曲线存在斜率为的切线,求实数的取值范围;(Ⅱ)求的单调区间;(Ⅲ)设函数,求证:当时,在上存在极小值.、(海淀区届高三上学期期中)已知函数,函数.(Ⅰ)已知直线是曲线在点处的切线,且与曲线相切,求的值;(Ⅱ)若方程有三个不同实数解,求实数的取值范围.、(石景山区届高三上学期期末)已知函数,.(Ⅰ)求函数的单调区间;(Ⅱ)若对任意,恒成立,求的取值范围.、(通州区届高三上学期期末)设函数.(Ⅰ)当=时,求曲线在点处的切线方程;(Ⅱ)设函数,证明:当∈时,>.、(西城区届高三上学期期末)已知函数,其中.(Ⅰ)如果曲线在处的切线的斜率是,求的值;(Ⅱ)如果在区间上为增函数,求的取值范围.。
2012年全国高考北京理科数学试题详细解析

B. 7 A. 5 8.【答案】C
C. 9
D. 11
【解析】若果树前 n 年的总产量 S 与 n 在图中对应 P ( S , n ) 点则前 n 年的年平均产量即为直 线 OP 的斜率由图易得当 n = 9 时,直线 OP 的斜率最大,即前 9 年的年平均产量最高. 【点评】 本题以函数的图象与图象变化为载体考查了斜率的几何意义, 其中正确分析出平均 产量的几何意义是解答本题的关键.
【解析】当 a = 0 时,如果 b = 0 同时等于零,此时 a + bi = 0 是实数,不是纯虚数,因此不
1
是充分条件;而如果 a + bi 已经为纯虚数,由定义实部为零,虚部不为零可以得到 a = 0 , 因此为必要条件。 【点评】本题考查复数的基本概念,必要条件、充分条件与充要条件的判断,考查基本知识 的掌握程度. 4.执行如图所示的程序框图,输出的 S 值为( )
x
① ∀x ∈ R , f ( x) < 0 或 g ( x) < 0 ; ② ∀x ∈ (−∞,−4) , f ( x) g ( x) < 0 。 则 m 的取值范围是_______。 14.【答案】 m ∈ (−4,−2) 【解析】根据 g ( x) = 2 − 2 < 0 ,可解得 x < 1 。由于题目中第一个条件的限制 ∀x ∈ R ,
A. 28 + 6 5
B. 30 + 6 5
C. 56 + 12 5
D. 60 + 12 5
7.【答案】B 【解析】从所给的三视图可以得到该几何体为三棱锥,如图所示,图中蓝色数字所表示的为 直接从题目所给三视图中读出的长度, 黑色数字代表通过勾股定理的计算得到的边长。 所求 表面积应为三棱锥四个面的面积之和,利用垂直关系和三角形面积公式,
2012年高考理科数学试题及答案-全国卷2

2012年高考数学试题(理) 第1页【共10页】2012年普通高等学校招生全国统一考试(新课标Ⅱ卷)理 科 数 学第Ⅰ卷一、选择题:(本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.)1. 已知集合A ={1, 2, 3, 4, 5},B ={(x ,y )| x ∈A , y ∈A , x —y ∈A },则B 中所含元素的个数为( )A 。
3B. 6C. 8D 。
102. 将2名教师,4名学生分成两个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由一名教师和2名学生组成,不同的安排方案共有( ) A. 12种B. 10种C 。
9种D 。
8种3。
下面是关于复数iz +-=12的四个命题中,真命题为( )P 1: |z |=2, P 2: z 2=2i , P 3: z 的共轭复数为1+i , P 4: z 的虚部为-1 。
A 。
P 2,P 3B 。
P 1,P 2C 。
P 2,P 4D. P 3,P 44。
设F 1,F 2是椭圆E : 12222=+b y a x )0(>>b a 的左右焦点,P 为直线23ax =上的一点,12PF F △是底角为30º的等腰三角形,则E 的离心率为( ) A 。
21B 。
32 C.43 D 。
54 5。
已知{a n }为等比数列,a 4 + a 7 = 2,a5 a6 = 8,则a 1 + a 10 =( )A. 7B. 5C. —5D. —76. 如果执行右边的程序框图,输入正整数N (N ≥2)和实数a 1, a 2,…,a N ,输入A 、B ,则( ) A 。
A +B 为a 1, a 2,…,a N 的和B 。
2B A +为a 1, a 2,…,a N 的算术平均数C 。
A 和B 分别是a 1, a 2,…,a N 中最大的数和最小的数D 。
A 和B 分别是a 1, a 2,…,a N 中最小的数和最大的数 7. 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )2012年高考数学试题(理) 第2页【共10页】A 。
2012北京数学理科(纯word版,含答案)
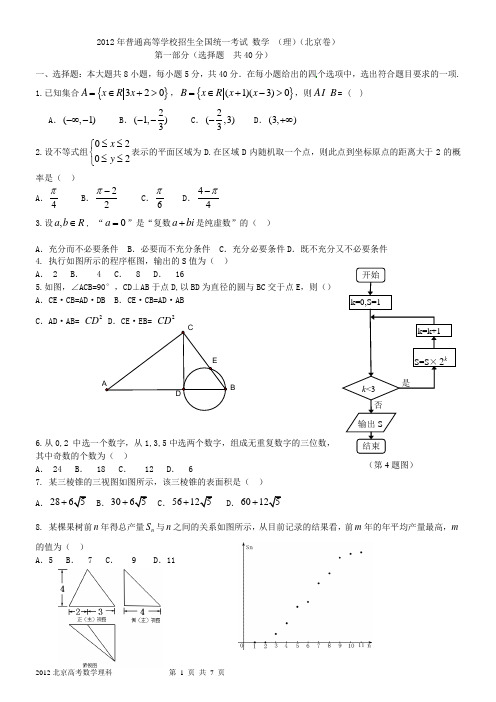
2012年普通高等学校招生全国统一考试 数学 (理)(北京卷)第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. 1.已知集合{}320A x R x =∈+>,{}(1)(3)0B x R x x =∈+->,则A B = ( ) A .(,1)-∞- B .2(1,)3-- C .2(,3)3- D .(3,)+∞2.设不等式组0202x y ≤≤⎧⎨≤≤⎩表示的平面区域为D.在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是( ) A .4π B .22π- C .6π D .44π- 3.设,a b R ∈, “0a =”是“复数a bi +是纯虚数”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分又不必要条件4. 执行如图所示的程序框图,输出的S 值为( ) A . 2 B . 4 C . 8 D . 165.如图,∠ACB=90°,CD ⊥AB 于点D,以BD 为直径的圆与BC 交于点E ,则() A .CE ·CB=AD ·DB B .CE ·CB=AD ·AB C .AD ·AB= 2CD D .CE ·EB= 2CD6.从0,2 中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数, 其中奇数的个数为( )A . 24B . 18C . 12D . 67. 某三棱锥的三视图如图所示,该三棱锥的表面积是( ) A.28+ B.30+ C.56+.60+8. 某棵果树前n 年得总产量n S 与n 之间的关系如图所示,从目前记录的结果看,前m 年的年平均产量最高,m 的值为( )A .5B . 7C . 9D .11(第4题图)B第二部分(非选择题 共110分) 二、填空题:本大题共6小题,每小题5分,共30分. 9. 直线2,1x t y t =+⎧⎨=--⎩(t 为参数)与曲线3cos 3sin x y =α⎧⎨=α⎩(α为参数)的交点个数为 .10.已知{}n a 为等差数列,n S 为其前n 项和.若112a =,23S a =,则2a = ;n S = . 11.在△ABC 中,若2a =,7bc +=,1cos 4B =-,则b = . 12.在直角坐标系xoy 中,直线l 过抛物线24y x =的焦点F,且与该抛物线相较于A 、B 两点,其中点A 在x 轴上方,若直线l 的倾斜角为60°,则△OAF 的面积为 .13.已知正方形ABCD 的边长为1,点E 是AB 边上的动点,则DE CB ⋅的值为 ; DE DC ⋅的最大值为 .14.已知()(2)(3)f x m x m x m =-++,()22x g x =-.若同时满足条件:①,()0x R f x ∀∈<或()0g x <;②(,4)x ∃∈-∞- ,()()0f x g x <. 则m 的取值范围是 . 三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题13分) 已知函数(sin cos )sin 2()sin x x xf x x-=.(1)求()f x 的定义域及最小正周期; (2)求()f x 的单调递增区间.16. (本小题14分)如图1,在Rt △ABC 中,∠C=90°,BC=3,AC=6,D,E 分别是AC ,AB 上的点, 且DE ∥BC ,DE=2,将△ADE 沿DE 折起到△A 1DE 的位置,使A 1C ⊥CD ,如图2. (1)求证:A 1C ⊥平面BCDE;(2)若M 是A 1D 的中点,求CM 与平面A 1BE 所成角的大小;(3)线段BC 上是否存在点P,使平面A 1DP 与平面A 1BE 垂直?说明理由. 17.(本小题13分)近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数(1)试估计厨余垃圾投放正确的概率; (2)试估计生活垃圾投放错误的概率;(3)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为,,a b c ,其中0a >,600a b c ++=.当数据,,a b c 的方差2S 最大时,写出,,a b c 的值(结论不要求证明),并求此时2S 的值. (注:方差2222121[()()()]n s x x x x x x n=-+-++- ,其中x 为12,,n x x x 的平均数) 18.(本小题13分)已知函数2()1f x ax =+(0a >),3()g x x bx =+.(1)若曲线()y f x =与曲线()y g x =在它们的交点(1,c )处具有公共切线,求,a b 的值; (2)当24a b =时,求函数()()f x g x +的单调区间,并求其在区间(,1]-∞-上的最大值.19.(本小题14分)已知曲线C: 22(5)(2)8()m x m y m R -+-=∈ (1)若曲线C 是焦点在x 轴的椭圆,求m 的范围;(2)设4m =,曲线C 与y 轴的交点为A,B (点A 位于点B 的上方),直线4y kx =+与曲线C 交于不同的两点M,N,直线1y =与直线BM 交于点G 求证:A,G,N 三点共线. 20.(本小题13分)设A 是由m n ⨯个实数组成的m 行n 列的数表,满足:每个数的绝对值不大于1,且所有数的和为零.记(,)S m n 为所有这样的数表构成的集合.对于(,)A S m n ∈,记()i r A 为A 的第i 行各数之和1i m ≤≤,()j c A 为A 的第j 列各数之和1j n ≤≤; 记()k A 为1|()|r A ,2|()|r A ,…,|()|m r A ,1|()|c A ,2|()|c A ,…,|()|n c A 中的最小值. (1)对如下数表A,求()k A 的值;(2)设数表A=(2,3)S 形如求()k A 的最大值;(3)给定正整数t ,对于所有的A ∈S(2,21t +),求()k A 的最大值.(李国波录入2012-6-8)参考答案 一、选择题1、D2、D3、B4、C5、A6、B7、B8、C 二、填空题9、2;10、1,1(1)4n n +;11、4;1213、1,1;14、(4,2)--; 三、解答题15、解:(1)由sin 0x ≠得,()x k k Z π≠∈,故()f x 的定义域为{|,}x R x k k Z π∈≠∈.因为(sin cos )sin 2()sin x x x f x x -==2cos (sin cos )x x x -=sin 2cos 21x x --)14x π--,所以()f x 的最小正周期22T ππ==. (2)函数sin y x =的单调递减区间为3[2,2]()22k k k Z ππππ++∈. 由222,()242k x k x k k Z ππππππ-≤-≤+≠∈得3,()88k x k x k k Z πππππ-≤≤+≠∈ 所以函数()f x 的单调递增区间为[,)8k k k Z πππ-∈,和3(,]()8k k k Z πππ+∈. 16.解:(1) ,AC BC DE BC ⊥∥∴DE AC ⊥∴1DE A D ⊥,DE CD ⊥(1A D CD D = )又 DE ⊥平面1A DC ,∴DE 1AC ⊥ 又∵1A C CD ⊥,(DE CD D = ) ∴1AC ⊥平面BCDE (2)如图,以C 为坐标原点,建立空间直角坐标系C xyz -,则(100A ,,,()020D ,,,M ,()300B ,,,()220E ,,,设平面1A BE 法向量为()n x y z = ,,,则10,0A B n BE n ⋅=⋅=∴(130A B =- ,,,()120BE =- ,,,∴3020x x y ⎧-=⎪⎨-+=⎪⎩令1y =,则2,x z ==∴(21n = 设CM 与平面1A BE 所成的角为θ∵(0CM =∴sin |cos ,|||||||CM n n CM CM n θ⋅=====⋅CM 与平面1A BE 所成角的大小45︒(3)线段BC 上不存在点P,使平面1A DP 与平面1ABE 垂直。
2012年高考理科数学北京卷-答案

数学(理科)答案解析
第Ⅰ卷
一、选择题
1.【答案】D
【解析】 ,利用二次不等式的解法可得 或 ,易得 .
【提示】求出集合 ,然后直接求解 .
【考点】集合间的基本运算.
2.【答案】D
【解析】题目中 表示的区域表示正方形区域,而动点 可以存在的位置为正方形面积减去四分之一的圆的面积部分,因此 ,故选D.
20.【答案】(Ⅰ)
(Ⅱ1
(Ⅲ)
【解析】(Ⅰ)由题意可知 , , , ,
∴
(Ⅱ)先用反证法证明 :
若 ,则 ,∴
同理可知 ,
∴ ,由题目所有数和为 ,即 ,
∴ 与题目条件矛盾
∴ .
易知当 时, 存在
∴ 的最大值为1.
(Ⅲ) 的最大值为 .
首先构造满足 的 :
, .
经计算知, 中每个元素的绝对值都小于1,所有元素之和为0,且 , , .
下面证明 是最大值.若不然,则存在一个数表 ,使得 .
由 的定义知 的每一列两个数之和的绝对值都不小于 ,而两个绝对值不超过1的数的和,其绝对值不超过2,故 的每一列两个数之和的绝对值都在区间 中.由于 ,故 的每一列两个数符号均与列和的符号相同,且绝对值均不小于 .
设 中有 列的列和为正,有 列的列和为负,由对称性不妨设 ,则 .另外,由对称性不妨设 的第一行行和为正,第二行行和为负.
【考点】由三视图求几何体的表面积.
8.【答案】C
【解析】由图可知6,7,8,9这几年增长最快,超过平均值,所以应该加入,因此选C.
【提示】由已知中图像表示某棵果树前 年的总产量 与 之间的关系,结合图像可得答案.
【考点】函数图像的应用.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市朝阳区2011-2012学年度高三年级第一学期期中统一考试数学测试题(理工类) 2011.11 (考试时间120分钟 满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分 注意事项:1.答第一部分前,考生务必将自己的姓名、考试科目涂写在答题卡上.考试结束时,将试题卷和答题卡一并交回.2.第一部分每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.第二部分不能答在试题卷上,请答在答题卡上. 第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. 1.设集合{}260M x x x =+-<,{}13N x x =≤≤,则M N 等于( )A .[]2,3 B .[]1,2 C .(]2,3 D .[)1,22. 已知向量a ,b 满足|a | = 8,|b | = 6, a ·b = 24,则a 与b 的夹角为( ) A .30︒ B .60︒ C .90︒D .120︒3. 已知函数()2sin()f x x ωϕ=+(0,0π)ωϕ><<的图象如图所示,则ω等于( )A .13B .32C .1D .24. 在各项均为正数的数列{}n a 中,对任意,m n *∈N 都有m n m n a a a +=⋅.若664a =,则9a 等于 ( )A .256B .510C .512D . 1024 5. “1a >”是“对任意的正数x ,不等式21a x x +≥成立”的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6. 设0x 是函数21()()log 3xf x x =-的零点.若00a x <<,则()f a 的值满足( )A .()0f a =B .()0f a <C .()0f a >D .()f a 的符号不确定7.已知函数)30(42)(2<<++=a ax ax x f ,其图象上两点的横坐标1x ,2x 满足21x x <, 且a x x -=+121,则有 ( ) A .)()(21x f x f > B . )()(21x f x f =C .)()(21x f x f <D .)(),(21x f x f 的大小不确定 8.设集合{}0123,,,S A A A A =,在S 上定义运算⊕:i j kA A A ⊕=,其中k 为i j +被4除的余数,,0,1,2,3i j =,则使关系式0()i i j A A A A ⊕⊕=成立的有序数对(,)i j 的组数为( )A .4B .3C .2D .1第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.9. 已知π3(,π),sin ,25αα∈=则πtan()4α+=__ _.10.已知等差数列{}n a 的前n 项和为n S .若22a =,158+=a a ,则6S =__.11.在ABC ∆中,π3A ∠=,3BC =,AB =,则C ∠=__ ;sin B = . 12. 在ABC ∆中,已知 (23,31)AB k k =++ ,(3,)AC k = ()k ∈R ,则BC=__;若90B ∠=︒,则k =__ _.13.已知函数12log (),40,()2cos ,0.x x f x x x --≤<⎧⎪=⎨⎪≤≤π⎩若方程()f x a =有解,则实数a 的取值范围是__ _.14.设函数()1f x x α=+()α∈Q 的定义域为[][],,b a a b -- ,其中0a b <<.若函数()f x 在区间[],a b 上的最大值为6,最小值为3,则()f x 在区间[],b a --上的最大值与最小值的和为__ _.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15. (本小题满分13分)设关于x 的不等式(1)0()x x a a --<∈R 的解集为M ,不等式2230x x --≤的解集为N .(Ⅰ)当1a =时,求集合M ; (Ⅱ)若M N ⊆,求实数a 的取值范围. 16. (本小题满分13分)已知向量a =(sin ,cos(π))x x -,b =(2cos ,2cos )x x ,函数()1f x =⋅a b +.(Ⅰ)求π()4f -的值; (Ⅱ)求函数()f x 在区间π0,2⎡⎤⎢⎥⎣⎦上的最大值和最小值,并求出相应的x 值.17. (本小题满分13分)设数列{}n a 的前n 项和为n S ,且221n n a S n =++()n *∈N .(Ⅰ)求1a ,2a ,3a ;(Ⅱ)求证:数列{}2n a +是等比数列;(Ⅲ)求数列{}n n a ⋅的前n 项和n T .18. (本小题满分13分)在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且3cos 4B =.(Ⅰ)求2sin 2cos 2A CB ++的值;(Ⅱ)若b =,求ABC ∆面积的最大值. 19. (本小题满分14分)设函数3211()(,,,0)32f x ax bx cx a b c a =++∈≠R 的图象在点(),()x f x 处的切线的斜率为()k x ,且函数1()()2g x k x x=-为偶函数.若函数()k x 满足下列条件:①(1)0k -=;②对一切实数x ,不等式211()22k x x ≤+恒成立.(Ⅰ)求函数()k x 的表达式;(Ⅱ)求证:1112(1)(2)()2nk k k n n +++>+ ()n *∈N . 20. (本小题满分14分)已知函数21()ln (1)2f x x ax a x=-+-(a ∈R 且0a ≠).(Ⅰ)求函数()f x 的单调区间;(Ⅱ)记函数()y F x =的图象为曲线C .设点11(,)A x y ,22(,)B x y 是曲线C 上的不同两点.如果在曲线C 上存在点00(,)M x y ,使得:①1202x x x +=;②曲线C 在点M 处的切线平行于直线AB ,则称函数()F x 存在“中值相依切线”. 试问:函数()f x 是否存在“中值相依切线”,请说明理由. 北京市朝阳区2011-2012学年度高三年级第一学期期中统一考试 数学测试题答案(理工类) 2011.11 一、选择题:(注:两空的填空,第一空3分,第一空2分) 三、解答题: (15)(本小题满分13分)解:(Ⅰ)当1a =时, 由已知得(2)0x x -<.解得02x <<.所以{|02}M x x =<<. …………………3分 (Ⅱ) 由已知得{}13N x x =-≤≤. …………………5分①当1a <-时, 因为10a +<,所以{|10}M x a x =+<<. 因为M N ⊆,所以110a -≤+<,解得21a -≤<-;……………8分 ②若1a =-时, M =∅,显然有M N ⊆,所以1a =-成立;……………10分 ③若1a >-时, 因为10a +>,所以{|01}M x x a =<<+. 又{}13N x x =-≤≤,因为M N ⊆,所以013a <+≤,解得12a -<≤.……………12分 综上所述,a 的取值范围是[2,2]-. ……………13分 (16)(本小题满分13分)解:(I )因为()f x =⋅a b +1=2sin cos cos(π)2cos 1x x x x +-⋅+ 22sin cos 2cos 1x x x =-+=sin 2cos2x x -, …………4分所以π()14f -=-. ……………6分 (II )由(I )得,()f x =sin 2cos2x x -)4x π-. …………8分 因为π0,2x ⎡⎤∈⎢⎥⎣⎦,所以π3π2,444x π⎡⎤-∈-⎢⎥⎣⎦. …………9分所以当242x ππ-=时,即8x 3π=时,()f x; …………11分当244x ππ-=-时,即0x =时,()f x 的最小值是1-. …………13分(17)(本小题满分13分) 解:(I )由题意,当1n =时,得1123a a =+,解得13a =.当2n =时,得2122()5a a a =++,解得28a =.当3n =时,得31232()7a a a a =+++,解得318a =.所以13a =,28a =,318a =为所求. ……………3分(Ⅱ) 因为221n n a S n =++,所以有11223n n a S n ++=++成立.两式相减得:11222n n n a a a ++-=+.所以122n n a a +=+()n *∈N ,即122(2)n n a a ++=+. …………5分所以数列{}2n a +是以125a +=为首项,公比为2的等比数列. ……………7分(Ⅲ)由(Ⅱ) 得:1252n n a -+=⨯,即1522n n a -=⨯-()n *∈N .则1522n n na n n -=⋅-()n *∈N . ……………8分设数列{}152n n -⋅的前n 项和为nP , 则01221512522532...5(1)252n n n P n n --=⨯⨯+⨯⨯+⨯⨯++⨯-⋅+⨯⋅,所以12312512522532...5(1)252n n n P n n -=⨯⨯+⨯⨯+⨯⨯++-⋅+⋅,所以1215(122...2)52n nn P n --=++++-⋅,即(55)25n n P n =-⋅+()n *∈N . ……………11分所以数列{}n n a ⋅的前n 项和n T =(1)(55)2522n n n n +-⋅+-⨯,整理得,2(55)25n n T n n n =-⋅--+()n *∈N . ……………13分(18)(本小题满分13分)解:(I )因为3cos 4B =,所以sin B =. …………1分 又22πsin 2cos 2sin cos cos 22A C BB B B +-+=+12sin cos (1cos )2B B B =+-=3244⨯+18=18+. ……………6分(II )由已知得2223cos 24a c b B ac +-==, …………7分又因为b =, 所以22332a c ac+-=. …………8分又因为223322a c ac ac +=+≥,所以6ac ≤,当且仅当a c ==ac 取得最大值. …………11分此时11sin 622ABC S ac B ∆==⨯=.所以ABC ∆的面积的最大值为. ……………13分(19)(本小题满分14分)(Ⅰ)解:由已知得:2()()k x f x ax bx c '==++. ……………1分 由1()()2g x k x x =-为偶函数,得21()2g x ax bx c x=++-为偶函数, 显然有12b =. …………2分又(1)0k -=,所以0a b c -+=,即12a c +=. …………3分又因为211()22k x x ≤+对一切实数x 恒成立,即对一切实数x ,不等式2111()0222a x x c -++-≤恒成立. …………4分显然,当12a =时,不符合题意. …………5分当12a ≠时,应满足10,21114()()0.422a a c ⎧-<⎪⎪⎨⎪∆=---≤⎪⎩注意到12a c +=,解得14a c ==. …………7分 所以2111()424k x x x =++. ……………8分(Ⅱ)证明:因为2221(1)()44n n n k n +++==,所以214()(1)k n n =+.………9分 要证不等式1112(1)(2)()2nk k k n n +++>+ 成立, 即证22211123(1)24nn n +++>++ . …………10分 因为21111(1)(1)(2)12n n n n n >=-+++++, …………12分 所以22211111111123(1)233412n n n +++>-+-++-+++112224n n n =-=++.所以1112(1)(2)()2n k k k n n +++>+ 成立. ……………14分 (20)(本小题满分14分)解:(Ⅰ)显然函数()f x 的定义域是(0,)+∞. …………1分由已知得,1(1)()1'()1a x x a f x ax a x x -+=-+-=-. …………2分⑴当0a >时, 令'()0f x >,解得01x <<; 令'()0f x <,解得1x >.所以函数()f x 在(0,1)上单调递增,在(1,)+∞上单调递减. …………3分 ⑵当0a <时,①当11a -<时,即1a <-时, 令'()0f x >,解得10x a <<-或1x >; 令'()0f x <,解得11x a -<<.所以,函数()f x 在1(0,)a -和(1,)+∞上单调递增,在1(,1)a -上单调递减; …………4分②当11a -=时,即1a =-时, 显然,函数()f x 在(0,)+∞上单调递增; ………5分③当11a ->时,即10a -<<时, 令'()0f x >,解得01x <<或1x a >-; 令'()0f x <,解得11x a <<-.所以,函数()f x 在(0,1)和1(,)a -+∞上单调递增,在1(1,)a -上单调递减.…………6分 综上所述,⑴当0a >时,函数()f x 在(0,1)上单调递增,在(1,)+∞上单调递减;⑵当1a <-时,函数()f x 在1(0,)a -和(1,)+∞上单调递增,在1(,1)a -上单调递减; ⑶当1a =-时,函数()f x 在(0,)+∞上单调递增;⑷当10a -<<时,函数()f x 在(0,1)和1(,)a -+∞上单调递增,在1(1,)a -上单调递减. ……………7分 (Ⅱ)假设函数()f x 存在“中值相依切线”. 设11(,)A x y ,22(,)B x y 是曲线()y f x =上的不同两点,且120x x <<,则211111ln (1)2y x ax a x =-+-,222221ln (1)2y x ax a x =-+-.2121ABy y k x x -=-22212121211(ln ln )()(1)()2x x a x x a x x x x ---+--=- 211221ln ln 1()(1)2x x a x x a x x -=-++-- …………8分曲线在点00(,)M x y 处的切线斜率0()k f x '=12()2x x f +'=12122(1)2x x a a x x +=-⋅+-+, …………9分依题意得:211221ln ln 1()(1)2x x a x x a x x --++--12122(1)2x x a a x x +=-⋅+-+. 化简可得:2121ln ln x x x x --122x x =+,即21lnxx=21212()x xx x-+21212(1)1xxxx-=+. …………11分设21xtx=(1t>),上式化为:2(1)4ln211ttt t-==-++,即4ln21tt+=+. …………12分令4()ln1g t tt=++,214'()(1)g tt t=-+=22(1)(1)tt t-+.因为1t>,显然'()0g t>,所以()g t在(1,)+∞上递增,显然有()2g t>恒成立.所以在(1,)+∞内不存在t,使得4ln21tt+=+成立.综上所述,假设不成立.所以,函数()f x不存在“中值相依切线”. ……………14分。
