2014下学期八年级竞赛试题(1)
华碧2014年八年级下数学竞赛试卷

华碧 2014年八年级下数学竞赛试卷(问卷)(时间:120分钟 满分:120分)一、选择题。
(每小题2分共30分)1、已知数a ,b-a ,则 ( )A. a>bB. a<bC. a≥bD. a≤b2、化简). ABC .D .3、函数中,自变量x 的取值范围是( ).A .x ≥-1B .x>2C .x>-1且x ≠2D .x ≥-1且x ≠24.过点P (-1,3)直线,使它与两坐标轴围成的三角形面积为5,•这样的直线可以作( ) (A )4条 (B )3条 (C )2条 (D )1条5、如图,长方体的长为15,宽10,高为20,一只蚂蚁如果沿着长方体的表面从点A 爬到点B ,需要爬行的最短距离是( )A .415 B. 25 C. 105+5 D. 356、在周长为20cm 的□ABCD 中,AB 不等于AD ,AC 、BD 相交于点O ,OE ⊥BD 交AD 于E ,则∆ABE 的周长为 ( )C 、8cmD 、10cm第6题图 第7题图 7.如左图所示,有一张直角三角形纸片,两直角边AC=5cm ,BC=10cm ,将△ABC 折叠,使点B 与点A 重合,折痕为DE ,则CD 的长为( )8.已知y 与x+3成正比例,并且x=1时,y=8,那么y 与x 之间的函数关系式为( )(A )y=8x (B )y=2x+6 (C )y=8x+6 (D )y=5x+39. 一辆汽车和一辆摩托车分别从A ,B 两地去同一城市,它们离A 地的路程随时间变化的图象如图所示.则下列结论错误..的是( ) A.摩托车比汽车晚到1 h B. A,B 两地的路程为20 km C.摩托车的速度为45 km/h D.汽车的速度为60 km/h第10题图 第11题图10. 如图,边长为1的正方形ABCD 绕点A 逆时针旋转30︒到正方形AB C D ''',图中阴影部分的面积为( ) A .12 BC.1 D.1-11.如图,P 是□ABCD 上一点.已知S △ABP =3,S △PCD =1,那么平行四边形ABCD的面积是 ( ) A .6 B .8 C .10 D .无法确定12、直线y kx b =+经过一、二、四象限,则直线y bx k =-的图象只能是( ) 13.无论k 为何值,一次函数(2k -1)x -(k -3)y -(k -11)=0的图像必经过定点( )A .(0,0)B .(0,11)C .(2,3)D .无法确定14.三角形的三边之比是7∶4∶5,周长等于32,那么这个三角形中最长的中位线为( ) A .7 B .14 C .5 D .1015、菱形的周长等于它的较短对角线长的4倍,则它的一组邻角是 ( ) A 、60°和120° B 、45°和135° C 、30°和150° D 、以上答案都不对第9题图二、填空题(每题2分,共30分)16.已知a 2b-ab 2=_________.17.(x ≥0)18、已知│x-3│,以x ,y 为两边长的等腰三角形的周长是_______.19、在实数范围内分解因式494-x =__________________.20.在直线l 上依次摆放着七个正方形(如图).已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S 1、S 2、S 3、S 4,则S 1+S 2+S 3+S 4=___________.21.如图,在△ABC 中,AB =AC =13,BC =10,D 是AB 的中点,过点D 作DE ⊥AC 于点E ,则DE 的长是______________.22.在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A 处。
八年级数学竞赛试题及参考答案

八年级数学竞赛试题及参考答案八年级数学竞赛试题(一)一、选择题(每小题5分,共30分) 1.已知2220082008,2ca b a b c k k +=-==++=,且那么的值为( ). A .4 B .14 C .-4 D .14- 2.若方程组312433x y k x y k x y x y +=+⎧<<-⎨+=⎩的解为,,且,则的取值范围是( ). A .102x y <-<B .01x y <-<C .31x y -<-<-D .11x y -<-< 3.计算:2399100155555++++++=( ).A .10151- B .10051- C .101514- D .100514-4.如图,已知四边形ABCD 的四边都相等,等边△AEF 的顶点E 、F 分别在BC 、CD 上,且AE=AB ,则∠C=( ). A .100° B .105° C .110° D .120°5.已知5544332222335566a b c d a b c d ====,,,,则、、、的大小关系是( ). A .a b c d >>> B .a b d c >>> C .b a c d >>> D .a d b c >>> 6.如果把分数97的分子、分母分别加上正整数913a b 、,结果等于,那么a b +的最小 值是( ).A .26B .28C .30D .32 二、填空题:(每小题5分,共30分)(第4题图)DCB(第15题图)EDCBA7.方程组200820092007200720062008x y x y -=⎧⎨-=⎩的解是 .8.如图,已知AB 、CD 、EF 相交于点O ,EF ⊥AB ,OG 为∠COF 的平分线,OH 为∠DOG 的平分线,若∠AOC :∠COG=4:7,则∠GOH= .9.小张和小李分别从A 、B 两地同时出发,相向而行,第一次在距A 地5千米处相遇,继续往前走到各地(B 、A )后又立即返回,第二次在距B 地4千米处两人再次相遇,则A 、B 两地的距离是 千米.10.在△ABC 中,∠A 是最小角,∠B 是最大角,且2∠B=5∠A ,若∠B 的最大值为m °,最小值为n °,则m °+n °= .11.已知21()()()04b c b c a b c a a a+-=--≠=,且,则 . 12.设p q ,均为正整数,且7111015p q <<,当q 最小时,pq 的值为 . 以下三、四、五题要求写出解题过程. 三、(本题满分20分)13.在一次抗击雪灾而募捐的演出中,晨光中学有A 、B 、C 、D 四个班的同学参加演出,已知A 、B 两个班共16名演员,B 、C 两个班共20名演员,C 、D 两个班共34名演员,且各班演员的人数正好按A 、B 、C 、D 次序从小到大排列,求各班演员的人数. 四、(本题满分20分)14.已知2211x x y y x y =+=+≠,,且. ⑴ 求证:1x y +=. ⑵ 求55x y +的值.五、(本题满分20分)15.如图,在△ABC 中AC >BC ,E 、D 分别是AC 、BC 上的点,且∠BAD=∠ABE ,AE=BD .求证:∠BAD=12∠C .G(第8题图)HOFED CBA参考答案一、选择题1.A 2.B 3.C 4.A 5.A 6.B 二、填空题: 7、21x y =⎧⎨=⎩ 8、72.5° 9、11 10、175° 11、2 12、68213、解:依题意得:A+B=16,B+C=20,C+D=34∵A <B <C <D ,∴A <8,B >8,B <10,C >10,C <17,D >17 由8<B <10且B 只能取整数得,B=9 ∴C=11,D=23,A=7答:A 、B 、C 、D 各班演员人数分别是7人、9人、11人、23人。
2013--2014年八年级数学竞赛-试卷
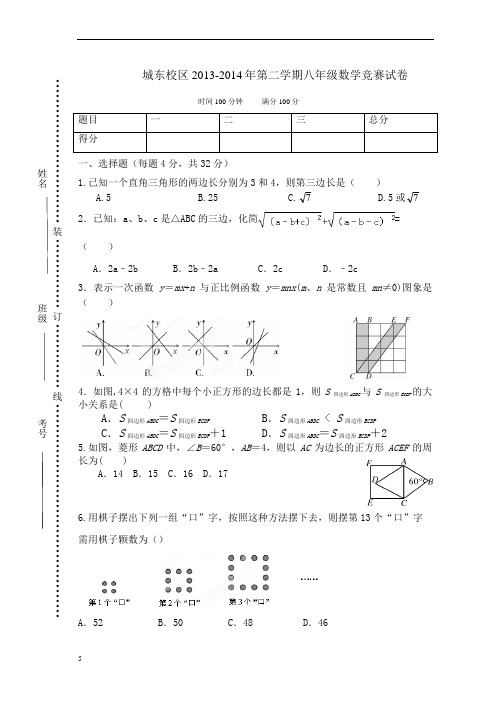
城东校区2013-2014年第二学期八年级数学竞赛试卷时间100 分钟 满分100分题目 一 二 三 总分 得分一、选择题(每题4分,共32分)1.已知一个直角三角形的两边长分别为3和4,则第三边长是( )A.5B.25C.7D.5或72.已知:a 、b 、c 是△ABC 的三边,化简=( )A .2a ﹣2bB .2b ﹣2aC .2cD .﹣2c3.表示一次函数y =mx +n 与正比例函数y =mnx (m 、n 是常数且mn ≠0)图象是( )4.如图,4×4的方格中每个小正方形的边长都是1,则S四边形ABDC与S四边形ECDF的大小关系是( )A .S 四边形ABDC =S 四边形ECDFB .S 四边形ABDC < S 四边形ECDF C .S 四边形ABDC =S 四边形ECDF +1D .S 四边形ABDC =S 四边形ECDF +25.如图,菱形ABCD 中,∠B =60°,AB =4,则以AC 为边长的正方形ACEF 的周长为( )A .14B .15C .16D .176.用棋子摆出下列一组“口”字,按照这种方法摆下去,则摆第13个“口”字需用棋子颗数为()A .52B .50C .48D .46·····························装··············订·············线··········································· 姓名班级 考号7. 直角三角形的两条直角边长为a,b,斜边上的高为h,则下列各式中总能成立的是 ( )A. ab=h 2B. a 2+b 2=2h 2C.a 1+b 1=h1 D.21a +21b=21h8.如图,在正方形ABCD 中,边长为2的等边三角形AEF 的顶点E 、F 分别在BC 和CD 上,下列结论:①CE =CF ②∠AEB =750③BE+DF =EF ④S 正方形ABCD =2+3,其中正确的序号是( ) 。
2013~2014年学年度第二学期竞赛

2013~2014年学年度第二学期竞赛八 年 级 语 文 卷不答,得分用于补偿必答题之失分,全卷最高分不得高于120分。
一、基础(24分)1、根据课文默写古诗文。
(10分)(1)无言独上西楼,月如钩。
。
(李煜《相见欢》)(1分) (2),!风雨不动安如山。
(杜甫《茅屋为秋风所破歌)(2分)(3)念天地之悠悠, 。
(陈子昂《登幽州台歌》)(1分) (4)《小石潭记》中,作者触景生情,寄寓自己孤寂凄清的失意心情的语句是:, 。
(2分)(5)默写王维的《送杜少府之任蜀州》这首诗的前四句。
(4分),。
,。
2、结合语境,给句中的拼音加上汉字。
(4分)(1)于是又点上一支烟,再继续写些为‘正人君子’之流所shēn wù tòng jí的文字。
( )(2)也许只有细菌分裂才能和它们相pì měi 。
( )(3)它还可以纠正自己的错误,继续保持它在冬季的jiān mò。
( ) (4)从那以后,我常在这棵月宫仙桂上尽兴玩耍,míng sī xiá xiǎng ,遨游在美妙的梦境中。
( )3、下列各项中加点的成语使用恰当的一项是( )(3分) A .知识愈浅薄的人愈是侃侃而谈....,知识渊博的人则往往出言谨慎。
B. 纪录片《舌尖上的中国》介绍了各地美食,丰富多彩,让人莫衷一是....。
C .环卫工人的劳动也许是具体而微....的,但又是不可缺少的,因为我们的城市需要“美容师”,他们应受到尊重。
D .对于各种网络游戏,一些年轻人沉溺其中,乐此不疲....,浪费了不少宝贵的青春时光。
4、下列对病句的修改不正确的一项是( )(3分)密封 线内 不答准题 姓名班级座号A.我们平时所用的调味品醋,含有氨基酸、钙、磷、铁和维生素B等成分,被皮肤吸收后可以改变面部皮肤营养缺乏。
(“改变”改为“改善”)B.虽然现在所学的一些专业课,对我们很陌生,学起来比较吃力,不过我相信,在老师的帮助下,只要下苦功,就一定能够学好。
2014初中数学联赛初二年级

.
17 n k 15
【答】144.
由条件得 7 k 8 ,由 k 的唯一性,得 k 1 7 且 k 1 8 ,所以 2 k 1 k 1 8 7 1 ,
8n9
n8 n9
n n n 9 8 72
所以 n 144 .
当 n 144 时,由 7 k 8 可得126 k 128 , k 可取唯一整数值 127. 8n9
()
A.21
B.20
C.31
D.30
【答】 C.
2014 年全国初中数学联合竞赛初二年级试题参考答案 第 1 页(共 4 页)
可以称出的重物的克数可以为 1、2、3、4、5、6、7、8、9、10、20、21、22、23、24、25、26、27、
28、29、30、31、32、33、34、35、36、37、38、39、40,共 31 种.
x 2, y 3, z 1, xyz 6 .
6.已知△ ABC 的三边长分别为 2,3,4, M 为三角形内一点,过点 M 作三边的平行线,交各边于
D 、 E 、 F 、 G 、 P 、 Q (如图),如果 DE FG PQ x ,则 x =
()
18
A.
13
20
B.
13
22
C.
13
24
PAE 1 (BAD CAE) 1 (66 30) 18 ,
2
2
所以 PAC PAE CAE 18 30 48 .
EP
C
D
A
4.已知 n 为正整数,且 n4 2n3 6n2 12n 25 为完全平方数,则 n =
.
【答】8.
易知 n 1 , n 2 均不符合题意,所以 n 3 ,此时一定有
2014年下八年级数学竞赛试题及答案

2014年下八年级数学竞赛试题1. 一辆汽车从湄江出发开往娄底.如果汽车每小时行使a 千米,则t 小时可以到达,如果汽车每小时行使b ()b a >千米,那么可以提前到达娄底的时间是( )小时..A at a b + B.bt a b + C.abta b+ D.bt at b -2. 分式方程()()1112x mx x x -=--+有增根,则m 的值为( ) A.0和3 B.1 C.1和2- D.33. 由下列条件可以作出唯一的等腰三角形的是( )A.已知等腰三角形的两腰B.已知一腰和一腰上的高C.已知底角的度数和顶角的度数 D .已知底边长和底边上的中线的长4. )A.(1x -B.(1x -C.(1x -+D.(1x -5. 当x =时,代数式()20033420052001x x --的值是( ) A.0 B.1- C.1 D.20032-6. 若34x -<<45x -=的x 值为( )A.2B.3C.4D.5 7. 设0a b <<,224a b ab +=,则a ba b+-的值为( )C.2D.3 8. 若不等式组211x a x a >-⎧⎨<+⎩无解,则a 的取值范围是( )A.2a <B.2a =C.2a >D.2a ≥9. 已知a 、b 为常数,若0ax b +>的解集是13x <,则0bx a -<的解集是( ) A.3x >- B.3x <- C.3x > D.3x <10. 在等腰ABC △中,AB AC =,中线BD 将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为( )A.7B.11C.7或11D.7或10二.填空题(共8小题,每小题5分,共40分)11. 如图ABC △中,AD 平分BAC ∠,且AB BD AC +=,若64B ∠=︒,则C ∠= .12. 若22013a x +=,22014b x +=,22015c x +=,且24abc =,则111a b c bc ac ab a b c++---的值为 .13. 一条线段的长为a ,若要使31a -,41a +,12a -这三条线段组成一个三角形,则a 的取值范围是 . 14. 方程1998x y +=的整数解有 组.15. 如图BD 是ABC △的一条角平分线,8AB =,4BC =,且24ABC S =△,则DBC △的面积是 .16. 若关于x 的方程212x ax +=--的解为正数,则a 的取值范围是 . 17. 关于x 的不等式332x m m -≤-的正整数解为1,2,3,4,则m 的取值范围是 . 18. 如果21a -和5a -是一个数m 的平方根,则m 的值为 .三.解答题(共5小题,每小题8分,共40分)19. 已知:在ABC △中,AD 是BC 边上的中线,E 是AD 上一点,延长BE 交AC 于F ,若AF EF =,求证:BE AC =.20. 若关于x 的分式方程311x m x x--=-无解,求m 的值.21. 已知有理数a ,b ,c 满足0a b c ++-=,求()2015a cb +-的值.22. 某商店准备购进甲、乙两种商品.已知甲商品每件进价15元,售价20元;乙商品每件进价35元,售价45元.(1)若该商店同时购进甲、乙两种商品共100件,恰好用去2700元,求购进甲、乙两种商品各多少件?(2)若该商店准备用不超过3100元购进甲、乙两种商品共100件,且这两种商品全部售出后获利不少于890元,问应该怎样进货,才能使总利润最大,最大利润是多少?(利润=售价﹣进价)23. 如图,已知在ABC △中,AB AC =,CE 是AB 边上的中线,延长AB 到D ,使BD AB =,连接CD .求证:12CE CD =.参考答案题号 1 2 3 4 5 6 7 8 9 10 答案DDDBABADBC二.填空题(共8小题)11、 32︒ 12、18 13、352a << 14、 4 15、 8 16、 a <2且a ≠﹣4 17、12≤m <15 18、 81或9三.解答题(共5小题,每小题10分,共40分)19、证明:如图,延长AD 到点G ,使得AD=DG ,连接BG .∵AD 是BC 边上的中线(已知),∴DC=DB ,在△ADC 和△GDB 中,∴△ADC ≌△GDB (SAS ), ∴CAD G ∠=∠,BG AC =,∵AF EF =,∴CAD AEF ∠=∠, 又∠BED=∠AEF (对顶角相等),∴∠BED=∠G ∴BE=BG ,又BG AC =, ∴BE=AC .20、解:去分母得x (x ﹣m )﹣3(x ﹣1)=x (x ﹣1),﹣mx ﹣3x+3=﹣x ,整理得(2+m )x ﹣3=0,∵关于x 的分式方程﹣=1无解,分两种情况:(1)当此方程的解为增根时,则x=1或0, 当x=1时,2+m ﹣3=0,解得m=1, 当x=0时,﹣3=0,无解;(2)当整式方程无解时,即当2+m=0时,方程(2+m )x ﹣3=0无解,即m=﹣2. 综上所述,m=1或﹣2.21.解:将等式整理配方,得)))2221122310a b c -+-+-=,110a -=220b -=310c -=,∴2a =,6b =,4c =,∴()()20152015201524600.a c b +-=+-==22、解:(1)设购进甲种商品x 件,购进乙商品y 件,根据题意得:,解得:,答:商店购进甲种商品40件,购进乙种商品60件;(2)设商店购进甲种商品a 件,则购进乙种商品(100﹣a )件, 根据题意列得:,解得:20≤a ≤22,∵a 为整数,故20a =,21,22.当20a =时,利润为:()()201520453580900-⨯+-⨯=元 当21a =时,利润为:()()201521453579895-⨯+-⨯=元 当22a =时,利润为:()()201522453578890-⨯+-⨯=元∴当a=20时,利润最大,最大利润为900元,此时乙种商品应购进数量为100﹣20=80, 答:应购进甲种商品20件,乙种商品80件,才能使总利润最大,最大利润为900元.23、证明:如图,延长CE 到F ,使EF=CE ,连接FB ,∵CE 是AB 边上的中线,∴AE=BE , 又∵∠BEF=∠AEC ,∴△AEC ≌△BEF , ∴FB=AC ,∠1=∠A , ∵BD=AB ,∴FB=BD ,∵∠3=∠A+∠ACB=∠1+∠2,即∠CBD=∠CBF ,又∵BC 为公共边,∴△CDB ≌△CFB ,∴CD=CF=2CE ,即CE=CD .。
2013-2014学年第二学期八年级数学竞赛试题[1]
![2013-2014学年第二学期八年级数学竞赛试题[1]](https://img.taocdn.com/s3/m/8bed276b1ed9ad51f01df2ec.png)
2013-2014学年第二学期八年级数学竞赛试题 班级 姓名请同学们把选择好的每题答案填到下面的答题卡里。
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 答案题号 15 16 17 18 19 20 21 22 23 24 25 答案选择题(共25小题每小题4分,全卷总分100分) 1. 如果a 、b 表示两个负数,且a <b ,则( ). (A)1>ba(B)ba <1(C)ba 11<(D)ab <12. a 、b 是有理数,下列各式中成立的是( ). (A)若a >b ,则a 2>b 2 (B)若a 2>b 2,则a >b (C)若a ≠b ,则|a |≠|b | (D)若|a |≠|b |,则a ≠b3. |a |+a 的值一定是( ). (A)大于零(B)小于零(C)不大于零(D)不小于零4. 若由x <y 可得到ax >ay ,应满足的条件是( ). (A)a ≥0(B)a ≤0(C)a >0(D)a <05. 若不等式(a +1)x >a +1的解集是x <1,则a 必满足( ). (A)a <0(B)a >-1(C)a <-1(D)a <16. 九年级(1)班的几个同学,毕业前合影留念,每人交0.70元.一张彩色底片0.68元,扩印一张相片0.50元,每人分一张.在收来的钱尽量用掉的前提下,这张相片上的同学最少有( ).(A)2人 (B)3人 (C)4人 (D)5人7. 不等式组⎩⎨⎧+>+<+1,159m x x x 的解集是x >2,则m 的取值范围是( ).(A)m ≤2(B)m ≥2 (C)m ≤1 (D)m ≥18、22424y x y xy x ++--有一个因式是y x 2-,另一个因式是( ) A .12++y x B .12-+y x C .12+-y x D .12--y x 9、把a 4-2a 2b 2+b 4分解因式,结果是( )A 、a 2(a 2-2b 2)+b 4B 、(a 2-b 2)2C 、(a -b)4D 、(a +b)2(a -b)210、已知a 为任意整数,且()2213a a +-的值总可以被(1)n n n ≠为自然数,且整除,则n 的值为( )A .13B .26C .13或26D .13的倍数 11、把x 2-y 2-2y -1分解因式结果正确的是( )。
2013-2014学年度下期八年级数学竞赛试题

2013-2014学年度下期八年级数学竞赛试题一、选择题(每小题4分,共40分)1、 下列式子一定是二次根式的是( )A .2--xB .xC .22+xD .22-x2、若x<0,则x x x 2-的结果是( )A .0B .—2C .0或—2D .23、下面的四组数中是勾股数的一组是( )A 2、3、4B 21、28、35C 12、13、14D 5、8、134、有一木工师傅测量了一个等腰三角形的腰、底边和高的长,但他把这三个数据与其它的数据弄混了,请你帮他找出来,是第( )组。
A 13、12、12B 12、12、8C 13、10、12D 5、8、45、若O 是四边形ABCD 对角线的交点,且OA=OB=OC=OD,则四边形ABCD 是 ( ) A.平行四边形 B.矩形 C.梯形 D.菱形6、平行四边形ABCD 的周长为40cm ,△ABC 的周长为25cm ,则对角线AC 的长为 ( )A.6cmB.15cmC.5cmD.16cm.7、已知平行四边形一边长为10,一条对角线长为6,则它的另一条对角线a的取值范围是()A.4<a<16B.14<a<26C.12<a<20D.7<a<138、若一次函数y=(3-k)x-k的图象经过第二、三、四象限,则k的取值范围是()A.k>3 B.0<k≤3 C.0≤k<3 D.0<k<39、如图,P是边长为1的菱形ABCD对角线AC上一动点,M、N分别是AB、BC的中点,则MP+NP的最小值是()1210、已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的解析式为()A.y=-x-2 B.y=-x-6 C.y=-x+10 D.y=-x-1二、填空题(每小题4分,共40分)11、若m<0,则332||mmm++= 。
12、若35-=x,则562++xx的值为。
13、一座桥横跨一江,桥长12米,一艘小船自桥北出发,向正南方驶去,因水流原因,到达南岸后,发现已偏离桥南头5米,则小船实际行驶了_______米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
八年级数学竞赛试题
一、选择题(每题4分,共32分)
1.若分式2
1
x +的值为正整数,则整数x 的值为( )
(A )0 (B )1 (C )0或1 (D )0或-1
2、 在△ABC 中,AC ⊥BC ,∠B=30º,CN 、CM 三等分∠ACB , AN:NM:MB 的值 (A)1:1:3 (B)1:1:2 (C)1:2:2 (D)1:2:3
3、若关于x 的方程|2x-1|+a=0无解,|3x-5|+b=0只有一个解,|4x-3|+c=0有两个解,则a,b,c 的大小关系是()(A)a>b>c (B)b>c>a (C)b>a>c(D)a>c>b
4、如图,在Rt △ABC 中,∠C =90°,D 为AC 上一点,且DA =DB =5,又△DAB 的面积为10,那么DC 的长是( ); A 、4 B 、3 C 、5 D 、4.5
5、如图,一块直角三角形的纸片,两直角边AC =6㎝,BC =8㎝,现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上,且与AE 重合,则CD 等于( ); A 、2㎝ B 、3㎝ C 、4㎝ D 、5㎝
6、已知,如图长方形ABCD 中,AB =3cm ,AD =9cm ,将此长方形折叠,使点B 与点D 重合,折痕为EF ,则△ABE 的面积为( ).
A 、6cm 2
B 、8cm 2
C 、10cm 2
D 、12cm 2 7.如图,将纸片△ABC 沿着D
E 折叠压平,且∠1+∠2=72°,则∠A =( ) A .72° B .24° C .36° D .18° 8.如图△ABC 中,AD 平分∠BAC ,且AB +BD =AC ,若∠B =62°,则∠C =__________.
二、填空题(每题4分,共32分) 9. 的值为时,则分式若y
xy x y
xy x y x ---+=-2232311 。
10. 化简2()a b
ab b ab
--÷
的结果为__________________. 11、有3堆硬币,每枚硬币的面值相同.小李从第1堆取出和第2堆一样多的硬币放入第2堆;又从第2堆中取出和第3堆一样多的硬币放人第3堆;最后从第3堆中取出和现存的第1堆一样多的硬币放人第1堆,这样每堆有16枚硬币,则原来第1堆有硬币___枚,第2堆有硬币____枚,第3堆有硬币_____枚.
12.观察下面一列有规律的数: 31,82,153,244,355,486,……根据规律可知第n 个数应是 (n 为整数)
13、若a=2005x+2004,b=2005x+2005,c=2005x+2006,代数式a 2+b 2+c 2-ab-bc-ca=
14、如图,P 为正方形ABCD 内一点,PA =1,PB =2,PC =3,则∠APB =_______ .
15.若2221
.013a
a a a +=++求的值为 。
16、若x 2
+mx-10=(x+a)(x+b),(a ,b 是整数),则m 值 为 。
(8题图)
A B C
D B
D E C A 1 2 (第7题图)
A B D C 第4题图 A C B E 第5题图
第6题班级______________________________________ 姓名____________________ 考场号________________ 考号
_______________
A B C D P
第14题图
2
三、解答下列各题
17(本题9分)如图,在△ABC中,AB=AC
(1)P为BC上的中点,求证:AB2-AP2=PB·PC;
(2)若P为B C上的任意一点,(1)中的结论是否成立,并证明;
(3)若P为BC延长线上一点,说明AB、AP、PB、PC之间的数量关系.
18、(本小题满分9分)
在一次远足活动中,某班学生分成两组,第一组由甲地匀速步行到乙地后原路
返回,第二组由甲地匀速步行经乙地继续前行到丙地后原路返回,两组同时出
发,设步行的时间为t(h),两组离乙地的距离分别为S1(km)和S2(km),图
10中的折线分别表示S1、S2与t之间的函数关系.
(1)甲、乙两地之间的距离为km,乙、丙两地之间的距离为
km;
(2
)求第二组由甲地出发首次到达乙地及由乙地到达丙地所用的时间分别
是多少?
(3)求图中线段AB所表示的S2与t间的函数关系式,并写出自变量t的
取值范围.
19.(本题满分9分)小明用下面的方法求出方程30
=的解,请你仿照
他的方法求出下面另外两个方程的解,并把你的解答过程填写在下面的表格中.
222
AD AC BD
=+;
附加题(本小题满分8分)如图所示,四边形OABC是矩形,点A、C的坐标分
别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),
过点D作直线y=-
1
2
x+b交折线OAB于点E.
(1)记△ODE的面积为S,求S与b的函数关系式;
(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边
形OA1B1C1,试探究OA1B1C1与矩形OABC的重叠部分的面积是否发生
变化,若不变,求出该重叠部分的面积;若改变,请说明理由.
班
级_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
姓
名_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
考
场
号_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
考
号
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
A
B C。
