初三数学圆及旋转题库
整理中考数学几何图形旋转试题经典问题及解答

几何图形旋转常见问题一、填空题1.如图1,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,那么它们的公共局部的面积等于.2.如图2,将一块斜边长为12cm,∠B=60°的直角三角板ABC,绕点C沿逆时针方向旋转90°至△A′B′C′的位置,再沿CB向右平移,使点B′刚好落在斜边AB上,那么此三角板向右平移的距离是cm.3.正△ABC的边长为3cm,边长为1cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA顺时针连续翻转〔如图3所示〕,直至点P第一次回到原来的位置,那么点P运动路径的长为cm.4.如图4,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,∠BCD=45°,将腰CD 以点D为中心逆时针旋转90°至ED,连结AE,CE,那么△ADE的面积是.二、解答题5.如图5-1,P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD 于点F.(1) 求证:BP=DP;(2) 如图5-2,假设四边形PECF绕点C按逆时针方向旋转,在旋转过程中是否总有BP=DP?假设是,请给予证明;假设不是,请用反例加以说明;(3) 试选取正方形ABCD的两个顶点,分别与四边形PECF的两个顶点连结,使得到的两条线段在四边形PECF绕点C按逆时针方向旋转的过程中长度始终相等,并证明你的结论 .6.如图6-1是一个美丽的风车图案,你知道它是怎样画出来的吗?按以下步骤可画出这个风车图案:在图6-2中,先画线段OA,将线段OA平移至CB处,得到风车的第一个叶片F1,然后将第一个叶片OABC绕点O逆时针旋转180°得到第二个叶片F2,再将F1、F2同时绕点O逆时针旋转90°得到第三、第四个叶片F3、F4.根据以上过程,解答以下问题:(1)假设点A的坐标为(4,0),点C的坐标为(2,1),写出此时点B的坐标;(2)请你在图6-2中画出第二个叶片F2;(3)在(1)的条件下,连接OB,由第一个叶片逆时针旋转180°得到第二个叶片的过程中,线段OB扫过的图形面积是多少?7.如图7,在直角坐标系中,点P0的坐标为(1,0),将线段OP按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn〔n为正整数〕.〔1〕求点P6的坐标;〔2〕求△P5OP6的面积;〔3〕我们规定:把点Pn (xn,yn)〔n=0,1,2,3,…〕的横坐标xn、纵坐标yn都取绝对值后得到的新坐标(|xn |,|yn|)称之为点Pn的“绝对坐标〞.根据图中点Pn的分布规律,请你猜测点Pn的“绝对坐标〞,并写出来.8.把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H 〔如图8〕.试问线段HG与线段HB相等吗?请先观察猜测,然后再证明你的猜测.9.如图9-1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片〔如图9-2〕,量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角形纸片摆成如图9-3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合〔在图9-3至图9-6中统一用F表示〕图9-1 图9-2 图9-3 小明在对这两张三角形纸片进展如下操作时遇到了三个问题,请你帮助解决.〔1〕将图9-3中的△ABF沿BD向右平移到图9-4的位置,使点B与点F 重合,请你求出平移的距离;F交DE于〔2〕将图9-3中的△ABF绕点F顺时针方向旋转30°到图9-5的位置,A1点G,请你求出线段FG的长度;交DE于点H,请证明:〔3〕将图9-3中的△ABF沿直线AF翻折到图9-6的位置,AB1AH﹦DH.图9-4 图9-5 图9-6参考答案一、1. 2. 6-2 3二、5. 解:〔1〕解法一:在△ABP与△ADP中,利用全等可得BP=DP.解法二:利用正方形的轴对称性,可得BP=DP.〔2〕不是总成立 .当四边形PECF绕点C按逆时针方向旋转,点P旋转到BC边上时,DP>DC>BP,此时BP=DP 不成立.〔3〕连接BE、DF,那么BE与DF始终相等.在图1-1中,可证四边形PECF为正方形,在△BEC与△DFC中,可证△BEC≌△DFC .从而有 BE=DF .6. 解:〔1〕B〔6,1〕〔2〕图略〔3〕线段OB扫过的图形是一个半圆.过B作BD⊥x轴于D.由〔1〕知B点坐标为〔6,1〕,∴OB2=OD2+BD2=62+12=37.∴线段OB扫过的图形面积是.7. 解:〔1〕根据旋转规律,点P6落在y轴的负半轴,而点Pn到坐标原点的距离始终等于前一个点到原点距离的倍,故其坐标为P6(0,26),即P6(0,64).〔2〕由可得,△P0OP1∽△P1OP2∽…∽△Pn-1OPn,设P1(x1,y1),那么y1=2sin45°=,∴.又∵,∴.〔3〕由题意知,OP0旋转8次之后回到x轴正半轴,在这8次中,点Pn分别落在坐标象限的平分线上或x轴或y轴上,但各点绝对坐标的横、纵坐标均为非负数,因此,点Pn的坐标可分三类情况:令旋转次数为n.①当n=8k或n=8k+4时〔其中k为自然数〕,点Pn 落在x轴上,此时,点Pn的绝对坐标为(2n,0);②当n=8k+1或n=8k+3或n=8k+5或n=8k+7时〔其中k为自然数〕,点Pn落在各象限的平分线上,此时,点P n的绝对坐标为,即.③当n=8k+2或n=8k+6时〔其中k为自然数〕,点Pn落在y轴上,此时,点P n的绝对坐标为(0,2n).8. 解:HG=HB.证法1:连结AH〔如图10〕.∵四边形ABCD,AEFG都是正方形,∴∠B=∠G=90°.由题意,知AG=AB,又AH=AH,∴Rt△AGH≌Rt△ABH〔HL〕.∴HG=HB.证法2:连结GB〔如图11〕.∵四边形ABCD,AEFG都是正方形,∴∠ABC=∠AGF=90°.由题意知AB=AG.∴∠AGB=∠ABG.∴∠HGB=∠HBG.∴HG=HB.9. 解:〔1〕图形平移的距离就是线段BC的长.∵在Rt△ABC中,斜边长为10cm,∠BAC=30°,∴BC=5cm.∴平移的距离为5cm.〔2分〕〔2〕∵∠A1FA=30°,∴∠GFD=60°.又∠D=30°,∴∠FGD=90°.在Rt△EFD中,ED=10 cm,∴ .∵FG=cm.〔3〕在△AHE与△DHB1中,∠FAB1=∠EDF=30°.∵FD=FA,EF=FB=FB1,∴FD-FB1=FA-FE,即AE=DB1.又∵∠AHE=∠DHB1,∴△AHE≌△DHB1〔AAS〕.∴AH=DH.。
中考数学压轴题之旋转(中考题型整理,突破提升)及详细答案

在△ DAG 与△ DCG 中, ∵ AD=CD,∠ ADG=∠ CDG,DG=DG, ∴ △ DAG≌ △ DCG. ∴ AG=CG. 在△ DMG 与△ FNG 中, ∵ ∠ DGM=∠ FGN,FG=DG,∠ MDG=∠ NFG, ∴ △ DMG≌ △ FNG. ∴ MG=NG 在矩形 AENM 中,AM=EN. 在 Rt△ AMG 与 Rt△ ENG 中, ∵ AM=EN, MG=NG, ∴ △ AMG≌ △ ENG. ∴ AG=EG ∴ EG=CG. (3)(1)中的结论仍然成立.
4.如图(1)所示,将一个腰长为 2 等腰直角△ BCD 和直角边长为 2、宽为 1 的直角△ CED 拼在一起.现将△ CED 绕点 C 顺时针旋转至△ CE’D’,旋转角为 a. (1)如图(2),旋转角 a=30°时,点 D′到 CD 边的距离 D’A=______.求证:四边形 ACED′ 为矩形; (2)如图(1),△ CED 绕点 C 顺时针旋转一周的过程中,在 BC 上如何取点 G,使得 GD’=E’D;并说明理由.
【答案】(1)详见解析;(2)FE·sin( -90°) 【解析】 【分析】 (1)由四边形 ABCD 是平行四边形得 AF∥ BE,所以∠ FAE=∠ BEA,由折叠的性质得 ∠ BAE=∠ FAE,∠ BEA=∠ FEA,所以∠ BAE=∠ FEA,故有 AB∥ FE,因此四边形 ABEF 是平行四 边形,又 BE=EF,因此可得结论; (2)根据点 M 在线段 BE 上和 EC 上两种情况证明∠ ENG=90°- ,利用菱形的性质得到
九年级数学: 旋转基础知识及专题练习(含答案)

旋转及综合专题一、旋转相关定义1、定义:把一个图形绕着某一点 O 转动一个角度的图形变换叫做旋转,点 O 叫做旋转中心,转动的角叫做旋转角。
2、如果图形上的点 P 经过旋转变为 P 1 ,那么这两个点叫做这个旋转的对应点。
3、(1)对应点到旋转中心的距离相等,即旋转中心在对应点所连线段的垂直平分线上;(2)对应点与旋转中心所连线段的夹角等于旋转角; (3)旋转前、后图形全等。
4、把一个图形绕着某一点旋转180︒ ,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心。
这两个图形的对称点叫做关于中心的对称点。
5、(1)关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心平分;(2)关于中心对称的两个图形是全等图形。
6、把一个图形绕着某一点旋转180︒ ,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心。
二、旋转相关结论如 图 , 将 ∆ABC 绕 点 A 逆 时 针 旋 转 α 角 到∆AB 1C 1 。
点 B 和点 B 1 为对应点,点 C 和C 1 为对 应点。
结论 1:旋转中心为对应点所连线段垂直平分 线的交点,也即对应点所连线段的垂直平分线 均经过旋转中心。
如图,线段 BB 1 的垂直平分 线l 1 、线段CC 1 的垂直平分线l 2 都经过旋转中心点 A 。
利用这个结论我们可以利用对应点坐标 求出旋转中心的坐标。
由于对应点所连线段的 垂直平分线均经过旋转中心,因此只需求出两 组对应点所连线段的垂直平分线解析式,然后 联立即可求出旋转中心坐标。
结论 2:对应点与旋转中心所构成的三角形均为等腰三角线,且等腰三角形顶角均等于旋转角α。
如图, ∆ABB 1 和 ∆ACC 1 均为等腰三角形, ∠BAB 1 = ∠CAC 1 = α。
结论 3:对应点与旋转中心所构成的三角形均相似。
如图, ∆BAB 1 ∽ ∆CAC 1 。
【特荐】九年级上册数学 人教版 圆和旋转(练习题)

期末复习---圆和旋转知识点一:圆的有关性质和概念例1.如图1,A,B,C是⊙O上三点,∠ACB=25°,则∠BAO的度数是()A.55° B.60° C.65° D.70°例2.如图2,点A、B、C是⊙O上的三点,若∠OBC=50°,则∠A的度数是()A.40° B.50° C.80° D.100°例3.如图3,⊙O的内接四边形ABCD中,∠BCD=138°,则∠BOD的度数是.图1 图2 图3例4.如图4,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为()A.215 B.8 C.210 D.213图4 图5例5.当宽为2cm的刻度尺的一边与圆相切时,另一边与图的两个交点处的度数如图5,那么该圆的半径为 cm.例6.如图,A为⊙O外一点,AB切⊙O于点B,AO交⊙O于C,CD⊥OB于E,交⊙O于点D,连接OD.若AB=12,AC=8.(1)求OD的长;(2)求CD的长.练习:1.下列命题中,正确的是( )① 顶点在圆周上的角是圆周角; ② 圆周角的度数等于圆心角度数的一半; ③ 90o的圆周角所对的弦是直径; ④ 不在同一条直线上的三个点确定一个圆; ⑤ 同弧所对的圆周角相等 A .①②③B .③④⑤C .①②⑤D .②④⑤2. 如图,⊙O 中OA BC ⊥,25CDA ∠=o,则AOB ∠的度数为 .3.如图3,△ABC 内接于圆O ,∠A=50°,∠ABC=60°,BD 是圆O 的直径,BD 交AC 于点E ,连接DC ,则∠AEB 等于( )A .70°B .110°C .90°D .120°图3 图4 图54.如图4,在⊙O 中,直径CD 垂直弦AB 于点E ,连接OB ,CB ,已知⊙O 的半径为2,AB =32,则∠BCD 的大小为 °5.如图5,四边形ABCD 内接于O e ,若四边形ABCO 是平行四边形,则ADC ∠的大小为 ( ) (A )45︒ (B )50︒ (C )60︒ (D )75︒知识点二:与圆有关的位置关系1.⊙O 的半径为5,圆心O 到直线l 的距离为3,则直线l 与⊙O 的位置关系是( )A . 相交B . 相切C . 相离D . 无法确定2. 如图,从圆O 外一点P 引圆O 的两条切线PA PB ,,切点分别为A B ,.如果60APB ∠=o,8PA =,那么弦AB 的长是( )A .4B .8C .43D .833. 已知⊙O 的半径是3,圆心O 到直线AB 的距离是3,则直线AB 与⊙O 的位置关系是 .第2题PBAOOBCDA【典例精析】例1如图,线段AB 经过圆心O ,交⊙O 于点A C ,,点D 在⊙O 上,连接AD BD ,,30A B ∠=∠=o.BD是⊙O 的切线吗?请说明理由.例2 如图,⊙O 的直径AB =4,点P 是AB 延长线上的一点,过P 点作⊙O 的切线,切点为C ,连结AC .(1)若∠CP A =30°,求PC 的长;(2)若点P 在AB 的延长线上运动,∠CP A 的平分线交AC 于点M . 你认为∠CMP 的大小是否发生变化?若变化,请说明理由;若不变化,求∠CMP 的大小.例3 如图,AB 是⊙O 的直径,BD 是⊙O 的弦,延长BD 到点C ,使DC BD =,连结AC ,过点D 作DE AC ⊥,垂足为E .(1)求证:AB AC =; (2)求证:DE 为⊙O 的切线;(3)若⊙O 的半径为5,60BAC ∠=o,求DE 的长.OAE CBMP O CBA练习:1. 如图,AB是圆的直径,MN切圆于P,AM⊥MN于M,BN⊥MN于N,如果AM=5,BN=3,那么⊙O的半径为____。
中考数学旋转综合题及详细答案

则∠ AFG=90°. ∵ ∠ ABH=∠ G=60°,AB=a,AG=2a,
∴ AH=AB×sin60°= 3 a,AF=AG×sin60°= 3 a. 2
∴ 点 F 到 BC 的最大距离为 3 a+ 3 a= 3 3 a. 22
∴ S△ BCF= 1 ×2a× 3 3 a= 3 3 a2.
2
22
PC=
=6.
考点:1.扇形面积的计算;2.正方形的性质;3.旋转的性质.
3.如图 1, ABCD 和 AEFG 是两个能完全重合的平行四边形,现从 AB 与 AE 重合时开 始,将 ABCD 固定不动, AEFG 绕点 A 逆时针旋转,旋转角为 α(0°<α<360°), AB=a,BC=2a;并发现:如图 2,当 AEFG 旋转到点 E 落在 AD 上时,FE 的延长线恰好通过 点 C.
(2)根据面积公式得出 S△ GHK=S 四边形 CKGH-S△ CKH= 1 x2-3x+9,根据△ GKH 的面积恰好等于 2
△
ABC 面积的
5
,代入得出方程 1
x2-3x+9=
5
1
×
×6×6,求出即可.
12
2
12 2
解:(1)BH 与 CK 的数量关系:BH=CK,理由是:
连接 OC,
由直角三角形斜边上中线性质得出 OC=BG, ∵ AC=BC,O 为 AB 中点,∠ ACB=90°, ∴ ∠ B=∠ ACG=45°,CO⊥AB, ∴ ∠ CGB=90°=∠ KGH, ∴ 都减去∠ CGH 得:∠ BGH=∠ CGK, 在△ CGK 和△ BGH 中
∴
1
x2﹣3x+9=
5
1
×
人教版初三旋转测试题及答案
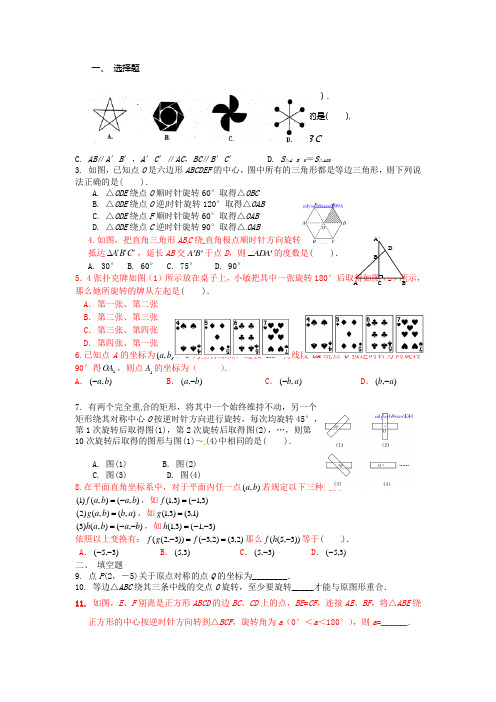
一、 选择题1.下列图形中,既是轴对称图形又是中心对称图形的是( ).2. 如图,△ABC 与△A ′B ′C ′成中心对称,下列说法不正确的是( ) A. S △ACB =S △A ′B ′C ′ B. AB =A ′B ′,A ′C ′=AC ,BC =B ′C ′C. AB ∥A ′B ′,A ′C ′∥AC ,BC ∥B ′C ′D. S △A ′B ′O =S △ACO3. 如图,已知点O 是六边形ABCDEF 的中心,图中所有的三角形都是等边三角形,则下列说法正确的是( ).A. △ODE 绕点O 顺时针旋转60°取得△OBCB. △ODE 绕点O 逆时针旋转120°取得△OABC. △ODE 绕点F 顺时针旋转60°取得△OABD. △ODE 绕点C 逆时针旋转90°取得△OAB4.如图,把直角三角形ABC 绕直角极点顺时针方向旋转90°后抵达C B A '''∆,延长AB 交B A ''于点D ,则A AD '∠的度数是( ). A. 30° B. 60° C. 75° D. 90°5.4张扑克牌如图(1)所示放在桌子上,小敏把其中一张旋转180°后取得如图(2)所示,那么她所旋转的牌从左起是( ). A .第一张、第二张 B .第二张、第三张 C .第三张、第四张D .第四张、第一张 (1) (2)6.已知点A 的坐标为),(b a ,O 为坐标原点,连接OA ,将线段OA 绕点O 按逆时针方向旋转90°得1OA ,则点1A 的坐标为( ).A .),(b a -B .),(b a -C .),(a b -D .),(a b -7. 有两个完全重合的矩形,将其中一个始终维持不动,另一个 矩形绕其对称中心O 按逆时针方向进行旋转,每次均旋转45°, 第1次旋转后取得图(1),第2次旋转后取得图(2),…,则第 10次旋转后取得的图形与图(1)~(4)中相同的是( ).A. 图(1)B. 图(2)C. 图(3)D. 图(4)8.在平面直角坐标系中,对于平面内任一点),(b a 若规定以下三种变换: ),(),()1(b a b a f -=,如)3,1()3,1(-=f ),(),()2(a b b a g =,如)1,3()3,1(=g ),(),()3(b a b a h --=,如)3,1()3,1(--=h依照以上变换有:)2,3()2,3())3,2((=-=-f g f 那么))3,5((-h f 等于( ). A .)3,5(-- B .)3,5( C .)3,5(- D .)3,5(- 二、 填空题9. 点P (2,-5)关于原点对称的点Q 的坐标为________.10. 等边△ABC 绕其三条中线的交点O 旋转,至少要旋转_____才能与原图形重合. 11. 如图,E 、F 别离是正方形ABCD 的边BC 、CD 上的点,BE =CF ,连接AE 、BF ,将△ABE 绕正方形的中心按逆时针方向转到△BCF ,旋转角为a (0°<a <180°),则a =______.A ’ DBA CB ’12. 如图,在Rt△ABC 中,∠ACB =90°,AC =BC =1,将Rt△ABC 绕点A 逆时针旋转30°后取得Rt△ADE ,点B 通过的路径为BD ,则图中阴影部份的面积是___________.13.在Rt△ABC 中,已知∠C =90°,∠B =50°,点D 在边BC 上,BD =2CD .把△ABC 绕着点D 逆时针旋转m (0<m <180)度后,若是点B 恰好落在初始Rt △ABC 的边上,那么m =_______.14. 如图,已知Rt △ABC 的周长为3.14,将△ABC 的斜边放在直线l 上,按顺时针方向在直线l 上转动两次, 转到△A 2B 1C 1位置,则AA 2=________.15. 图中是正比例函数与反比例函数的图象,相交于A 、B 两点, 其中点A 的坐标为(1,2),别离以点A 、B 为圆心,以1个单位长 度为半径画圆,则图中两个阴影部份面积的和是________.16.如图,在Rt △ABC 中,∠ACB =90º, ∠BAC=60º,AB =6.Rt △AB ´C ´可以看做是由 Rt △ABC 绕A 点逆时针方向旋转60º取得的, 则线段B ´C 的长为____________. 三、 解答题17. 如图,四边形ABCD 绕点点O 旋转后,极点A 的对应点为点E .试确定旋转后的四边形.18.在平面直角坐标系中,△ABC 的极点坐标是A (-7,1),B (1,1),C (1,7),线段DE 的端点坐标是D (7,-1),E (-1,-7).(1)试说明如何平移线段AC ,使其与线段ED 重合; (2)将△ABC 绕坐标原点O 逆时针旋转,使AC 的 对应边为DE ,请直接写出点B 的对应点F 的坐标; (3)画出(2)中的△DEF ,并和△ABC 同时绕坐标 原点O 逆时针旋转90°,画出旋转后的图形.19. 如图(1),△ABC 和△CEF 是两个大小不等的等边三角形,且有一个公共极点C ,连接(第11题) A B CDFE 300ECDAB(第12题)(第13题)AF和BE.(1)线段AF和BE有如何的大小关系?请证明你的结论;(2)将图(1)中的△CEF绕点C旋转必然的角度,取得图(2),(1)中的结论还成立吗?作出判断并说明理由;(3)若是将图(1)中的△ABC绕点C旋转必然的角度,请你画出一个变换后的图形(草图即可),那么(1)中的结论还成立吗?作出判断,没必要说明理由;(4)按照以上证明、说理、画图,归纳你的发现.(1) (2)(第19题)20. 李兵同窗家买了新房,准备装修地面,为节约开支,购买了两种质量相同、颜色相同的残缺地砖,现已加工成如图(1)所示的等腰直角三角形,李兵同学设计出如图(2)所示的四种图案:(1)请问你喜欢哪一种图案,并简述该图案的形成进程;(2)请你利用平移、旋转、轴对称等知识再设计一幅与上述不同的图案.(1)(2)(第20题)21. 如图,在△ABC中,∠BAC=120°,以BC为边向形外作等边三角形BCD,把△ABD绕着点D按顺时针方向旋转60°后取得△ECD.若AB=3,AC=2,求∠BAD的度数与AD的长.(第21题)22.△ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上.(1)作出△ABC关于y轴对称的△A1B1C1,并写出点C1的坐标;(2)作出△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标.(第22题)23.如图(1)(2)(3),在□ABCD中,AB⊥AC,AB=1,BC=5,对角线AC、BD相交于点O,将直线AC绕点O顺时针旋转.别离交BC、AD于点E、F.(1)试说明在旋转进程中,线段AF与EC总维持相等;(2)如图(2),证明:当旋转角为90o时,四边形ABEF是平行四边形;(3)在旋转进程中,四边形BEDF可能是菱形吗?若是不能,请说明理由;若是能,说明理由,并求出此时AC绕点O顺时针旋转的度数.(1)(2)(3)(第23题)附加题(共10分,不计入总分)24. 已知在正方形ABCD中,E为对角线BD上一点,过点E作EF⊥BD交BC于点F,连接DF,G为DF的中点,连接EG、CG.(1)求证:EG=CG;(2)将图(1)中△BEF绕点B逆时针旋转45°,如图(2)所示,取DF中点G,连接EG、CG.问(1)中的结论是不是仍然成立?若成立,请给出证明;若不成立,请说明理由;(3)将图(2)中△BEF绕点B旋转任意角度,如图(3)所示,再连接相应的线段,问(1)中的结论是不是仍然成立?通过观察你还能得出什么结论?(均不要求证明)(1) (2)(3)(第24题)第二十三章综合提优测评卷1.D2. D3. C4.B5.A6. C7. B8.B9. (-2,5) 10. 120°11.90 12.1π613.80和12014. 3.14 15. π16.3716. △CPS旋转取得△EPQ.17. (1)连接OA、OE、OB、AC.(2)以OB为一边作∠BOF,使∠BOF=∠AOE.(3)在射线OF上截取OF=OB;再别离以E、F为圆心,以AC、AD为半径在线段EF的右上侧画弧,两弧交于点G;再分别以E、G为圆心,以AD、CD为半径在线段EG的右边画弧,两弧交于点H.(4)连接EF、FG、GH、HE.四边形EFGH就是四边形ABCD绕点O旋转后的图形.(第17题)18.(1)将线段AC先向右平移6个单位,再向下平移8个单位.(其他平移方式也可)(2)F(-1,-1)(3)画出如图所示的正确图形:(第18题)19. (1)AF=BE.证明如下:∵△ABC和△CEF是等边三角形,∴AC=BC,CF=CE,∠ACF=∠BCE=60°.∴△AFC≌△BEC.∴AF=BE.(2)第(1)题的结论成立.理由如下:∵△ABC和△CEF是等边三角形,∴AC=BC,CF=CE,∠ACB=∠FCE=60°.∴∠ACB-∠FCB=∠FCE-∠FCB,即∠ACF=∠BCE.∴△AFC≌△BEC.∴AF=BE.(3)此处图形不唯一.如图,题(1)中的结论仍成立.(第19题)(4)按照以上证明、说理、画图,归纳如下:大小不等的等边三角形ABC 和等边三角形CEF 有且仅有一个公共极点C ,则以点C 为旋转中心,任意旋转其中一个三角形,都有AF =BE .20. 略 21. ∠BAD =60°,AD =522. (1)图略,点C 1的坐标为(-3,2); (2)图略,点C 2的坐标(-3,-2). 23.略 提示:(1)证△AOF ≌△COE ;(2)证EF ∥AB ;(3)当EF ⊥AB 时,四边形BEDF为菱形,旋转角为45o.24. (1)在Rt △FCD 中,∵ G 为DF 的中点,∴ CG =12FD .同理,在Rt △DEF 中,EG =12FD .∴ CG =EG .(2)(1)中结论仍然成立,即EG =CG .连接AG ,过点G 作MN ⊥AD 于点M ,与EF 的延长线交于点N . 在△DAG 与△DCG 中,∵ AD =CD ,∠ADG =∠CDG , DG =DG ,∴ △DAG ≌△DCG .∴ AG =CG . 在△DMG 与△FNG 中,∵ ∠DGM =∠FGN ,FG =DG ,∠MDG =∠NFG , ∴ △DMG ≌△FNG .∴ MG =NG . 在矩形AENM 中,AM =EN . 在Rt △AMG 与Rt △ENG 中, ∵ AM =EN ,MG =NG , ∴ △AMG ≌△ENG .∴ AG =EG .∴ EG =CG . (3)(1)中的结论仍然成立,即EG =CG .其他的结论还有EG ⊥CG .。
九年级上册数学同步练习题库:图形的旋转(简答题:较易)

图形的旋转(简答题:较易)1、如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.(1)求证:△BCD≌△FCE;(2)若EF∥CD,求∠BDC的度数.2、如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C (﹣1,3).(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.3、如图是一个4×4的正方形网格,每个小正方形的边长为1.请你在网格中以左上角的三角形为基本图形,通过平移、对称或旋转变换,设计一个精美图案,使其满足:①既是轴对称图形,又是以点O为对称中心的中心对称图形;②所作图案用阴影标识,且阴部分面积为4.4、如图,上面的平面图形绕轴旋转一周,可以得出下面的立体图形,请你把有对应关系的平面图形与立体图形连接起来.5、(12分)如图,以点P(﹣1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=,其中∠BAC=90°,将△ABC绕点P旋转180°,得到△MCB.(1)求B、C两点的坐标;(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.6、如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,的顶点都在格点上,点的坐标为.(1)把向上平移5个单位后得到对应的,画出,并写出的坐标;(2)以原点为对称中心,再画出关于原点对称的,并写出点的坐标.7、如图,在直角坐标系中,Rt△AOB的两条直角边OA,OB分别在x轴的负半轴,y轴的负半轴上,且OA=2,OB=1.将Rt△AOB绕点O按顺时针方向旋转90°,再把所得的像沿x轴正方向平移1个单位,得△CDO.(1)写出点A,C的坐标;(2)求点A和点C之间的距离.8、在图中,将大写字母A绕它上侧的顶点按逆时针方向旋转90°,作出旋转后的图案9、如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD ∠ABD (填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是;(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD=AD;(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明).10、问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足关系时,仍有EF=BE+FD.【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:=1.41,=1.73)11、在平面直角坐标系中,△ABC的顶点坐标是A(-7,1),B(1,1),C(1,7).线段DE的端点坐标是D(7,-1),E(-1,-7).(1)试说明如何平移线段AC,使其与线段ED重合;(2)将△ABC绕坐标原点O逆时针旋转,使AC的对应边为DE,请直接写出点B的对应点F的坐标;(3)画出(2)中的△DEF,并和△ABC同时绕坐标原点O逆时针旋转90°.画出旋转后的图形.12、如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).(1)请直接写出点A关于原点O对称的点的坐标;(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,写出点B的对应点的坐标;(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.13、如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求完成下列步骤:(1)画出将△ABC向上平移3个单位后得到的△A1B1C1,(2)画出将△A1B1C1绕点C1按顺时针方向旋转90°后所得到的△A2B2C1.14、如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网格线的交点),按要求画出四边形AB1C1D1和四边形AB2C2D2.(1)以A为旋转中心,将四边形ABCD顺时针旋转90°,得到四边形AB1C1D1;(2)以A为位似中心,将四边形ABCD作位似变换,且放大到原来的两倍,得到四边形AB2C2D2.15、如图,△ABC是边长为12的等边三角形,D是BC的中点,E是直线AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E的运动过程中,DF的最小值是.16、如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.(1)画出△A1B1C,直接写出点A1、B1的坐标;(2)求在旋转过程中,△ABC所扫过的面积.17、△ABC在平面直角坐标系中的位置如图所示,A(-1,4),B(-2,2),C(0,1),将△ABC沿y轴翻折得到△A1B1C1,再将△A1B1C1绕点O旋转180°得到△A2B2C2.写出各点坐标。
中考数学初中数学 旋转(大题培优 易错 难题)及详细答案

中考数学初中数学 旋转(大题培优 易错 难题)及详细答案一、旋转1.在△ABC 中,AB=AC ,∠BAC=α(︒<<︒600α),将线段BC 绕点B 逆时针旋转60°得到线段BD 。
(1)如图1,直接写出∠ABD 的大小(用含α的式子表示); (2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE 的形状并加以证明; (3)在(2)的条件下,连结DE ,若∠DEC=45°,求α的值。
【答案】(1)1302α︒-(2)见解析(3)30α=︒【解析】解:(1)1302α︒-。
(2)△ABE 为等边三角形。
证明如下:连接AD ,CD ,ED ,∵线段BC 绕点B 逆时针旋转60︒得到线段BD , ∴BC=BD ,∠DBC=60°。
又∵∠ABE=60°,∴1ABD 60DBE EBC 302α∠=︒-∠=∠=︒-且△BCD 为等边三角形。
在△ABD 与△ACD 中,∵AB=AC ,AD=AD ,BD=CD ,∴△ABD ≌△ACD (SSS )。
∴11BAD CAD BAC 22α∠=∠=∠=。
∵∠BCE=150°,∴11BEC 180(30)15022αα∠=︒-︒--︒=。
∴BEC BAD ∠=∠。
在△ABD 和△EBC 中,∵BEC BAD ∠=∠,EBC ABD ∠=∠,BC=BD , ∴△ABD ≌△EBC (AAS )。
∴AB=BE 。
∴△ABE 为等边三角形。
(3)∵∠BCD=60°,∠BCE=150°,∴DCE 1506090∠=︒-︒=︒。
又∵∠DEC=45°,∴△DCE 为等腰直角三角形。
∴DC=CE=BC 。
∵∠BCE=150°,∴(180150)EBC 152︒-︒∠==︒。
而1EBC 30152α∠=︒-=︒。
∴30α=︒。
(1)∵AB=AC ,∠BAC=α,∴180ABC 2α︒-∠=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1讲:旋转1一、填空题1.如图,△AOB旋转到△A′OB′的位置.若∠AOA′=90°,则旋转中心是点______.旋转角是______.点A的对应点是______.线段AB的对应线段是______.∠B的对应角是______.∠BOB′=______.2.如图,△ABC绕着点O旋转到△DEF的位置,则旋转中心是______.旋转角是______.AO=______,AB=______,∠ACB=∠______.1题图 2题图 3题图3.如图,正三角形ABC绕其中心O至少旋转______度,可与其自身重合.4.一个平行四边形ABCD,如果绕其对角线的交点O旋转,至少要旋转______度,才可与其自身重合.5.钟表的运动可以看作是一种旋转现象,那么分针匀速旋转时,它的旋转中心是钟表的旋转轴的轴心,经过45分钟旋转了______度.6.旋转的性质是对应点到旋转中心的______相等;对应点与旋转中心所连线段的夹角等于______;旋转前、后的图形之间的关系是______.7.把一个图形绕着某一个点旋转______,如果它能够与另一个图形______,那么称这两个图形关于这个点对称或中心对称,这个点叫做______,这两个图形中的对应点叫做关于中心的______.8.关于中心对称的两个图形的性质是:(1)关于中心对称的两个图形,对称点所连______都经过______,而且被对称中心所______.(2)关于中心对称的两个图形是______.9.线段不仅是轴对称图形,而且是______图形,它的对称中心是______.10.平行四边形是______图形,它的对称中心是____________.11.圆不仅是轴对称图形,而且是______图形,它的对称中心是______.12.若线段AB、CD关于点P成中心对称,则线段AB、CD的关系是______.13.如图,若四边形ABCD与四边形CEFG成中心对称,则它们的对称中心是______,点A的对称点是______,E的对称点是______.BD∥______且BD=______.连结A,F的线段经过______,且被C点______,△ABD≌______.13题图 15题图14.若O点是□ABCD对角线AC、BD的交点,过O点作直线l交AD于E,交BC于F.则线段OF 与OE的关系是______,梯形ABFE与梯形CDEF是______图形.15.如图,用等腰直角三角板画∠AOB=45°,并将三角板沿OB方向平移到如图所示的虚线处后绕点M按逆时针方向旋转22°,则三角板的斜边与射线OA的夹角为______°.16.如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形A′B′C′D′,则它们的公共部分的面积等于______.17.在平面直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点O按逆时针方向旋转60°得到P1,延长OP1到点P2,使OP2=2OP1,再将点P2绕着原点O按逆时针方向旋转60°,得点P3,则P3的坐标是______.18.如图,已知梯形ABCD中,AD∥BC,∠B=90°,AD=3,BC=5,AB=1,把线段CD绕点D逆时针旋转90°到DE位置,连结AE,则AE的长为______.16题图 18题图 19题图19.如图,以等腰直角三角形ABC的斜边AB为边作等边△ABD,连结DC,以DC为边作等边△DCE,B,E在C,D的同侧.若,2AB则BE=______.20.如图,已知D,E分别是正三角形的边BC和CA上的点,且AE=CD,AD与BE交于P,则∠BPD______°.20题图二、选择题1.下图中,不是旋转对称图形的是( ).2.有下列四个说法,其中正确说法的个数是( ).①图形旋转时,位置保持不变的点只有旋转中心;②图形旋转时,图形上的每一个点都绕着旋转中心旋转了相同的角度;③图形旋转时,对应点与旋转中心的距离相等;④图形旋转时,对应线段相等,对应角相等,图形的形状和大小都没有发生变化A.1个B.2个C.3个D.4个3.如图,把菱形ABOC绕点O顺时针旋转得到菱形DFOE,则下列角中不是旋转角的为( ).A.A.∠BOF B.∠AODB.C.∠COE D.∠COF4.如图,若正方形DCEF旋转后能与正方形ABCD重合,则图形所在平面内可作为旋转中心的点共有( )个.A.1 B.2C.3 D.45.下面各图中,哪些绕一点旋转180°后能与原来的图形重合?( ).A.①、④、⑤B.①、③、⑤C.②、③、⑤D.②、④、⑤6.下列图形中,不是..中心对称图形的是( ).A.圆B.菱形C.矩形D.等边三角形7.以下四个图形中,既是轴对称图形又是中心对称图形的有( ).A.4个B.3个C.2个D.1个8.下列图形中,是中心对称图形的有( ).A.1个B.2个C.3个D.4个9.下列图形中,是轴对称图形而不是中心对称图形的是( ).10.下列图形中,既是中心对称图形又是轴对称图形的是( ).A.等边三角形B.菱形C.等腰梯形D.平行四边形11.数学课上,老师让同学们观察如图所示的图形,问:它绕着圆心O旋转多少度后和它自身重合?甲同学说:45°;乙同学说:60°;丙同学说:90°;丁同学说:135°.以上四位同学的回答中,错误的是( ).A.甲B.乙C.丙D.丁12.如图,在平面直角坐标系中,△ABC和△DEF为等边三角形,AB=DE,点B,C,D在x轴上,点A,E,F在y轴上,下面判断正确的是( ).A.△DEF是△ABC绕点O顺时针旋转90°得到的B.△DEF是△ABC绕点O逆时针旋转90°得到的C.△DEF是△ABC绕点O顺时针旋转60°得到的D.△DEF是△ABC绕点O顺时针旋转120°得到的13.以下图的边缘所在直线为轴将该图案向右翻折后,再绕中心旋转180°,所得到的图形是( ).三、解答题14.已知:如图,四边形ABCD及一点P.求作:四边形A′B′C′D′,使得它是由四边形ABCD绕P点顺时针旋转150°得到的.15.已知:如图,当半径为30cm的转动轮按顺时针方向转过120°角时,传送带上的物体A向哪个方向移动?移动的距离是多少?16.已知:如图,F是正方形ABCD中BC边上一点,延长AB到E,使得BE=BF,试用旋转的性质说明:AF=CE且AF⊥CE.17.已知:如图,若线段CD是由线段AB经过旋转变换得到的.A.求作:旋转中心O点.18.已知:如图,P为等边△ABC内一点,∠APB=113°,∠APC=123°,试说明:以AP、BP、CP为边长可以构成一个三角形,并确定所构成三角形的各内角的度数.19.已知:如图,四边形ABCD与四边形EFGH成中心对称,试画出它们的对称中心,并简要说明理由.20.如图,有一块长方形钢板,工人师傅想把它分成面积相等的两部分,请你在图中画出作图痕迹.21.已知:三点A(-1,1),B(-3,2),C(-4,-1).(1)作出与△ABC关于原点对称的△A1B1C1,并写出各顶点的坐标;(2)作出与△ABC关于P(1,-2)点对称的△A2B2C2,并写出各顶点的坐标.22.已知:直线l的解析式为y=2x+3,若先作直线l关于原点的对称直线l1,再作直线l1关于y轴的对称直线l2,最后将直线l2沿y轴向上平移4个单位长度得到直线l3,试求l3的解析式.23.如图,将给出的4张扑克牌摆成第一行的样子,然后将其中的1张牌旋转180°成第二行的样子,你能判断出被旋转过的1张牌是哪一张吗?为什么?四、综合题1.已知:如图,四边形ABCD中,∠D=60°,∠B=30°,AD=CD.求证:BD2=AB2+BC2.2.已知:如图,E是正方形ABCD的边CD上任意一点,F是边AD上的点,且FB平分∠ABE.A.求证:BE=AF+CE.3.已知:如图,在四边形ABCD中,∠B+∠D=180°,AB=AD,E,F 分别是线段BC ,CD 上的点,且BE +FD =EF .求证:.21BAD EAF ∠=∠4.已知:如图,Rt △ABC 中,∠ACB =90°,D 为AB 中点,DE 、DF 分别交AC 于E ,交BC 于F ,且DE ⊥DF .如果CA =CB ,求证:AE 2+BF 2=EF 2;如果CA <CB ,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.第2讲:旋转的应用(直击中考)FE DC B A NM E FAC B A BCDNMA1、四边形ABCD 中,∠ABC =60度,∠ADC =120度,求证:BD =AD+CD2、正方形ABCD 中,E 为BC 上的一点,F 为CD 上的一点,BE+DF=EF ,求∠EAF 的度数.3、D 为等腰Rt ABC ∆斜边AB 的中点,DM ⊥DN,DM,DN 分别交BC,CA 于点E,F 。
(1) 当MDN ∠绕点D 转动时,求证DE=DF 。
(2) 若AB=2,求四边形DECF 的面积。
0120BDC ∠=,以4、如图,ABC ∆是边长为3的等边三角形,BDC ∆是等腰三角形,且D 为顶点做一个060角,使其两边分别交AB 于点M ,交AC 于点N ,连接MN ,则AMN ∆的周长为 ;5、(2010年朝阳一模) 23.(本小题满分7分)请阅读下列材料:问题:如图1,在等边三角形ABC 内有一点P ,且PA=2, PB=3, PC=1.求∠BPC 度数的大小和等边三角形ABC 的边长.李明同学的思路是:将△BPC 绕点B 顺时针旋转60°,画出旋转后的图形(如图2).连接PP ′,可得△P ′PC 是等边三角形,而△PP ′A 又是直角三角形(由勾股定理的逆定理可证).所以∠AP ′B=150°,而∠BPC=∠AP ′B=150°.进而求出等边△ABC 的边长为7.问题得到解决.请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD 内有一点P ,且PA=5,BP=2,PC=1.求∠BPC 度数的大小和正方形ABCD 的边长.6、已知:PA=2,PB=4,以AB 为一边作正方形ABCD,使P 、D 两点落在直线AB 的两侧.如图,当∠APB=45°时,求AB 及PD 的长;7、(2009年崇文一模)25.(本小题满分8分)图3 图1图2在等边△ABC 的两边AB 、AC 所在直线上分别有两点M 、N ,D 为△ABC 外一点,且∠MDN =60°,∠BDC =120°,BD =CD .探究:当点M 、N 分别在直线AB 、AC 上移动时,BM 、NC 、MN 之间的数量关系及△AMN 的周长Q 与等边△ABC 的周长L 的关系.(Ⅰ)如图①,当点M 、N 在边AB 、AC 上,且DM =DN 时,BM 、NC 、MN 之间的数量关系是____________;此时 LQ____________;(Ⅱ)如图②,当点M 、N 在边AB 、AC 上,且当DM ≠DN 时,猜想(Ⅰ)问的两个结论还成立吗?写出你的猜想并加以证明;(Ⅲ)如图③,当点M 、N 分别在边AB 、CA 的延长线上时,若AN =x ,则Q =________(用x 、L 表示).8、(2009年崇文二模)以ABC ∆的两边AB 、AC 为腰分别向外作等腰Rt ABD ∆和等腰Rt ACE ∆,90,BAD CAE ∠=∠=︒连接DE ,M 、N 分别是BC 、DE 的中点.探究:AM 与DE 的位置关系及数量关系.(1)如图① 当ABC ∆为直角三角形时,AM 与DE 的位置关系是 , 线段AM 与DE 的数量关系是 ;(2)将图①中的等腰Rt ABD ∆绕点A 沿逆时针方向旋转︒θ(0<θ<90)后,如图②所示,(1)问中得到的两个结论是否发生改变?并说明理由. 9、(2009年丰台一模)23.如图1,在ABC △中,ACB ∠为锐角,点D 为射线BC 上一点,联结AD ,以AD 为一边且在AD 的右侧作正方形ADEF . (1)如果AB AC =,90BAC =∠,①当点D 在线段BC 上时(与点B 不重合),如图2,线段CF BD 、所在直线的位置关系为 __________ ,线段CF BD 、的数量关系为 ;②当点D 在线段BC 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由; (2)如果AB AC ≠,BAC ∠是锐角,点D 在线段BC 上,当ACB ∠满足什么条件时,CF BC ⊥(点C F 、不重合),并说明理由. 图1ABDFEC图2ABDECFF图3ABDC E10、(2009中考真题)24.在□ABCD中,过点C作CE⊥CD交AD于点E,将线段EC绕点E逆时针旋转90°得到线段EF(如图①).(1)在图①中画图探究:①当P1为射线CD上任意一点(P1不与C点重合)时,连结EP1,将线段EP1绕点E逆时针旋转90°得到线段EG1.判断直线FG1与直线CD的位置关系并加以证明;②当P2为线段DC的延长线上任意一点时,连结EP2,将线段EP2绕点E逆时针旋转90°得到线段EG2.判断直线G1G2与直线CD的位置关系,画出图形并直接写出你的结论.第3讲:圆的基本概念及垂径定理一、基础知识填空1.由圆的定义可知:(1)圆上的各点到圆心的距离都等于________;在一个平面内,到圆心的距离等于半径长的点都在________.因此,圆是在一个平面内,所有到一个________的距离等于________的________组成的图形.(2)要确定一个圆,需要两个基本条件,一个是________,另一个是________,其中,________确定圆的位置,______确定圆的大小.2.连结______________的__________叫做弦.经过________的________叫做直径.并且直径是同一圆中__________的弦.3.圆上__________的部分叫做圆弧,简称________,以A,B为端点的弧记作________,读作________或________.4.圆的________的两个端点把圆分成两条弧,每________都叫做半圆.5.在一个圆中_____________叫做优弧;_____________叫做劣弧.6.半径相等的两个圆叫做____________.圆是______对称图形,它的对称轴是______________________;圆又是______对称图形,它的对称中心是____________________.垂直于弦的直径的性质定理是____________________________________________.平分________的直径________于弦,并且平分________________________________.二、填空题7.如下图,(1)若点O为⊙O的圆心,则线段__________是圆O的半径;线段________是圆O的弦,其中最长的弦是______;______是劣弧;______是半圆.(1)(2)若∠A=40°,则∠ABO=______,∠C=______,∠ABC=______.8.圆的半径为5cm,圆心到弦AB的距离为4cm,则AB=______cm.9.如图,CD为⊙O的直径,AB⊥CD于E,DE=8cm,CE=2cm,则AB=______cm.7题9题10题10.如图,⊙O的半径OC为6cm,弦AB垂直平分OC,则AB=______cm,∠AOB=______.11.如图,AB为⊙O的弦,∠AOB=90°,AB=a,则OA=______,O点到AB的距离=______.12.如图,⊙O的弦AB垂直于CD,E为垂足,AE=3,BE=7,且AB=CD,则圆心O到CD的距离是______.13.如图,P为⊙O的弦AB上的点,P A=6,PB=2,⊙O的半径为5,则OP=______.14.如图,⊙O的弦AB垂直于AC,AB=6cm,AC=4cm,则⊙O的半径等于______cm.14题图15.已知:如图,在同心圆中,大圆的弦AB交小圆于C,D两点.(1)求证:∠AOC=∠BOD;(2)试确定AC与BD两线段之间的大小关系,并证明你的结论.16.已知:如图,AB是⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E,若AB=2DE,∠E=18°,求∠C及∠AOC的度数.17.已知:如图,△ABC,试用直尺和圆规画出过A,B,C三点的⊙O.18.11.已知:如图,AB是⊙O的直径,弦CD交AB于E点,BE=1,AE=5,∠AEC=30°,求CD的长.19.已知:如图,试用尺规将它四等分.20.今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何.(选自《九章算术》卷第九“句股”中的第九题,1尺=10寸).21.已知:⊙O的半径OA=1,弦AB、AC的长分别为2,3,求∠BAC的度数.22.已知:⊙O的半径为25cm,弦AB=40cm,弦CD=48cm,AB∥CD.求这两条平行弦AB,CD之间的距离.23.已知:如图,A,B是半圆O上的两点,CD是⊙O的直径,∠AOD=80°,B是的中点.(1)在CD上求作一点P,使得AP+PB最短;(2)若CD=4cm,求AP+PB的最小值.24.如图,有一圆弧形的拱桥,桥下水面宽度为7.2m,拱顶高出水面2.4m,现有一竹排运送一货箱从桥下经过,已知货箱长10m,宽3m,高2m(竹排与水面持平).问:该货箱能否顺利通过该桥?第4讲:弧、弦、圆心角一、基础知识填空1.______________的______________叫做圆心角.2.在同圆或等圆中,两个圆心角及它们所对的两条弧、两条弦中如果有一组量相等,那么______________________.3.在圆中,圆心与弦的距离(即自圆心作弦的垂线段的长)叫做弦心距,不难证明,在同圆或等圆中,如果两条弦相等,那么它们的弦心距也______.反之,如果两条弦的弦心距相等,那么_____________________.4._________在圆上,并且角的两边都_________的角叫做圆周角.5.在同一圆中,一条弧所对的圆周角等于_________圆心角的_________.6.在同圆或等圆中,____________所对的圆周角____________.7._________所对的圆周角是直角.90°的圆周角______是直径.8.如图,若五边形ABCDE是⊙O的内接正五边形,则∠BOC=______,∠ABE=______,∠ADC=______,∠ABC=______.8题图 9题 10题9.如图,若六边形ABCDEF是⊙O的内接正六边形,则∠AED=______,∠FAE=______,∠DAB=______,∠EFA=______.10.如图,ΔABC是⊙O的内接正三角形,若P是上一点,则∠BPC=______;若M是上一点,则∠BMC=______.二,选择题11.在⊙O中,若圆心角∠AOB=100°,C是上一点,则∠ACB等于( ).A.80°B.100°C.130°D.140°12.在圆中,弦AB,CD相交于E.若∠ADC=46°,∠BCD=33°,则∠DEB等于( ).A.13°B.79°C.38.5°D.101°13.如图,AC是⊙O的直径,弦AB∥CD,若∠BAC=32°,则∠AOD等于( ).A.64°B.48°C.32°D.76°13题 14题 15题14.如图,弦AB,CD相交于E点,若∠BAC=27°,∠BEC=64°,则∠AOD等于( ).A.37°B.74°C.54°D.64°15.如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于( ).A.69°B.42°C.48°D.38°16.如图,△ABC内接于⊙O,∠A=50°,∠ABC=60°,BD是⊙O的直径,BD交AC于点E,连结DC,则∠AEB等于( ).A.70°B.90°C.110°D.120°17.⊙O中,M为的中点,则下列结论正确的是( ).A.AB>2AM B.AB=2AMC.AB<2AM D.AB与2AM的大小不能确定三、解答题18.已知:如图,A、B、C、D在⊙O上,AB=CD.求证:∠AOC=∠DOB.19.已知:如图,P是∠AOB的角平分线OC上的一点,⊙P与OA相交于E,F点,与OB相交于G,H点,试确定线段EF与GH之间的大小关系,并证明你的结论.20.已知:如图,AB为⊙O的直径,C,D为⊙O上的两点,且C为的中点,若∠BAD=20°,求∠ACO的度数.21.如图,⊙O中,AB为直径,弦CD交AB于P,且OP=PC,试猜想与之间的关系,并证明你的猜想.22.如图,⊙O中,直径AB=15cm,有一条长为9cm的动弦CD在上滑动(点C与A,点D与B不重合),CF⊥CD交AB于F,DE⊥CD交AB于E.(1)求证:AE=BF;(2)在动弦CD滑动的过程中,四边形CDEF的面积是否为定值?若是定值,请给出证明并求这个定值;若不是,请说明理由.23.已知:如图,△ABC内接于⊙O,BC=12cm,∠A=60°.求⊙O的直径.24.已知:如图,AB是⊙O的直径,弦CD⊥AB于E,∠ACD=30°,AE=2cm.求DB长.25.已知:如图,△ABC内接于圆,AD⊥BC于D,弦BH⊥AC于E,交AD于F.求证:FE=EH.26.已知:如图,⊙O的直径AE=10cm,∠B=∠EAC.求AC的长.27.已知:如图,△ABC内接于⊙O,AM平分∠BAC交⊙O于点M,AD⊥BC于D.求证:∠MAO=∠MAD.28.已知:如图,AB是⊙O的直径,CD为弦,且AB⊥CD于E,F为DC延长线上一点,连结AF交⊙O于M.求证:∠AMD=∠FMC.第5讲:点和圆的位置关系一、基础知识填空1.平面内,设⊙O的半径为r,点P到圆心的距离为d,则有d>r⇔点P在⊙O______;d=r⇔点P在⊙O______;d<r⇔点P在⊙O______.2.平面内,经过已知点A,且半径为R的圆的圆心P点在___________________________________.3.平面内,经过已知两点A,B的圆的圆心P点在______________________________________ ____________________.4._____________________________________________确定一个圆.5.在⊙O上任取三点A,B,C,分别连结AB,BC,CA,则△ABC叫做⊙O的______;⊙O叫做△ABC 的______;O点叫做△ABC的______,它是△ABC___________的交点.6.锐角三角形的外心在三角形的___________部,钝角三角形的外心在三角形的__________一、___部,直角三角形的外心在________________.7.若正△ABC外接圆的半径为R,则△ABC的面积为___________.8.若正△ABC的边长为a,则它的外接圆的面积为___________.9.若△ABC中,∠C=90°,AC=10cm,BC=24cm,则它的外接圆的直径为___________.10.若△ABC内接于⊙O,BC=12cm,O点到BC的距离为8cm,则⊙O的周长为___________.二、选择题1.已知:A,B,C,D,E五个点中无任何三点共线,无任何四点共圆,那么过其中的三点作圆,最多能作出( ).A.5个圆B.8个圆C.10个圆D.12个圆2.下列说法正确的是( ).A.三点确定一个圆B.三角形的外心是三角形的中心C.三角形的外心是它的三个角的角平分线的交点D.等腰三角形的外心在顶角的角平分线上3.下列说法不正确的是( ).A.任何一个三角形都有外接圆B.等边三角形的外心是这个三角形的中心C.直角三角形的外心是其斜边的中点D.一个三角形的外心不可能在三角形的外部4.正三角形的外接圆的半径和高的比为( ).A.1∶2 B.2∶3 C.3∶4 D.1∶35.已知⊙O的半径为1,点P到圆心O的距离为d,若关于x的方程x2-2x+d=0有实根,则点P( ).A.在⊙O的内部B.在⊙O的外部C.在⊙O上D.在⊙O上或⊙O的内部6.如图,△ABC内接于⊙O,若AC=BC,弦CD平分∠ACB,则下列结论中,正确的个数是( ).①CD是⊙O的直径②CD平分弦AB③CD⊥AB ④=⑤=A.2个B.3个C.4个D.5个7. 如图,CD 是⊙O 的直径,AB ⊥CD 于E ,若AB =10cm ,CE ∶ED =1∶5,则⊙O 的半径是( ).A .cm 25B .cm 34C .cm 53D .cm 628. 如图,AB 是⊙O 的直径,AB =10cm ,若弦CD =8cm ,则点A 、B 到直线CD的距离之和为( ). A .12cm B .8cm C .6cm D.4cm9. △ABC 内接于⊙O ,OD ⊥BC 于D ,若∠A =50°,则∠BOD 等于( ).A .30°B .25°C .50°D .100° 10. 有四个命题,其中正确的命题是( ).①经过三点一定可以作一个圆②任意一个三角形有且只有一个外接圆③三角形的外心到三角形的三个顶点的距离相等 ④在圆中,平分弦的直径一定垂直于这条弦 A .①、②、③、④ B .①、②、③ C .②、③、④ D .②、③11. 在圆内接四边形ABCD 中,若∠A ∶∠B ∶∠C =2∶3∶6,则∠D 等于( ).A .67.5°B .135°C .112.5° D.45°三、解答题1.已知:如图,△ABC .作法:求件△ABC 的外接圆O .2.在平面直角坐标系中,作以原点O 为圆心,半径为4的⊙O ,试确定点A (-2,-3),B (4,-2),)2,32(-C 与⊙O 的位置关系.3.在直线123-=x y 上是否存在一点P ,使得以P 点为圆心的圆经过已知两点A (-3,2),B (1,2).若存在,求出P 点的坐标,并作图.4.如图,AC 是⊙O 的直径,∠1=46°,∠2=28°,则∠BCD =______.5.如图,AB 是⊙O 的直径,若∠C =58°,则∠D =______.4题图 5题图 6题6.如图,AB 是⊙O 的直径,弦CD 平分∠ACB ,若BD =10cm ,则AB =______,∠BCD =______. 7.若△ABC 内接于⊙O ,OC =6cm ,cm 36 AC ,则∠B 等于______. 三、解答题8.已知:如图,⊙O 中,AB =AC ,OD ⊥AB 于D ,OE ⊥AC 于E . 求证:∠ODE =∠OED .9.已知:如图,AB 是⊙O 的直径,OD ⊥BC 于D ,AC =8cm ,求OD 的长.10. 已知:如图,点D 的坐标为(0,6),过原点O ,D 点的圆交x 轴的正半轴于A 点.圆周角∠OCA =30°,求A 点的坐标.11.已知:如图,试用尺规作图确定这个圆的圆心.12.已知:如图,半圆O的直径AB=12cm,点C,D是这个半圆的三等分点.求∠CAD的度数及弦AC,AD和围成的图形(图中阴影部分)的面积S.第6讲: 直线和圆的位置关系(一)一、基础知识填空1.直线与圆在同一平面上做相对运动时,其位置关系有______种,它们分别是______________________________.2.直线和圆_________时,叫做直线和圆相交,这条直线叫做____________.直线和圆_________时,叫做直线和圆相切,这条直线叫做____________. 这个公共点叫做_________.直线和圆____________时,叫做直线和圆相离. 3.设⊙O 的半径为r ,圆心O 到直线l 的距离为d ,_________⇔直线l 和圆O 相离; _________⇔直线l 和圆O 相切; _________⇔直线l 和圆O 相交.4.圆的切线的性质定理是__________________________________________. 5.圆的切线的判定定理是__________________________________________.6.已知直线l 及其上一点A ,则与直线l 相切于A 点的圆的圆心P 在____________________________________________________________________________________.7.经过圆外一点作圆的切线,______________________________叫做这点到圆的切线长.从圆外一点可以引圆的______条切线,它们的____________相等.这一点和____________平分____________.8.三角形的三个内角的平分线交于一点,这个点到__________________相等.9.__________________的圆叫做三角形的内切圆,内切圆的圆心是____________,叫做三角形的____________.10.设等边三角形的内切圆半径为r ,外接圆半径为R ,边长为a ,则r ∶R ∶a =______.11.设O 为△ABC 的内心,若∠A =52°,则∠BOC =____________.11.已知:如图,PA ,PB 分别与⊙O 相切于A ,B 点,C 为⊙O 上一点,∠ACB =65°,则∠APB 等于( ).A .65°B .50°C .45°D .40°11题图 12题12.如图,△ABC 中,∠A =60°,BC =6,它的周长为16.若⊙O 与BC ,AC ,AB 三边分别切于E ,F ,D 点,则DF 的长为( ).A .2B .3C .4D .6 13.下面图形中,一定有内切圆的是( ).A .矩形B .等腰梯形C .菱形D .平行四边形 14.等边三角形的内切圆半径、外接圆半径和高的比是( ).A .3:2:1B .3:2:1C .2:3:1D .1∶2∶3二、解答题1.已知:Rt△ABC中,∠C=90°,BC=5cm,AC=12cm,以C点为圆心,作半径为R的圆,求:(2)当R为何值时,⊙C和直线AB相离?(2)当R为何值时,⊙C和直线AB相切?(3)当R为何值时,⊙C和直线AB相交?2.已知:如图,P是∠AOB的角平分线OC上一点.PE⊥OA于E.以P点为圆心,PE长为半径作⊙P.求证:⊙P与OB相切.3.已知:如图,△ABC内接于⊙O,过A点作直线DE,当∠BAE=∠C时,试确定直线DE与⊙O的位置关系,并证明你的结论.4.已知:如图,割线ABC与⊙O相交于B,C两点,E是的中点,D是⊙O上一点,若∠EDA=∠AMD.求证:AD是⊙O的切线.5.已知:如图,Rt△ABC中,∠ACB=90°,以AC为直径的半圆O交AB于F,E是BC的中点.(1)求证:直线EF是半圆O的切线.2.6.已知:如图,△ABC 中,AD ⊥BC 于D 点,.21BC AD 以△ABC 的中位线为直径作半圆O ,试确定BC 与半圆O 的位置关系,并证明你的结论.7.已知:如图,△ABC 中,AC =BC ,以BC 为直径的⊙O 交AB 于E 点,直线EF ⊥AC 于F .(1)求证:EF 与⊙O 相切.8.已知:如图,以△ABC 的一边BC 为直径作半圆,交AB 于E ,过E 点作半圆O 的切线恰与AC 垂直,试确定边BC 与AC 的大小关系,并证明你的结论.9.已知:如图,PA 切⊙O 于A 点,PO ∥AC ,BC 是⊙O 的直径.请问:直线PB 是否与⊙O 相切?说明你的理由.10.已知:如图,PA切⊙O于A点,PO交⊙O于B点.PA=15cm,PB=9cm.求⊙O的半径长.11.已知:如图,从两个同心圆O的大圆上一点A,作大圆的弦AB切小圆于C点,大圆的弦AD切小圆于E点.求证:(1)AB=AD;(2)DE=BC.12.已知:如图,PA,PB分别与⊙O相切于A,B两点.求证:OP垂直平分线段AB.13.已知:如图,△AB C.求作:△ABC的内切圆⊙O.14.已知:如图,PA,PB,DC分别切⊙O于A,B,E点.(1)若∠P=40°,求∠COD;(2)若PA=10cm,求△PCD的周长.15.已知:如图,⊙O是Rt△ABC的内切圆,∠C=90°.若AC=12cm,BC=9cm,求⊙O的半径r;若AC=b,BC=a,AB=c,求⊙O的半径r.16.已知:如图,△ABC的三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r.求△ABC的面积S.17.已知:如图,⊙O内切于△ABC,∠BOC=105°,∠ACB=90°,AB=20cm.求BC、AC的长.18.已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.2.求⊙O的面积.19.已知:如图,AB是⊙O的直径,F,C是⊙O上两点,且=,过C点作DE⊥AF的延长线于E点,交AB的延长线于D点.(1)试判断DE与⊙O的位置关系,并证明你的结论;(2)试判断∠BCD与∠BAC的大小关系,并证明你的结论.20.已知:如图,PA,PB分别是⊙O的切线,A,B为切点,AC是⊙O的直径,∠BAC=35°,求∠P 的度数.21.已知:如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D 作DE⊥AC,垂足为E.求证:AB=AC;求证:DE为⊙O的切线;若⊙O的半径为5,∠BAC=60°,求DE的长.22.已知:如图,⊙O 是Rt △ABC 的外接圆,AB 为直径,∠ABC =30°,CD 是⊙O 的切线,ED ⊥AB 于F .(3)判断△DCE 的形状并说明理由;(4)设⊙O 的半径为1,且213-=OF ,求证△DCE ≌△OCB .23.已知:如图,AB 为⊙O 的直径,PQ 切⊙O 于T ,AC ⊥PQ 于C ,交⊙O 于D . 求证:AT 平分∠BAC ;若,3,2==TC AD 求⊙O 的半径.第7讲圆和圆的位置关系1.没有______的两个圆叫做这两个圆相离.当两个圆相离时,如果其中一个圆在另一个圆的______,叫做这两个圆外离;如果其中有一个圆在另一个圆的______,叫做这两个圆内含.2.____________的两个圆叫做这两个圆相切.这个公共点叫做______.当两个圆相切时,如果其中的一个圆(除切点外)在另一个圆的______,叫做这两个圆外切;如果其中有一个圆(除切点外)在另一个圆的______,叫做这两个圆内切.3.______的两个圆叫做这两个圆相交,这两个公共点叫做这两个圆的______以这两个公共点为端点的线段叫做两圆的______.4.设d是⊙O1与⊙O2的圆心距,r1,r2(r1>r2)分别是⊙O1和⊙O2的半径,则⊙O1与⊙O2外离⇔d________________________;⊙O1与⊙O2外切⇔d________________________;⊙O1与⊙O2相交⇔d________________________;⊙O1与⊙O2内切⇔d________________________;⊙O1与⊙O2内含⇔d________________________;⊙O1与⊙O2为同心圆⇔d____________________.5.各条边______,并且各个______也都相等的多边形叫做正多边形.6.把一个圆分成n(n≥3)等份,依次连结各等分点所得的多边形是这个圆的______.7.一个正多边形的______________叫做这个正多边形的中心;______________叫做正多边形的半径;正多边形每一边所对的______叫做正多边形的中心角;中心到正多边形的一边的__________叫做正多边形的边心距.8.正n边形的每一个内角等于__________,它的中心角等于__________,它的每一个外角等于______________.9.设正n边形的半径为R,边长为a n,边心距为r n,则它们之间的数量关系是______.这个正n 边形的面积S n=________.10.正八边形的一个内角等于_______,它的中心角等于_______.11.正六边形的边长a,半径R,边心距r的比a∶R∶r=_______.12.同一圆的内接正方形和正六边形的周长比为_______.13.如图,在12×6的网格图中(每个小正方形的边长均为1个单位),⊙A的半径为1,⊙B的半径为2,要使⊙A与静止的⊙B相切,那么⊙A由图示位置需向右平移______个单位.二、选择题14.若两个圆相切于A点,它们的半径分别为10cm、4cm,则这两个圆的圆心距为( ).A.14cm B.6cmC.14cm或6cm D.8cm7-,则这两个圆的圆心距可取的整数值的个数是15.若相交两圆的半径分别是17+和1( ).A.1B.2 C.3 D.416.10.等边三角形的外接圆面积是内切圆面积的( ).17. 已知正方形的周长为x ,它的外接圆半径为y ,则y 与x 的函数关系式是( ).A .x y 42=B .x y 82=C .x y 21=D .x y 22=18. 有一个长为12cm 的正六边形,若要剪一张圆形纸片完全盖住这个圆形,则这个圆形纸片的半径最小是( ).A .10cmB .12cmC .14cmD .16cm二.解答题19. 已知:如图,⊙O 1与⊙O 2相交于A ,B 两点.求证:直线O 1O 2垂直平分AB .20. 已知:如图,⊙O 1与⊙O 2外切于A 点,直线l 与⊙O 1、⊙O 2分别切于B ,C 点,若⊙O 1的半径r 1=2cm ,⊙O 2的半径r 2=3cm .求BC 的长.21. 已知:如图,两圆相交于A ,B 两点,过A 点的割线分别交两圆于D ,F 点,过B 点的割线分别交两圆于H ,E 点.求证:HD ∥EF .22. 已知:相交两圆的公共弦的长为6cm ,两圆的半径分别为cm 23,cm 5,求这两个圆的圆心距.23.如图,工地放置的三根外径是1m的水泥管两两外切,求其最高点到地平面的距离.24.已知:如图,⊙O1与⊙O2相交于A,B两点,圆心O1在⊙O2上,过B点作两圆的割线CD,射线DO1交AC于E点.(1)求证:DE⊥AC.25.已知:如图,⊙O1与⊙O2相交于A,B两点,过A点的割线分别交两圆于C,D,弦CE∥DB,连结EB,试判断EB与⊙O2的位置关系,并证明你的结论.26.如图,点A,B在直线MN上,AB=11cm,⊙A,⊙B的半径均为1cm.⊙A以每秒2cm的速度自左向右运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(s)之间的关系式为r=1+t(t≥0).(2)试写出点A,B之间的距离d(cm)与时间t(s)之间的函数表达式;(3)问点A出发多少秒时两圆相切?。
