强度折剪
剪切计算及常用材料强度
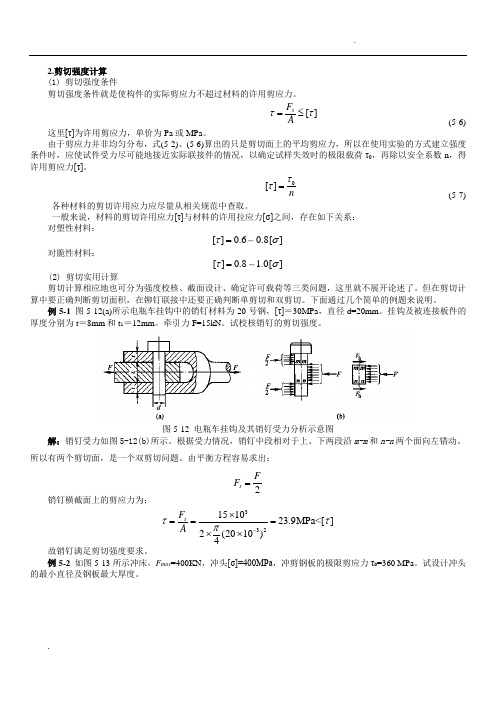
2.剪切强度计算 (1) 剪切强度条件剪切强度条件就是使构件的实际剪应力不超过材料的许用剪应力。
[]sF A ττ=≤(5-6)这里[τ]为许用剪应力,单价为Pa 或MPa 。
由于剪应力并非均匀分布,式(5-2)、(5-6)算出的只是剪切面上的平均剪应力,所以在使用实验的方式建立强度条件时,应使试件受力尽可能地接近实际联接件的情况,以确定试样失效时的极限载荷τ0,再除以安全系数n ,得许用剪应力[τ]。
[]n ττ=(5-7)各种材料的剪切许用应力应尽量从相关规范中查取。
一般来说,材料的剪切许用应力[τ]与材料的许用拉应力[σ]之间,存在如下关系: 对塑性材料:[]0.60.8[]τσ= 对脆性材料:[]0.8 1.0[]τσ=(2) 剪切实用计算剪切计算相应地也可分为强度校核、截面设计、确定许可载荷等三类问题,这里就不展开论述了。
但在剪切计算中要正确判断剪切面积,在铆钉联接中还要正确判断单剪切和双剪切。
下面通过几个简单的例题来说明。
例5-1 图5-12(a)所示电瓶车挂钩中的销钉材料为20号钢,[τ]=30MPa ,直径d=20mm 。
挂钩及被连接板件的厚度分别为t =8mm 和t 1=12mm 。
牵引力F=15kN 。
试校核销钉的剪切强度。
图5-12 电瓶车挂钩及其销钉受力分析示意图解:销钉受力如图5-12(b)所示。
根据受力情况,销钉中段相对于上、下两段沿m-m 和n-n 两个面向左错动。
所以有两个剪切面,是一个双剪切问题。
由平衡方程容易求出:2s F F =销钉横截面上的剪应力为:332151023.9MPa<[]2(2010)4s F A ττπ-⨯===⨯⨯故销钉满足剪切强度要求。
例5-2 如图5-13所示冲床,F max =400KN ,冲头[σ]=400MPa ,冲剪钢板的极限剪应力τb =360 MPa 。
试设计冲头的最小直径及钢板最大厚度。
图5-13 冲床冲剪钢板及冲剪部分受力示意图解:(1) 按冲头压缩强度计算dmax max2=[]4F FdAσσπ=≤所以3max644400100.034 3.4[]40010Fd m cmπσπ⨯⨯≥===⨯⨯(2) 按钢板剪切强度计算t钢板的剪切面是直径为d高为t的柱表面。
第四章 剪切强度试验

t为试样厚度,单位为mm。
第四章 剪切强度试验
第五节 剪切试验结果分析与处理
4 开缝试验 本试验适合薄片状材料。当试样受拉时,在x—x截面受剪切作用,故式中
6、剪断后若发生弯曲,或断口出现楔形、椭圆形等剪切截面,则试验结果 无效,应重新取样进行试验。
第四章 剪切强度试验
第五节 剪切试验结果分析与处理
试样剪断后,记下最大载荷,按以下公式计算抗剪强度。 1 单剪试验剪切强度按下式计算
τ= p/ so 式中 τ—为抗剪强度,单位为N/mm²;
p—为试样被剪断的最大载荷,单位为N; so—为试样原始横截面积,单位为mm²。 2 双剪试验剪切强度按下式计算
第四节剪切试验的操作要点第四章剪切强度试验1试验前需测量试样的直径精度不低于001mm或板厚横截面积计算精确到001mm2试验机应按jjg13983拉力压力和万能材料试验机检定规程进行检定
第四章 剪切强度试验
第一节 剪切试验原理
在图4-1中,沿截面m—m假想地 将试样分成两部分,并取左边 为研究对象。由平衡关系可知, 在m—m面上分布的内力系的合 力必然是一个平行于P的Q力, 且由平衡条件
得 PQ=0
P=Q
在图4-2所示的双剪切中,用同 样的方法可以求出剪力:
Q=P/2
第四章 剪切强度试验
第二节 剪切试样
1、双剪切圆柱试样 试样直径和长度随实际需要并根据夹具而定,一般取5,10, 15mm。
2、用于冲孔的板状试样
薄板金属不能做成圆柱试样时,可用冲孔剪切试验。板状试样厚 度一般小于5mm。
剪切计算常用材料强度

2.剪切强度计算 (1) 剪切强度条件剪切强度条件就是使构件的实际剪应力不超过材料的许用剪应力。
[]sF A ττ=≤(5-6)这里[τ]为许用剪应力,单价为Pa 或MPa 。
由于剪应力并非均匀分布,式(5-2)、(5-6)算出的只是剪切面上的平均剪应力,所以在使用实验的方式建立强度条件时,应使试件受力尽可能地接近实际联接件的情况,以确定试样失效时的极限载荷τ0,再除以安全系数n ,得许用剪应力[τ]。
[]n ττ=(5-7)各种材料的剪切许用应力应尽量从相关规范中查取。
一般来说,材料的剪切许用应力[τ]与材料的许用拉应力[σ]之间,存在如下关系: 对塑性材料:[]0.60.8[]τσ=对脆性材料:[]0.8 1.0[]τσ=(2) 剪切实用计算剪切计算相应地也可分为强度校核、截面设计、确定许可载荷等三类问题,这里就不展开论述了。
但在剪切计算中要正确判断剪切面积,在铆钉联接中还要正确判断单剪切和双剪切。
下面通过几个简单的例题来说明。
例5-1 图5-12(a)所示电瓶车挂钩中的销钉材料为20号钢,[τ]=30MPa ,直径d=20mm 。
挂钩及被连接板件的厚度分别为t =8mm 和t 1=12mm 。
牵引力F=15kN 。
试校核销钉的剪切强度。
图5-12 电瓶车挂钩及其销钉受力分析示意图解:销钉受力如图5-12(b)所示。
根据受力情况,销钉中段相对于上、下两段沿m-m 和n-n 两个面向左错动。
所以有两个剪切面,是一个双剪切问题。
由平衡方程容易求出:2s FF =销钉横截面上的剪应力为:332151023.9MPa<[]2(2010)4s F A ττπ-⨯===⨯⨯故销钉满足剪切强度要求。
例5-2 如图5-13所示冲床,F max =400KN ,冲头[σ]=400MPa ,冲剪钢板的极限剪应力τb =360 MPa 。
试设计冲头的最小直径及钢板最大厚度。
图5-13 冲床冲剪钢板及冲剪部分受力示意图解:(1) 按冲头压缩强度计算dmax max2=[]4F F d Aσσπ=≤所以0.034 3.4d m cm ≥===(2) 按钢板剪切强度计算t钢板的剪切面是直径为d 高为t 的柱表面。
强度折减法

强度折减法
强度折减法是一种用于减轻原材料的热处理强度的方法,它是在适当的温度和时间下添加低碳或微合金钢进行热处理,以降低原材料强度的一种方法。
这种方法可以有效地减少热处理后的材料强度,从而改变机械性能和物理性能,实现生产过程中的改性目的。
强度折减法的工作原理:当金属材料在热处理操作时,在温度一定的情况下,添加适量的低碳或微合金钢将使原材料内部组织形成低碳锭晶,这种低碳锭晶具有更低的强度、塑性和韧性,从而改变了原始材料的组织结构,使其具有更低的强度,从而达到了强度折减的目的。
强度折减法具有许多优点。
首先,它可以有效地减轻原材料的热处理强度,从而改变机械性能和物理性能,实现生产过程中的改性目的。
其次,它的施工简单快捷,操作条件和工艺可以根据实际情况调整,减少金属材料的热处理工艺,节约设备的成本,实现金属材料的加工速度,缩减生产周期。
此外,这种方法还具有良好的可控性。
由于影响折减量的主要因素是加入低合金钢的厚度和温度,经验证,采用适当的操作模式可以控制到位,只要调整加入低合金钢的厚度和温度,就可以实现对原材料强度的有效折减。
即使是强度折减法,也有一些缺点。
首先,它可能会引起金属材料的综合性能下降,特别是硬度和耐腐蚀性,因此,在采用强度折减法之前,应该考虑到金属材料的综合性能。
其次,它会影响产品的外
观,如果采用过热处理,则会导致表面脆化和棱角粗糙,出现粗糙的表面,从而影响产品的外观。
通过以上介绍,我们可以清楚地看到,强度折减法是一种有效的减轻原材料的热处理强度的方法,具有许多优点,但也有一些缺点,因此,在采用强度折减法之前,应该充分考虑到金属材料的综合性能,并选择合适的热处理工艺和温度,才能达到技术要求和生产要求。
剪切计算及常用材料强度..

2.剪切强度计算(1) 剪切强度条件剪切强度条件就是使构件的实际剪应力不超过材料的许用剪应力。
[]sF A ττ=≤(5-6)这里[τ]为许用剪应力,单价为Pa 或MPa 。
由于剪应力并非均匀分布,式(5-2)、(5-6)算出的只是剪切面上的平均剪应力,所以在使用实验的方式建立强度条件时,应使试件受力尽可能地接近实际联接件的情况,以确定试样失效时的极限载荷τ0,再除以安全系数n ,得许用剪应力[τ]。
[]n ττ= (5-7) 各种材料的剪切许用应力应尽量从相关规范中查取。
一般来说,材料的剪切许用应力[τ]与材料的许用拉应力[σ]之间,存在如下关系:对塑性材料: 对脆性材料: (2) 剪切实用计算剪切计算相应地也可分为强度校核、截面设计、确定许可载荷等三类问题,这里就不展开论述了。
但在剪切计算中要正确判断剪切面积,在铆钉联接中还要正确判断单剪切和双剪切。
下面通过几个简单的例题来说明。
例5-1 图5-12(a)所示电瓶车挂钩中的销钉材料为20号钢,[τ]=30MPa ,直径d=20mm 。
挂钩及被连接板件的厚度分别为t =8mm 和t 1=12mm 。
牵引力F=15kN 。
试校核销钉的剪切强度。
图5-12 电瓶车挂钩及其销钉受力分析示意图解:销钉受力如图5-12(b)所示。
根据受力情况,销钉中段相对于上、下两段沿m-m 和n-n 两个面向左错动。
所以有两个剪切面,是一个双剪切问题。
由平衡方程容易求出:销钉横截面上的剪应力为:故销钉满足剪切强度要求。
例5-2 如图5-13所示冲床,F max =400KN ,冲头[σ]=400MPa,冲剪钢板的极限剪应力τb =360 MPa 。
试设计冲头的最小直径及钢板最大厚度。
图5-13 冲床冲剪钢板及冲剪部分受力示意图解:(1) 按冲头压缩强度计算d所以(2) 按钢板剪切强度计算t钢板的剪切面是直径为d 高为t 的柱表面。
所以例5-3 如图5-14所示螺钉受轴向拉力F 作用,已知[τ]=0.6[σ],求其d :h 的合理比值。
剪切计算及常用材料强度

剪切计算及常用材料强度Document number:WTWYT-WYWY-BTGTT-YTTYU-2018GT2.剪切强度计算(1) 剪切强度条件剪切强度条件就是使构件的实际剪应力不超过材料的许用剪应力。
[]sFAττ=≤(5-6) 这里[τ]为许用剪应力,单价为Pa或MPa。
由于剪应力并非均匀分布,式(5-2)、(5-6)算出的只是剪切面上的平均剪应力,所以在使用实验的方式建立强度条件时,应使试件受力尽可能地接近实际联接件的情况,以确定试样失效时的极限载荷τ0,再除以安全系数n,得许用剪应力[τ]。
[]nττ=(5-7) 各种材料的剪切许用应力应尽量从相关规范中查取。
一般来说,材料的剪切许用应力[τ]与材料的许用拉应力[σ]之间,存在如下关系:对塑性材料:[]0.60.8[]τσ=对脆性材料:[]0.8 1.0[]τσ=(2) 剪切实用计算剪切计算相应地也可分为强度校核、截面设计、确定许可载荷等三类问题,这里就不展开论述了。
但在剪切计算中要正确判断剪切面积,在铆钉联接中还要正确判断单剪切和双剪切。
下面通过几个简单的例题来说明。
例5-1 图5-12(a)所示电瓶车挂钩中的销钉材料为20号钢,[τ]=30MPa,直径d=20mm。
挂钩及被连接板件的厚度分别为t=8mm和t1=12mm。
牵引力F=15kN。
试校核销钉的剪切强度。
图5-12 电瓶车挂钩及其销钉受力分析示意图解:销钉受力如图5-12(b)所示。
根据受力情况,销钉中段相对于上、下两段沿m-m和n-n两个面向左错动。
所以有两个剪切面,是一个双剪切问题。
由平衡方程容易求出:2sFF=销钉横截面上的剪应力为:332151023.9MPa<[]2(2010)4sFAττπ-⨯===⨯⨯故销钉满足剪切强度要求。
例5-2如图5-13所示冲床,F max=400KN,冲头[σ]=400MPa,冲剪钢板的极限剪应力τb=360 MPa。
试设计冲头的最小直径及钢板最大厚度。
有限元强度参数折减法

27
2021/4/22
2在岩土介质与支挡结构共同作用中的应 用
传统的极限平衡方法可以求出岩士介质作用在支挡 结构上的推力,而不知道推力的分布。对推力分布 作不同的假设求得的支挡结构内力有很大差异,从 而降低了计算的精度。强度折减有限元法的应用, 有助于考虑岩土介质与支挡结构的共同作用,获得 支挡结构上真实的推力分布状况,它们是在土体处 于极限平衡状态下获得的
33
2021/4/22
1.27
k1
强左
)度 图 的折 反 变减 映 化系 了 过数 塑 程( 性
依应 次变 为分
布
区
随
1.25 1.26
34
2021/4/22
参考文献:
有限元强度折减法在土坡与岩坡中的应用 郑颖人, 赵尚毅
有限元极限分析法及其在岩土工程中的应用 郑颖人, 赵尚毅,邓楚键等
岩土工程极限分析有限元法及其应用 郑颖人 赵尚毅
24
2021/4/22
1.3折线型滑动面边坡稳定分析算例
下图 所示为两个直线滑面组成折线型滑体ABMCD, 滑块ABCD 面积433 m2,滑面AB = 20 m,倾角y1 = 15°,AD = 25 m,DC = 19.32 m,BC =19.82 m,滑块 BCM 面积196.5 m2,滑面BM =28.03 m,倾角y 2 = 45°,CM = 19.82 m,CM 面上施加有线性变化的面 荷载,PM = 400 kPa,PC = 0,岩体重度g =20kN/m3, 弹性模量 E = 109 Pa。计算方法同上,在滑动面 AB, BM 上布置接触单元,通过有限元强度折减,得到不 同参数的安全系数如表
有限元强度参数折减法及其在岩 土极限分析中的应用
剪切计算常用材料强度

2.剪切强度计算 (1) 剪切强度条件剪切强度条件就是使构件的实际剪应力不超过材料的许用剪应力。
[]sF A ττ=≤(5-6)这里[τ]为许用剪应力,单价为Pa 或MPa 。
由于剪应力并非均匀分布,式(5-2)、(5-6)算出的只是剪切面上的平均剪应力,所以在使用实验的方式建立强度条件时,应使试件受力尽可能地接近实际联接件的情况,以确定试样失效时的极限载荷τ0,再除以安全系数n ,得许用剪应力[τ]。
[]n ττ=(5-7)各种材料的剪切许用应力应尽量从相关规范中查取。
一般来说,材料的剪切许用应力[τ]与材料的许用拉应力[σ]之间,存在如下关系: 对塑性材料:[]0.60.8[]τσ=对脆性材料:[]0.8 1.0[]τσ=(2) 剪切实用计算剪切计算相应地也可分为强度校核、截面设计、确定许可载荷等三类问题,这里就不展开论述了。
但在剪切计算中要正确判断剪切面积,在铆钉联接中还要正确判断单剪切和双剪切。
下面通过几个简单的例题来说明。
例5-1 图5-12(a)所示电瓶车挂钩中的销钉材料为20号钢,[τ]=30MPa ,直径d=20mm 。
挂钩及被连接板件的厚度分别为t =8mm 和t 1=12mm 。
牵引力F=15kN 。
试校核销钉的剪切强度。
图5-12 电瓶车挂钩及其销钉受力分析示意图解:销钉受力如图5-12(b)所示。
根据受力情况,销钉中段相对于上、下两段沿m-m 和n-n 两个面向左错动。
所以有两个剪切面,是一个双剪切问题。
由平衡方程容易求出:2s FF =销钉横截面上的剪应力为:332151023.9MPa<[]2(2010)4s F A ττπ-⨯===⨯⨯故销钉满足剪切强度要求。
例5-2 如图5-13所示冲床,F max =400KN ,冲头[σ]=400MPa ,冲剪钢板的极限剪应力τb =360 MPa 。
试设计冲头的最小直径及钢板最大厚度。
图5-13 冲床冲剪钢板及冲剪部分受力示意图解:(1) 按冲头压缩强度计算dmax max2=[]4F F d Aσσπ=≤所以0.034 3.4d m cm ≥===(2) 按钢板剪切强度计算t钢板的剪切面是直径为d 高为t 的柱表面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
tanφi = ( tanφ) / Zi
( 2)
式中 Zi 为强度折减系数 。若某一问题的解接近临 界平衡状态 ,就将安全系数 f s 取为对应的 Zi 。 至于临界平衡状态的定义也有很多 [1~7 ] , 一般认 为 ,对于给定的强度参数 ci 和φi , 若能在给定的迭代 次数内收敛 ,而对于稍低于 ci 和φi 的参数 ci′ 和φi′,在 给定的迭代次数内不能收敛 , 就认为结构已达到临界 平衡状态 。由于无法准确确定 “给定的迭代次数” ,因 此这一定义在使用上尚有不便 ,这里 ,将临界平衡状态 定义为当边坡内的塑性区能够形成潜在的滑移通道时 的状态 。这一定义在本质上与文献 [ 4 ] 是一致的 ,但使 用上更简单 ,文献 [ 4 ] 取临界平衡态为边坡内的广义塑 性剪应变等值线由坡底至坡顶连通时的时刻 。
( 5) 若已达到了极限状态 , 取安全系数 f s = Zi , 结
式中 h 为 深 度 ;γ 为 容 重 ; K 为 侧 压 系 数 , K = ν 。 1 - ν 顺便指出 ,式 ( 4) 所定义的应力场也适用于这样一 个岩石圆柱 : 柱体的圆周面及底部被施以滑动简支约 束 ,而上表面自由 。对于上述应力场 ,认为应处处满足
第 24 卷 第5期 2002 年 9 月
岩 土 工 程 学 报
Chinese Journal of Geotechnical Engineering
Vol. 24 No. 5 Sept. , 2002
求解安全系数的有限元法
Finite ele ment metho d for solving the factor of safety
假定此种岩石充满了半无限空间 , 其中的应力场 仅为自重应力场 ( 按弹性力学的规定) ,则有 σ γh 1 =σ 2 = - K σ h 3 = - γ
( 4)
4 算 法
建议的用有限元法计算安全系数的算法如下 : ( 1) 由式 ( 7) 求得参数 β; ( 2) 给定一强度折减系数 Zi , 由式 ( 2) 求得 ci ,φi ; ( 3) 由式 ( 9) 求得 Ei 和ν i : sinφi 1 ν 1 i = 2 β ( 9) ν E Ei = ν i ( 4) 以 Ei ,ν i 和 ci ,φ i 为参数作有限元分析 ;
ZHENG Hong1 ,2 ,LI Chun2guang2 ,Lee C. F. 3 , GE Xiu2run2
( 1 . China Three Gorges University , Yichang 443002 , China ; 2 . Institute of Rock and Soil Mechanics , The Chinese Academy of Sciences , Wuhan 430071 , China ; 3 . De2 partment of Civil Engineering , The University of Hong Kong , Hong Kong , China)
Key words :factor of safety ;finite element ; limit equilibrium
有下列强度参数 ci 和φi 的题目 :
1 前 言
Ξ
ci = c/ Zi
数十年来 ,虽然涌现出不少优秀的数值分析方法 , 但传统的极限平衡法仍然是评价边坡和其他水工建筑 物安全性的首选方法 。极限平衡法中最重要的概念是 安全系数 ,安全系数的定义方法有多种 [1 ] ,但目前最为 工程师们所接受的还是基于强度储备概念的安全系数 定义 ,本文也将沿用这一概念 。 从本质上讲 ,若将材料视为理想弹塑性材料 ,则利 用有限元法可以求得结构的安全系数 ,而且 ,有限元法 还具有传统的极限平衡法无可比拟的优势 [1~7 ] : 首先 , 可以了解结构随强度恶化而呈现出的渐进失稳过程 ; 其次 ,可以得到极限状态下的失效形式 。 本文简述了求解安全系数的有限元方法 , 分析了 现有方法中的一些问题 ,指出在对材料的抗剪强度参数 c 和 φ 折扣的同时 ,必须按照一定的规则对材料的刚度 参数 E 和 ν作相应调整 ,才能得到合理的结果 ,并且以 一个均质边坡为例 ,说明了本文方法的合理性。
图1 均质边坡的有限元模型 ( 单元 :698 , 节点 :757)
Fig. 1 The FE model of a homogenous slope ( elem :698 ,node :757)
式中 φi 和ν i 对应于折减系数 Z i ;β为常数 ,则 φ β = sin ( 7) 1 - 2ν 其中 φ 和ν为岩石真实的参数 。由式 ( 3) , β ≥1 。 当 Zi →∞时 , 必有 φi →0 , ci →0 。由式 ( 6 ) 可知 ν 0 . 5 , 岩石表现为无抗剪强度但又不可压缩的水 , i → 由此可见式 ( 6) 在此意义上的合理性 。 随着 ci 和φi 的降低 ,ν i 将增大 , 而 Ei 将减小 , 因
cc = c/ f s
的弹模 E 通常以 MPa 为单位 ,泊松比 ν通常在 0. 3 以
Ξ 基金项目 : 香港 RGC - CA99/ 00 ,EG01 及武汉市科委 991002024 资
tanφc = ( tanφ) / f s
( 1)
在用有限元法寻找 f s 时 ,通常需要求解一系列具
3 强度折减系数 Zi 与弹性常数 E ,ν之
间的关系
一般情况下 ,一种岩石的强度参数 c 和φ 越高 ,其 弹模 E 越高 ,泊松比 ν越低 。如硬岩的弹模 E 通常以
GPa 为单位 , 泊松比 ν通常在 0. 25 以下 ; 而软岩和土
2 安全系数的有限元方法
基于强度储备概念的安全系数 f s 的定义为 : 当材 料的抗剪强度参数 c 和φ分别用其临界强度参数 cc 和 φc 所代替后 ,结构将处于临界平衡状态 ,其中
sinφ ≥1 - 2ν
( 3)
为式 ( 6 ) 已经定义了 ν i 的变化规律 。按照下式定义
Ei :
ν = Const Eν i i = E
( 8)
式中 E 和ν为岩石真实的参数 。需指出的是 , 式 ( 8) 仅是为了满足 “强度越高 , E 越高而ν 越低”而建议 的 , 尚缺乏必要的力学基础 。事实上 , 即使不对 E 作 调整 , 只要能确保式 ( 3) 成立 , 则仍然可以得到令人满 意的安全系数 。
用文献 [ 8 ] 建议的位移控制法 ( DCM) 求解了本问 题 , 与经典的载荷控制法 (LCM) 相比 , DCM 有更好的收 敛性和稳定性 。本构积分采用了文献 [ 9 ] 建议的自适 应算法 。 图 2 给出了不对 E ,ν作调整和按照式 ( 9) 对 E ,ν 作调整的塑性区分布图 。这里的塑性区是基于 Gauss 点的状态而绘制的 , 即当一个四边形单元内的任意一
助项目 收稿日期 :2001 - 10 - 20
© 1995-2004 Tsinghua Tongfang Optical Disc Co., Ltd. All rights reserved.
第5期
郑 宏 , 等 1 求解安全系数的有限元法
627
上 。然而 ,迄今为止 , 在利用有限元法寻求安全系数 时 ,都仅仅是对强度参数 c 和φ 折扣 ,没有考虑随着强 度参数的降低 ,应对刚度参数 E 和ν作相应调整 。下 面证明这样做是有问题的 。 首先证明岩石类材料 , 若其满足 Mohr2Coulomb 准 则 ,则其摩擦角 φ 和泊松比ν应满足不等式 :
否则 ,若 sinφ < 1 - 2ν ,则该半无限空间或受约岩柱 内 ,一定深度以下的岩石都将处于塑性状态 ; 特别地 , 若 c = 0 ,则整个半无限空间或岩柱都处于塑性状态 , 而这显然有违于实际情况 。故对满足 Mohr2Coulomb 准 则的岩石类材料 ,其摩擦角 φ 和泊松比ν之间必存在 关系式 ( 3) 。笔者查阅的岩石大都满足式 ( 3) 。 基于以上分析 ,在对边坡进行有限元分析时 ,如果 仅对强度参数 c 和φ 折扣 ,很多情况下塑性区将首先 出现在边坡深部而不是边帮 ; 当 c 和φ 值降低到一定 程度时 ,由于深部的塑性区已经贯通了整个模型 ,导致 计算结果不收敛 ,而潜在滑移通道上的塑性区却可能 尚未贯通 ,从而使得计算出来的安全系数偏小 。 在对强度参数 c 和 φ 折扣时 , 为了保持式 ( 3) 成 立 ,可假定始终有如下关系式成立 : sinφi = β( 1 - 2ν i)
郑 宏1 ,2 ,李春光2 ,李焯芬3 ,葛修润2
(1. 三峡大学 ,湖北 宜昌 443002 ; 2. 中国科学院武汉岩土力学研究所 ,湖北 武汉 430071 ; 3. 香港大学 土木工程系 ,香港)
摘 要 : 分析了目前在利用弹塑性有限元法求解安全系数时所存在的一些问题 ,指出在对强度参数折扣的同时 ,必需满足 φ 和ν不 等式 : sinφ ≥1 - 2ν ,才能使所求得的安全系数接近于经典的极限平衡法 。 关键词 : 安全系数 ; 有限元 ; 极限平衡 中图分类号 :TU 457 文献标识码 :A 文章编号 :1000 - 4548 (2002) 05 - 0626 - 03 作者简介 : 郑 宏 ,男 (1964 - ) ,博士 ,三峡大学特聘教授 ,中国科学院武汉岩土力学研究所研究员 。1985 年毕业于东北工学院机械 系 ,现从事岩土力学数值分析研究和软件开发 。
Mohr2Coulomb 准则 ,即
( 1 + sinφ) σ )σ 1 - ( 1 - sinφ 3 ≤2 ccosφ ( 5)
将式 ( 4) 代入式 ( 5) ,同时令 h → ∞ ,得
sinφ ≥ 1 - K ν பைடு நூலகம் 1 - 2 1 + K
束分析 , 否则取一个新的强度折减系数 Zi 重复 ( 2) 步 。
