六年级奥数 阴影图形面积(三角形专练)
六年级奥数练习(阴影面积)1

六年级奥数练习题(圆和组合图形)1、算出圆内正方形的面积为多少2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是多少平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是多少4.右图中三角形是等腰直角三角形,阴影部分的面积是(平方厘米).5.三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB长40厘米, BC长厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积为 .7.扇形的面积是平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是度.8.图中扇形的半径OA=OB=6厘米.45=∠AOB, AC垂直OB于C,那么图中阴影部分的面积是平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是平方厘米.12.如图,半圆S1的面积是平方厘米,圆S2的面积是平方厘米.那么长方形(阴影部分的面积)是多少平方厘米13.如图,已知圆心是O,半径r=9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米)14.3(≈π13、如图,求阴影部分的面积 .14、大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大平方厘米.212112215、在一个半径是厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取,结果精确到1平方厘米)16、如图所求,圆的周长是厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π17.下图中正方形部分是一个水池,其余部分是草坪,已知正方形的面积是300平方米,草坪的面积是多少平方米17、已知:ABCD 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .18、如图:阴影部分的面积是多少四分之一大圆的半径为r .(计算时圆周率取722)19、已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.20.如图{图在下面}两个连在一起的轮轴,已知小轮的半径是3分米,当这个小轮转3圈时,大轮正好转一圈,只蜜蜂分别沿着阴影部分的边缘飞1次,那只蜜蜂飞过的路线最长(3个正方形的边长都为4m )23.将半径分别是3厘米和2厘米的两个半圆如图放置,求阴影部分的周长24.求阴影部分的面积25.一个圆环外直径是内直径的二分之三倍,圆环面积150cm ,求外圆的面积26.一个长方形的面积是20平方厘米,如果在这个长方DCB AGF形里画一个最大的半圆形,这个半圆形是多少平方厘米因为这个半圆的直径是长方形的长,半径是宽,说明长方形的长是宽的2倍。
六年级奥数---阴影部分的面积
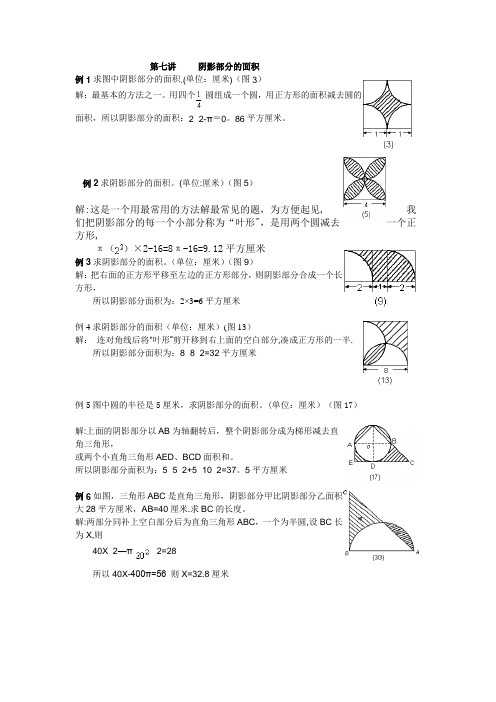
第七讲阴影部分的面积例1求图中阴影部分的面积.(单位:厘米)(图3)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0。
86平方厘米。
例2求阴影部分的面积。
(单位:厘米)(图5)解:这是一个用最常用的方法解最常见的题,为方便起见, 我们把阴影部分的每一个小部分称为“叶形",是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米例3求阴影部分的面积。
(单位:厘米)(图9)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例4求阴影部分的面积(单位:厘米)(图13)解:连对角线后将"叶形”剪开移到右上面的空白部分,凑成正方形的一半.所以阴影部分面积为:8×8÷2=32平方厘米例5图中圆的半径是5厘米,求阴影部分的面积。
(单位:厘米)(图17)解:上面的阴影部分以AB为轴翻转后,整个阴影部分成为梯形减去直角三角形,或两个小直角三角形AED、BCD面积和。
所以阴影部分面积为:5×5÷2+5×10÷2=37。
5平方厘米例6如图,三角形ABC是直角三角形,阴影部分甲比阴影部分乙面积大28平方厘米,AB=40厘米.求BC的长度。
解:两部分同补上空白部分后为直角三角形ABC,一个为半圆,设BC长为X,则40X÷2—π÷2=28所以40X-400π=56 则X=32.8厘米例8。
求阴影部分的面积.(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米巩固练习:1求阴影部分的面积.(单位:厘米)(图7)2.大正方形的边长为6厘米,小正方形的边长为4厘米。
求阴影部分的面积。
(图32)3。
六年级下册奥数试题-几何专题 全国通用(含答案) (1)

小学奥数几何专题1、(★★)如图,已知四边形ABCD 中,AB=13,BC=3,CD=4,DA=12,并且BD 与AD 垂直,则四边形的面积等于多少?[思 路]:显然四边形ABCD 的面积将由三角形ABD 与三角形BCD 的面积求和得到.三角形ABD 是直角三角形,底AD 已知,高BD 是未知的,但可以通过勾股定理求出,进而可以判定三角形BCD 的形状,然后求其面积.这样看来,BD 的长度是求解本题的关键.解:由于BD 垂直于AD ,所以三角形ABD 是直角三角形.而AB=13,DA=12,由勾股定理,BD 2=AB 2-AD 2=132—122=25=52,所以BD=5.三角形BCD 中BD=5,BC=3,CD=4,又32十42=52,故三角形BCD 是以BD 为斜边的直角三角形,BC 与CD 垂直.那么:ABCD S 四边形=ABD S ∆+BCD S∆=12×5÷2+4×3÷2=36.. 即四边形ABCD 的面积是36. 2、(★★)如图四边形土地的总面积是48平方米,三条线把它分成了4个小三角形,其中2个小三角形的面积分别是7平方米和9平方米.那么最大的一个三角形的面积是________平方米;[分析]:剩下两个三角形的面积和是 48-7-9=32 ,是右侧两个三角形面积和的2 倍,故左侧三角形面积是右侧对应三角形面积的2倍,最大三角形面积是 9×2=18。
3.(★★)将下图中的三角形纸片沿虚线折叠得到右图,其中的粗实线图形面积与原三角形面积之比为2:3。
已知右图中3个阴影的三角形面积之和为1,那么重叠部分的面积为多少?[思 路]:小升初中常把分数,百分数,比例问题处理成份数问题,这个思想一定要养成。
解:粗线面积:黄面积=2:3绿色面积是折叠后的重叠部分,减少的部分就是因为重叠才变少的,这样可以设总共3份,后来粗线变2份,减少的绿色部分为1份,所以阴影部分为2-1=1份,7 94、(★★)求下图中阴影部分的面积:【解】如左下图所示,将左下角的阴影部分分为两部分,然后按照右下图所示,将这两部分分别拼补在阴影位置。
【奥数题】人教版小学数学六年级上册三角形中的计算奥数思维拓展(试题)含答案与解析
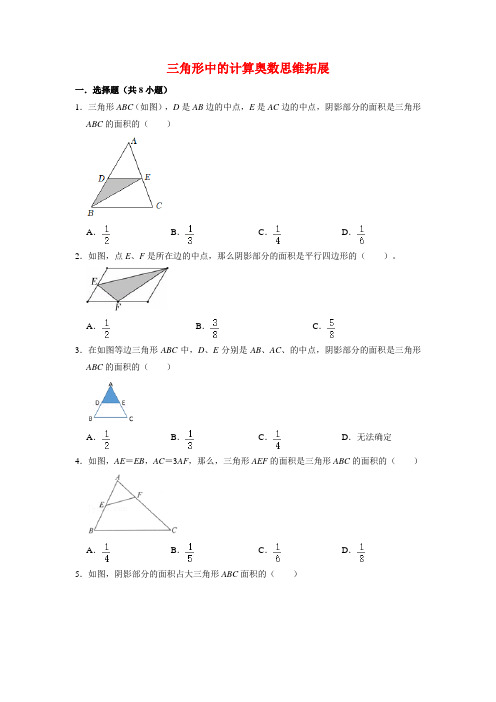
三角形中的计算奥数思维拓展一.选择题(共8小题)1.三角形ABC(如图),D是AB边的中点,E是AC边的中点,阴影部分的面积是三角形ABC的面积的()A.B.C.D.2.如图,点E、F是所在边的中点,那么阴影部分的面积是平行四边形的()。
A.B.C.3.在如图等边三角形ABC中,D、E分别是AB、AC、的中点,阴影部分的面积是三角形ABC的面积的()A.B.C.D.无法确定4.如图,AE=EB,AC=3AF,那么,三角形AEF的面积是三角形ABC的面积的()A.B.C.D.5.如图,阴影部分的面积占大三角形ABC面积的()A.B.C.D.无法确定6.如图,把三角形ABC的一条边延长一倍到D,把它的另一条边延长2倍到E,得到一个较大的三角形,那么,三角形ABC的面积是三角形ADE的面积的()A.B.C.D.7.如图中,DE=2BE,那么阴影部分面积是长方形面积的()A.B.C.8.如图,在三角形ABC中,E、D、G分别是AB、BC、AD的中点,图中与三角形ADE面积相等的三角形还有()A.0个B.1个C.2个D.3个二.填空题(共8小题)9.如图中阴影部分的面积是12平方厘米,BD:CD=4:5,三角形ADC的面积是平方厘米。
10.如图,三角形ABC的面积27cm2,,三角形AED的面积是cm2。
11.如图,AD=DB,AE=EF=FC。
已知阴影部分的面积是5平方厘米,三角形ABC的面积是平方厘米。
12.如图,直角梯形ABCD的上底是5厘米,下底是7厘米,高是4厘米,且三角形ADE、ABF和四边形AECF的面积相等,则三角形AEF的面积是.13.如图每个小长方形的长2厘米,宽1厘米,阴影部分面积占长方形面积的%.14.在△ABC中,BD=2DC,AE=BE,已知△ABC的面积是18平方厘米,则四边形AEDC的面积等于平方厘米。
15.如图梯形中E是BC的中点,F是DC的中点,线段EF把梯形分成甲、乙两个部分,面积比是21:4,那么梯形的上底AB与下底CD的长度比是。
小学数学奥数六年级阴影面积练习题

阴影面积(二)例题讲解例1、如图,直角三角形ABC的面积是45,分别以B、C为圆心,3为半径画圆。
己知图中阴影部分的面积是35. 58。
请问:∠A是多少度?(π取3.14)练习2、如图,三角形ABC是一个等腰三角形,它的面积等于200。
分别以B、C 为圆心,6为半径画圆。
已知图中阴影部分的面积是168.6。
请问:∠A是多少度?(π取3.14)例3 、如图(1)是一个直径是6厘米的半圆,AB是直径。
如图(2)所示,让A点不动,把整个半圆逆时针转600,此时B点移动到C点。
请问:图中阴影部分的面积是多少平方厘米?(π取3.14)练习3、如图(1)是一个半径为4厘米的半圆,AB是直径。
如图(2)所示,让A点不动,把整个半圆顺时针转300,此时B点移动到C点。
请问:图中阴影部分的面积是多少平方厘米?(π取3.14,结果保留2 位小数)例4、如图,一只小狗被拴在一个边长为4米的正方形的建筑物的一个顶点处,四周都是空地。
绳长刚好够小狗走到建筑物外墙边的任一位置,小狗的活动范围能有多少平方米?(建筑外墙不可逾越,小狗身长忽略不计,π取3.14)练习4、如图,一只猫被拴在一个边长为4米的正五边形建筑物的一个顶点处,四周都是空地。
绳长刚好够猫走到建筑物外墙边的任一位置,猫的活动范围能有多少平方米?(建筑外墙不可逾越,猫身长忽略不计,π取3.14)例5 、如图(1),正方形的边长是4厘米,圆形的半径是1厘米。
当圆形绕正方形滚动一周又回到原来位置时,扫过的面积有多大?(π取3.14)(2)如图,等边三角形的边长是6厘米,而圆形的半径是l厘米。
当圆形绕等边三角形滚动一周又回到原来位置时,其扫过的面积有多大?(π取3.14)练习5、如图,正方形的边长是2厘米,圆形的半径是1厘米。
当圆形绕正方形滚动一周又回到原来位置时,扫过的面积有多大?(π取3.14)过手练习1、如图,三角形ABC为等边三角形,边长为2,D为BC边中点。
小学奥数-三角形的面积竞赛题

图形的面积竞赛题1. 如下图,把三角形ABC的一条边AB延长1倍到D,把它的另一边AC延长2倍到E,得到一个较大的三角形ADE,三角形ADE的面积是三角形ABC面积的______倍.2. 如下图,在三角形ABC中, BC=8厘米, AD=6厘米,E、F分别为AB和AC的中点.那么三角形EBF的面积是______平方厘米.4. 下图中,三角形ABC的面积是30平方厘米,D是BC的中点,AE的长是ED的长的2倍,那么三角形CDE的面积是______平方厘米.5. 现有一个5×5的方格表(如下图)每个小方格的边长都是1,那么图中阴影部分的面积总和等于______.6. 下图正方形ABCD边长是10厘米,长方形EFGH的长为8厘米,宽为5厘米.阴影部分甲与阴影部分乙的面积差是______平方厘米.7. 如图所示,一个矩形被分成A、B、C、D四个矩形.现知A的面积是2cm2,B的面积是4cm2,C的面积是6cm2.那么原矩形的面积是______平方厘米.8. 有一个等腰梯形,底角为450,上底为8厘米,下底为12厘米,这个梯形的面积应是______平方厘米.9. 已知三角形ABC的面积为56平方厘米、是平行四边形DEFC的2倍,那么阴影部分的面积是______平方厘米.10. 如图,长方形ABCD中, AB=24cm,BC=26cm,E是BC的中点,F、G分别是AB、CD的四等分点, H为AD上任意一点,求阴影部分面积.11、下图所示,ABCD是边长为8厘米的正方形,三角形ABF的面积比三角形CEF的面积大10平方厘米,阴影部分的面积是多少平方厘米?12、正方形ABCD的边长是4厘米,CG=3厘米,长方形DEFG的长DG=5厘米,那么它的宽DE是多少厘米。
13、如右图大小两个长方形对应边的距离均为5厘米。
如果两个长方形之间的面积为600平方厘米,那么小长方形的周长是多少厘米?14、如右图,长方形ABCD中,阴影部分的面积和是15平方厘米,四边形EFGH 的面积是多少平方厘米?13、四个相同的长方形拼成一个面积为100平方厘米的大正方形,每个长方形的周长是多少厘米?8、下图所示,ABCD 是边长为8厘米的正方形,三角形ABF 的面积比三角形CEF 的面积大10平方厘米,阴影部分的面积是多少平方厘米?13. 有两张正方形纸,它们的边长都是整厘米数,大的一张的面积比小的一张多44平方厘米.大、小正方形纸的边长分别是多少?10. 下图中,在长方形内画了一些直线,已知边上有三块面积分别是13,35,49.那么图中阴影部分的面积是______.3. 如下图,,41,31AC CD BC BE ==那么,三角形AED 的面积是三角形ABC 面积的______.二、解答题11.已知正方形的面积是50平方厘米,三角形ABC两条直角边中,长边是短边的2.5倍,求三角形ABC的面积.1、右图,平行四边形ABCD中,E、F分别是AD、CD的中点。
(完整版)六年级奥数练习(阴影面积)1
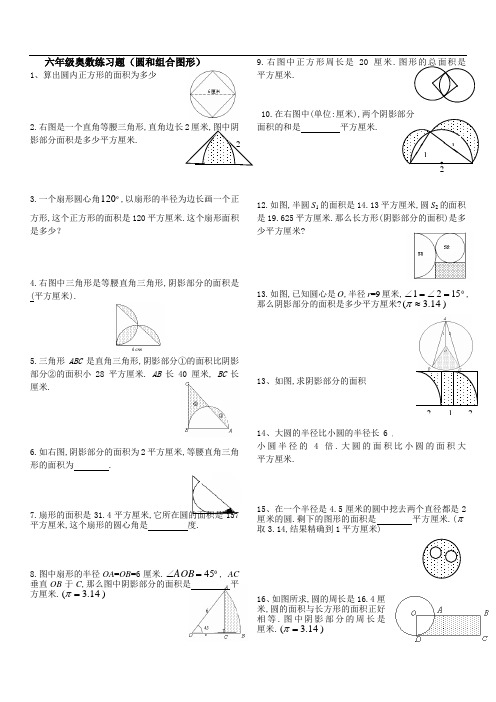
六年级奥数练习题(圆和组合图形)1、算出圆内正方形的面积为多少 2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是多少平方厘米. 3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是多少? 4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB 长40厘米, BC 长厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积为 .7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是平方厘米. 10.在右图中(单位:厘米),两个阴影部分 面积的和是 平方厘米.12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π13、如图,求阴影部分的面积 .14、大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面平方厘米.15、在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)16、如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是厘米.)14.3(=π2 1 2112217.下图中正方形部分是一个水池,其余部分是草坪,已知正方形的面积是300平方米,草坪的面积是多少平方米?17、已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .18、如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率取722)19、已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.20.如图{图在下面}两个连在一起的轮轴,已知小轮的半径是3分米,当这个小轮转3圈时,大轮正好转一圈,21.3只蜜蜂分别沿着阴影部分的边缘飞1次,那只蜜蜂飞过的路线最长?(3个正方形的边长都为4m )23.将半径分别是3厘米和2厘米的两个半圆如图放置,求阴影部分的周长24.求阴影部分的面积25.一个圆环外直径是内直径的二分之三倍,圆环面积150cm ,求外圆的面积26.一个长方形的面积是20平方厘米,如果在这个长方形里画一个最大的半圆形,这个半圆形是多少平方厘米?因为这个半圆的直径是长方形的长,半径是宽,说明长方形的长是宽的2倍。
小学六年级阴影部分面积专题复习经典例题(含答案)

小学六年级阴影部分面积专题复习经典例题(含答案)欢迎下载研究必备资料,本文主要涉及组合图形的面积计算。
以下是各题的解答和点评:1.求如图阴影部分的面积。
(单位:厘米)分析:阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积。
利用梯形和半圆的面积公式代入数据即可解答。
解答:$(4+6)\times4\div2\div2-3.14\times2^2=10-6.28=3.72$(平方厘米)。
答案:阴影部分的面积是3.72平方厘米。
点评:组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用。
2.如图,求阴影部分的面积。
(单位:厘米)分析:根据图形可以看出,阴影部分的面积等于正方形的面积减去4个扇形的面积。
正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积。
解答:扇形的半径是:$10\div2=5$(厘米);$10\times10-3.14\times5\times5=100-78.5=21.5$(平方厘米)。
答案:阴影部分的面积为21.5平方厘米。
点评:组合图形的面积计算需要注意各部分之间的关系,特别是涉及到圆形时需要注意半径的计算。
3.求如图阴影部分面积。
(单位:厘米)解答:该题缺少图形,无法回答。
4.求出如图阴影部分的面积:单位:厘米。
解答:该题缺少图形,无法回答。
5.求如图阴影部分的面积。
(单位:厘米)解答:该题缺少图形,无法回答。
6.求如图阴影部分面积。
(单位:厘米)解答:该题缺少图形,无法回答。
7.计算如图中阴影部分的面积。
单位:厘米。
解答:该题缺少图形,无法回答。
8.求阴影部分的面积。
单位:厘米。
解答:该题缺少图形,无法回答。
9.如图是三个半圆,求阴影部分的周长和面积。
(单位:厘米)分析:阴影部分可以看成是两个半圆和一个矩形组成的,可以分别计算各部分的周长和面积再相加。
解答:矩形的长和宽分别为$8-4\pi$和$4$,面积为$(8-4\pi)\times4=32-16\pi$(平方厘米);半圆的半径为$4$,周长为$2\pi r=8\pi$(厘米),面积为$\pi r^2=16\pi$(平方厘米)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
阴影图形面积···(一)三角形专练
一、知识要点
1、计算平面图形的面积时,有些问题在已知条件与所求问题之间找不出任何联系,会使你感到
无从下手。
这时,如果我们能认真观察图形,分析、研究已知条件,并加以深化,再运用我们已有的基本几何知识,适当添加辅助线,搭一座连通已知条件与所求问题的小“桥”,便会使你顺利达到目的。
有一些平面图形的面积计算必须借助于图形本身的特点,添加一些辅助线,运用平移旋转、剪拼组合等方法,对图形进行恰当合理的变形,在经过分析推导,才能寻求出解题的途径。
2、对于三角形的面积一般有以下几种变换关系:
等底等高的三角形面积相等;等底的三角形面积比等于高之比;等高的三角形面积比等于底之比。
很多四边形的面积都可以转换成三角形面积 3、对于圆的面积变换关系:
圆面积比等于半径比的平方;熟练掌握圆环的面积;外圆内方的面积;外方内圆的面积
二、例题精讲
例1 已知如图,ABC ∆的面积是82cm 。
ED AE =,BC BD 3
2
=。
求阴影部分的面积。
(阴影部分为AEF ∆和BED ∆)
【思路导航】阴影部分为两个三角形,但AEF ∆的面积无法直接计 算。
由于ED AE =,连接DF ,可知EDF AEF S S ∆∆=(等底等高) 采用移补的方法,将所求阴影部分转化为求三角形BDF 的面积。
因为BC BD 3
2
=
,所以DCF BDF S S ∆∆=2。
又因为ED AE =,所以 =∆ABF S DCF BDF S S ∆∆=2。
因此,DCF ABC S S 5=∆。
由于28cm S ABC =∆,所以26.158cm S DCF =÷=∆,则阴影
部分的面积为22.326.1cm =⨯。
B
A
F
D
E
C
课堂练习
1、如图(1)所示,ED AE =,BD BC 3=,2
30cm S ABC =∆。
求阴影部分的面积。
(阴影部分为AEF ∆和BED ∆)
图(1)
2、如图(2)所示,ED AE =,BD DC 31
=,221cm S ABC =∆。
求阴影部分的面积。
(阴影部分为AEF ∆和BED ∆)
图(2)
3、如图(3)所示,AE DE 2
1
=,DC BD 2=,25cm S EBD =∆。
求三角形ABC 的面积。
A
B
C
D
F
E
B
A
F D
E
C
B
A
F
D
E
C
图(3)
例2 如图所示,在三角形ABC 中,三角形ACD DCE BDE ,,的面积分别是902cm ,302cm ,282cm 。
那么三角形ADE 的面积所多少?
【思路导航】解法一:BCD BDE ∆∆和的面积比是
4
3
309090=+=∆∆BCD BDE S S , 以BD 为底的这两个三角形高的比等于它们的面积比,这样 以AD 为底的ADE ACD ∆∆和的高之比也是
4
3
, ADE ACD ∆∆和的面积比等于高的比:
43=∆∆ACD ADE S S ,所以2214
3
28cm S ADE =⨯=∆。
解法二:BDC ADC ∆∆和同高,
30
7309028=+=∆∆BDC ADC S S ,则30:7:=BD AD ,BDE ADE ∆∆与同高,307==∆∆BD AD S S BDE ADE ,22130
7
90cm S ADE =⨯=∆。
课堂练习
如图所示,在三角形ADE 中,三角形CDE BCE ABC ,,的面积分别是502cm ,242cm ,372cm 。
求三角形BDC 的面积。
例3 如图所示,四边形ABCD 的对角线BD 被F E ,两点三等分,且四边形AECF 的面积是152cm 。
求四边形ABCD 的面积。
【思路导航】由于F E ,三等分BD ,所以三角形AFD AEF ABE ,,是
E
A
D
B E C
A
C
D
E
B
A
D
F
等底等高的三角形,它们的面积相等。
同理,三角形CFD CEF CBE ,,的 面积也相等,由此可知,三角形ABD 的面积是三角形AEF 面积的3倍, 三角形BCD 的面积是三角形CEF 面积的3倍,从而得出四边形ABCD 的面积是四边形AECF 面积的3倍。
245315cm =⨯
课堂练习
1、如图所示,四边形ABCD 的对角线BD 被G F E ,,三点四等分,且四边形AECG 的面积为152cm 。
求四边形ABCD 的面积。
2、如图所示,已知四边形ABCD 的对角线BD 被G F E ,,三点四等分,且阴影部分(四边形DEBF )的面积为152cm 。
求四边形ABCD 的面积。
3、如图所示,正方形ABCD 的边长24cm ,F E ,分别是BC CD , 的中点,BE 与DF 交于点G 。
求阴影部分(BFG ∆)的面积。
F E
.
G A
B
C
D
F
A
D
G
.
E
B C
A
B
C
D
E
F
G
例4 如图所示,DO BO 2=,阴影部分(OBC ∆)的面积是42
cm ,那么梯形ABCD 的面积是多少?
【思路导航】因为DO BO 2=,取BO 中点E ,连接AE 。
根据 三角形等底等高面积相等的性质。
可知CDA DBC S S ∆∆=,
2
4cm S S DOA COB ==∆∆,类似可得每个三角形的面积。
所以,
2224cm S CDO =÷=∆,2
1234cm S DAB =⨯=∆
2182412cm S ABCD =++=梯形。
课堂练习
1、如图所示,阴影部分(AOD ∆)的面积是42
cm ,AO OC 2=。
求梯形ABCD 的面积。
2、如图所示,已知AO OC 2=,2
14cm S BOC =∆。
求梯形ABCD 的面积。
A
B
C
D
O
A
B
C
D
O
A B
C
D
O
3、如图所示,已知2
6cm S AOB =∆,AO OC 3=。
求梯形ABCD 的面积。
例5 如图所示,长方形ADEF 的面积是16,三角形ADB 的面积是3,三角形ACF 的面积是4,求三角形ABC 的面积是。
【思路导航】连结AE (如图5.57),则三角形AEC 的面积是16÷2-4=4。
因为△ACF 与△AEC 等高,且面积相等。
所以,CF=CE 。
同理,△ABE 的
面积是16÷2-3=5,则BD :BE=3:5。
即AF DE BE 85
85==。
BCE ∆与
ACF ∆等高,所以5.28
5
4=⨯=∆BCE S 。
从而,△ABC 的面积是16-(3+4+2.5)
=6.5。
课堂练习
1、如图所示,长方形ABCD 的面积是202
cm ,三角形ADF 的面积是52
cm ,三角形ABE 的面积
是72
cm 。
求三角形AEF 的面积。
2、如图所示,长方形ABCD 的面积是202
cm ,226,4cm S cm S AFD ABE ==∆∆。
求三角形AEF A B
C
D
O
A
B
C
D E
F
A
D
3、如图所示,长方形ABCD 的面积是242
cm ,24cm S S AFD ABE ==∆∆,求三角形AEF 的面积。
A
B
C
D E
F。
