高一数学《正弦函数、余弦函数的性质》(课件)
合集下载
5.3.1正弦函数余弦函数的图象与性质(第1课时)课件高一上学期数学

π
的图象向右平移 个单位长度,得到
2
g(x)的图象.
3.函数y=1-sin x,x∈[0,2π]的大致图象是( B )
1 2 3 4 5 6 7 8 9 10
解析 当 x=0 时,y=1;当
当
3π
x= 时,y=2;当
2
π
x=2 时,y=0;当
x=π 时,y=1;
x=2π 时,y=1.结合选项中的图象可知 B 正确.故选 B.
π
3
2
2π
0
1
1
2
3
规律方法
用“五点法”画函数y=Asin x+b(A≠0)或y=Acos x+b(A≠0)在[0,2π]
上的简图的步骤.
(1)列表:
x
0
sin x(或cos x) 0(或1)
y
π
2
1(或0)
b(或A+b) A+b(或b)
π
3π
2
2π
0(或-1)
-1(或0)
0(或1)
b(或-A+b)
解 将 y= 1-cos 2 化为 y=|sin x|,
即 y=
sin(2π ≤ ≤ π + 2π,∈Z),
-sin(π + 2π < < 2π + 2π,∈Z).
因此首先作出函数y=sin x的图象,然后将图象在x轴下方的部分翻折到上
方即可得到函数y=|sin x|的图象,其图象如图所示.
x的取值集合为
解析 当
π
2
,m),则m=
2π
4π
{x∣ 3 +2kπ<x< 3 +2kπ,k∈Z}
5.3.1正弦函数余弦函数的图象与性质(第2课时)课件高一上学期数学

变式训练1
求函数y=cos|x|的最小正周期.
解 因为cos(-x)=cos x,所以y=cos|x|=cos x,从而函数y=cos|x|与y=cos x的图
象一样,因此周期相同,为2π.
探究点二
正弦、余弦函数的最值(值域)
1.正、余弦函数的最值的理解
【例2】 求函数y=4-cos 3x取得最大值、最小值时的自变量x的集合,并分
π
f(x+2 )=
sin( +
即函数满足
π
)
2
+ cos( +
π
)
2
=|cos x|+|-sin x|=|cos x|+|sin x|=f(x),
π
π
f(x+2 )=f(x),因此函数的一个周期是2 ,因此选
BCD.
1 2 3 4
2.函数y=3-sin ax(a≠0,x∈R)的值域是( B )
别写出最大值、最小值.
解 ∵-1≤cos 3x≤1,
∴-1≤-cos 3x≤1.
∴3≤4-cos 3x≤5.
∴当 cos 3x=-1 时,3x=2kπ+π,即
2π
x=
3
y 取得最大值 5,相应的自变量 x
2π
的集合为{x|x=
3
当 cos 3x=1 时,3x=2kπ,即
+
π
(k∈Z)时,
3
+
π
求形如y=asin2x+bsin x+c,a≠0,x∈R的函数的值域或最大(小)值时,可以通
过换元,令t=sin x,将原函数转化为关于t的二次函数,利用配方法求值域或
5.4.2 正弦函数、余弦函数的性质(2)课件高一上学期数学人教A版(2019)必修第一册

例题讲解 LOGO
例5 求下列函数的最大值,最小值,并写出取最值时自变量x的集合.
(1)y cos x 1, x R;(2)y 3sin 2x, x R.
整体代换
【解析】(2)令z=2x,使函数y=-3sin 2x取得最大值的x的集合,
就是使y=sin z取得最小值的z的集合z z
由
2x
z
1
2
探究新知 LOGO
例7 求下列函数的值域:
(1) y 3 2 cos(2x );(2) y cos2 x 4 cos x 5.
3
解:(1) -1 cos(2x ) 1-2 2 cos(2x ) 2,
3
3
1 3 2 cos(2x ) 5,即y=3 2 cos(2x )的值域为[1,5].
3
3
(2) y cos2 x 4 cos x 5 (cos x 2)2 1,
令t cos x,则t [1,1]
y (t 2)2 1在[1,1]上单调递减
当t= 1时,ymax (1 2)2 1 10 当t=1时,ymin (1 2)2 1 2 故y cos2 x 4 cos x 5的值域为[2,10].
课堂练习 LOGO
1.求函数y=2sin( x),x∈R 的单调递增区间;
4
解:y
2 s in(
x)
2sin(x
)
4
4
由 2k x 3 2k (k Z), 得 3 2k x 7 2k (k Z)
2
42
4
4
故y 2sin( - x)的单调增区间为[3 2k , 7 2k ](k Z ).
课堂练习 LOGO
课堂小结 LOGO
课堂小结
1.4.1(公开课课件)正弦函数、余弦函数的图像

实 一 一对应
唯一确定
角
正 弦
数
一对多 值
定义:任意给定的一个实数x,有唯一确定的值sinx与 之对应。由这个法则所确定的函数 y=sinx叫做正弦
函数,y=cosx叫做余弦函数,二者定义域为R。
第3页,共28页。
二、正弦函数 y =sinx(x∈R)的图象
1.几何法作图:
问题:如何作出正弦函数的图象?
(3) 连线(用光滑的曲线顺次连结五个点)
1-
-
-
-1
o
6
2
3
2 3
5
7
6
6
4 3
3 5 23
-1 -
第26页,共28页。
图象的最高点
(0,1) (2 ,1)
与x轴的交点
11 6
2
x
(
2
,0)
(
3 2
,0)
图象的最低点 ( ,1)
课堂小结
1.正、余弦函数的图象每相隔2π个单位重复出现,因此, 只要记住它们在[0,2π]内的图象形态,就可以画出正弦 曲线和余弦曲线.
正弦函数、余弦函数的图象
第1页,共28页。
1.正弦线、余弦线的概念
设任意角α的终 边与单位圆交于点P. 过点P做x轴的垂线, 垂足为M.
则有向线段MP叫做角α的正弦线. 有向线段OM叫做角α的余弦线.
2. 三角函数值的符号判断
y α 的终边
P(x,y)
oMx
第2页,共28页。
一、正弦函数的定义:
有何联系?
第17页,共28页。
练习:(1)作函数 y=1+3cosx,x∈[0,2π]的简图 (2)作函数 y=2sinx-1,x∈[0,2π]的简图
高中数学必修一课件:正弦函数、余弦函数的性质(第1课时)

∴函数f(x)=sin34x+3π 2 为偶函数.
③f(x)=
(1-cos2x)+sin 1+sin x
x
=
sin2x+sin 1+sin x
x
=sin
x,但函数应满足1+sin
x≠
0,∴函数的定义域为{x|x∈R,且x≠2kπ+32π,k∈Z}.
∵函数的定义域不关于原点对称,
∴该函数既不是奇函数也不是偶函数.
思考题3 (1)判断下列函数的奇偶性.
①f(x)=sin
x-tan x
x;
②f(x)=lg(1-sin x)-lg(1+sin x);
③f(x)=1-cossi2nx
; x
④f(x)= 1-cos x+ cos x-1.
【答案】 ①偶函数 ②奇函数 ③非奇非偶函数 ④既是奇函数又是偶 函数
(2)函数f(x)=7sin(23x+152π)是( A )
(2)若本例(1)中的“偶函数”改为“奇函数”,“π”改为“
11π 12
”,其他
条件不变,结果如何?
【解析】 f5π 3 =f5π 3 -111π2 ×2=f-π6 =-fπ6 =-sin π6 =-12.
(3)若本例(1)中的条件不变,求当x∈[-π,0]时函数的解析式.
【解析】 因为f(x)是偶函数,所以f(-x)=f(x), 因为x∈0,π2 时,f(x)=sin x, 所以当x∈-π2 ,0时,-x∈0,π2 ,所以 f(-x)=sin(-x)=-sin x=f(x), 即当x∈-π2 ,0时,f(x)=-sin x,
π (2)已知函数f(x)= 2sin(x+ 4 +φ)是奇函数,则φ的值可以是( B )
A.0
B.-π4
《余弦函数、正切函数的图像与性质》课件1

,0 2
正切函数y=tanx的主要性质: x | x , 1. 定义域: 2 2.值域:实数集R. 3.周期性:周期是π. 4.奇偶性:由tan(-x)=-tan(x),知正切函 数是奇函数,它的图象关于原点成中心 对称. 5.单调性:正切函数在每一个开区间 , 内都是增函数.
• 小结 1.通过本节学习,应掌握余弦函数 图象的画法.
2.会用“五点法”画出余弦曲线简图. 3.能结合余弦函数图象理解余弦函数的 性质(定义域、值域、周期性、奇偶性、 单调性)
正切函数的图象与性质
• 学习目标 1.理解利用正切线画出正切函数图象 的方法 2.掌握正切函数的图象与性质 3.会画正切函数简图
• 课堂练习二 1.判断下列函数的奇偶性 (1)f(x)=|x|+cosx; (2)f(x)=sinx+cosx; (3)f(x)=cosx|sinx|+sinx|cosx|. 2.已知f(x)是定义在R上的奇函数, 且x>0时, f(x)=sinx+cosx,则在定义域R 上,f(x)=___________. 3.已知函数y=a-bcos3x的最大值为6,最小值为-2, 求a,b的值. 4.求y=cos2x的单调区间. 5.教材56页-4,5.
• 学法指导: 1. 余弦曲线是中心对称图形,其所有的 ,0 对称中心坐标是_____________ ; 2 2.余弦曲线是轴对称图形,其所有的对 x , 称轴方程是_______________. 余弦曲线的对称轴一定是过余弦曲线的 最高点或最低点,此时余弦值为最大值 或最小值.
• 余弦型函数 y Acosx A0, 0的 2 定义域R;值域[-A,A];周期 T . 当 时 y Acos(x ) 为偶函数, 当 2 时y Acos(x )为奇函数; 对称轴由x 求得 x 对称中心横坐标由 x 求得. 2 其单调区间求法与正弦型函数相同。
正切函数y=tanx的主要性质: x | x , 1. 定义域: 2 2.值域:实数集R. 3.周期性:周期是π. 4.奇偶性:由tan(-x)=-tan(x),知正切函 数是奇函数,它的图象关于原点成中心 对称. 5.单调性:正切函数在每一个开区间 , 内都是增函数.
• 小结 1.通过本节学习,应掌握余弦函数 图象的画法.
2.会用“五点法”画出余弦曲线简图. 3.能结合余弦函数图象理解余弦函数的 性质(定义域、值域、周期性、奇偶性、 单调性)
正切函数的图象与性质
• 学习目标 1.理解利用正切线画出正切函数图象 的方法 2.掌握正切函数的图象与性质 3.会画正切函数简图
• 课堂练习二 1.判断下列函数的奇偶性 (1)f(x)=|x|+cosx; (2)f(x)=sinx+cosx; (3)f(x)=cosx|sinx|+sinx|cosx|. 2.已知f(x)是定义在R上的奇函数, 且x>0时, f(x)=sinx+cosx,则在定义域R 上,f(x)=___________. 3.已知函数y=a-bcos3x的最大值为6,最小值为-2, 求a,b的值. 4.求y=cos2x的单调区间. 5.教材56页-4,5.
• 学法指导: 1. 余弦曲线是中心对称图形,其所有的 ,0 对称中心坐标是_____________ ; 2 2.余弦曲线是轴对称图形,其所有的对 x , 称轴方程是_______________. 余弦曲线的对称轴一定是过余弦曲线的 最高点或最低点,此时余弦值为最大值 或最小值.
• 余弦型函数 y Acosx A0, 0的 2 定义域R;值域[-A,A];周期 T . 当 时 y Acos(x ) 为偶函数, 当 2 时y Acos(x )为奇函数; 对称轴由x 求得 x 对称中心横坐标由 x 求得. 2 其单调区间求法与正弦型函数相同。
5.4.2正弦函数余弦函数的性质(第2课时)课件-高一上学期数学人教A版2

当堂达标
2.函数 f(x)= 3sin2x-π4,x∈R 的最小正周期为(
)
π A.2
B.π
C.2π
D.4π
【解析】 因为 3sin12x+4π-π4= 3sin12x-π4+2π = 3sin12x-π4,即 f(x+4π)=f(x),所以函数 f(x)的最小正周期为 4π.
当堂达标
3.函数 f(x)=sinx+π6的一个递减区间是(
(1)cos 150°与 cos 170°;(2)sin 5π与 sin-75π. 【解】 (1)因为 90°<150°<170°<180°,函数 y=cos x 在区间[90°,180°]
上是减函数,所以 cos 150°>cos 170°.
(2)sin-75π=sin-2π+35π=sin 35π=sinπ-25π=sin 25π.因为 0<π5<25π<π2,
)
A.-π2,π2
B.[-π,0]
C.-23π,23π
D.π2,23π
【解析】 令 x+π6∈π2+2kπ,32π+2kπ,k∈Z,
得 x∈π3+2kπ,43π+2kπ,k∈Z,
k=0 时,区间π3,43π是函数 f(x)的一个单调递减区间,
而π2,23π⊆π3,43π.故选 D.
当堂达标
4.比较下列各组数的大小:
函数 y=sin x 在区间0,π2上是增函数,
所以 sin
π 5<sin
25π,即 sin
π5<sin-75π.
课堂小结
正弦、余弦函数的奇偶性、单调性
函数
奇偶性
正弦函数 奇函数
余弦函数 偶函数
单调性(单调区间)
5-4-2 第2课时 正弦函数、余弦函数的性质课件-高一上学期数学人教A版(2019)必修第一册
π
π
π
由 y=cosx+6,x∈0,2,可得 x+ ∈ , ,
6 6 3
1
3
∴ − ≤ cos( + ) ≤
2
6
2
1
所以函数的值域为- ,
2
3
.
2
解三角不等式
当x∈[0,2π]时,求不等式 cos ≥
y
集.
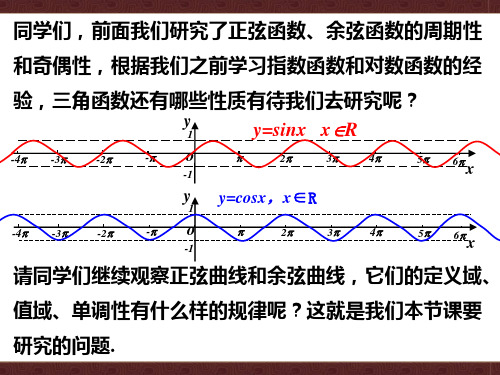
, ∪ [ , ]
值域、单调性有什么样的规律呢?这就是我们本节课要
研究的问题.
学习
目标
1. 理 解 正 弦 函 数 、 余 弦
2.能够利用函数的单调
函数的单调性具有周期
性解决比较函数值的大
性变化的规律,通过一
小以及求函数的最值、
个周期内的单调性进而
值域等问题.
研究在整个定义域上的
性质.
问题1:类比以往对函数性质的研究,正弦函数、余
使函数 y cos x, x R 取得最小值的x的集合
{x | x (2k 1) , k Z}
函数 y cos x 1, x R 的最大值是1+1=2;最小值是
-1+1=0.
例3.下列函数有最大、最小值吗?如果有,请写出取最大、最
小值时的自变量x的集合,并说出最大、最小值分别是什么.
5π
π
π
即 2kπ- 6 ≤2x≤2kπ+6(k∈Z),
令 2kπ-π≤2x-6≤2kπ(k∈Z),
5π
π
∴kπ-12≤x≤kπ+12(k∈Z).
5π
π
π
π
由 y=cosx+6,x∈0,2,可得 x+ ∈ , ,
6 6 3
1
3
∴ − ≤ cos( + ) ≤
2
6
2
1
所以函数的值域为- ,
2
3
.
2
解三角不等式
当x∈[0,2π]时,求不等式 cos ≥
y
集.
, ∪ [ , ]
值域、单调性有什么样的规律呢?这就是我们本节课要
研究的问题.
学习
目标
1. 理 解 正 弦 函 数 、 余 弦
2.能够利用函数的单调
函数的单调性具有周期
性解决比较函数值的大
性变化的规律,通过一
小以及求函数的最值、
个周期内的单调性进而
值域等问题.
研究在整个定义域上的
性质.
问题1:类比以往对函数性质的研究,正弦函数、余
使函数 y cos x, x R 取得最小值的x的集合
{x | x (2k 1) , k Z}
函数 y cos x 1, x R 的最大值是1+1=2;最小值是
-1+1=0.
例3.下列函数有最大、最小值吗?如果有,请写出取最大、最
小值时的自变量x的集合,并说出最大、最小值分别是什么.
5π
π
π
即 2kπ- 6 ≤2x≤2kπ+6(k∈Z),
令 2kπ-π≤2x-6≤2kπ(k∈Z),
5π
π
∴kπ-12≤x≤kπ+12(k∈Z).
5π
π
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、奇偶性
正弦函数是奇函数、余弦函数是偶函数
正弦、余弦曲线
y 1
-2 -
o -1 y 1
x
2 3 4
-2
-
o -1
x
2 3 4
正弦、余弦曲线
y 1
-2 -
o -1 y 1
x
2 3 4
-2
-
o -1
x
2 3 4
(3) 单调性
2 2 2k ]( k Z )上都是增函数,其值从 1增大到1, 3 在每一个闭区间 [ 2k , 2k ]( k Z )上 2 2 都是减函数,其值从1减小到 1. 正弦函数在每一个闭区 间 [
正弦函数、余弦函数的性质
1. 函数周期性
对于函数f(x),如果存在一个非零常数
T, 使得当x取定义域内的每一个值时,都有
f(x+T)=f(x),那么函数f(x)就叫做周期函数,
非零常数T叫做这个函数的周期.
函数y A sin(x ), x R及函数y A cos(x ), x R的周期T 2
2
时取得最大值 1,
3 当且仅当 x 2k 时取得最小值 1. 2
余弦函数当且仅当 x 2k时取得最大值 1, 当且仅当 x 2k 时取得最小值 1.
正弦、余弦曲线
y 1
-2 -
o -1 y 1
x
2 3 4
-2
-
o -1
x
2 3 4
(5) 对称性
【例2】利用三角函数的单调 性,比较下列 各组数的大小 (1) sin(
18 10 23 17 ( 2) cos( )与 cos( ). 5 4
)与 sin(
Байду номын сангаас
);
1 【例3】求函数y sin( x ), x [2 , 2 ] 2 3 的单调递增区间
1 【例3】求函数y sin( x ), x [2 , 2 ] 2 3 的单调递增区间
【练习】求函数 y 3 sin( 2 x 的单调递减区间 .
4
), x [0, ]
1、数形结合理解记忆正弦函数和余弦
函数的性质;
2、注意复合函数的单调性要根据内外
层单调性来确定;
3、注意三角函数的有界性的应用.
2k ,
由余弦函数的周期性可 知: 余弦函数在每一个闭区 间[ 2k , 2k ]上 都是增函数,其值从 1增大到 1, 在每个闭区间 [2k , 2k ]上都是减函数, 其值从1减小到 1.
(4) 最大值与最小值
正弦函数当且仅当 x 2k
【例1】下列函数有最大值、 最小值吗? 如果有, 请写出取最大值、最小 值时的自变量 x的集合, 并说出最大值、最小值 分别是什么 (1) y cos x 1, x R ( 2) y 2 sin 2 x , x R 1 ( 3) y 3 sin( x ), x R 2 4
正弦函数y=sinx既是轴对称图形,也是中心 对称图形 其对称轴是直线x=kπ+ (k∈Z) 2 对称中心是(kπ,0)
(5) 对称性
正弦函数y=sinx既是轴对称图形,也是中心 对称图形 其对称轴是直线x=kπ+ (k∈Z) 2 对称中心是(kπ,0) 余弦函数y=cosx既是轴对称图形,也是中心 对称图形 对称轴是直线x=kπ (k∈Z) 对称中心是(kπ+ ,0) 2
