椭圆切线的几个性质

合集下载

椭圆两平行切线性质的再讨论

一
（＋７（＋）一ｏ～证ｚ手ｚ２ …，题～．命得。）
ｌ
。一
＝＝
’ ’ 一二ｚ一—声
＋ —
Ｚ２１＿１－ｍ１
’ Βιβλιοθήκη 类似可得推广３双曲线过焦点的对称轴ｚ上且在中心Ｏ的同侧两点Ｍ，线段ＭＮ所在半轴上的顶Ｎ，点Ｅ，线段若，０Ｎ的长度成等比数列，０Ｅ，过
・
３・２
中学数学月刊
２００９年第１ｌ期
十３＋４１０，四点Ａ，Ｂ，共圆，Ｆ１ — ８。则Ｆ，ＨＰ
．
Ｐ — Ｐ・ｌ又因为Ｐ — Ｐ２故Ｐ・ＢＨＡＰＢ，ＨＦ，ＡＰ
ＰＦｌ・ＰＦ２．
—
因为四点Ａ，Ｂ，共圆，Ｆ，Ｈ记ＦＡ＝－Ｂ
（）Ｆ１一Ｔ２，Ｆ２一ＴＦ１１ＴＩＦ２Ｔ１２；
丁Ｆ１ｌ・ＴＦ＝ＴＦ・ＴＦ（［］；１２２１２２文１）
（）５ＡＢ・ＡＴ１一ＡＦｌ・ＡＦ２，Ｂ・ＢＴ２一Ａ
ＢＦ１・ＢＦ２；
（）若两条平行切线是定直线，焦点对第６则
ｚ）一壁２竺一ｚｚ三
ｍｍ。
一．＋。则
学，０９）０（・２８）
椭圆两平行切线性质的再讨论
高志雄（苏省姜堰中学江２５０）２５Ｏ
文［３１读后受益匪浅，又觉意犹未尽．文但本

椭圆上任意点的切线公式结论

椭圆上任意点的切线公式结论1. 椭圆的基本概念嘿，朋友们，今天咱们聊聊椭圆这个有趣的家伙。

说到椭圆，大家可能会想到蛋，或者是那些好看的足球。

没错，椭圆就是个比圆形更“灵活”的形状，它可以在我们的眼前变得更扁，也可以更长。

简单来说，椭圆就是一个特殊的曲线，它是由两个焦点和很多点组成的，所有点到这两个焦点的距离之和都是相等的。

是不是有点像我们生活中的那些琐碎事情，总是得在各个方面找到平衡，才能让日子过得更滋润？椭圆的标准方程长得有点复杂，但其实也不难理解。

它的公式是这样的：(frac{x^2{a^2 + frac{y^2{b^2 = 1)。

这里的(a)和(b)就像是椭圆的两条腿，一个长一个短，决定了椭圆的形状。

如果你想象一下，(a)是横向的长度，(b)是纵向的长度，二者结合起来，就形成了椭圆这个优雅的身姿。

2. 切线的概念接下来，我们来聊聊切线。

切线这个词听起来有点高大上，但其实它的意思就是一条“摩擦”椭圆的直线。

想象一下，你在滑滑梯的时候，刚好碰到一个小石头，那瞬间你就偏离了原来的轨道，这个“偏离”就像切线跟椭圆的关系一样。

切线与椭圆在某一点相接，却不相交，这就是切线的魅力所在。

那为什么要研究切线呢？生活中很多时候，我们需要找到一个方向，或者说是一个“出口”。

比如说，想要在复杂的生活中寻找到一条简洁的路径，切线就像是给你指路的那盏明灯，让你在迷雾中找到前行的方向。

2.1 切线公式说到这儿，咱们不得不提到椭圆上任意点的切线公式。

这可是个干货！公式是这样的：对于椭圆 (frac{x^2{a^2 + frac{y^2{b^2 = 1) 上的点 ((x_0, y_0))，切线的方程可以表示为：frac{xx_0{a^2 + frac{yy_0{b^2 = 1。

这看起来是不是有点拗口？但其实，这个公式的意思是：只要你知道椭圆的形状和某个点的位置，你就可以轻松地找到切线的方向。

这就像你知道了自己的目标之后，自然就能制定出行动计划。

椭圆切线的几个典型性质

2006 年第 15 期数学通讯
29
椭圆切线的几个典型性质
崔宝法
( 海盐县元济高级中学 ,浙江 314300)
中图分类号 : O123. 3 文献标识码 : A 文章编号 : 0488 - 7395 (2006) 15 - 0029 - 02
对于椭圆的切线 , 在全日制普通高级中学教科书 ( 必修) 数学第二册 ( 上) 中虽略有涉及 , 但没有作进一步的讨论与研究 . 事实上 , 椭圆的切线作为和椭圆位置关系最特殊的直线 , 有着它自身所独有的一些典型性质 . 下面给出其中几条性质 , 并加以证明 . 性质 1 椭圆的任意一条切线与切点处的两条焦半径所成的角相等 . 证如图 1 ,设椭圆方程为
2
收稿日期 :2006 - 04 - 04 ) ,男 ,浙江海盐人 ,浙江海盐县元济高级中学高级教师 . 作者简介 : 崔宝法 (1958 —
30
数学通讯 2006 年第 15 期 ) , 两焦点的坐标为 F1 ( c , 一点为 P ( acosθ, bsinθ 0) , F2 ( - c ,0 ) , 则 P 点处的切线方程为 sinθ
x 轴的交点) ,
则法线 PT 的方程为
a y0 x - b x0 y = ( a - b ) x0 y0 ,
2 2 2 2
1 ( a > b > 0) 的两个
焦点 , P 为椭圆外任一点 , PQ , PQ′ 为椭圆的两条切线 , T , T′ 为切点 . 作点 F1 关于直线 PT 的对称点 F1 ′ ,则 ∠F1 ′ TQ = ∠F1 TQ . 又根据性质 1 , 有 ∠PTF2 = ∠QTF1 , ∴ ∠F1 ′ TQ = ∠F2 TP , ∴ F2 , T , F1 ′ 三点共线 , ∴ | F2 F1 ′ | = | F2 T| + | TF1 ′ |

椭圆外一点的切线斜率之积

椭圆外一点的切线斜率之积椭圆是一种常见的几何图形，它具有许多独特的性质和特点。

其中一个重要的性质是，对于椭圆上的任意一点，它的切线斜率都可以通过该点与椭圆中心的连线来计算。

而对于椭圆外一点，其切线斜率之积也有着一定的规律和特点。

我们来看一下椭圆的基本性质。

椭圆是一个平面内到两个定点的距离之和等于常数的点的集合。

这两个定点称为椭圆的焦点，常数称为椭圆的长轴长度。

椭圆的中心是两个焦点的中点，短轴长度等于长轴长度的一半。

对于椭圆上的任意一点P，它的切线斜率可以通过以下公式来计算： k = -b^2x / a^2y其中，a和b分别是椭圆的长轴和短轴长度，x和y分别是点P的横坐标和纵坐标。

这个公式的推导可以通过对椭圆方程进行求导得到。

现在，我们来考虑一个椭圆外的点Q，它与椭圆的距离为d。

我们可以通过以下公式来计算点Q到椭圆上最近的点P的坐标：x = a^2xQ / (a^2 + b^2d^2)^0.5y = b^2yQ / (a^2 + b^2d^2)^0.5其中，xQ和yQ分别是点Q的横坐标和纵坐标。

这个公式的推导可以通过对点Q到椭圆上的切线斜率进行求导得到。

现在，我们来考虑点Q到椭圆上最近的点P的切线斜率。

根据上面的公式，我们可以得到：k = -b^2x / a^2y = -b^2(a^2xQ / (a^2 + b^2d^2)^0.5) / a^2(b^2yQ / (a^2 + b^2d^2)^0.5) = -axQ / byQ因此，点Q到椭圆上最近的点P的切线斜率为-k，即：k1 = axQ / byQ现在，我们来考虑点Q到椭圆上最远的点P的切线斜率。

根据椭圆的对称性，最远的点P与最近的点P关于椭圆中心对称。

因此，最远的点P的切线斜率为-k1，即：k2 = -axQ / byQ因此，点Q到椭圆上最近和最远的点P的切线斜率之积为：k1 * k2 = -(axQ / byQ)^2 = -a^2xQ^2 / b^2yQ^2这个式子告诉我们，点Q到椭圆上最近和最远的点P的切线斜率之积只与点Q的坐标有关，与椭圆的长轴和短轴长度无关。

椭圆的切线的性质和判定

椭圆的切线的性质和判定
切线的定义
首先我们来回顾一下什么是切线。

在几何学中，切线是指与给定曲线相切的直线。

对于椭圆而言，切线是与椭圆相切并且仅在切点与椭圆相交的一条直线。

切线的性质
椭圆的切线具有以下性质：
1. 切线与椭圆的切点处的切线方向与椭圆的切点处的切线方向相同。

2. 切线与椭圆的切点处的切线垂直于椭圆的法线。

法线是指与椭圆切点处切线垂直的直线。

3. 具有相同斜率的直线可以视为同一条切线。

4. 切线与椭圆的切点处的切线与椭圆的对称轴相交于同一点。

切线的判定方法
确定一条直线是否是椭圆的切线可以通过以下方法进行判定：
1. 求解切点坐标：设直线方程为y = kx + b，将其代入椭圆方程x^2/a^2 + y^2/b^2 = 1中，得到一个关于x的二次方程。

解这个二次方程，得到两个解x1和x2。

将x1和x2带入直线方程中求解出对应的y1和y2。

这样得到的两个点(x1, y1)和(x2, y2)就是直线与椭圆的切点。

2. 验证切线性质：将直线的斜率代入椭圆的导数方程dy/dx = -b^2x/a^2y，如果二者相等，说明这条直线是椭圆的切线。

总结
椭圆的切线具有一些独特的性质，包括与切点处的切线方向相同、与切点处的切线垂直的法线、具有相同斜率的直线视为同一条
切线等。

判定一条直线是否是椭圆的切线可以通过求解切点坐标和验证切线性质来进行。

希望本文对你理解椭圆的切线的性质和判定方法有所帮助！。

高中切线的概念

高中切线的概念高中数学中的切线是一个重要的概念。

在学习曲线与函数图像的性质时，我们经常会遇到需要求切线的问题。

下面我将详细介绍什么是高中数学中的切线，以及切线的性质和求解方法。

首先，我们来理解什么是切线。

切线是指在某一点上与曲线相切的直线。

具体来说，对于一个函数曲线上的一点P，如果这个点P有一个邻近点Q，且点Q在曲线上，那么通过点P和点Q的直线就是曲线在点P处的切线。

了解了什么是切线后，我们来看看切线的性质。

首先，切线与曲线在相切点处的切点总是相等的。

也就是说，如果一条直线与曲线在某一点P处相切，那么这条直线与曲线在这一点的斜率相等。

这是因为切线是曲线在某一点的“最佳逼近线”，所以它们在这一点上的斜率应该是相同的。

另外，切线与曲线在相切点处的切点还有一个重要性质：切线与曲线在这一点处的切点所在的直线与切线重合。

换句话说，切线与曲线在相切点处还有相同的导数。

这个性质很有用，因为我们可以通过求导数来求解切线的斜率，从而得到切线的方程。

那么我们来看看如何求解切线的方程。

首先，我们需要知道函数在某一点的导数。

导数是函数在某一点的切线斜率，所以通过求导数可以得到切线的斜率。

具体而言，对于一条函数曲线f(x)，在点P(x0, f(x0))处的切线斜率即为f'(x0)。

所以我们可以通过求导的方法来求解切线的斜率。

如果已知函数在点P处的切线斜率，那么切线的方程可以通过点斜式方程来表示。

具体而言，切线的方程可以表示为y-f(x0)=f'(x0)(x-x0)，其中(x0, f(x0))为切线与曲线的相切点。

通过代入这个方程，我们可以得到切线的具体表达式。

最后，还有一种情况需要注意，那就是当曲线是一个圆或椭圆时，切线有可能有无数条。

这是因为圆或椭圆在某一点的切线是与曲线相切的直线，而圆或椭圆上的每一点都可以与圆或椭圆相切，所以切线有无数条。

在计算切线方程时，我们需要给定切点的具体坐标才能确定一条切线。

椭圆切线的几个性质

R R2 RA RB Rc
R
当且仅当△ ABC 为正三角形时取等号.
参考文献 [ 1] 李耀文. 关于垂足三角形的一个恒等式. 中学数学.
2004. 6. [ 2] 高庆计. 垂足三角形旁切圆半径之间的一个恒等
式. 福建中学数学. 2005. 6. 24
椭圆切线的几个性质
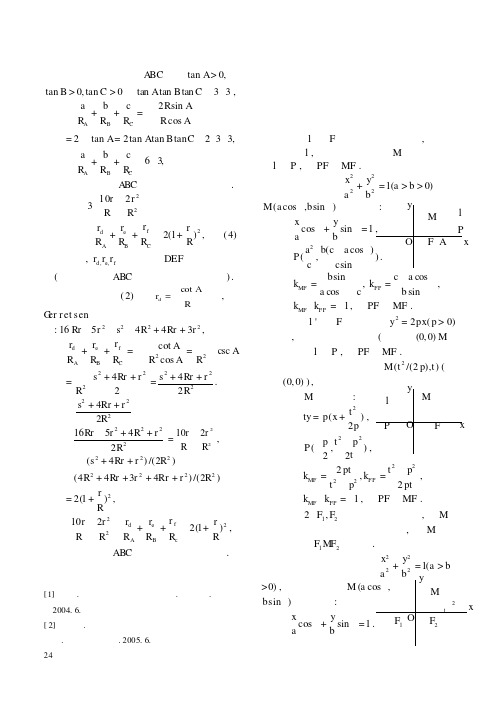
福建长乐七中谢星恩黄玉惠林世中
= t 2 p2 2 pt
,
∴ kMF kFP = 1 , ∴ PF ⊥MF .
性质 2 F1 , F2 是椭圆的两个焦点, 若 M是
椭圆上异于长轴两端点的任一点, 则 M 点的
切线平分△ F1 MF2 的外角.
x2 y2
证明
设椭圆的方程为 a 2
+ b2
= 1(a > b y
> 0) , 过椭圆上一点 M (a cosθ,
证明 ∵在锐角△ ABC 中有 tan A> 0,
tan B > 0, tan C > 0 且 tan Atan Btan C ≥3 3 ,
∑ a b c
2Rsin A
∴++=
RA RB RC
Rcos A
= 2∑tan A= 2tan Atan BtanC ≥2 3 3,
故
a
+
b +
c
≥6
3,
RA RB RC
≥16Rr 5r 2 + 4R2 + r 2 = 10r 2r 2 ,
2 R2
R R2
又∵ (s2 + 4Rr + r 2 ) /(2R2 )
≤(4R2 + 4Rr + 3r 2 + 4Rr + r 2 ) /(2R2 )

2椭圆切线的几个有趣性质及其证明

2椭圆切线的几个有趣性质及其证明椭圆是一个非常重要的椭圆几何学中的基本图形。

它具有很多有趣的性质，其中包括切线的性质。

本文将介绍椭圆切线的几个有趣性质及其证明。

1.切线与法线垂直我们首先证明椭圆上任意一点的切线与该点的法线垂直。

设椭圆的方程为$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$，点$ P(x_0, y_0)$在椭圆上。

我们知道，椭圆的一般方程为$ \frac{x^2}{a^2} +\frac{y^2}{b^2} = k^2$，所以我们可以得到$ x_0^2/a^2 + y_0^2/b^2 = 1 $。

对该方程求导，我们得到$ \frac{2x_0}{a^2} +\frac{2y_0}{b^2}y^\prime = 0 $。

根据点斜式可得直线的斜率为$ y^\prime = -\frac{a^2y_0}{b^2x_0} $，而直线的法线的斜率为$ y^\prime = \frac{b^2x_0}{a^2y_0} $，我们可以看出两条直线的斜率互为相反数，所以切线与法线垂直。

2.任意两条切线的交点我们接着证明任意两条椭圆切线的交点在椭圆的两个焦点上。

设椭圆的两条切线分别为$l_1$和$l_2$，对应的交点为$A$和$B$。

设椭圆的两个焦点为$F_1$和$F_2$。

我们要证明$AF_1+AF_2=BF_1+BF_2$。

首先，连接$ AF_1$和$ AF_2$，可以得到$ \Delta AF_1F_2 $为等腰三角形。

同理，连接$ BF_1$和$ BF_2$，可以得到$ \Delta BF_1F_2 $为等腰三角形。

而在椭圆几何学中，我们知道，三角形的高是两底边之和的一半。

所以$ AF_1+AF_2 = BF_1 + BF_2 $，即交点$ A$和$ B$在椭圆的两个焦点上。

3.切线与椭圆的两个焦点的连线的夹角我们继续证明切线与椭圆的两个焦点的连线的夹角相等。

椭圆的切点弦方程公式推导

椭圆的切点弦方程公式推导1.定义椭圆及其性质：椭圆是一个平面上的几何图形，它由平面上到两个定点F1和F2的距离之和恒定于常数2a的点P构成。

此外，椭圆还有一个重要性质，就是通过椭圆上的两个点和椭圆上与这两点垂直的直径，必定存在一条唯一的切线。

2.确定椭圆的标准方程：椭圆的标准方程是x^2/a^2+y^2/b^2=1，其中a和b是椭圆的半长轴和半短轴的长度。

3.确定椭圆上特定点的切线方程：假设椭圆上的一点P位于第一象限，其坐标为(x0,y0)。

要求得P的切线方程，需要先求得椭圆上过点P的切线的斜率k。

4.求切线的斜率：设椭圆上的点P的坐标为(x0,y0)，则与切线垂直直径的斜率为-x0/y0，而切线的斜率为-y0/x0。

由此可得切线的斜率k=-y0/x0。

5.求切点的坐标：切线方程需要通过切点，因此需要求出切点的坐标。

设切点的坐标为(x1,y1)，则切线方程为y-y1=k(x-x1)。

6. 求椭圆上的点 P 的坐标：代入椭圆的标准方程，得到 x0^2/a^2+ y0^2/b^2 = 1、由此可得 y0 = sqrt(b^2 - (b^2/a^2)*x0^2)。

7. 代入切线斜率得到切点的坐标：代入切线斜率 k 和切点的坐标(x1, y1)，得到 k = -sqrt(b^2 - (b^2/a^2)*x0^2)/x1，再整理得 x1 = b^2*x0/sqrt(a^2*y0^2 + b^2*x0^2) 和 y1 = -a^2*y0/sqrt(a^2*y0^2 + b^2*x0^2)。

8.代入切点坐标得到切线方程：将切点的坐标(x1,y1)代入切线方程y-y1=k(x-x1)，整理得y=(b^2*y0-a^2*y1)x+a^2y1-b^2y0。

至此，推导得到了椭圆的切点弦方程公式为y=(b^2*y0-a^2*y1)x+a^2y1-b^2y0，其中(x0,y0)为椭圆上的点的坐标，(x1,y1)为切点的坐标。

椭圆二级结论大全及证明过程mp4

椭圆二级结论大全及证明过程1. 引言椭圆是数学中重要的几何形状之一，在几何、代数和解析几何等领域都有广泛的应用。

椭圆的性质和结论是数学研究的重点之一，其中椭圆的二级结论是椭圆几何中的重要内容之一。

在本文中，我们将对椭圆的二级结论进行全面而系统的总结，包括结论的表述以及证明过程，并附带mp4视频演示，以帮助读者更好地理解和掌握椭圆的相关知识。

2. 椭圆的基本概念在介绍椭圆的二级结论之前，我们首先需要了解椭圆的基本概念和性质。

椭圆是指平面上到两个定点F1和F2的距离之和为常数2a（a>0）的动点的轨迹。

椭圆的定义可以用代数方程x^2/a^2 + y^2/b^2 =1（a>b>0）来表示。

椭圆具有许多特殊的性质，例如焦点、准线、长轴、短轴等，这些性质对于理解椭圆的二级结论至关重要。

3. 椭圆的二级结论椭圆的二级结论是指关于椭圆性质的一系列重要结论，涉及到椭圆的各种几何特性和性质。

这些结论在椭圆的研究和应用中起着重要作用，对于深入理解椭圆的性质和应用具有重要意义。

下面我们将逐一介绍椭圆的二级结论及其证明过程。

3.1 椭圆的焦点性质椭圆的焦点性质是指椭圆上任意一点到两个焦点的距离之和等于椭圆的长轴长度。

具体而言，对于椭圆上的任意一点P(x, y)，其到两个焦点F1和F2的距离之和等于2a。

这一性质是椭圆的基本特征之一，也是椭圆的二级结论中的重要内容。

证明过程：可以通过椭圆的定义和几何推理来证明椭圆的焦点性质。

根据椭圆的定义可知，点P到两个焦点的距离分别为√(x-ae)^2 +y^2 和√(x+ae)^2 + y^2，其中e为椭圆的离心率。

然后利用距离定理和代数运算，可以证明√(x-ae)^2 + y^2 + √(x+ae)^2 + y^2 = 2a，证明得证。

3.2 椭圆的切线性质椭圆的切线性质是指切线与法线的交点在椭圆长轴上。

具体而言，对于椭圆上的任意一点P(x, y)，其切线和法线在交点处的斜率乘积等于-1，且交点在椭圆的长轴上。

高考椭圆的知识点

高考椭圆的知识点椭圆是高中数学中常见的一个几何图形，也是高考数学中的重点内容之一。

下面将详细介绍高考椭圆的知识点。

一、椭圆的定义椭圆可以定义为平面上到两个定点的距离之和等于常数的点的轨迹。

这两个定点称为焦点，两个焦点之间的距离称为焦距。

椭圆的形状由焦距和常数决定。

二、椭圆的基本要素1. 焦点和直径：椭圆有两个焦点，焦点的位置决定了椭圆的形状和大小。

椭圆的长轴是通过两个焦点的直线，它的长度称为椭圆的长径；椭圆的短轴是垂直于长轴的直线，它的长度称为椭圆的短径。

2. 中心：椭圆的中心是长轴和短轴的交点，也是椭圆的对称中心。

3. 长径和短径：椭圆的中心到椭圆上任意一点的距离称为椭圆半径，椭圆的长径是指长轴的一半，短径是指短轴的一半。

4. 离心率：椭圆的离心率是一个0到1之间的实数，它表示椭圆的扁平程度。

离心率为0时，椭圆退化为一个点；离心率为1时，椭圆变为一条直线。

三、椭圆的方程1. 标准方程：椭圆的标准方程可以表示为（x-h）^2/a^2 + （y-k）^2/b^2 = 1，其中(h, k)是椭圆的中心坐标，a是长轴的一半，b是短轴的一半。

2. 参数方程：椭圆的参数方程可以表示为x = h + a*cosθ，y = k + b*sinθ，其中(h, k)是椭圆的中心坐标，a是长轴的一半，b是短轴的一半，θ是参数。

四、椭圆的性质1. 对称性：椭圆具有两个对称轴，分别是长轴和短轴，以中心为对称中心。

2. 焦点性质：椭圆上任意一点到两个焦点的距离之和等于常数（焦距）。

3. 切线性质：椭圆上任意一点的切线和从该点出发指向焦点的直线的夹角等于切线斜率的相反数。

4. 弦长性质：椭圆上任意一条弦的长度等于焦点到弦中点的距离与焦距之和。

5. 面积性质：椭圆的面积可以用公式S = πab表示，其中a是长轴的一半，b是短轴的一半。

五、椭圆在高考中的应用1. 椭圆的参数方程可以用来描述物体在椭圆轨道上的运动。

2. 椭圆的性质可以应用于建筑结构中的设计和力学分析。

椭圆的简单几何性质教学设计

椭圆的简单几何性质教学设计导语：椭圆是几何学中一个重要的概念，理解椭圆的性质对于数学学科的学习具有重要意义。

因此，本文将设计一个针对椭圆的简单几何性质的教学内容，旨在帮助学生更好地理解和掌握椭圆的基本特点。

一、引入在教学开始之前，可以通过引入椭圆的概念来激发学生对该主题的兴趣。

可以让学生观察并描述一些椭圆的实例，例如椭圆形的轮胎、篮球等，进而引出椭圆的定义和性质。

二、椭圆的定义在引入概念之后，需要给出椭圆的严格定义。

椭圆可以定义为平面上到两个定点之和等于一定值的点的集合。

这个定义可以通过几何图形的展示和实例的校验来让学生更好地理解。

三、椭圆的性质1. 椭圆的焦点性质：椭圆的焦点是与椭圆的定义密切相关的内容。

可以通过推导和演示来给出焦点的定义和特点，包括焦点在椭圆的几何中心线上、到椭圆边界上任意一点的距离之和等于定值等。

2. 椭圆的长轴和短轴：椭圆还有两条重要的中垂线，分别为长轴和短轴。

可以通过给出椭圆的参数方程，并引导学生通过参数方程来推导出椭圆的长轴和短轴的关系。

3. 椭圆的离心率：椭圆的离心率是衡量椭圆形状的重要参数，可以通过定义和计算公式来介绍离心率的概念，并让学生通过计算椭圆形状不同的例子的离心率来理解其意义和特点。

4. 椭圆的切线性质：椭圆切线是垂直于椭圆边界的直线。

可以通过直角三角形的性质以及切线与半径的关系来推导出椭圆的切线性质，并通过具体的几何图形和实例来应用这一性质。

5. 椭圆的对称性：椭圆具有许多对称轴，其中包括两条主轴和许多副轴。

可以通过示意图和实例来介绍和验证椭圆的对称性，以及对称轴的特点。

四、椭圆的应用在学习了椭圆的基本性质之后，可以引导学生思考椭圆在实际问题中的应用。

例如，椭圆的形状适用于人造卫星轨道、搭桥拱形等各种实际问题。

可以通过展示实际案例、进行讨论和解决具体问题的方式，让学生将椭圆的性质与实际应用相联系。

五、教学扩展对于那些对椭圆性质有较好掌握的学生，可以引导他们进行更深入的探究和研究。

圆锥曲线切线的一条性质

圆锥曲线切线的一条性质圆锥曲线是数学中一个十分重要的概念，是把一个平面上的点P 与两个不同的定点 F1 和 F2 连接起来，如果点 P 到这两个定点的距离之和等于定长，则这个点 P 就被称作圆锥曲线的点。

常见的圆锥曲线有椭圆、双曲线和抛物线。

而圆锥曲线切线的性质，也是圆锥曲线中最为重要的概念之一。

在圆锥曲线的各个部分上，切线的性质不尽相同，下面我们将就椭圆、双曲线和抛物线三类圆锥曲线切线的性质进行介绍。

1. 椭圆的切线性质椭圆的切线性质有以下几点：（1）椭圆任意一个点 P 的切线斜率等于点 P 处切线所对应的切线方程的导数值；（2）椭圆任意一个点 P 的切线分别在椭圆的两焦点 F1 和F2 处的切线分别垂直于两个焦点之间的连线；（3）椭圆的长半轴是椭圆上最长的直径，因此椭圆的切线斜率不会超过此直径的斜率，而椭圆的短半轴的切线斜率也不会小于直径的斜率；（4）同时，由于椭圆上每个点的切线都垂直于椭圆的两焦点连线，因此椭圆中垂线段的长度与每条切线的斜率成反比例关系。

2. 双曲线的切线性质双曲线的切线性质与椭圆有着很大的不同，主要表现在以下几点：（1）双曲线两个极限上的切线都是与对应焦点连线垂直的直线；（2）双曲线的每个点处都存在两条切线，且它们与两个焦点连线之间的夹角相等；（3）双曲线上的切线的斜率可以超过横轴的斜率，因此双曲线的切线可以是无限大或无限小。

3. 抛物线的切线性质抛物线与椭圆和双曲线相比，切线的性质有着一些相似之处，但也有一些不同：（1）抛物线上任意一点处的切线与此点的切线垂线段长度相等；（2）抛物线的顶点处斜率为零，顶点的两侧顶点分别为正无穷和负无穷点，与双曲线类似；（3）抛物线的孪生点（即对称于抛物线对称轴上的两个点）处的切线斜率相等；（4）由于抛物线的拋物线顶点一般是关键点，因此与顶点相关的切线性质也更加重要，此处不仅包括顶点处的切线斜率，还包括拋物线斜轴上单位长度的切线斜率。

综上所述，圆锥曲线切线的性质是圆锥曲线研究中最基础的概念之一，对于圆锥曲线的证明和运用有着十分重要的地位。

椭圆切线与坐标轴围成的面积

椭圆切线与坐标轴围成的面积1. 引言椭圆是数学中的一种基本曲线，它的形状类似于拉长的圆形。

椭圆在几何学、物理学、工程学等领域中都有广泛的应用。

本文将探讨椭圆切线与坐标轴围成的面积，带领读者深入了解这一问题。

2. 椭圆的定义与性质椭圆可以通过以下定义来描述：给定一个平面上的两个焦点F1和F2以及一个常数2a，椭圆是满足到焦点F1和F2的距离之和等于常数2a的所有点的集合。

椭圆的一些基本性质如下：•椭圆的中心位于焦点连线的中点，记为O；•椭圆的长轴是通过两个焦点的直线段，长度为2a；•椭圆的短轴是通过中心垂直于长轴的直线段，长度为2b；•椭圆的离心率e小于1，且与长轴、短轴的关系为e^2 = 1 - (b^2 / a^2)。

3. 椭圆切线的定义与性质椭圆上的切线是与椭圆相切的直线。

切线与椭圆的交点称为切点。

椭圆上的每一点都存在唯一的切线。

椭圆切线的一些性质如下：•切线与椭圆的切点在椭圆上；•切线与椭圆的切点到两个焦点的距离之和等于椭圆的长轴；•切线与椭圆的切点到中心的距离等于椭圆的半径。

4. 椭圆切线与坐标轴围成的面积的推导我们考虑椭圆在第一象限中的情况。

设椭圆的方程为(x^2 / a^2) + (y^2 / b^2) = 1，其中a和b分别是椭圆的长轴和短轴。

首先，我们需要求解椭圆上点(x, y)处的切线斜率。

根据椭圆的方程，我们可以得到y关于x的导数为dy/dx = -b^2x / (a^2y)。

切线的斜率为切点处的导数值，即dy/dx。

设切线与椭圆的交点为(x0, y0)，代入切线的斜率公式，我们可以得到切点处的切线方程为y - y0 = (dy/dx)|(x=x0)(x - x0)。

接下来，我们需要找到切线与x轴和y轴的交点。

当切线与x轴相交时，y = 0，代入切线方程可以求解出切点的横坐标x0。

同理，当切线与y轴相交时，x = 0，代入切线方程可以求解出切点的纵坐标y0。

我们可以得到切线与x轴和y轴的交点分别为(x0, 0)和(0, y0)。

几何中的切线性质

几何中的切线性质几何学是研究空间和形状的分支学科，其中切线是一个重要的概念。

切线是一条与曲线相切于一点的直线，它具有一些独特的性质。

本文将介绍几何中的切线性质，以及它们在实际生活和工程应用中的重要性。

一、切线的定义和操作方法在几何中，切线是一条直线与曲线在某一点处仅有一个公共点的直线。

切线的构造方法有多种，其中最常见的是使用切线与曲线的斜率。

对于一条曲线上的点P(x, y)，可以通过求解斜率等于曲线在该点处的导数来找到切线的斜率。

然后使用点斜式或一般式等方法构造切线。

最后，通过求解曲线与切线的交点找到切线方程。

二、切线的性质1. 切线与曲线在切点处垂直切线与曲线在切点处的相切点垂直于切线。

这一性质可以通过切线与曲线的斜率相乘等于-1来证明。

因为切线的斜率是曲线在切点处的导数，所以导数与切线的斜率相乘等于-1。

2. 切线的斜率等于曲线在切点处的斜率切线的斜率等于曲线在切点处的斜率。

这可以通过导数的定义来证明。

导数定义为曲线在某一点上的切线斜率。

3. 切线与曲线在切点处只有一个公共点切线与曲线在切点处仅有一个公共点，不会与曲线有额外的交点。

这一性质是切线的定义之一。

4. 切线与曲线的切点在曲线上切线与曲线的切点必定在曲线上。

这是因为切线与曲线在切点处有且只有一个公共点。

三、切线性质的应用切线性质在实际生活和工程应用中有着重要的作用。

以下是一些应用示例：1. 圆的切线圆的切线是从圆的外部过一点的直线，它与圆只有一个公共点。

圆的切线性质在几何构造和机械设计中广泛应用。

2. 行星轨道和行星之间的切线行星的轨道是椭圆，而行星之间的连接线是切线。

这一性质在天文学和航天工程中使用。

3. 斜面上的运动斜面上的物体在没有垂直分量的力影响下，只受到切向力的作用。

这一性质在机械工程和物理学中起着重要作用。

四、结论切线是几何学中一个重要的概念，具有独特的性质和应用。

切线与曲线在切点处垂直，切线的斜率等于曲线在切点处的斜率，切线与曲线在切点处只有一个公共点，并且切线与曲线的切点在曲线上。

椭圆二级结论高频考点

椭圆二级结论高频考点引言椭圆是一种重要的几何形状，在数学和应用中都有广泛的应用。

椭圆的性质和特点在各类考试中经常被问及，而椭圆的二级结论是其中一个高频考点。

本文将深入探讨椭圆二级结论的相关知识点，包括定义、性质及应用。

定义椭圆可以通过以下定义得到：给定两个焦点F和F’和一条长度为2a的线段作为定长，所有与这条线段和焦点的距离之和等于定长的点所组成的轨迹被称为椭圆。

其中，焦点F和F’到椭圆上的任意一点的距离之和等于2a。

二级结论1：椭圆的离心率椭圆的离心率是一个重要的参数，用来衡量椭圆的平扁程度。

离心率的定义可以通过焦距长度和长轴长度的比值得到。

数学上，椭圆的离心率e可以表示为：e=c a其中，c是焦距长度，a是长轴长度。

离心率e的取值范围为0到1，当e=0时，椭圆退化为一条线段；当e=1时，椭圆退化为一条抛物线。

二级结论2：椭圆的焦点与直径的中点椭圆的焦点与直径的中点之间有一个有趣的关系。

对于一个椭圆，任意一条直径的中点到焦点的距离之和等于长轴长度。

具体来说，设直径的中点为M，焦点为F和F’，则有MF + MF’ = 2a。

二级结论3：椭圆的切线与法线性质椭圆的切线与法线是椭圆性质的重要组成部分。

对于椭圆上的一点P，通过该点的切线和法线与椭圆的几何关系如下：切线•切线是指通过椭圆上一点的直线，且与椭圆相切于该点。

•切线与该点处的椭圆弧相切，且切线与椭圆的切点处的切线垂直。

•椭圆上任意一点处的切线的斜率等于该点处的导数。

•两条切线中点连线的中点在椭圆上。

法线•法线是指通过椭圆上一点的直线，且与椭圆的切线垂直于该点。

•法线与该点处的椭圆弧相切。

•椭圆上任意一点处的法线的斜率等于该点处的导数的负倒数。

应用椭圆的二级结论在数学和应用问题中具有广泛的应用。

以下是一些常见的应用场景：圆锥曲线及天体力学椭圆是圆锥曲线中的一种，而圆锥曲线在天体力学中有着广泛的应用。

例如，奇焦椭圆轨道可以用来描述行星绕太阳运动的轨迹。

椭圆的切线

椭圆的切线与椭圆有且仅有一个交点的直线，就叫做椭圆的切线。

二者公共点，叫做切点。

经过切点且与切线垂直的直线，叫做该椭圆的法线。

即直线L与椭圆C切于点P。

即P点为切点。

过切点P且与切线L垂直的直线即是法线。

椭圆（Ellipe）是平面内到定点F1、F2的距离之和等于常数（大于，F1F2，）的动点P的轨迹，F1、F2称为椭圆的两个焦点。

其数学表达式为：，PF1，+，PF2，=2a（2a>，F1F2，）。

椭圆是圆锥曲线的一种，即圆锥与平面的截线。

椭圆的周长等于特定的正弦曲线在一个周期内的长度。

扩展资料：切线法线定理1：设F1、F2为椭圆C的两个焦点，P为C上任意一点。

若直线AB切椭圆C于点P，且A和B在直线上位于P的两侧，则∠APF1=∠BPF2。

（也就是说，椭圆在点P处的切线即为∠F1PF2的外角平分线所在的直线）。

定理2：设F1、F2为椭圆C的两个焦点，P为C上任意一点。

若直线AB为C在P点的法线，则AB平分∠F1PF2。

椭圆的面镜（以椭圆的长轴为轴，把椭圆转动180度形成的立体图形，其内表面全部做成反射面，中空）可以将一些焦点发出的光线全部反射到另一个焦点处；椭圆的透镜（一些截面为椭圆）有汇聚光线的作用（也叫凸透镜），老花眼镜、放大镜和远视眼镜都是这种镜片（这些光学性质可以通过反证法证明）。

例如：有一个圆柱，被截得到一个截面，下面证明它是一个椭圆（用上面的第一定义）：将两个半径与圆柱半径相等的半球从圆柱两端向中间挤压，它们碰到截面的时候停止，那么会得到两个公共点，显然他们是截面与球的切点。

设两点为F1、F2对于截面上任意一点P，过P做圆柱的母线Q1、Q2，与球、圆柱相切的大圆分别交于Q1、Q2则PF1=PQ1、PF2=PQ2，所以PF1+PF2=Q1Q2由定义1知：截面是一个椭圆，且以F1、F2为焦点用同样的方法，也可以证明圆锥的斜截面（不通过底面）为一个椭圆。

数学高考知识点椭圆切线

数学高考知识点椭圆切线椭圆是高考中常出现的一个重要的几何形状，掌握相关知识点对于考生来说是非常关键的。

其中一个重要的概念就是椭圆的切线。

在本文中，我将深入解析椭圆切线的相关内容，帮助读者加深理解。

首先，让我们回顾一下椭圆的定义和性质。

椭圆是一个平面上所有距离两个定点F1和F2的距离之和等于常数2a的点的集合。

这两个定点被称为焦点，2a则是椭圆的长轴长度。

对称轴是连接两个焦点并且垂直于椭圆长轴的线段，它的长度被称为椭圆的短轴，记作2b。

此外，焦点之间的距离等于两个焦半径之和的两倍，即F1F2=2c。

根据椭圆的定义，我们可以得到一个重要的性质，即椭圆上的任意一点到两个焦点的距离之和等于常数2a。

接下来，我们来讨论椭圆的切线。

切线是曲线与其某一点相切的直线。

对于椭圆而言，每一条切线与曲线相切的点都位于椭圆的外部。

这是因为对于椭圆上的所有点，到焦点的距离之和等于常数2a，所以任意一条线如果不与椭圆有交点，那么它就不满足这个条件。

因此，只有位于椭圆外部的点才有可能与椭圆相切。

要求椭圆的切线，我们可以利用椭圆的几何性质来推导。

首先，我们可以通过将椭圆的切线与椭圆的法线相交于一点，来确定椭圆上一点的切线。

椭圆的法线是与切线垂直的直线，通过椭圆上的点，并且与该点的切线相交于一点。

在椭圆上，法线与切线的相交点将构成一个直角。

这是椭圆的一个重要性质，也是我们求解切线的关键。

我们可以根据这个性质得到一个重要的结论：椭圆的切线和法线的斜率互为相反数。

具体来说，设椭圆的方程为x^2/a^2+y^2/b^2=1，点P(x0,y0)为椭圆上的一点，点P处的切线的斜率为k，则椭圆的法线的斜率为-1/k。

这个结论可以通过利用椭圆方程求解导数来得到，但是在此不做详细推导。

利用这个结论，我们可以通过已知椭圆上一点的坐标和斜率，求解该点处的切线方程。

例如，假设我们已知椭圆的方程为x^2/4+y^2/9=1，要求椭圆上点P(2,-3)处的切线方程。

椭圆外一点的切线方程

椭圆外一点的切线方程
椭圆是一种常见的平面图形，其由一组点构成，满足到两个定点的距离之和为常数的性质。

在椭圆上取一点P，我们可以通过求出该点处椭圆的切线方程来研究椭圆的性质。

具体来说，我们先求出椭圆的参数方程，即：
x = a*cos(t)
y = b*sin(t)
其中a和b分别是椭圆的半长轴和半短轴，t是参数。

接下来，我们考虑椭圆上一点P(x0,y0)，以及该点的切线L。

设切线L的斜率为k，则L的方程为：
y-y0 = k*(x-x0)
由于P在椭圆上，因此有：
(x0/a)^2 + (y0/b)^2 = 1
同时，P处于L上，因此有：
y0 = k*x0 - k*x + y
将L的方程代入上式，得到：
(x0/a)^2 + ((k*x0 - k*x + y)/b)^2 = 1
化简后得到一个关于x的二次方程：
(k^2/a^2 + 1/b^2)*x^2 - 2*k*y0/b^2*x + (y0^2/b^2 - 1) = 0 由于L是切线，因此该方程有且只有一个解，即判别式为0：
(-2*k*y0/b^2)^2 - 4*(k^2/a^2 + 1/b^2)*(y0^2/b^2 - 1) = 0 解出k，带入L的方程即可得到切线方程。