人教版数学八年级下册19.2.3 一次函数与方程、不等式同步练习(解析版)
19-2-3 一次函数与方程、不等式同步训练 人教版数学八年级下册

19.2.3一次函数与方程、不等式同步训练一、单选题1.若直线y=﹣2x﹣4与直线y=4x+b的交点在第二象限,则b的取值范围是()A.﹣4<b<8B.﹣4<b<0C.b>8D.﹣2≤b≤82.一次函数的图象交x轴于(2,0),交y轴于(0,3),当函数值大于0时,x的取值范围是()A.x>2B.x<2C.x>3D.x<33.如图,在平面直角坐标系中,一次函数y=ax+b经过A,B两点,若点B的坐标为(3,0),则不等式ax+b>0的解是()A.x>0B.x>3C.x<0D.x<34.如图,在平面直角坐标系中,直线y=x−2与y=kx+b(k<0)相交于点M,点M的纵坐标为1,则关于x的不等式x−2≤kx+b的解集是()A.x≤1B.x<3C.x≤3D.x<15.用图象法解某二元一次方程组时,在同一平面直角坐标系中作出相应的两个一次函数图象,如图,则所解的二元一次方程组为().A .{y =−x +2y =2x −1B .{y =2x −1y =32x −12C .{y =2x −1y =−32x +52D .{y =−x +2y =32x −126.如图,直线y =kx +b 经过点A(−1,m)和点B(−2,0),直线y =2x 过点A ,则不等式2x <kx +b <0的解集为( )A .x <−2B .−2<x <−1C .−2<x <0D .−1<x <07.如图,直线y =k 1x +b 1与x 轴交于点(-4,0),直线y =k 2x +b 2与x 轴交于点(3,0),则不等式组{k 1x +b 1>0k 2x +b 2>0的解集是( )A .x >−4B .x <3C .-4<x <3D .x <−4或x >38.已知一次函数y =kx +b 的图象如图所示,当x <1时,y 的取值范围是( )A.-2<y<0B.-4<y<0C.y<-2D.y<-4二、填空题9.已知方程kx+b=0的解为x=3,那么直线y=kx+b与x轴的交点坐标为_____ 10.在平面直角坐标系中,如果点P的横坐标和纵坐标相等,则称点P为和谐点,请写出x−1图像上和谐点的坐标:__________.函数y=3411.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x 的方程kx+b=0的解为________.12.一次函数y=mx-n(m,n为常数)的图象如图所示,则不等式mx-n≥0的解集是______________.x+b的图像交于点P.下面有四个结13.如图,已知正比例函数y1=ax与一次函数y2=12论:①a<0;①b<0;①当x>0时,y1>0;①当x<−2时,y1>y2.其中正确的是______.(填序号)14.如图,已知一次函数y=mx+n的图像经过点P(−2,3),则关于x的不等式mx−m+n< 3的解集为_______.三、解答题15.如图,在平面直角坐标系中,直线y=−2x+10与x轴交于点B,与y轴交于点C,与直x交于点A,点M是y轴上的一个动点,设M(0,m).线y=12(1)若MA+MB的值最小,求m的值;(2)若直线AM将△ACO分割成两个等腰三角形,请求出m的值,并说明理由.16.如图,一次函数y=kx+b的图象经过点A(﹣2,6),与x轴交于点B,与正比例函数y=3x的图象交于点C,点C的横坐标为1.(1)求AB的函数表达式;S△BOC,求点D的坐标.(2)若点D在y轴负半轴,且满足S△COD=1317.如图,直线l1的函数解析式为y=−2x+4,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.(1)求直线l2的函数解析式;(2)求△ADC的面积;(3)在直线l2上是否存在点P,使得△ADP面积是△ADC面积的2倍?如果存在,请求出P坐标;如果不存在,请说明理由.18.已知直线y=kx+b经过点B(1,4),且与直线y=﹣x﹣11平行.(1)求直线AB的解析式并求出点C的坐标;(2)根据图象,写出关于x的不等式0<2x﹣4<kx+b的解集;(3)现有一点P在直线AB上,过点P作PQ①y轴交直线y=2x﹣4于点Q,若线段PQ的长为3,求P点坐标.。
19.2.3 一次函数与方程、不等式-2020-2021学年八年级数学下(人教版)(解析版)

19.2.3一次函数与方程、不等式一、单选题1.如图,已知一次函数y =kx+b 的图象经过点A(5,0)与B(0,﹣4),那么关于x 的不等式kx+b <0的解集是( )A .x <5B .x >5C .x <﹣4D .x >﹣4【答案】A【解析】 由题意可得:一次函数y =kx +b 中,y <0时,图象在x 轴下方,x <5,则关于x 的不等式kx +b <0的解集是x <5, 故选A .2.以方程组21y x y x =-+⎧⎨=+⎩的解为坐标的点在( )A .第一象限B .第二象限C .第三象限D .第四象限 【答案】A【分析】解方程组求得方程组的解,然后依据各象限内点的坐标特点求解即可.【解析】根据题意得:21x x -+=+, 解得:12x =,将12x=代入2y x=-+得32y=,故该点的坐标为13,22⎛⎫ ⎪⎝⎭.故选:A.【点睛】本题主要考查的是一次函数与二元一次方程组,求得方程组的解是解题的关键.3.以一个二元一次方程组中的两个方程作为一次函数画图象,所得的两条直线()A.有一个交点B.有无数个交点C.没有交点D.以上都有可能【答案】D【分析】二元一次方程组中的两个方程的解的个数可能有一个,或两个方程有无数个解,或无解,因而以一个二元一次方程组中的两个方程作为一次函数画图象,所得的两条直线有一个交点或有无数个交点或没有交点.【解析】解:由于方程组的解即为两个函数的交点坐标,而方程组的解有三种可能:①方程组无解;①有一个解;①有无数个解(此时两直线重合);所以A,B,C的情况都有可能.故选D.【点睛】一次函数的解析式就是二元一次方程,因而把方程组的解中的x的值作为横坐标,以y的值为纵坐标得到的点,就是一次函数的图象的交点坐标.方程组解的个数就是直线交点的个数.4.如图,一次函数y 1=x +b 与一次函数y 2=kx +3的图象交于点P (1,2),则关于不等式x +b >kx +3的解集是( )A .x >0B .x <0C .x >1D .x <1【答案】C【分析】 观察函数图象得到当x >1时,函数1y x b =+的图象都在23y kx =+的图象上方,所以关于x 的不等式x+b >kx+3的解集为x >1.【解析】解:当x >1时,函数1y x b =+的图象都在23y kx =+的图象上方,则x+b >kx+3,即不等式x+b >kx+3的解集为x >1.故选:C .【点睛】本题考查了一次函数与一元一次不等式:从函数图象的角度看,就是由函数的图像在平面直角坐标系内的高低位置来确定自变量的取值范围,掌握数型结合是解题的关键.5.若二元一次方程组35,31x y x y -=⎧⎨-=-⎩无解,则直线35y x =-与31y x 的位置关系为( )A .平行B .垂直C .相交D .重合【答案】A【解析】【分析】 二元一次方程可以化为一次函数,两个二元一次方程组的解就是两个函数的交点。
人教版八年级数学 下册 第十九章 19.2.3 一次函数与方程、不等式 同步练习题(含答案)

第十九章变量与函数19.2.3 一次函数与方程、不等式一、选择题1、直线y=-x+4和y=2x-5直线的交点坐标是()A、(3,1)B、(1,3)C、(3,2)D、(2,3)2、一次函数y=kx+b的图象如图所示,不等式kx+b>0的解集是()A.x>2B. x>4B.C. x<2 D. x<43、如图,直线y=kx+b经过点A(-1,-2)和点B(-2,0),直线y=2x过点A,则不等式2x<kx+b<0的解集为()A.x<-2 B.-2<x<-1 C.-2<x<0 D.-1<x<0第3题图第4题图4、同一直角坐标系中,一次函数y1=k1x+b与正比例函数y2=k2x的图象如图,则满足y1≥y2的x 取值范围是()A.x≤﹣2 B.x≥﹣2 C.x<﹣2 D.x>﹣25、一次函数y=3x-4的图象是一条直线,它由无数个点组成的,那么方程3x-y=4的解有( )A.1个B.2个C.3个D.无数个二、填空题6、若解方程x+2=3x-2得x=2,则当x_________时直线y=x+ 2 上的点在直线y=3x-2上相应点的上方.7、如图,平面直角坐标系中,经过点B(﹣4,0)的直线y=kx+b与直线y=mx+2相交于点A(-32,-1),则不等式mx+2<kx+b<0的解集为_____.8、若方程2x=4的解使关于x的一次不等式(a-1)x<a+5成立,则a的取值范围是9、以方程2x-y=1的解为坐标的点都在一次函数 ______的图像上。
10、如图,直线y=kx+b上有一点P(-1,3),回答下列问题:(1)关于x的方程kx+b=3的解是_______.(2)关于x的不等式kx+b>3的解是________.(3)关于x的不等式kx+b-3<0的解是______.三、解答题11、一次函数y=2x-a与x轴的交点是点(-2,0)关于y轴的对称点,求一元一次不等式2x-a≤0的解集.12、如图所示的折线ABC 表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t (分钟)之间的函数关系的图象.(1)写出y与t 之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?13、我校为开展研究性学习,准备购买一定数量的两人学习桌和三人学习桌,若购买1张两人学习桌,1张三人学习桌需230元;若购买2张两人学习桌,3张三人学习桌需590元.(1)求两人学习桌和三人学习桌的单价;(2)学校欲投入资金不超过6600元,购买两种学习桌共60张,以至少满足137名学生的需求,有几种购买方案?并求哪种购买方案费用最低?14、如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.(1)正方体的棱长为________cm.(2)求线段AB对应的函数解析式,并写出自变量x的取值范围.(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.15、我市某镇组织20辆汽车装运完A,B,C三种脐橙共100吨到外地销售.按计划,20辆车都要装运,每辆汽车只能装运同一种脐橙,且必须装满.根据下表提供的信息,解答以下问题.脐橙品种 A B C每辆汽车运载量/吨65 4每吨脐橙获得/百元121610(1)设装运A x之间的函数关系式.(2)如果装运每种脐橙的车辆数都不少于4辆,那么车辆的安排方案有几种?并写出每种安排方案.(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.参考答案:一、1、C 2、C 3、B 4、A 5、D二、6、y=3x7、﹣4<x<﹣3 2【解析】根据函数的图像,可知不等式mx+2<kx+b<0的解集就是y=mx+2在函数y=kx+b的下面,且它们的值小于0的解集是﹣4<x<﹣3 2 .故答案为:﹣4<x<﹣3 2 .8、x=3, x<39、y=2x-110、(1)x=-1;(2)x>-1;(3)x<-1;(4)x≤-1;(5)x>-1.解析:(1)因为P(-1,3)在一次函数y=kx+b图像上,所以kx+b=3得解为x=-1.(2) 不等式kx+b>3,恰好是一次函数y=kx+b函数值大于3的部分,对应的x>-1.(3)因为kx+b-3<0所以kx+b<3, 恰好是一次函数y=kx+b函数值大小于3的部分对应的x<-1.(4)观察图象可知,点(-1,3)在函数y=-3x上,构造函数y=-3x如解图.y=-3x比y=kx +b图像“高”的部分,∴不等式-3x≥kx+b的解为x≤-1.(5)不等式(k+3)x+b>0可变形为kx+b>-3x,仿照(4)可得x>-1.三、11、解:∵(-2,0)关于y轴得对称点为(2,0),把(2,0)在y=2x-a得0=4-a,解得a=4.当a=4时,2x-4≤0,解得x≤2.12、①当0<t≤3时,y=2.4;当t>3时,y=t-0.6.②2.4元;6.4元13、解:(1)设两人桌每张x元,三人桌每张y元,根据题意得,解得x=100,y=130.(2)设两人桌m张,则三人桌(60﹣m)张,根据题意可得,解得40≤m≤43.∵m为正整数,∴m为40、41、42、43,共有4种方案,设费用为W,W=100m+130(60﹣m)=﹣30m+7800,m=43时,W最小为6510元.14、【解析】(1)由题意可得:12秒时,水槽内水面的高度为10cm,12秒后水槽内高度变化趋势改变,故正方体的棱长为10cm.答案:10(2)设线段AB对应的函数解析式为:y=kx+b, ∵图象过A(12,10),B(28,20), ∴{12k +b =10,28k +b =20,解得{k =58,b =52, ∴线段AB对应的解析式为 y=58x+52(12≤x≤28).(3)∵28-12=16(s),∴没有立方体时,水面上升10cm,所用时间为16秒, ∵前12秒有立方体的存在,导致水面上升速度加快了4秒, ∴将正方体铁块取出,又经过4秒恰好将此水槽注满.15、解:(1)根据题意,装运A 种脐橙的车辆数为x ,装运B 种脐橙的车辆数为y ,那么装运C 种脐橙的车辆数为(20-x -y ),则有6x +5y +4(20-x -y )=100,整理得y =-2x +20(0≤x ≤10,且x 为整数).(2)由(1)知,装运A ,B ,C 三种脐橙的车辆数分别为x ,-2x +20,x ,由题意得-2x +20≥4,解得x ≤8.又∵x ≥4,∴4≤x ≤8.∵x 为整数,∴x 的值为4,5,6,7,8,∴安排方案共有5种.方案一:装运A 种脐橙4车,B 种脐橙12车,C 种脐橙4车; 方案二:装运A 种脐橙5车,B 种脐橙10车,C 种脐橙5车; 方案三:装运A 种脐橙6车,B 种脐橙8车,C 种脐橙6车; 方案四:装运A 种脐橙7车,B 种脐橙6车,C 种脐橙7车; 方案五:装运A 种脐橙8车,B 种脐橙4车,C 种脐橙8车.(3)设利润为W 百元,则W =6x ×12+5(-2x +20)×16+4x ×10=-48x +1600(4≤x ≤8).∵-48<0,∴W 的值随x 的增大而减小.W 最大=-48×4+1 600=1 408(百元)=14.08(万元).。
八年级数学下册 《19.2.3一次函数与方程、不等式》同步练习题含答案

《19.2.3一次函数与方程、不等式》同步练习题一、选择题(每小题只有一个正确答案)1.如图,函数y=2x和y=ax+4的图象相交于点A(m, 2),则不等式2x<ax+4的解集为()A. x>3B. x<1C. x>1D. x<32.一次函数y=kx+b的图象如图所示,不等式kx+b>0的解集是()A. x>2B. x>4C. x<2D. x<412则关于x的不等式kx+b>mx+n的解集是()A. x>2B. x<2C. x>1D. x<14.观察函数y1和y2的图象,当x=0,两个函数值的大小为()A. y1>y2B. y1<y2C. y1=y2D. y1≥y25.观察下列图像,可以得出不等式组310{0.510xx+>-+>的解集是( )A. x <13 B. -13<x <0 C. 0<x <2 D. -13<x <2 6.如图,已知直线11y k x m =+和直线22y k x n =+交于点()1,2P -,则关于x 的不等式()12k k x m n ->-+的解是( ).A. 2x >B. 1x >-C. 12x -<<D. 1x <-7.已知方程kx+b=0的解是x=3,则函数y=kx+b 的图象可能是( )A. B. C. D.二、填空题8.如图,平面直角坐标系中,经过点B (﹣4,0)的直线y=kx+b 与直线y=mx+2相交于点A(-32,-1),则不等式mx+2<kx+b <0的解集为_____.9.函数y=kx+b 的图象如图所示,则方程kx+b=0的解为________,不等式kx+b>0的解集为_________,不等式kx+b -3>0的解集为________.10.一次函数y=kx+b 的图象经过A(-1,1)和B(-√7 ,0),则不等式组0<kx +b <−x 的解为________________.11.已知一次函数的图象过点()35,与()49--,,那么这个函数的解析式是__________,则该函数的图象与y 轴交点的坐标为__________________. 12.如图,直线y =kx +b 上有一点P (-1,3),回答下列问题:(1)关于x 的方程kx +b =3的解是_______. (2)关于x 的不等式kx +b >3的解是________. (3)关于x 的不等式kx +b -3<0的解是______. (4)求不等式-3x ≥kx +b 的解. (5)求不等式(k+3)x +b >0的解.三、解答题13.画出函数y =2x -4的图象,并回答下列问题: (1)当x 取何值时,y >0?(2)若函数值满足-6≤y ≤6,求相应的x 的取值范围.14.已知:直线y =2x +4与x 轴交于点A ,与y 轴交于点B ,坐标原点为O . (1)求点A ,点B 的坐标.(2)求直线y =2x +4与x 轴、y 轴围成的三角形的面积. (3)求原点O 到直线y =2x +4的距离.15.在平面直角坐标系xoy 中,已知一次函数()10y mx m =≠与()20y kx b k =+≠相交于点()12A ,,且()20y kx b k =+≠与y 轴交于点()03B ,. (1)求一次函数1y 和2y 的解析式; (2)当120y y >>时,求出x 的取值范围.16.已知直线y=kx+5交x 轴于A ,交y 轴于B 且A 坐标为(5,0),直线y=2x ﹣4与x 轴于D ,与直线AB 相交于点C . (1)求点C 的坐标;(2)根据图象,写出关于x 的不等式2x ﹣4>kx+5的解集; (3)求△ADC 的面积.参考答案1.B【解析】∵函数y =2x 的图象经过点A(m, 2), ∴2m =2, 解得:m =1, ∴点A(1, 2),当x <1时,2x <ax +4,即不等式2x <ax +4的解集为x <1. 故选:B . 2.C【解析】kx+b >0即是一次函数的图象在x 轴的上方,由图象可得x <2,故选C. 3.B【解析】试题解析:根据表可得1y kx b =+ 中y 随x 的增大而减小;2y mx n =+中y 随x 的增大而增大.且两个函数的交点坐标是(2,1).则当2x < 时, kx b mx n +>+. 故选B . 4.A【解析】试题解析:由图可知:当x=0时,y 1=3,y 2=2, y 1>y 2 . 故选A . 5.D【解析】由图象知,函数y =3x +1与x 轴交于点1,03⎛⎫- ⎪⎝⎭即当x >13-时,函数值y 的范围是y >0,因而当y >0时,x 的取值范围是x >13-,函数y =3x +1与x 轴交于点(2,0),即当x <2时,函数值y 的范围是y >0,因而当y >0时,x 的取值范围是x <2,所以,原不等式组的解集是13-<x <2,故选D.6.B【解析】根据图形,找出直线y 1在直线y 2上方部分的x 的取值范围即可. 解:由图形可,当x >−1时,k 1x +m >k 2x +n , 即(k 1−k 2)x >−m +n ,所以,关于x 的不等式(k 1−k 2)x >−m +n 的解集是x >−1. 故选B. 7.C【解析】试题解析:由于方程kx+b=0的解是x=3,即x=3时,y=0,所以直线y=kx+b 经过点(3,0), 故选C. 8.﹣4<x <﹣32【解析】根据函数的图像,可知不等式mx+2<kx+b <0的解集就是y=mx+2在函数y=kx+b 的下面,且它们的值小于0的解集是﹣4<x <﹣32. 故答案为:﹣4<x <﹣32. 9. x=1 x<1 x<0【解析】由图可知,函数y=kx+b 的图象和x 轴相交于点(1,0),和y 轴相交于点(0,3), ∴方程kx+b=0的解为:x=1; 不等式kx+b>0的解集为:x<1; 不等式kx+b -3>0的解集为:x<0.故答案为:(1). x=1 (2). x<1 (3). x<0.10.-√7 <x<-1【解析】试题解析:由题意可得:一次函数图象在y=1的下方时x <-1,在y=0的上方时x >-√7,∴关于x 的不等式0<kx+b <1的解集是-√7<x <-1. 故答案为:-√7<x <1. 11. y=2x-1 (0,-1)【解析】设该一次函数的解析式为y =kx +b (k ≠0).将点(3, 5)和(-4, -9)分别代入该一次函数的解析式,得35{49k b k b +=-+=-,解之,得2{1k b ==-, ∴该一次函数的解析式为y =2x -1.∵函数图象与y 轴交点的横坐标为零, 又∵当x =0时, 2011y =⨯-=-,∴该函数的图象与y 轴交点的坐标为(0, -1). 故本题应依次填写:y =2x -1;(0, -1).12.(1)x =-1;(2)x >-1;(3)x <-1;(4)x ≤-1;(5)x >-1.【解析】试题分析:(1)利用一次函数图像性质与一元一次方程的关系.(2)(3)(4)(5)利用一次函数图像性质与一元一次不等式的关系试题解析:(1)因为P(-1,3)在一次函数y=kx+b图像上,所以kx+b=3得解为x=-1.(2) 不等式kx+b>3,恰好是一次函数y=kx+b函数值大于3的部分,对应的x>-1.(3)因为 kx+b-3<0所以kx+b<3, 恰好是一次函数y=kx+b函数值大小于3的部分对应的x<-1.(4)观察图象可知,点(-1,3)在函数y=-3x上,构造函数y=-3x如解图.y=-3x比y=kx+b图像“高”的部分,∴不等式-3x≥kx+b的解为x≤-1.(5)不等式(k+3)x+b>0可变形为kx+b>-3x,仿照(4)可得x>-1.13.(1)x>2 (2)-1≤x≤5【解析】试题分析求出函数图象与两坐标轴的交点,利用两点法作出图象即可;(1)求出直线与x轴的交点,再根据y>0确定x的取值范围;(2)分别求出y=6和y=-6时x的值,根据-6≤y≤6,求相应的x的取值范围.试题解析:函数y=2x-4的图象如图所示:(1)令y=0,则2x-4=0,解得:x=2由图象得:当x>2时,y>0;(2)当y=6时,则2x-4=6解得:x=5;当y=-6时,则2x-4=-6解得:x=-1∵-6≤y≤6,∴-1≤x≤5.14.(1)B:(0,4)(2)4(3)4√55【解析】试题分析:(1)分别令x=0、y=0求解即可得到与坐标轴的交点坐标;(2)根据三角形的面积公式列式计算即可得解;(3)先根据勾股定理求出AB的长,再利用面积法可求出原点O到直线y=2x+4的距离.(1)∵y=2x+4,当y=0时,2x+4=0,2x=−4x=−2.∴A:(−2,0).当x =0时,y =4, ∴B:(0,4).(2)∵A:(−2,0)B:(0,4) ∴OA =2 OB =4 ∴S △AOB =12×2×4=4(3)作OM ⊥AB 于M 点.∵OA =2 OB =4,∴AB =2√5,∴OA ×OB =AB ×OM2×4=2√5×OMOM =4√55, ∴点O 到直线y =2x +4的距离为4√55. 15.(1) 23y x =-+ ;(2) 1<<3x .【解析】∵一次函数()10y mx m =≠过点()12A ,∴2m = ∴12y x =;又∵一次函数()20y kx b k =+≠经过点()12A ,, ()03B , ∴2{3k bb=+=;解得: 1{ 3k b =-=∴23y x =-+;(2)1<<3x.16.(1)C(3,2);(2) x>3;(3)3.【解析】(1)根据点A的坐标利用待定系数法可求出直线AB的解析式,联立直线AB、CD 的解析式方程组,通过解方程即可求出点C的坐标;(2)根据直线AB、CD的上下位置关系结合点C的坐标,即可得出不等式2x-4>kx+5的解集;(3)利用一次函数图形上点的坐标特征可求出点D的坐标,再根据三角形的面积公式即可求出△DC的面积.解:(1)∵直线y=kx+5经过点A(5,0),∴5k+5=0解得k=-1∴直线AB的解析式为:y=-x+5;5{24y xy x=-+=-,解得:3{2xy==,∴点C(3,2)(2)观察函数图象可知:当x>3时,直线y=2x-4在直线y=-x+5的上方,∴不等式2x-4>kx+5的解集为x>3.(3)把y=0代入y=2x﹣4得2x﹣4=0.解得x=2∴D(2,0)∵A(5,0),C(3,2)∴AD=3S △ADC =1232=3。
2020-2021学年八年级数学人教版下册 19.2.3一次函数与方程、不等式 同步习题(含答案)
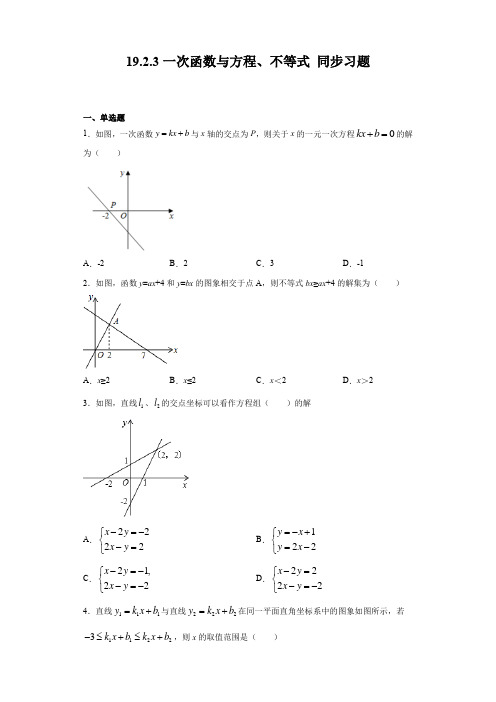
19.2.3一次函数与方程、不等式 同步习题一、单选题1.如图,一次函数y kx b =+与x 轴的交点为P ,则关于x 的一元一次方程0kx b +=的解为( )A .-2B .2C .3D .-12.如图,函数y =ax +4和y =bx 的图象相交于点A ,则不等式bx ≥ax +4的解集为( )A .x ≥2B .x ≤2C .x <2D .x >23.如图,直线1l 、2l 的交点坐标可以看作方程组( )的解A .2222x y x y -=-⎧⎨-=⎩B .122y x y x =-+⎧⎨=-⎩C .21,22x y x y -=-⎧⎨-=-⎩D .2222x y x y -=⎧⎨-=-⎩4.直线111y k x b =+与直线222y k x b =+在同一平面直角坐标系中的图象如图所示,若11223k x b k x b -≤+≤+,则x 的取值范围是( )A .1x ≤-B .51x -<≤C .51x -≤<-D .11x -≤≤5.用图象法解二元一次方程组020kx y b x y -+=⎧⎨-+=⎩时,小英所画图象如图所示,则方程组的解为( )A .12x y =⎧⎨=⎩B .21x y =⎧⎨=⎩C .12.5x y =⎧⎨=⎩D .13x y =⎧⎨=⎩6.已知方程组2300x y ax y c -+=⎧⎨-+=⎩的解为11x y =-⎧⎨=⎩,则一次函数23y x =+与y ax c =+的图像的交点坐标是( ) A .(-1,1)B .(1,-1)C .(2,-2)D .(-2,2)7.一次函数1y kx b =+与2y mx n =+的图象如图所示,则以下结论:①0k >;①0b >;①0m >;①0n >;①当3x =时,12y y >,正确的个数是( )A .1个B .2个C .3个D .4个8.若直线y kx b =+经过点()1,0和()0,1-,则下列说法正确的是( )A .1b =B .函数值y 随着x 增大而减小C .关于x 的方程0kx b +=的解是1x =-D .关于x 的不等式0kx b +>的解集是1x >9.如图,一次函数3y x =-+与一次函数2y x m =+的图象交于点()2,n -,则关于x 的不等式组3023x x m x -+>⎧⎨+>-+⎩的解集为( )A .2x >-B .3x <C .23x -<<D .03x <<10.如图,正比例函数1y ax =与一次函数212y x b =+的图象交于点P .下面四个结论:①0a <; ①0b <;①不等式12ax x b >+的解集是2x <-; ①当0x >时,120y y >.其中正确的是( )A .①①B .①①C .①①D .①①二、填空题11.已知一次函数y =ax +b (a 、b 是常数),x 与y 的部分对应值如下表:不等式ax +b >0的解集是_____.12.如图,直线y kx b =+经过点(,2)A m -和点(2,0)B -,直线2y x =过点A ,则不等式02x kx b >>+的解集为_______________.13.如图,已知函数y =ax +b (a ,b 为常数且a ≠0)和函数y =kx (k 为常数且k ≠0) 的图象交于点P ,则根据图象可得,关于x 的不等式ax +b >kx 的解集是___________.14.如图,已知函数y ax b =+和y kx =的图象交于点P ,则二元一次方程组y ax b y kx=+⎧⎨=⎩的解是________.15.已知下表中的点(x ,y )都在函数y =x +n 的图像上,下列结论:①y 随x 的增大而增大;①当x >0时,y >2;①x +n =0的解为x =﹣2.其中正确的结论有____(填序号).三、解答题16.已知直线y=kx+b 经过点A (5,0),B (1,4).(1)求直线AB 的解析式;(2)根据图象,写出关于x 的不等式2x ﹣4>kx+b 的解集.17.如图,一次函数12y x m =-+与正比例函数2y kx =的图象交于点A(2,1); (1)求出m ,k 的值.(2)若12y y >,请直接写出x 的取值范围.18.如图,直线1:1l y x =+与直线2:l y mx n =+相交于点(1,)P b .(1)直接写出1x mx n +>+的解集;(2)将1y x =+与y mx n =+组成方程组,不解方程组,请直接写出它的解. (3)直线3:l y nx m =+是否也经过点P ?请说明理由.参考答案1.A 2.A 3.A 4.D 5.D 6.A 7.C 8.D 9.C 10.D 11.x <1 12.-1<x <0 13.x <-2 14.42x y =-⎧⎨=-⎩15.①①①16.(1)y=-x+5;(2)x>3. 17.(1)15,2m k ==;(2)2x <. 18.(1)1x >;(2)12x y =⎧⎨=⎩;(3)经过,理由略。
19.2.3 一次函数与方程、不等式 人教版八年级数学下册课时练习(含答案)

19.2.3一次函数与方程、不等式1.如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )A.x=2B.x=0C.x=-1D.x=-32.下列图象中,以方程-2x+y-2=0的解为坐标的点组成的图象是( )3.一次函数y=kx+b的图像如图所示,则方程kx+b=0的解为( ).A.x=2B.y=2C.x=-1D.y=-14.如图,直线y=kx+b交坐标轴于A(﹣2,0)、B(0,3)两点,则不等式kx+b>0的解集是( )A.x>﹣2B.x>3C.x<﹣2D.x<35.如图,直线y=kx+b与y轴交于点(0,3)、与x轴交于点(a,0),当a满足﹣3≤a<0时,k的取值范围是()A.﹣1≤k<0B.1≤k≤3C.k≥1D.k≥36.如图,直线y=kx+b经过点A(3,1)和点B(6,0),则不等式0<kx+b<1解集为( )A.x<0B.0<x<3C.x>6D.3<x<67.如图,是在同一坐标系内作出的一次函数l1.l2的图象,设l1:y=k1x+b1,l2:y=k2x+b2,则方程组的解是()A. B. C. D.8.当自变量x_______时,函数y=5x+4的值大于0;当x_______时,函数的值小于0.9.如图,已知函数y=x+b和y=ax+3图像交点为P,则不等式x+b>ax+3解集为_____.10.已知点A(0,m)和点B(1,n)都在函数y=﹣3x+b的图象上,则m n.(在横线上填“>”、“<”或“=”)11.已知两条直线y=kx-2和y=2x+b相交于点(-2,4),则这两条直线与y轴所围成的三角形的面积为_______.12.如图,平面直角坐标系中,▱OABC的顶点A坐标为(6,0),C点坐标为(2,2),若直线y=mx+2平分▱OABC的周长,则m的值为.13.某公园计划在健身区铺设广场砖,现有甲、乙两个工程队参加竞标,甲工程队铺设广场砖的造价y甲(元)与铺设面积x(m2)的函数关系如图所示;乙工程队铺设广场砖的造价y乙(元)与铺设面积x(m2)满足函数关系式为y乙=kx.(1)根据图写出甲工程队铺设广场砖的造价y甲(元)与铺设面积x(m2)的函数关系式;(2)如果狮山公园铺设广场砖的面积为1600 m2,那么公园选择哪个工程队施工更合算?14.已知一次函数y=-2x+4,完成下列问题:(1)求此函数图像与x轴、y轴的交点坐标;(2)画出此函数的图像;观察图像,当0≤y≤4时,x的取值范围是;(3)平移一次函数y=-2x+4的图像后经过点(-3,1),求平移后的函数表达式.15.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).(1)求b的值;(2)不解关于x,y的方程组,请你直接写出它的解;(3)直线l3:y=nx+m是否也经过点P?请说明理由.参考答案1.D2.B3.C4.A.5.C6.D7.B8.答案为:>-0.8,<-0.89.答案为:x>110.答案为:>.11.答案为:1012.答案为:﹣0.25.13.解:(1)y甲=(2)当k>45时,选择甲工程队更合算;当0<k<45时,选择乙工程队更合算;当k=45时,选择两个工程队的花费一样.14.解:(1)当x=0时y=4,∴函数y=-2x+4的图像与y轴的交点坐标为(0,4);当y=0时,-2x+4=0,解得:x=2,∴函数y=-2x+4的图像与x轴的交点坐标(2,0).(2)图像略;观察图像,当0≤y≤4时,x的取值范围是0≤x≤2.(3)设平移后的函数表达式为y=-2x+b,将(-3,1)代入得:b+6=1,∴b=-5,∴y=-2x-5.答:平移后的直线函数表达式为:y=-2x-5.15.解:(1)2 (2)x=1,y=2; (3)经过点P。
人教版八年级下册 19.2.3《一次函数与方程、不等式》同步训练( 解析版)

=
1x+ 3
4 的图象相交于(–1,1),(2,2)两点.当 3
y1 y2 时,x 的取值范围是( )
A.x<–1
B.x<–1 或 x>2
C.x>2
D.–1<x<2
10.已知一次函数 y = ax + b 的图象过第一、二、四象限,且与 x 轴交于点(2,0), 则关于 x 的不等式 a(x −1) − b 0 的解集为
人教版八年级下册 19.2.3《一次函数与方程、不等式》 同步训练(带解析)
一、单选题
1.已知一次函数 y = kx + b 的图象如图所示,当 x 2 时,y 的取值范围是 ( )
A. y −4 B. −4 y 0 C. y 2 D. y 0
2.如图,函数 y1=﹣2x 与 y2=ax+3 的图象相交于点 A(m,2),则关于 x 的不等 式﹣2x>ax+3 的解集是( )
13. x 3
【解析】
解: y2 − y1 = (k2x + b2 ) − (k1x + b1 ) = (k2 − k1 ) x + b2 − b1
由图象可知:在交点的左侧, y2 y1
即当 x 3 时, y2 − y1 0
∴ (k2 − k1 ) x + b2 − b1 0 的解集是 x 3 .
M (3, −1) ,则关于 x 的不等式 −x + a 2x + b 的解集为 ( )
A. x 3
B. x 3
C. x −1
D. x −1
7.如图,直线 y = −x + 2 与 y = ax + b ( a 0 且 a,b 为常数)的交点坐标为(3,﹣ 1),则关于 x 的不等式 −x + 2 ax + b 的解集为( )
新人教版八年级数学下册19.2.3 一次函数与方程、不等式(同步练习)
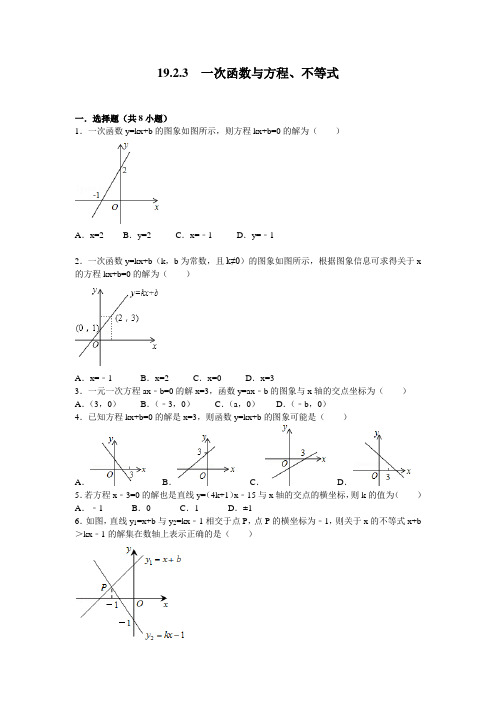
19.2.3 一次函数与方程、不等式一.选择题(共8小题)1.一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为()A.x=2 B.y=2 C.x=﹣1 D.y=﹣12.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x 的方程kx+b=0的解为()A.x=﹣1 B.x=2 C.x=0 D.x=33.一元一次方程ax﹣b=0的解x=3,函数y=ax﹣b的图象与x轴的交点坐标为()A.(3,0)B.(﹣3,0)C.(a,0)D.(﹣b,0)4.已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是()A.B.C.D.5.若方程x﹣3=0的解也是直线y=(4k+1)x﹣15与x轴的交点的横坐标,则k的值为()A.﹣1 B.0 C.1 D.±16.如图,直线y1=x+b与y2=kx﹣1相交于点P,点P的横坐标为﹣1,则关于x的不等式x+b >kx﹣1的解集在数轴上表示正确的是()A.B.C.D.7.如图,直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2,则关于x的不等式﹣x+m >nx+4n>0的整数解为()A.﹣1 B.﹣5 C.﹣4 D.﹣38.如图,一次函数y=kx+b的图象经过A、B两点,则不等式kx+b<0的解集是()A.x<0 B.0<x<1 C.x<1 D.x>1二.填空题(共10小题)9.若直线y=2x+b与x轴交于点(﹣3,0),则方程2x+b=0的解是_________.10.如图是一次函数y=kx+b的图象,则方程kx+b=0的解为_________.11.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=0的解为_________.12.如图,已知直线y=ax﹣b,则关于x的方程ax﹣1=b的解x=_________.13.如图,直线y=kx+b分别交x轴和y轴于点A、B,则关于x的方程kx+b=0的解为_________.14.如图,已知函数y=2x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),根据图象可得方程2x+b=ax﹣3的解是_________.15.如图,已知函数y=2x+b与函数y=kx﹣3的图象交于点P,则不等式kx﹣3>2x+b的解集是_________.16.如图,直线y=kx+b过A(﹣1,2)、B(﹣2,0)两点,则0≤kx+b≤﹣2x的解集为_________.17.一次函数y1=kx+b与y2=x+a的图象如图,则kx+b>x+a的解集是_________.18.如图,函数y=kx和的图象相交于A (a,2),则不等式的解集为_________.三.解答题(共4小题)19.如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:(1)方程kx+b=0的解;(2)式子k+b的值;(3)方程kx+b=﹣3的解.20.如图,直线l1:y=2x与直线l2:y=kx+3在同一平面直角坐标系内交于点P.(1)写出不等式2x>kx+3的解集:_________;(2)设直线l2与x轴交于点A,求△OAP的面积.21.在平面直角坐标系x0y中,直线y=kx+b(k≠0)过(1,3)和(3,1)两点,且与x轴、y轴分别交于A、B两点,求不等式kx+b≤0的解.22.在直角坐标系xOy中,直线y=kx+b(k≠0)经过(﹣2,1)和(2,3)两点,且与x 轴、y轴分别交于A、B两点,求不等式kx+b≥0的解集.(赠品,不喜欢可以删除)数学这个家伙即是科学界的“段子手”,又是“心灵导师”一枚。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
19.2.3 一次函数与方程、不等式基础闯关全练1.直线y=3x+9与x 轴的交点坐标是( )A .(0,-3)B .(-3,0)C .(0,3)D .(3,0)2.直线y=2x+b 与并轴的交点坐标是(2,0),则关于x 的方程2x+b=0的解是x=_______. 3.一次函数y=ax+b 的图象如图19-2-3-1所示,则不等式ax+b ≥0的解集是( )A .x ≥2B .x ≤2C .x ≥4D .x ≤44.如图19-2-3-2所示,一次函数y=kx+b (k <0)的图象经过点A(2,3).当y <3时,x 的取值范围是_______.5. 一次函数y=7-4x 和y=1-x 的图象的交点坐标为_______,则方程组⎩⎨⎧=+=+1,74y x y x 的解为_______. 能力提升全练1.如图19-2-3-3,直线y=-x+m 与y=nx+4n(n ≠0)的交点的横坐标为-2.则关于x 的不等式-x+m >nx+4n >0的整数解为( )A .-1B .-5C .-4D .-3 2.已知直线y=2x-4与y=5-x.(1)在同一直角坐标系中画出它们的图象; (2)求出它们的交点A 的坐标;(3)求出这两条直线与y 轴围成的三角形的面积.三年模拟全练 一、选择题1.如图19-2-3-4,函数y=kx+b 与y=mx+n 的图象交于点P(1,2),那么关于x ,y 的方程组⎩⎨⎧+=+=n mx y b kx y ,的解是( )A .⎩⎨⎧==21y x B .⎩⎨⎧==12y x C .⎩⎨⎧==32y x D .⎩⎨⎧==31y x2.如图19-2-3-5,一次函数y=k+b(k≠0)过点A(-11,0),B(-1,1),则关于x的不等式O<kx+b<-x的解集为()A.O<x<1 B.x<-1 C.-11<x<-1 D.-11<x<1 二、填空题3.如图19-2-3-6,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可知关于x的不等式3x+b>ax-3的解集是_______.三、解答题4.如图19-2-3-7,直线l₁:y=2x与直线l₂:y=kx+3在同一平面直角坐标系内交于点P.(1)直接写出不等式2x>kx+3的解集.(2)设直线l₂与x轴交于点A,求△OAP的面积.五年中考全练一、选择题1.如图19-2-3-8,直线y=kx+3经过点(2,0),则关于x的不等式kx+3>0的解集是()A.x>2 B.x<2 C.x≥2 D.x≤2二、填空题2.已知二元一次方程组⎩⎨⎧-=+-=-22,5yxyx的解为⎩⎨⎧=-=,1,4yx则在同一平面直角坐标系中,直线l₁:y=x+5与直线l₂:y=-x21-1的交点坐标为_______.3.如图19-2-3-9,一次函数y=-x-2与y=2x+m的图象交于点P(n,-4),则关于x的不等式组⎩⎨⎧----+2,22<<xxmx的解集为_______.三、解答题4.如图19-2-3-10,直线l₁:y=2x+1与直线l₂:y=mx+4相交于点P(1,b).(1)求b,m的值;(2)垂直于x轴的直线x=a与直线l₁,l₂分别交于点C,D,若线段CD长为2,求a的值.核心素养全练已知甲、乙两车分别从相距300千米的A、B两地同时出发,相向而行,甲到B地后立即返回,图19-2-3-11是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.(1)请直接写出甲、乙两车离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数关系式,并标明自变量x的取值范围:(2)它们在行驶的过程中有几次相遇?求出每次相遇的时间.19.2.3一次函数与方程、不等式1.B当y=0时,3x+9=0,解得x=-3.故直线与x轴的交点坐标为(-3,0).2.答案2解析由一次函数与一元一次方程的关系可知一次函数图象与x轴交点的横坐标即为一元一次方程的解,即x=2.3.B通过观察图象可以看出ax+b≥0的解集是x≤2,故选B.4.答案x>2解析因为直线呈下降趋势,点A的坐标为(2,3),所以求当y<3时x的取值范围,即求直线上纵坐标小于3的点所对应的横坐标的取值集合,从图象上可以看出x的取值范围为x>2.5.答案(2,-1);⎩⎨⎧-==12yx解析在同一直角坐标系中作出一次函数y=7-4x与y=1-x的图象,如图所示,由图象可知交点坐标为(2,-1).由y=7-4x,得4x+y=7.由y=1-x,得x+y=1,故方程组⎩⎨⎧=+=+1,74yxyx的解为⎩⎨⎧-==12yx.1.D ∵直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,且x<-2时,y=-x+m 的图象在y=nx+4n的图象的上方,∴关于x的不等式-x+m>nx+4n的解集为x<-2.令y=nx+4n=0,得x=-4,∴nx+4n >0的解集是x >-4, ∴-x+m >nx+4n >0的解集是-4<x <-2, 故所求的整数解为-3. 2.解析(1)如图.(2)因为点A 同时在两条直线上,所以点A 的坐标就是方程组⎩⎨⎧-=-=x y x y 5,42的解.解方程组得⎩⎨⎧==,,23y x 所以点A 的坐标为(3,2). (3)由图象可知BC=9,故两条直线与y 轴围成的三角形的面积CAB△S =21BC •|x |A =21×9×3=227. 一、选择题1.A 方程组的解就是两函数图象的交点P 的横、纵坐标,即x=1.y=2.故选A .2.C 构造函数y=-x ,则函数y=-x 与已知函数y=kx+b 都经过点B (-1,1),即B 是两函数图象的交点,结合图象可知:当x <-1时,一次函数y=kx+b(k ≠0)的图象在y=-x 的图象的下方,即kx+b <-x ,因为函数y=kx+b 的图象与x 轴的交点为A (-11,0),所以当x >-11时,kx+b >0.所以关于x 的不等式0<kx+b <-x 的解集为-11<x <-1.故选C . 二、填空题3.答案x >-2解析 ∵函数y=3x+b 和y=ax-3的图象交于点P(-2,-5),当x >-2时,函数y=3x+b 的图象在函数y=ax-3的图象的上方,∴不等式3x+b >ax-3的解集是x >-2. 三、解答题4.解析(1)从题图中得出当x >1时,y=2x 的图象在y=kx+3图象的上方,∴不等式2x >kx+3的解集为x >1. (2)把x=1代入y=2x ,得y=2,∴点P 的坐标为(1,2),∵点P 在直线y=kx+3上,∴2=k+3,解得k=-1, ∴直线l ₂:y=-x+3,当y=0时,由0=-x+3得x=3,∴点A 的坐标为(3,0), ∴OAP△S =21×3×2=3.一、选择题1.B 由题图可知,函数y=kx+3随着x 的增大而减小,与x 轴的交点为(2,0),若kx+3>0,即y >0,即求y=kx+3的图象在x 轴上方时x 的取值范围,故不等式kx+3>0的解集为x <2.二、填空题2.答案(-4,1)解析y=x+5即x-y=-5,y=-21x-1即x+2y=-2,所以二元一次方程组⎩⎨⎧-=+-=-22,5y x y x 的解即两直线交点的坐标,所以直线l ₁:y=x+5与直线l ₂:y=-21x-1的交点坐标为(-4,1). 3.答案-2<x <2解析 ∵y=-x-2过点P(n ,-4), ∴-n-2=-4,解得n=2. ∴P 点的坐标为(2,-4),观察图象知2x+m <-x-2的解集为x <2. 解不等式-x-2<0可得x >-2. ∴不等式组⎩⎨⎧----+02,22<<x x m x 的解集是-2<x <2.三、解答题4.解析(1)把点P(1,b)代入y=2x+1,得b=3,把(1,3)代入y=mx+4得3=m+4.解得m=-1.(2)由(1)知直线l ₂的解析式为y=-x+4,故直线x=a 与直线l ₁的交点C 的坐标为(a ,2a+1),与直线l ₂的交点D 的坐标为(a ;-a+4). ∵CD=2,∴|2a+1-(-a+4)|=2,即|3a-3|=2. ∴3a-3=2或3a-3=-2,∴a=3135或. 核心素养全练解析 (1)⎪⎩⎪⎨⎧≤-≤≤=),4273(80540),30(100x x x x y <甲⎪⎭⎫ ⎝⎛≤≤=215040x x y 乙.(2)由题意可知有两次相遇, ①当O ≤x ≤3时,100x+40x=300.解得x=715(符合题意); ②当3<x ≤427时,(540-80x)+40x=300,解得x=6(符合题意).综上所述,两车第一次相遇的时间为第715小时,第二次相遇的时间为第6小时.。
