共顶点等腰三角形产生相似三角形模型
相似三角形12种基本模型证明

相似三角形12种基本模型证明相似三角形是指拥有相同形状但不同大小的三角形。
在三角形中,如果它们的对应角度相等,那么它们就是相似三角形。
相似三角形一般用比例关系表示。
下面是相似三角形12种基本模型的证明:1. AAA相似模型如果两个三角形的三个角分别相等,则它们是相似的。
证明:三角形的三个角之和为180度。
如果两个三角形的三个角分别相等,那么它们的三个角和也相等,即这两个三角形的三个角和相等,因此它们是相似的。
2. AA相似模型如果两个三角形中有两个对应角相等,则它们是相似的。
证明:假设两个三角形的对应角分别为A和A’,B和B’,C和C’。
由于A和A’相等,B和B’相等,那么它们的第三个对应角C和C’也必须相等。
因此,这两个三角形的三个角分别相等,它们是相似的。
3. SSS相似模型如果两个三角形的三条边分别成比例,则它们是相似的。
证明:假设两个三角形的三条边为a, b, c和a’, b’, c’。
由于它们是成比例的,即a/a’= b/b’= c/c’,那么它们的三边比例相等,即它们是相似的。
4. SAS相似模型如果两个三角形中有两条边成比例,且夹角相等,则它们是相似的。
证明:假设两个三角形的两条边为a, b和a’, b’,夹角为C和C’。
由于它们是成比例的,即a/a’= b/b’,那么它们的三边比例相等。
又由于它们的夹角相等,即C = C’,因此它们是相似的。
5. ASA相似模型如果两个三角形中有两个角相等,且它们对应的两条边成比例,则它们是相似的。
证明:假设两个三角形的两个对应角分别为A和A’,B和B’,且对应的两条边分别为a, a’和b, b’。
由于它们的两条边成比例,即a/a’= b/b’,那么它们的三边比例相等。
又由于它们的两个角相等,即A = A’,因此它们是相似的。
6. HL相似模型如果两个三角形中有一条边和一条斜边分别成比例,且这两条边夹角相等,则它们是相似的。
证明:假设两个三角形的一条边为b,斜边为c,且夹角为C,另一个三角形的一条边为b’,斜边为c’,且夹角为C’。
三角形相似基本模型

三角形相似基本模型一、引言三角形是几何学中最基本的图形之一,而相似三角形则是三角形中的重要概念之一。
相似三角形是指具有相同形状但大小不同的两个三角形。
在实际生活中,我们经常会遇到需要利用相似三角形来解决问题的情况。
本文将介绍三种常见的三角形相似基本模型,并通过具体例子来说明其应用。
二、模型一:角-角相似在角-角相似模型中,两个三角形的对应角度相等。
具体来说,如果两个三角形的角度分别为A、B、C和A'、B'、C',且满足A=A'、B=B'、C=C',那么这两个三角形是相似的。
例如,已知三角形ABC与三角形A'B'C'的角度分别为∠A=40°、∠B=60°、∠C=80°,且∠A'=40°、∠B'=60°、∠C'=80°,则可以得出三角形ABC与三角形A'B'C'是相似的。
在实际应用中,我们可以利用角-角相似模型解决一些测量问题。
例如,在无法直接测量某个角度时,我们可以利用已知的相似三角形来计算出该角度的近似值。
三、模型二:边-边-边相似在边-边-边相似模型中,两个三角形的对应边长成比例。
具体来说,如果两个三角形的边长分别为a、b、c和a'、b'、c',且满足a/a'=b/b'=c/c',那么这两个三角形是相似的。
例如,已知三角形ABC的边长分别为AB=4cm、BC=6cm、AC=8cm,而三角形A'B'C'的边长分别为A'B'=8cm、B'C'=12cm、A'C'=16cm,则可以得出三角形ABC与三角形A'B'C'是相似的。
在实际应用中,我们经常会遇到需要测量无法直接测量的边长的情况。
中考数学几何专项——相似模型(相似三角形)

相似模型【相似模型一:A 字型】 特征 模型结论DE ∥BCCBCBBC D E ADA E DA AD:AB=AE:AC=DE:BC 顺着比∠B=∠AEDCB CBDA EDAAD:AC=AE:AB=DE:BC 反着比AD×AB=AE×AC 顺着乘∠B =∠ACDCBED AAD:AC=AC:AB=CD:BC AC²=AD×AB当∠ BAC=90°AD B CB①△ABD ∽△CBA AB ²=BD×BC ②△ACD ∽△BCAAC²=CD×BC③△ADB ∽△CDA AD²=BD×CD特征 模型结论AC ∥BDAD B CO DB A CC A OD BAD B CODBACCAO D B① △BD0∽△ACO ② DO:0C=BO:0A=BD:AC 交叉比③ △AOD 与△C0B 不相似∠B=∠C(也叫蝴蝶型相似)A D BC ODBACCAD B CODBACC① △AOC ∽△DOB② AO:OD=0C:0B=AC:BDAO×OB=OC×0D 顺着比,交叉乘 ③ △BOC∽△DOA特征 模型 结论成比例线段共端点① △ABC ∽△ADE② △ABD∽△ACE特征 模型结论AB ∥EF ∥CDFEBCD AF EDCBA图2① 有两对A 字型相似△BEF ∽△BCD △DEF∽△DAB ② 有一对X 型相似△AEB ∽△DEC ③111AB CD EF+=特征模型结论ECD BAA BDC EEDCBA90度,45度; 120度,60度60°45°图2图1旋转N M 60°120°E D CB A 45°ED C B A ①△ABN ∽△MAN ∽△MCA ②△ABD ∽△CAE ∽△CBA【相似模型六:三角形内接矩形模型】 特征模型结论矩形EFGH 或正方形EFGH 内接与三角形H G FED C BA【相似模型七:十字模型】 特征 模型 结论正方形①若AF=BE,则AF ⊥BE ②若AF ⊥BE ,则AF=BE,长方形PEAB CD矩形ABCD 中,CE ⊥BD ,则△CDE ∽△BCD ,CE CDBD BC平行四边形△GME ∽△HNF△MED ≌△BFA三角形MED CAB在△ABC 中,AB =AC ,AB ⊥AC ,①D 为中点,②AE ⊥BD ,③BE :EC=2:1,④∠ADB =∠CDE ,⑤∠AEB =∠CED ,⑥∠BMC =135°,⑦2BMMC =,这七个结论中,“知二得五”【A 型,X 型,三平行模型】1.如图,在△ABC 中,EF ∥DC ,∠AFE =∠B ,AE =6,ED =3,AF =8,则AC =_________,CDBC=_________.F E DCBABCDE FA2.如图,AB ∥CD ,线段BC ,AD 相交于点F ,点E 是线段AF 上一点且满足∠BEF =∠C ,其中AF =6,DF =3,CF =2,则AE =_________.3.如图,在Rt △ABD 中,过点D 作CD ⊥BD ,垂足为D ,连接BC 交AD 于点E ,过点E 作EF ⊥BD 于点F ,若AB =15,CD =10,则BF :FD =_____________.FEBCAN MEDCBA4.如图,在□ABCD 中,E 为BC 的中点,连接AE ,AC ,分别交BD 于M ,N ,则BM :DN =_____________.5.如图所示,AB ∥CD ,AD ,BC 相交于点E ,过E 作EF ∥AB 交BD 于点F .则下列结论:①△EFD ∽△ABD ;②EF BF CD BD =;③1EF EF FD BF AB CD BD BD +=+=;④111AB CD EF+=.其中正确的有___________. F EDCBA图26.在△ABC 中,AB=9,AC=6,点M 在边AB 上,且AM=3,点N 在AC 边上.当AN= 时,△AMN 与原三角形相似.7.如图,在△ABC 中,∠C=90°,AC=8,BC=6,D 是边AB 的中点,现有一点P 位于边AC 上,使得△ADP 与△ABC 相似,则线段AP 的长为 .8.如图,已知O 是坐标原点,点A.B 分别在y x 、轴上,OA=1,OB=2,若点D 在x 轴下方,且使得△AOB 与△OAD 相似,则这样的点D 有 个.9.如图,在Rt △ACB 中,∠C=90°,AC=16cm ,BC=8cm ,动点P 从点C 出发,沿CA 方向运动;动点Q 同时从点B 出发,沿BC 方向运动,如果点P 的运动速度均为4cm/s ,Q 点的运动速度均为2cm/s ,那么运动几秒时,△ABC 与△PCQ 相似.10.将△ABC的纸片按如图所示的方式折叠,使点B落地边AC上,记为点B',折叠痕为EF,已知AB=AC=8,BC=10,若以点B'.F.C为顶点的三角形与△ABC相似,那么BF的长度是.11.如图,在中,,,是角平分线.求证:(1)(2)12.如图,四边形中,平分,,,为的中点.(1)求证:;(2)与有怎样的位置关系?试说明理由;(3)若,,求的值.13.如图,在中,为上一点,,,,于,连接.(1)求证:;(2)找出图中一对相似三角形,并证明.14.如图,在中,,分别是,上的点,,的平分线交于点,交于点.(1)试写出图中所有的相似三角形,并说明理由(2)若,求的值.15.如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.(1)求BD的长;(2)若△DCN的面积为2,求四边形ABNM的面积.16.如图,在中,于点,于点,连接,求证: ..17.如图,在△ABC中,DE∥FG∥BC,AD∶DF∶FB=1∶2∶3,若EG=3,则AC=________.图1 图218..如图,平行于BC的直线DE把△ABC分成的两部分面积相等.则ADAB= _________.19.如图所示,AD=DF=FB, DE∥FG∥BC,则S1:S2:S3=__________.20.如图,在矩形ABCD中,对角线AC,BD相交于点O,OE⊥BC于点E,连接DE交OC于点F,作FG⊥BC于点G,则线段BG与GC的数量关系是___.21. 如图,已知点C 为线段AB 的中点,CD ⊥AB 且CD=AB=4,连接AD ,BE ⊥AB ,AE 是∠DAB 的平分线,与DC 相交于点F ,EH ⊥DC 于点G ,交AD 于点H ,则HG 的长为 .22.如图1,在△ABC 中,点D 、E 、Q 分别在边AB 、AC 、BC 上,且DE ∥BC ,AQ 交DE 于点P . (1)求证: ;(2)如图,在△ABC 中,∠BAC =90°,正方形DEFG 的四个顶点在△ABC 的边上,连接AG 、AF ,分别交DE 于M 、N 两点.如图2,若AB =AC =1,直接写出MN 的长;如图3,求证MN 2=DM【母子型】1、已知:如图,△ABC 中,∠ACB=90°,CD ⊥AB 于D ,S △ABC=20,AB=10。
三角形相似模型总结

三角形相似模型总结
嘿,朋友们!今天咱就来好好唠唠三角形相似模型总结。
你们看啊,就说那相似三角形,不就好比是一对双胞胎嘛!两个三角形长得有点像,但又不完全一样。
比如说,咱有两个三角形,一个大的,一个小的,嘿,它们的角都一样大!这就叫相似呀!
就像一次数学测验里,有这样一道题,给你两个三角形,让你判断是不是相似。
你就得瞪大眼睛,瞅瞅它们的角,再看看它们边的比例是不是一样。
要是角相等,边的比例也对得上,那它们就是相似三角形没跑啦!
还有啊,相似三角形的性质也超级重要呢!比如对应边是成比例的,对应角相等。
这就好像两个小伙伴,有很多相同的地方,但又有各自的特点。
记得有次和同学一起做练习题,看到个三角形,我们很快就发现了它和另一个相似三角形的关系,那种感觉,哇,太爽了!
再来想想,相似三角形的判定也很有意思呀!就像要给三角形贴上一个“相似”的标签一样,得满足那些条件才行。
像是三边对应成比例,两角对应相等,这不就好比是进入一个秘密社团的密码嘛!
相似三角形在生活中也有很多用处呢!好比建筑师要盖房子,就得用相似三角形的知识来确保结构稳固。
咱平时看到的那些高楼大厦,说不定就有相似三角形在里面帮忙呢!
哎呀呀,三角形相似模型真的是太有趣太有用啦!总结起来就是,它就像一把神奇的钥匙,能打开好多数学难题的大门,能让我们发现生活中那些隐藏的数学奥秘。
大家一定要好好掌握它呀!。
初中-八年级-等腰直角三角形中的常用模型
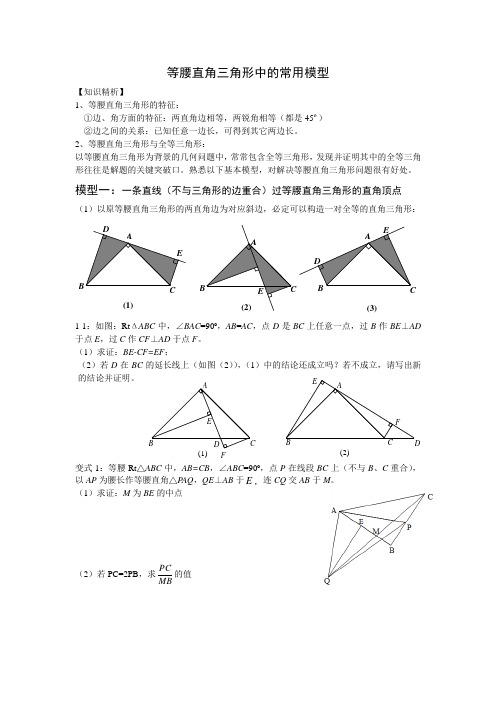
等腰直角三角形中的常用模型【知识精析】1、等腰直角三角形的特征:①边、角方面的特征:两直角边相等,两锐角相等(都是45º)②边之间的关系:已知任意一边长,可得到其它两边长。
2、等腰直角三角形与全等三角形:以等腰直角三角形为背景的几何问题中,常常包含全等三角形,发现并证明其中的全等三角形往往是解题的关键突破口。
熟悉以下基本模型,对解决等腰直角三角形问题很有好处。
模型一:一条直线(不与三角形的边重合)过等腰直角三角形的直角顶点(1)以原等腰直角三角形的两直角边为对应斜边,必定可以构造一对全等的直角三角形:1-1:如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作BE ⊥AD 于点E ,过C 作CF ⊥AD 于点F 。
(1)求证:BE-CF=EF ;(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗?若不成立,请写出新的结论并证明。
变式1:等腰Rt △ABC 中,AB=CB ,∠ABC =90º,点P 在线段BC 上(不与B 、C 重合),以AP 为腰长作等腰直角△P AQ ,QE ⊥AB 于E ,连CQ 交AB 于M 。
(1)求证:M 为BE 的中点(2)若PC=2PB ,求MBPC 的值(3)(1)(2)F E D C B A A B C D E F (1)(2)以原等腰直角三角形的两直角边为对应直角边,必定可以构造一对全等的直角三角形:1-2:如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作BE ⊥AD 于点E ,交AC 于点G ,过C 作CF ⊥AC 交AD 的延长线与于点F 。
(1)求证:BG=AF ;(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗?若不成立,请写出新的结论并证明。
变式1:如图,在R t △ABC 中,∠ACB =45º,∠BAC =90º,AB=AC ,点D 是AB 的中点,AF ⊥CD于H 交BC 于F ,BE ∥AC 交AF 的延长线于E ,求证:BC 垂直且平分DE .变式2:等腰Rt △ABC 中,AC=AB ,∠BAC =90°,点D 是AC 的中点,AF ⊥BD 于点E ,交BC 于点F ,连接DF ,求证:∠1=∠2。
共顶点等腰三角形产生相似三角形模型(整理者14232)

共顶点等腰三角形产生相似三角形模型今天研究一个难度较低但结论还比较有趣的模型。
前面研究过两个有点类似的模型,当时起名个人是从模型构造出发分别叫旋转放缩对称直角三角形和互补旋转放缩等腰三角形模型,现在想想既复杂拗口,又没点穿本质,还不如直接叫共顶点直角三角形产生等腰三角形和共顶点等腰三角形产生直角三角形模型好点。
所以今天这个就直接叫共顶点等腰三角形产生相似三角形模型了。
模型构造:一:任意作一等腰三角形ABC,∠A为顶角。
然后将其绕A旋转180°得△AED。
二:将△AED绕A进行旋转及放缩,得到新的等腰三角形AED三:连BD,CE(注意对应,不是BE和CD),分别作其中垂线,交于F点。
结论:△DFB∽△EFC,且∠DFB=∠EFC=180°-∠BAC。
证明:由边角边基本全等模型易证△EAB∽△DAC①则有BE=DC,可推出△EFB≌△CFD②,从而∠EFB=∠CFD即∠DFB=∠CFE,△DFB ∽△EFC。
接下来推为什么产生的两新的相似的等腰三角形顶角和原等腰三角形顶角互补:由①,∠ADG=GEH,则∠GHE=∠DAE;由②,∠HEI=∠FCI,则∠EHI=∠EFC。
又∠EHI+∠GHE=180°,则有∠EFC+∠DAE=∠EFC=∠BAC=180°。
由于等腰△ABC形状可以改变,△ADE可以任意旋转放缩,给出的图形是否以偏概全结论是否任意情况都成立呢?应该是都成立的。
尽管形状改变,过程和推导都大同小异,仅再举一情形进行证明。
在此图延长BE和DC交于G。
由△AED≌△ADC,可推∠EGD=∠BAC。
再由△EBF≌△CDF,可推∠GDF+∠EBF=180°,所以在四边形GBFD中,∠BFD+∠EGD=∠BFD+∠BAC=180°。
模型应用:。
共顶点等腰三角形旋转模型的基本做法与结论

共顶点等腰三角形旋转模型的基本做法与结论共顶点等腰三角形旋转模型是数学中常见的几何问题,它涉及到旋转、对称等概念与性质。
本文将以共顶点等腰三角形旋转模型为主题,探讨其基本做法与结论。
一、问题描述我们考虑一个共顶点等腰三角形ABC,其中AB=AC,以A为顶点作一条直线AD,且AD与BC相交于点D。
现在,我们将等腰三角形ABC绕点D进行旋转,旋转角度为θ,求旋转后的三角形A'B'C'的性质。
二、基本做法1. 确定旋转后的三角形根据旋转的定义,我们知道旋转是将一个图形绕着某个点旋转一定角度,得到一个新的图形。
在本题中,我们将等腰三角形ABC绕点D旋转,因此旋转后的三角形为A'B'C'。
2. 确定旋转角度旋转角度θ是一个关键的参数,它决定了旋转后的图形与原图形的关系。
在本题中,我们需要确定旋转角度θ的值。
3. 分析旋转后的三角形性质旋转后的三角形A'B'C'与原三角形ABC之间存在一些性质的关系,我们需要分析旋转后的三角形的各个性质,如边长、角度等。
三、结论通过对共顶点等腰三角形旋转模型的分析和计算,我们得出以下结论:1. 旋转后的三角形A'B'C'也是一个等腰三角形,即A'B' = A'C';2. 旋转后的三角形A'B'C'与原三角形ABC共顶点A,即A'、B'、C'三点共线。
这些结论可以通过具体的计算和证明进行验证,但在本文中我们不做具体的推导和证明。
四、实际应用共顶点等腰三角形旋转模型在几何学中具有重要的应用价值。
例如,在建筑设计中,我们常常需要通过旋转来生成对称的图形,而共顶点等腰三角形旋转模型就是一种常用的方法。
通过对旋转后的图形进行分析,我们可以更好地理解建筑物的结构和形态,并进行合理的设计和规划。
在计算机图形学中,共顶点等腰三角形旋转模型也是一种常见的变换操作。
相似三角形的特殊情况等腰三角形

相似三角形的特殊情况等腰三角形相似三角形是指在形状相似的三角形中,对应角度相等,对应边长成比例。
而等腰三角形是指具有两边长度相等的三角形。
在相似三角形中,有一种特殊情况,即两个三角形的对应边长比例为1:1,即边长相等,这样的相似三角形也就是等腰三角形。
下面将详细介绍相似三角形的特殊情况等腰三角形。
一、相似三角形的概念相似三角形指的是具有相同形状但大小不同的三角形。
也就是说,它们的对应角顶点对应的角度相等,对应边长成比例关系。
二、等腰三角形的概念等腰三角形是指具有两边长度相等的三角形。
在等腰三角形中,两边被称为等腰边,另一边被称为底边。
三、相似三角形的特殊情况等腰三角形在相似三角形中,存在一种特殊情况,即两个三角形的对应边长比例为1:1,也就是边长相等。
根据相似三角形的定义,可以得出以下结论:当两个三角形的对应边长比例为1:1时,这两个三角形一定是相似的,并且是等腰三角形。
四、等腰三角形的性质1. 等腰三角形的底角(底边两边所夹的角)相等。
证明:设等腰三角形ABC的底边为BC,两边相等的边为AB和AC。
已知AB=AC,所以∠ABC=∠ACB,即底角相等。
2. 等腰三角形的高线(从顶点到底边的垂线)同时也是中位线、角平分线和对称轴。
证明:由等腰三角形的性质可知,高线BD同时也是角平分线和对称轴。
同时,由三角形的中位线性质可知,BD也是中位线。
因此,等腰三角形的高线同时具有这四个性质。
五、例题解析现给出一个相似三角形的特殊情况等腰三角形的例题,来加深我们对这个概念的理解。
已知三角形ABC与三角形ABD相似,且AD=BD,证明三角形ABC是等腰三角形。
解:根据已知条件,可以得出两个结论:三角形ABC与三角形ABD相似,且AD=BD。
由相似三角形的定义可知,对应角度相等,对应边长成比例关系。
所以∠BAC=∠BAD,∠ABC=∠ABD,并且AC/AD=BC/BD。
又因为AD=BD,所以AC=BC,即两边相等,因此三角形ABC是等腰三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
共顶点等腰三角形产生相似三角形模型
今天研究一个难度较低但结论还比较有趣的模型。
前面研究过两个有点类似的模型,当时起名个人是从模型构造出发分别叫旋转放缩对称直角三角形和互补旋转放缩等腰三角形模型,现在想想既复杂拗口,又没点穿本质,还不如直接叫共顶点直角三角形产生等腰三角形和共顶点等腰三角形产生直角三角形模型好点。
所以今天这个就直接叫共顶点等腰三角形产生相似三角形模型了。
模型构造:一:任意作一等腰三角形ABC,∠A为顶角。
然后将其绕A旋转180°得△AED。
二:将△AED绕A进行旋转及放缩,得到新的等腰三角形AED
三:连BD,CE(注意对应,不是BE和CD),分别作其中垂线,交于F点。
结论:△DFB∽△EFC,且∠DFB=∠EFC=180°-∠BAC。
证明:由边角边基本全等模型易证△EAB∽△DAC①
则有BE=DC,可推出△EFB≌△CFD②,从而∠EFB=∠CFD即∠DFB=∠CFE,△DFB ∽△EFC。
接下来推为什么产生的两新的相似的等腰三角形顶角和原等腰三角形顶角互补:由①,∠ADG=GEH,则∠GHE=∠DAE;由②,∠
HEI=∠FCI,则∠EHI=∠EFC。
又∠EHI+∠GHE=180°,则有∠EFC+∠DAE=∠EFC=∠BAC=180°。
由于等腰△ABC形状可以改变,△ADE可以任意旋转放缩,给出的图形是否以偏概全结论是否任意情况都成立呢?应该是都成立的。
尽管形状改变,过程和推导都大同小异,仅再举一情形进行证明。
在此图延长BE和DC交于G。
由△AED≌△ADC,可推∠EGD=∠BAC。
再由△EBF≌△CDF,可推∠GDF+∠EBF=180°,所以在四边形GBFD中,∠BFD+∠EGD=∠BFD+∠
BAC=180°。
模型应用:。
