第9讲 矩形单元和6节点三角形单元
有限元 2-3弹性力学平面问题(2.4矩形单元,2.5六节点三角形单元)

j m
p)
有限单元法
土木工程学院
P-12/40
单元应力矩阵:
[S ] = [D ] [B ] = [Si
式中:
E [Si ] = 4ab 1 − μ 2
Sj
Sm
Sp
]
(
)
⎤ ⎡ μaηi (1 + ξ iξ ) ⎥ ⎢ bξ (1 + η iη ) ⎥ (i, j , m, p ) ⎢ μbξ (1 + η η ) ( ) 1 η ξ ξ a + i i i i ⎥ ⎢ 1 1 μ μ − − ⎢ aη i (1 + ξ iξ ) bξ i (1 + ηiη )⎥ ⎥ ⎢ 2 ⎦ ⎣ 2
[
]
或 Li = 1 (ai + bi x + ci y ) (i, j, m ) 2A
(2 − 5 − 1)
i
Yi
Xj
Yj
X m Ym
Xp
] Y ]
p
T
(2 − 4 − 3)
三、单元位移函数和形函数
单元共有8个位移分量,将结点位移分量全 部作为已知边界条件,则位移函数可取为:
u = α1 + α 2 x + α 3 y + α 4 xy
v = α 5 + α 6 x + α 7 y + α 8 xy
(2 − 4 − 4)
{ } [ ]{ }
[ ][ ]
[ ]
矩形单元自然具有相同关系,只是[B], [S] 的内容有所区别。 仿照三角形单元:
0 ⎫ ⎧∂ ∂x ⎪ ⎪⎡ N i [B ] = [H ][N ] = ⎨ 0 ∂ ∂y ⎬⎢ ⎪∂ ∂y ∂ ∂x ⎪⎣ 0 ⎩ ⎭ 0 " Np Ni " 0 0 ⎤ = [ Bi ⎥ Np⎦ Bj Bm Bp ]
9第2章弹性力学平面问题及空间问题有限元

假定的位移函数是多项式,它是连续函数,可以肯定,在单元内部位移函数是单值连续的。由于单 元的位移函数 u 、 v 都是坐标 x 、 y 的线性函数,在单元边界上位移也是线性变化的,两个相邻单元在 公共节点上具有相同的节点位移,因而相邻单元在公共边界上位移连续,即协调条件得到满足。 由上面分析可以看出,三角形常应变单元的位移模式可以保证计算结果的收敛。
px
py
px
py ]
T
(2-1-7b)
(2 )若在 jm 边上受线性分布的水平方向的面力,它在 j 点的集度为 q ,在 m 点的集度为零 (如图 2-5) 。可预计由该面力求得的等效节点载荷只有 R xj 、
R xm ,其余节点载荷分量必为零。
将 jm 边上的分布面力写成 s 的函数,为
s { p} [ (1 ) q 0]T l 在 jm 边上的形函数也需用变量 s 表示,根据形函数的含义,
Ve
[k ii ] [k ij ] [ k im ] [k ji ] [k ij ] [k jm ] [k mi ] [ k mj ] [k mm ]
式中, t 为单元的厚度,当单元划分得足够小时,可以认为每个单元的厚度 t 为常值。子阵为
(2-1-5)
[k rs ] [ Br ]T [ D][B s ]tA
101
二、 单元刚度矩阵 1、单元几何矩阵 [ B ] 有了单元的位移模式,利用平面问题的几何方程求得应变分量
0 x x u e e 0 { } [ L][ N ]{} [B ]{} y y v xy y x
理学有限元讲稿等效载荷

(4)结构整体刚度矩阵的集成
建立每个单元的刚度矩阵,如对单元③可表示为:
注意单元节点编号(i,j,m)与整体节点编号的对应关系: (i, j, m)=(5, 3, 2)
其中,[kii]=[k55]表示单元③的节点5作用单位位移时在节点5产生的节点力;它应与总刚阵子阵[K55]迭加;[kij]=[k53]表示单元③的节点3作用单位位移时在节点5产生的节点力;它应与总刚阵子阵[K53]迭加;[kij]=[k52]表示单元③的节点2作用单位位移时在节点5产生的节点力;它应与总刚阵子阵[K52]迭加等,
(4)结构整体刚度矩阵的集成
对结构分析建立整体刚度矩阵的方法,是利用单元“节点的平衡方程”。用具体例题说明如下。
a
a
a
a
1
2
3
4
5
6
X2
X1
Y1
i
j
m
i
j
m
m
i
j
j
i
m
1
2
3
4
由于该结构有6个节点,节点自由度为12,即需要确定的节点位移参量为12个,应列出12个线性方程。这样,线性方程组的系数矩阵,也即总刚度矩阵有1212个元素,按(x, y)分块后有66子矩阵。
(8)精度较高的平面单元简介
如前所述,线性位移模式的单元为常应变单元,当单元尺寸较大时会产生明显误差。为减少离散化带来的误差,使所求得位移和应力能更好反映真实状态,可采用具有较高阶次位移插值函数的单元,即精度较高的平面单元。对平面问题,常用的较高精度单元是矩形单元和六节点三角形单元。
(8)精度较高的平面单元简介
在描述轴对称问题时,采用圆柱坐标(r,,z)比较方便。用相距dr的两个圆柱面,互成d角的两个垂直面,和两个相距dz的水平面,从弹性体中分离出一个小的微元体,用rr表示径向正应力,表示环向正应力,zz表示轴向正应力,剪应力分量rz=zr。
有限元课件_矩形单元
将(b)式代入,得
B1
式中
N i b 1 Bi ab 0 N a i
B2
B3
B4
e
(g)
0 b i 1 0 0 N 1 a i 0 a 1 i 0 4ab a i 1 0 b i 1 0 N i b
(i=1,2,3,4)
(3-49)
由虎克定律我们可以得出用节点位移表示的单元应力,即
D S1
S2
S3
S4
e
(3-50)
返回
式中Si Βιβλιοθήκη D Bi E2
(i=1,2,3,4)
(h)
对于平面应力问题
Si
4ab 1
a i 1 0 b i 1 0 b 1 a i 1 0 i 0 1 1 a i 1 0 b i 1 0 2 2
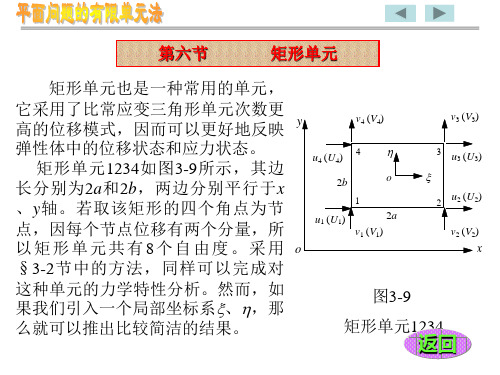
第六节
矩形单元
矩形单元也是一种常用的单元, 它采用了比常应变三角形单元次数更 高的位移模式,因而可以更好地反映 弹性体中的位移状态和应力状态。 矩形单元 1234 如图 3-9 所示,其边 长分别为 2a 和 2b ,两边分别平行于 x 、 y 轴。若取该矩形的四个角点为节 点,因每个节点位移有两个分量,所 以矩形单元共有8个自由度。采用 §3-2 节中的方法,同样可以完成对 这种单元的力学特性分析。然而,如 果我们引入一个局部坐标系、,那 么就可以推出比较简洁的结果。
(3-48)
其中 (xi , yi)是节点i的整体坐标,i =1,2,3,4。
返回
在局部坐标系中,节点i的坐标是(i , i ),其值分别 为±1。取位移模式
第九讲 有限元
x 0 y 1 2 xy 2(1 )
平面应变问题弹性矩阵D
6. 单元刚度矩阵
[ K e ] [ B]T [ D][B]d (vol)
V
a b
a b
[ B]T [ D][B]tdxdy t——厚度
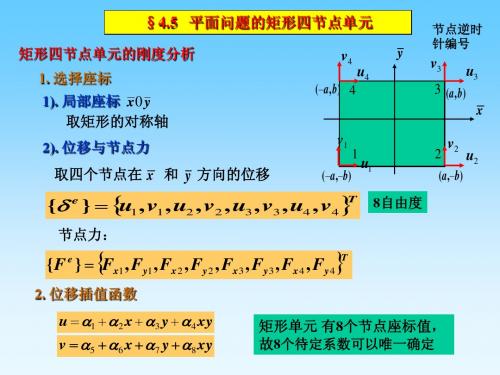
§4.5 平面问题的矩形四节点单元
矩形四节点单元的刚度分析 1. 选择座标 1). 局部座标 x0 y 取矩形的对称轴 2). 位移与节点力
v4
( a , b ) 4
y
节点逆时 针编号
u4
v3
3 (a , b)
u3
x
v1
(a,b)
1
T
取四个节点在 x 和 y 方向的位移
e
u1
8自由度
2
v2
u2
v 5 6 x 7 y 8 xy
矩形单元 有8个节点座标值, 故8个待定系数可以唯一确定
u 1 2 x 3 y 4 xy
v 5 6 x 7 y 8 xy
1 2 3 u 1 x y xy 0 0 0 0 4 0 0 0 0 1 x y xy 5 v 6 7 8
e E T T A
Fx1 N1 F 0 y1 N Fx 2 2 F t 0 y2 N3 Fx 3 0 F y3
E
0 0 N1q y N1 0 0 0 dxdy t N q dxdy N 2 q y 2 y 0 0 N 3q y N3
[B]——矩形4节点单元几何矩阵 简写成:
六节点三角形单元

3、应力矩阵
根据应力-应变关系,可以计算单元中的应力,得到式(228)同样形式
{ } [D]{} [S][ ]e
(7-11)
应力矩阵[S]具有与式(2-29)同样形式
[S] [D][B]
将[S]写成子矩阵形式 [S] [Si S j Sl Sm ]
(7-12) (7-13)
其中
(7-17)
上式对应平面应力情形。对于平面应变情形,只须将上式 中的E、作相应的改变。
5、等价节点力 单元体积力和表面力引起的节点力仍可用式(2-45)和 (2-46)进行计算。
{FV } A[N ]T {qV }hdxdy
T
{FS}
[N]
l
{qS }hdl
(2-45) (2-46)
(7-2)
式中形函数为 :
Ni
1 4
1
x a
1
y b
பைடு நூலகம்
N
j
1 4
1
x a
1
y b
Nl
1 4
1
x a
1
y b
Nm
1 4
1
x a
1
u a1 a2x a3 y a4xy
v
a5
a6
x
a7
y
a8
xy
(7-1)
在上式表示的位移模式中,a1, a2, a3, a5, a6, a7, a8
反映了单元的刚体位移和常
应变。在单元的边界(x=±a
有限元分析与应用大作业

有限元分析及应用大作业课程名称: 有限元分析及应用班级:姓名:试题2:图示薄板左边固定,右边受均布压力P=100Kn/m作用,板厚度为0.3cm;试采用如下方案,对其进行有限元分析,并对结果进行比较。
1)三节点常应变单元;(2个和200个单元)2)四节点矩形单元;(1个和50个单元)3)八节点等参单元。
(1个和20个单元)图2-1 薄板结构及受力图一、建模由图2-1可知,此薄板长和宽分别为2m和1.5m,厚度仅为0.3cm,本题所研究问题为平面应力问题。
经计算,平板右边受均匀载荷P=33.33MPa,而左边被固定,所以要完全约束个方向的自由度,如图2-2所示。
取弹性模量E=2.1×11Pa,泊松比μ=0.3。
P=33.33MPa图2-2 数学模型二、第一问三节点常应变单元(2个和200个单元)三节点单元类型为PLANE42,设置好单元类型后,实常数设置板厚为0.3M。
采用2个单元的网格划分后的结果如图2-3,200个单元的网格划分图如图2-6所示。
约束的施加方式和载荷分布如图2-2中所示。
约束右边线上节点全部自由度。
计算得到的位移云图分别如图2-4、7所示,应力云图如图2-5、8所示。
图2-3 2个三角形单元的网格划分图图2-4 2个三角形单元的位移云图图2-5 2个三角形单元的应力云图图2-7 200个三角形单元的位移云图三、第二问四节点矩形单元的计算四节点单元类型为PLANE42,设置好单元类型后,实常数设置板厚为0.3M。
采用1个单元的网格划分后的结果如图2-9,50个单元的网格划分图如图2-12所示。
约束的施加方式和载荷分布如图2-2中所示。
约束右边线上节点全部自由度。
计算得到的位移云图分别如图2-10、11所示,应力云图如图2-13、14所示。
图2-9 1个四边形单元的网格划分图图2-11 1个四边形单元的应力云图图2-12 50个四边形单元的网格划分图图2-13 50个四边形单元的位移云图图2-14 50个四边形单元的应力云图四、第三问八节点等参单元的计算四节点单元类型为PLANE82,设置好单元类型后,实常数设置板厚为0.3M。
有限元第三章 单元类型及单元刚度矩阵

Fξ j(2) x
l
0 1
x xi x xj
二、一维单元及其单元刚度阵
1.杆单元
●一次杆单元
根据形状函数的定义,我们知道,形状函数是 描述或反映单元内点位移与单元节点位移的关系。 对于上述问题,已知节点位移为ui,uj,而要求节点 间任一内点的位移,显然可以根据线性插值来计算 (二点一次拉氏插值),即
一、形状函数类型及其特征
在第二章中,曾经讨论过单元内点位移函数假设 适应满足的4项原则。
●包含单元的刚体位移 ●包含单元的常应变状态 ●保证不偏惠各坐标轴 ●保证单元内位移连续
体现位移函数完备性 体现位移函数几何不变性 体现位移函数协调性
一、形状函数类型及其特征
要保证位移函数的几何不变性,位移函数多项 式的各项应根据帕斯卡三角形来选择。
二、一维单元及其单元刚度阵
1.杆单元 杆单元受轴向力,在单元端点处无弯矩和扭矩作用,
将此单元独立出来进行受力分析时为二力杆。根据单元 形状函数的阶次,又可分为一次杆单元和二次杆单元。
●一次杆单元 单元有两个节点,如图所示,编号为i、j,采用局部
坐标 ,记 x l,并取i为x坐标的原点,则有
F i(1)
二、一维单元及其单元刚度阵
1.杆单元 元素的计算
●二次杆单元
k22 E l2 A 0 l(421 )2d xE 3 l A 7 k33 E l2 A 0 l(4142)2d xE 3 l A 16
k 12 E l2 0 lA (42 1 )4 (2 1 )d x E 3 l A 1
一、形状函数类型及其特征
ngrange型形状函数,这时节点广义位移为节 点位移,不含节点位移导数,它与单元的几何形状、 单元节点分布和节点数有关。所以,该类形状函数 在单元几何形状、节点分布和节点数一定时也随之 确定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6节点三角形单元
第四章 平面问题高精度单元
§4.3
•
6节点三角形单元简介
显然单元满足完备性要求。由于该位移模式决定了单元边界上位 移呈二次抛物线分布,相邻单元公共边界上有三个公共节点,正 好能够保证相邻单元在边界上位移的连续性,因而是协调元,单
元满足收敛条件。
• • 该单元应变、应力随坐标完全呈线性变化,属于高精度单元。 进行广义坐标代换后位移模式仍可写成标准形式:
1 Li xm L j L ym m
§4.3
6节点三角形单元简介
利用上面变换式,三角形单元上的任何多项式函数可以方便地在 两种坐标之间转换。
面积坐标的各种形式幂函数在三角形上的积分有很简便的计算公式。
•
面积坐标表示的6节点三角形单元形函数
根据形函数性质直接构造出用面积坐标表示的形函数如下:
形函数矩阵经过微分算子矩阵作用后得到3×8应变矩阵:
0 b y 0 b y 0 b y 0 b y 1 B 0 a x 0 a x 0 a x 0 ax 4ab a x b y a x b y a x b y a x b y
§4.2
Nk N 0 0 Nk
矩形单元
Nl 0 0 Nl Nm 0 0 Nm Nn 0 0 Nn
形函数矩阵
•
各形函数为:
1 x y (1 )(1 ) 4 a b 1 x y N l (1 )(1 ) 4 a b 1 x y N m (1 )(1 ) 4 a b 1 x y N n (1 )(1 ) 4 a b Nk
T
第四章 平面问题高精度单元
§4.2
•
矩形单元
单元内位移多项式设4项,为双线性多项式:
u a1 a2 x a3 y a4 xy v a5 a6 x a7 y a8 xy
通过节点坐标和节点位移代入,把广义坐标(多项式系数)a1
~ a8
代换为节点位移分量后得到插值形式的位移函数:
第四章 平面问题高精度单元
§4.1
提高有限元求解精度的途径
三、建立高精度单元的原理和途径 • 原理:提高单元位移模式多项式的阶次,从而增强单元拟合局部区 域位移、应力变化的能力。 • • 途径:主要是增加单元的节点数。 对平面问题,先考虑采用4节点矩形单元和6节点三角形单元。
第四章 平面问题高精度单元
第四章 平面问题高精度单元
§4.2
•
矩形单元
由平面问题物理方程(应力~应变关系)得到:
DB S
e
e
•
对于矩形单元,其单元上应力、应变不再是常数,而是一定程度 上呈线性变化,即:x方向正应变、正应力随y坐标线性变化;y
方向正应变和正应力随x坐标线性变化。因此,在一定条件下,
u N k uk Nl ul N mum N nun Ni ui
v N k vk Nl vl N mvm N n vn Ni vi
• 写成矩阵形式为:
u e N v
其中
N 为形函数矩阵
第四章 平面问题高精度单元
第4章 平面问题高精度单元
4.1 提高有限元求 解精度的途径 4.2 矩形单元 4.3 6节点三角形 单元简介
简单三角形单元缺点 提高有限元求解精度的途径 高精度单元的原理
单元位移模式 单元应力、应变 单元刚度矩阵 矩形单元讨论
单元简介 面积坐标 单元位移模式
第四章 平面问题高精度单元
§4.1
提高有限元求解精度的途径
因此,单元内任一点的面积坐标满足关系: Li+ Lj+ Lm=1 即3个面积坐标只有2个面积坐标是独立的。
•
面积坐标与直角坐标之间有确定的变换关系,因此,对三角形单
元的描述完全可以用面积坐标进行。
直角坐标表示面积坐标
不难导出下列变换关系:
1 Li (ai bi x ci y ) 2A
第四章 平面问题高精度单元
§4.2
•
•
矩形单元
显然,上述形函数满足形函数性质。
由于边界平行于坐标轴,矩形单元位移模式沿单元边界(x,y方向) 都是线性变化,沿其他方向则按2次函数变化。称为“双线性”位 移函数。
•
由于单元位移在单元边界上线性变化,而单元之间的公共边界上
有2个公共节点,所以单元边界间的位移是连续的,单元满足协调 性条件。
精度会高一阶。
( b y ) ( a x ) ( b y ) ( a x ) ( b y ) ( a x ) ( b y ) ( a x ) E (b y ) S (a x ) (b y ) (a x ) (b y ) (a x ) (b y ) (a x ) 2 4ab(1 ) 1 1 1 1 1 1 1 1 (a x ) (b y ) (a x ) (b y ) (a x ) (b y ) (a x ) ( b y ) 2 2 2 2 2 2 2 2
(i, j, m)
显然,面积坐标与3节点三角形单元的形函数完全相同。
第四章 平面问题高精度单元
§4.3
6节点三角形单元简介
bi bj bm ci 1 cj x y cm
Li ai 1 矩阵形式: L j aj L 2 A a m m
一、简单三角形单元的缺点 • • 三节点三角形单元精度低,收敛慢,在单元内不能反映应力应变 的变化。 这是因为该单元只有 3 个节点,单元自由度少,单元位移模式只 能是线性函数,描述单元内位移变化的能力差。
二、提高有限元求解精度的途径 • • 第一个途径是对某一种特定类型的单元采用网格加密,依靠单元 的收敛性提高求解精度; 第二个途径是对一定的单元网格和单元尺寸,采用高精度单元以 提高求解精度。
•
•
第四章 平面问题高精度单元
§4.3 一、单元概述
•
6节点三角形单元简介
三角形单元天然具有很好的几何适应性,如果增加三角形单元位移模式
多项式的阶数,就能成为实用的单元。考虑图示6节点三角形单元,单 元每边中点设一个节点,则单元有12个自由度,因此位移模式恰好取完
全二次多项式:
u 1 2 x 3 y 4 xy 5 x 2 6 y 2 v 7 8 x 9 y 10 xy 11x 2 12 y 2
•
和简单三角形单元一样,矩形单元位移 模式中包含了完全一次多项式,所以满
足完备性条件。因此矩形单元的收敛性
得到保证。
第四章 平面问题高精度单元
§4.2 二、单元应变和应力
矩形单元
单元位移模式代入平面问题几何方程:
x x y 0 xy y 0 e e N B y x
面积坐标表示直角坐标 不难导出下列变换关系:
x xi Li x j L j xm L m y yi Li y j L j ym Lm
1 1 矩阵形式: x x i y y i
第四章 平面问题高精度单元
1 xj yj
• •
矩形单元
4节点矩形单元采用了双线性位移模式,应力基本上沿坐标轴呈线 性变化,因而精度比3节点三角形单元高。 由于位移模式在单元边界上线性变化,并且根据单元公共边界上 两个共同节点位移插值得到,单元的协调性得到满足,同时也满 足完备性,因此单元是收敛的。 单元要求两对边平行于坐标轴,因而不能模拟复杂几何边界,单 元网格疏密不能过渡,这是矩形单元的固有缺点。矩形单元可以 与3节点三角形单元结合使用。 如果突破几何上的限制,成为任意方位的任意四边形单元,便可 成为实用的单元。
第四章 平面问题高精度单元
§4.2
矩形单元
三、矩形单元刚度矩阵
• 矩形单元刚度矩阵导出的原理和方法同简单三角形单元。计算式如下:
k a b B DBhdxdy
e a b
T
•
可以通过积分计算出精确的刚度矩阵元素,见P51。
第四章 平面问题高精度单元
§4.2 四、矩形单元讨论
•
三角形中任意一点的位置用三个参数来表示,
称为面积坐标。面积坐标(Li, Lj, Lm)定义 为三个比值:
Ai Li A Aj Lj A Aj Lm A
第四章 平面问题高精度单元
三角形单元上的面积坐标
A为三角形面积,显然有: Ai Aj Am A
§4.3
•
6节点三角形单元简介
•
•
采用面积坐标后,单元刚度矩阵和等效节点力的计算都比较方便。
6节点三角形单元列式推导原理与其它单元相同。
第四章 平面问题高精度单元
第四章 平面问题高精度单元
§4.2
矩形单元
一、矩形单元及其位移模式
• 矩形单元边长分别为2a、2b。取4个 顶点为节点。不失一般性地假设矩 形的2个对称轴分别为x,y轴。每节 点2个位移分量,因此单元共8个自 由度。 • 单元节点编号为 k,l,m,n
单元节点位移列阵为:
uk
e
vk
ul
vl
um vm un vn
u N i ui
i 1 6 6
v N i vi
i 1
•
但是,采取如前面3节点单元建立形函数的办法过于复杂,下面介 绍用三角形单元的面积坐标描述单元位移模式和形函数的方法。
