《有限元基础教程》_【ANSYS算例】4.7.1(3) 基于3节点三角形单元的矩形薄板分析(GUI)及命令流
有限元法基础及ANSYS应用教学设计

有限元法基础及ANSYS应用教学设计引言有限元法是一种非常常用的工程计算方法,通过该方法可以准确地计算出各种物理现象的模拟结果。
ANSYS是目前常用的有限元分析软件之一,该软件可实现对比较复杂结构和系统的数值模拟和分析,是工程领域中不可或缺的软件工具。
本文将介绍有限元法的基础知识,并结合ANSYS,探讨有限元法在工程实践中的应用。
有限元法基础知识有限元方法的基本原理有限元法是一种数值计算方法,它是将所研究的物理系统或结构抽象成一个有限元网络,再在这个网络上进行数值计算。
该方法是建立在解微积分和微分方程的基础上的,将视物体或构件为非连续介质的复杂数学模型,将其分成许多小的部分,用有限数量的节点模拟实际结构的运动或应力状态,并根据节点间相对移动和形变计算所需的力、扭矩和剪切力等物理量。
有限元分析的基本原理是利用高阶数学方法将任意运动连续物体近似为一组由有限个基本单元组成的离散带单元坐标系统,从而求解结构变形、应力、热力学效应、电磁效应等问题。
有限元法的优点和缺点有限元法的优点是可以准确地进行对各种结构或系统的分析和计算,可有效预测其行为特性;另外,有限元法可以模拟各种极端条件,非常适合在实验难以进行的情况下进行数值模拟。
但是,有限元法也存在缺点,可能需要更高的技能和更长的时间才能理解分析结果,以及程序的使用需要相应的计算机资源。
有限元法的步骤有限元法的求解是由以下三个基本步骤组成:1.建立模型。
在这一步骤中,需要选择合适的有限元模型,并确定其的物理性质。
通常,这需要通过CAD系统(计算机辅助设计)或其他仿真软件来完成。
2.确定边界条件。
在这一步骤中,需要根据具体的情况进行约束,并确定边界条件,以便应用合适的力学知识来解决分析问题。
在ANSYS软件中,定义边界条件是至关重要的一步。
3.解决方程组。
在最后一个步骤中,需要解决有限元模型的方程组,并通过计算来获得所需的结果。
具体来讲,可以使用如MATLAB等数值计算软件来完成解决方程组的工作。
有限元分析基础教程

有限元分析基础教程前言有限元分析已经在教学、科研以及工程应用中成为重要而又普及的数值分析方法和工具;该基础教程力求提供具备现代特色的实用教程。
在教材的内容体系上综合考虑有限元方法的力学分析原理、建模技巧、应用领域、软件平台、实例分析这几个方面,按照教科书的方式深入浅出地叙述有限元方法,并体现出有限元原理“在使用中学习,在学习中使用”的交互式特点,在介绍每一种单元的同时,提供完整的典型推导实例、MATLAB实际编程以及ANSYS应用数值算例,并且给出的各种类型的算例都具有较好的前后对应性,使学员在学习分析原理的同时,也进行实际编程和有限元分析软件的操作,经历实例建模、求解、分析和结果评判的全过程,在实践的基础上深刻理解和掌握有限元分析方法。
一本基础教材应该在培养学员掌握坚实的基础理论、系统的专业知识方面发挥作用,因此,教材不但要提供系统的、具有一定深度的基础理论,还要介绍相关的应用领域,以给学员进一步学习提供扩展空间,本教程正是按照这一思路进行设计的;全书的内容包括两个部分,共分9章;第一部分为有限元分析基本原理,包括第1章至第5章,内容有:绪论、有限元分析过程的概要、杆梁结构分析的有限元方法、连续体结构分析的有限元方法、有限元分析中的若干问题讨论;第二部分为有限元分析的典型应用领域,包括第6章至第9章,内容有:静力结构的有限元分析、结构振动的有限元分析、传热过程的有限元分析、弹塑性材料的有限元分析。
在基本原理方面,以基本变量、基本方程、求解原理、单元构建等一系列规范的方式进行介绍;在阐述有限元分析与应用方面,采用典型例题、MATLAB程序及算例、ANSYS算例的方式,以体现出分析建模的不同阶段和层次,引导学员领会有限元方法的实质,还提供有大量的练习题。
本教程的重点是强调有限元方法的实质理解和融会贯通,力求精而透,强调学员综合能力(掌握和应用有限元方法)的培养,为学员亲自参与建模、以及使用先进的有限元软件平台提供较好的素材;同时,给学员进一步学习提供新的空间。
ANSYS有限元全套学习资料第一章

第 1章
概述
欢迎 !
• 欢迎使用ANSYS/LS-DYNA 显式动力学 培训手册!
SF=0 隐式方法
SF 0
S F = ma
显式方法
概述
… 显式-隐式方法的比较
隐式时间积分: • 时间t+Dt 时计算平均加速度-位移:
u t Dt K1 FtaDt
线性问题:
– 当[K] 是线性时无条件稳定 – 可以采用大的时间步
非线性问题:
– 通过一系列线性逼近(Newton-Raphson) 来获得解 – 要求对非线性刚度矩阵[K]求逆 – 收敛需要小的时间步 – 对于高度非线性问题无法保证收敛
Jobname.K
• • • • 在执行ANSYS SOLVE命令后自动生成的LS-DYNA 输入文件 包括存在于ANSYS数据库中的几何、载荷和材料数据 ASCII 输入文件 100% 相容于 LS-DYNA 版本960 能自动地通过EDWRITE命令生成:
Solution > Write Jobname.K
• • 完美的显式和隐式求解技术的结合 ANSYS 前后处理:
– 所有的显式动力学特定的命令有EDxx前缀
– 用户化ANSYS GUI能有效的执行显式问题 – 支持所有的固体建模和布尔操作 – 允许直接输入IGES, Pro/E, ACIS, Parasolid等几何模型 – 支持所有的ANSYS自由网格划分技术 – 可以使用APDL 和优化设计 – 支持所有的通用后处理器特性和动画宏 – 专业的时间-历程后处理器
有限元法基础及ANSYS应用(电子教案)

《有限元法基础及ANSYS应用》电子教案第一章绪论1.1有限元法概述1.1.1 有限元法的发展及基本思想随着现代工业、生产技术的发展,不断要求设计高质量、高水平的大型、复杂和精密的机械及工程结构。
为此目的,人们必须预先通过有效的计算手段,确切地预测即将诞生的机械和工程结构,在未来工作时所发生的应力、应变和位移。
但是传统的一些方法往往难以完成对工程实际问题的有效分析。
弹性力学的经典理论,由于求解偏微分方程边值问题的困难,只能解决结构形状和承受载荷较简单的问题,对于几何形状复杂、不规则边界、有裂缝或厚度突变,以及几何非线性、材料非线性等问题往往遇到很多麻烦,试图按经典的弹性力学方法获得解析解是十分困难的,甚至是不可能的。
因此,需要寻求一种简单而又精确的数值分析方法。
有限元法正是适应这种要求而产生和发展起来的一种十分有效的数值计算方法。
这个方法起源于20世纪50年代中期航空工程中飞机结构的矩阵分析。
1960年美国的克劳夫(C lo ug h)采用此方法进行飞机结构分析时,首次将这种方法起名为“有限单元法”(finite element method),简称“有限元法”。
有限单元法的基本思想,是在力学模型上将一个原来连续的物体离散成为有限个具有一定大小的单元,这些单元仅在有限个节点上相连接,并在节点上引进等效力以代替实际作用于单元上的外力。
对于每个单元,根据分块近似的思想,选择一种简单的函数来表示单元内位移的分布规律,并按弹性理论中的能量原理(或用变分原理)建立单元节点力和节点位移之间的关系。
最后,把所有单元的这种关系式集合起来,就得到一组以节点位移为未知量的代数方程组,解这些方程组就可以求出物体上有限个离散节点上的位移。
图1.1是用有限元法对直齿圆柱齿轮的轮齿进行的变形和应力分析,其中图1.1(a)为有限元模型,图1.1(b)是最大切应力等应力线图。
在图1.1(a)中采用8节点四边形等参数单元把轮齿划分成网格,这些网格称为单元;网格间互相连接的点称为节点;网格与网格的交界线称为边界。
02-02有限元分析基础-ANSYS基础操作

二、ANSYS基本操作
1.2 交互式启动(建议使用)
二、ANSYS基本操作
2.用户界面 2.1 主窗口
二、ANSYS基本操作
2.2 Output Windows(输出窗口)
显示程序的文本信息,以简单形式显示 过程数据等信息。
二、ANSYS基本操作
3.ANSYS的数据库 ANSYS采用通用的集中式数据库存储所用模 型数据的数据及分析结果。数据模型包括实 体模型、有限元模型和材料参数等,数据模 型通过前处理器写入数据库。载荷及约束通 过求解器写入数据库;分析结果通过后处理 器写入数据库。
二、ANSYS基本操作
下面介绍常用数据操作: 3.1 存储数据库(两种方式) (1) Save as Jobname.db,相当于直接保存 (2) Save as……,相当于另存为…… 3.2 恢复数据库(两种导入方式) (1) Resume Jobname.db,恢复当前保存数据 (2) Resume from……,不改变当前数据,导 入指定文件名的数据
二、ANSYS基本操作
(4)定义单元 在命令行(输入窗口)输入命令: ET,1,Plane42 然后选择Element Type>Add/Edit/Delete…, 单击Option,K3项选择Plane strs w/thk。
二、ANSYS基本操作
(5)定义实常数 Preprocessor>Real Contants>Add,弹出 Plane42常实数窗口,单击OK,设置THK
0
0
4
0.005-0.10来自二、ANSYS基本操作
(2)定义直线 Preprocessor>modeling>Creat>Lines>Lines >Straight Line
研究生有限元ansys实例操作
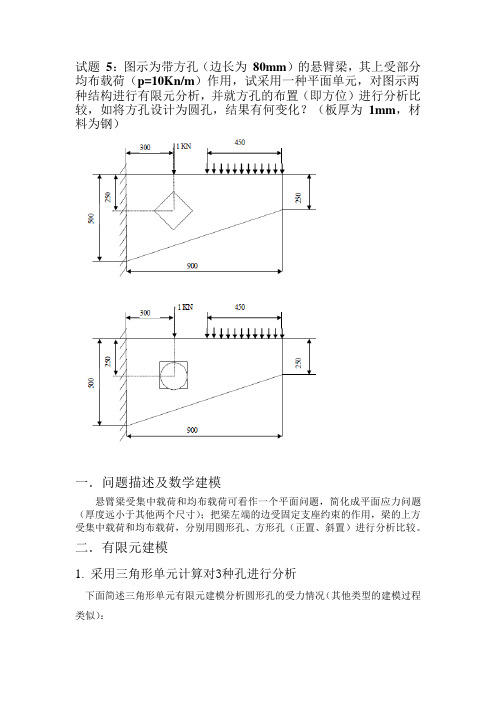
试题5:图示为带方孔(边长为80mm)的悬臂梁,其上受部分均布载荷(p=10Kn/m)作用,试采用一种平面单元,对图示两种结构进行有限元分析,并就方孔的布置(即方位)进行分析比较,如将方孔设计为圆孔,结果有何变化?(板厚为1mm,材料为钢)一.问题描述及数学建模悬臂梁受集中载荷和均布载荷可看作一个平面问题,简化成平面应力问题(厚度远小于其他两个尺寸);把梁左端的边受固定支座约束的作用,梁的上方受集中载荷和均布载荷,分别用圆形孔、方形孔(正置、斜置)进行分析比较。
二.有限元建模1. 采用三角形单元计算对3种孔进行分析下面简述三角形单元有限元建模分析圆形孔的受力情况(其他类型的建模过程类似):1.进入ANSYS【开始】→【程序】→ANSYS 12.0→File→change directory→Job Name:problem5→Run2.设置计算类型ANSYS Main Menu: Preferences→select Structural→OK3.选择单元类型单元是三节点常应变单元,可以用四节点退化表示。
ANSYS Main Menu: Preprocessor→Element Type→Add/Edit/Delete →Add →select Solid Quad 4 node 42→OK (back to Element Types window) →Options…→select K3: Plane Stress→OK→Close (the Element Type window)4. 定义材料参数材料为钢,可查找钢的参数并在有限元中定义,其中弹性模量E=210Gpa,泊松比v=0.3。
ANSYS Main Menu: Preprocessor →Material Props →Material Models →Structural →Linear →Elastic →Isotropic →input EX:2.1e11, PRXY:0.3→OK 5. 生成几何模型✓生成特征点ANSYS Main Menu: Preprocessor →Modeling →Create →Keypoints →In Active CS →依次输入六个点的坐标:input:1(0,0),2(900,250),3(900,500),4(0,500),5(300, 500),6(450,500)→OK✓生成坝体截面ANSYS Main Menu: Preprocessor →Modeling →Create →Areas →Arbitrary →Through KPS →依次连接1,2,3,6,5,4这六个特征点→OK6.网格划分ANSYS Main Menu: Preprocessor →Meshing→Size Cntrls→Manualsize→Lines →Picked Lines→选择梁外轮廓线→Size=40→Apply选择轮齿对称轴→Size=20→OkANSYS Main Menu: Preprocessor →Meshing →Mesh Tool→Mesh: Areas, Shape: Tri, Free→Mesh→Pick All (in Picking Menu) →Close( the Mesh Tool window)7.模型施加约束✓分别给左侧边施加全约束ANSYS Main Menu: Solution →Define Loads →Apply →Structural →Displacement →On lines→选择左侧边→OK →select:ALL DOF→OK✓给梁的上边施加集中载荷和分布载荷ANSYS Main Menu: Solution →Define Loads →Apply →Structural →Force →On Keypoints →拾取5节点Lab2: UY ,值为-1000→OKANSYS Main Menu: Solution →Define Loads →Apply →Structural →Pressure → On Lines→拾取5节点和6节点中间的线段FY,值为4500→OK8. 分析计算ANSYS Main Menu: Solution →Solve →Current LS →OK(to close the solve Current Load Step window) →OK9. 结果显示确定当前数据为最后时间步的数据ANSYS Main Menu: General Postproc →Read Result→Last Set查看在外力作用下的变形ANSYS Main Menu: General Postproc →Plot Results →Deformed Shape→select Def + Undeformed →OK查看节点位移分布情况Contour Plot →Nodal Solu… →select: DOF solution→Displacement vector sum→OK查看节点应力分布情况Contour Plot →Nodal Solu…→select: Stress→Stress intensity→Def + Undeformed→OK10. 退出系统ANSYS Utility Menu: File→Exit…→Save Everything→OK三.结果分析1.圆孔梁变形图,节点位移图,节点应力图2.斜置方孔变形图,节点位移图,节点应力图3.正置方孔变形图,节点位移图,节点应力图4. 将三种方案进行比较5.结论由实际情况可推知坝体X 向的变形和所受应力都为正,Y 向的变形和所受力均为负上面的结果与实际结果基本相符。
ansys有限元基础教程

ansys有限元基础教程ANSYS是一款常用的有限元分析软件,广泛应用于工程设计和科学研究领域。
本文将介绍ANSYS的有限元基础教程,帮助读者快速上手使用该软件。
首先,我们需要了解有限元分析的基本原理。
有限元分析是一种将复杂结构模型离散为大量小块(有限单元)的方法,通过求解每个小块的力学行为,最终得到整个结构的应力、位移等参数。
在ANSYS中,用户需要首先创建一个几何模型,然后将其划分为多个有限单元,并设置每个单元的材料属性、约束条件和载荷。
创建几何模型时,ANSYS提供了多种建模工具,如直线、弧线、曲面等。
用户可以通过这些工具创建出与实际结构相似的几何模型。
在模型创建完成后,我们需要划分为有限单元。
ANSYS提供了丰富的单元类型,如点单元、线单元、面单元和体单元等。
在划分单元时,用户需要根据问题的特点选择适合的单元类型。
接下来,我们需要设置材料属性、约束条件和载荷。
材料属性包括材料的弹性模量、泊松比等,用户需要在ANSYS中定义这些参数。
约束条件主要是结构的边界条件,如固支条件、约束位移等。
用户需要将这些约束条件设置好以便进行分析。
载荷包括静载荷和动载荷,用户需要根据实际情况设置相应的载荷。
在设置完模型、单元和边界条件后,我们可以进行有限元分析。
ANSYS提供了多种分析类型,如静力分析、热传导分析和模态分析等。
用户需要选择适当的分析类型,并设置相应的参数。
然后,ANSYS将自动进行计算,并给出结构的应力、位移等结果。
最后,用户还可以对计算结果进行后处理。
ANSYS提供了丰富的后处理工具,如绘制应力云图、绘制位移变形图等。
通过这些工具,用户可以直观地了解结构的受力情况和变形情况。
综上所述,ANSYS的有限元基础教程主要包括模型创建、单元划分、材料设定、约束条件设置、载荷设置、分析类型选择、计算求解和后处理等步骤。
通过学习这些基础知识,读者可以快速上手使用ANSYS进行有限元分析,为工程设计和科学研究提供有力的支持。
ansys三角形和四边形单元

一、概述在有限元分析中,选择合适的单元类型对于模拟结果的准确性和可靠性至关重要。
在ANSYS软件中,三角形和四边形单元是常用的两种单元类型,它们在不同的工程问题中具有各自的特点和适用范围。
本文将对ANSYS中的三角形和四边形单元进行介绍和分析,以期帮助工程师和研究人员在实际工程中做出正确的选择。
二、三角形单元的特点和适用范围1. 三角形单元是由三个节点和三个自由度构成的平面单元,适用于对称轴或面对称加载条件的问题。
它具有较好的形状适应性,可以适应复杂的几何形状。
2. 三角形单元适用于轻负载和小变形条件下的结构分析,例如弹性力学问题和轻负载的非线性分析。
3. 由于三角形单元仅有三个节点,所以对于边界条件和加载较复杂的问题,可能需要引入大量的单元来进行建模,从而增加了计算量和求解时间。
4. 三角形单元在非线性分析和大变形条件下的模拟效果较差,容易产生“锯齿”效应和收敛性问题。
三、四边形单元的特点和适用范围1. 四边形单元是由四个节点和四个自由度构成的平面单元,适用于矩形和正交结构的问题。
它具有简单的几何形状和稳定的性能。
2. 四边形单元适用于大变形和非线性条件下的结构分析,例如接触问题、塑性问题和大变形的非线性弹性力学问题。
3. 四边形单元相对于三角形单元具有更好的计算稳定性和收敛性,适用于对称和非对称加载条件的问题。
4. 由于四边形单元具有较好的几何适应性和稳定性,所以在建模过程中可以减少单元数量,从而降低了计算量和求解时间。
5. 在一些规则的结构问题中,四边形单元可能出现局部变形的问题,需要适当处理。
四、结论和建议在实际工程中,选择合适的单元类型是非常重要的。
根据上述分析,对于对称轴或面对称加载条件的问题可以选择三角形单元,而对于大变形和非线性条件下的问题可以选择四边形单元。
根据实际的工程需求和计算资源,也可以选择合适的单元类型,进行合理的建模和分析。
希望本文能够为工程师和研究人员在使用ANSYS软件进行有限元分析时提供一定的参考和帮助,使得模拟结果更加准确和可靠。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【ANSYS 算例】4.7.1(3) 基于3节点三角形单元的矩形薄板分析
如图4-20所示为一矩形薄平板,在右端部受集中力100 000N F =作用,材料常数为:弹性模量7110Pa E =⨯、泊松比1/3μ=,板的厚度为0.1m t =,在ANSYS 平台上,按平面应力问题完成相应的力学分析。
(a) 问题描述 (a) 有限元分析模型
图4–20 右端部受集中力作用的平面问题(高深梁)
解答 在ANSYS 平台上,完成的分析如下。
1. 基于图形界面的交互式操作(step by step)
(1) 进入ANSYS(设定工作目录和工作文件)
程序 → ANSYS Interactive →Working directory (设置工作目录) →Initial jobname (设置工作文件名): 2D3Node →Run → OK
(2) 设置计算类型
ANSYS Main Menu : Preferences… → Structural → OK
(3) 选择单元类型
ANSYS Main Menu : Preprocessor →Element Type →Add/Edit/Delete… →Add… →Solid :Quad 4node 42 →OK (返回到Element Types 窗口) → Options… →K3: Plane Strs w/thk(带厚度的平面应力问题) →OK →Close
(4) 定义材料参数
ANSYS Main Menu : Preprocessor →Material Props →Material Models →Structural →Linear →Elastic → Isotropic: EX:1.0e7 (弹性模量),PRXY: 0.33333333 (泊松比) → OK → 鼠标点击该窗口右上角的“ ”来关闭该窗口
(5) 定义实常数以确定平面问题的厚度
ANSYS Main Menu: Preprocessor →Real Constant s… →Add/Edit/Delete →Add →Type 1→ OK →Real Constant Set No: 1 (第1号实常数), THK: 0.1 (平面问题的厚度) →OK →Close (6) 生成单元模型
生成4个节点
ANSYS Main Menu: Preprocessor →Modeling → Create → Nodes → On Working Plane →输入节点1的x,y,z 坐标(2,1,0),回车→输入节点2的x,y,z 坐标(2,0,0),回车→输入节点3的x,y,z 坐标(0,1,0),回车→输入节点4的x,y,z 坐标(0,0,0),回车→OK
定义单元属性
ANSYS Main Menu: Preprocessor →Modeling → Create → Elements → Elem Attributes →Element type number:1 →Material number:1→Real constant set number:1 →OK
生成单元 ANSYS Main Menu: Preprocessor →Modeling → Create → Elements → User Numbered → Thru Nodes →Number to assign to element:1→Pick nodes:2,3,4→OK →Number to assign to element:2→Pick nodes:3,2,1→OK
(7) 模型施加约束和外载
左边两个节点施加X,Y 方向的位移约束
ANSYS Main Menu: Solution → Define Loads → Apply →Structural → Displacement → On
Nodes→鼠标选取节点3,4→OK →Lab2 DOFs to be constrained: UX,UY,V ALUE:0→OK 右边两个节点施加Y方向的集中力载荷
ANSYS Main Menu: Solution→Define Loads →Apply →Structural →Force/Moment →On Nodes→鼠标选取节点1,2→OK→Direction: FY→V ALUE: -0.5e5 →OK
(8) 分析计算
ANSYS Main Menu: Solution →Solve →Current LS→OK→Close (Solution is done! ) →关闭文字窗口
(9) 结果显示
ANSYS Main Menu: General Postproc →Plot Results→Deformed Shape …→Def + Undeformed →OK (返回到Plot Results) →Contour Plot→Nodal Solu …→Stress, Von Mises, Undisplaced shape key: Deformed shape with Undeformed model→OK (还可以继续观察其他结果)
(10) 退出
ANSYS Utility Menu: File→ Exit …→ Save Everything→OK
2 完整的命令流
!%%%%%%% [ANSYS算例]4.7.1(3) %%%% begin %%%%%
/PREP7 !进入前处理
!=====设置单元和材料
ET,1,PLANE42 !定义单元类型
KEYOPT,1,3,3 !带厚度的平面应力问题
MP,EX,1,1.0e7 !定义材料弹性模量
MP,PRXY,1,0.33333333 !定义材料泊松比
R,1,0.1 !定义实常数(平板厚度0.1)
!------定义4个节点
N,1,2,1,0,,,, !节点1,坐标(2,1,0)
N,2,2,0,0,,,, !节点2,坐标(2,0,0)
N,3,0,1,0,,,, !节点3,坐标(0,1,0)
N,4,0,0,0,,,, !节点4,坐标(0,0,0)
!------设置划分网格的单元和材料类型
TYPE,1 !设置单元类型1
MAT,1 !设置材料类型1
TSHAP,LINE !设置由节点连成直边的单元
!-------生成单元
EN,1,2,3,4 !由4个节点生成一个单元
EN,2,3,2,1 !由4个节点生成另一个单元
!-------施加约束位移
D,3,,,,,,UX,UY,UZ,,, !对3号节点, 完全位移约束
D,4,,,,,,UX,UY,UZ,,, !对4号节点, 完全位移约束
!-------施加载荷
F,1,FY,-0.5e5 !对1号节点, 施加FY=-0.5e5
F,2,FY,-0.5e5 !对2号节点, 施加FY=-0.5e5
!=====进入求解模块
/solu !求解模块
solve !求解
finish !退出所在模块
!=====进入一般的后处理模块
/POST1 !进入后处理
PLDISP,1 !计算的变形位移显示(变形前与后的对照)
!%%%%%%% [ANSYS算例]4.7.1(3) %%%% end %%%%%。
