第8-9讲 矩形单元和6节点三角形单元
人教版六年级数学上册《第八单元 数学广角——数与形》全单元教学课件PPT优秀公开课课件

课堂小结
这节课你们都学会了哪些知识?
数与形有着紧密的联系,在一定条件下可以相 互转化。当用数形结合的方法解决问题时,使 许多问题的解决变得很简单。
方法一
用一个圆 表示“1”
1 2 1 4
11 2 +4 =
1 2
1 2
1
2
11 48
11 2 +4
1 +8 =
探究新知
画图探索规律 方法一
1 2
11
1
48
16
1+ 2
1+1+1 4 8 16
=
1
1
2
64
11 48
1 1Байду номын сангаас32 16
11111 1
2
+
4
+
8
+ 16
+ 32
+ 64
=
1
2
1
11 48
1 32
8 + 2 = 26 9 27 27
……
所以原式的结果是1
课堂练习
找规律填空 2
2×4=8
22
242
2 (8) 8 2
2 16 64 (16) 2
从上到下外围数字 都是2,内部数字都 是它的左上角与右 上角两个数字的积。
8×2=16
课堂练习
计算
1-
1 2
-
1 4
-
1 8
-1-116 32
1 64
小兰
妈妈
爸爸
巩固练习
黄岩岛是我国南沙群岛的一个小岛,渔产丰富。一天,某渔 船离开港口前往这个海域捕鱼。捕捞一段时间后,发现一外 国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告, 并立即返航,渔政船接到报告后,立即从此港口出发赶往黄 岩岛。渔政船及渔船与港口的距离s和渔船离开港口的时间t 之间的关系如图所示。(假设渔船与渔政船沿同一航线航行)
六节点三角形单元

(7-26)
(4)面积坐标的积分公式 下面给出面积坐标的幂函数积分公式。它们在计算单元 刚度矩阵和等效结点载荷时有用。
在三角形单元上进行积分时,有
a!b!c! 2A A L L L dxdy (a b c 2)!
a i b j c m
(7-27)
在三角形某一边(设ij边,边长为l)上进行积分时,有
可能达到较高的精度。图7-1悬臂梁分别采用高、低阶单元 计算就是一个典型的例子。
P
A B
h
4h 悬臂深梁
常应变单元:A=0.866 B=0.619
• •
解析解:A=1.0 B=1.0
• •
• •
图7-1
高阶单元:A=0.99 B=0.99
选择位移模式时,第2章提到要考虑解的收敛性,即要考虑 到位移模式的完备性和协调性。实际操作中,一般应考虑 位移模式的对称性。这是因为,有限元位移模式的选择实 由低价至高阶,顺序选取,组成多项式。多项式中的项数
Ai Li A
y
Am Lj Lm A A
j
Aj
(7-21)
m
Ai P · Am Aj
i
x
图7-5
其中A为三角形ijm的面积,Ai, Aj, Am分别为三角形的Pjm,
Pmi, Pijd的面积。这三个比值Li, Lj, Lm称为P点的面积坐标。 由于 则
Ai Ai Am A
Li L j Lm 1
一是不能适应斜线及曲线边界,二是不便于采用大小不同 的单元。 7.3 六节点三角形单元 1、位移模式 在三角形单元i, j, m的各边中点增设一个节点, 使每个单元具有6个节点, y j 得到图7-4所示的六节点 i • 三角形单元。 m • m • 这种单元具有12个 自由度,可以采用完全 二次多项式的位移模式:
平面单元的有限元法

u
1
5
3
2
y
2x
3
5
2
y
则单元刚体位移为
v
4
5
2
3
x
6
y
3
2
5
u
1
5
3
2
y
v
4
5
2
3
x
记为
u v
1 4
0 y 0x
显然,位移函数包含 了单元的刚体位移 (平动和转动)
u v
j j
um
vm
[I]是单位矩阵,
[N]称为形函数矩阵,
Ni只与单元节点坐标有关,称为 单元的形状函数
4-2 平面问题的常应变(三角形)单元
据弹性力学几何方程得单元的应变分量
u
x y
xy
x
4-1 有限单元法的计算步骤
弹性力学平面问题的有限单元法包括五个主要步骤: 1、所分析问题的数学建模 2、离散化 3、单元分
析 4、整体分析与求解 5、结果分析
图 3-1
4-2 平面问题的常应变(三角形)单元
有限单元法的基础是用所谓有限个单元的集合 体来代替原来的连续体,因而必须将连续体简化为 由有限个单元组成的离散体。对于平面问题,最简 单,因而最常用的单元是三角形单元。因平面问题 的变形主要为平面变形,故平面上所有的节点都可 视为平面铰,即每个节点有两个自由度。单元与单 元在节点处用铰相连,作用在连续体荷载也移置到 节点上,成为节点荷载。如节点位移或其某一分量 可以不计之处,就在该节点上安置一个铰支座或相 应的连杆支座。如图3-1
第08讲特殊平行四边形单元整体分类总复习(原卷版)

第08讲特殊平行四边形章节分类总复习考点一矩形的判定与性质【知识点睛】❖矩形的判定方法:①有一个角是直角的平行四边形是矩形; ②有三个角是直角的四边形是矩形;③四个角都相等的四边形是矩形; ④对角线相等的平行四边形是矩形;⑤对角线相等且互相平分的四边形是矩形.❖矩形的性质①矩形的对边平行且相等; ②矩形的四个角都是直角;③矩形的对角线相等且互相平分; ④矩形既是轴对称图形,又是中心对称图形。
【类题训练】1.如图,在矩形ABCD中,AC、BD交于点O,DE⊥AC于点E,∠AOD=124°,则∠CDE 的度数为()A.62°B.56°C.28°D.30°2.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E是边AD的中点,点F在对角线AC上,且,连接EF.若AC=10,则EF的长为()A.B.3C.4D.53.如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=2,∠ABE=45°,则DE的长为()A.2﹣2B.﹣1C.﹣1D.24.如图,矩形ABCD和矩形BDEF,点A在EF边上,设矩形ABCD和矩形BDEF的面积分别为S1、S2,则S1与S2的大小关系为()A.S1=S2B.S1>S2 C.S1<S2D.3S1=2S25.如图,在平行四边形ABCD中,M、N是BD上两点,BM=DN,连接AM、MC、CN、NA,添加一个条件,使四边形AMCN是矩形,这个条件是()A.MB=MO B.OM=AC C.BD⊥AC D.∠AMB=∠CND6.如图,在矩形COED中,点D的坐标是(1,3),则CE的长是()A.3B.C.D.47.如图,在矩形ABCD中,AB=12,AD=10,点P在AD上,点Q在BC上,且AP=CQ,连结CP、QD,则PC+QD的最小值为()A.22B.24C.25D.268.如图,在▱ABCD中,下列条件①AC=BD;②∠1+∠3=90°;③OB=AC;④∠1=∠2,能判断▱ABCD是矩形的有()A.1个B.2个C.3个D.4个9.如图,在矩形ABCD中,AB=4,BC=6,E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为()A.B.C.D.10.定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.如图,在平面直角坐标系xOy中,矩形OABC的边OA=3,OC=4,点M(2,0),在边AB存在点P,使得△CMP为“智慧三角形”,则点P的坐标为()A.(3,1)或(3,3)B.(3,)或(3,3)C.(3,)或(3,1)D.(3,)或(3,1)或(3,3)11.如图所示,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为.12.矩形ABCD中,AB=8,AD=4,点A是y轴正半轴上任意一点,点B在x轴正半轴上.连接OD.则OD的最大值是.13.如图,矩形ABCD中,AC的垂直平分线MN与AB交于点E,连接CE.若∠CAD=70°,则∠DCE=°.14.如图,P是矩形ABCD的边AD上一个动点,矩形的两条边AB、BC的长分别为6和8,那么点P到矩形的两条对角线AC和BD的距离之和是.15.如图,在矩形ABCD中,AB=6,BC=8,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,则DE的长是.17.矩形ABCD与矩形CEFG如图放置,点B、C、E共线,点C、D、G共线,连接AF,取AF的中点H,连接GH.若BC=EF=3,CD=CE=1,则GH=.18.如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是.19.如图,在三角形ABC中,点O是AC边上的一个动点,过点O作直线MN平行于BC,设MN交∠ACB的角平分线于点E,交∠ACB的外角平分线于F.问:(1)求证:OE=OF;(2)若CE=12,CF=5,求OC的长;(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.20.如图,在平行四边形ABCD中,连接BD,E为线段AD的中点,延长BE与CD的延长线交于点F,连接AF,∠BDF=90°.(1)求证:四边形ABDF是矩形;(2)若AD=10,BD=8,求△BCF的面积.考点二菱形的判定与性质【知识点睛】❖菱形的判定方法:①有一组邻边相等的平行四边形是菱形;②四条边相等的四边形是菱形;③对角线互相垂直的平行四边形是菱形;④对角线互相垂直平分的四边形是菱形。
苏教版四年级数学上册第八单元《垂线和平行线》说课稿

苏教版四年级数学上册第八单元《垂线和平行线》说课稿一. 教材分析苏教版四年级数学上册第八单元《垂线和平行线》是小学数学中的重要内容。
本节课的主要内容有:了解垂直与平行的含义,学会用直角三角形判断两条直线是否垂直,能用直尺和三角板画垂直线和平行线,以及能在实际情境中识别垂直与平行。
教材通过丰富的图片和实际情境,激发学生的学习兴趣,让学生在观察、操作、交流活动中,自主探索和发现垂直与平行的特征和性质,培养学生的空间观念和动手操作能力。
二. 学情分析四年级的学生已经学习了直线、射线和线段的基本概念,对图形的观察和操作能力有一定的提高。
但是,对于垂直与平行的概念,学生可能还比较陌生,需要通过实际的操作和观察来理解和掌握。
此外,学生对于用直尺和三角板画垂直线和平行线的方法,可能还需要一定的指导和练习。
三. 说教学目标1.知识与技能:学生能理解垂直与平行的含义,学会用直角三角形判断两条直线是否垂直,能用直尺和三角板画垂直线和平行线。
2.过程与方法:学生通过观察、操作、交流等活动,探索垂直与平行的特征和性质,培养学生的空间观念和动手操作能力。
3.情感态度与价值观:学生感受数学与生活的联系,培养学习数学的兴趣和信心。
四. 说教学重难点1.教学重点:学生能理解垂直与平行的含义,学会用直角三角形判断两条直线是否垂直,能用直尺和三角板画垂直线和平行线。
2.教学难点:学生能灵活运用垂直与平行的知识,解决实际问题。
五. 说教学方法与手段1.教学方法:采用情境导入、观察操作、交流探讨、总结提升的教学方法,引导学生自主探索和发现垂直与平行的特征和性质。
2.教学手段:利用多媒体课件、直尺、三角板、图片等教学辅助工具,为学生提供丰富的学习资源,提高学生的学习兴趣和效果。
六. 说教学过程1.情境导入:通过展示生活中的垂直与平行的例子,如电梯、黑板、道路等,引导学生观察和思考,引出本节课的主题。
2.观察操作:学生分组合作,用直尺和三角板尝试画出垂直线和平行线,观察和交流各自的成果,总结垂直与平行的特征和性质。
2019年秋部编版六年级上册数学 第8单元 数学广角——数与形 教案

第8单元数学广角——数与形单元学习目标总览数形结合是一种非常重要的数学思想,把数与形结合起来解决问题可使复杂的问题变得更简单,使抽象的问题变得更直观。
有时候,图形中隐含着数的规侓,可利用数的规侓来解决图形的问题。
有时候,利用图形来直观地解释一些比较抽象的数学原理与事实,让人一目了然。
1.通过数与形的教学,使学生初步学会一种重要的解题方法与策略。
促进学生数学思维的发展。
2.借助相关图形的操作与剪拼等情境,实现数与形之间的转化。
3.通过数与形的训练,让学生感受到数学之美。
运用数形结合解决问题1课时1.引导学生数形结合,相互印证。
形的问题中包含数的规律,数的问题也可以用形来帮助解决,教学时,要让学生通过解决问题体会到数与形的这种完美结合。
既可以从数的角度出发,让学生看看可以怎样用图形来表示数的规律,也可以让学生寻找图形中所包含的数的规律。
通过数与形的对应关系,互相印证结果,感受数学的魅力。
2.使学生感受到用形来解决数的有关问题的直观性与简捷性。
图形的直观、形象的特点,决定了化数为形往往能够达到以简驭繁的目的。
例如,例2中,用举例的方法求出等比数列的有限和,都不能证明无限多项相加的结果为1。
但是如果用圆或线段的图形加以说明,学生则比较容易理解当一个数无限趋近于1时,其结果就是1。
一个极其抽象的极限问题,由于用图形来解决,就变得十分直观和便捷了。
3.引导学生从不同的角度探索数与形的通用模式。
小学阶段,虽然不要求写出一个数列的通式,但可以通过数形结合的方法,利用图形的规律,从不同的角度,用自己的语言描述出数列的通用模式。
运用数形结合解决问题课时目标导航算术与图形的转换。
(教材第107~108页例1、例2)1.使学生认识到数形结合的思想可以使某些抽象的数学问题直观化、生动化,能够变抽象思维为形象思维。
2.使学生能够感受到数与形可以互相转化,树立数与形相结合是数学解题的思想方法。
3.使学生加深对数形结合思想方法的认识,充分感受数形结合在小学数学学习中的应用。
第九讲 有限元
x 0 y 1 2 xy 2(1 )
平面应变问题弹性矩阵D
6. 单元刚度矩阵
[ K e ] [ B]T [ D][B]d (vol)
V
a b
a b
[ B]T [ D][B]tdxdy t——厚度
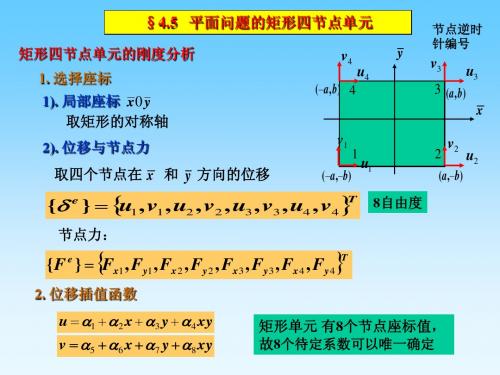
§4.5 平面问题的矩形四节点单元
矩形四节点单元的刚度分析 1. 选择座标 1). 局部座标 x0 y 取矩形的对称轴 2). 位移与节点力
v4
( a , b ) 4
y
节点逆时 针编号
u4
v3
3 (a , b)
u3
x
v1
(a,b)
1
T
取四个节点在 x 和 y 方向的位移
e
u1
8自由度
2
v2
u2
v 5 6 x 7 y 8 xy
矩形单元 有8个节点座标值, 故8个待定系数可以唯一确定
u 1 2 x 3 y 4 xy
v 5 6 x 7 y 8 xy
1 2 3 u 1 x y xy 0 0 0 0 4 0 0 0 0 1 x y xy 5 v 6 7 8
e E T T A
Fx1 N1 F 0 y1 N Fx 2 2 F t 0 y2 N3 Fx 3 0 F y3
E
0 0 N1q y N1 0 0 0 dxdy t N q dxdy N 2 q y 2 y 0 0 N 3q y N3
[B]——矩形4节点单元几何矩阵 简写成:
六节点三角形单元

3、应力矩阵
根据应力-应变关系,可以计算单元中的应力,得到式(228)同样形式
{ } [D]{} [S][ ]e
(7-11)
应力矩阵[S]具有与式(2-29)同样形式
[S] [D][B]
将[S]写成子矩阵形式 [S] [Si S j Sl Sm ]
(7-12) (7-13)
其中
(7-17)
上式对应平面应力情形。对于平面应变情形,只须将上式 中的E、作相应的改变。
5、等价节点力 单元体积力和表面力引起的节点力仍可用式(2-45)和 (2-46)进行计算。
{FV } A[N ]T {qV }hdxdy
T
{FS}
[N]
l
{qS }hdl
(2-45) (2-46)
(7-2)
式中形函数为 :
Ni
1 4
1
x a
1
y b
பைடு நூலகம்
N
j
1 4
1
x a
1
y b
Nl
1 4
1
x a
1
y b
Nm
1 4
1
x a
1
u a1 a2x a3 y a4xy
v
a5
a6
x
a7
y
a8
xy
(7-1)
在上式表示的位移模式中,a1, a2, a3, a5, a6, a7, a8
反映了单元的刚体位移和常
应变。在单元的边界(x=±a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.1 提高有限元求 解精度的途径 4.2 矩形单元 4.3 6节点三角形 单元简介
简单三角形单元缺点 提高有限元求解精度的途径 高精度单元的原理
单元位移模式 单元应力、应变 单元刚度矩阵 矩形单元讨论
单元简介 面积坐标 单元位移模式
第四章 平面问题高精度单元
§4.1
提高有限元求解精度的途径
u N i ui
i 1 6 6
v N i vi
i 1
•
但是,采取如前面3节点单元建立形函数的办法过于复杂,下面介 绍用三角形单元的面积坐标描述单元位移模式和形函数的方法。
第四章 平面问题高精度单元
§4.3
6节点三角形单元简介
二、面积坐标下6节点三角形单元分析
• 面积坐标的定义如图所示。
因此,单元内任一点的面积坐标满足关系: Li+ Lj+ Lm=1 即3个面积坐标只有2个面积坐标是独立的。
•
面积坐标与直角坐标之间有确定的变换关系,因此,对三角形单
元的描述完全可以用面积坐标进行。
直角坐标表示面积坐标
不难导出下列变换关系:
1 Li (ai bi x ci y ) 2A
6节点三角形单元
第四章 平面问题高精度单元
§4.3
•
6节点三角形单元简介
显然单元满足完备性要求。由于该位移模式决定了单元边界上位 移呈二次抛物线分布,相邻单元公共边界上有三个公共节点,正 好能够保证相邻单元在边界上位移的连续性,因而是协调元,单
元满足收敛条件。
• • 该单元应变、应力随坐标完全呈线性变化,属于高精度单元。 进行广义坐标代换后位移模式仍可写成标准形式:
Ni (2Li 1) Li (i 1,2,3)
N 4 4 L1 L2 N 5 4 L2 L3 N 6 4 L3 L1
第四章 平面问题高精度单元
§4.3
6节点三角形单元简介
不难验证,上述6个形函数满足形函数的2个主要性质:
N i ( Pj ) ij
N
i
1
Ni (2Li 1) Li (i 1,2,3) N 4 4 L1L2 N 5 4 L2 L3 N 6 4 L3 L1
一、简单三角形单元的缺点 • • 三节点三角形单元精度低,收敛慢,在单元内不能反映应力应变 的变化。 这是因为该单元只有3个节点,单元自由度少,单元位移模式只 能是线性函数,描述单元内位移变化的能力差。
二、提高有限元求解精度的途径 • • 第一个途径是对某一种特定类型的单元采用网格加密,依靠单元 的收敛性提高求解精度; 第二个途径是对一定的单元网格和单元尺寸,采用高精度单元以 提高求解精度。
精度会高一阶。
(b y ) (a x ) (b y ) (a x ) (b y ) (a x ) (b y ) (a x ) E (b y ) S (a x ) (b y ) (a x ) (b y ) (a x ) (b y ) (a x ) 2 4ab(1 ) 1 1 1 1 1 1 1 1 (a x ) (b y ) (a x ) (b y ) (a x ) (b y ) (a x ) ( b y ) 2 2 2 2 2 2 2 2
第四章 平面问题高精度单元
§4.1
提高有限元求解• 原理:提高单元位移模式多项式的阶次,从而增强单元拟合局部区 域位移、应力变化的能力。 • • 途径:主要是增加单元的节点数。 对平面问题,先考虑采用4节点矩形单元和6节点三角形单元。
第四章 平面问题高精度单元
形函数矩阵经过微分算子矩阵作用后得到3×8应变矩阵:
0 b y 0 b y 0 b y 0 b y 1 B 0 a x 0 a x 0 a x 0 ax 4ab a x b y a x b y a x b y a x b y
•
和简单三角形单元一样,矩形单元位移 模式中包含了完全一次多项式,所以满
足完备性条件。因此矩形单元的收敛性
得到保证。
第四章 平面问题高精度单元
§4.2 二、单元应变和应力
矩形单元
单元位移模式代入平面问题几何方程:
x x y 0 xy y 0 N e B e y x
第四章 平面问题高精度单元
§4.2
•
•
矩形单元
显然,上述形函数满足形函数性质。
由于边界平行于坐标轴,矩形单元位移模式沿单元边界(x,y方向) 都是线性变化,沿其他方向则按2次函数变化。称为“双线性”位 移函数。
•
由于单元位移在单元边界上线性变化,而单元之间的公共边界上
有2个公共节点,所以单元边界间的位移是连续的,单元满足协调 性条件。
§4.2
矩形单元
一、矩形单元及其位移模式
• 矩形单元边长分别为2a、2b。取4个 顶点为节点。不失一般性地假设矩 形的2个对称轴分别为x,y轴。每节 点2个位移分量,因此单元共8个自 由度。 • 单元节点编号为 k,l,m,n
单元节点位移列阵为:
uk
e
vk
ul
vl
um vm un vn
•
•
采用面积坐标后,单元刚度矩阵和等效节点力的计算都比较方便。
6节点三角形单元列式推导原理与其它单元相同。
第四章 平面问题高精度单元
第四章 平面问题高精度单元
(i, j, m)
显然,面积坐标与3节点三角形单元的形函数完全相同。
第四章 平面问题高精度单元
§4.3
6节点三角形单元简介
bi bj bm ci 1 c j x cm y
Li ai 1 矩阵形式: L j a j L 2 A a m m
• •
矩形单元
4节点矩形单元采用了双线性位移模式,应力基本上沿坐标轴呈线 性变化,因而精度比3节点三角形单元高。 由于位移模式在单元边界上线性变化,并且根据单元公共边界上 两个共同节点位移插值得到,单元的协调性得到满足,同时也满 足完备性,因此单元是收敛的。 单元要求两对边平行于坐标轴,因而不能模拟复杂几何边界,单 元网格疏密不能过渡,这是矩形单元的固有缺点。矩形单元可以 与3节点三角形单元结合使用。 如果突破几何上的限制,成为任意方位的任意四边形单元,便可 成为实用的单元。
1 Li xm L j ym Lm
§4.3
6节点三角形单元简介
利用上面变换式,三角形单元上的任何多项式函数可以方便地在 两种坐标之间转换。
面积坐标的各种形式幂函数在三角形上的积分有很简便的计算公式。
•
面积坐标表示的6节点三角形单元形函数
根据形函数性质直接构造出用面积坐标表示的形函数如下:
•
•
第四章 平面问题高精度单元
§4.3 一、单元概述
•
6节点三角形单元简介
三角形单元天然具有很好的几何适应性,如果增加三角形单元位移模式
多项式的阶数,就能成为实用的单元。考虑图示6节点三角形单元,单 元每边中点设一个节点,则单元有12个自由度,因此位移模式恰好取完
全二次多项式:
u 1 2 x 3 y 4 xy 5 x 2 6 y 2 v 7 8 x 9 y 10 xy 11x 2 12 y 2
u N k uk Nl ul N mum N nun Ni ui
v N k vk Nl vl N mvm N n vn Ni vi
• 写成矩阵形式为:
u e N v
其中
N 为形函数矩阵
第四章 平面问题高精度单元
第四章 平面问题高精度单元
§4.2
矩形单元
三、矩形单元刚度矩阵
• 矩形单元刚度矩阵导出的原理和方法同简单三角形单元。计算式如下:
k a b B DBhdxdy
e a b T
•
可以通过积分计算出精确的刚度矩阵元素,见P51。
第四章 平面问题高精度单元
§4.2 四、矩形单元讨论
T
第四章 平面问题高精度单元
§4.2
•
矩形单元
单元内位移多项式设4项,为双线性多项式:
u a1 a2 x a3 y a4 xy v a5 a6 x a7 y a8 xy
通过节点坐标和节点位移代入,把广义坐标(多项式系数)a1
~ a8
代换为节点位移分量后得到插值形式的位移函数:
•
三角形中任意一点的位置用三个参数来表示,
称为面积坐标。面积坐标(Li, Lj, Lm)定义 为三个比值:
Ai Li A Aj Lj A Aj Lm A
第四章 平面问题高精度单元
三角形单元上的面积坐标
A为三角形面积,显然有: Ai Aj Am A
§4.3
•
6节点三角形单元简介
面积坐标表示直角坐标 不难导出下列变换关系:
x xi Li x j L j xm L m y yi Li y j L j ym Lm
1 1 矩阵形式: x x i y y i
第四章 平面问题高精度单元
1 xj yj
§4.2
Nk N 0 0 Nk
矩形单元
Nl 0 0 Nl Nm 0 0 Nm Nn 0 0 Nn
形函数矩阵
•
各形函数为:
1 x y (1 )(1 ) 4 a b 1 x y N l (1 )(1 ) 4 a b 1 x y N m (1 )(1 ) 4 a b 1 x y N n (1 )(1 ) 4 a b Nk
