西北工业大学自动控制原理 (23)
《自动控制原理》(卢京潮,西北工业大学)第二章习题及答案
∴
G ( s) =
4 ⎤ ⎡ −1 k (t ) = L−1 [G ( s )] = L−1 ⎢ + = 4e − 2 t − e − t ⎥ s + 1 s + 2 ⎣ ⎦
- 16 -2-10 Nhomakorabea已知系统传递函数
C ( s) 2 &(0) = 0 , , 且初始条件为 c(0) = −1 ,c = 2 R ( s ) s + 3s + 2
(1) (3) 原式 =
−1 1 3 1 1 + − + + 3 2 2( s + 2) 4( s + 2) 8( s + 2) 24s 3( s + 3)
− t 2 − 2 t t − 2 t 3 − 2 t 1 −3t 1 ∴ x(t)= e + e − e + e + 4 4 8 3 24
1 s 1 1 s +1 1 1 1 2 − 2 = − ⋅ + ⋅ (4) 原式 = 2 2 s s + 2 s + 2 2 s 2 ( s + 1) + 1 2 ( s + 1) 2 + 1
化,试推导 id = f (ud ) 的线性化方程。 解 解得 将 i d = 10 −14 (e 将 i (0) = 2.19 × 10 A 代入 i d = 10 −14 (e
−3
ud
u d / 0.026
− 1)
ud 0 = 0.679V
u d / 0.026
− 1) 在( u d 0 , i0 )处展开为泰勒级数,
∴ X (s) = ∴ X ( s) =
e− s 1 e −3s 1 ( s ) − 2 (2 s + ) + 2 s 2 s 2
西北工业大学—自动控制原理

ur
u u a m up
l
消去中间变量得:
Tm l l k 1 k 2 k 3 k 4 k m l k 1k 2 k 3 k m u a ─二阶线性定常微分方程
即: l
1 k1k 2 k 3k 4 k m kk kk l l 1 2 3 m ua Tm Tm Tm
R 1 1 uc uc ur L LC LC
── 2 阶线性定常微分方程
(2)弹簧—阻尼器机械位移系统 分析 A、B 点受力情况
A x 0 ) k2x0 k1 (x i x A ) f(x
A
B
由 k 1 ( x i x A ) k1 x A 解出 x A x i
第一章:自动控制理论的一般概念 §1.1 引言 §1.2 自动控制理论发展概述 发展过程: 19 世纪
呼应 与西方工业革命发展相
时域 复域 频域
20 世纪 60 年代初
古典控制理论 (单入/出)
与航天技术发展相呼应
现(近)代控制理论 (多入 / 出)
2.
闭环(信号有反向作用) 特点:复杂、抗干扰能力强、精度高、有稳定性问题。
3.
复合(前向联系、反向作用) 特点:性能要求高时用之。 例如:炉温系统可以采用开环或闭环的。
闭环控制工作原理:
给定量:使c跟踪r 外部作用: 干扰量:使c偏离r
控制目的:排除干扰因素、影响、使被控量随给定量变化。 负反馈原理——构成闭环控制系统的核心
0
at e
t 0 t 0
L[f ( t )] e at e st dt e sa t dt
0 0
西北工业大学—自动控制原理

联系并准备
实验二:典型环节模拟 实验三:二阶系统特征参数对性能的影响
联系地点: 实验大楼 12 楼
联 系 人: 杨建华 (实验中心主任)
§3.5
线性系统的稳定性分析
§3.5.1 稳定性的概念 lim k(t) 0 t
§3.5.2 稳定的充要条件
系统闭环特征方程的所有根都具有负的实部 或所有闭环特征根均位于左半s平面
自动控制原理
西北工业大学自动化学院
自动控制原理教学组
自动控制原理
本次课程作业(9)
3 — 8, 9, 10
自动控制原理
(第 9 讲) §3 线性系统的时域分析与校正
§3.1 概述 §3.2 一阶系统的时间响应及动态性能 §3.3 二阶系统的时间响应及动态性能 §3.4 高阶系统的阶跃响应及动态性能 §3.5 线性系统的稳定性分析 §3.6 线性系统的稳态误差 §3.7 线性系统时域校正
§3.5
线性系统的稳定性分析(2)
§3.5.2 稳定的充要条件
根据系统稳定的定义,若 lim k(t) 0 ,则系统是稳定的。
t
必要性: (s) M (s) bm (s z1 ) (s z2 ) (s zm ) D(s) an(s 1 ) (s 2 ) (s n )
充分性:
C(s) (s)
解. 列劳斯表
s5 1
0
s4 2
0
s3 80
00
s2 e0
-2
s1 16 /e
0
s0 -2
-1
-2
列辅助方程: 2s4 2 0
d 2s4 2 8s3 0
ds
第一列元素变号一次,有一个正根,系统不稳定
§3.5
西北工业大学自动控制原理考试试题汇总

装订线注:2. 命题教师和审题教师姓名应在试卷存档时填写。
共4页 第1页学号:姓名:自动控制原理试题A (56学时)答案及评分标准一、答案:A C B B A D C D C B评分标准:每小题2分二、1、答案:()12314()12314123141C S R S G G G G G G G G G G H G G H G +++--=评分标准:15分(按步骤给分)2、答案:%16.3 1.4s σ=s =% t 评分标准:10分,每一问5分3、答案:(1)*13K ω=-==12a d = d 3K (2) 13<<15评分标准:15分 第一问10分,第二问5分4、答案:(1) (2) K=80K <<评分标准: 15分 第一问8分,第二问7分 5、答案:(1) ()(1)(11020K G s s ss ++=)033.4γ=- K=100(2) 3.1251()1001c s G s s ++=(3) 0100(3.1251)()(1)(1)(10011020'57.7c s GG s s s s s γ+⎧⎪⎪+++⎨⎪=⎪⎩=) 评分标准:25分 第一问10分,第二问5分,第三问10分装订线注:2. 命题教师和审题教师姓名应在试卷存档时填写。
共4页 第1页学号:姓名:自动控制原理试题B (56学时)答案及评分标准一、 答案:C D B A B C A D C B评分标准:每小题2分二、1、答案:%16.3 1.4s σ=s =% t评分标准:10分,每一问5分2、答案:(1)*13K ω=-==12a d = d 3K (2) 13<<评分标准:15分 第一问10分,第二问5分 3、答案:()12314()12314123141C S R S G G G G G G G G G G H G G H G +++--=评分标准:15分(按步骤给分) 4、答案: (1) ()(1)(11020K G s s s s )++= K=10033.4γ=-(2) 3.12511001c S G S ++=(3) 0100(3.1251)()(1)(1)(1001)1020'57.7c s GG s s s s s γ+⎧⎪⎪+++⎨⎪=⎪⎩=评分标准:25分 第一问10分,第二问5分,第三问10分5、 答案:(1) (2) K=80K <<15评分标准: 15分 第一问8分,第二问7分诚信保证本人知晓我校考场规则和违纪处分条例的有关规定,保证遵守考场规则,诚实做人。
《自动控制原理》卢京潮主编课后习题答案西北工业大学出版社
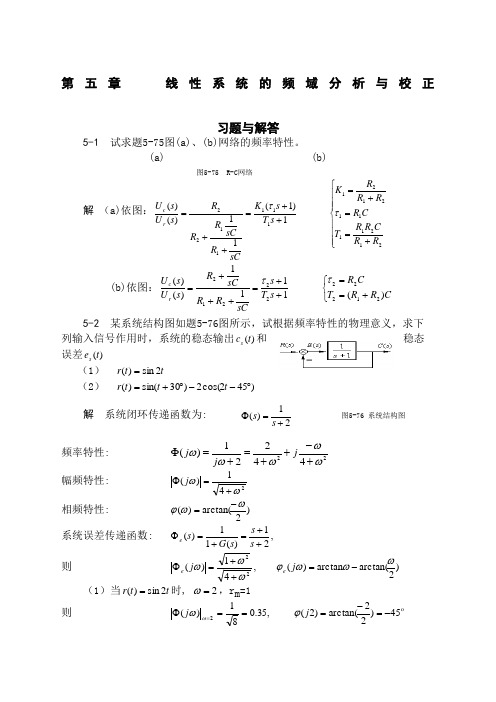
第五章 线性系统的频域分析与校正习题与解答5-1 试求题5-75图(a)、(b)网络的频率特性。
(a) (b)图5-75 R-C 网络解 (a)依图:⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(R R C R R T C R RR R K s T s K sC R sC R R R s U s U r c ττ (b)依图:⎩⎨⎧+==++=+++=C R R T CR s T s sCR R sC R s U s U r c)(1111)()(2122222212ττ 5-2 某系统结构图如题5-76图所示,试根据频率特性的物理意义,求下列输入信号作用时,系统的稳态输出)(t c s 和稳态误差)(t e s(1) t t r 2sin )(=(2) )452cos(2)30sin()(︒--︒+=t t t r 解 系统闭环传递函数为: 21)(+=Φs s 图5-76 系统结构图 频率特性: 2244221)(ωωωωω+-++=+=Φj j j 幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-=系统误差传递函数: ,21)(11)(++=+=Φs s s G s e 则 )2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e(1)当t t r 2sin )(=时, 2=ω,r m =1 则 ,35.081)(2==Φ=ωωj ο45)22arctan()2(-=-=j ϕ(2) 当 )452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωω5-3 若系统单位阶跃响应 试求系统频率特性。
解 ss R s s s s s ss C 1)(,)9)(4(3698.048.11)(=++=+++-= 则 )9)(4(36)()()(++=Φ=s s s s R s C 频率特性为 )9)(4(36)(++=Φωωωj j j5-4 绘制下列传递函数的幅相曲线:解 ()()()12G j K j K e j ==-+ωωπ幅频特性如图解5-4(a)。
821西北工业大学自动控制原理考试大纲

题号:821
《自动控制原理》
考试大纲
考试内容
正确理解自动控制原理课程中的有关概念。
掌握结构图等效变换方法和梅森公式。
能根据结构图熟练求取系统的传递函数。
掌握代数稳定判据及其应用;掌握系统稳态误差的分析和计算方法;掌握一、二阶系统典型响应的特点以及模型参数与动态性能之间的关系,并能熟练分析与计算系统的动态性能,了解附加闭环零、极点对系统动态性能的影响。
能熟练绘制系统根轨迹(包括广义根轨迹)并分析系统性能随参数的变化规律,掌握有关的计算方法。
掌握频率响应与频率特性的概念;掌握典型环节的频率特性,能熟练绘制系统的开环频率特性;掌握由频率特性确定传递函数的方法;掌握频域稳定判据;理解三频段的意义,掌握稳定裕度计算和系统性能估算的方法;正确理解闭环频率特性及相应的特征量。
掌握频域串联校正方法;掌握反馈校正和复合校正方法。
掌握差分方程,能熟练推导离散系统的脉冲传递函数;熟练掌握离散系统的稳定性分析方法和稳态误差计算方法。
了解非线性系统运动的特点,重点掌握运用描述函数法进行非线性系统稳定性及自振分析的方法。
一般掌握相平面法。
注重各章概念的融会贯通以及解题方法的综合运用。
西北工业大学《自动控制原理》习题解答

《自动控制原理》习题解答西北工业大学自动化教研室第一章习题及答案1-3图1-3 (a),(b)所示均为调速系统。
(1) 分别画出图1-24(a)、图(b)所示系统的方框图。
给出图1-24(a) 所示系统正确的反馈连线方式。
(2) 指出在恒值输入条件下,图1-24(a),(b) 所示系统中哪个是有差系统,哪个是无差系统,说明其道理。
图1-3 调速系统工作原理图解图1-3 (a)正确的反馈连接方式如图1-3 (a)中虚线所示。
(1) 系统方框图如图解1-10所示。
(2) 图1-3 (a) 所示的系统是有差系统,图1-3 (b) 所示的系统是无差系统。
图1-3 (a)中,当给定恒值电压信号,系统运行达到稳态时,电动机转速的恒定是以发电机提供恒定电压为条件,对应发电机激磁绕组中电流一定是恒定值。
这意味着放大器前端电压是非零的常值。
因此,常值偏差电压存在是系统稳定工作的前提,故系统有差。
图1-3 (b)中,给定恒定电压,电动机达到稳定转速时,对应发电机激磁绕组中的励磁电流恒定,这意味着执行电动机处于停转状态,放大器前端电压必然为0,故系统无差。
1-4图1-4 (a),(b)所示的系统均为电压调节系统。
假设空载时两系统发电机端电压均为110V,试问带上负载后,图1-4(a),(b)中哪个能保持110V不变,哪个电压会低于110V?为什么?图1-4 电压调节系统工作原理图解带上负载后,开始由于负载的影响,图1-4(a)与(b)系统的端电压都要下降,但图(a)中所示系统能恢复到110V,而图(b) 所示系统却不能。
理由如下:图(a)系统,当u低于给定电压时,其偏差电压经放大器K放大后,驱动电机D转动,经I增大,发电机的输出电压会升高,从而使偏差电减速器带动电刷,使发电机F的激磁电流j压减小,直至偏差电压为零时,电机才停止转动。
因此,图(a)系统能保持110V不变。
图(b)系统,当u低于给定电压时,其偏差电压经放大器K后,直接使发电机激磁电流增大,提高发电机的端电压,使发电机G 的端电压回升,偏差电压减小,但不可能等于零,因i=0,发电机就不能工作。
自动控制原理西北工业大学课件

Routh s3 s2 s1
s0
2
1+0.6K
3
K
3(1+0.6K)-2K 0 3
K
3-0.2K>0 K<15 K>0
10 < K <15
§3.6.4
动态误差系数法(1)
动态误差系数法
用静态误差系数法只能求出稳态误差
值
ess
lim
t
e(t )
;而稳态误差随时间变化的
规律无法表达。
用动态误差系数法可以研究动态误差 es (t )
(((32GKK2K))()K(Ktttss)ttG)GKKKD2(2((ttt(,sss,s22ss)))02()::s.1007.K1140时s1s时0K0ss121710tK(10212K201s40t0t0K,0t110st0101)0K00010Kt00tt)tst0s0s000K30vn00.Kv50.t14t5s10Ks9100021t50101Kn0K30,0n0t00.t51K02nt
1
0
G2(s) s
线性系统的时域分析与校正
第三章小结
时域分析法小结(1)
自动控制原理1~3章测验题
一. 单项选择题 ( 在每小题的四个备选答案中,选出一
个正确的答案,将其题号写入题干的○内,每小题
1分,共 分 ) 1.适合于应用传递函数描述的系统是
○
A.非线性定常系统; B.线性时变系统; C.线性定常系统; D.非线性时变系统。
i0
E(s) Φ e (s).R(s)
C0 R(s) C1sR(s) C2s2 R(s) Ci si R(s)
es (t ) C0 r(t ) C1r(t ) C2r(t ) Cir (i) (t ) Cir (i) (t ) i0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
K ( s 1)
G(s) 2
s s( 1)
1
§5.3.4 最小相角系统和非最小相角系统(3)
非最小相角系统
—— 在右半s平面存在开环零、极点或带纯延时环节的系统
★ 非最小相角系统相角变化的绝对值一般 比最小相角系统的大
★ 非最小相角系统未必不稳定 ★ 非最小相角系统未必一定要画0根轨迹 ★ 最小相角系统由L()可以唯一确定G(s)
GX
jGY
令
Im[ G( j)] GY 0
得
g 20 4.47
代入实部 GX ( g ) 0.4167
G(g ) 0.4167 h 1 1 2.4
G( jg ) 0.4167
§5.5
稳定裕度 (6)
解法II:由Bode图求 , h。
由L(): 得
G(s)
s(
5 s 1)(
非最小相角系统由L()不能唯一确定G(s)
课程回顾
奈奎斯特稳定判据 Z P 2N
0 闭环系统不稳定 Z 0 闭环系统稳定
0 有误!
Z: 在右半s平面中的闭环极点个数 P: 在右半s平面中的开环极点个数 N: 开环幅相曲线GH(j)包围[G]平面(-1, j0)点的圈数
注意问题
1. 当[s]平面虚轴上有开环极点时,奈氏路径要从其右边 绕出半径为无穷小的圆弧;[G]平面对应要补充大圆弧
2 g
tan 90
g2 20
g 4.47
20
h
1
g
2 g
22
2 g
ห้องสมุดไป่ตู้
102
g 4.47
2.4
G( jg )
100
(7.6 dB)
§5.5
稳定裕度 (5)
(2.2)将G(j)分解为实部、虚部形式
G( j )
100
j(2 j )(10 j )
1200 j100(20 2 ) (4 2 )(100 2 )
2. N 的最小单位为二分之一
§5.4.3
对数稳定判据 (4)
例2
G(s)
1000 s(s2 25)(0.2s 1)
40
s[( s )2 1]( s 1)
5
5
G( j0) 0
G( j0 ) 90
G( j5 ) 135
G( j5 ) 315
G( j) 0 360
N N N 0 1 1 Z P 2N 0 2 (1) 2
s( s 1)
1
求K:
K c
G( j)
c
2 c 1
K
c2 1
1
K c2 1
K 2 c 1
§5.3.4 最小相角系统和非最小相角系统(2)
⑴
⑵
⑶
⑷
G( j0 ) 90 G( j) 0 90
G( j0 ) 90 G( j) 0 90
G( j0 ) 90 G( j) 0 90
自动控制原理
(第 23 讲)
§5.5 稳定裕度
§5.5.1 稳定裕度的定义 §5.5.2 稳定裕度的计算
§5.5
稳定裕度 (1)
系统动态性能
稳定程度
时域(t) 频域()
稳定边界
稳定程度
虚轴 (-1,j0)
阻尼比 x 到(-1,j0)的距离
稳定裕度
(开环频率指标)
§5.5
稳定裕度 (2)
§5.5.1 稳定裕度的定义
自动控制原理
(第 23讲)
§5. 线性系统的频域分析与校正
§5.1 §5.2 §5.3 §5.4 §5.5 §5.6 §5.7 §5.8 §5.9
频率特性的基本概念 幅相频率特性(Nyquist图) 对数频率特性(Bode图) 频域稳定判据 稳定裕度 利用开环频率特性分析系统的性能 闭环频率特性曲线的绘制 利用闭环频率特性分析系统的性能 频率法串联校正
§5.4.3
对数稳定判据 (5)
例3 G(s)
Ks 3
(0.2s 1)( s 1)(5s 1)
G( j0) 00 G( j0 ) 0270 G( j) K0
K1 N N N 0 0 0
Z P 2N 0 20 0
K 2 N N N 0 1 1
Z P 2N 0 2 (1) 2
截止频率 ωc
相角裕度
G( jωc ) 1 180 G( jc )
相角交界频率ωg G( jωg ) 180
幅值裕度 h
h 1
G( jg )
, h 的几何意义
, h 的物理意义
系统在
h
相角 幅值
方面的稳定储备量
一般要求
40 h 2
§5.5
稳定裕度 (3)
§5.5.2 稳定裕度的计算
例4
G(s)
s(
s
5 1)(
s
1)
s(s
100 2)(s
10)
,求
,
h。
2 10
解法I:由幅相曲线求 , h。
100
(1)令 G( jωc ) 1 c c2 22 c2 102
c2[c4 104c2 400] 10000
试根得 c 2.9
180 G( jc ) 180 (2.9)
s
1)
2 10
5
10
G(
jc )
1
c
c
2
1
c2
c 10 3.16 2.9
180 G( jc ) 180 (3.16)
180 90 arctan 3.16 arctan 3.16
2
10
90 57.67 17.541 14.8 18.5
g 210 4.47
h 1 G( j4.47)
自动控制原理
西北工业大学自动化学院
自动控制原理教学组
自动控制原理
本次课程作业(23)
5 — 20(用坐标纸), 21, 22 5 — 23, 24 (选做)
§5.3.4 最小相角系统和非最小相角系统(1)
例8 开环系统Bode图如图所示,求 G(s)。
K ( s 1)
解 依题有 G(s) 2
1 2.4 0.4167
§5.5
稳定裕度 (7)
6( s 1)
例5
G(s)
2.5
s( s 1)( s 1)( s
,求 , h。
1)
2 5 12.5
解.作L()求 c
法I: 法II:
6 2.5
c 2 G( jc ) 1
c
62 2.5
4.8
6 c
2.5
c
c
2
11
62
2.5c
c
62 2.5
180 90 arctan 2.9 arctan 2.9
2
10
90 55.4 16.1 18.5
§5.5
稳定裕度 (4)
(2.1)令 ( g ) 180
90 arctan g arctan g
2
10
可得 arctan g arctan g 90
2
10
g g
2 10
1
4.8
180 G( jc )
180 arctan 4.8 90 arctan 4.8 arctan 4.8 arctan 4.8
