南邮信号与系统课后答案精选精品PPT课件

合集下载

南邮信号与系统答案第6章

∞
信号与系统 · 习题解答
⎧ 1 k = 0,1,2,3 ⎪ *（3） f (k ) = ⎨− 1 k = 4,5,6,7 ⎪0 其它 ⎩
第5页
解法一：f (k ) = δ (k ) + δ (k − 1) + δ (k − 2) + δ (k − 3)
− δ (k − 4) − δ (k − 5) − δ (k − 6) − δ (k − 7) ↔ 1 + z −1 + z − 2 + z −3 − z − 4 − z −5 − z −6 − z −7 1 − ( z −1 ) 4 1 − ( z −1 ) 4 (1 − z − 4 ) 2 z z 4 −1 2 = − z −4 = = [ 4 ] −1 −1 −1 z −1 z 1− z 1− z 1− z
信号与系统 ·Z变换式，试求f(0)，f(1)，f(2)和f(∞)。 z 2 − 2z (1) F ( z ) = 2 ( z − 1)( z + 0.5)
解：由初值定理：f (0) = lim F ( z ) = 0 z →∞
f (1) = lim z[ F ( z ) − f (0)] = 1
1
L
1 2
3
0
4
k
f (k ) = δ (k ) + δ (k − 2) + δ (k − 4) + L + δ (k − 2m) + L ↔ 1+ z
−2 ∞
+z
−4
+L+ z
− 2m
+L
2
1 m 1 z = ∑( 2 ) = = 2 1 z −1 m=0 z 1− 2 z 解法二： 1 1 1 z 1 z z2 k f (k ) = ε (k ) + (−1) ε (k ) ↔ + = 2 2 2 2 z −1 2 z +1 z −1

南京邮电通信原理课件

(a)
(b) 1 0 0 1
an
+E 0
bn (0)
1
1
0 (e)
1
1
1
0
(f)
4
6.1 数字基带信号及其频谱特性

单极性(NRZ)波形：该波形的特点是电脉冲之间无间隔，极性单一，易于用TTL、CMOS电路产生；缺点是有直流分量，要求传输线路具有直流传输能力，因而不适应有交流耦合的远距离传输，只适用于计算机内部或极近距离的传输。双极性(NRZ)波形：当“1”和“0”等概率出现时无直流分量，有利于在信道中传输，并且在接收端恢复信号的判决电平为零值，因而不受信道特性变化的影响，抗干扰能力也较强。单极性归零(RZ)波形：信号电压在一个码元终止时刻前总要回到零电平。通常，归零波形使用半占空码，即占空比为 50%。从单极性RZ波形可以直接提取定时信息。与归零波形相对应，上面的单极性波形和双极性波形属于非归零(NRZ)波形，其占空比等于100％。双极性归零(RZ)波形：兼有双极性和归零波形的特点。使得接收端很容易识别出每个码元的起止时刻，便于同步。
G1 ( f ) g1 (t )e j 2 ft dt

15
6.1 数字基带信号及其频谱特性
于是
U T ( f ) U T ( f )U T ( f ) 2

m N n N

N
N
N
am an e j 2 f ( n m )TS [G0 ( f ) G1 ( f )][G0 ( f ) G1 ( f )]
N
E[ U T ( f ) ] (2 N 1)Ts
2
即可求得u (t)的功率谱密度 2 (2 N 1) P(1 P) G0 ( f ) G1 ( f ) Pu ( f ) lim N (2 N 1)Ts

南邮信号与系统答案第5章

信号与系统 · 习题解答
第11页
5-8 试用单位阶跃序列表示图示离散信号。 (b) f (k)
2
3
2
1 −2 −1 0 1 2 3
4 5
6
−1
k
解：f 2 (k ) = ε (k + 2) + ε (k ) + ε (k − 2) − 4ε (k − 4) + ε (k − 6)
信号与系统 · 习题解答
10 5
k<0 k =0 k ≥1
∴ f1 (k − 1) + f 2 (k + 1) 0 k <0 ⎧ ⎪ =⎨ 1 k =0 ⎪2 k + k − 1 k ≥ 1 ⎩
2
1
−1 0 1 2
L
3 k
信号与系统 · 习题解答
第5页
*（4） f1 (k − 1) ⋅ f 2 (k + 1) 解：
f1 (k − 1) ⋅ f 2 (k + 1) ⎧ 0 ⎪ =⎨ 0 ⎪2 k (k − 1) ⎩ ⎧ 0 =⎨ k ⎩2 (k − 1) k <0 k =0 k ≥1 k <1 k ≥1
⎧C1 = 0 解得 C1 = 0 ， ⎪ 2 ⎨ 2 2 C2 = ⎪2[C1 cos 3 π + C2 sin 3 π ] = 2 3 ⎩
2 2 sin kπ 所以 yzi (k ) = 2 ⋅ 3 3
k
k ≥0
信号与系统 · 习题解答
第19页
5-15 试求下列差分方程的单位函数响应（1） y (k + 2) + 3 y (k + 1) + 2 y (k ) = x(k + 1) + x(k )

南邮信与系统课后答案

(3)Hz2z32zz11
解：
Hz的极点z1为 1，z2
1 2
即在单位圆上有z1 单1极，点且 z2 12位于单位圆内
因此系统为临界稳定。
5-17 对下列差分方程描系述统的画出模拟图。
( 1 ) y k 5 y k 1 6 y k 2 x k 3 x k 2
解： 1 由零极点图可得：
H
z
H
0
z
z
1 z
1
2
lim h k 1 h
k
3
由终值定理知：
h lim z 1 H z 1
z1
3
即
lim z
z1
1H
0
z
z
1 z
1
1 3
2
解得
:H
0
1 2
1z
H z 2 z 1 z 1
2
2 由 H z 可写出系统的差分方程
k0
yk
y zs k
y zi k
1 2
2 3
1k
1 3
2k ,
k0
5-11 某离散系统得模图拟5图1所如示。
Y ( s)
X (s)
z 1
z 1
3 4
1 8
求：1 求H z
Yz ； X z
2 单位函数响应hk；
3 写出系统的差分方程；
4 求系统的单位阶跃响应gk 。
解： 1 对加法器列方程得：
为：
yk 2 1 yk 1 1 yk 1 xk 1
2
2
2
对齐次方程 y k 2 1 y k 1 1 y k 0 进行 Z 变换：
2
2

71南京邮电学院《信号与系统》信号37911PPT课件

两边取傅氏变换，用时域微分性质，得 10
[a n (j)n a n 1 (j)n 1 a 1 (j) a 0 ]Y () [b m (j)m b m 1 (j)m 1 b 1 (j) b 0 ]X () Y () b a m n ( (j j) )m n a b n m 1 1 ( (jj) )n m 1 1 a b 1 1 ( (jj) ) a b 0 0X ()
3.7 相关函数和谱密度 (只讲3.7.1)
T
周期信号 fT (t) 的平均功率为
P
1 T
2 T
f
2 T
(
t
)
d
t
2
平均功率也可以在频域内获得，称为帕什瓦尔
定理：
P Fn 2
n
描述平均功率随频率的分布情况。
Fn 2 ~n0 称为功率信号的功率谱。 1
非周期信号有 f (t )
1.能量信号：有能量谱密度；
态响应；直观了解输入、输出信号频谱和
系统的频率特性。
9
讨论信号作用于线性系统时在频域中求解零状态响应的方法，又称频域分析法。频域分析法的理论基础是时域卷积定理。一. 系统函数 H()的意义
由线性时不变系统的数学模型
a ny (n )(t) a n 1 y (n 1 )(t) a 1 y '(t) a 0 y (t) b m x (m )(t) b m 1 x (m 1 )(t) b 1 x '(t) b 0 x (t)
E
1
F()2d
2
3
E21 F()2d1 0F()2d
上式称为帕什瓦尔等式，或能量等式。表明能量信号的能量不仅可以从时域中求取，也可以从频域中求取。定义： Ef ()F()2 为能量谱密度。简称能

信号与系统课后习题附参考答案

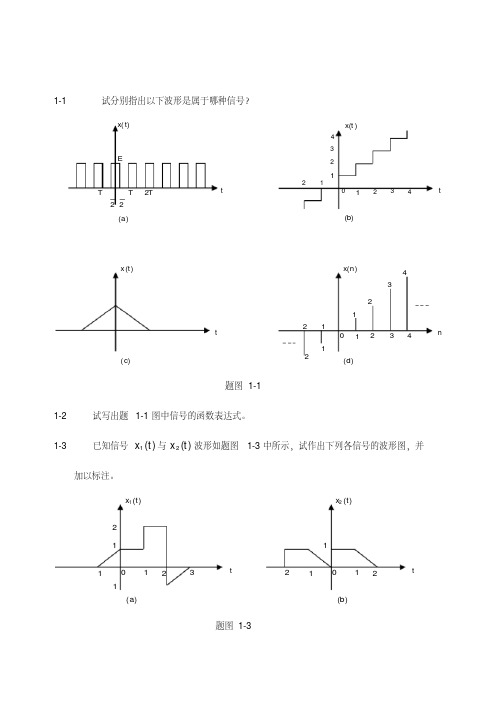
1-1试分别指出以下波形是属于哪种信号？题图1-11-2 试写出题1-1图中信号的函数表达式。

1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示，试作出下列各信号的波形图，并加以标注。

题图1-3t)(2t x )(b 12112t)(1t x )(a 121123122T T2TEt)(t x )(a t)(t x )(b 13124023412t)(t x )(c n)(n x )(d 2213012112344⑴)2(1t x ⑵)1(1t x ⑶)22(1t x ⑷)3(2tx ⑸)22(2t x ⑹)21(2t x ⑺)(1t x )(2t x ⑻)1(1t x )1(2tx ⑼)22(1t x )4(2tx 1-4 已知信号)(1n x 与)(2n x 波形如题图1-4中所示，试作出下列各信号的波形图，并加以标注。

题图1-4⑴)12(1n x ⑵)4(1n x ⑶)2(1n x ⑷)2(2n x ⑸)2(2n x ⑹)1()2(22n x n x ⑺)2(1nx )21(2n x ⑻)1(1n x )4(2nx ⑼)1(1nx )3(2nx 1-5 已知信号)25(t x 的波形如题图1-5所示，试作出信号)(t x 的波形图，并加以标注。

题图1-5t)25(t x 110232523n)(2n x )(b 2213121124n)(1n x )(a 22131142134212321231-6 试画出下列信号的波形图：⑴)8sin()sin()(t t t x ⑵)8sin()]sin(211[)(t t t x ⑶)8sin()]sin(1[)(t t t x ⑷)2sin(1)(t tt x 1-7 试画出下列信号的波形图：⑴)(1)(t u e t x t⑵)]2()1([10cos )(t u t u t e t x t⑶)()2()(t u e t x t⑷)()()1(t u et x t ⑸)9()(2tu t x ⑹)4()(2tt x 1-8试求出以下复变函数的模与幅角，并画出模与幅角的波形图。

信号与系统4教学ppt

上两式称为双边拉普拉斯变换对，可以表示为
f (t) F (s)
拉氏变换扩大了信号的变换范围。
变换域的内在联系
时域函数 f (t)傅氏变换频域函数 F ()
时域函数 f (t)拉氏变换复频域函数 F (s)
4.1.2 单边拉普拉斯变换
考虑到：1. 实际信号都是有始信号，即 t 0时，f (t) 0
作业
连续信号与系统的复频域分析概述
傅里叶变换（频域）分析法
– 在信号分析和处理方面十分有效：分析谐波成分、系统的频率响应、波形失真、取样、滤波等
– 要求信号满足狄里赫勒条件 – 只能求零状态响应 – 反变换有时不太容易
拉普拉斯变换（复频域）分析法
– 在连续、线性、时不变系统的分析方面十分有效 – 可以看作广义的傅里叶变换 – 变换式简单 – 扩大了变换的范围 – 为分析系统响应提供了规范的方法
但反变换的积分限并不改变。
以后只讨论单边拉氏变换：
（1）f (t) 和 f (t) (t) 的拉氏正变换 F(s) 是一样的。
（2）反之，当已知 F(s) ，求原函数时，也无法得到 t < 0 时的 f (t) 表达式。
例如，常数 1 和 (t) 的（单边）拉普拉斯变换是一
样的。
单边拉氏变换的优点：
0
可见： L[tn (t)] n L[tn1 (t)]
s
依次类推：
L[tn (t)]
n s
n
1 s
n
s
22 s
1 s
1 s
n! sn1
特别是 n=1 时，有
L[t (t)]
1 s2
拉普拉斯变换与傅里叶变换的关系
1. 0 0 ：只有拉氏变换而无傅氏变换

南京邮电大学《信号与系统》信号与系统3

2
2
2 5cos(3t 36.9) 2cos(6t 60) cos(9t 30)
单边幅度频谱：
An
5
2 1
0
3
单边相位频谱：
n
36.9
6
9 n0
30 0
3
6 9 n0
《信号与系统》SIG 6N0ALS AND SYSTEMS ZB
(2) 双边频谱
f (t) 2 5cos(3t 36.9) 2cos(6t 60) cos(9t 30)
例：试将图示周期矩形脉冲
f (t)
A
信号 f (t)展开为(1)三角型和
(2)指数型傅里叶级数。
解：(1) f (t)是偶函数，故只含有常
数项和余弦T项。 2
2
T
t
a0
1 T
2
f (t)dt 2 T
2 Adt A
0
T
2
an
2 T
2
f (t) cosn0tdt
4 T
2 Acosn0tdt
0
2
4 A sin( n0 ) 2 A sin( n0 )
n0T
2
n
2
《f 信(t) 号 A与T 系统n1》n2ASIsGinN(nA2L0S)AcoNsnD0StYSTEMS ZB
(2) 指数型傅立叶级数
T
Fn
1 T
2 f (t)e jn0tdt 1
T
T
2 Ae jn0tdt
2
2
2 2.5[e j(3t36.9 ) e j(3t36.9 ) ]
当 f (t)是实奇函数时，则 Fn是虚奇函数。
（利《用信号Fn与的系计统算》公S式IG可N以A证LS明AN）D SYSTEMS ZB

信号与系统教材课后答案、参考用第四章作业参考答案36页PPT

x(t)F1
X()
c 2
sincct
/2ejct/2ej/2
2c sincct
/2ejct/2ej/2
c sinc
2
t/2 e e j(ct/2/2) j(ct/2/2)
c
c 2
2
ct
sinct
/2cos(ct
/2/2)
2t sin2ct /2
例1、某低频信号f(t)的最高频率分量为fm=1kHz，该信号经
1
1
2
(e
j t
e
jt ) e
jk t / 2 dt
40
4 2j 0
1
2
(e
j ( 2 t ) / 2
e j ( 2 t ) ) dt
8j 0
1 8j
2 j (2
e j ( 2 t ) / 2 k)
|
2 0
j
2 (2
k)
e j ( 2 t ) / 2
|
2 0
1 2 (( 1 ) k 1 )
T0 x2(t)ejk0tdt
1 1 2(t1)ejktdtejk (1)k 2 1
从而：
c k c 1 k c 2 k1 2 ( 1 )k,k 0 , 1 , 2
l ) 0/2,T04
c k
1 T0
x ( t ) e jk 0 t dt
T0
1
2
sin
te jk t / 2 dt
1
/
2
)
je j sin(( (
) T 1 / 2 ) sin((
)T1 / 2 ) )
2
( )T1 / 2
( )T1 / 2

南邮信号与系统课后答案第一章

所以为非能非功信号
1-7 判断下列信号是能量信号，还是功率信号或者都不是。
(1)
பைடு நூலகம்
1
k
解：显然该信号为离散周期信号，因此是功率信号
1-8 判断下列系统是否为线性系统，是否为时不变系统，并简单说明理由。其中y(t)、y(k)为系统的完全响应， q(0)为系统的初始状态，x(t)、x(k) 为系统的激励。
1-6 判断下列信号是能量信号，还是功率信号或者都不是。
(3) 2e3t
解：E lim 2e
T T T
3t
dt lim
2
T
T T
4e 6t dt
2 lime 6T e6T 3 T
2 1 T 1 1 6T 3t P lim 2e dt lim e e 6T T 2T T 3 T T 由罗必塔法则 2 lim e 6T T
第一章信号与系统的基本概念
作
业
南京邮电大学通信与信息工程学院信息工程系
1-1 判断下面的信号是否为周期信号，如果是，确定其基本周期。
2
4 sin 2t ut 4
解：因为t 0时，ut 0，所以为非周期信号
4
cos2t 2 cos5t
(4)
yt 3q0x3t
解：不满足分解性，因此为非线性系统。
当x1 t xt td 时，y1 t 3q0x3t td yt td 3q0x3t td 所以为时变系统
1-10 判断下列系统是否为因果系统，并简单说明理由。
(5) yk 2 2 yk 1 yk xk 1 3xk

南京邮电大学信号与系统习题3

A f (t)
A 2
−τ τ 0 − 2
τ τ
2
t
解：信号 f (t)可以分解为：可以分解为：
《信号与系统》SIGNALS AND SYSTEMS
A A f (t) = gτ (t) + g2τ (t) 2 2 Aτ ωτ ↔ Sa( ) + AτSa(ωτ) 2 2
ZB
3-26 已知
f (t) = f1(t) + f2(t)的频谱密度函数 F(ω) = 4Sa(ω) − j
−20 0
20
ZB
f2(t) 3-34 已知图所示锯齿脉冲 f (t)的傅 f (t) 已知图(a)所示锯齿脉冲 1 1 1 jω jω 里叶变换 F(ω) = (e − jωe −1)， −1 0 t 0 1 2t ω2 (a) (c) 利用傅里叶变换的性质，求图(c) 利用傅里叶变换的性质，求图、(f) 所示信号的傅里叶变换。所示信号的傅里叶变换。解:(c) f2(t) = f (t −1) + f (−t +1) = f (t −1) + f [−(t −1)] ↔ F(ω)e− jω + F(−ω)e− jω = [F(ω) + F(−ω)]e− jω
ZB
3-33 试应用调制定理，求题示信号试应用调制定理，的傅里叶变换，并画出频谱图。的傅里叶变换，并画出频谱图。解： (t) = ε (t + π ) −ε (t − π )cos20t f

π − 5 5 5 π π 2π π Sa( ω) Qε (t + ) −ε (t − ) ↔ 5 5 5 5
双边相位频谱：双边相位频谱：
2π 2π θn 2π 5 1 5 −8 3 3 1 3 0 2π 8 nω0 8 nω0 2π −5 −1 2π − − − 《信号与系统》SIGNALS AND SYSTEMS ZB 3 3 3

南邮信号与系统课后答案第三章

3-14
如题图 3 14 所示信号 f t F ，在不求出前提下，求
1
F 的
f t
(1) F 0 F 0
-1
0
1
t
解： F 0 F 0

f t e
j t
dt
0

f t dt
f 1 t
1
(a)
2 5
0
-1
2 5
t
2 2 解： f 1 t cos 10 t u t u t cos 10 tg 4 t 5 5 5 2 f t g 4 t Sa F 5 5 5 4 f 1 t 1 2
y 1 t
H 2
cos 2 t
4 5
sin 2 t cos 2 t 127
4 5 Ae
j

另解：
1 j2 1 j2
j
e
j 127

y t A cos 2 t cos 2 t 127

1 10
g 10 t Sa 5 1 10 5
1 10 , A 10
Sa 5 t 2
g 10
对称性
u 5 u 5

g 10

5
3-8
已知 f t F ，求下列函数的傅里叶
2 j
F e
2 j
t ( 6 ) t 2 f 2

南京邮电大学信号与系统习题2

2
t
t

( c ) 当 2 t 3时, y (t ) （ 2)d 2
1
2 1
0 1 2
2
( d ) 当 3 t 4时,
t 2
2 1 0 1 2
(e) 当 t 4时, y (t ) 0
ZB

《信号与系统》SIGNALS AND SYSTEMS
t
2 1 0 1 2

(b) 当 1 t 2时, y (t ) （ 2)d 2
1

t
x( ) h( ) (t ) x( ) h( ) (t ) x( ) h( ) (t ) x x x
2 2 2 t 2 1
0 1 2
2

2 1
0
2

(a ) 当 t 1时, y (t ) 0
(b) 当 1 t 2时, y ( t ) （ 2 t ) d 2
h(t ) x( ) h( ) 2 t
2 1
0
t 1
h(t ) x( ) h( ) 2 t
2
h(t ) x( ) h( ) 2 t
e e

(5) et (t ) * cost (t )
2t t
e e

2 ( t )
d e
2t

t
t
e 2t (e t 0) e
t
e d

t
e(t ) cosd (t ) et
t
0

e cosd (t )
《信号与系统》SIGNALS AND SYSTEMS 3

南邮数字信号处理吴镇扬-课后习题详细答案-DSP期末复习PPT课件

• 解：
DTxF n T n0 xnn0ejwn
n
令 n ' n n 0 xn ' e jw n ' n 0xn ' e jw ' jn w 0
n '
n '
e jw 0 nxn 'e jw ' n e jw 0 D n T xn ' F e jT w 0X n e jw
•pp 34： 1.5 (3)
1
X Z x n Z n 0 . 5 n u n 1 Z n 0 . 5 n Z n
n
n
n
变量 n ' n 替换 0 .5 n 'Z n ' 0 .5 1 Z n '
n ' 1
n ' 1
0
Re[z]
• pp 34： 1.5 (2n Z n0 .5 n u n Z n0 .5 n Z n
n
n
n 0
n 00 .5 Z 1 n 1 0 1 .5 Z 1 ,0 .5 Z 1 1 1 0 1 .5 Z 1 ,0 .5 Z
n ' 1
n ' 1
•变量替换易出问题
1 0 . 0 5 . 5 1 Z 1 Z 1 0 1 . 5 Z 1 ,0 . 5 1 Z 1 1 0 1 . 5 Z 1 ,Z 0 . 5
零点：z
2z 1 2z
0
z
z
1 2
j Im[z]
极点： z 1
收敛域：
2 z
1
2
1/2
DSP考试题型
• 填空题20分(每空1分) • 判断题10分(每题2分) • 简答题10分 • 画图题15分 • 计算题45分

南京邮电学院《信号与系统》第二次习题课

Fn
S a(n )
10
A F()
包络线是一取样函数，
其图形如左
2 2
零交点位置 2 , 4
即当 nk(k1,2,3 ) 时，频谱的幅值为0。
10
此时
n 1,2 0,3 0, 0
频率 n 0 f5 K 0 ,1 H K 0Z ,1 H 0K 5Z H 0 Z 所以不能选出50 KHz，100 KHz频率分量。
2. Fn ~n0 是偶函数； Fn~n0 是奇函数。
3. 偶函数；奇函数，奇虚函数和偶谐函数的特点。
4. 单边频谱、双边频谱会画。实偶函数的频谱是实偶函数；
实奇函数的频谱是虚奇函数。 5. 周期信号的功率谱 Fn 2 ~n0
平均功率: P T 1 T 2 T 2f2(t)dt, P n F n2A 0 22 1n 1A n 2
再均移位 5.7、放大 5 倍，即可。
（四）非周期能量信号的能量谱密度：
F() 2 ~
非周期能量信号的能量：
E f2(t)d t, E 1F ()2d
2
信号的脉冲宽度和频带宽度
单个矩形脉冲： t2
（五）系统不失真传输的条件：
时域表示：
y(t)K x(ttd)
频域表示： H () H ( ( )) K td
f4(t)
-1 0 1 t -2
f3(t)f1( t)
F1()
R 1()j1 I()
f4(t) f1 ( t)
F1()
R 1()j1 I()
f5(t) 2
f5 (t) f1 (t) f1 ( t)
-1 0 1 t -2
F 1()F 1( )
2j I1()
3 f6(t) -1 0 1

南京邮电学院《信号与系统》信号2-1

an1
h 0 (n1)
0 0
(t)dt
a0
0
0 h0 (t)dt
0
(t)dt
0
上式左边只第一项不为零，其他项为零
an
[h0(n1)
(0
)
h ( n1) 0
(0
)]
1
单位冲激信h0(号n1引) (0起 ) 的 at1=n 0+时的n个初始条件为
h0(n2)
(0
)
h ( n3) 0
(0
)
h0 (0 ) 0
Rc
+_vc (t)
vc (t) c dvc (t) (t)
R
dt
vc (t)
1 c
1t
e Rc (t)
2先计算系统的阶跃响应s(t)，然后利用冲激响应h(t)与阶跃响应 s(t)的关系求冲激响应
h(t)与s(t)的关系（线性时不变系统）
(t) s(t) (t t) s(t t)
h0 (t) (k1et k2e3t ) (t)
代入初始条件：hh0'0(0(0))k1 k1
k2
3k
0
2
1
解得k1
1 2
,
k
2
1 2
h0 (t)
(1 2
e t
1 e3t ) (t)
2
2 (t)作用下的响应为2h0 (t) '(t)作用下的响应为h'0 (t)
h(t)
h'0
(t)
2h0 (t)
) (t),
L
1 R
R
R
h(t)
ds(t)
1
t
(1 e

南京邮电学院《信号与系统》第一次习题课

此时F1() 与F2(t-)无重叠， F1(t) ＊F2(t) =0;
b.当-1≤t-0.5（头部进入）并且t-3.5<-1（尾部
没有进入）时，即 -0.5≤t<2.5，如图④
图④ F2(t-)
F1()
此时
-3.5+t -1 0 -0.5+t
t 0.5
y(t) 1
F10 ( )F 2[(t 1) (t 1)]
-1 0 1 tt
F2(t) 3
01 4 t
F2 (t)
(t 1)[ (t 1) (t 4)]
F3(t) 2 24
0
t
-2
F3(t) 2t[(t) (t 1)] 2(t 2)[(t 1) (t 3)] 2(t 4)[(t 3) (t 4)]
四、已知函数的波形如图所示：
f1(t) 1
0 123
f2(t)
(1)
(1)
1
t
t
-0.5 (1)
1.5
求： (a) f 1(t) f 2(t)
f3(t)
(1)
(1)
-1 0 1
t
(b) f 1(t) f 3(t) f 3(t)
(c) {[ f 1(t) f 3(t)][(t 1) (t 3)]} f 3(t)
c.当t-3.5≥-1（尾部进入）并且t-0.5<3（头部没有出来）时，即 2.5≤t<3.5，如图⑤
图⑤
F2(t-) F1()
-1 –3.5+t-0.5+t 3
此时
t 0.5
y(t) t3.5 F10 ( )F20 (t )d
d.当t-3.5<3（尾部没有出来），t-0.5≥3（头部已出来）时，即 3.5≤t<6.5，如图⑥

南京邮电学院《信号与系统》信号 7

随着系统内部结构的复杂程度的增加，六十年代中期提出了状态变量分析法。其实质：
将网络方程列写成关于“状态变量”的一组一阶微分(差分)方程组。也就是说，描述系统最少需要列写多少个一阶方程来表征它。
这个“最少个数”称为：网络复杂度。
显然，全电阻网络不需要用微分方程来描述它，故，网络复杂度为零。
如果系统的全部状态变量的变化规律已经求出，那么，系统中的任何变量(电压或电流)只需要用状态变量的代数方程来描述。
已知微分方程 H(s) 模拟图建立状态方程
例：
d 3y(t) d 2 y(t) d y(t)
d v(t )
dt3 8 dt2 19 dt 12y(t) 4 dt 10v(t)
得
4s 10 H(s) s3 8s2 19s 12
v(t) q (3) q"
4
q' q
10
y(t)
8
19
状态矢量所描述的空间称为状态空间。
状态矢量所包含的状态变量的个数称为状态空间的维数，或系统的阶数。也就是网络复杂度。
用状态变量来描述和分析系统的方法称为状态变量分析法。
状态变量分析法步骤： 1. 选定状态变量； 2. 建立状态方程(一组一阶微分或差分方程)；
即，建立状态变量与输入之间的关系。 3. 建立输出响应与输入激励关系的输出方程
D x1(k ) 1
2
y(k)
D x2 (k ) 1
3
x1(k 1) 2x1(k ) v(k ) x2 (k 1) 3x2 (k ) v(k )
y(k) x1(k) x2 (k)
状态方程写成矩阵形式：
x1 ( k
1)
2
0
x1 ( k

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

如图所示，试求该系统的零状态响应。
xk
hk
4
3 2
4
2 1
-2 -1 0 1 2 3 k
-2
-1 0 1 2 3 4 k
-1
解： xk 4, 2,3,2 hk 4,,1,2,1
4 2 3 2 4 1 2 1
4 2 3 2 8 4 6 4 4 2 3 2 16 8 12 8 16 12 22 5 2 7 2
k
1
uk
4 3
1k 1
8 3
0.5k 1 u k
2 3
1k 2
4 3
0.5k 2
k 1
k 1
2 3
1k
2
4 3
0.5k 2
4 3
1k
1
8 3
0.5k 1
uk
2 3
1k
1 3
0.5k
4 3
1k
4 3
0.5k
uk
21k 0.5k uk
2-25 计算下列卷积
2 2 e3tut
hh00
1 0 2 1
c1c1 0.02.55cc22
0 1
c1
c2
2
3 4
3
h0
k
2 3
1k
4 3
0.5k
uk
1
hk h0 k 2 2h0 k 1
2 3
1k 2
4 3
0.5k 2
uk
1
2
2 3
1k 1
4 3
0.5k 1 u k
2 3
1k 2
4 3
0.5k 2
第二章信号与系统的时域分析
作业
1
2-1 绘出下列信号的波形，注意它们的区别。
2 tut
3 t 1ut
1
0
1t
0
1t
-1
6 t 1ut 1
7 tut ut 1
0
1t
1
0
1t
2-5 试写出题图2-5各信号的解析表达式。
f1 t
2
1
f5 t
3
3e2t
0
1
2
t
01
23
t
(a)
(e)
-3
解： (a) : f1t ut 1 ut 3ut 1 ut 2
t4
ut 5
1
1
t 5e5tut 5
2-32 系统的激励xt和冲激响应ht如题图2 32所示，试画出xt ht的波形图。
xt
2
ht
(1) (1)
-2 0
2t
(b)
-1 0 1 t
解： xt ht xt t 1 t 1
xt 1 xt 1
xt ht
2
-3 -1 0 1
3
t
2-39 计算下列序列的离散卷积
k 1 2 k 2 2uk 3
k 1 2uk 2
另解：原式 uk 1 k k 1
uk 1 uk 2 k 1 2uk 2
5 akuk akuk
k
k
解：原式 an akn uk ak 1uk
n0
n0
ak (k 1)uk (k 1)akuk
2-40 某离散系统的输入信号xk 和单位脉冲响应hk
t 3
2-17 计算下列各积分的值。
2
3 t2 2t 1 t 5dt 0
解：原式＝0
5
e j2t t 3 t 3dt
e e 解：原式 j2t j2t e j6 e j6 2 cos 6
t 3
t 3
2-19 已知系统的微分方程为yt 3yt 2 yt 2xt xt，试求系统的冲激响应ht 。
2 uk 1uk uk 2
解：原式 uk 1uk uk 1uk 2
k
k 2
1uk 1 1uk 3
n1
n1
kuk 1 k 2uk 3
k k 1 k 2 uk 3 k 2uk 3
k k 1 k k 2 22
解：原式 e3tut 2 e3tut 2ut
e e t 3 2d u t 2 e3 d 2 3 2
0
0
3
03
6 et 1u t 1 et4ut 4
解：原式 t4 e 1et 4d u t 5 1
t e5t
t4
1d u t 5
e5t
2-43 求下列离散系统的零状态响应。
2
或f2k 2 k n n1
2-8 已知信号 f t 如图所示
（1）用阶跃信号表示 f t
（2）画出 f 2t 2 的波形
（3）画出
f
t 2
1
的波形
（4）画出 df t 的波形
dt
（5）画出 f 1t 的波形
解：
(1) f k 2ut 2 4ut 2 2ut 4
f t
2
-2 0 2 4 t
-2
题图(a)
f 2t 2 f 2t 1
2
-2 0 1
t
-2 （2）
f
t 2
1
f
1 2
t
2
2
f t
2
-6
-2
0
-2
6t
（3）
df t
dt
(2)
(2)
-2 0 2 4 t
-2
题图(a)
f 1t
8
4
-2 0 2 4 t
(4) （4）
-2 0
2
-2 （5）
4t
k
2-12 已知yk f i，求yk 、yk i0
2-23 设描述某离散系统的差分方程为
yk 2 0.5yk 1 0.5yk xk 2 2xk 1
求系统的单位脉冲响应hk 。
解：设h0 k 2 0.5h0 k 1 0.5h0 k k
特征方程： 2 0.5 0.5 0
特征根：1 1， 2 0.5
h0 k c11k c2 0.5k uk 1
解：设h0t 3h0 t 2h0 t t
特征方程：2 3 2 0 特征根：1 1，2 2
h0 t c1et c2e2t ut
hh00
0 0
0 1
cc11c22c2
0
1
cc2111
h0 t et e2t ut
ht 2h0 t h0 t
2 2e2t et ut et e2t ut 3e2t et ut
解：
k 1
k
yk yk 1 yk f i f i f k 1
i0
i0
k
k 1
yk yk yk 1 f i f i f k
i0
i0
2-16 化简下列各式。
2 t2 t t 1
解：原式＝ t 2 t t 1 0 t 1
6 et1 t 3
解：原式 et1 t 3 e4 t 3
(e)
:
f5 t
3e2t
cos 2t
3
2
ut
1
或f5
t
3e2t
cos
2t
2
ut
1
或f5 t 3e2t sin 2tut 1
2-6 试写出题图2-6各序列的解析表达式。
f1k
2
2
1
f2 k
2
2
1
-2 -1 0 1 2 3 k
-1
-2 -1 0 1 2 3 k
(a)
(b)
解： (a) : f1k 2 k 1 k 2 k 1 k 2 (b) : f2 k 2uk 1 2uk 3