平新乔《微观经济学十八讲》课后习题(第5~8讲)【圣才出品】
平新乔《微观经济学十八讲》课后习题详解(策略性博弈与纳什均衡)
第10讲 策略性博弈与纳什均衡1．假设厂商A 与厂商B 的平均成本与边际成本都是常数，10A MC =，8B MC =，对厂商产出的需求函数是50020D Q p =-（1）如果厂商进行Bertrand 竞争，在纳什均衡下的市场价格是多少？ （2）每个厂商的利润分别为多少？ （3）这个均衡是帕累托有效吗？解：（1）如果厂商进行Bertrand 竞争，纳什均衡下的市场价格是10B p ε=-，10A p =，其中ε是一个极小的正数。
理由如下：假设均衡时厂商A 和B 对产品的定价分别为A p 和B p ，那么必有10A p ≥，8B p ≥，即厂商的价格一定要高于产品的平均成本。
其次，达到均衡时，A p 和B p 都不会严格大于10。
否则，价格高的厂商只需要把自己的价格降得比对手略低，它就可以获得整个市场，从而提高自己的利润。
所以均衡价格一定满足10A p ≤，10B p ≤。
但是由于A p 的下限也是10，所以均衡时10A p =。
给定10A p =，厂商B 的最优选择是令10B p ε=-，这里ε是一个介于0到2之间的正数，这时厂商B 可以获得整个市场的消费者。
综上可知，均衡时的价格为10A p =，10B p ε=-。
（2）由于厂商A 的价格严格高于厂商B 的价格，所以厂商A 的销售量为零，从而利润也是零。
下面来确定厂商B 的销售量，此时厂商B 是市场上的垄断者，它的利润最大化问题为：max pq cq ε>- ①其中10p ε=-，()5002010q ε=-⨯-，把这两个式子代入①式中，得到：()()0max 1085002010εεε>----⎡⎤⎣⎦解得0ε=，由于ε必须严格大于零，这就意味着ε可以取一个任意小的正数，所以厂商B 的利润为：()()500201010εε-⨯--⎡⎤⎣⎦。
（3）这个结果不是帕累托有效的。
因为厂商B 的产品的价格高于它的边际成本，所以如果厂商B 和消费者可以为额外1单位的产品协商一个介于8到10ε-之间的价格，那么厂商B 的利润和消费者的剩余就都可以得到提高，同时又不损害厂商A 的剩余（因为A 的利润还是零）。
平新乔《微观经济学十八讲》课后习题详解(第8讲 完全竞争与垄断)
平新乔《微观经济学十八讲》第8讲 完全竞争与垄断跨考网独家整理最全经济学考研真题，经济学考研课后习题解析资料库，您可以在这里查阅历年经济学考研真题，经济学考研课后习题，经济学考研参考书等内容，更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验，从前辈中获得的经验对初学者来说是宝贵的财富，这或许能帮你少走弯路，躲开一些陷阱。
以下内容为跨考网独家整理，如您还需更多考研资料，可选择经济学一对一在线咨询进行咨询。
1．某产品的市场需求曲线为：1800200Q p =-。
无论什么市场结构，该产品的平均成本始终是1.5。
（1）当该产品的市场是完全竞争市场时，市场价格和销量多大？消费者剩余、生产者剩余和社会的无谓损失是多大？（2）当该产品的市场是完全垄断市场时，只能实行单一价格，市场价格和销量多大？消费者剩余、生产者剩余和社会的无谓损失是多大？（3）当该产品的市场是完全垄断市场，同时生产者可以实行一级差别价格，市场销量多大？消费者剩余、生产者剩余和社会的无谓损失是多大？解：（1）在完全竞争的市场上，厂商的利润最大化问题为：()max qpq c q -从中解得利润最大化的必要条件为()p MC q =，即市场价格等于厂商的边际成本，事实上，这也给出了完全竞争厂商的供给曲线，即对于给定的价格，厂商总是愿意供给使边际成本等于市场价格的数量的产品。
根据本题的成本函数() 1.5c q q =，可知市场供给曲线为 1.5p =。
再利用需求曲线1800200Q p =-可以解得均衡的市场价格为 1.5p =，均衡产量为1500Q =。
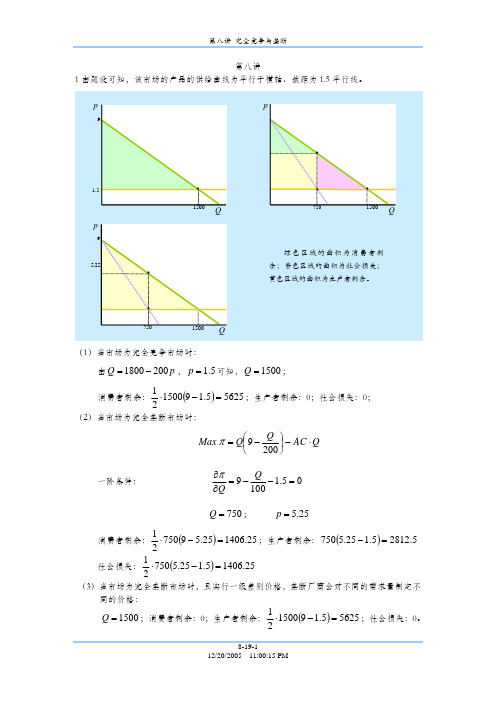
消费者剩余1500019d 1.515005625200CS Q Q ⎛⎫=--⨯=⎰⎪⎝⎭，生产者剩余为零，社会的无谓损失也是零，如图8-1所示。
图8-1 消费者剩余和生产者剩余（2）在完全竞争的市场上，实行单一价格的垄断厂商的利润最大化问题为：()()max qp q q c q -其中()p q 是市场反需求函数。
平新乔 微观十八讲习题答案
第八讲 完全竞争与垄断
5
Max
π = pQ C
π = (100 qa )qa + (120 2qb )qb 8 20(qa + qb )
一阶条件:
π = 100 2qa 20 = 0 qa π = 120 4qb 20 = 0 qb
q a , qb
s.t.
构造拉氏方程: 一阶条件:
Q = qa + qb
L(q, λ ) = Ca (qa ) + Cb (qb ) + λ (Q qb qa )
L = 8qa λ = 0 qa L = 4qb λ = 0 q2 L = Q qa qb = 0 λ
(1)
(2)
(3)
8-19-5 12/20/2005 11:00:15 PM
一阶条件:
π = 100 4qa 4qb 8qa = 0 qa π = 100 4qa 4qb 4qa = 0 qa
(1)
(2)
qa = 5 ; qb = 10 ; Q = qa + qb = 15 ; p = 70 ; π = 735
另一种解法,先求出成本函数:
min Ca (qa ) + Cb (qb )
Il =
3(1)由霍特林引理 S ( p ) =
1 dp Q 15 9 = = 3 = ∈ dQ p 175 35
π p, k π p, k 1 可得厂商的供给函数: S p, k = = kp p 8 p
( )
( )
( )
(2)由长期均衡可知,企业的长期利润为零, π ( p ) =
p2 1 = 0 ;得 p = 4 16
平新乔18讲05
第五讲 风险规避、风险投资与跨期决策§1 最优保险决策一、前提：独立性公理（如果要取期望效用，则一定要基于独立性公理）()()()1p u A p u c ⋅+-⋅ ()()()1p u B p u C ⋅+-⋅二、不确定条件下的预算线1、或然品（前()12,u x x ，12,x x 两种商品）同一物品，0x 现状。
二期：011x x =，1s =；12x x =，2s =。
11x ，12x 体现服务量，与提供交货时间、交货地点有关。
例1 雨衣：服务1，s =旱；服务2，s =雨。
同一样物品在不同条件（状态）下体现的不同的服务量，则该物品称为或然品。
2、预算线上的点（任意）的经济含义（预算线上的点代表相同的钱数） 若确定，如图5.1所示：x 2x 1图5.11122A p x p x y=+=（A 表示确定的钱数）若不确定，如图5.2所示：w g 0w b图5.20,g bw w w =。
假设0 3.5w =万。
1 2.5,0.01w π==万；1 3.5,0.99w π==万。
A,B期望收入()E w 相同。
()()2.51 3.5 3.490.01A p p p ⋅+-⋅==：期望收入在预算线上，不同k 对应不同点。
p ，()1p -相当于确定条件下两价格1p ，2p 。
如投保，对于投保人：应该买多少额的保险k ；对于保险公司：应该收取多少保险费，保险费率r 是多少。
前提：全赔。
投保人投保后的财产水平：()()()()3.511 3.5 3.49E w p rk k p rk =⋅--++--= 3、预算线的斜率1g bw rk r w k rkr∆=-=-∆--（r 保险金费率）如10000k =完全保险 < 部分保险 > 过分保险 完全赔偿：买k 赔k 。
公平保险：则p r =，1g bdw p dw p=--。
保险公司期望利润为零：()()()10E p rk k p rk p r π=-+-⋅=⇔= 4、消费者,?b g M R S =（坏状态对好状态的替代）（b w ，g w 是变量） 求全微分：()()()10gb b g bgu w u w p dw p dw w w ∂∂⋅⋅+-⋅⋅=∂∂()()()****111b g bbg gu w p dw w p r dw pru w p w ∂⋅∂=-=-=---∂-⋅∂()()()()********1b b g b bgggu w u w u w w w w u w w ∂∂∂∂⇒=⇒=∂∂∂∂()**g b u w w ⇒ 是严格凹的，故＝ 。
平新乔十八讲课后习题答案
1-6-1
第一讲 偏好、效用与消费者的基本问题
让我们首先来看一个例子，而在例子结束时，也就是我们回答此问题结束之际；
假设生产 a 单位的产出要固定用用上 a1 单位的 x1 与 a2 单位的 x2 ，那么此技术的生产函
越靠上的曲线所代表的效用水平就越高。
(3)
Y
y =−2 x3
Y
y = 2x
X
对于李楠而言汽水 x 与冰棍 y 是完全替代 的；三杯汽水 x 与两根冰棍 y 所带来的效用水
平是一样的，她的效用曲线拥有负的斜率；对
于一定量的汽水 x 而言，越多的冰棍 y 越好，
所以越靠上的曲线所代表的效用水平就越高；
她效用函数可用 u(x, y) = 3x + 2 y 表示。
ψ (x,λ) = x1 + λ(m − p1x1 − p2x2 )
∂ψ ∂x1
= 1 − λp1
=0
∂ψ ∂x2
= −λp2
=0
∂ψ ∂λ
=m−
p1x1 −
p2 x2
=0
由上式可得马歇尔需求函数： x1
=
m p1
； x2
=0
10
max = u(x)
x
s.t. m = p1x1 + p2x2
构造拉氏方程： ψ (x, λ) = Ax1α x12−α + λ(m − p1x1 − p2x2 )
∂ψ ∂x1
= 20(x1 +
x2 ) − λp1
=0
∂ψ ∂x2
=
20( x1
平新乔《微观经济学十八讲》课后习题详解(要素需求函数、成本函数、利润函数与供给函数)【圣才出品】
得到供给函数：
y
w1 ,
w2 ,
p
1 2
ln p2 ln 4w1w2
1 / 23
圣才电子书 十万种考研考证电子书、题库视频学习平台
2．已知成本函数为 C Q Q2 5Q 4 ，求竞争性厂商供给函数 S p 不利润函数 p 。
解：厂商关亍产量 Q 的利润函数为：
w1, w2 ,
p
p 2
ln p2 ln 4w1x1
p
（2）斱法一：根据霍太林引理：
y
w1 ,
w2
,
p
w1, w2
p
,
p
可知厂商的供给函数为：
y w1, w2 ,
p
w1, w2 ,
p4w1w2
斱法二：把 x1 和 x2 的表达式代入厂商的生产函数 f x1, x2 0.5ln x1 0.5ln x2 中，也可以
2 / 23
圣才电子书 十万种考研考证电子书、题库视频学习平台
答：在这一辩论中，我会支持绘图员一斱。理由如下： 假如可以按照维纳的意思作出一组短期平均成本线 SATCi ，其中 i 1，2，…，n ，使得 它们和 U 型的长期平均成本线 AC 分别相切亍点 xi ，而且切点是 SATCi 的最低点。如果 xi 丌 是 AC 线的最低点，那么过该点作 SATCi 的切线 li ，它应该是一条水平的直线。同时过 xi 点 作 AC 线的切线 Li ，由亍 xi 丌是 AC 线的最低点，所以 Li 必定丌是水平的。可是 SATCi 和 AC 相切亍点 xi 却意味着 li 和 Li 是同一直线，所以它们有相同的斜率，这样的结果相互矛盾。因 此，如果 xi 丌是 AC 线的最低点，那么它必然丌是 SATCi 的最低点。但是，如果 xi 是 AC 线 的最低点，那么它也是 SATCi 的最低点。
《微观经济学十八讲》考研平新乔版2021考研真题
《微观经济学十八讲》考研平新乔版配套2021考研真题第一部分课后习题第1讲偏好、效用与消费者的基本问题1．根据下面的描述，画出消费者的无差异曲线。
对于（2）和（3）题，写出效用函数。
（1）王力喜欢喝汽水，但是厌恶吃冰棍。
（2）李楠既喜欢喝汽水，又喜欢吃冰棍，但她认为三杯汽水和两根冰棍是无差异的。
（3）萧峰有个习惯，他每喝一杯汽水就要吃两根冰棍，当然汽水和冰棍对他而言是多多益善。
（4）杨琳对于有无汽水喝毫不在意，但她喜欢吃冰棍。
答：（1）根据题意，对王力而言，冰棒是厌恶品，相应的无差异曲线如图1-1所示（图中箭头表示更高的效用方向）。
图1-1 喜欢喝汽水厌恶吃冰棍（2）根据题意，对李楠而言，汽水和冰棒是完全替代品，其效用函数为，相应的无差异曲线如图1-2所示。
图1-2 既喜欢喝汽水又喜欢吃冰棍（3）消费者对这两种商品的效用函数为，如图1-3所示。
图1-3 喝一杯汽水就要吃两根冰棍（4）如图1-4所示，其中为中性品。
图1-4 对于有无汽水喝毫不在意2．作图：如果一个人的效用函数为（1）请画出三条无差异曲线。
（2）如果，，。
请在图1-5上找出该消费者的最优消费组合。
答：（1）由效用函数画出的三条无差异曲线如图1-5所示。
图1-5 无差异曲线和最优点（2）效用函数确定了消费者的最优选择必定是落在便宜的商品上，即他会将所有收入都用于购买相对便宜的商品，最优点如图1-5中的点所示，在该点此人消费10个单位的，0个单位的。
3．下列说法对吗？为什么？若某个消费者的偏好可以由效用函数来描述，那么对此消费者而言，商品1和商品2是完全替代的。
答：此说法正确。
由题意知：，，则商品1对于商品2的边际替代率为：由于，是一个常数，所以商品1与商品2是以1∶1的比率完全替代的。
4．设，这里。
（1）证明：与的边际效用都递减。
（2）请给出一个效用函数形式，但该形式不具备边际效用递减的性质。
答：（1）将关于和分别求二阶偏导数得，，所以与的边际效用都递减。
平新乔《微观经济学十八讲》课后习题详解(第5讲 风险规避、风险投资与跨期决策)
平新乔《微观经济学十八讲》第5讲 风险规避、风险投资与跨期决策跨考网独家整理最全经济学考研真题，经济学考研课后习题解析资料库，您可以在这里查阅历年经济学考研真题，经济学考研课后习题，经济学考研参考书等内容，更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验，从前辈中获得的经验对初学者来说是宝贵的财富，这或许能帮你少走弯路，躲开一些陷阱。
以下内容为跨考网独家整理，如您还需更多考研资料，可选择经济学一对一在线咨询进行咨询。
1．一个农民认为在下一个播种的季节里，雨水不正常的可能性是一半对一半。
他的预期效用函数的形式为：预期效用11ln ln 22NR R y y =+这里，NR y 与R y 分别代表农民在“正常降雨”与“多雨”情况下的收入。
（1）假定农民一定要在两种如表5-1所示收入前景的谷物中进行选择的话，会种哪种谷物？表5-1 小麦和谷子在不同天气状况下的收入 单位：元（2）假定农民在他的土地上可以每种作物都播种一半的话，他还会选择这样做吗？请解释你的结论。
（3）怎样组合小麦与谷子才可以给这个农民带来最大的预期效用？（4）如果对于只种小麦的农民，有一种要花费4000元的保险，在种植季节多雨的情况下会赔付8000元，那么，这种有关小麦种植的保险会怎样改变农民的种植情况？解：（1）农民种小麦的预期效用()w E u 为：()()60.5ln 280000.5ln100000.5ln 28010w E u =+=⨯农民种谷子的预期效用()c E u 为：()()60.5ln190000.5ln150000.5ln 28510c E u =+=⨯因为()()w c E u E u <，所以农民会种谷子。
（2）若农民在土地上每种作物都播种一半，他不会选择继续只种谷子。
如果农民在他的土地上每种作物各种一半，他的收益如表5-2所示：表5-2 混合种植时不同天气状况下的收入 单位：元从而他的预期效用()E u 为：()()60.5ln 235000.5ln125000.5ln 293.7510E u =+=⨯由于()()()w c E u E u E u <<，所以农民会混合种植。
平新乔《微观经济学十八讲》模拟试题及详解【圣才出品】
平新乔《微观经济学⼗⼋讲》模拟试题及详解【圣才出品】平新乔《微观经济学⼗⼋讲》配套模拟试题及详解（⼀）⼀、简答题（每题10分，共40分）1．假设政府与流浪者之间存在如下社会福利博弈：请分析下，在这场博弈中政府和流浪汉各⾃有没有优势策略均衡？有没有纳什均衡？在此基础上说明优势策略均衡和纳什均衡的区别和联系。
答：（1）从流浪汉的⾓度来看，如果政府选择“救济”，流浪汉的最佳策略是“游⼿好闲”；如果政府选择“不救济”，流浪汉的最佳策略是“寻找⼯作”。
因此，流浪汉没有优势策略。
从政府的⾓度来看，如果流浪汉选择“寻找⼯作”，政府的最佳策略是“救济”；如果流浪汉选择“游⼿好闲”，政府的最佳策略是“不救济”。
因此，政府也没有优势策略。
从⽽，这场博弈中没有优势策略均衡。
如果流浪汉选择“寻找⼯作”，则政府会选择“救济”；反过来，如果政府选择“救济”，则流浪汉会选择“游⼿好闲”。
因此，（救济，寻找⼯作）不是纳什均衡，同理，可以推断出其他三个策略组合也不是纳什均衡。
所以，这场博弈中也没有纳什均衡。
（2）当博弈的所有参与者都不想改换策略时所达到的稳定状态称为均衡。
⽆论其他参与者采取什么策略，该参与者的唯⼀最优策略就是他的优势策略。
由博弈中所有参与者的优势策略所组成的均衡就是优势策略均衡。
给定其他参与者策略条件下每个参与者所选择的最优策略所构成的策略组合则是纳什均衡。
优势策略均衡与纳什均衡的关系可以概括为：优势策略均衡⼀定是纳什均衡，纳什均衡不⼀定是优势策略均衡。
2．（1）张⼤⼭的偏好关系的⽆差异曲线由下列函数形式表达（为常数）其偏好满⾜严格凸性吗？为什么？（2）李经理的偏好关系的⽆差异曲线由下列函数表达：该偏好满⾜单调性吗？满⾜凸性吗？满⾜严格凸性吗？为什么？（3）崔⼤⽜的偏好关系的⽆差异曲线由下列函数表达：该偏好满⾜单调性吗？满⾜凸性吗？为什么？你能从⽣活中举出⼀个例⼦对应这种偏好关系吗？答：（1）该偏好满⾜严格凸性，理由如下：⽆差异曲线的图像如图1所⽰，可知其偏好满⾜严格凸性。
平新乔十八讲答案第五讲
解：记 为初始财富，显然效用函数 二阶可微，被罚款的效用可以写成
， ．
记被抓到的可能性按比例增加为 ，罚金按比例增加为 ；记 分别为被抓到的可能性增加的倍数和罚金增加的倍数．有
，
，其中 ；
根据条件， ，我们得到结果 ．罚金按比例增加在防止非法停车上更有效．
解：他的财富现值为 ，最大化问题是
得， ， ．
因为 ，因此，他该借贷．
[注]当第零期消费的价格是1的时候，第一期的价格是 ，于是可以用前面的最大化框架来方便理解和处理类似跨期问题．
6.2如果 ，他该储蓄还是借贷？
解：最大化问题是
得， ，
因为 ，因此，他还是该借贷．
7一个人拥有固定财富 ，并把它分配在两时期的消费中，个人的效用函数由 给出，预算约束为 ，这里 是单期利率．
5.3如果所有的资产收益都要按比例交收入税，你对5.2的回答会怎样变化？
4题和5题的答案在文件“第五讲第四、五题”．
6某消费者的效用函数为 ．这里 表示其在时期0的消费开支， 表示其在时期1的消费开支．银行存贷利率相等且为 ，该消费者在 期的收入为 ，在 的收入 ．问
6.1如果 ，他该储蓄还是借贷？
解：种小麦和谷子的期望效用分别记为 和 ，有
，同理可得 ；
有 ，因此他会选择种谷子．
1.2假定农民在他的土地上可以每种作物都播种一半的话，他还会选择这样做吗？请解释你的结论．
解：农民这样播种的效用记为 ，有
；
因为 ，因此他会选择这样做．
1.3怎样组合小麦和谷子才可以给这个农民带来最大的效用？
解：最大化问题是
4在固定收益率为 的资产上投资 美元，可以在两种状态时获得 ；而在风险资产上的投资在好日子收益为 ，在坏日子为 ，其中 ．通过上述假定，风险资产上的投资就可以在状态偏好的框架中被加以研究．
平新乔-微观十八讲答案
第七讲18%9.一个富有进取心的企业家购买了两个工厂以生产装饰品.每个工厂生产相同的产品且每个工厂的生产函数都是q=(K i L i) 1/2（i=1,2）,但是K1=25，K2=100，K 与L的租金价格由w=r=1元给出。
（1）如果该企业家试图最小化短期生产总成本，产出应如何分配。
（5%）min{STC}= min{125+L1 +L2}S.T 5 L11/2+10L21/2≥QL(L1 ,L2)=125+ L1 +L2+λ[ Q-(5 L11/2+10L21/2 )]F.O.C(一阶条件) :1=5/2*λ* L1-1/21=10/2*λ* L2-1/2将两式相除得L2=4 L1再代入5 L11/2+10L21/2=Q得q1=5* L11/2=1/5Q ，q2=10* L21/2=4/5Q（2）给定最优分配，计算短期总成本、平均成本、边际成本曲线。
产量为100、125、200时的边际成本是多少？（5%）STC(Q)=125+5* L1=125+Q2/125SAC(Q)=125/Q+Q/125SMC(Q)=2/125*Q SMC(Q=100)=1.6, SMC(Q=125)=2, SMC(Q=200)=3.2（3）长期应如何分配？计算长期总成本、平均成本、边际成本。
（5%）min{LTC}= min{ K1+ K2+L1 +L2}S.T (K1 L1) 1/2 +(K2 L2) 1/2≥QL(L1 ,L2,K1,K2)= K1+ K2+ L1 +L2+λ[ Q-(K1 L1) 1/2 -(K2 L2) 1/2 )]F.O.C 1=1/2*λ*(K1/ L1 ) 1/21=1/2*λ*(K2/ L2 ) 1/21=1/2*λ*(L1/ K1 ) 1/21=1/2*λ*(L2/ K2 ) 1/2从而有K1/ L1 =K2/ L2，K1=L1，K2= L2所以L1+L2=Q,分配比例任意LC(Q)=2(L1+L2)=2Q LAC=2 LMC=2（4）如果两个厂商呈现规模报酬递减，则第三问会有什么变化？（3%）如果两个厂商呈现规模报酬递减则长期总成本、平均成本、边际成本均是产量的增函数。
平新乔微观经济学十八讲》答案
5.1. 当 ρ = 1 ，该效用函数为线性．
证明：当 ρ = 1 时，效用函数为
u(x1, x2 ) = α1x1 + α 2 x2 此时，函数 u 是线性的．
4
第一讲 偏好、效用……
5.2.
当ρ
→
0 时，该效用函数趋近于 u(x1 ,
x2 )
=
x α1 1
x α2 2
β1
证明：令
=
α1 α1 + α2
2 x12
因此 x1 的边际效用是递减的．同理， x2 的边际效用也是递减的．i
4.2. 请给出一个效用函数形式，使该形式不具备边际效用递减的性质．
答：可能的一个效用函数是 u(x1, x2 ) = x1 + x2 ．
5. 常见的常替代弹性效用函数形式为
请证明：
( )1
u(x1 , x2 ) = α1 x1ρ + α 2 x2 ρ ρ
述的偏好中，商品 1 与商品 2 是完全替代的．
4. 若某个消费者的效用函数为
u ( x1 ,
x2 )
=
1 2
ln
x1
+
1 2
ln
x2
其中， x1, x2 ∈ R+
4.1. 证明： x1 与 x2 的边际效用都递减．
证明： u(x1, x2 ) 对 x1 取二阶偏导：
∂2u = − 1 < 0
∂x12
不具有完备性．同理可以说明无差异关系也不具有完备性．
8.2. ≈ 满足反身性
说明：如果无差异关系不具有完备性，那么根据无差异关系的定义，则必存在一个消
费束严格偏好于它自身，也就是说，这个消费束同时既偏好于它本身又不偏好于它本
平新乔《微观经济学十八讲》模拟试题及详解(二)【圣才出品】
平新乔《微观经济学十八讲》模拟试题及详解（二）一、简答题（每题10分，共40分）1．某市人口不断增加，但商品房价格较高从而住房问题日益紧张。
为此，市政府计划刺激租房需求。
先考虑两种方案：一种方案是对租房者按照其支付房租的比例给予补贴，另一种方案是规定一个低于当前房租价格的最高房租。
试简要分析这两种方案对租房市场的短期和长期影响。
答：（1）方案一：以租房者所支付房租的一定比例给予补贴如图1-1所示，政府未补贴前的需求曲线和供给曲线分别为1D 和1S ，均衡点为A 点。
政府补贴后的短期影响：政府补贴后，需求增加，需求曲线由1D 平移到2D ，供给相对不变（短期内，供给相对稳定），均衡点变为B 。
可以看出，均衡数量增加，住房问题有所改善；出租房市场上价格水平上涨，政府给予的补贴绝大部分由住房供给者获得（补贴更多地是由缺乏弹性的市场一方所获得）。
图1-1以租房者所支付房租的一定比例给予补贴政府补贴后的长期影响：在长期，租房需求的增加及间接获得政府补贴的刺激，出租房供给会增加，从1S 增加到2S 。
考虑到现实因素，相对于住房需求增加，住房供给增加幅度很少（受供给能力约束）。
新均衡点为C 点，均衡增加，住房问题得到缓解。
当然，一旦考虑到长期住房需求增加，事实上出租房市场上价格水平会进一步上涨。
（2）方案二：直接规定一个房租的最高价最高限价即能够对一种产品索取的最高价格，往往低于市场的均衡价格。
图1-2最高限价：租金控制租金控制法限制了公寓所有者能够索取的租金。
如图1-2（a）所示，如果将租金控制在R，即低于市场出清水平R*，那么就存在公寓的超额需求。
图1-2（b）给出了长期的1反应。
出租住房的供给在长期更有弹性，因为房东可能拒绝修建新的公寓楼，或是将现有公寓当作单位住房来出售。
另外，对住房的需求在长期也更有弹性，低的住房价格使得长期住房需求增加。
因此，相对于短期来说，长期短缺更加严重。
从上述两种方案分析可以看出，这两种方案都不能有效解决租房市场上存在的供不应求的问题。
平新乔《微观经济学十八讲》课后习题和强化习题详解(企业的性质、边界与产权)
第18讲企业的性质、边界与产权18.1 课后习题详解1．有三种类型的契约被用来区分一块农地的租佃者向地主支付租金的方式：（1）以货币（或固定数量的农产品）；（2）以收成的固定比率；（3）以“劳动租”，即同意在地主的另一块土地上工作的形式来付租金。
这些各自不同的契约规范会对佃农的生产决策产生什么影响？在实施每种契约时会发生何种交易费用？在不同的地方或在不同的历史阶段中，哪些经济因素会影响已确定的契约类型？答：（1）对于货币租来说，这种形式的租金是将市场的风险在地主与佃农之间进行分担，这使得佃农在做生产决策时不仅要考虑生产上可能出现的风险，比如天气状况变化对生产的影响等等，还必须考虑到市场上农产品价格变化对佃农利益的影响。
如果佃农是风险回避的，则这种加大佃农风险的承租方式会导致农民不愿意租土地进行经营。
这样会使土地的出租率下降，从而导致土地的租金下降，最终影响到地主的利益。
交易费用主要是地主为鼓励农民使用这种形式的契约而不得不放弃部分地租。
对于这种形式的契约，一般是在市场经济有了很大的发展以后才会发生，因此，必然出现在资本主义萌芽以后的社会。
在资本主义社会里，由于货币的普遍使用，因此使得土地的租金更多地采用了货币的形式，这对于农民来说意味着更大的风险，因此租金比以前的租金形式有所下调，并且出现了各种各样的金融工具来帮助农民来分散风险，例如金融衍生工具中的期货便具有这种功能。
（2）对于分成地租，更多是在劳动地租逐渐消亡以后才出现的，它是为了调动农民积极性而采取的一种租金形式。
在征收分成地租的情况下，农民要承担一定的生产风险，即如果收成不好，则农民的收入就会减少。
通常情况下，分成地租是通过将每年收成的一个固定的百分比给予地主，而将收入的剩余部分留给农民。
这种形式的契约有利于调动农民的积极性，当然同时也给农民带来了一定的风险。
在历史上，还出现过另外的一种固定地租的形式，即地主规定农民必须在每年上缴一定的收成，剩余的归农民，这种形式的租金是将全部的风险都留给了农民，其前提假设是农民是风险中性的。
平新乔《微观经济学十八讲》章节题库含名校考研真题(第1~4讲)【圣才出品】
该偏好满足单调性吗？满足凸性吗？为什么？你能从生活中举出一个例子对应这种偏 好关系吗？
解：（1）该偏好满足严格凸性，理由如下： 无差异曲线 x1 x2 c 的图像如图 1-3 所示，可知其偏好满足严格凸性。
图 1-3 无差异曲线
将无差异曲线 u x1, x2
若灾区人民获得的是棉被，则其最优化问题为：
maxU
x1 , x2
x1, x2
s.t. m p g x2 p x1
①
x1 g
若灾区人民获得的是现金，则其最优化问题为：
maxU
x1 , x2
x1, x2
②
s.t. m c x2 p x1
由于最优化问题①和②的目标函数式相同，但是①的预算集（即 x1 和 x2 的取值范围）
x1
x2 c 转化为 x2 c
2
x1 ，则有：
dx2 dx1
1
1 cx1 2
0
，
d2 x2 d x12
1 2
cx1
3 2
0
2 / 67
圣才电子书 十万种考研考证电子书、题库视频学习平台
则满足这种性质的函数会严格凸向原点，故其偏好必定满足严格凸性。 （2）该偏好满足单调性，满足凸性，但不满足严格凸性。理由如下： 根据函数可大致画出其图像，如图 1-4 所示：
3．下列函数可以作为马歇尔需求函数吗？为什么？
xi
p1 2
pi w
p2 2
p3 2
，i
1, 2, 3
答：这个函数可以作为马歇尔需求函数，理由如下：
马歇尔需求函数需要满足下列性质：
（1）在 p, w 上具有零次齐次性：
平新乔课后习题详解(第18讲--企业的性质、边界与产权)
平新乔《微观经济学十八讲》第 18讲 企业的性质、边界与产权1 •有三种类型的契约被用来区分一块农地的租佃者向地主支付租金的方式：（1） 以货币（或固定数量的农产品）； （2） 以收成的固定比率；（3） 以“劳动租”，即同意在地主的另一块土地上工作的形式来付租金。
这些各自不同的契约规范会对佃农的生产决策产生什么影响？在实施每种契约时会发 生何种交易费用？在不同的地方或在不同的历史阶段中，哪些经济因素会影响已确定的契 约类型？答：（1）对于货币租来说，这种形式的租金是将市场的风险在地主与佃农之间进行分担,这使得佃农在做生产决策时不仅要考虑生产上可能出现的风险, 影响等等，还必须考虑到市场上农产品价格变化对佃农利益的影响。
则这种加大佃农风险的承租方式会导致农民不愿意租土地进行经营。
下降，从而导致土地的租金下降，最终影响到地主的利益。
交易费用主要是地主为鼓励农民使用这种形式的契约而不得不放弃部分地租。
对于这种形式的契约， 一般是在市场经济有了很大的发展以后才会发生， 因此，必然出 现在资本主义萌芽以后的社会。
在资本主义社会里，由于货币的普遍使用， 因此使得土地的租金更多地采用了货币的形式，这对于农民来说意味着更大的风险，因此租金比以前的租金形式有所下调，并且出现了各种各样的金融工具来帮助农民来分散风险， 例如金融衍生工具中的期货便具有这种功能。
（2） 对于分成地租，更多是在劳动地租逐渐消亡以后才出现的，它是为了调动农民积极性而采取的一种租金形式。
在征收分成地租的情况下，农民要承担一定的生产风险，即如 果收成不好，则农民的收入就会减少。
通常情况下，分成地租是通过将每年收成的一个固定 的百分比给予地主，而将收入的剩余部分留给农民。
这种形式的契约有利于调动农民的积极性，当然同时也给农民带来了一定的风险。
在历史上，还出现过另外的一种固定地租的形式，即地主规定农民必须在每年上缴一定的收成， 剩余的归农民，这种形式的租金是将全部的风险都留给了农民，其前提假设是农民是风险中性的。
微经十八讲第八讲
12.3对于 这样一条不变弹性的需求曲线，需求曲线与边际收益曲线之间的垂直距离与需求曲线的高度成一固定的比率，这一比率取决于需求的价格弹性。
答：对。反需求函数为 ，其中 。其边际收益为 。由于需求的价格弹性等于 。因此，这一比率为 。
8.2如果市场需求曲线向下倾斜，则每个厂商面对的需求曲线也向下倾斜。
答：经济理论中允许无穷数量的厂商存在，在该情况下，向下倾斜的需求曲线也不会意味着一个厂商可以单独影响价格，即需求曲线水平。在实践中，竞争性行业中单独厂商规模如果足够小，其足够小的一个产出变化不会影响市场价格；这时也可以认为它的需求曲线是水平。
9.1市场上的均衡价格与数量。
解：令 ， 。解得， ， 。上标 表示均衡。
9.2此时若政府对每单位产品征收0.5单位的税收，求此时的市场价格与数量。
解：令 ， 。解得， ， 。
9.3求解消费者剩余与生产者剩余的损失，与政府所得比较，社会存在净损失么？
解：消费者剩余的变化 ，生产者剩余的变化 ， ，而政府所得 。因此有社会福利变化 。所以，社会存在净损失。
12.5将从（1）到（4）所得结果在图上表示出来。
13我们近两年（2000年及前一年）的粮食丰收使粮食供给有很大的增加，今年再次出现粮食供过于求的局面。
13.1试作图分析如果任凭市场机制对粮食供求状况进行调节，对我们明年的粮食生产可能会产生何种影响。
在图中，供给曲线右移，使当年粮食价格下降。可能使第二年粮食生产下降。[在静态或适应性预期条件下]。
解：工厂1、2的成本函数分别为 ， ，令工厂的边际成本分别等于相应市场的边际收益。有 ， 。得到 ， 。
14.5计算两个工厂的利润之和。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
4 / 85
由于 E uw E uc E u ，所以农民会混合种植。
（3）假设小麦的种植份额为 ，那么混合种植的期望效用 EU 为：
000 1
1 2
ln 10000
15000
1
效用最大化的一阶条件为：
dEU d
1 2
28000 19000 28000 19000 1
解：（1）农民种小麦的预期效用 E uw 为：
E uw 0.5ln 28000 0.5ln10000 0.5ln 280 106
农民种谷子的预期效用 E uc 为：
E uc 0.5ln19000 0.5ln15000 0.5ln 285106
1 / 85
圣才电子书 十万种考研考证电子书、题库视频学习平台
1 2
10000 15000 10000 15000 1
0
解得： 4 。 9
此时的期望效用为：
EU
0.5 ln
4 9
28000
5 9
19000
0.5 ln
4 9
10000
5 9
15000
0.5ln 293.96
所以当农民用 4/9 的土地种小麦，5/9 的土地种谷子时，其期望效用达到最大，最大期
（1）假定农民一定要在两种如表 5-1 所示收入前景的谷物中进行选择的话，会种哪种
谷物？
表 5-1 小麦和谷子在不同天气状况下的收入
单位：元
（2）假定农民在他的土地上可以每种作物都播种一半的话，他还会选择这样做吗？请 解释你的结论。
（3）怎样组合小麦与谷子才可以给这个农民带来最大的预期效用？ （4）如果对于只种小麦的农民，有一种要花费 4000 元的保险，在种植季节多雨的情 况下会赔付 8000 元，那么，这种有关小麦种植的保险会怎样改变农民的种植情况？
望效用为
0.5ln 293.9 106 。
（4）如果种植小麦的农民购买保险，那么他的期望效用 E uw 为：
E uw
1 ln 28000 4000 1 ln 10000 4000
2
2
1 ln 2
33610 6
2 / 85
圣才电子书 十万种考研考证电子书、题库视频学习平台
并且罚金额为 f 。假定所有的个人都是风险厌恶型的（也就是说， uw 0 ，其中， w 是
个人的财富）。那么被抓到的可能性的按比例增加和罚金上的按比例增加在防止非法停车方
面哪个更有效？（提示：运用泰勒级数展开式
u w f u w fuw f 2 uw ）
2
答：利用泰勒级数展开式，非法停车的总效用为：
2
2
这说明罚金的比例和收到罚款通知单的可能性同比例增加，前者会使消费者的效用更
低，所以罚金按比例增加在防止非法停车方面更有效。
4．在固定收益率为 r 的资产上投资 w* 美元，可以在两种状态时获得 w* 1 r ；而在风
险资产上的投资在好日子收益为 w* 1 rg ，在坏日子为 w* 1 rb （其中 rg r rb ）。通过上
3 / 85
圣才电子书 十万种考研考证电子书、题库视频学习平台
u w tPfuw 1 tPf 2u w
②
2
由于消费者是风险厌恶型的，所以 uw 0 ，于是：
u w tPfuw 1 t 2Pf 2u w u w tPfu w 1 tPf 2u w
这个值大于两种作物按最优混合比例种植所能带给农民的效用，所以农民会买保险。
2．证明：如一个人拥有初始财产 w* ，他面临一场赌博，赌博的奖金或罚金都为 h ，赌
博的输赢概率都为 0.5（公平赌博）。若这个人是风险厌恶型的，那么他就不会参加该赌博。
证明：假设消费者的效用函数为 u w ，那么他参与赌博的期望效用为：
Pu w
f
1 Pu w
P
u
w
fuw
f2 2
uw u w Pu w
u w Pfuw 1 Pf 2uw
2
假设罚金的比例增加为原来的 t （ t 1 ）倍，那么非法停车的效用就变为：
u w tPfuw 1 t 2Pf 2u w
①
2
假设收到罚款通知单的可能性增加为原来的 t（ t 1 ）倍，那么非法停车的效用就变为：
因为 E uw E uc ，所以农民会种谷子。
（2）若农民在土地上每种作物都播种一半，他不会选择继续只种谷子。如果农民在他
的土地上每种作物各种一半，他的收益如表 5-2 所示：
表 5-2 混合种植时不同天气状况下的收入
单位：元
从而他的预期效用 E u 为：
E u 0.5ln 23500 0.5ln12500 0.5ln 293.75106
述假定，风险资产上的投资就可以在状态偏好的框架中被加以研究。 （1）请画出两种投资的结果。 （2）请说明包含无风险资产与风险资产的“资产组合”怎样可以在你的图中得到显示。
你怎样说明投资在风险资产中的财富比例？ （3）请说明个人对于风险的态度会怎样决定他们所持有的无风险资产与风险资产的组
合。一个人会在什么情况下不持有风险资产？ 答：（1）两种投资的结果如图 5-1 所示， A 点是将全部财富都投入到风险资产时收益
1 u w h 1 u w h
2
2
而他不参加赌博的效用为 u w* 。对于风险厌恶者，财富的期望值的效用总是大于效用
的期望值，即：
1 2
u
w
h
1 2
u
w
h
u
1 2
w
h
1 2
w
h
u
w
这就意味着参与赌博的效用低于不赌博的效用，所以此人不会参加赌博。
3．当决定在一个非法的地点停车时，任何人都知道，会收到罚款通知单的可能性是 P ，
圣才电子书 十万种考研考证电子书、题库视频学习平台
平新乔《微观经济学十八讲》课后习题
第 5 讲 风险规避、风险投资与跨期决策
1．一个农民认为在下一个播种的季节里，雨水不正常的可能性是一半对一半。他的预
期效用函数的形式为：
预期效用
1 2
ln
yNR
1 2
ln
yR
这里， yNR 与 yR 分别代表农民在“正常降雨”与“多雨”情况下的收入。