参数估计教程
华东师范大学茆诗松《概率论与数理统计教程》第6章 参数估计.
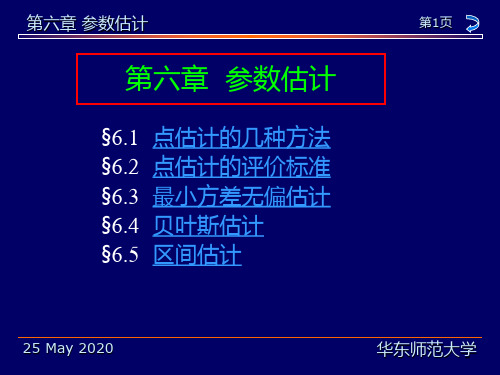
ˆ (a , , a ), j j 1 k
其中
1 n j a j xi n i1
j 1, , k ,
25 November 2018
华东师范大学
第六章 参数估计
第7页
例6.1.2 设总体服从指数分布,由于EX=1/, 即 =1/ EX,故 的矩法估计为
ˆ 1/ x
华东师范大学
第六章 参数估计
第8页
例 6.1.3 x1, x2, …, xn 是来自 (a,b) 上的均匀分布 U(a,b) 的样本, a 与 b 均是未知参数,这里 k=2 , 由于
ab EX , 2 (b a ) 2 Var( X ) , 12
不难推出
a EX 3Var( X ), b EX 3Var( X ),
L( ) ( ) [2 (1 )] [(1 ) ]
2 n1 n2 2 n3
2
n2
2 n1 n 2
(1 )
2 n3 n2
其对数似然函数为
ln L( ) (2n1 n2 ) ln (2n3 n2 ) ln(1 ) n2 ln 2
1 n n n 2 2 ln L( , ) 2 ( xi ) ln ln(2) 2 i 1 2 2
2
25 November 2018
华东师范大学
第六章 参数估计
第14页
将 lnL(, 2) 分别关于两个分量求偏导并令 其为0, 即得到似然方程组
ln L( , 2 ) 1 n 2 ( xi ) 0 i 1 ln L( , 2 ) 1 n n 2 4 ( xi ) 2 0 2 2 i 1 2
参数估计步骤

参数估计步骤
参数估计是统计学中的一个关键任务,用于从收集到的数据中推断未知的参数值。
以下是一般的参数估计步骤:
1.明确问题和目标:
确定需要估计的参数是什么。
明确估计的目标,例如点估计还是区间估计。
2.选择合适的概率分布:
基于问题的性质和数据的特征,选择一个合适的概率分布,如正态分布、泊松分布等。
3.建立统计模型:
建立描述数据生成过程的统计模型,包括参数和概率分布。
4.收集数据:
收集与问题相关的数据样本。
5.选择估计方法:
选择合适的估计方法,如最大似然估计、最小二乘法、贝叶斯估计等,取决于问题和模型。
6.构建估计统计量:
基于所选的估计方法,构建相应的估计统计量。
7.计算估计值:
使用收集到的数据计算估计统计量的具体值。
8.评估估计的性能:
评估估计的精确性和效果,考虑估计的方差、置信区间等。
9.进行假设检验(可选):
如果需要,进行假设检验以验证估计的显著性。
10.解释和报告结果:
将估计结果进行解释,并报告估计的点值或区间。
11.敏感性分析:
进行敏感性分析,考虑不同假设和参数值对估计的影响。
12.持续监测和更新:
定期监测估计的性能,如果有新数据可用,可以更新估计。
这些步骤的具体实施取决于问题的性质、数据的特点以及所选择的统计方法。
在实际应用中,研究人员需要根据具体情况灵活运用这些步骤。
统计学教程(含spss)四参数估计

从一批灌装产品中,随机抽取20灌,得样本方差为0.0025。试以95%的置 信度,估计总体方差的存在区间。
n 1 s2 2 n 1 s2
2 2
2 1 2
n 1 s2
2 0.025
2
n 1 s2
2 0.975
19 0.0025 2 19 0.0025
32.8523
8.90655
自正态总体抽样时,总体均值与总体中位数相同,而中位数的 标准误差大约比均值的标准误差大25%。因此,样本均值更有效。
x 的抽样分布
M e的抽样分布
____
X
有效性
一致性
如果 lim
P
1(为任意小数,n
为样本容量)
n
则称 为的满足一致性标准的点估计量
ˆ1的抽样分布 ˆ2的抽样分布
x s 2 p 均为一致性估计量
X~N, 2
x__
~
N
, 2 n
__
Z x ~N 0,1
n
P Z
Z Z
1
2
2
P Z
2
__
x n
Z
1
2
显著性水平
22
2
Z 2
置信度
1
0
P_x_ Z
2
n
__
x Z 2
1
n
2
Z 2
显著性水平α下,μ在1- α置信水平下的置信区间:
__
x
Z
2
__
n , x Z 2
f x
x
n
x 2
f x
1
e 2 2 x
2
x
抽样分布
E(x)
参数估计的一般步骤

参数估计的一般步骤引言:参数估计是统计学中一项重要的任务,它用于根据样本数据来推断总体参数的值。
参数估计的一般步骤包括确定估计方法、选择样本、计算估计值和进行推断。
本文将详细介绍参数估计的一般步骤,并以人类的视角进行描述,使读者更好地理解和应用这些步骤。
一、确定估计方法在参数估计中,首先需要确定合适的估计方法。
估计方法可以分为点估计和区间估计两种。
点估计方法通过单个数值来估计参数的值,例如最大似然估计和矩估计。
区间估计方法则通过一个区间来估计参数的范围,例如置信区间估计。
选择合适的估计方法是参数估计的第一步。
二、选择样本在确定了估计方法后,接下来需要选择合适的样本进行参数估计。
样本应当具有代表性,能够反映总体的特征。
为了保证样本的代表性,可以使用随机抽样方法来选择样本。
通过合理选择样本,可以减小估计误差,提高参数估计的准确性。
三、计算估计值在选择好样本后,需要计算参数的估计值。
对于点估计方法,可以使用最大似然估计或矩估计等方法来计算参数的估计值。
对于区间估计方法,可以使用置信区间估计来计算参数的范围。
计算估计值时,需要根据样本数据和估计方法进行相应的计算,确保估计结果的准确性。
四、进行推断在计算得到估计值后,需要进行推断,即根据估计值对总体参数进行推断。
对于点估计方法,可以直接使用估计值作为总体参数的估计值。
对于区间估计方法,可以使用置信区间来表示总体参数的范围。
通过推断可以了解总体参数的可能取值范围,帮助做出正确的决策和预测。
总结:参数估计的一般步骤包括确定估计方法、选择样本、计算估计值和进行推断。
在进行参数估计时,需要选择合适的估计方法和样本,计算出估计值,并进行相应的推断。
参数估计在统计学中扮演着重要的角色,它帮助我们根据样本数据来推断总体参数的值,从而更好地了解和应用统计学。
通过本文的介绍,希望读者能够更好地理解和应用参数估计的一般步骤。
《参数估计方法》课件

目录
• 参数估计方法概述 • 点估计 • 区间估计 • 最大似然估计法 • 最小二乘估计法 • 贝叶斯估计法
01
参数估计方法概述
参数估计方法的定义
参数估计方法的定
义
参数估计方法是一种统计学中的 方法,它通过分析样本数据来估 计未知的参数值。这些参数可以 描述总体特性的程度,如平均值 、方差等。
使得它容易进行统计推断。
最小二乘估计法的应用场景
线性回归分析
最小二乘估计法是线性回归分析中最常用的 参数估计方法,用于预测一个因变量与一个 或多个自变量之间的关系。
时间序列分析
在时间序列分析中,最小二乘估计法可用于拟合和 预测时间序列数据,例如ARIMA模型。
质量控制
在质量控制中,最小二乘估计法可用于拟合 控制图,以监测过程的稳定性和预测异常情 况。
区间估计
区间估计是一种更精确的参数估计方法,它给出未知参数的一个置信区间,即有较大的把握认为未知参数落在这个区 间内。例如,用样本均值和标准差来估计总体均值的置信区间。
贝叶斯估计
贝叶斯估计是一种基于贝叶斯定理的参数估计方法,它根据先验信息和样本数据来推断未知参数的后验 概率分布。贝叶斯估计能够综合考虑先验信息和样本数据,给出更加准确的参数估计结果。
贝叶斯估计法的性质
01
02
03
贝叶斯估计法是一种主观概率估 计方法,因为它依赖于先验信息 的可信度和准确性。
先验信息的不确定性可以通过引 入一个先验分布来表达,该分布 描述了先验信息中未知参数的可 能取值及其概率。
贝叶斯估计法的后验概率分布可 以用于推断未知参数的估计值和 不确定性程度。
贝叶斯估计法的应用场景
3
matlab教程参数估计及假设检验

[muratio,sgmratio]=fugailv(0,1,1000,200,0.05) [muratio,sgmratio]=fugailv(10,2,2000,500,0.01) [muratio,sgmratio]=fugailv(4,6,5000,400,0.025)
2、其它分布的参数估计
要依据该g( ).
参数估计
点估计 区间估计
点估计 —— 估计未知参数的值。 区间估计—— 根据样本构造出适当的区间, 使它以一定的概率包含未知参数或未知参 数的已知函数的真值。
(一)点估计的求法 1、矩估计法 基本思想是用样本矩估计总体矩 .
(1). 取容量充分大的样本(n>50),按中心极限定理, 它近似地服从正态分布; (2).使用Matlab工具箱中具有特定分布总体的估计命令. 10[muhat, muci] = expfit(X,alpha)----- 在显著性水平 alpha下,求指数分布的数据X的均值的点估计及其区间 估计. 20 [lambdahat, lambdaci] = poissfit(X,alpha)----- 在显 著性水平alpha下,求泊松分布的数据X 的参数的点估 计及其区间估计. 30[phat, pci] = weibfit(X,alpha)----- 在显著性水平alpha 下,求Weibull分布的数据X 的参数的点估计及其区间 估计.
的无约束最优化问题。
方法: ①最速下降法 ②Newton(牛顿)法及其修正的方法。 ③共轭方向法和共轭梯度法 ④变尺度法(拟牛顿法) 等等 详见北京大学出版社 高惠璇编著《统计计算》 P359------P379
二、假设检验
统计推断的另一类重要问题是假设检验问题。 在总体的分布函数完全未知或只知其形式,但 不知其参数的情况,为了推断总体的某些未知 特性,提出某些关于总体的假设。 对总体X的分布律或分布参数作某种假设,根据 抽取的样本观察值,运用数理统计的分析方法, 检验这种假设是否正确,从而决定接受假设或拒 绝假设.
Eviews_教程

Eviews 教程(案例介绍)一、单方程计量经济模型参数估计与统计检验例1 为了研究税收(T )发展状况,选择国内生产总值(GDP )、财政支出(GE )为影响因素,建立计量经济模型分析因素之间的经济关系。
选取下表的有关统计数据,模型如下:t t t t GE GDP T μβββ+++=210税收收入等有关统计数据 单位:亿元借助该财政收入模型案例,采用Eviews6.0估计模型中参数,并进行相关的统计检验,确定最终模型。
Eviews软件模型分析过程如下:1.创建工作文件启动Eviews软件,在主菜单上依次单击File→New→Workfile,选择数据类型(时间序列或非时间序列),并输入样本区间和工作文件名,创建工作文件的子窗口如图1-1所示。
图1-1 创建工作文件2.建立变量组Eviews软件建立变量组可采用三种途径:(1)在主菜单上依次单击Quick→Empty Group,在数据编辑窗口中单击Edit+/-,并按上行健↑,这样可依次输入变量名;(2)在主菜单上依次单击Objects→New Objects,在对话框中选择“Group”并定义文件名,在数据编辑窗口中首先按上行健↑,这样可依次输入变量名;(3)在主菜单上Eviews命令框中直接输入命令:Data T GDP GT CPI(命令及变量名之间用空格分隔),将直接出现已定义变量名称的数据编辑窗口。
图1-2 数据编辑窗口3.输入经济变量的样本数据在图1-2所示的数据编辑窗口中,在“NA”的位置可输入各经济变量的样本数据,输入样本数据后及时予以保存。
样本数据也可以从有关Office软件的各类表格中进行数据的复制;也可以通过Eviews 软件本身生产新的变量数据序列,如在主菜单上依次单击Quick→Generate Series、或者在工作文件(Workfile)窗口中单击Generate,在弹出窗口中输入方程式,如图1-3所示。
图1-3 生产新变量数据序列4.估计模型参数在主菜单上依次单击Quick→Estimate Equation,弹出对话框,在“Specification”选项卡中输入模型中被解释变量、常数项、解释变量序列,并选择估计方法及样本区间,如图1-4所示,估计结果如图1-5。
SPSS18教程7章总体参数的估计

§5.3 区间估计
• 1. 样本中的支持率为 90% , 即用样本 样本中的支持率为90 90% 比例作为对总体比例的点估计 • 2. 估计范围为 90%±3%(±3% 的误差 ) , 估计范围为90 90% 的误差) 即区间(93% 87% 即区间(93%,87%)。 • 3. 如用类似的方式 , 重复抽取大量 如用类似的方式, 样本量相同的)样本时, (样本量相同的)样本时,产生的大 量类似区间中有些会覆盖真正的 p , 而有些不会; 但其中大约有95 95% 而有些不会 ; 但其中大约有 95% 会覆 盖真正的总体比例。 盖真正的总体比例。
§5.3 区间估计
• 这样得到的区间被称为总体比例 的 这样得到的区间被称为总体比例p的 置信度(confidence level)为 95%的 置信度 为 的 置信区间(confidence interval)。这 置信区间 。 置信水平或 里的置信度又称置信水平 里的置信度又称 置信水平 或 置信系 数。 • 显然置信度的概念又是大量重复抽 样时的一个渐近概念。 样时的一个渐近概念。
• 如果我们想知道桂林人认可某饮料 的比例, 的比例,人们只有在桂林人中进行 抽样调查以得到样本, 抽样调查以得到样本,并用样本中 认可该饮料的比例来估计真实的比 例。 • 从不同的样本得到的结论也不会完 全一样。 全一样。虽然真实的比例在这种抽 样过程中永远也不知道; 样过程中永远也不知道;但可以知 道估计出来的比例和真实的比例大 致差多少。 致差多少。
描描描统
449.0104 447.4124 450.6084 448.9500 30.287 5.50339 439.60 461.10 21.50 8.18
§5.2 点估计
• 那么,什么是好估计量的标准呢? 那么,什么是好估计量的标准呢? • 一种统计量称为无偏估计量 estimator)。 (unbiased estimator)。 • 所谓的 无偏性 (unbiasedness) 就是 : 所谓的无偏性 (unbiasedness)就是 无偏性(unbiasedness) 就是: 虽然每个样本产生的估计量的取值 不一定等于参数, 不一定等于参数 , 但当抽取大量样 本时, 本时 , 那些样本产生的估计量的均 值会接近真正要估计的参数。 值会接近真正要估计的参数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录参数估计 ________________________________________________________________________________ 3第一节抽样推断的基本概念与原理 ________________________________________________________ 3一、抽样推断的特点和作用 _____________________________________________________________ 3二、重复抽样与不重复抽样 _____________________________________________________________ 4三、抽样误差与抽样平均误差 ___________________________________________________________ 4四、抽样推断的理论基础 _______________________________________________________________ 6五、参数估计的基本步骤 _______________________________________________________________ 7第二节参数估计中的点估计 ______________________________________________________________ 7一、总体参数的点估计 _________________________________________________________________ 7二、点估计量的优良标准 _______________________________________________________________ 7第三节参数估计中的区间估计 ____________________________________________________________ 8一、参数估计的精度与抽样平均误差计算 _________________________________________________ 8二、参数估计的误差范围与概率度 _______________________________________________________11三、总体参数的区间估计 ______________________________________________________________ 12第四节抽样组织方式及其参数估计 _______________________________________________________ 13一、简单随机抽样 ____________________________________________________________________ 13二、分层抽样 ________________________________________________________________________ 14三、机械抽样 ________________________________________________________________________ 16四、整群抽样 ________________________________________________________________________ 16第五节必要样本容量的确定 _____________________________________________________________ 17一、平均数的必要样本容量 ____________________________________________________________ 17二、成数的必要样本容量 ______________________________________________________________ 18三、影响必要样本容量的因素 __________________________________________________________ 19 习题 ___________________________________________________________________ 错误!未定义书签。
第六章参数估计统计抽样推断是统计学研究的重要内容,它包括两大核心内容:参数估计(Parameter Estimation)和假设检验(Hypothesis Testing)。
两者都是根据样本资料,运用科学的统计理论和方法,参数估计对所要研究的总体参数,进行合乎数理逻辑的推断;假设检验对先前提出的某个陈述,进行检验判断真伪。
2005年中国消费者协会的主题是“健康·维权”。
想象你是中国消费者协会的官员,负责治理缺斤少两的不法行为。
假如你知道可口可乐公司,他们生产的一种瓶装雪碧,包装上标明其净含量是500ml,在市场上随机抽取了50瓶,测得到其平均含量为499.5ml,标准差为2.63ml。
你拿着这些数据可能做两件事:一是你做一个估计:该种包装的雪碧平均含量在498.77-500.23ml之间,然后向消协写份报告;二是你做一个裁决:说“可口可乐公司有欺骗消费者的行为”的证据不足。
前者是参数估计;后者是假设检验。
学习参数估计和假设检验要注意:(1)明确要研究的问题,并给出正确的提法;(2)确定合适的统计量,统计量也可以认为是统计推断模型,不论是参数估计还是假设检验,都要通过统计量来进行,构造的统计量是否可行,直接关系到统计推断的效果,因此要仔细研究和比较统计量的性质;(3)统计参数估计和假设检验是根据样本资料对总体进行认识的,这就要求样本资料必须要有代表性,否则不可能客观反映总体的情况;(4)参数统计与非参数统计方法的主要区别,在于前者在处理问题的时候总是从已确知的分布出发,所以在进行统计参数推断时,要能够掌握统计量的精确分布即统计量的抽样分布;(5)给出推断结果的合理解释。
本章首先集中说明抽样推断中的常用术语,然后主要介绍参数估计的基本原理,点估计和区间估计的方法,以及必要样本容量的测算。
第一节抽样推断的基本概念与原理抽样推断是按照随机性原则,从研究对象中抽取一部分进行观察,并根据所得到的观察数据,对研究对象的数量特征作出具有一定可靠程度的估计和推断,以达到认识总体的一种统计方法。
例如,要检验某种工业产品的质量,我们只需从中抽取一小部分产品进行检验,并用计算出来的合格率来估计全部产品的合格率,或是根据合格率的变化来判断生产线是否出现了异常。
一、抽样推断的特点和作用(一)抽样推断的特点抽样推断方法与其它统计调查方法相比,具有省时、省力、快捷的特点,从而能以较小的代价及时获得总体的有关信息。
1. 根据样本资料对总体的数量特征作出具有一定可靠性的估计和推断。
我们可以用样本的平均数或成数来估计总体的平均数或成数。
抽样调查与全面调查相比,虽然目的一致,都是为了达到对总体数量的认识,但是达到目的的手段和途径完全不同:抽样推断是通过科学的推断达到目的的,全面调查是通过综合汇总达到目的的。
2. 按照随机性原则从全部总体中抽取样本单位。
所谓随机性原则,就是在抽选样本单位时,总体中每一个单位都有相等被抽中的机会,样本单位的抽中与否完全是偶然的。
遵循随机性原则抽取样本是为了保证样本对总体具有充分的代表性,避免人为的误差。
也只有按随机性原则抽样,才能根据样本的数量特征对总体的数量特征进行科学的估计,从而达到推断总体的目的。
3. 抽样推断必然会产生抽样误差,这是抽样推断方法本身所决定的。
抽样误差是可以事先通过一定的资料加以计算的,并在抽样过程中可以采取一定的措施来控制误差的范围,从而保证抽样推断的结果达到一定的可靠程度,但抽样误差是不可能消灭的。
(二)抽样推断的作用1. 某些现象不可能进行全面调查,为了解其全面资料就必须采用抽样推断方法。
如对那些有破坏性或消耗性的产品进行质量检验,象炮弹的杀伤半径的检验、灯泡的使用寿命的检验、人体的白血球的检验等,都是不可能进行全面调查的,而只能采用抽样推断的方法。
另外,对于无限总体或总体的范围过大时,就很难进行全面调查了。
例如,对江河湖海中的鱼尾数、大气或海洋的污染情况等,都属于这种情况。
2. 某些理论上可以进行全面调查的现象,采用抽样推断可以达到事半功倍的效果。
如要了解全国城乡居民的家庭收入状况,从理论上讲可以挨门逐户进行全面调查,但是调查范围太大,调查单位太多,实际上难以办到,也没有必要。
采用抽样推断既可以节省人力、物力、费用和时间,提高调查结果的时效性,又能达到和全面调查同样的目的和效果。
3. 抽样推断可以对全面调查的结果进行评价和修正。
全面调查涉及范围广,调查单位多,工作量大,参加人员多,因而发生登记性和计算性的误差就多。
所以,在全面调查后,还可以再抽取一部分单位重新调查一次,计算其差错比率,并以此为依据对全面调查的资料进行修正,这样就可以进一步提高全面调查资料的准确性。
由于抽样推断中调查的范围小,可以多调查一些项目,或从事某项更深入的专题调查,以补充全面调查的不足。
全国人口普查就是有短表和长表之分,短表用于全面调查,长表用于抽样调查。
4. 抽样推断可用于工业生产过程中的质量控制。
在工业产品成批或大量连续生产过程中,采用抽样推断方法可以检验生产工艺过程是否正常,及时提供有关信息,便于采取相应措施,进行质量控制,保证生产质量稳定,防止损失。
5. 利用抽样推断的原理,可以对某些总体的假设进行检验,来判断假设的真伪,为决策提供依据。
如某地上一年度居民家庭年收入35000元,本年度抽样调查结果显示居民家庭年收入33000元,这是否意味着该地居民家庭收入水平下降了呢?我们还不能下这个结论,最好通过假设检验,检验这两年居民家庭收入是否存在显著性统计差异,才能判断该地本年度居民家庭收入是否低于上年度水平。
总之,抽样推断是一种科学实用的统计方法,在自然科学与社会科学领域都有着广泛的应用。
二、重复抽样与不重复抽样抽样推断首先要抽取样本,就具体方法而言有重复抽样与不重复抽样之分。
1. 重复抽样重复抽样又叫有放还抽样或重置抽样。
它是每抽出一个样本单位后,把结果记录下来,随即将该单位放回到总体中去,使它和其余的单位在下一次抽选中具有同等被抽中的机会。
在重复抽样过程中,总体单位数始终保持不变,并且同一个单位有多次被抽中的可能性。
2. 不重复抽样不重复抽样又叫无放还抽样或不重置抽样。
它是每抽出一个样本单位后,把结果记录下来,该单位就不再放回到总体中去参加以后的抽选。
