(完整版)哈工大选修课LINEARALGEBRA试卷及答案,推荐文档
哈工大选修课 LINEAR ALGEBRA 试卷及答案

LINEAR ALGEBRAANDITS APPLICATIONS 姓名:易学号:成绩:1. Definitions(1) Pivot position in a matrix; (2) Echelon Form; (3) Elementary operations;(4) Onto mapping and one-to-one mapping; (5) Linearly independence.2. Describe the row reduction algorithm which produces a matrix in reduced echelon form.3. Find the 33⨯ matrix that corresponds to the composite transformation of a scaling by 0.3, a rotation of 90︒, and finally a translation that adds (-0.5, 2) to each point of a figure.4. Find a basis for the null space of the matrix361171223124584A ---⎡⎤⎢⎥=--⎢⎥⎢⎥--⎣⎦5. Find a basis for Col A of the matrix1332-9-2-22-822307134-111-8A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦6. Let a and b be positive numbers. Find the area of the region bounded by the ellipse whose equation is22221x y ab+=7. Provide twenty statements for the invertible matrix theorem. 8. Show and prove the Gram-Schmidt process. 9. Show and prove the diagonalization theorem.10. Prove that the eigenvectors corresponding to distinct eigenvalues are linearly independent.Answers:1. Definitions(1) Pivot position in a matrix:A pivot position in a matrix A is a location in A that corresponds to a leading 1 in the reduced echelon form of A. A pivot column is a column of A that contains a pivot position.(2) Echelon Form:A rectangular matrix is in echelon form (or row echelon form) if it has the following three properties:1.All nonzero rows are above any rows of all zeros.2.Each leading entry of a row is in a column to the right of the leading entry of the row above it.3.All entries in a column below a leading entry are zeros.If a matrix in a echelon form satisfies the following additional conditions, then it is in reduced echelon form (or reduced row echelon form):4.The leading entry in each nonzero row is 1.5.Each leading 1 is the only nonzero entry in its column.(3)Elementary operations:Elementary operations can refer to elementary row operations or elementary column operations.There are three types of elementary matrices, which correspond to three types of row operations (respectively, column operations):1.(Replacement) Replace one row by the sum of itself anda multiple of another row.2.(Interchange) Interchange two rows.3.(scaling) Multiply all entries in a row by a nonzero constant.(4)Onto mapping and one-to-one mapping:A mapping T : n →m is said to be onto m if each b in m is the image of at least one x in n.A mapping T : n →m is said to be one-to-one if each b in m is the image of at most one x in n.(5)Linearly independence:An indexed set of vectors {V1, . . . ,V p} in n is said to be linearly independent if the vector equationx 1v 1+x 2v 2+ . . . +x p v p = 0Has only the trivial solution. The set {V 1, . . . ,V p } is said to be linearly dependent if there exist weights c 1, . . . ,c p , not all zero, such that c 1v 1+c 2v 2+ . . . +c p v p = 02. Describe the row reduction algorithm which produces a matrix in reduced echelon form. Solution: Step 1:Begin with the leftmost nonzero column. This is a pivot column. The pivot position is at the top. Step 2:Select a nonzero entry in the pivot column as a pivot. If necessary, interchange rows to move this entry into the pivot position. Step 3:Use row replacement operations to create zeros in all positions below the pivot. Step 4:Cover (or ignore) the row containing the pivot position and cover all rows, if any, above it. Apply steps 1-3 to the submatrix that remains. Repeat the process until there all no more nonzero rows to modify. Step 5:Beginning with the rightmost pivot and working upward and to the left, create zeros above each pivot. If a pivot is not 1, make it 1 by scaling operation.3. Find the 33⨯ matrix that corresponds to the composite transformation of a scaling by 0.3, a rotation of 90︒, and finally a translation that adds (-0.5, 2) to each point of a figure. Solution:If ψ=π/2, then sin ψ=1 and cos ψ=0. Then we have ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−−→−⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡110003.00003.01y x y x scale⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-−−→−110003.00003.0100001010y x R o t a t e⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-−−−→−110003.00003.0100001010125.0010001y x T r a n s l a t eThe matrix for the composite transformation is ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-10003.00003.0100001010125.0010001⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=10003.00003.0125.0001010⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=125.0003.003.004. Find a basis for the null space of the matrix 361171223124584A ---⎡⎤⎢⎥=--⎢⎥⎢⎥--⎣⎦Solution:First, write the solution of A X=0 in parametric vector form: A ~ ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---00002302101000201, x 1-2x 2 -x 4+3x 5=0 x 3+2x 4-2x 5=0 0=0The general solution is x 1=2x 2+x 4-3x 5, x 3=-2x 4+2x 5, with x 2, x 4, and x 5 free. ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+--+=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡10203012010001222325425454254254321x x x x x x x x x x x x x x x xu v w=x 2u+x 4v+x 5w (1)Equation (1) shows that Nul A coincides with the set of all linear conbinations of u, v and w . That is, {u, v, w}generates Nul A. In fact, this construction of u, v and w automatically makes them linearly independent, because (1) shows that 0=x 2u+x 4v+x 5w only if the weights x 2, x 4, and x 5 are all zero.So {u, v , w} is a basis for Nul A.5. Find a basis for Col A of the matrix 1332-9-2-22-822307134-111-8A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦Solution: A ~ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---07490012002300130001, so the rank of A is 3. Then we have a basis for Col A of the matrix: U = ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0001, v = ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0013and w = ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--07496. Let a and b be positive numbers. Find the area of the region bounded by the ellipse whose equation is22221x y ab+=Solution:We claim that E is the image of the unit disk D under the linear transformation Tdetermined by the matrix A=⎥⎦⎤⎢⎣⎡b a 00, because if u= ⎥⎦⎤⎢⎣⎡21u u , x=⎥⎦⎤⎢⎣⎡21x x , and x = Au, then u 1 =ax 1 and u 2 =bx 2It follows that u is in the unit disk, with 12221≤+u u , if and only if x is in E , with1)()(2221≤+b x a x . Then we have{area of ellipse} = {area of T (D )} = |det A| {area of D} = ab π(1)2= πab7. Provide twenty statements for the invertible matrix theorem.Let A be a square n n ⨯ matrix. Then the following statements are equivalent. That is, for a given A, the statements are either all true or false. a. A is an invertible matrix.b. A is row equivalent to the n n ⨯ identity matrix.c. A has n pivot positions.d. The equation Ax = 0 has only the trivial solution.e. The columns of A form a linearly independent set.f. The linear transformation x → Ax is one-to-one.g. The equation Ax = b has at least one solution for each b in n.h. The columns of A spann.i. The linear transformation x → Ax maps nonton.j. There is an n n ⨯ matrix C such that CA = I. k. There is an n n ⨯ matrix D such that AD = I. l. A T is an invertible matrix. m. If 0A ≠, then ()()T11T A A --=n. If A, B are all invertible, then (AB)* = B *A *o. T**T )(A )(A =p. If 0A ≠, then ()()*11*A A --=q. ()*1n *A 1)(A --=-r. If 0A ≠, then ()()L11L A A --= ( L is a natural number )s. ()*1n *A K)(KA --=-t. If 0A ≠, then *1A A1A =-8. Show and prove the Gram-Schmidt process.Solution:The Gram-Schmidt process:Given a basis {x 1, . . . , x p } for a subspace W of n, define11x v = 1112222v v v v x x v ⋅⋅-=222231111333v v v v x v v v v x x v ⋅⋅-⋅⋅-=. ..1p 1p 1p 1p p 2222p 1111p p p v v v v x v v v v x v v v v x x v ----⋅-⋅⋅⋅-⋅⋅-⋅⋅-=Then {v 1, . . . , v p } is an orthogonal basis for W. In additionSpan {v 1, . . . , v p } = {x 1, . . . , x p } for p k ≤≤1 PROOFFor p k ≤≤1, let W k = Span {v 1, . . . , v p }. Set 11x v =, so that Span {v 1} = Span {x 1}.Suppose, for some k < p, we have constructed v 1, . . . , v k so that {v 1, . . . , v k } is an orthogonal basis for W k . Define1k w1k 1k x p r o j x v k+++-= By the Orthogonal Decomposition Theorem, v k+1 is orthogonal to W k . Note that proj Wk x k+1 is in W k and hence also in W k+1. Since x k+1 is in W k+1, so is v k+1 (because W k+1 is a subspace and is closed under subtraction). Furthermore, 0v 1k ≠+ because x k+1 is not in W k = Span {x 1, . . . , x p }. Hence {v 1, . . . , v k } is an orthogonal set of nonzero vectors in the (k+1)-dismensional space W k+1. By the Basis Theorem, this set is an orthogonal basis for W k+1. Hence W k+1 = Span {v 1, . . . , v k+1}. When k + 1 = p, the process stops.9. Show and prove the diagonalization theorem. Solution:diagonalization theorem:If A is symmetric, then any two eigenvectors from different eigenspaces are orthogonal. PROOFLet v 1 and v 2 be eigenvectors that correspond to distinct eigenvalues, say, 1λand 2λ. T o show that 0v v 21=⋅, compute2T 12T 11211v )(A v v )v (λv v λ==⋅ Since v 1 is an eigenvector ()()2T12T T1Avv v A v ==)(221v v Tλ=2122T12v v λv v λ⋅==Hence ()0v v λλ2121=⋅-, but ()0λλ21≠-, so 0v v 21=⋅10. Prove that the eigenvectors corresponding to distinct eigenvalues are linearly independent. Solution:If v 1, . . . , v r are eigenvectors that correspond to distinct eignvalues λ1, . . . , λr of an n n ⨯ matrix A.Suppose {v 1, . . . , v r } is linearly dependent. Since v 1 is nonzero, Theorem, Characterization of Linearly Dependent Sets, says that one of the vectors in the set is linear combination of the preceding vectors. Let p be the least index such that v p +1 is a linear combination of he preceding (linearly independent) vectors. Then there exist scalars c 1, . . . ,c p such that 1p p p 11v v c v c +=+⋅⋅⋅+ (1) Multiplying both sides of (1) by A and using the fact that Av k = λk v k for each k, we obtain 111+=+⋅⋅⋅+p p p Av Av c Av c11111++=+⋅⋅⋅+p p p p p v v c v c λλλ (2) Multiplying both sides of (1) by 1+p λ and subtracting the result from (2), we have0)()(11111=-+⋅⋅⋅+-++p p p p c v c λλλλ (3) Since {v 1, . . . , v p } is linearly independent, the weights in (3) are all zero. But none of the factors 1+-p i λλ are zero, because the eigenvalues are distinct. Hence 0=i c for i = 1, . . . ,p. But when (1) says that 01=+p v , which is impossible. Hence {v 1, . . . , v r } cannot be linearly dependent and therefore must be linearly independent.。
(北师大版)哈尔滨市高中数学选修4-4第一章《坐标系》检测题(含答案解析)

一、选择题1.在同一平面直角坐标系中,经过伸缩变换22x xy y ''=⎧⎨=⎩后,曲线C 变为曲线()()22561x y -++=,则曲线C 的对称中心是( )A .()5,6-B .5,32⎛⎫-⎪⎝⎭C .()10,12-D .5,62⎛⎫-⎪⎝⎭2.已知点P 的极坐标是1,2π⎛⎫⎪⎝⎭,则过点P 且垂直极轴的直线方程是( ) A .12ρ=B .1cos 2ρθ=C .12cos ρθ=-D .2cos ρθ=-3.极坐标方程2cos22cos 1ρθρθ-=表示的曲线是( ) A .圆B .椭圆C .抛物线D .双曲线4.圆5cos ρθθ=-的圆心极坐标是( )A .45,3π⎛⎫ ⎪⎝⎭B .5,3π⎛⎫ ⎪⎝⎭C .25,3π⎛⎫ ⎪⎝⎭D .55,3π⎛⎫ ⎪⎝⎭5.在同一平面直角坐标系中,经过伸缩变换53x xy y''=⎧⎨=⎩后,曲线C 变为曲线2241x y ''+=,则曲线C 的方程为( )A .2225361x y +=B .2291001x y +=C .10241x y +=D .22281259x y +=6.在极坐标系中,已知圆C 经过点6P π⎛⎫⎪⎝⎭,,圆心为直线sin 4πρθ⎛⎫+= ⎪⎝⎭轴的交点,则圆C 的极坐标方程为 A .4cos ρθ=B .4sin ρθ=C .2cos ρθ=D .2sin ρθ=7.在球坐标系中,点3,,46P ππ⎛⎫ ⎪⎝⎭和点33,,46Q ππ⎛⎫⎪⎝⎭之间的距离为( )A B .C .D8.在直角坐标系xOy 中,直线l 的方程为0x =,以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,则l 的极坐标方程为( )A .sin 32πρθ⎛⎫+= ⎪⎝⎭ B .sin 32πρθ⎛⎫-= ⎪⎝⎭C .sin 62πρθ⎛⎫+= ⎪⎝⎭ D .sin 62πρθ⎛⎫-= ⎪⎝⎭9.已知曲线C 与曲线5ρ=5sin?θθ-关于极轴对称,则曲线C 的方程为( )A .10cos ρ=-π-6θ⎛⎫ ⎪⎝⎭ B .10cos ρ=π-6θ⎛⎫ ⎪⎝⎭ C .10cos ρ=-π6θ⎛⎫+⎪⎝⎭D .10cos ρ=π6θ⎛⎫+⎪⎝⎭10.在极坐标系中,曲线1:2cos C ρθ=,曲线2:4C πθ=,若曲线1C 与2C 交于,A B 两点,则线段AB 的长度为( ) A .2BC.D .111.在极坐标系中,直线cos()4ρθπ-=ρ的公共点的个数为A .1B .2C .0D .无法确定12.若曲线2 1x ty t=-⎧⎨=-+⎩(t为参数)与曲线ρ=B , C 两点,则BC 的值为( ) ABCD二、填空题13.已知直线l的极坐标方程为2sin()4πρθ-=A的极坐标为7)4π,则点A 到直线l 的距离为____.14.在平面直角坐标系xOy 中,圆22:(1)(1)1C x y -+-=,以坐标原点O 为极点,x 轴正半轴为极轴,直线l 的极坐标方程为(0)2πθαα=<<,直线l 交圆C 于,A B 两点,P 为,A B 中点.若||||AB OP ⋅,则α=________.15.求圆心为(3,)6C π,半径为3的圆的极坐标方程为 ___________________.16.在极坐标系中,直线sin cos 1ρθρθ-=被曲线1ρ=截得的线段长为_____________. 17.在极坐标系中,已知(2,)6A π,5(4,)6B π,则A ,B 两点之间的距离AB 为__________.18.在极坐标系中,O 是极点,设点(1,)6A π,(2,)2B π,则OAB ∆的面积是__________.19.在直角坐标系xOy 中,曲线C 1的参数方程为2x cosay =⎧⎪⎨=⎪⎩(α为参数),在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,曲线C 2的方程为ρ(cos θ-sin θ)+1=0,则C 1与C 2的交点个数为________. 20.过点P (2,4π)并且与极轴垂直的直线的方程是___________________________. 三、解答题21.在极坐标系中,已知直线l 过点1,0A ,且其向上的方向与极轴的正方向所成的最小正角为3π,求:(1)直线的极坐标方程; (2)极点到该直线的距离. 22.在平面直角坐标系xOy 中,圆C 的参数方程为22cos ,2sin x y αα=+⎧⎨=⎩(α为参数),以点O 为极点,x 轴的正半轴为极轴建立极坐标系. (1)求圆C 的极坐标方程;(2)过极点O 作直线与圆C 交于点A ,求OA 的中点所在曲线的极坐标方程.23.以平面直角坐标系的坐标原点O 为极点,以x 轴的非负半轴为极轴,以平面直角坐标系的长度为长度单位建立极坐标系. 已知直线l 的参数方程为23{12x ty t=-=-+ (为参数),曲线的极坐标方程为2sin 4cos ρθθ= . (1)求曲线C 的直角坐标方程;(2)设直线与曲线C 相交于A B 、两点,求AB .24.在直角坐标系xOy 中,已知曲线221:(1)1C x y -+=以坐标原点O 为极点,以x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为2cos()336πρθ-=(1)求曲线1C 的极坐标方程;(2)已知点(4,0)M ,直线l 的极坐标方程为3πθ=,它与曲线1C 的交点为O ,P ,与曲线2C 的交点为Q ,求MPQ 的面积.25.在平面直角坐标系xOy 中,圆C 的参数方程为3cos ,3sin x m a y α=+⎧⎨=⎩(α为参数,m 为常数).在以原点O 为极点、以x 轴的非负半轴为极轴的极坐标系中,直线l 的极坐标方程为cos 24πρθ⎛⎫-= ⎪⎝⎭若直线l 与圆C 有两个公共点,求实数m 的取值范围. 26.已知平面直角坐标系xOy ,直线l 过点3)P ,且倾斜角为α,以O 为极点,x 轴的非负半轴为极轴建立极坐标系,圆C 的极坐标方程为24cos()103πρρθ---=.(1)求直线l 的参数方程和圆C 的标准方程;(2)设直线l 与圆C 交于M 、N 两点,若||||PM PN -=,求直线l 的倾斜角α的值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】根据题意,点(,)x y ''在曲线()()22561x y -++=上,由伸缩变换公式22x xy y ''=⎧⎨=⎩,将其代入()()22561x y -++=中化简,将其变形为标准方程即可求解. 【详解】解:由题意,点(,)x y ''在曲线()()22561x y -++=上,()()22561x y ''∴-++=,又22x x y y '==⎩'⎧⎨,()()()22225125261324x y x y ⎛⎫∴-++=⇒-++= ⎪⎝⎭,所以曲线C 的对称中心是5,32⎛⎫- ⎪⎝⎭.故选:B 【点睛】本题考查伸缩变换公式的应用, 关键是将变换后的量代入方程进行化简,考查理解辨析能力及运算求解能力,属于基础题.2.C解析:C 【分析】把极坐标化为直角坐标,求出直线的直角坐标方程,再化为极坐标方程. 【详解】1,2P π⎛⎫⎪⎝⎭的直角坐标是1,02⎛⎫- ⎪⎝⎭,∴过P 且与极轴垂直的直线的直角坐标方程为12x =-,其极坐标方程为1cos 2ρθ=-,即12cos ρθ=-.故选:C . 【点睛】本题考查求直线的极坐标方程,解题时利用极坐标与直角坐标的互化求解.3.D解析:D 【分析】将极坐标方程化为直角坐标方程,就可以得出结论; 【详解】解:极坐标方程2cos22cos 1ρθρθ-=可化为:()222cos sin 2cos 1ρθθρθ--=,2221x y x ∴--=,即22(1)2x y --=,它表示中心在()1,0的双曲线. ∴极坐标方程2cos22cos 1ρθρθ-=表示的曲线是双曲线.故选:D . 【点睛】本题研究极坐标问题,我们的解法是将极坐标方程化为直角坐标方程,再进行研究,属于中档题.4.D解析:D 【分析】先把圆的极坐标方程化成直角坐标方程求出圆心的直角坐标为5(,22-,再把直角坐标化成极坐标得解. 【详解】由题得25cos sin ρρθθ=-,所以22225,50x y x x y x +=-∴+-+=,所以圆心的坐标为5(,2--,即5(,2.所以该点的极径5ρ==,极角θ在第四象限,且5tan 3θθπ==. 所以圆心极坐标是5(5,)3π. 故选:D 【点睛】本题主要考查极坐标和直角坐标的互化,考查圆的一般方程,意在考查学生对这些知识的理解掌握水平.5.A解析:A 【分析】将伸缩变换53x xy y''=⎧⎨=⎩代入曲线2241x y ''+=中即可解.【详解】解:把53x x y y ''=⎧⎨=⎩代入曲线2241x y ''+=,可得:()()225431x y +=,即2225361x y +=,即为曲线C 的方程. 故选:A . 【点睛】考查平面直角坐标系的伸缩变换,题目较为简单. 伸缩变换:设点(,)P x y 是平面直角坐标系中的任意一点,在变换,(0):,(0)x x y y λλϕμμ'=⋅>⎧⎨'=⋅>⎩的作用下,点(,)P x y 对应到点(,)P x y ''',称ϕ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换. 6.A解析:A 【分析】求出圆C 的圆心坐标为(2,0),由圆C 经过点6P π⎛⎫⎪⎝⎭,得到圆C 过极点,由此能求出圆C 的极坐标方程. 【详解】在sin 4πρθ⎛⎫+= ⎪⎝⎭0θ=,得2ρ=, 所以圆C 的圆心坐标为(2,0). 因为圆C 经过点6P π⎛⎫⎪⎝⎭,,所以圆C 的半径2r =,于是圆C 过极点,所以圆C 的极坐标方程为4cos ρθ=. 故选A 【点睛】本题考查圆的极坐标方程的求法,考查直角坐标方程、参数方程、极坐标方程的互化等基础知识,考查运算求解能力,考查函数与方程思想,属于中档题.7.C解析:C 【解析】 【分析】先化,P Q 两点的球坐标化为直角坐标,再利用两点间距离公式求解 【详解】将,P Q 两点的球坐标化为直角坐标,得,4242P Q -⎝⎭⎝⎭,所以||PQ ==故选:C 【点睛】本题考查球坐标与直角坐标的转化,考查距离公式,是基础题8.C解析:C 【解析】 【分析】利用cos ,sin x y ρθρθ==,将直线的直角坐标方程转化为极坐标方程,并利用辅助角公式进行化简,由此得出正确选项. 【详解】因为cos sin 2 sin 06x πρθθρθ⎛⎫=+= ⎪⎝⎭,所以l 的极坐标方程为 sin 62πρθ⎛⎫+= ⎪⎝⎭.故选C. 【点睛】本小题主要考查直角坐标方程化为极坐标方程,考查三角函数辅助角公式,属于基础题.9.B解析:B 【解析】 【分析】将方程5sin ρθθ=-化为直角坐标方程,然后求出该方程关于极轴对称的方程,再转化为极坐标方程即可. 【详解】 ∵5sin ρθθ=-,∴2cos 5sin ρθρθ=-,将222,?,?x y cos x sin y ρρθρθ=+==代入上式,得225x y y +=-,∴曲线关于极轴对称的曲线C 的直角坐标方程为225x y y +=+,化为极坐标方程为5sin ρθθ=+,即ρ=θ+5sin θ=10co πs 6θ⎛⎫- ⎪⎝⎭. 故选B . 【点睛】(1)进行极坐标方程与直角坐标方程互化的关键是抓住互化公式:x =ρcos θ,y =ρsin θ,ρ2=x 2+y 2,ytan xθ=(x ≠0). (2)进行极坐标方程与直角坐标方程互化时,要注意ρ,θ的取值范围及其影响;要善于对方程进行合理变形,并重视公式的逆向与变形使用;要灵活运用代入法和平方法等技巧.10.B解析:B 【解析】 【分析】分别将曲线1C ,2C 的极坐标方程化为普通方程,根据直线与圆相交,利用点到直线的距离公式结合垂径定理,可得结果 【详解】 根据题意, 曲线()222221:22cos 211C cos x y xx y ρθρρθ==+=-+=曲线2:4C y x πθ==,则直线与圆相交,圆的半径为1,圆心到直线y x =的距离为d ==设AB 长为m ,则有22212m d r ⎛⎫+= ⎪⎝⎭,即211142m +=解得m =(舍负)故线段AB 故选B 【点睛】本题主要考查的是极坐标与直角坐标方程的互化,圆的方程以及直线与圆的位置关系,是一道基础题11.A解析:A 【解析】将直线cos 4πρθ⎛⎫-= ⎪⎝⎭22x y +=20x y +-=;将圆ρ=化为直角坐标方程为222x y +=,其圆心坐标为()0,0又圆心()0,0到直线20x y +-=的距离为d ==所以直线20x y +-=与圆222x y +=相切,所以直线cos 4πρθ⎛⎫-= ⎪⎝⎭ρ只有一个公共点.故选A .12.C解析:C 【分析】分析:把参数方程化为普通方程,把极坐标方程化为直角坐标方程,利用直线与圆相交的弦长处理方法计算.详解:曲线21x ty t =-⎧⎨=-+⎩的普通方程为10x y +-=,曲线ρ=228x y +=,圆心O 到直线的距离为d ==r =∴BC ==C . 点睛:直线与圆相交的弦长有两种方法:一是代数方法,一是几何方法,代数法就是由直线与圆方程联立方程组解得交点坐标,再由两点间距离公式求得弦长,常用的是几何方法:用垂径定理,即求出圆心到直线的距离d ,则弦长l =二、填空题13.【解析】直线的直角坐标方程为点的直角坐标为所以点到直线的距离为解析:2【解析】直线l 的直角坐标方程为1y x -= ,点A 的直角坐标为(2,2)- ,所以点A 到直线l 的距离522. 14.或【分析】把圆方程化为极坐标方程设对应的极径是用表示出则由此计算可得结论【详解】由题意圆的一般方程为化为极坐标方程将代入得成立设对应的极径是则∴∴∴(舍去)又∴或∴或故答案为:或【点睛】本题考查直角解析:12π或512π【分析】把圆方程化为极坐标方程,设,,A B P 对应的极径是120,,ρρρ,用α表示出12,ρρ,则12AB ρρ=-,122OP ρρ+=,由此计算可得结论.【详解】由题意圆的一般方程为222210x y x y +--+=,化为极坐标方程22(cos sin )10ρρθθ-++=,将θα=代入得22(cos sin )10ρραα-++=,24(cos sin )40αα∆=+->成立, 设,,A B P 对应的极径是120,,ρρρ,则122(cos sin )ρραα+=+,121ρρ=,∴120cos sin 2ρρραα+==+,∴AB 12ρρ=-===0cos )AB OP ραα==+=4sin 2(1sin 2)3αα+=,(2sin 21)(2sin 23)0αα-+=,∴1sin 22α=(32-舍去), 又(0,)2πα∈,∴26πα=或526πα=.∴12πα=或512πα=. 故答案为:12π或512π. 【点睛】本题考查直角坐标方程与直角坐标方程的互化,考查极坐标的应用,以极点为顶点的射线上两点,A B 对应的极径是12,ρρ,则12AB ρρ=-,线段AB 中点对应的极径为122ρρ+.15.【分析】求出圆心的直角坐标写出圆的直角坐标方程再利用转化成极坐标方程【详解】由题:圆心为直角坐标为所以圆的标准方程:化简得:所以其极坐标方程为:故答案为:【点睛】此题考查曲线直角坐标方程与极坐标方程解析:3sin ρθθ=+【分析】求出圆心的直角坐标,写出圆的直角坐标方程,再利用cos ,sin x y ρθρθ==转化成极坐标方程. 【详解】由题:圆心为(3,)6C π,直角坐标为0033cos 3sin 662x y ππ====,所以圆C 的标准方程:223(()92x y +-=,化简得:2230x y y +--=,cos ,sin x y ρθρθ==,2cos 3sin ρθρθ=+,所以其极坐标方程为:3sin ρθθ=+.故答案为:3sin ρθθ=+【点睛】此题考查曲线直角坐标方程与极坐标方程之间的互相转化,通过几何关系转化固然轻松,当几何关系寻找比较困难时,考虑直角坐标与极坐标的直接代换,虽计算量稍大,但通式通法一定能求解.16.【解析】【分析】首先将极坐标化为直角坐标然后利用弦长公式求弦长即可【详解】直线的极坐标方程化为直角坐标方程即:曲线的极坐标方程化为直角坐标方程即:则圆心到直线的距离:由弦长公式可得弦长为:【点睛】本【解析】【分析】首先将极坐标化为直角坐标,然后利用弦长公式求弦长即可.【详解】直线sin cos 1ρθρθ-=的极坐标方程化为直角坐标方程即:10x y -+=,曲线1ρ=的极坐标方程化为直角坐标方程即:221x y +=,则圆心到直线的距离:d ==== 【点睛】 本题主要考查极坐标与直角坐标的互化,圆想弦长公式及其应用等知识,意在考查学生的转化能力和计算求解能力.17.【分析】先利用直角坐标与极坐标间的关系即利用ρcosθ=xρsinθ=y 进行代换将极坐标化成直角坐标再在直角坐标系中算出两点间的距离即可【详解】根据x=ρcosθy=ρsinθ点的直角坐标为:故答案解析:【分析】先利用直角坐标与极坐标间的关系,即利用ρcosθ=x ,ρsinθ=y ,进行代换将极坐标化成直角坐标,再在直角坐标系中算出两点间的距离即可.【详解】根据x=ρcosθ,y=ρsinθ,点52,,4,66A B ππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,的直角坐标为:A B AB -∴==),(), ,故答案为【点睛】本题考查点的极坐标和直角坐标的互化,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,本题解题的关键是能进行极坐标和直角坐标的互化.18.【解析】分析:由题意结合三角形面积公式整理计算即可求得三角形的面积详解:的面积点睛:本题主要考查三角形面积公式的应用极坐标的几何意义等知识意在考查学生的转化能力和计算求解能力【解析】分析:由题意结合三角形面积公式整理计算即可求得三角形的面积.详解:OAB 的面积11sin 12232OAB S OA OB π=⨯⨯⨯=⨯⨯= 点睛:本题主要考查三角形面积公式的应用,极坐标的几何意义等知识,意在考查学生的转化能力和计算求解能力.19.2【解析】由曲线C2的方程为p (cosθ﹣sinθ)+1=0∴x ﹣y+1=0即y=x+1;将曲线C1的参数方程化为普通方程为∴消去y 整理得:7x2+8x ﹣8=0△>0∴此方程有两个不同的实根故C1与解析:2【解析】由曲线C 2的方程为p (cosθ﹣sinθ)+1=0,∴x ﹣y+1=0.即y=x+1;将曲线C 1的参数方程化为普通方程为22143x y +=. ∴消去y 整理得:7x 2+8x ﹣8=0.△>0,∴此方程有两个不同的实根,故C 1与C 2的交点个数为2.故答案为2.点睛:这个题目考查的是直线和曲线的交点个数的判断问题;一般直线和椭圆,直接联立判△>0则由两个交点,△<0无交点,△=0,只有一个交点.直线和双曲线则数形结合的情况较多,比较直线和双曲线的渐近线的斜率,从而得到交点个数.20.【解析】设是直线上任意一点如图由于所以应填答案解析:cos ρθ【解析】设(,)M ρθ是直线上任意一点,如图,由于2222OH =⨯=,所以cos 2OH ρθ==,应填答案cos 2ρθ=。
(完整版)哈工大选修课LINEARALGEBRA试卷及答案,推荐文档

LINEAR ALGEBRAANDITS APPLICATIONS 姓名:易学号:成绩:1. Definitions(1) Pivot position in a matrix;(2) Echelon Form;(3) Elementary operations;(4) Onto mapping and one-to-one mapping;(5) Linearly independence.2. Describe the row reduction algorithm which produces a matrix in reduced echelon form.3. Find the matrix that corresponds to the composite transformation of a scaling by 0.3, 33⨯a rotation of , and finally a translation that adds (-0.5, 2) to each point of a figure.90︒4. Find a basis for the null space of the matrix361171223124584A ---⎡⎤⎢⎥=--⎢⎥⎢⎥--⎣⎦5. Find a basis for Col of the matrixA 1332-9-2-22-822307134-111-8A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦6. Let and be positive numbers. Find the area of the region bounded by the ellipse a b whose equation is22221x y a b +=7. Provide twenty statements for the invertible matrix theorem.8. Show and prove the Gram-Schmidt process.9. Show and prove the diagonalization theorem.10. Prove that the eigenvectors corresponding to distinct eigenvalues are linearly independent.Answers:1. Definitions(1) Pivot position in a matrix:A pivot position in a matrix A is a location in A that corresponds to a leading 1 in the reduced echelon form of A. A pivot column is a column of A that contains a pivot position.(2) Echelon Form:A rectangular matrix is in echelon form (or row echelon form) if it has the following three properties:1. All nonzero rows are above any rows of all zeros.2. Each leading entry of a row is in a column to the right of the leading entry of the row above it.3. All entries in a column below a leading entry are zeros.If a matrix in a echelon form satisfies the following additional conditions, then it is in reduced echelon form (or reduced row echelon form):4. The leading entry in each nonzero row is 1.5. Each leading 1 is the only nonzero entry in its column.(3) Elementary operations:Elementary operations can refer to elementary row operations or elementary column operations.There are three types of elementary matrices, which correspond to three types of row operations (respectively, column operations):1. (Replacement) Replace one row by the sum of itself anda multiple of another row.2. (Interchange) Interchange two rows.3. (scaling) Multiply all entries in a row by a nonzero constant.(4) Onto mapping and one-to-one mapping:A mapping T : R n → R m is said to be onto R m if each b in R m is the image of at least one x in R n.A mapping T : R n → R m is said to be one-to-one if each b in R m is the image of at most one x in R n.(5) Linearly independence:An indexed set of vectors {V1, . . . ,V p} in R n is said to be linearly independent if the vector equationx 1v 1+x 2v 2+ . . . +x p v p = 0Has only the trivial solution. The set {V 1, . . . ,V p } is said to be linearly dependent if there exist weights c 1, . . . ,c p , not all zero, such thatc 1v 1+c 2v 2+ . . . +c p v p = 02. Describe the row reduction algorithm which produces a matrix in reduced echelon form.Solution:Step 1:Begin with the leftmost nonzero column. This is a pivot column. The pivot position is at the top.Step 2:Select a nonzero entry in the pivot column as a pivot. If necessary, interchange rows to move this entry into the pivot position.Step 3:Use row replacement operations to create zeros in all positions below the pivot.Step 4:Cover (or ignore) the row containing the pivot position and cover all rows, if any, above it. Apply steps 1-3 to the submatrix that remains. Repeat the process until there all no more nonzero rows to modify.Step 5:Beginning with the rightmost pivot and working upward and to the left, create zeros above each pivot. If a pivot is not 1, make it 1 by scaling operation.3. Find the matrix that corresponds to the composite transformation of a scaling by 0.3, 33⨯a rotation of , and finally a translation that adds (-0.5, 2) to each point of a figure.90︒Solution:If ψ=π/2, then sin ψ=1 and cos ψ=0. Then we have⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−−→−⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡110003.00003.01y x y x scale ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-−−→−110003.00003.010*******y x Rotate⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-−−−→−110003.00003.0100001010125.0010001y x Translate The matrix for the composite transformation is⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-10003.00003.0100001010125.0010001⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=10003.00003.0125.0001010⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=125.0003.003.004. Find a basis for the null space of the matrix361171223124584A ---⎡⎤⎢⎥=--⎢⎥⎢⎥--⎣⎦Solution:First, write the solution of A X=0 in parametric vector form:A ~ , ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---000023021010002001x 1-2x 2 -x 4+3x 5=0x 3+2x 4-2x 5=00=0The general solution is x 1=2x 2+x 4-3x 5, x 3=-2x 4+2x 5, with x 2, x 4, and x 5 free.⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+--+=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡10203012010001222325425454254254321x x x x x x x x x x x x x x x xu v w=x 2u+x 4v+x 5w (1)Equation (1) shows that Nul A coincides with the set of all linear conbinations of u, v and w. That is, {u, v, w}generates Nul A. In fact, this construction of u, v and w automatically makes them linearly independent, because (1) shows that 0=x 2u+x 4v+x 5w only if the weights x 2, x 4, and x 5 are all zero.So {u, v, w} is a basis for Nul A.5. Find a basis for Col of the matrixA 1332-9-2-22-822307134-111-8A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦Solution:A ~ , so the rank of A is 3.⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---07490012002300130001Then we have a basis for Col of the matrix:A U = , v = and w = ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0001⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0013⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--07496. Let and be positive numbers. Find the area of the region bounded by the ellipse a b whose equation is22221x y a b+=Solution:We claim that E is the image of the unit disk D under the linear transformation Tdetermined by the matrix A=, because if u= , x=, and x = Au, then ⎥⎦⎤⎢⎣⎡b a 00⎥⎦⎤⎢⎣⎡21u u ⎥⎦⎤⎢⎣⎡21x x u 1 = and u 2 = a x 1bx 2It follows that u is in the unit disk, with , if and only if x is in E , with12221≤+u u1)()(2221≤+x a x . Then we have{area of ellipse} = {area of T (D )}= |det A| {area of D} = ab π(1)2 = πab7. Provide twenty statements for the invertible matrix theorem.Let A be a square matrix. Then the following statements are equivalent. That is, for a n n ⨯given A, the statements are either all true or false.a. A is an invertible matrix.b. A is row equivalent to the identity matrix.n n ⨯c. A has n pivot positions.d. The equation Ax = 0 has only the trivial solution.e. The columns of A form a linearly independent set.f. The linear transformation x Ax is one-to-one.→g. The equation Ax = b has at least one solution for each b in R n .h. The columns of A span R n .i. The linear transformation x Ax maps R n onto R n .→j. There is an matrix C such that CA = I.n n ⨯k. There is an matrix D such that AD = I.n n ⨯l. A T is an invertible matrix.m. If , then 0A ≠()()T11T A A --=n. If A, B are all invertible, then (AB)* = B *A *o. T**T )(A )(A =p. If , then 0A ≠()()*11*A A--=q. ()*1n *A 1)(A --=-r. If , then ( L is a natural number )0A ≠()()L 11L A A--=s. ()*1n *A K)(KA --=-t. If , then 0A ≠*1A A1A =-8. Show and prove the Gram-Schmidt process.Solution:The Gram-Schmidt process:Given a basis {x 1, . . . , x p } for a subspace W of R n , define11x v = 1112222v v v v x x v ⋅⋅-= 222231111333v v v v x v v v v x x v ⋅⋅-⋅⋅-=. ..1p 1p 1p 1p p 2222p 1111p p p v v v v x v v v v x v v v v x x v ----⋅-⋅⋅⋅-⋅⋅-⋅⋅-=Then {v 1, . . . , v p } is an orthogonal basis for W. In additionSpan {v 1, . . . , v p } = {x 1, . . . , x p } for pk ≤≤1PROOFFor , let W k = Span {v 1, . . . , v p }. Set , so that Span {v 1} = Span p k ≤≤111x v ={x 1}.Suppose, for some k < p, we have constructed v 1, . . . , v k so that {v 1, . . . , v k } is an orthogonal basis for W k . Define1k w 1k 1k x proj x v k +++-=By the Orthogonal Decomposition Theorem, v k+1 is orthogonal to W k . Note that proj Wk x k+1 is in W k and hence also in W k+1. Since x k+1 is in W k+1, so is v k+1 (because W k+1 is a subspace and is closed under subtraction). Furthermore, because x k+1 is not in W k = Span {x 1, . . . , 0v 1k ≠+x p }. Hence {v 1, . . . , v k } is an orthogonal set of nonzero vectors in the (k+1)-dismensional space W k+1. By the Basis Theorem, this set is an orthogonal basis for W k+1. Hence W k+1 = Span {v 1, . . . , v k+1}. When k + 1 = p, the process stops.9. Show and prove the diagonalization theorem.Solution:diagonalization theorem:If A is symmetric, then any two eigenvectors from different eigenspaces are orthogonal.PROOFLet v 1 and v 2 be eigenvectors that correspond to distinct eigenvalues, say,and . To 1λ2λshow that , compute0v v 21=⋅ Since v 1 is an eigenvector2T 12T 11211v )(Av v )v (λv v λ==⋅()()2T 12T T 1Av v v A v ==)(221v v Tλ= 2122T 12v v λv v λ⋅==Hence , but , so ()0v v λλ2121=⋅-()0λλ21≠-0v v 21=⋅10. Prove that the eigenvectors corresponding to distinct eigenvalues are linearly independent.Solution:If v 1, . . . , v r are eigenvectors that correspond to distinct eignvalues λ1, . . . , λr of an n n ⨯matrix A.Suppose {v 1, . . . , v r } is linearly dependent. Since v 1 is nonzero, Theorem, Characterization of Linearly Dependent Sets, says that one of the vectors in the set is linear combination of the preceding vectors. Let p be the least index such that v p +1 is a linear combination of he preceding (linearly independent) vectors. Then there exist scalars c 1, . . . ,c p such that (1)1p p p 11v v c v c +=+⋅⋅⋅+Multiplying both sides of (1) by A and using the fact that Av k = λk v k for each k, we obtain111+=+⋅⋅⋅+p p p Av Av c Av c (2)11111++=+⋅⋅⋅+p p p p p v v c v c λλλMultiplying both sides of (1) by and subtracting the result from (2), we have1+p λ (3)0)()(11111=-+⋅⋅⋅+-++p p p p c v c λλλλSince {v 1, . . . , v p } is linearly independent, the weights in (3) are all zero. But none of the factors are zero, because the eigenvalues are distinct. Hence for i = 1, . . . , p.1+-p i λλ0=i cBut when (1) says that , which is impossible. Hence {v 1, . . . , v r } cannot be linearly 01=+p v dependent and therefore must be linearly independent.。
大学数学实验智慧树知到答案章节测试2023年黑龙江工程学院

绪论单元测试1.MATLAB是matrix&laboratory两个词的组合,意为矩阵工厂(矩阵实验室)。
()A:错B:对答案:B2.MATLAB和、c语音并称为三大数学软件。
()A:对B:错答案:B3.MATLAB的基本数据单位是矩阵.( )A:对B:错答案:A4.matlab的优点有以下哪些?( )A:高效的数值计算及符号计算功能,能使用户从繁杂的数学运算分析中解脱出来;B:具有完备的图形处理功能,实现计算结果和编程的可视化;C:友好的用户界面及接近数学的自然化语言,使学者易于学习和掌握;D:功能丰富的应用工具箱(如信号处理工具箱、通信工具箱等) ,为用户提供了大量方便实用的处理工具。
答案:ABCD5.MATLAB只能做高数、线代、概率的计算题,不能做其他的。
()A:对B:错答案:B6.matlab主要应用于以下哪些领域()A:工程计算、控制设计B:信号处理与通讯C:金融建模设计与分析等领域D:图像处理、信号检测答案:ABCD7.本课程仅仅学习了matlab的冰山一角。
()A:对B:错答案:A8.matlab也加入了对C,FORTRAN,C++,JAVA的支持。
()A:对B:错答案:A9.本课程只研究在matlab在高等数学、概率论、线性代数三大学科中的简单应用,姑且把matlab当做一个大型的计算器。
()A:对B:错答案:A10.“mathematica 可能是数学界最好的狙击枪,但MATLAB能给你一座军火库。
“这句话形容了矩阵运算、数据可视化、GUI(用户界面)设计、甚至是连接其他编程语言,MATLAB都能轻松实现。
()A:错B:对答案:B第一章测试1.定义变量的命令为syms ()A:错B:对答案:B2.正弦函数的函数命令为sinx ()A:错B:对答案:A3.余弦函数的函数命令为cos(x) ()A:对B:错答案:A4.matlab不区分输入法的半角和全角()A:对B:错答案:B5.matlab不区分函数命令的大小写()A:对B:错答案:B6.指数函数的函数命令为e^x ()A:对B:错答案:B7.floor(x)是指对x朝-∞方向取整()A:错B:对答案:B8.plot命令可以画离散数据的函数曲线图()A:错B:对答案:B9.ezplot命令可以画连续函数的曲线图()A:对B:错答案:A10.正切函数tanx 可以直接用plot命令画0到pi之间的图形()A:错B:对答案:A第二章测试1.计算极限:()A:-1/exp(1/3)B:1/exp(1/3)C:1D:0答案:B2.计算极限:()A:2B:-1C:1D:0答案:A3.计算极限:()A:INFB:-3/5C:0D:3/5答案:D4.计算极限:()A:-1/3B:0C:1/3D:1答案:C5.计算极限:()A:1B:0C:INFD:-1答案:B6.计算极限:()A:1B:0C:INFD:-1答案:D7.计算极限:()A:INFB:0C:1D:-1答案:B8.计算极限:()A:1/exp(1/3)B:-1/2C:0D:1/2答案:D9.计算极限:( )A:0B:2C:-1D:1答案:A10.计算极限:( )A:1B:-1C:0D:2答案:A第三章测试1.求由参数方程确定的函数的导数。
最新数学理科选修4-4《极坐标》完整版-经典习题及详细答案

数学理科选修4-4第一讲《极坐标》习题一.选择题1.已知⎪⎭⎫ ⎝⎛-3,5πM ,下列所给出的不能表示点的坐标的是( ) A .⎪⎭⎫ ⎝⎛-3,5π B .⎪⎭⎫ ⎝⎛34,5π C .⎪⎭⎫ ⎝⎛-32,5π D .⎪⎭⎫ ⎝⎛--35,5π2.点()3,1-P ,则它的极坐标是( ) A .⎪⎭⎫ ⎝⎛3,2π B .⎪⎭⎫ ⎝⎛34,2π C .⎪⎭⎫ ⎝⎛-3,2π D .⎪⎭⎫ ⎝⎛-34,2π3.极坐标方程⎪⎭⎫⎝⎛-=θπρ4cos 表示的曲线是( ) A .双曲线 B .椭圆 C .抛物线 D .圆4.圆)sin (cos 2θθρ+=的圆心坐标是( )A .⎪⎭⎫ ⎝⎛4,1π B .⎪⎭⎫ ⎝⎛4,21π C .⎪⎭⎫ ⎝⎛4,2π D .⎪⎭⎫⎝⎛4,2π5.在极坐标系中,与圆θρsin 4=相切的一条直线方程为( ) A .2sin =θρ B .2cos =θρ C .4cos =θρ D .4cos -=θρ6、 已知点()0,0,43,2,2,2O B A ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛--ππ则ABO ∆为( ) A 、正三角形 B 、直角三角形 C 、锐角等腰三角形 D 、直角等腰三角形 7、)0(4≤=ρπθ表示的图形是( )A .一条射线B .一条直线C .一条线段D .圆8、直线αθ=与1)cos(=-αθρ的位置关系是( )A 、平行B 、垂直C 、相交不垂直D 、与有关,不确定9.两圆θρcos 2=,θρsin 2=的公共部分面积是( ) A.214-πB.2-πC.12-πD.2π10.已知点1P 的球坐标是)4,,32(1πϕP ,2P 的柱坐标是)1,,5(2θP ,求21P P .A .2B .3C .22D .22二.填空题11.极坐标方程52sin 42=θρ化为直角坐标方程是12.圆心为⎪⎭⎫⎝⎛6,3πC ,半径为3的圆的极坐标方程为 13.已知直线的极坐标方程为22)4sin(=+πθρ,则极点到直线的距离是 14、在极坐标系中,点P ⎪⎭⎫⎝⎛611,2π到直线1)6sin(=-πθρ的距离等于____________。
黑龙江省哈尔滨工业大学附中2024-2025学年八年级上学期9月月考物理试题

黑龙江省哈尔滨工业大学附中2024-2025学年八年级上学期9月月考物理试题一、单选题1.刻度尺是实验室中常用的一种测量工具,它用来测量()A.时间B.温度C.长度D.质量2.如图所示,小明正跑着下电扶梯。
旁边有人提醒道:“这样很危险,乘电扶梯时应该站着不动。
”这里“站着不动”是相对于()A.商场里的地面B.人所站的阶梯C.展柜里的商品D.迎面而上的乘客3.如图所示声波的波形图,下列说法正确的是A.乙、丁的响度和音色相同B.甲、丁的音调和响度相同C.甲、乙的音调和响度相同D.丙、丁的音色和响度相同4.小李同学在校园运动会上,参加了初中男子组50m短跑比赛。
他正常完成比赛所用的时间可能为()A.0.8s B.8s C.8min D.8h5.对于匀速直线运动,下列说法中正确的是()A.物体运动的速度越大,通过的路程越长B.物体运动的速度越大,所用的时间越少C.物体运动的速度与路程成正比,与时间成反比D.速度的大小不变,与路程和时间无关6.“复兴号”高速列车正在平直的轨道上匀速行驶,下图中的四个图像能反映列车在做匀速直线运动的是()A.B.C.D.7.对于声音的产生,下列说法正确的是A.只有固体的振动才能发声B.声音是由物体的振动产生的C.物体不振动也能发声D.振动停止后,发声体仍能发声8.北宋沈括在他的著作《梦溪笔谈》中提到:行军宿营,士兵枕着皮制的箭筒睡在地上,可尽早听到来袭敌人的马蹄声。
这样做能尽早听到马蹄声的主要原因是()A.声音在土地中传播的速度比在空气中快B.使马蹄声的音调变高了C.改变了马蹄声的音色D.提高了士兵的听力9.目前,全球的气候均在变暖,近150年来,全球平均气温升高了1℃,这个数字在气象学上是个不可忽视的大数字。
对这种现象,有些科学家认为:可能是由于大量排放二氧化碳而造成的温室效应。
科学家提出这种观点是属于科学探究中的()A.猜想与假设B.提出问题C.进行实验与收集证据D.得出结论、作出解释10.甲、乙两列火车在平直铁轨上匀速前进,它们行驶的路程比是3℃1,所用的时间比是2℃3,则两列车行驶的速度比是()A.9℃8B.8℃9C.9℃2D.2℃111.下列几种估测最符合实际情况的是()A.人步行的速度约为5m/s B.全新的2B铅笔长约18cmC.人心脏跳动一次的时间大约1min D.一张试卷的厚度大约1cm12.琵琶演奏者通过按住琴弦的不同位置来改变声音的()A.响度B.音调C.音色D.速度二、多选题13.声音在某些介质中的传播速度如表所示,分析表格信息,关于声速推断正确的是()A.声速大小与介质有关B.声速大小与温度有关C.声音在固体中的传播速度一定比在液体中快D.声音从空气传到水中,它的传播速度将变慢14.如图所示,图甲是小车甲运动的s t-图象,图乙是小车乙运动的v t-图象。
自动控制原理课件(哈工大)自测题答案
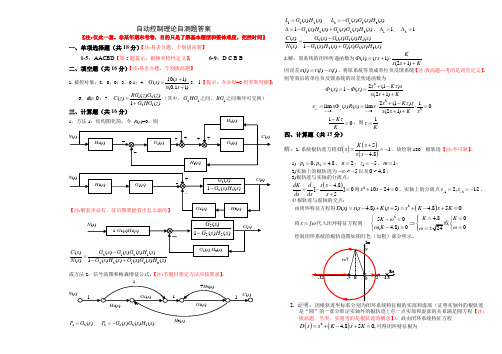
一、单项选择题(共18分)【注:易丢分题,个别拔高题】1-5:AACBD 【第5题提示:据频率特性定义】; 6-9:D C B B 二、填空题(共16分)【注:易丢分题,个别拔高题】1.被控对象;2.0,0;3.0.1;4.10(1)()(0.11)s G s s s +=+5.1【提示:令分母=0用劳斯判据】;6.0=e ;7.1221()()()1()RG z G z C z G HG z =+(其中,21G HG 之间、1RG 之间顺序可交换)三、计算题(共16分)22123()()C s N s122()()L G s H s =, 2123()()()L G s G s H s =-221231()()()()()G s H s G s G s H s ∆=-+,11∆=, 21∆=212122123()()()()()()1()()()()()G s G s G s H s C s N s G s H s G s G s H s -=-+ 2.解:原系统的闭环传递函数为()(1)(21)Ks s s s KΦτ=+⋅++因误差)()()(t c t r t e -=,将原系统等效成单位负反馈系统【注:拔高题---考的是误差定义】,则等效后的单位负反馈系统的误差传递函数为22(1)()1()(21)e s K ss s s s KτΦΦ+-=-=++22002(1)1lim ()()lim 0(21)ss e s s s K s e s s R s s s s K s τ→→+-=Φ=⋅⋅=++10K K τ-=,则1Kτ= 四、计算题(共15分) 解:1.系统根轨迹方程()()()514.8K s G s s s +==--,故绘制180°根轨迹【注:不可缺】。
1) 120, 4.8p p ==,2n =;15z =-,1m =; 2)实轴上的根轨迹为~5-∞-以及0~4.8;3)根轨迹与实轴的分离点:()4.8[]05s s dK dds ds s -=-=+则210240s s +-=,实轴上的分离点122,12x x s s ==-。
2022年黑龙江省哈尔滨工业大学附属中学校高二学业水平测试数学练习试题(1)

一、单选题二、多选题1. 已知抛物线的焦点为,准线为,为上一点,过作的垂线,垂足为. 若,则( )A.B.C.D.2. 已知数列是递减的等比数列,的前项和为,若,,则=( )A .54B .36C .27D .183. 互相垂直且有公共原点的两条数轴构成平面直角坐标系,但如果平面坐标系中两条坐标轴不垂直,则这样的坐标系称为“斜坐标系”.如图,在斜坐标系中,过点作两坐标轴的平行线,其在轴和轴上的截距,分别作为点的坐标和坐标,记.若斜坐标系中,轴正方向和轴正方向的夹角为,则该坐标系中和两点间的距离为()A .2B .1C.D.4.已知函数,则的一个充分不必要条件是( ).A.B.C .3D.5. 如图甲(左),圣索菲亚教堂是哈尔滨的标志性建筑,其中央主体建筑集球、圆柱、棱柱于一体,极具对称之美.为了估算索菲亚教堂的高度,在索菲亚教堂的正东方向找到一座建筑物,高约为40,如图乙(右),在它们之间的地面上的点(三点共线)处测得楼顶、教堂顶的仰角分别是和,在楼顶处测得塔顶的仰角为,则估算索菲亚教堂的高度约为()A .50B .55C .60D .706. 下列函数中,既是偶函数又在上单调递增的函数是A.B.C.D.7. 已知定义在上的函数,满足,函数的图象关于点中心对称,对于任意、,,都有成立.则的解集为( )A.B.C.D.8. 从一批含有13件正品,2件次品的产品中不放回地抽3次,每次抽取1件,设抽取的次品数为ξ,则E (5ξ+1)=( )A .2B .1C .3D .49. 某城市为吸引和留住人才,推出“共有产权房”政策,由政府出资30%(1~4级人才)或20%(5~7级人才)垫付首付,支持高层次人才到本区购房落户.以下是某小区5套共有产权房成交价格y (单位:万元)与住房面积x (单位:m 2)之间的统计数据(成交价格受面积、楼层、位置等因素影响)2022年黑龙江省哈尔滨工业大学附属中学校高二学业水平测试数学练习试题(1)2022年黑龙江省哈尔滨工业大学附属中学校高二学业水平测试数学练习试题(1)三、填空题四、解答题面积x /m 28095105110125价格y /万元120142161171186若y 与x 之间具有线性相关关系,根据表中数据可求得y 关于x 的回归方程为,则下列说法正确的是( )A.B .变量x 与y 具有负相关关系C .当住房面积增加1m 2时,其价格增加约0.98万元D .根据回归方程估计,若住房面积为150m 2,则成交价格约为202万元10. 已知,,,四点在球心为,半径为5的球面上,且满足,,设,的中点分别为,,则( )A .点有可能在上B.线段的长有可能为7C.四面体的体积的最大值为20D.四面体的体积的最大值为5611.质点和同时出发,在以原点为圆心,半径为的上逆时针作匀速圆周运动.的角速度大小为,起点为与轴正半轴的交点;的角速度大小为,起点为射线与的交点.则当与重合时,的坐标可以为( )A.B.C.D.12.已知函数,则( )A.函数的图象关于点对称B .函数在区间上单调递增C.函数的图象向左平移个单位长度所得到的图象所对应的函数为偶函数D .函数在区间上恰有3个零点13. 已知,则______.14. 已知椭圆与双曲线有公共的焦点,为右焦点,为坐标原点,双曲线的一条渐近线交椭圆于点,且点在第一象限,若,则椭圆的离心率等于_________.15. 袋中有6个大小相同的球,其中1个红球,m 个白球,n 个黑球,现依次取球,每次取出一个,取出不放回,直到取出的球中有两种不同颜色的球时结束,已知取到1个红球1个白球的概率为,则__________,用表示终止时取球的次数,则随机变量的数学期望__________.16. 已知函数满足,且函数与函数互为反函数.(1)求函数、解析式;(2)函数在上有零点,求实数的取值范围.17. 随着新高考改革的不断深入,高中学生生涯规划越来越受到社会的关注.一些高中已经开始尝试开设学生生涯规划选修课程,并取得了一定的成果.下表为某高中为了调查学生成绩与选修生涯规划课程的关系,随机抽取50名学生的统计数据.成绩优秀成绩不够优秀总计选修生涯规划课151025不选修生涯规划课61925总计212950(Ⅰ)根据列联表运用独立性检验的思想方法分析:能否有的把握认为“学生的成绩是否优秀与选修生涯规划课有关”,并说明理由;(Ⅱ)如果从全校选修生涯规划课的学生中随机地抽取3名学生,求抽到成绩不够优秀的学生人数的分布列和数学期望(将频率当作概率计算).参考附表:0.1000.0500.0100.0012.7063.841 6.63510.828参考公式,其中.18. 已知中的三个内角A,B,C所对的边分别为a,b,c,角B为钝角,且.(1)求角B的大小;(2)若点D在AC边上,满足,且,,求BC边的长.19. 某乡镇在实施乡村振兴的进程中,大力推广科学种田,引导广大农户种植优良品种,进一步推动当地农业发展,不断促进农业增产农民增收.为了解某新品种水稻品种的产量情况,现从种植该新品种水稻的不同自然条件的田地中随机抽取400亩,统计其亩产量x(单位:吨(t)).并以此为样本绘制了如图所示的频率分布直方图.(1)求这400亩水稻平均亩产量的估计值(同一组中的数据用该组区间的中点值代表,精确到小数点后两位);(2)若这400亩水稻的灌溉水源为河水和井水,现统计了两种水源灌溉的水稻的亩产量,并得到下表:亩产量超过0.7t 亩产量不超过0.7t合计河水灌溉18090270井水灌溉7060130合计250150400能否有95%的把握认为亩产量与所用灌溉水源相关?0.1000.0500.0100.001k0 2.706 3.841 6.63510.828附:.20. 某省农科院为支持省政府改善民生,保证冬季蔬菜的市场供应举措,深入开展了反季节蔬菜的相关研究,其中一项是冬季大棚内的昼夜温差x(℃)与反季节蔬菜种子发芽数y(个)之间的关系,经过一段时间观测,获得了下列一组数据(y值为观察值):温差x(℃)89101112发芽数y(个)2324262730(1)在所给坐标系中,根据表中数据绘制散点图,并判断y与x是否具有明显的线性相关关系(不需要说明理由);(2)用直线l的方程来拟合这组数据的相关关系,若直线l过散点图中的中间点(即点(10,26)),且使发芽数的每一个观察值与直线l上对应点的纵坐标的差的平方之和最小,求出直线l的方程;(3)用(2)中求出的直线方程预测当温度差为15℃时,蔬菜种子发芽的个数.21. 某研究小组在电脑上进行人工降雨模拟实验,准备用A、B、C三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其实验数据统计如下:方式实施地点大雨中雨小雨模拟实验总次数A甲4次6次2次12次B乙3次6次3次12次C丙2次2次8次12次假定对甲、乙、丙三地实施的人工降雨彼此互不影响,请你根据人工降雨模拟实验的统计数据:(1)求甲、乙、丙三地都恰为中雨的概率;(2)考虑到旱情和水土流失,如果甲地恰需中雨或小雨即达到理想状态,乙地必须是大雨才达到理想状态,丙地只要是大雨或中雨即达到理想状态,记“甲、乙、丙三地中达到理想状态的个数”为随机变量X,求随机变量X的分布列和均值E(X).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
LINEAR ALGEBRAANDITS APPLICATIONS 姓名:易学号:成绩:1. Definitions(1) Pivot position in a matrix;(2) Echelon Form;(3) Elementary operations;(4) Onto mapping and one-to-one mapping;(5) Linearly independence.2. Describe the row reduction algorithm which produces a matrix in reduced echelon form.3. Find the matrix that corresponds to the composite transformation of a scaling by 0.3, 33⨯a rotation of , and finally a translation that adds (-0.5, 2) to each point of a figure.90︒4. Find a basis for the null space of the matrix 361171223124584A ---⎡⎤⎢⎥=--⎢⎥⎢⎥--⎣⎦5. Find a basis for Col of the matrixA 1332-9-2-22-822307134-111-8A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦6. Let and be positive numbers. Find the area of the region bounded by the ellipse a b whose equation is22221x y a b +=7. Provide twenty statements for the invertible matrix theorem.8. Show and prove the Gram-Schmidt process.9. Show and prove the diagonalization theorem.10. Prove that the eigenvectors corresponding to distinct eigenvalues are linearly independent.Answers:1. Definitions(1) Pivot position in a matrix:A pivot position in a matrix A is a location in A that corresponds to a leading 1 in the reduced echelon form of A. A pivot column is a column of A that contains a pivot position.(2) Echelon Form:A rectangular matrix is in echelon form (or row echelon form) if it has the following three properties:1. All nonzero rows are above any rows of all zeros.2. Each leading entry of a row is in a column to the right of the leading entry of the row above it.3. All entries in a column below a leading entry are zeros.If a matrix in a echelon form satisfies the following additional conditions, then it is in reduced echelon form (or reduced row echelon form):4. The leading entry in each nonzero row is 1.5. Each leading 1 is the only nonzero entry in its column.(3) Elementary operations:Elementary operations can refer to elementary row operations or elementary column operations.There are three types of elementary matrices, which correspond to three types of row operations (respectively, column operations):1. (Replacement) Replace one row by the sum of itself anda multiple of another row.2. (Interchange) Interchange two rows.3. (scaling) Multiply all entries in a row by a nonzero constant.(4) Onto mapping and one-to-one mapping:A mapping T : R n → R m is said to be onto R m if each b in R m is the image of at least one x in R n.A mapping T : R n → R m is said to be one-to-one if each b in R m is the image of at most one x in R n.(5) Linearly independence:An indexed set of vectors {V1, . . . ,V p} in R n is said to be linearly independent if the vector equationx 1v 1+x 2v 2+ . . . +x p v p = 0Has only the trivial solution. The set {V 1, . . . ,V p } is said to be linearly dependent if there exist weights c 1, . . . ,c p , not all zero, such thatc 1v 1+c 2v 2+ . . . +c p v p = 02. Describe the row reduction algorithm which produces a matrix in reduced echelon form.Solution:Step 1:Begin with the leftmost nonzero column. This is a pivot column. The pivot position is at the top.Step 2:Select a nonzero entry in the pivot column as a pivot. If necessary, interchange rows to move this entry into the pivot position.Step 3:Use row replacement operations to create zeros in all positions below the pivot.Step 4:Cover (or ignore) the row containing the pivot position and cover all rows, if any, above it. Apply steps 1-3 to the submatrix that remains. Repeat the process until there all no more nonzero rows to modify.Step 5:Beginning with the rightmost pivot and working upward and to the left, create zeros above each pivot. If a pivot is not 1, make it 1 by scaling operation.3. Find the matrix that corresponds to the composite transformation of a scaling by 0.3, 33⨯a rotation of , and finally a translation that adds (-0.5, 2) to each point of a figure.90︒Solution:If ψ=π/2, then sin ψ=1 and cos ψ=0. Then we have⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−−→−⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡110003.00003.01y x y x scale ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-−−→−110003.00003.010*******y x Rotate⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-−−−→−110003.00003.0100001010125.0010001y x Translate The matrix for the composite transformation is⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-10003.00003.0100001010125.0010001⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=10003.00003.0125.0001010⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=125.0003.003.004. Find a basis for the null space of the matrix361171223124584A ---⎡⎤⎢⎥=--⎢⎥⎢⎥--⎣⎦Solution:First, write the solution of A X=0 in parametric vector form:A ~ , ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---000023021010002001x 1-2x 2 -x 4+3x 5=0x 3+2x 4-2x 5=00=0The general solution is x 1=2x 2+x 4-3x 5, x 3=-2x 4+2x 5, with x 2, x 4, and x 5 free.⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+--+=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡10203012010001222325425454254254321x x x x x x x x x x x x x x x xu v w=x 2u+x 4v+x 5w (1)Equation (1) shows that Nul A coincides with the set of all linear conbinations of u, v and w. That is, {u, v, w}generates Nul A. In fact, this construction of u, v and w automatically makes them linearly independent, because (1) shows that 0=x 2u+x 4v+x 5w only if the weightsx 2, x 4, and x 5 are all zero.So {u, v, w} is a basis for Nul A.5. Find a basis for Col of the matrix A 1332-9-2-22-822307134-111-8A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦Solution:A ~ , so the rank of A is 3.⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---07490012002300130001Then we have a basis for Col of the matrix:A U = , v = and w = ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0001⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0013⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--07496. Let and be positive numbers. Find the area of the region bounded by the ellipse a b whose equation is22221x y a b+=Solution:We claim that E is the image of the unit disk D under the linear transformation Tdetermined by the matrix A=, because if u= , x=, and x = Au, then ⎥⎦⎤⎢⎣⎡b a 00⎥⎦⎤⎢⎣⎡21u u ⎥⎦⎤⎢⎣⎡21x x u 1 =and u 2 = a x 1bx 2It follows that u is in the unit disk, with , if and only if x is in E , with 12221≤+u u1)()(2221≤+x a x . Then we have{area of ellipse} = {area of T (D )}= |det A| {area of D} = ab π(1)2 = πab7. Provide twenty statements for the invertible matrix theorem.Let A be a square matrix. Then the following statements are equivalent. That is, for a n n ⨯given A, the statements are either all true or false.a. A is an invertible matrix.b. A is row equivalent to the identity matrix.n n ⨯c. A has n pivot positions.d. The equation Ax = 0 has only the trivial solution.e. The columns of A form a linearly independent set.f. The linear transformation x Ax is one-to-one.→g. The equation Ax = b has at least one solution for each b in R n .h. The columns of A span R n .i. The linear transformation x Ax maps R n onto R n .→j. There is an matrix C such that CA = I.n n ⨯k. There is an matrix D such that AD = I.n n ⨯l. A T is an invertible matrix.m. If , then 0A ≠()()T11T A A --=n. If A, B are all invertible, then (AB)* = B *A *o. T**T )(A )(A =p. If , then 0A ≠()()*11*A A--=q. ()*1n *A 1)(A --=-r. If , then ( L is a natural number )0A ≠()()L 11L A A--=s. ()*1n *A K)(KA --=-t. If , then 0A ≠*1A A1A =-8. Show and prove the Gram-Schmidt process.Solution:The Gram-Schmidt process:Given a basis {x 1, . . . , x p } for a subspace W of R n , define11x v = 1112222v v v v x x v ⋅⋅-= 222231111333v v v v x v v v v x x v ⋅⋅-⋅⋅-=. ..1p 1p 1p 1p p 2222p 1111p p p v v v v x v v v v x v v v v x x v ----⋅-⋅⋅⋅-⋅⋅-⋅⋅-=Then {v 1, . . . , v p } is an orthogonal basis for W. In additionSpan {v 1, . . . , v p } = {x 1, . . . , x p } for pk ≤≤1PROOFFor , let W k = Span {v 1, . . . , v p }. Set , so that Span {v 1} = Span p k ≤≤111x v ={x 1}.Suppose, for some k < p, we have constructed v 1, . . . , v k so that {v 1, . . . , v k } is an orthogonal basis for W k . Define1k w 1k 1k x proj x v k +++-=By the Orthogonal Decomposition Theorem, v k+1 is orthogonal to W k . Note that proj Wk x k+1 is in W k and hence also in W k+1. Since x k+1 is in W k+1, so is v k+1 (because W k+1 is a subspace and is closed under subtraction). Furthermore, because x k+1 is not in W k = Span {x 1, . . . , 0v 1k ≠+x p }. Hence {v 1, . . . , v k } is an orthogonal set of nonzero vectors in the (k+1)-dismensional space W k+1. By the Basis Theorem, this set is an orthogonal basis for W k+1. Hence W k+1 = Span {v 1, . . . , v k+1}. When k + 1 = p, the process stops.9. Show and prove the diagonalization theorem.Solution:diagonalization theorem:If A is symmetric, then any two eigenvectors from different eigenspaces are orthogonal.PROOFLet v 1 and v 2 be eigenvectors that correspond to distinct eigenvalues, say, and . To 1λ2λshow that , compute0v v 21=⋅ Since v 1 is an eigenvector2T 12T 11211v )(Av v )v (λv v λ==⋅()()2T 12T T 1Av v v A v ==)(221v v Tλ= 2122T 12v v λv v λ⋅==Hence , but , so ()0v v λλ2121=⋅-()0λλ21≠-0v v 21=⋅10. Prove that the eigenvectors corresponding to distinct eigenvalues are linearly independent.Solution:If v 1, . . . , v r are eigenvectors that correspond to distinct eignvalues λ1, . . . , λr of an n n ⨯matrix A.Suppose {v 1, . . . , v r } is linearly dependent. Since v 1 is nonzero, Theorem, Characterization of Linearly Dependent Sets, says that one of the vectors in the set is linear combination of the preceding vectors. Let p be the least index such that v p +1 is a linear combination of he preceding (linearly independent) vectors. Then there exist scalars c 1, . . . ,c p such that (1)1p p p 11v v c v c +=+⋅⋅⋅+Multiplying both sides of (1) by A and using the fact that Av k = λk v k for each k, we obtain111+=+⋅⋅⋅+p p p Av Av c Av c (2)11111++=+⋅⋅⋅+p p p p p v v c v c λλλMultiplying both sides of (1) by and subtracting the result from (2), we have1+p λ (3)0)()(11111=-+⋅⋅⋅+-++p p p p c v c λλλλSince {v 1, . . . , v p } is linearly independent, the weights in (3) are all zero. But none of thefactors are zero, because the eigenvalues are distinct. Hence for i = 1, . . . , p. 1+-p i λλ0=icBut when (1) says that , which is impossible. Hence {v 1, . . . , v r } cannot be linearly 01=+p v dependent and therefore must be linearly independent.。
