回归直线
最小二乘法拟合回归直线的注意事项

最小二乘法是一种常用的回归分析方法,用于拟合一条直线以描述自变量和因变量之间的关系。
在实际应用中,最小二乘法可以帮助我们找到最符合观测数据的线性模型,从而进行预测和分析。
然而,最小二乘法也存在一些注意事项,需要我们在使用时特别留意。
下面将详细介绍最小二乘法拟合回归直线的注意事项。
一、数据的准备在使用最小二乘法拟合回归直线之前,首先需要准备好观测数据。
数据的准备包括收集样本数据、对数据进行清洗和处理,确保数据的准确性和完整性。
还需要对数据进行可视化分析,探索自变量和因变量之间的关系。
只有在数据准备充分的情况下,才能保证最小二乘法的拟合结果具有可靠性和有效性。
二、线性关系的验证在使用最小二乘法进行回归分析时,需要验证自变量和因变量之间是否存上线性关系。
线性关系的验证可以通过散点图、相关系数等统计手段进行分析。
如果自变量和因变量之间呈现非线性关系,那么使用最小二乘法拟合回归直线可能会导致模型拟合不佳,影响数据分析的准确性。
三、异常值的处理在进行最小二乘法拟合回归直线时,需要注意异常值的存在。
异常值可能会对拟合结果产生较大影响,导致模型失真。
需要对异常值进行识别和处理,可以采用箱线图、3σ原则等方法进行异常值的识别,并对异常值进行必要的调整或剔除。
四、多重共线性的检测在多元最小二乘法中,需要特别注意自变量之间是否存在多重共线性。
多重共线性会导致自变量之间存在高度相关性,从而使得最小二乘法的拟合结果不稳定,模型的解释性降低。
需要通过方差膨胀因子(VIF)等方法进行多重共线性的检测,并在必要时进行变量的调整或剔除。
五、残差的验证在进行最小二乘法拟合回归直线后,需要对模型的残差进行验证。
残差是预测值与观测值之间的差异,通过对残差的分析可以检验模型的拟合程度和预测效果。
可以使用残差图、残差分布等方法进行残差的验证,确保模型的残差符合正态分布和独立同分布的假设。
六、模型的解释和评价在使用最小二乘法拟合回归直线后,需要对模型进行解释和评价。
回归直线方程r的求法

回归直线方程r的求法
在统计学和数据分析中,回归分析是一种用来研究变量之间关
系的方法。
其中,线性回归是最简单和最常用的一种回归分析方法。
线性回归的目标是找到一条直线,使得这条直线能够最好地拟合观
测到的数据点。
求解回归直线方程r的方法通常涉及以下步骤:
1. 收集数据,首先需要收集相关的数据,包括自变量(X)和
因变量(Y)的数值。
这些数据可以通过实验、观测或调查获得。
2. 绘制散点图,将收集到的数据绘制成散点图,以便直观地观
察自变量和因变量之间的关系。
3. 确定回归方程,线性回归的目标是找到一条直线,使得所有
数据点到这条直线的距离之和最小。
这可以通过最小二乘法来实现,即通过最小化残差平方和来确定回归方程的系数。
4. 求解回归直线方程,一旦确定了回归方程的系数,就可以得
到回归直线方程r。
一般来说,回归直线方程r的一般形式为,Y =
aX + b,其中a和b分别为回归方程的系数。
5. 拟合直线,最后一步是将回归直线方程r拟合到散点图上,以便评估回归方程对数据的拟合程度。
通过以上步骤,我们可以求解回归直线方程r,并用这条直线来描述自变量和因变量之间的关系。
这样的回归分析可以帮助我们理解变量之间的关系,并用于预测和决策制定。
01第一节 直线回归

【例8.2】 试计算【例8.1】资料回归截距α的95%和99%置信区间。 对于【例8.1】资料,因为 , , , ,
所以,
,
于是总体回归截距α的95%和99%置信区间分别为: [582.1816-2.228×147.3153, 582.1816+2.228×147.3153] [582.1816-3.169×147.3153, 582.1816+3.169×147.3153] 即[253.9631, 910.40]和[115.3394, 1049.0238]。 这说明在研究雏鹅重与70日龄重的关系时,总体回归截距α在 [253.9631,910.40]区间内,其可靠度为95%;在[115.3394, 1049.0238]区间内,其可靠度为99%。
2、总体回归系数β的置信区间 统计学已证明
服从自由度为n-2的t公布,其中,
叫做样本回归系数标准误,由(8-15)式计算。可以导出β的95%、 99%置信区间为:
(8-16)
(8-17) 【例8.3】 求出【例8.1】资料总体回归系数β的95%和99%置信区间。 对于【例8.1】资料,因为 , ,
,
所以总体回归系数β的95%和99%置信区间分别为: [21.7122-2.228×1.4849, 21.7122+2.228×1.4849] [21.7122-3.169×1.4849, 21.7122+3.169×1.4849] 即[18.4038, 25.0206]和[17.0066, 26.4178]。 这说明雏鹅重和70日龄重的总体回归系数β在[18.4038, 25.0206]区间 内,其可靠度为95%;在[17.0066, 26.4178]区间内,其可靠度为99%。
回归直线方程计算
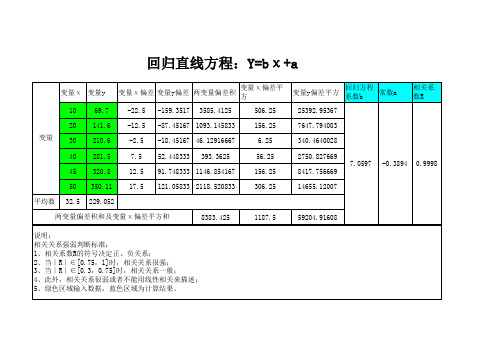
两变量偏差积和及变量χ偏差平方和
说明: 相关关系强弱判断标准: 1、相关系数R的符号决定正、负关系; 2、当∣R∣∈[0.75,1]时,相关关系很强; 3、当∣R∣∈[0.3,0.75]时,相关关系一般; 4、此外,相关关系很弱或者不能用线性相关来描述; 5、绿色区域输入数据,蓝色区域为计算结果。
yba变量变量y变量偏差变量y偏差变量偏差平方变量y偏差平方回归方程系常数a相关系数r两变量偏差积和及变量偏差平方和说明
回归直线方程: 回归直线方程:Y=bχ+a
变量χ 变量y 10 20 变量 30 40 45 50 平均数 32.5 210.6 281.5 320.8 350.11 229.052 8383.425 1187.5 59204.91608 -2.5 7.5 12.5 17.5 -18.45167 46.12916667 52.448333 393.3625 6.25 56.25 156.25 306.25 340.4640028 2750.827669 7.0597 91.748333 1146.854167 121.05833 2118.520833 8417.756669 14655.12007 -0.3894 0.9998 69.7 141.6 变量χ偏差 变量y偏差 两变量偏差积 -22.5 -12.5 -159.3517 3585.4125 变量χ偏差平 方 506.25 156.25 变量y偏差平方 25392.95367 7647.794003 回归方程 常数a 系数b 相关系 数R
直线回归的步骤

直线回归的步骤回归分析是一种用来研究变量之间关系的统计方法,其中最常用的方法是直线回归。
直线回归可以用来描述两个变量之间的线性关系,也可以用来预测一个变量的值。
本文将介绍直线回归的基本概念和步骤。
一、直线回归的基本概念直线回归的基本概念包括自变量、因变量、回归线和残差。
自变量是用来解释因变量的变量,又称为解释变量或独立变量。
因变量是需要解释的变量,又称为被解释变量或依赖变量。
回归线是自变量和因变量之间的最佳拟合直线,可以用来描述两个变量之间的线性关系。
残差是回归线与实际数据之间的差异,也就是预测值与实际值之间的误差。
二、直线回归的步骤直线回归的步骤包括数据收集、数据处理、回归分析和结果解释。
1. 数据收集直线回归的第一步是收集数据。
数据可以通过实验、调查或观察等方式获得。
收集数据时需要注意数据的准确性和可靠性,避免数据的误差和偏差。
2. 数据处理数据处理是指对收集到的数据进行清洗、整理和统计。
数据清洗是指对数据进行筛选和修正,去除异常值和缺失值等。
数据整理是指对数据进行排序和归纳,方便后续的分析和处理。
数据统计是指对数据进行描述性统计和推断性统计,包括均值、方差、标准差、相关系数等指标的计算。
3. 回归分析回归分析是直线回归的核心步骤。
回归分析可以分为简单线性回归和多元线性回归两种类型。
简单线性回归是指只有一个自变量和一个因变量的回归模型,多元线性回归是指有多个自变量和一个因变量的回归模型。
简单线性回归的回归模型可以表示为:Y = a + bX + e其中,Y是因变量,X是自变量,a是截距,b是斜率,e是误差项。
多元线性回归的回归模型可以表示为:Y = a + b1X1 + b2X2 + … + bnXn + e其中,Y是因变量,X1、X2、…、Xn是自变量,a是截距,b1、b2、…、bn是斜率,e是误差项。
回归分析的目的是找到最佳拟合直线,即使得残差最小的直线。
最小二乘法是用来求解最佳拟合直线的一种方法。
回归直线方程公式详解及例题

回归直线方程公式详解及例题回归直线方程,听起来是不是有点严肃?这玩意儿就像是数学里的“小白兔”,看起来很复杂,但其实乍一看也不过是个简单的小家伙。
让咱们聊聊这个直线方程的由来,还有怎么用它解决问题。
说白了,就是用一条直线把一堆数据给“牵”起来,让我们看清楚它们之间的关系。
就像在赶集一样,把各种水果摆成一排,想要了解哪个最受欢迎。
这里,最常见的回归直线方程是y = mx + b。
听起来不算复杂吧?不过咱们慢慢来,不急。
y代表咱们要预测的东西,比如说,你想知道你的成绩和学习时间的关系,那y就可以是你的成绩;x就是你花在学习上的时间。
m,这个家伙叫做斜率,表示的是y和x之间的关系,简单来说就是学习时间每增加一个小时,成绩大概能提高多少分。
b则是当你啥都不做时,你的成绩是多少,这个也很重要,没错,人生不就是这么回事吗?想象一下,拿出一根铅笔和一张纸,把这些点点画出来。
每个点就代表了一次测量,比如说你在不同时间学习的成绩。
画得可真像一幅抽象画,虽然一开始没法看出什么,但如果仔细一看,就能发现某种趋势。
这就是回归分析的魔力,它能帮你找到这些点之间的规律。
慢慢地,这些点就会聚成一条线,给你展示出学习时间和成绩之间的关系。
再来聊聊如何计算这些参数。
有很多软件和工具可以帮你做这些。
但如果你想亲自尝试,手动计算也是个不错的选择。
先得算出这些数据的平均值,接着用这些平均值来计算m和b。
想象一下,m的计算就像是在算你朋友圈里哪个小伙伴总是抢着买单。
搞定这些,y = mx + b就能顺利出炉了。
说到这里,有些小伙伴可能会想,回归直线到底有什么用呢?这玩意儿其实是个超有用的工具。
比如说,商家可以用它预测销量,学校可以分析成绩趋势,甚至天气预报也会用到。
想想看,如果你知道晴天和下雨天的概率,你是不是就能提前决定穿哪双鞋?这不就是让生活更简单吗?回归直线也有它的局限性。
毕竟,生活可不是总那么简单。
数据点就像是小孩子一样顽皮,根本不愿意听话,完全不按常理出牌。
回归直线法的计算方法

回归直线法的计算方法
1. 嘿,你知道回归直线法的计算方法吗?就好比你想知道你的成绩和努力之间的关系一样!比如说,你观察每次复习时间和对应的考试成绩,这就是在找它们之间的那条“线”呀!
2. 哇塞,回归直线法算起来其实不难哦!就像你找最喜欢的那条小路回家一样自然。
比如统计不同月份的销售额和广告投入,这不就是在寻找它们之间的关联嘛!
3. 告诉你哦,回归直线法计算方法超有趣的!好比你去拼凑一幅拼图,要找到最合适的那些碎片拼在一起。
就像研究温度和冰淇淋销量的关系,多有意思呀!
4. 嘿呀,学回归直线法的计算方法其实很有成就感呢!就像是你自己搭建了一座小桥,连接起不同的点。
好比根据身高和体重的数据分析,多神奇呀!
5. 哎呀,回归直线法的计算,那可是有门道的哟!就像解开一个神秘的密码。
比如说研究每天跑步里程和体能提升的关系,这就是在破解密码呀!
6. 哇哦,回归直线法计算可别小瞧呀!就好像在黑暗中找到那一丝光亮。
比如观察施肥量和作物产量的关联,这不就是在探索奥秘嘛!
7. 嘿嘿,回归直线法的计算方法很值得探究呢!就跟你寻找宝藏的路线一样刺激。
像分析游戏时间和游戏技巧提升的关系,多带劲呀!
8. 哟呵,回归直线法的算法,真的很吸引人呀!就像追寻一道美丽的彩虹。
比如说确定工作时间和工作效率的联系,这不是很好玩嘛!
9. 总之呢,回归直线法的计算方法真的很有用,学会它,就像掌握了一把打开知识大门的钥匙,能让你发现好多有趣的关系和规律,不是吗?。
直线回归法公式

直线回归法公式直线回归法公式1. 简介直线回归法是一种用于建立变量之间线性关系的统计方法。
它通过找到一条最佳拟合直线,以最小化观测值与拟合值之间的误差,来预测因变量的值。
直线回归法广泛应用于经济学、统计学和机器学习等领域。
2. 简单线性回归简单线性回归是直线回归法的最基本形式,用于建立一个自变量和一个因变量之间的线性关系。
其回归方程可以用以下公式表示:y=β0+β1x+ϵ其中,y是因变量,x是自变量,β0和β1是回归系数,ϵ是误差。
举个例子来说明简单线性回归公式的应用。
假设我们要研究一个国家的人口增长与经济增长之间的关系。
我们收集了一系列年份和对应的人口数量和GDP增长率数据。
我们可以使用简单线性回归来建立人口数量(因变量)与GDP增长率(自变量)之间的关系模型。
3. 多元线性回归多元线性回归是在简单线性回归的基础上进一步扩展,用于建立多个自变量和一个因变量之间的线性关系。
其回归方程可以用以下公式表示:y=β0+β1x1+β2x2+⋯+βp x p+ϵ其中,y是因变量,x1,x2,…,x p是自变量,β0,β1,β2,…,βp是回归系数,ϵ是误差。
举个例子来说明多元线性回归公式的应用。
假设我们要研究一个公司的销售额与广告投入、产品价格、季节性因素等变量之间的关系。
我们可以使用多元线性回归来建立销售额(因变量)与广告投入、产品价格、季节性因素等(自变量)之间的关系模型。
4. 最小二乘法最小二乘法是直线回归法中常用的参数估计方法,用于寻找最佳拟合直线。
其原理是最小化观测值与拟合值之间的误差平方和。
最小二乘法通过最小化以下目标函数来估计回归系数:nmin∑(y i−y î)2i=1其中,y i是观测值,y î是拟合值,n是观测值的数量。
使用最小二乘法可以得到最优的回归系数,使得拟合直线与观测值之间的误差最小化。
5. 总结直线回归法是一种用于建立变量之间线性关系的统计方法。
简单线性回归和多元线性回归是直线回归法的两种形式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 解:由以上分析,现对做x与Y相关性检验 (1)作统计假设: x与Y不具有线性相关关系 (2)由小概率0.05与n-2在附表中查得 r0.05 =0.632 (3) L ( x x ) x n x 47 . 6
n n 2 2 2 xx i i i 1 i 1
L xy L yy x 1 n
y
x
2
xy
3.计算相关系数,说明相关密切程度和方向
r
2
n xy n x
x
y
r
x
2
n y
2
y
2
4.计算参数a、b,建立直线回归方程 y c a bx n xy x y y b x b a n x x n n
i 1
n
( x i x )( y i y ) ( yi y )
2
x ,
i 1
n
i
y i n x y 37 . 2
2
i 1
n
i 1
n
yi
2
n y 1 n
36 . 9 y i 159 . 1
i 1
n
x i 158 . 8 ,
y
i 1
2 2
2
(y
i 1 n i 1
n
i
i 1 n i 1
n
yi n y
2
n
xi ,
y
1
n
yi
相关系数的取值范围及意义
1.r 的取值范围为[-1,1] 2. r 1 ,称完全相关,既存在线性函数关系 r =1,称完全正相关 r =-1,称完全负相关 3.r =0,称零相关,既不存在相关关系 4. r <0,称负相关
5. r >0,称正相关
6.
r 愈大,表示相关关系愈密切
例1 根据下表资料,计算居民年可支配收 入与消费支出之间的相关系数。
10户居民年收入和消费支出相关表 单位:千元
年收入 18 25 45 60 62 75 88 92 98 99
消费支出 15 20 30 40 42 53 60 65 78 70
第九章 相关与回归分析
• 教学目的:通过本章的学习使学生掌握相关分析和回归分析的基 本原理和方法,并理解相关分析和回归分析的区别和联系。
• 教学重点:简单相关系数的计算、取值范围;简单直线回归方程
的拟合及拟合好坏的判断。
• 教学学时:本章将用4个学时介绍。
变量之间的关系
1.确定性关系
与销售量 2.非确定性关系 量与价格
n
r
37.2 47.6 56.9
0.71
r > r0.05,即有95%的把握认为具有相关关系, (4) 回归直线方程是y=34.92+0.78x
相关分析和回归分析的步骤: 1.根据资料确定自变量x和因变量y 2.根据资料计算以下总和数: x
序号 x y x2 y2 xy
y
2
2 2
56234 279.8 203.3
0.988
• 计算结果说明居民的消费支出与可支配收 入之间存在着高度相关的关系。
例2
• 为了了解某地母亲身高与女儿身高的 相关关系,随机 测得10对母女的身高如下表所示
母高 x 159 160 160 163 159 154 159 158 159 157 156
函数关系,例如商品销售额
相关关系,例如商品需求
变量之间相关关系的示意图
正相关
线性相关 相关关系 非线性相关
负相关
二、相关系数及其计算
1.变量之间线性相关关系的密切程度的度量 2.两个变量之间线性相关程度的度量,也称简单相 关系数 3.根据样本数据计算而的得相关系数,称为样本相 关系数,记为 r
样本相关系数 x 和 y 的样本相关系数为
Y2
225 400 900 1600 1764 2809 3600 4225 4900 6084 26507
xy
270 500 1350 2400 2604 3975 5280 5980 6930 7644 36933
• 将表中数据代入简捷公式,可得 • r
10 36933 662 473 10 51656 (662) 10 26507 (473)
相关系数计算表
可支配收入 (千元)x
18 25 45 60 62 75 88 92 98 99 662
消费支出 (千元)y
15 20 30 40 42 53 60 65 78 70 473
x2
324 625 2025 3600 3844 5625 7744 8464 9801 9604 57656
r L xy L xx L yy
L xx L xy L yy x 1
( 10.1 )
2
其中
(x
i 1
n
i
x)
i 1
n
xi n x
2
2
( 10.2 ) ( 10.3 )
(x
i 1
n
i
x )( y i y ) பைடு நூலகம்y)
2
i 1
n
xi yi n x y
159 160 161 161 155 162 157 162 女高 158 y 请做一元回归分析,并预测母亲身高为161时,女儿身高为多少?
检验的步骤
• (1)做统计假设:x与Y不具有线性相关关系 • (2)根据小概率0.05(或0.01)与n-2在附表中 查出r的一个临界值 r0.05 • (3)根据样本相关关系系数计算公式算出r值 • (4)做统计推断,如果 r r0.05 • 表明有95%的把握认为具有相关关系; r0.05 r≤ • 我们就没有理由拒绝原来的假设,这时寻找回归 直线方程就毫无意义了
