第八章稳恒电流的磁场
稳恒磁场
二、电流的磁效应 二、电流的磁效应
I
S N •磁针和磁针 •在磁场 中运动的 电荷受到 的磁力 •磁铁与载流导 线的相互作用 S N S N
•电流的磁效应
I I
•载流导 线与载流 导线的相 互作用
三、磁场 三、磁场
1、概念
在运动电荷(或电流)周围空间存在的一种特殊形式的物质。
2、磁场的特性
•磁场对磁体、运动电荷或载流导 线有磁场力的作用; •载流导线在磁场中运动时,磁场 力要作功——磁场具有能量。
∧
Idl
r
R Idl’ θ
dB ⊥
dB dB//
P dB’
μ0 Idl sin(d l r ) μ0 Idl dB = = sin 90° 4π r2 4π r 2
分解 dB
dB ⊥ = dB cos θ
dB// = dB sin θ
电流对称
2
∫ dB
⊥
=0
μ0 I B = ∫ dB // = 4π
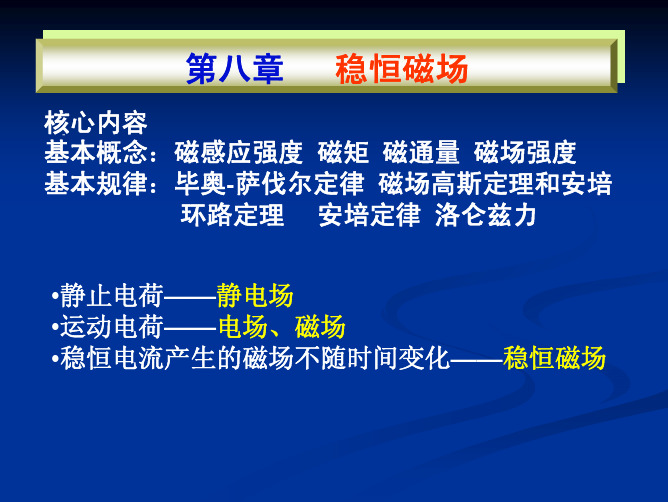
第八章 第八章
稳恒磁场 稳恒磁场
核心内容 基本概念:磁感应强度 磁矩 磁通量 磁场强度 基本规律:毕奥-萨伐尔定律 磁场高斯定理和安培 环路定理 安培定律 洛仑兹力 •静止电荷——静电场 •运动电荷——电场、磁场 •稳恒电流产生的磁场不随时间变化——稳恒磁场
一、电流 一、电流
8.1 电流 current
线圈所包围的面积
I
en
pm
其中 e n 与电流环绕方向符合右手螺旋法则
μ 0 IπR μ 0 pm B = (1)当x=0时,有 BO = = = 3 3 2( R 2 + x 2 ) 3 2 2R 2πR 2πR
2
μ0 I
机械工业出版社大学物理 第08章 稳恒磁场02-安培力、磁力矩

§8.6 磁介质对磁场的影响
能够对磁场有影响的物质称为磁介质。
一、磁导率
vv v B B0 B'
磁介质中的 总磁感强度
真空中的 磁感强度
介质磁化后的 附加磁感强度
实验表明: B r B0
相对磁导率
r
B B0
磁导率 r0
——表示磁介质磁化对磁场的影响
25
磁介质的分类
顺磁质 抗磁质 铁磁质
BIdl sin
因 dl rd
π
F BIr0 sin d
BI 2r
r
y
dF
rC
Idl
r
d
Bo
r
r
r
F BI 2r j BI AB j
B
I
Ax
17
例2 求如图不规则的平面载流导线
在均匀磁场中所受的力。
已知
r B
和
I。
y
dF
r B
r
解:
取一r 段电流r元
r
Idrl
dF Idl B
解 M NBISsin
得
π,
2
M Mmax
M NBIS 50 0.05 2 (0.2)2 N m
M 0.2N m
23
第八章 稳恒磁场
8.1 电流与电动势 8.2 磁场 磁感应强度 8.3 毕奥-萨伐尔定律 8.4 安培环路定理 8.5 磁场载流导体的作用 8.6 磁介质对磁场的影响 8.7 铁磁质
b
B
d vd+
+ +Fm +
+q
- - - - -
霍耳电压 UH
+
I UH
第08章稳恒磁场00-电流与电动 比奥萨伐尔定律

cos sin R
dBx 4π r
3
o
r
2 2
x
0 IRdl
r R x
2
2
0 IR 2 π R Bx dl 3 0 4πr
0 I R 2 3 2 r
0 I R Bx 3 2 2 (x2 R2)
B Bxi
18
B Bxi
讨论:
(1)若
I
o
R
2
0 nI L B 0 nI cos 2 1/ 2 2 2 2 L / 4 R
(2)无限长的螺线管
L R
则:
即:1 π, 2 0
B 0nI
24
π (3)半无限长螺线管 1 , 2 0 2
1 B 0 nI 2
(4)磁感应强度的小的分布
dB
I
r r0 / sin y r0 ct g 2 dy r0d / sin 0 I dB sin d
4 π r0
o r0
y
*
dB
z
Id y
1
r
P
x
C
14
B dB
C
D
0 I
4 π r0
2
1
sin d
B 的方向沿 z 轴的负方向。
I
(2 )
R B x 0 I 0 o B0 2R
I
(4) I R
o
(5)
0 I B0 2 R 2
R1
R2
R
o
( 3)
B0
0 I
4R
I
I
稳恒磁场
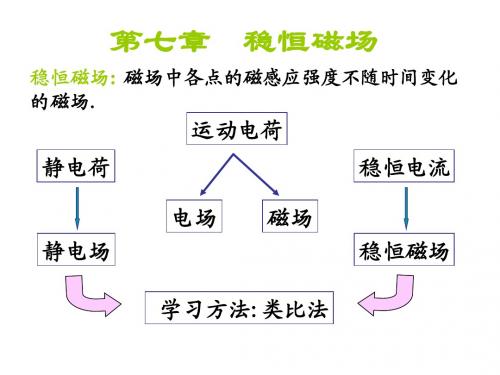
安培定律
一、安培力
安培力:电流元在磁场中受到的磁力. 安培力:电流元在磁场中受到的磁力. 一个自由电子受的洛仑兹力为: 一个自由电子受的洛仑兹力为
f 洛 = qv × B = −ev × B
电流元所受磁力: 电流元所受磁力
方向: 方向:×
v
dl
B
I
设截面积为S,单位体积电子数为 设截面积为 单位体积电子数为n 单位体积电子数为
1 2 m = NISn = NI πR n 2
方向:与 B 成600夹角. 夹角. 方向: (2)此时线圈所受力矩的大小为: )此时线圈所受力矩的大小为:
)60
0
B
3 2 πR M = mB sin60 = NIB 4 方向: m× B 方向: ×
0
n
即垂直于 B向上,从上往下俯视,线圈是逆时针转动。 向上,从上往下俯视,线圈是逆时针转动。
1T = 1N ⋅ S ⋅ m−1 ⋅ C−1
磁通量
一、磁力(感)线 磁力( 直线电流的磁力线
磁场的高斯定理
圆电流的磁力线
通电螺线管的磁力线
I
I
I
I
通量(通过一定面积的磁力线数目) 二、磁通量(通过一定面积的磁力线数目)
v v dΦ = B ⋅ dS
v v Φ = ∫s B ⋅ dS
单位
1Wb= 1T ⋅ m
I
该式对任意形状的线圈都适用. 该式对任意形状的线圈都适用.
例1如图,求圆心O点的 B . 如图,求圆心 点的 I O
• × R
B=
µ0 I
4R
I
O• •
R
B=
µ0 I
8R
R
• •O
第八章 恒定电流的磁场(一)

一. 选择题: [ D ]1. 载流的圆形线圈(半径a 1 )与正方形线圈(边长a 2 )通有相同电流I .若两个线圈的中心O 1 、O 2处的磁感强度大小相同,则半径a 1与边长a 2之比a 1∶a 2为 (A) 1∶1 (B)π2∶1 (C)π2∶4 (D)π2∶8[B ]2.有一无限长通电流的扁平铜片,宽度为a ,厚度不计,电流I 在铜片上均匀分布,在铜片外与铜片共面,离铜片右边缘为b 处的P 点(如图)的磁感强度B的大小为(A) )(20b a I+πμ. (B) b b a a I +πln 20μ.(C) b b a b I +πln 20μ. (D) )2(0b a I +πμ.[ D ]3. 如图,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I 从a 端流入而从d 端流出,则磁感强度B沿图中闭合路径L 的积分⎰⋅Ll Bd 等于(A) I 0μ. (B) I 031μ.(C) 4/0I μ. (D) 3/20I μ.提示[ B ] 4. 图中,六根无限长导线互相绝缘,通过电流均为I ,区域Ⅰ、Ⅱ、Ⅲ、Ⅳ均为相等的正方形,哪一个区域指向纸内的磁通量最大?(A) Ⅰ区域. (B) Ⅱ区域.(C) Ⅲ区域.(D) Ⅳ区域.(E) 最大不止一个.提示:加原理判断磁场和磁感应强度的叠根据无限长直导线产生[ C ]5. 在半径为R 的长直金属圆柱体内部挖去一个半径为r 的长直圆柱体,两柱体轴线平行,其间距为a ,如图.今在此导体上通以电流I ,电流在截面上均匀分布,则空心部分轴线上O ′点的磁感强度的大小为(A) 2202R a a I ⋅πμ (B) 22202R r a a I -⋅πμ (C) 22202r R a a I -⋅πμ (D) )(222220ar R a a I -πμ 二. 填空题1.在匀强磁场B 中,取一半径为R 的圆,圆面的法线n与B成60°角,如图所示,则通过以该圆周为边线的如图所示的任意曲面S 的磁通量==⎰⎰⋅Sm S B d Φ221R B π-提示:2. 一长直载流导线,沿空间直角坐标Oy 轴放置,电流沿y 正向.在原点O 处取一电流元l I d ,则该电流元在(a ,0,0)点处的磁感强度的大小为 204aI d lπμ 方向为Z轴负方向提示:ⅠⅡⅢⅣ aRr O O ′I任意曲面3. 一个密绕的细长螺线管,每厘米长度上绕有10匝细导线,螺线管的横截面积为10cm 2.当在螺线管中通入10 A 的电流时,它的横截面上的磁通量为)(1046W b -⨯π. (真空磁导率μ0 =4π×10-7 T ·m/A)提示:为S 1L21提示:根据安培环路定理5. 一质点带有电荷q =8.0×10-10 C ,以速度v =3.0×105 m ·s -1在半径为R =6.00×10-3 m 的圆周上,作匀速圆周运动.该带电质点在轨道中心所产生的磁感强度B =__6.67×10-7(T ),该带电质点轨道运动的磁矩p m =_7.2×10-7(Am 2)___.(μ0 =4π×10-7 H ·m -1)提示:6. 如图所示,在宽度为d 的导体薄片上有电流I 沿此导体长度方向流过,电流在导体宽度方向均匀分布.导体外在导体中线附近处P 点的磁感强度B的大小为dI20μ提示7. 在一根通有电流I 的长直导线旁,与之共面地放着一个长、宽各为a 和b 的矩形线框,线框的长边与载流长直导线平行,且二者相距为b ,如图所示.在此情形中,线框内的磁通量Φ = 2ln 20a Iπμ提示:俯视图三.计算题1.将通有电流I 的导线在同一平面内弯成如图所示的形状,求D 点的磁感强度B的大小.解:其中3/4圆环在D 处的场 )8/(301a I B μ=AB 段在D 处的磁感应强度 )221()]4/([02⋅=b I B πμ BC 段在D 处的磁感应强度 )221()]4/([03⋅=b I B πμ1B 2B 3B方向相同,故D 点处总的磁感应强度为)223(40321ba I B B B B +=++=ππμ 2..已知半径为R 的载流圆线圈与边长为a 的载流正方形线圈的磁矩之比为2∶1,且载流圆线圈在中心O 处产生的磁感应强度为B 0,求在正方形线圈中心O '处的磁感强度的大小.解:设圆线圈磁矩为1m P 方线圈磁矩为2m P 则211R I P m π= 222a I P m = 由已知条件得: )2/(2122a I R I π=正方形一边在其中心产生的磁感应强度为 )2/(201a I B πμ=正方形各边在其中心产生的磁感应强度大小相等,方向相同,因此中心/O 处的总的磁感应强度的大小为3120200/222aI R a I Bμπμ== 由 RI B 2100μ=得 012μRB I =所以 03/0)/2(B a R B =3. 如图所示,半径为R ,线电荷密度为λ (>0)的均匀带电的圆线圈,绕过圆心与圆平面垂直的轴以角速度ω 转动,求轴线上任一点的B的大小及其方向.解: 圆线圈的总电荷 λπR q 2= ,转动时等效的电流为λωωπλπR R T q I ===/22, 代入环形电流在轴线上产生磁场的公式得2/32230)(2y R R B B y +==ωλμ 方向沿y 轴正向。
稳恒电流的磁场的散度和旋度

从而得到
−
d dt
∫ ρdV
V
=
0
表示全空间的总电荷守恒。
毕奥-萨伐尔定律
∫ K
B
=
μ0
4π
V
′
K J(
x′) r3
×
rK
dV
′
K dB
K K r dB 垂直于JdV ′与
所形成的平面 rK
μ0是真空中的磁导率。
K JdV ′
μ0
=
4π
×107
N A2
磁场的矢势
( ) K
∇
×
⎛ ⎜
⎝
A g
⎞ ⎟ ⎠
),
求电荷分布为ρ(rK)=ρ0e−αr的电势和电场强度, 其中α为常数
=
g
KK
∇× A + A×(∇g )
g2
∇
×
K J(
xK′)
=
r(∇
×
K J(
xK′))
+
JK ( xK′)
×
(∇r
)
r
r2
K J(
xK′)
×
(∇r
)
=
r2
=
K J(
xK′)
×
K r
r3
磁场的矢势
∫ K
B
=
μ0
4π
V
′
K J (x′)
Kr 3
×
K r
dV
′
∫ = μ0 ∇ × J (x′) dV ′
∫V
∇⋅
G JdV
=
−∫V
∂ρ
dV ∂t
∇⋅
K J
+
∂ρ
习题解答---大学物理第八章习题 2

专业班级_____ 姓名________学号________第八章稳恒电流的磁场一、选择题:1、在磁感应强度为B的均匀磁场中作一半径为r的半球面S,S边线所在平面的法线方向单位矢量n与B的夹角为α,则通过半球面S的磁通量为:[ D ](A)Br2π(B)Br22π(C)απsin2Br-(D)απcos2Br-。
2、无限长直导线在P处弯成半径为R的圆,当通以电流I时,则在圆心O点的磁感应强度大小等于:[ D ](A)RIπμ20(B)RI4μ(C)0(D))11(2πμ-RI(E))11(4πμ+RI3、电流由长直导线1沿切向经a点流入一个电阻均匀分布的圆环,再由点沿切向从圆环流出,经长直导线2返回电源(如图)。
已知直导线上的电流强度为I,圆环的半径为R,且a、b和圆心O在同一直线上。
设长直载流导线1、2和分别在O点产生的磁感应强度为1B、2B、3B,则圆心处磁感应强度的大小[ C ](A)0=B,因为0321===BBB。
(B)0=B, 因为虽然01≠B,02≠B,但021=+BB,03=B。
(C)0≠B,因为01≠B,02≠B,03≠B。
(D)0≠B,因为虽然03=B,但021≠+BB。
4、磁场由沿空心长圆筒形导体的均匀分布的电流产生,圆筒半径为R,x坐标轴垂直圆筒轴线,原点在中心轴线上,图(A )——(E )哪一条表示x B -的关系?[ D ] 5、无限长直圆柱体,半径为R ,沿轴向均匀流有电流,设圆柱体内(R r <)的磁感应强度为i B ,圆柱体外(r> R )的磁感应强度为e B 。
则有:[ B ] (A)i B 、e B 均与r 成正比。
(B) i B 、e B 均与r 成反比。
(C)i B 与r 成反比,e B 与r 成正比。
(D) i B 与r 成正比,e B 与r 成反比。
6、如右图所示,在磁感应强度为B的均匀磁场中,有一圆形载流导线,a 、b 、c 是其上三个长度相等的电流元,则它们所受安培力大小的关系为[ B ](A )c b a F F F >>。
稳恒电流的磁场

将线圈置于磁场中,当磁场发生变化时,线圈中产生感应电流,并 受到磁场的作用力而发生旋转,实现电磁驱动。
霍尔效应实验
将导体置于磁场中,当电流通过导体时,在导体两侧产生电势差, 这种现象称为霍尔效应,可用于测量磁场强度。
电磁感应现象实验
法拉第实验
通过在导线线圈中切割磁感线,发现导线中产生 感应电流,即电磁感应现象。
稳恒电流的磁场
https://
REPORTING
• 磁场和电流的关系 • 稳恒电流产生的磁场 • 磁场对稳恒电流的作用 • 稳恒电流的磁场应用 • 实验与观察
目录
PART 01
磁场和电流的关系
REPORTING
WENKU DESIGN
安培环路定律
安培环路定律是描述磁场和电流之间关系的物理定律,它指出磁场和电流之间的 关系是线性的,即磁场是由电流产生的,并且电流的存在会导致周围空间中磁场 的形成。
电流在磁场中的受力分析
02
根据左手定则,可以判断电流在磁场中受到的力的方向。
电磁感应
03
当导线在磁场中做切割磁感线运动时,导线中会产生感应电动
势,从而产生感应电流。
PART 03
磁场对稳恒电流的作用
REPORTING
WENKU DESIGN
洛伦兹力
定义
洛伦兹力是指带电粒子在磁场中 所受到的力,其大小与带电粒子 的电荷量、速度和磁感应强度有
磁场对电流的作用力
磁场对电流的作用力是指电流在磁场中受到的力,这个力的 大小和方向取决于电流和磁场的相互位置和方向。
磁场对电流的作用力遵循安培定律,其数学表达式为: F=IBLsinθ,其中F表示作用力,I表示电流,B表示磁场强度,L 表示导线长度,θ表示电流和磁场方向的夹角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
51第八章 稳恒磁场§8-1、电流的磁场【基本内容】一、毕奥—萨伐尔定律设有通电导线L ,在L 上以电流元l Id ,l Id 到场点P 的矢径为r,如图6.1,则l Id 在场点所产生的B d为:304r r l Id B d⨯=πμ 大小:20si n 4r Idl dB θπμ=;方向:由l Id 与r的右手定则确定。
真空中磁导率)/(/104270A m T A N ⋅⨯=-πμ二、磁场叠加原理:在若干个电流或电流元产生的磁场中,某点的磁感应强度等于各个电流或电流元单独存在时在该点所产生的磁感应强度的矢量和。
即∑=iiB B或⎰=B d B三、常见载流体的磁场分布1、载流直导线的磁场分布θπμsin 40aIB =半无限长直导线的磁场分布:aI B πμ40=无限长直导线的磁场分布: a I B πμ20=2、通电圆环轴线上的磁场 2/32220)(2x R I R B +=μ 圆心处x=0:RI B 200μ=图不图6.1r∆SI 0稳d BPm Id lIθ图6.1q v I AFB R21图6.3x xPR 0I图6.2θ0aPθ52 对长为L 的圆弧:0022B B R L B πθπ==3、长直螺线管、密绕螺绕环内的磁场nI B 0μ=【典型例题】利用磁场叠加原理求磁场毕萨定律是计算电流产生磁场的一般方法,应按矢量积分的方法计算。
磁场叠加原理:⎰∑==B d B B B ii ,步骤:1、取电流元l Id 并求l Id 产生的B d ,2、由磁场叠原理求B:(1) 若各B d的方向相同,则直接积分⎰=dB B ; (2) 若各B d的方向不相同,则正交分解后积分j B i B B dB B dB B y x y y x x+=⇒==⎰⎰,【例8-1】 闭合载流导线弯成如图例6-1所示的形状,载有电流I ,试求:半圆圆心O 处的磁感应强度。
【解】 闭合导线是由直导线和圆弧线组成,根据载流直导线和圆弧导线产生的磁场公式,可求得各段直线和圆弧线在O 点产生的磁感应强度分别为:0==CD AB B BRI R I B B FA DE ⋅=⋅==πμππμ1624sin 2400 方向:垂直纸面向外。
RI R I B EF ⋅=⋅⨯=πμππμ824sin 24200方向:垂直纸面向外。
RIRIBBCO422100μμ=⨯=⋂方向:垂直纸面向里。
)2(4200-=--=⋂ππμRIB B BB DE EF BCO方向:垂直纸面向里。
【例8-2】 在一半径R 的无限长半圆柱形金属薄片中 ,自上而下地有电流I 通过,如图例6-2所示,试求圆柱轴线上任一点P【解】 建立例6-2图解坐标系,取宽为dL的无限长直导线,其通有电流 dl RIdI π=该电流元在O处产生磁感应强度B d大小:θπμπμd RI R dI dB 20022==R例6-1图例D0AFExP 4R2RRRBC IIR 例6-1图例6DBCAFExP+Qb4R2RRR 例6-2图Rθ例6-2图解xd BθdLIy53方向:各B d方向不同。
iRI B d RI B dBcoc dB RId R I B dB dB y y x x 20020200200cos 2sin 2sin πμθθπμθπμθθπμθππ-===⇒-=-=-=⇒-=⎰⎰【例8-3】 一内半径为a ,外半径为b 的均匀带电圆环,绕过环心O 且与环平面垂直的轴线以角速度ω逆时针方向旋转,如图例6-3。
环上所带电量为+Q,求环心O 处的磁感应强度。
【解】 该圆环的面电荷密度)(22ab Q-=πσ在圆环上取半径为r,长为dr 的小圆环,如图例6-3图解: 其带电量:rdr dq πσ2=当带电圆环旋转时,产生圆形电流:rdr dI σωπω==2该圆形电流在O 点处产生的磁感应强度大小:dr rdI dB σωμμ00212==方向:垂直纸面向外。
环心O 处的磁感应强度)(2)(2121000b a Q a b dr B ba +=-==⎰πωμσωμσωμ 方向:垂直纸面向外。
§8-2、磁场定理【基本内容】一、磁场的高斯定律1、磁感应线磁感应线上每一点的切线方向表示该处磁感应强度的方向;磁感应线的疏密程度表示磁感应强度的大小;磁感应线是无头无尾的闭合曲线。
2、磁通量:垂直通过某一面积元dS 的磁感应线的根数。
dS B S d B d m θφcos =⋅=通过有限面积S 的磁通量则为:dS B S d B SSm ⎰⎰⎰⎰=⋅=θφcos3、磁场的高斯定理通过任意闭合曲面的磁通量为零:x例6-2图D例6-2图解R dLEd B Iy2Rθθ例6-3图例6-3图解+Qωdrωrb a54 0=⋅⎰⎰SS d B意义:稳恒磁场是无源场,自然界中没有磁单极存在。
二、安培环路定理1、定理的内容:在稳恒磁场中,磁感应强度沿任意闭合路径的线积分等于通过该闭合环路所包围的的所有电流强度I 的代数和的μ0倍。
∑⎰=⋅内I l d B l0μ⎰⋅ll d B:磁感应强度沿任意闭合回路的积分(环流)。
∑内I:闭合回路所包围的电流的代数和。
I 的正负:由所取回路的方向按右手定则确定。
2、定理的意义稳恒磁场是一非保守场,是有旋场。
【典型例题】用安培环路定理可求解某些磁场的B,这些磁场分布有对称性,即激发磁场的电流分布,要有一定的对称性。
例如(1)无限长均匀载流圆柱体,无限长均匀载流圆柱面和无限长载流直线产生的磁场B在垂直于圆柱轴线的平面上,以轴线上的任一点为圆心,半径为r 的圆周上各点的B的大小相等,方向沿该点的切线。
若安培环路取这样的圆周,且通过需求B 的点,则可用安培环路定理方便地求出该点的B(2)载流长直螺线管,除去边缘效应管内是匀强磁场,方向沿螺线管的轴线,由于磁场分布的对称性,可方便地用安培环路定理求出这种情况中的B。
(3)螺绕环,螺绕环内的磁力线是以环心为圆心的同心圆,这种情况也可用安培环路定理求出B。
步骤:(1)选取积分回路l ,(2)求B沿l 的环流⎰⋅ll d B ,(3)求l 所包围电流强度的代数和,(4)由∑⎰=⋅内I l d B l0μ 求B 。
【例8-4】如例6-4图所示,在半径为R 长直圆柱形导体内,开一个半径为r 圆柱形空洞,空洞的轴线与导体的轴线平行,相距为d ,在导体中沿轴线方向通有均匀分布的电流,其电流密度为j 。
(1) 求O 、/O 处的磁感强度; (2) 证明空腔内磁场均匀。
【解】 将此导体等效地看作一个半径为R ,电流均匀分布的大圆柱体,与另一个半径为r 、电流密度55大小相等、方向相反的小圆柱体组合而成,而磁感应强度应为两圆柱体的磁感应强度叠加而成。
(1)O 轴上一点的磁感应强度为2010B B B O +=10B 和20B分别为大圆柱和小圆柱在O 轴上一点产生的磁感应强度,如图例6-4题解,由安培环路定理求得djr r j d d I B B 222,020********μππμπμ=⋅===故 djr B 2200μ=,方向:垂直于/OO 轴向上。
/O 轴上一点的磁感应强度为/20/10/B B B O +=/10B 和/20B 分别为大圆柱和小圆柱在/O 轴上一点产生的磁感应强度。
/10B 22202010jdd j d d I μππμπμ=⋅==0/20=B故 /10/0B B =20jdμ=,方向:垂直于/OO 轴向上。
(2) 设空腔内任一点P 距O 为1r ,距/O 为2r ,明显d r r=-21。
大圆柱和小圆柱在P 点的磁场大小为1B 22102110jr r j r μππμ=⋅=,2B 22202220jr r j r μππμ=⋅= 方向垂直于1r 和2r ,可得1B 102r j ⨯=μ,2B 20)(2r j ⨯-=μP 点的合磁感强度为21B B B +=102r j ⨯=μ+20)(2r j ⨯-μ=⇒B d j r r j ⨯=-⨯2)(20210μμ大小 =B jd 2μ,方向垂直于/OO 轴向上。
例6-4图Or题解例6-4图OO //ROdr 1r 2BB 1j-jd B 2j56 【讨论】这种设想用用反向电流填充空腔的方法称为补偿法,它使不对称的系统变成两个对称系统的组合,便于利用已知的结果。
【例8-5】 一根半径为R 的长直圆柱形导体载有电流I ,导体内电流均匀分布。
如图例6-5所示。
在圆柱半径和轴/OO 所确定的平面内有一假想的矩形平面S ,长为L ,宽为R 。
求在何位置时,通过S 的磁通量最大。
【解】以/OO 为轴的圆环为安培环路,当圆环半径R r <时,有220r RI l d B ππμ⋅=⋅⎰ 可求得202R Ir B πμ=同样,当R r >时,rIB πμ20=设矩形平面S 的一边与轴线相距x ,则通过S 的磁通量为 R R x IL x R R IL Ldr r I Ldr R Ir BdSS d B R x R Rx ++-=⋅+⋅==⋅=Φ⎰⎰⎰⎰⎰⎰+ln2)(42202220020πμπμπμπμ舍去)或()15(21)15(210012202122020R x R x R Rx x R x IL RILx dx d +-=-=⇒=-+⇒=+⋅+-⇒=Φπμπμ 故当R x )15(21-=时,磁通量有最大值。
【讨论】根据磁场的特征,随着x 的增加,磁通量逐渐增加,当x 达到某一值时,磁通量开始减少,直至为0。
因此,本题求极大值时,不必求二阶导数。
§8-3、磁场对运动电荷和电流的作用【基本内容】一、磁场对载流导线的作用1、安培定律B l Id F d⨯=⎰⨯=LB l Id F+I IO /dr OO /dr 1r 2B 1B j-jj题解例6-4图B 2例6-5图xLROO /IR57大小:θsi n IdlB dF =; 方向:由B l Id⨯的方向决定。
若导线上的B 处处相同,则B L I F⨯=2、电流强度“安培”的定义:设在真空中,两根无限长的平行直导线相距1米,通有大小相同的稳恒电流I ,若导线每米长度上所受的力为2×10-7N ,则每根导线中电流强度的大小规定为1“安培”。
二、磁场对载流线圈的作用1、通过闭合线圈的磁矩m P:n S I P m∆=0I 0为通过线圈的电流强度、ΔS 为线圈的面积、n为线圈的法向单位矢量,如图6.4。
2、匀强磁场中的载流线圈磁矩为m P 的线圈在均匀磁场中:(1)0=合F ,无平动加速度;(2)B P M m ⨯=,若0≠M ,则产生转动。
讨论: (1) 当2/πθ=时,M 最大。
(2) 当0=θ时,M=0,线圈在稳定平衡位置;当πθ=时,M=0,线圈在不稳定平衡位置。
