三角形相似 复习
相似三角形专题复习
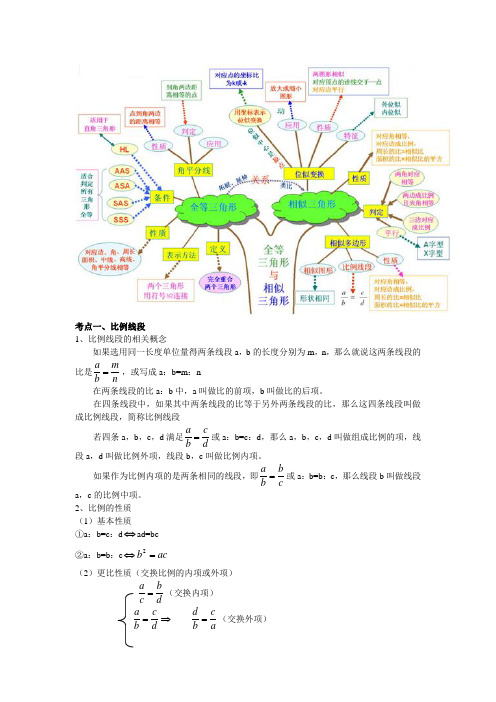
考点一、比例线段 1、比例线段的相关概念如果选用同一长度单位量得两条线段a ,b 的长度分别为m ,n ,那么就说这两条线段的比是a mb n=,或写成a :b=m :n 在两条线段的比a :b 中,a 叫做比的前项,b 叫做比的后项。
在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段,简称比例线段若四条a ,b ,c ,d 满足a cb d=或a :b=c :d ,那么a ,b ,c ,d 叫做组成比例的项,线段a ,d 叫做比例外项,线段b ,c 叫做比例内项。
如果作为比例内项的是两条相同的线段,即cbb a =或a :b=b :c ,那么线段b 叫做线段a ,c 的比例中项。
2、比例的性质 (1)基本性质①a :b=c :d ⇔ad=bc ②a :b=b :c ac b =⇔2(2)更比性质(交换比例的内项或外项)dbc a =(交换内项) ⇒=dcb a ac bd =(交换外项)abc d =(同时交换内项和外项) (3)反比性质(交换比的前项、后项):cda b d c b a =⇒= (4)合比性质:dd c b b a d c b a ±=±⇒= (5)等比性质:ba n f db m ec a n fd b n m fe d c b a =++++++++⇒≠++++==== )0( 3、黄金分割把线段AB 分成两条线段AC ,BC (AC>BC ),并且使AC 是AB 和BC 的比例中项,叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点,其中AC=215-AB ≈0.618AB 考点二、平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例。
推论:(1)平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边。
相似三角形性质和判定复习

相似三角形复习【知识要点】1、相似三角形的定义三边对应成_________,三个角对应________的两个三角形叫做相似三角形. 2、相似三角形的判定方法1.两个三角形相似,一般说来必须具备下列六种图形之一:2. 两个角对应相等的两个三角形__________.3. 两边对应成_________且夹角相等的两个三角形相似.4. 三边对应成比例的两个三角形___________.性质:⎪⎪⎩⎪⎪⎨⎧比的平方、对应面积比等于相似比、对应周长比等于相似、对应边成比例、对应角相等4321判定:⎪⎩⎪⎨⎧、三边对应成比例夹角相等、两边对应成比例,且、两角对应相等3211.相似比:相似三角形对应边的比叫做相似比。
当相似比等于1时,这两个三角形不仅形状相同,而且大小也 相同,这样的三角形我们就称为全等三角形。
全等三角形是相似三角形的特例。
2. 相似三角形的判定:①两角对应相等,两三角形相似。
②两边对应成比例,且夹角相等,两三角形相似。
③三边对应成比例,两三角形相似。
3. 相似三角形的性质:①相似三角形的对应角相等。
②相似三角形的对应线段(边、高、中线、角平分线)成比例。
③相似三角形的周长比等于相似比,面积比等于相似比的平方。
FEC【典型例题】1、如图在4×4的正方形方格中,△ABC 和△DEF 的顶点都在长为1的小正方形顶点上. (1)填空:∠ABC=______,BC=_______. (2)判定△ABC 与△DEF 是否相似?2、如图所示,D 、E 两点分别在△ABC 两条边上,且DE 与BC 不平行,请填上一个你认为适合的条件_________,使得△ADE ∽△ABC .并证明3、如图,在△ABC 中,AB =AC ,点D 、E 、F 分别在AB 、BC 、AC 边上,DE=DF ,∠EDF =∠A .(1)求证:BCABEF DE =.(2)证明:BDE ∆与EFC ∆相似。
4、已知,如图,CD 是Rt ABC ∆斜边上的中线,DE AB ⊥交BC 于F ,交AC 的延长线于E , 说明:⑴ ADE ∆∽FDB ∆; ⑵DF DE CD ∙=2.5、已知:如图,□AB C D 中E 为AD 的中点,AF :AB =1:6,EF 与AC 交于M 。
相似三角形复习

相似三角形复习关键信息项:1、相似三角形的定义及性质定义:____________________________性质:____________________________2、相似三角形的判定方法方法:____________________________示例:____________________________3、相似三角形的应用应用场景:____________________________解题思路:____________________________11 相似三角形的定义相似三角形是指三角分别相等,三边成比例的两个三角形。
两个三角形相似用符号“∽”表示。
111 相似比相似三角形对应边的比称为相似比。
相似比为 1 时,两个三角形全等。
112 相似三角形的性质1、相似三角形的对应角相等,对应边成比例。
2、相似三角形的对应高的比、对应中线的比与对应角平分线的比都等于相似比。
3、相似三角形周长的比等于相似比。
4、相似三角形面积的比等于相似比的平方。
12 相似三角形的判定方法1、两角分别相等的两个三角形相似。
2、两边成比例且夹角相等的两个三角形相似。
3、三边成比例的两个三角形相似。
121 直角三角形相似的判定1、一个锐角相等的两个直角三角形相似。
2、两条直角边成比例的两个直角三角形相似。
3、斜边和一条直角边成比例的两个直角三角形相似。
122 判定方法示例例如,在三角形 ABC 和三角形 A'B'C'中,如果∠A =∠A',∠B =∠B',那么三角形 ABC ∽三角形 A'B'C'。
又比如,在三角形 ABC 和三角形 A'B'C'中,如果 AB / A'B' = AC / A'C' 且∠A =∠A',那么这两个三角形相似。
13 相似三角形的应用131 应用场景1、测量物体的高度,如测量旗杆、大树等的高度。
相似三角形判定复习(一)

A E
C
二、证明题: 证明题: 1.D为 ABC中AB边上一点 边上一点, 1.D为△ABC中AB边上一点, ∠ACD= ∠ ABC. A 2=AD AB. 求证: 求证:AC =AD·AB. 2.△ABC中 BAC是直角 是直角, 2.△ABC中,∠ BAC是直角,过斜 边中点M而垂直于斜边BC BC的直线 边中点M而垂直于斜边BC的直线 CA的延长线于 的延长线于E AB于D,连 交CA的延长线于E,交AB于D,连AM. 求证: 求证:① △ MAD ∽△ MEA B ② AM2=MD · ME D 如图,AB∥CD,AO=OB, 3. 如图,AB∥CD,AO=OB, E DF=FB,DF交AC于 DF=FB,DF交AC于E, 求证: 求证:ED2=EO · EC. A
复习( 复习(一)
一、相似三角形的判定定理: 相似三角形的判定定理:
A'
定理1 两角对应相等,两三角形相似。 定理1:两角对应相等,两三角形相似。 ∠A' ∠A= ∠A ⇒△ABC∽△A'B'C' B' ABC∽△ B C C' ∠B' ∠B= ∠B A 定理2 两组边的比相等且夹角相等, 定理2:两组边的比相等且夹角相等, 两三角形相似。 两三角形相似。 AB BC = ABC∽△ B C A 'B ' B ' C ' ⇒ △ABC∽△A'B'C' ∠B' ∠B= ∠B B C 定理3 三组边的比相等,两三角形相似。 定理3:三组边的比相等,两三角形相似。
解: ∵ DE∥BC ∴∠ADE= ∠B, ∠EDC=∠DCB=∠A ① ∵ DE∥BC ∴△ADE ∽ △ABC D ② ∵ ∠A= ∠DCB, ∠ADE= ∠B ∴△ADE∽ △CBD ③ ∵ △ADE ∽ △ABC B △ADE ∽ △CBD ∴ △ABC ∽ △CBD ④ ∵ ∠DCA= ∠DCE, ∠A= ∠EDC ∴ △ADC ∽ △DEC
第二十四章-相似三角形-复习ppt课件

1
一、本章知识结构图
放缩与相似形
比例线段
相
比例线段
似
三角形一边的平行线
相似三角形
判定 性质
平面向量
实数与向量相乘
向量的线性运算
2
回顾与思考
一、相似形
1. 各角对应相等,各边对应成比例的两个多边形叫相 似多边形. 2. 三个角对应相等,三条边对应成比例的两个三角形 叫相似三角形.两个相似三角形用“∽”表示,读做 “相似于”.
(2) 以连接后的这两个向量为邻边向量 构造平行四边形
(3) 这个平行四边形的对角线向量就是 这两个向量的和向量与差向量
3.向量加法和减法的三角形法则 加法: 一终二起,一起二终 减法: 共起点指向被减
9
五、典例精析,复习新知
2.如图,在△ABC中,AB=AC=27,D在AC上,且 BD=BC=18,DE//BC交AB于E,则DE= 分析:由△ABC∽△BCD,列出比例式,求出CD,再用 △ABC∽△AED A答案:10
称比例线段.此时也称这四条线段成比例.
4
➢ 线段的比要注意以下几点: • 线段的比是正数 • 单位要统一 • 线段的比与线段的长度无关
如果 (b=d=f≠0),
那么
如果,
,那么ad=bc.
如果ad=bc(a、b、c、d都不等于0),那么
.
5
三、相似三角形的判定与性质 方法1:通过定义(不常用)
方法2:平行于三角形一边的直线与其他两边(或延 长线)相交,所构成的三角形与原三角形相似; 方法3:两对应角相等的,两三角形相似. 方法4:两边对应成比例且夹角相等,两三角形相似. 方法5:三边对应成比例的,两三角形相似.
相似三角形期末复习

2 : 3
2 : 3
4 : 9
2、如图:已知∠ABC=∠CDB=90°,AC=5cm,BC=3cm,当BD取多少cm时 △ABC和△BDC相似?
4
D
A
B
C
5
3
三,相似三角形的应用
例1:古代的数学家想出了一种测量金字塔高度的方法:为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′,比较棒子的影长A′B′与金字塔的影长AB,即可近似算出金字塔的高度OB,如果O′B′=1,A′B′=2,AB=274, 求金字塔的高度OB。
即
a b b c
= ,
(或 a:b=b:c),
那么线段 b 叫做a 和 c 的比例中项.
2
ac
b
=
即:
一.比例线段
如图,点 C 把线段 AB 分成两条线段 AC 和 BC ,
如果
AC
AB
AC
BC
=
那么称线段 AB 被点 C 黄金分割(golden section),
点 C 叫做线段 AB 的黄金分割点,
∴ =
AD AE
AC AB
∴ AD·AB=AE·AC
作业:如图,正方形ABCD中,E是DC中点,FC= BC. 求证: AD·EF=AE·EC
证明:∵四边形ABCD是正方形
∴BC=CD=AD,∠D=∠C=90°
∵E是BC中点,FC= BC
∴
∴
∴△ADE∽△ECF(两边对应成比例且夹角相等,两三角形相似)
(1)对应角相等,对应边成比例 (2)相似三角形对应高、中线的比等于相似比 (3)相似三角形周长之比等于相似比,面积比等于相似比的平方
------万州德澳中学初三数学备课组
相似三角形复习1

A D B M C
D
C O
2. 如图,AB∥CD,AO=OB, DF=FB,DF交AC于E, 求证:ED2=EO ·EC.
E A B
F
△ABC中,∠ BAC是直角,过斜边中点M而垂直于 斜边BC的直线交CA的延长线于E, 交AB于D,连AM. 求证:① △ MAD ~△ MEA
E
② AM2=MD ·ME
证明:①∵∠BAC=90°
M为斜边BC中点 ∴AM=BM=BC/2 ∴ ∠B= ∠MAD A D 又 ∵ ∠B+ ∠BDM=90° B C ∠E+ ∠ADE= 90° M ∠BDM= ∠ADE ② ∵ △MAD∽ △MEA ∴∠B=∠E AM ME ∴∠MAD= ∠E ∴ MD AM 又 ∵ ∠DMA= ∠AME 2 即AM =MD· ME ∴△MAD∽ △MEA
AC BC BC BD
b 时,即当
BD
1 时, B
D
a 2 b2 BD
2 2
时,
△ABC∽ △BDC, ∴ BD b a b
答:略.
a
将两块完全相同的等腰直角三角板摆成如图的样子,假 设图形中的所有点、线都在同一平面内,则图中有相似 (不包括全等)三角形吗?如有,把它们一 一写出来. A 解:有相似三角形,它们是: △ADE∽ △BAE, △BAE ∽ △CDA ,△ADE∽ △CDA 1 2 E C ( △ADE∽ △BAE ∽ △CDA ) B D G
1.平行线分线段成比例定理及推论 对应高,中线,角平分线 的比等于相似比 对应周长的比等于相似比
相 似 三 角 形
2.性质
面积比等于相似比的平方
1.平行
3.判定
2.AA 3.SAS 4.SSS
相似三角形的复习

相似三角形的性质
1、相似三角形的对应角相等; 、相似三角形的对应角相等; 2、相似三角形的对应线段(边、高、中线、 、相似三角形的对应线段( 中线、 角平分线)成比例,且等于相似比; 角平分线)成比例,且等于相似比; 3、相似三角形的周长比等于相似比; 、相似三角形的周长比等于相似比; 4、相似三角形的面积比=(相似比)2 、相似三角形的面积比 (相似比) 5、直角三角形被斜边上的高分成的两个直 、 角三角形和原三角形相似。 角三角形和原三角形相似。
AB CD EF
还成立吗?如果成立,请给出证明;如果不成立,请说明理 还成立吗?如果成立,请给出证明;如果不成立, ;(2)请找出S 之间的关系式, 由;( )请找出 △ABD,S△BED和S△BDC之间的关系式,并 给出证明。 给出证明。 A A E C E C
B
F
D
B
F
D
由三角形相似证线段成比例的一般步骤: 三角形相似证线段成比例的一般步骤: 证线段成比例的一般步骤 1、先看这些线段确定哪两个可能相似的三 、 角形; 角形; 2、再找这两个三角形相似所需要的条件; 2、再找这两个三角形相似所需要的条件; 3、如这两个三角形不相似,则采用其它办 、如这两个三角形不相似, 中间比代换等 如找中间比代换等); 法(如找中间比代换等); (注意:当无法用三角形相似来证明线段成 注意: 比例时,可试着用引平行线的方法。) 引平行线的方法 比例时,可试着用引平行线的方法。)
F
1、如图 ABCD中,G是BC延长线上的一点, 、 延长线上的一点, 中 是 延长线上的一点 AG与BD交于点 ,与DC交于 点,则图中相似的 与 交于点E, 交于F点 交于点 交于 三角形共有( 三角形共有(D )对。 A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形相似 复习
教学目的:提高学生对三角形相似判定定理的认识及应用能力。
教学重点:三角形相似判定定理的认识及应用 教学难点:三角形相似判定与性质综合应用。
教学内容:
一复习知识要点:
1、相似三角形的定义:对应角相等,对应边成比例的三角形
2、相似三角形的判定定理及其推论
判定定理1:两角对应相等的两个三角形相似.
判定定理2:两边对应成比例且夹角相等,两个三角形相似. 判定定理3:三边对应成比例的两个三角形相似 3、直角三角形被斜边上的高分成的两个直角三角形 和原三角形相似 4.相似三角形的性质
(1)相似三角形对应角相等,对应边成比例.
(2)相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.
(3)相似三角形周长的比等于相似比. 5。
三角形的中位线定理:平行于第三边且等于第三边的 一半.6 梯形中位线:等于上、下底和的一半且平行于底边。
7图形的变换与坐标 二例题讲解:
例2. D 为△ABC 中AB 边上一点,∠ACD= ∠ ABC. 求证:AC2=AD ·AB
2如图在4×4的正方形方格中,△
ABC 和△DEF 的顶点都在长为1的小正方形顶点上(1)填空:∠ABC=_____,BC=_______. 2)判定△ABC 与△DEF 是否相似?
【。
