(完整版)专题:二次根式重难点综合题型
初中数学实数(二次根式)重难点题型梳理归纳

实数章末重难点题型汇编【考点1 无理数的概念】【方法点拨】无限不循环小数又叫做无理数。
在理解无理数时,要抓住“无限不循环”这一实质,归纳起来有三类:(135,2等;(2)有特定意义的数,如圆周率π,或化简后含有π的数,如13π等; (3)有特定结构的数,如0.1010010001…等; 【例1】(2019春•博兴县期中)在3.14、√12、227、−√5、√273、2π、0.2020020002这六个数中,无理数有( ) A .1个 B .2个C .3个D .4个【答案】解:3.14、227、√273、0.2020020002是有理数,√12、−√5、2π是无理数,无理数的个数是3,故选:C .【变式1-1】(2018春•新罗区校级期中)下列说法中 ①无限小数都是无理数 ②无理数都是无限小数③﹣2是4的平方根 ④带根号的数都是无理数.其中正确的说法有( ) A .3个B .2个C .1个D .0个【答案】①无限不循环小数都是无理数,故①错误;②无理数都是无限不循环小数,故②正确;③﹣2是4的平方根,故③正确;④带根号的数不一定都是无理数,故④错误;故选:B .【变式1-2】(2018秋•东台市期中)下列实数中,√12、√93、−17、π2、﹣3.14、√0.1、√−273、0、0.3232232223…(相邻两个3之间依次增加一个2),无理数的个数是( ) A .2个B .3个C .4个D .5个【答案】解:√12=2√3,√0.1=√1010,√−273=−3,则无理数有:√12、√93、π2、√0.1、0.3232232223…,共5个.故选:D .【变式1-3】(2019秋•安宁区校级期中)在下列各数中是无理数的有( )−√(−5)2、√36、17、0、﹣π、√113、3.1415、√15、2.010101…(相邻两个1之间有1个0).A .1个B .2个C .3个D .4个故选:C .【考点2 无理数的估算】【方法点拨】无理数的估算,关键掌握二次根式的性质,能对根式进行估算. 【例2】(2018春•巫山县期中)估计√13+12的值在( ) A .1到2之间 B .2到3之间 C .3到4之间 D .4到5之间【答案】解:∵3<√13<4,∴4<√13+1<5,∴√13+12的值在2到3之间.故选:B . 【点睛】此题主要考查了估算无理数的大小,正确得出√13的取值范是解题关键. 【变式2-1】(2019春•北流市期中)设n 为正整数,且n <√83<n +1,则n 的值为( )A .6B .7C .8D .9【答案】解:∵√81<√83<√100,∴9<√83<10,又∵n 为正整数,∴n =9.故选:D .【变式2-2】(2019春•嘉陵区)已知a ,b 分别是6−√13的整数部分和小数部分,则2a ﹣b 的值是( )A .√13−2B .2−√13C .√13D .9−√13【答案】解:∵3<√13<4,∴6−√13的整数部分是2,即a =2,6−√13的小数部分是6−√13−2=4−√13,即b =4−√13,∴2a ﹣b =4﹣4+√13=√13;故选:C . 【变式2-3】(2019春•郯城县期中)若a 是√10−1的整数部分,b 是5+√5的小数部分,则a (√5−b )的值为( ) A .6B .4C .9D .3√5【答案】解:∵2<√10−1<3,∴a =2,又∵7<5+√5<8,∴5+√5的整数部分为7∴b =5+√5−7=√5−2; ∴a (√5−b )=2×(√5−√5+2)=4.故选:B .【考点3 实数的大小比较】【方法点拨】实数大小比较常见方法有:倒数法、作差法、作商法、放缩法、两边平方法等等.【例3】(2019秋•河北期中)已知a =√7−√5,b =√5−√3,c =3−√7,则a 、b 、c 三个数的大小关系是( ) A .b >c >aB .b >a >cC .a >b >cD .c >a >b【答案】解:∵a =√7−√5,b =√5−√3,c =3−√7,∴1a=√7−√5=√7+√52, 1b=√5−√3=√5+√32,1c =3−√7=3+√72,∵√7>√3,∴1a >1b , ∵3>√5,∴1a<1c,∴1c>1a>1b,∴b >a >c .故选:B .【变式3-1】(2019春•洪山区期中)比较实数:2、√5、√73的大小,正确的是( )A .√73<2<√5 B .2<√73<√5 C .√5<√73<2D .2<√5<√73【答案】解:∵2=√4<√5,∴2<√5,∵√73<√83=2,∴√73<2,∴√73<2<√5.故选:A .【变式3-2】(2019春•淮北期中)比较√3−1与√32的大小,结果是( ) A .前者大 B .后者大C .一样大D .无法确定【答案】解:∵√3−1−√32=√32−1<√42−1=1﹣1=0,∴√3−1−√32<0,∴√3−1<√32,∴比较√3−1与√32的大小,结果是后者大.故选:B .【变式3-3】(2019秋•乐山校级期中)已知a =√2−1,b =√6−2,c =2√2−√6,那么a 、b 、c 的大小关系是( ) A .a <b <cB .c <b <aC ..b <a <cD ..c <a <b【答案】解:∵a ﹣c =√2−1﹣(2√2−√6)=√6−(1+√2)≈2.449﹣2.414>0,∴a >c ;∵a ﹣b =√2−1﹣(√6−2)=√2+1−√6≈2.414﹣2.449<0, ∴a <b ,∴c <a <b .故选:D .【考点4 二次根式相关概念】【方法点拨】(1a a ≥0)的式子叫做二次根式。
《二次根式》知识点总结-题型分类-复习专用.doc

《二次根式》题型分类知识点一:二次根式的概念 【知识要点】二次根式的定义:形如五的戎子叫二次根式,其中么叫被开 方数,只有当么是一个非负数时,石才有意义.【典型例题】题型一:二次根式的判定【例1】下列各式1)卫,2)底,3)-存714)扬,5)』(-A 6)举一反三:1、 使代数式有意义的X 的取值范围是x-4( )A 、x>3 B. x > 3C 、 x>4D 、 x 》3且XH 42、 若式子丁鼻有意义,则x 的取值范围\l x — 3是 _____________ .题型去二次根式定义的运用【例 31 若 y= Qx-5 +』5-x ,则 x+y= _______________7)J/著换三:若x 、y 都是实数,且yr 求xy 的值1、下列各式中,一定是二次根式的是( )A 、乔B 、V^IOC 、yfa + lD 、题型二:二次根式有意义【例2】J 兀-2有意义的x 的取值范围是 ---------已知a 是亦整数部分,b 是 亦的小数部分, 求a-b 的值。
V5V 3,其中是二次根式的是 ------------ (填序号). 举一反三: 2、在丽、Vl + x 2 、的中是二次根式的个数有 ------- 个3、当。
取什么值时,代数式血 + 1+1取值最小, 并求出这个最小值。
知识点二:二次根式的性质【知识要点】1.非负性:V^(a>0)是一个非负数.2. (V^)2 =a(a>0).注意:此性质既可正用,也可反用,反用的意义在于,可以把任意一个非负数或非负代数式写成完全 平方的形式:a = (7a)2(a>0)4.公式=\a\=l a^~^ 与(Va)2 =a(a>0)的区别与联系-a(a < 0)(1) 品表示求一个数的平方的算术根,a 的范围是一切实数. (2) (需尸表示一个数的算术平方根的平方,a 的范围是非负数. (3) Q 和(石尸的运算结果都是非负的.【典型例题】題型二:二次根式的牲廣2(公式(石)2二a(a > 0)的运用)注意:此性质可作公式记住,后面根式运算中经常用到.f 例5】化简:卜一1| + (丁^二5)2的结果为()A 、4-2aB 、0C 、2a —4D 、4举一反三:在实数范围内分解因式:才-3二 _________________ ; 題型去二次根式餉濒3(公式7^? = |a| = J a(a ~0)的应用)注意:(1)字母不一定是正数.-a(a < 0)(2) 能开得尽方的因式移到根号外时,必须用它的算术平方根代替.(3) 可移到根号内的因式,必须是非负因式,如果因式的值是负的,应把负号留在根号外.f 例6】已知x<2,则化简J(x —2)2的结果是A % x — 2B 、兀+ 2C. —X — 2D. 2 — x3.=|a|= <a(a > 0)-a(a < 0)举一反三:1、根式J(-3)2的值是()A. -3B. 3 或-3C. 3D. 9那么|疑-2a |可化简为()2、已知a<0,A. - aB. aC. 一3aD. 3a【例71如果表示a, b两个实数的点在数轴上的位置如图所示,那么化简| a-b | + J(a + b)2的结果等于() ---- ----- -- --- Ab a oA. -2bB. 2bC. -2aD. 2a举一反三:实数a在数轴上的位置如图所示:化简:0-1| +J(Q-2)2= ______________ . 寸—()j-*-I:例811、把二次根式agl化简,正确的结果是( )A. J—aB. — J-aC. — -VaD.2、__________________________________________________________ 把根号外的因式移到根号内:当b>0时,-V7 = ; (。
二次根式易错题和重点题

二次根式易错题和重点题摘要:一、二次根式的基本概念1.二次根式的定义2.二次根式的性质二、二次根式的运算1.二次根式的加减法2.二次根式的乘除法3.二次根式的指数运算三、二次根式的化简1.完全平方公式2.平方差公式3.分母有理化四、二次根式的应用1.求解二次方程2.计算几何图形的面积和周长3.应用二次根式的实际问题正文:二次根式是数学中常见的一种表达形式,它涉及到许多基本概念和运算。
首先,我们需要了解二次根式的定义和性质,这是解决二次根式问题的关键。
一、二次根式的基本概念二次根式,通常表示为√a,其中a是一个正实数。
它表示的是一个数的平方根,即a的算术平方根。
根据定义,我们可以知道二次根式的值必须是非负的。
此外,二次根式还有一些重要的性质,如:1.√a = a2.√a * √b = √(ab)3.(√a) = a二、二次根式的运算二次根式的运算主要包括加减法、乘除法和指数运算。
1.二次根式的加减法:对于两个二次根式√a和√b,它们的和与差分别为√(a + b)和√(a - b)。
2.二次根式的乘除法:二次根式的乘法可以简单地将根号下的数相乘,即√a * √b = √(ab)。
而除法运算则较为复杂,通常需要利用分母有理化来解决。
3.二次根式的指数运算:二次根式的指数运算可以表示为(√a),它的结果是a的1/2次方。
三、二次根式的化简二次根式的化简是解决二次根式问题的关键。
化简的方法主要包括完全平方公式、平方差公式和分母有理化。
1.完全平方公式:对于一个二次根式√(a + b),我们可以通过完全平方公式将其化简为√(a + b) = √a + √b。
2.平方差公式:对于一个二次根式√(a - b),我们可以通过平方差公式将其化简为√(a - b) = √a - √b。
3.分母有理化:在涉及到分数的二次根式中,我们可以通过分母有理化来化简。
例如,将√(a/b)化简为√(a/b) * √(b/b) = √(ab/b) = √(a/b)。
二次根式知识点梳理及经典练习(超详细)

二次根式知识点梳理及经典练习知识点1:二次根式的概念1.二次根式的定义:形如的式子叫二次根式,其中叫被开方数,只有当是一个非负数时,才有意义.题型一:二次根式的判定【例1】下列各式1)22211,2)5,3)2,4)4,5)(),6)1,7)2153x a a a --+---+,其中是二次根式的是_________(填序号). [练一练]:1、下列各式中,一定是二次根式的是( ) A 、a B 、10- C 、1a + D 、)0(≥a a2、在a 、2a b 、1x +、21x +、3中是二次根式的个数有______题型二:二次根式有意义【例2】若式子13x -有意义,则x 的取值范围是 .[练一练]:1、使代数式43--x x 有意义的x 的取值范围是( )A 、x>3B 、x ≥3C 、 x>4D 、x ≥3且x ≠42、使代数式221x x -+-有意义的x 的取值范围是3、如果代数式mn m 1+-有意义,那么,直角坐标系中点P (m ,n )的位置在( )A 、第一象限B 、第二象限C 、第三象限D 、第四象限题型三:二次根式定义的运用[练一练]:A.-1 B.1 C.2 D.3题型四:二次根式的整数部分与小数知识点2:二次根式的性质常用到.注意:(1)字母不一定是正数.(2)能开得尽方的因式移到根号外时,必须用它的算术平方根代替.(3)可移到根号内的因式,必须是非负因式,如果因式的值是负的,应把负号留在根号外.题型一:二次根式的双重非负性【例4】若()2240a c -+-=,则=+-c b a .[练一练]:1、若0)1(32=++-n m ,则m n +的值为 。
2、已知y x ,为实数,且()02312=-+-y x ,则y x -的值为( ) A .3 B .– 3 C .1 D .– 13、已知直角三角形两边x 、y 的长满足|x 2-4|+652+-y y =0,则第三边长为______.4、若1a b -+互为相反数,则()2005_____________a b -=。
八年级数学二次根式章末重难点题型(举一反三)(沪科版)
专题1.1 二次根式章末重难点题型【沪科版】【考点1 二次根式相关概念】【方法点拨】1.二次根式:形如a (0 a )的代数式叫做二次根式. 2.最简二次根式:(1)被开方数的因数是整数,因式是整式; (2)被开方数中不含能开得尽方的因数或因式.3.同类二次根式:几个二次根式化成最简二次根式以后,如果被开方数相同,像这样的二次根式称为同类二次根式.【例1】(2019春•浉河区校级月考)在式子,,,(y ≤0),和(a <0,b <0)中,是二次根式的有( ) A .3个B .4个C .5个D .6个 【变式1-1】(2019春•莱芜期中)二次根式:①;②;③;④;⑤中最简二次根式是( ) A .①②B .③④⑤C .②③D .只有④ 【变式1-2】(2019春•左贡县期中)二次根式:①; ②; ③; ④中,与是同类二次根式的是()A.①和②B.①和③C.②和④D.③和④(2019春•海阳市期中)若两个最简二次根式和是同类二次根式,则n的值是()【变式1-3】A.﹣1B.4或﹣1C.1或﹣4D.4【考点2 二次根式有意义条件】【方法点拨】二次根式有意义的条件,关键是掌握二次根式中的被开方数是非负数.分式分母不为零.【例2】(2019春•泰山区期中)式子在实数范围内有意义的条件是()A.x≥1B.x>1C.x<0D.x≤0【变式2-1】(2019春•西湖区校级期中)为使有意义,x的取值范围是()A.x≥﹣2且x≠2B.x>﹣2且x≠2C.x>2D.x>2或x≤﹣2【变式2-2】(2018春•西华县期中)使代数式有意义的整数x有()A.5个B.4个C.3个D.2个【变式2-3】(2019秋•安岳县校级期中)如果有意义,则x的取值范围()A.x≥3B.x≤3C.x>3D.x<3【考点3 利用二次根式性质化简符号】【方法点拨】二次根式的化简求值,掌握二次根式的性质和绝对值的性质是解题的关键.【例3】(2019春•海阳市期中)把a根号外的因式移入根号内,运算结果是()A.B.C.﹣D.﹣【变式3-1】(2019春•汉阳区期中)已知ab<0,则化简后为()A.a B.﹣a C.a D.﹣a【变式3-2】(2018春•宜兴市期中)(a﹣1)变形正确的是()A.﹣1B.C.﹣D.﹣【变式3-3】(2019春•城区校级期中)化简﹣x,得()A.(x﹣1 )B.(1﹣x)C.﹣(x+1 )D.(x﹣1 )【考点4 利用二次根式的性质化简】【方法点拨】二次根式的性质:(1))()(02≥=a a a(2)⎪⎩⎪⎨⎧<-=>==)()()(00002a a a a a a a【例4】(2019春•庐阳区校级期中)实数a ,b 在数轴上的位置如图所示,则化简的结果是( )A .a ﹣b +3B .a +b ﹣1C .﹣a ﹣b +1D .﹣a +b +1 【变式4-1】(2019春•丰润区期中)若2<a <3,则=( ) A .5﹣2aB .1﹣2aC .2a ﹣1D .2a ﹣5【变式4-2】(2018秋•海淀区校级期中)实数a 、b 、C 在数轴上的位置所示,那么化简|c +a |+﹣的正确结果是( )A .2b ﹣cB .2b +cC .2a +cD .﹣2a ﹣c【变式4-3】(2018春•汉阳区期中)若0<x <1,则﹣等于( )A .B .﹣C .﹣2xD .2x【考点5 二次根式的乘除运算】 【方法点拨】掌握二次根式的乘除法则 (1)),(00≥≥=⋅b a ab b a(2)),(00>≥=b a b aba 【例5】(2019春•邗江区校级期中)计算: (1)÷ (2)÷3×【变式5-1】(2018秋•松江区期中)计算:•(﹣)÷(a>0)【变式5-2】(2019秋•闸北区期中)计算:【变式5-3】(2019春•新泰市期中)化简下列式子:•3.【考点6 利用二次根式性质求代数式的值】【例6】(2019春•萧山区期中)已知,,求下列式子的值:(1)a2b+ab2;(2)a2﹣30b+b2;(3)(a﹣2)(b﹣2).【变式6-1】(2019春•芜湖期中)已知,,分别求下列代数式的值;(1)x2+y2;(2).【变式6-2】(2019春•长白县期中)已知﹣=2,求的值.【变式6-3】(2018秋•通川区校级期中)已知x=,y=,求:(1)x2y﹣xy2的值;(2)x2﹣xy+y2的值.【考点7 二次根式的加减运算】【方法点拨】二次根式的运算法则:二次根式相加减,先把各个二次根式化成最简,再把同类二次根式合并.【例7】(2019春•武昌区期中)计算:(1)(2)【变式7-1】(2019春•萧山区期中)计算下列各式:(1);(2)+4﹣+.【变式7-2】(2018春•襄城区期中)计算:(1)﹣+﹣(2)﹣﹣+2【变式7-3】(2018春•罗山县期中)(1)(2)【考点8 二次根式的混合运算】【例8】(2019春•泰兴市校级期中)计算:(1)(2)3【变式8-1】(2019春•广东期中)计算(1)()÷(2)(3)2﹣()()【变式8-2】(2019春•杭锦后旗期中)计算:(1)﹣×+(2)(2﹣)2018(2+)2019﹣2×|﹣|﹣()0【变式8-3】(2019春•莱州市期中)计算:(1)(2)【考点9 分母有理化的应用】【例9】(2019春•西城区校级期中)阅读下述材料:我们在学习二次根式时,熟悉的分母有理化以及应用其实,有一个类似的方法叫做“分子有理化”与分母有理化类似,分母和分子都乘以分子的有理化因式,从而消掉分子中的根式比如:﹣==分子有理化可以用来比较某些二次根式的大小,也可以用来处理一些二次根式的最值问题.例如:比较﹣和﹣的大小可以先将它们分子有理化如下:﹣=﹣=因为﹣>+,所以﹣<﹣再例如:求y=﹣的最大值.做法如下:解:由x+2≥0,x﹣2≥0可知x≥2,而y=﹣=当x=2时,分母﹣有最小值2,所以y的最大值是2解决下述两题:(1)比较3﹣4和2的大小;(2)求y=+﹣的最大值和最小值.【变式9-1】(2019春•微山县期中)【阅读材料】材料一:把分母中的根号化去,使分母转化为有理数的过程,叫做分母有理化通常把分子、分母乘以同一个不等于0的式子,以达到化去分母中根号的目的例如:化简解:材料二:化简的方法:如果能找到两个实数m,n,使m2+n2=a,并且mn=b,那么=m±n例如:化简解:+1【理解应用】(1)填空:化简的结果等于;(2)计算:①;②.【变式9-2】(2018秋•吴江区期中)阅读材料:黑白双雄、纵横江湖;双剑合璧、天下无敌.这是武侠小说中的常见描述,其意是指两个人合在一起,取长补短,威力无比.在二次根式中也有这种相辅相成的“对子”.如:,=3,它们的积不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式,于是,二次根式除法可以这样理解:如:,.像这样,通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.解决问题:(1)4﹣的有理化因式可以是,分母有理化得.(2)计算:①已知x=,求x2+y2的值;②.【变式9-3】(2019秋•唐河县期中)阅读下列材料,然后回答问题:在进行二次根式运算时,我们有时会碰上如、这样的式子,其实我们还可以将其进一步化简:==;===﹣1.以上这种化简过程叫做分母有理化.还可以用以下方法化简:====﹣1.请任用其中一种方法化简:①;②.【考点10 二次根式的应用】【例10】(2018春•嘉祥县期中)阅读理解:对于任意正整数a,b,∵(﹣)2≥0,∴a﹣2+b≥0,∴a+b≥2,只有当a=b时,等号成立;结论:在a+b≥2 (a、b均为正实数)中,只有当a=b时,a+b有最小值2.根据上述内容,回答下列问题:(1)若a+b=9,≤;(2)若m>0,当m为何值时,m+有最小值,最小值是多少?【变式10-1】(2019•太原一模)阅读与计算:请阅读以下材料,并完成相应的任务.古希腊的几何学家海伦在他的《度量》一书中给出了利用三角形的三边求三角形面积的“海伦公式”:如果一个三角形的三边长分别为a、b、c,设p=,则三角形的面积S=.我国南宋著名的数学家秦九韶,曾提出利用三角形的三边求面积的“秦九韶公式”(三斜求积术):如果一个三角形的三边长分别为a、b、c,则三角形的面积S=.(1)若一个三角形的三边长分别是5,6,7,则这个三角形的面积等于.(2)若一个三角形的三边长分别是,求这个三角形的面积.【变式10-2】已知一个三角形的三边长分别为12,,.(1)求此三角形的周长P(结果化成最简二次根式);(2)请你给出一个适当的a的值,使P为整数,并求出此时P的值.【变式10-3】斐波那契(约1170﹣1250,意大利数学家)数列是按某种规律排列的一列数,他发现该数列中的每个正整数都可以用无理数的形式表示,如第n(n为正整数)个数a n可表示为[()n﹣()n].(1)计算第一个数a1;(2)计算第二个数a2;(3)证明连续三个数之间a n﹣1,a n,a n+1存在以下关系:a n+1﹣a n=a n﹣1(n≥2);(4)写出斐波那契数列中的前8个数.【考点1 二次根式相关概念】【方法点拨】1.二次根式:形如a (0 a )的代数式叫做二次根式. 2.最简二次根式:(1)被开方数的因数是整数,因式是整式; (2)被开方数中不含能开得尽方的因数或因式.3.同类二次根式:几个二次根式化成最简二次根式以后,如果被开方数相同,像这样的二次根式称为同类二次根式.【例1】(2019春•浉河区校级月考)在式子,,,(y ≤0),和(a <0,b <0)中,是二次根式的有( ) A .3个B .4个C .5个D .6个【分析】根据二次根式的定义:一般地,我们把形如(a ≥0)的式子叫做二次根式进行分析即可. 【答案】解:式子,,(y ≤0),(a <0,b <0)是二次根式,共4个,故选:B .【点睛】此题主要考查了二次根式定义,关键是注意被开方数为非负数. 【变式1-1】(2019春•莱芜期中)二次根式:①;②;③;④;⑤中最简二次根式是( ) A .①②B .③④⑤C .②③D .只有④【分析】判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是. 【答案】解:③==|a ﹣1|,被开方数含有开得尽方的因式,不是最简二次根式;④==,被开方数含有分母,不是最简二次根式; ⑤==,被开方数含有小数(分数),不是最简二次根式;因此只有①②符合最简二次根式的条件. 故选:A .【点睛】根据最简二次根式的定义,最简二次根式必须满足两个条件: (1)被开方数不含分母;(2)被开方数不含能开得尽方的因数或因式.被开方数是多项式时,还需将被开方数进行因式分解,然后再观察判断.【变式1-2】(2019春•左贡县期中)二次根式:①;②;③;④中,与是同类二次根式的是()A.①和②B.①和③C.②和④D.③和④【分析】根据同类二次根式的定义解答即可.【答案】解:∵,,,∴与是同类二次根式的是①和③故选:B.【点睛】此题主要考查了同类二次根式的定义,即:化成最简二次根式后,被开方数相同,这样的二次根式叫做同类二次根式.需要注意化简前,被开方数不同也可能是同类二次根式.(2019春•海阳市期中)若两个最简二次根式和是同类二次根式,则n的值是()【变式1-3】A.﹣1B.4或﹣1C.1或﹣4D.4【分析】根据最简二次根式以及同类二次根式即可求出答案.【答案】解:由题意可知:n2﹣2n=n+4,∴解得:n=4或n=﹣1,当n=4时,n+4=8>0,此时不是最简二次根式,不符合题意,当n=﹣1时,n+4=3>0,综上所述,n=﹣1故选:A.【点睛】本题考查二次根式,解题的关键是正确理解最简二次根式以及同类二次根式,本题属于基础题型.【考点2 二次根式有意义条件】【方法点拨】二次根式有意义的条件,关键是掌握二次根式中的被开方数是非负数.分式分母不为零.【例2】(2019春•泰山区期中)式子在实数范围内有意义的条件是()A.x≥1B.x>1C.x<0D.x≤0【分析】直接利用二次根式有意义的条件分析得出答案.【答案】解:式子在实数范围内有意义的条件是:x﹣1>0,解得:x>1.故选:B.【点睛】此题主要考查了二次根式有意义的条件,正确把握定义是解题关键.【变式2-1】(2019春•西湖区校级期中)为使有意义,x的取值范围是()A.x≥﹣2且x≠2B.x>﹣2且x≠2C.x>2D.x>2或x≤﹣2【分析】根据二次根式有意义的条件题意可得2x+4≥0,再根据分式有意义的条件可得3x﹣6≠0,再解即可.【答案】解:由题意得:2x+4≥0,且3x﹣6≠0,解得:x≥﹣2且x≠2,故选:A.【点睛】此题主要考查了分式和二次根式有意义的条件,分式有意义,分母不为0;二次根式的被开方数是非负数.【变式2-2】(2018春•西华县期中)使代数式有意义的整数x有()A.5个B.4个C.3个D.2个【分析】直接利用二次根式的得出x的取值范围,进而得出整数x的值.【答案】解:∵代数式有意义,∴x+3>0,3﹣3x≥0,解得:x>﹣3,x≤1,则﹣3<x≤1,故代数式有意义的整数x有:﹣2,﹣1,0,1,共4个数.故选:B.【点睛】此题主要考查了二次根式有意义的条件,正确得出x的取值范围是解题关键.【变式2-3】(2019秋•安岳县校级期中)如果有意义,则x的取值范围()A.x≥3B.x≤3C.x>3D.x<3【分析】根据二次根式中的被开方数是非负数和分式分母不为零的条件可得3﹣x<0,再解即可.【答案】解:由题意得:3﹣x<0,解得:x>3,故选:C.【点睛】此题主要考查了二次根式有意义的条件,关键是掌握二次根式中的被开方数是非负数.分式分母不为零.【考点3 利用二次根式性质化简符号】【方法点拨】二次根式的化简求值,掌握二次根式的性质和绝对值的性质是解题的关键.【例3】(2019春•海阳市期中)把a根号外的因式移入根号内,运算结果是()A.B.C.﹣D.﹣【分析】根据二次根式的性质,可得答案.【答案】解:a根号外的因式移到根号内,化简的结果是﹣,故选:D.【点睛】本题考查了二次根式的性质,注意化简后不能改变原数的大小.【变式3-1】(2019春•汉阳区期中)已知ab<0,则化简后为()A.a B.﹣a C.a D.﹣a【分析】根据算术平方根和绝对值的性质=|a|,进行化简即可.【答案】解:∵a2≥0,ab<0,∴a<0,b>0,∴=|a|=﹣a,故选:B.【点睛】本题考查了二次根式的化简求值,掌握算术平方根和绝对值的性质是解题的关键.【变式3-2】(2018春•宜兴市期中)(a﹣1)变形正确的是()A.﹣1B.C.﹣D.﹣【分析】直接利用二次根式的性质化简得出答案.【答案】解:∵有意义,∴1﹣a>0,∴a﹣1<0,∴(a ﹣1)=﹣=﹣.故选:C .【点睛】此题主要考查了二次根式的性质与化简,正确化简二次根式是解题关键. 【变式3-3】(2019春•城区校级期中)化简﹣x,得( )A .(x ﹣1 )B .(1﹣x )C .﹣(x +1 )D .(x ﹣1 )【分析】根据已知式子得出x <0,再根据二次根式的性质把根号内的因式移入根号外,最后合并即可. 【答案】解:∵要使和有意义,必须x <0,∴﹣x =﹣x﹣x •(﹣)=﹣x+=(1﹣x ), 故选:B .【点睛】本题考查了二次根式的性质和化简的应用,能把各个部分根式化成最简根式是解此题的关键. 【考点4 利用二次根式的性质化简】 【方法点拨】二次根式的性质:(1))()(02≥=a a a(2)⎪⎩⎪⎨⎧<-=>==)()()(00002a a a a a a a【例4】(2019春•庐阳区校级期中)实数a ,b 在数轴上的位置如图所示,则化简的结果是( )A .a ﹣b +3B .a +b ﹣1C .﹣a ﹣b +1D .﹣a +b +1【分析】根据二次根式的性质以及绝对值的性质即可求出答案. 【答案】解:由数轴可知:﹣1<a <0<2<b , ∴a +1>0,b ﹣2>0, ∴原式=|a +1|﹣|b ﹣2| =a +1﹣b +2=a﹣b+3,故选:A.【点睛】本题考查二次根式,解题的关键是熟练运用二次根式的性质,本题属于基础题型.【变式4-1】(2019春•丰润区期中)若2<a<3,则=()A.5﹣2a B.1﹣2a C.2a﹣1D.2a﹣5【分析】根据二次根式的性质解答即可.【答案】解:因为2<a<3,所以=a﹣2﹣(3﹣a)=a﹣2﹣3+a=2a﹣5,故选:D.【点睛】此题考查二次根式的性质,关键是根据二次根式的性质解答.【变式4-2】(2018秋•海淀区校级期中)实数a、b、C在数轴上的位置所示,那么化简|c+a|+﹣的正确结果是()A.2b﹣c B.2b+c C.2a+c D.﹣2a﹣c【分析】先由数轴知c<b<0<a,且|c|>|a|,据此得出c+a<0,a﹣b>0,再根据绝对值性质和二次根式的性质2化简可得.【答案】解:由数轴知c<b<0<a,且|c|>|a|,则c+a<0,a﹣b>0,∴原式=﹣c﹣a﹣b﹣(a﹣b)=﹣c﹣a﹣b﹣a+b=﹣2a﹣c,故选:D.【点睛】本题主要考查二次根式的性质与化简,解题的关键是掌握二次根式的性质2:=|a|.【变式4-3】(2018春•汉阳区期中)若0<x<1,则﹣等于()A.B.﹣C.﹣2x D.2x【分析】首先利用完全平方公式化简,进而利用二次根式的性质求出即可.【答案】解:﹣=﹣=﹣=|x +|﹣|x ﹣| ∵0<x <1, ∴x ﹣<0,∴原式=x ++x ﹣=2x . 故选:D .【点睛】此题主要考查了二次根式的性质与化简,正确利用完全平方公式是解题关键. 【考点5 二次根式的乘除运算】 【方法点拨】掌握二次根式的乘除法则 (1)),(00≥≥=⋅b a ab b a(2)),(00>≥=b a b aba 【例5】(2019春•邗江区校级期中)计算: (1)÷ (2)÷3×【分析】(1)根据二次根式的性质把除式变形,根据二次根式的乘法法则计算; (2)根据二次根式的乘除法法则计算即可. 【答案】解:(1)÷=×= =;(2)÷3×=××==.【点睛】本题考查的是二次根式的乘除法、二次根式的性质,掌握二次根式的乘除法法则是解题的关键.【变式5-1】(2018秋•松江区期中)计算:•(﹣)÷(a>0)【分析】直接利用二次根式的性质化简进而得出答案.【答案】解:•(﹣)÷(a>0)=﹣•a2b÷=﹣9a2=﹣.【点睛】此题主要考查了二次根式的乘除运算,正确化简二次根式是解题关键.【变式5-2】(2019秋•闸北区期中)计算:【分析】利用除以一个数等于乘以这个数的倒数转化后利用二次根式的乘法运算法则进行计算即可.【答案】解:原式=(2×6)=12=4【点睛】本题考查了二次根式的乘除法运算,解题的关键是能够了解法则并能熟练的将除法转化为乘法进行运算.【变式5-3】(2019春•新泰市期中)化简下列式子:•3.【分析】直接利用二次根式的乘除运算法则化简得出答案.【答案】解:原式=2ab×3×(﹣2)=﹣12ab•a2=﹣12a3b.【点睛】此题主要考查了二次根式的乘除运算,正确化简二次根式是解题关键.【考点6 利用二次根式性质求代数式的值】【例6】(2019春•萧山区期中)已知,,求下列式子的值:(1)a2b+ab2;(2)a2﹣30b+b2;(3)(a﹣2)(b﹣2).【分析】(1)先分解因式,然后将a、b的值代入求值;(2)先变形,然后将a、b的值代入求值;(3)直接代入求值.【答案】解:(1)a2b+ab2=ab(a+b)=()=1×2;(2)a2﹣30b+b2=(a+b)2﹣2ab﹣30b=2﹣﹣30=(2)2﹣2﹣30+60=78﹣30;(3)(a﹣2)(b﹣2)=()()=()=5﹣4.【点睛】本题考查了根式的化简求值,适当对整式进行变形是解题的关键.【变式6-1】(2019春•芜湖期中)已知,,分别求下列代数式的值;(1)x2+y2;(2).【分析】(1)先将x、y进行分母有理化,得到x=﹣1,y=+1,再求出x﹣y与xy的值,然后根据完全平方公式得出x2+y2=(x﹣y)2+2xy,再整体代入即可;(2)将所求式子变形为,再整体代入即可.【答案】解:(1)∵=﹣1,=+1,∴x﹣y=﹣2,xy=2﹣1=1,∴x2+y2=(x﹣y)2+2xy=(﹣2)2+2×1=6;(2)∵x2+y2=6,xy=1,∴原式===6.【点睛】本题考查二次根式的化简求值,分母有理化,解题的关键是运用完全平方公式以及整体思想,本题属于基础题型.【变式6-2】(2019春•长白县期中)已知﹣=2,求的值.【分析】利用已知结合完全平方公式求出x2+=34,进而代入求出即可.【答案】解:∵﹣=2,∴(﹣)2=4,∴x+=6,∴(x+)2=36,∴x2+=34,∴==4.【点睛】此题主要考查了二次根式的化简求值,正确利用完全平方公式是解题关键.【变式6-3】(2018秋•通川区校级期中)已知x=,y=,求:(1)x2y﹣xy2的值;(2)x2﹣xy+y2的值.【分析】先将x和y的值分母有理化后,计算xy和x+y的值,再分别代入(1)和(2)问代入计算即可.【答案】解:∵x===3+2,y===3﹣2,∴xy==1,x+y=3+2+3﹣2=6,∴(1)x2y﹣xy2,=xy(x﹣y),=1×,=4;(2)x2﹣xy+y2,=(x+y)2﹣3xy,=62﹣3×1,=36﹣3,=33.【点睛】本题主要考查了二次根式的化简求值,在解答时应先化简x和y的值,并利用提公因式法和完全平方公式将所求式子进行变形是关键.【考点7 二次根式的加减运算】【方法点拨】二次根式的运算法则:二次根式相加减,先把各个二次根式化成最简,再把同类二次根式合并.【例7】(2019春•武昌区期中)计算:(1)(2)【分析】(1)直接化简二次根式进而合并得出答案;(2)直接化简二次根式进而合并得出答案.【答案】解:(1)原式=2+3﹣=0;(2)原式=×3+6×﹣5=2+3﹣5=0.【点睛】此题主要考查了二次根式的加减运算,正确化简二次根式是解题关键.【变式7-1】(2019春•萧山区期中)计算下列各式:(1);(2)+4﹣+.【分析】(1)首先化简二次根式,然后再合并同类二次根式;(2)首先化简二次根式,然后再合并同类二次根式.【答案】解:(1)原式=2++2﹣=+2;(2)原式=3+2﹣4+=5﹣.【点睛】此题主要考查了二次根式的加减,关键是掌握二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变.【变式7-2】(2018春•襄城区期中)计算:(1)﹣+﹣(2)﹣﹣+2【分析】(1)首先化简二次根式进而合并得出答案;(2)首先化简二次根式进而合并得出答案.【答案】解:(1)原式=6﹣4+3﹣5=﹣;(2)原式=﹣﹣+10=9.【点睛】此题主要考查了二次根式的加减运算,正确化简二次根式是解题关键.【变式7-3】(2018春•罗山县期中)(1)(2)【分析】(1)先进行二次根式、三次根式的化简,然后进行加减合并.(2)先去绝对值符号,然后化简二次根式,最后进行合并运算.【答案】解:(1)原式=9﹣3+=;(2)原式=﹣+﹣1﹣3+=2﹣4.【点睛】本题主要考查了二次根式的加减运算,要先进行二次根式的化简,然后再进行合并运算.【考点8 二次根式的混合运算】【例8】(2019春•泰兴市校级期中)计算:(1)(2)3【分析】(1)先化简各二次根式,再进一步计算可得;(2)先化简各二次根式、除法转化为乘法,再进一步计算可得.【答案】解:(1)原式=(2﹣)﹣3(+)=2﹣﹣﹣3=﹣﹣;(2)原式=••(﹣)=﹣2.【点睛】本题主要考查二次根式混合运算,解题的关键是掌握二次根式的混合运算顺序和运算法则.【变式8-1】(2019春•广东期中)计算(1)()÷(2)(3)2﹣()()【分析】(1)先化简各二次根式,再计算括号内的加减,最后计算除法即可得;(2)利用完全平方公式和平方差公式计算可得.【答案】解:(1)原式=(5+4﹣3)÷2=6÷2=3;(2)原式=19﹣6﹣3+4=20﹣6.【点睛】本题主要考查二次根式的混合运算,解题的关键是熟练掌握二次根式的混合运算顺序和运算法则及完全平方公式、平方差公式.【变式8-2】(2019春•杭锦后旗期中)计算:(1)﹣×+(2)(2﹣)2018(2+)2019﹣2×|﹣|﹣()0【分析】(1)根据二次根式的乘除法则运算;(2)根据积的乘方和零指数幂的意义计算.【答案】解:(1)原式=﹣+2=4﹣+2=4+;(2)原式=[(2﹣)(2+)]2018•(2+)﹣2×﹣1=(4﹣3)2018•(2+)﹣﹣1=2+﹣﹣1=1.【点睛】本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.【变式8-3】(2019春•莱州市期中)计算:(1)(2)【分析】(1)根据二次根式的加减法和除法可以解答本题;(2)根据平方差公式和完全平方公式可以解答本题.【答案】解:(1)=(9﹣2+)÷4=8÷4=2;(2)=[()+3][()﹣3]=()2﹣18=3﹣6+6﹣18=﹣9﹣6.【点睛】本题考查二次根式的混合运算,解答本题的关键是明确二次根式混合运算的计算方法.【考点9 分母有理化的应用】【例9】(2019春•西城区校级期中)阅读下述材料:我们在学习二次根式时,熟悉的分母有理化以及应用其实,有一个类似的方法叫做“分子有理化”与分母有理化类似,分母和分子都乘以分子的有理化因式,从而消掉分子中的根式比如:﹣==分子有理化可以用来比较某些二次根式的大小,也可以用来处理一些二次根式的最值问题.例如:比较﹣和﹣的大小可以先将它们分子有理化如下:﹣=﹣=因为﹣>+,所以﹣<﹣再例如:求y=﹣的最大值.做法如下:解:由x+2≥0,x﹣2≥0可知x≥2,而y=﹣=当x=2时,分母﹣有最小值2,所以y的最大值是2解决下述两题:(1)比较3﹣4和2的大小;(2)求y=+﹣的最大值和最小值.【分析】(1)利用分子有理化得到3﹣4=,2﹣=,然后比较3+4和2+的大小即可得到3﹣4与2﹣的大小;(2)利用二次根式有意义的条件得到0≤x≤1,而y=+,利用当x=0时,有最大值1,有最大值1得到所以y的最大值;利用当x=1时,有最小值﹣1,有最下值0得到y的最小值.【答案】解:(1)3﹣4==,2﹣==,而3>2,4>,∴3+4>2+,∴3﹣4<2﹣;(2)由1﹣x≥0,1+x≥0,x≥0得0≤x≤1,y=+,当x=0时,+有最小值,则有最大值1,此时有最大值1,所以y的最大值为2;当x=1时,+有最大值,则有最小值﹣1,此时有最下值0,所以y的最小值为﹣1.【点睛】本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后合并同类二次根式即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.【变式9-1】(2019春•微山县期中)【阅读材料】材料一:把分母中的根号化去,使分母转化为有理数的过程,叫做分母有理化通常把分子、分母乘以同一个不等于0的式子,以达到化去分母中根号的目的例如:化简解:材料二:化简的方法:如果能找到两个实数m,n,使m2+n2=a,并且mn=b,那么=m±n例如:化简解:+1【理解应用】(1)填空:化简的结果等于;(2)计算:①;②.【分析】(1)根据分母有理化法则计算;(2)①根据完全平方公式、二次根式的性质化简;②先把原式分母有理化,再合并同类二次根式即可.【答案】解:(1)原式===4+,故答案为:4+;(2)①===﹣;②原式=﹣1+﹣+4﹣+…+﹣=﹣1.【点睛】本题考查的是分母有理化、二次根式的化简,掌握分母有理化法则、二次根式的性质是解题的关键.【变式9-2】(2018秋•吴江区期中)阅读材料:黑白双雄、纵横江湖;双剑合璧、天下无敌.这是武侠小说中的常见描述,其意是指两个人合在一起,取长补短,威力无比.在二次根式中也有这种相辅相成的“对子”.如:,=3,它们的积不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式,于是,二次根式除法可以这样理解:如:,.像这样,通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.解决问题:(1)4﹣的有理化因式可以是,分母有理化得.(2)计算:①已知x=,求x2+y2的值;②.【分析】(1)找出各式的分母有理化因式即可;(2)①将x与y分母有理化后代入原式计算即可得到结果.②原式各项分母有理化,合并即可得到结果.【答案】解:(1)4﹣的有理化因式可以是4+,==,故答案为:4+,;(2)①当x====2+,y====2﹣时,x2+y2=(x+y)2﹣2xy=(2++2﹣)2﹣2×(2+)×(2﹣)=16﹣2×1=14.②原式=﹣1+﹣+﹣+…+﹣=﹣1.【点睛】此题考查了分母有理化,正确选择两个二次根式,使它们的积符合平方差公式是解答问题的关键.【变式9-3】(2019秋•唐河县期中)阅读下列材料,然后回答问题:在进行二次根式运算时,我们有时会碰上如、这样的式子,其实我们还可以将其进一步化简:==;===﹣1.以上这种化简过程叫做分母有理化.还可以用以下方法化简:====﹣1.请任用其中一种方法化简:①;②.【分析】①根据平方差公式分母有理化即可求解;②把分子5变为12﹣7,再根据平方差公式分解因式,再约分计算即可求解.【答案】解:①==;②===2﹣.【点睛】本题主要考查了分母有理化,解题的关键是找准有理化因式.【考点10 二次根式的应用】【例10】(2018春•嘉祥县期中)阅读理解:对于任意正整数a,b,∵(﹣)2≥0,∴a﹣2+b≥0,∴a+b≥2,只有当a=b时,等号成立;结论:在a+b≥2 (a、b均为正实数)中,只有当a=b时,a+b有最小值2.根据上述内容,回答下列问题:(1)若a+b=9,≤;(2)若m>0,当m为何值时,m+有最小值,最小值是多少?【分析】(1)根据a+b≥2 (a、b均为正实数),进而得出即可;(2)根据a+b≥2 (a、b均为正实数),进而得出即可.【答案】解:(1)∵a+b≥2 (a、b均为正实数),∴a+b=9,则a+b≥2,即≤;故答案为:;(2)由(1)得:m+≥2,即m+≥2,当m=时,m=1(负数舍去),故m+有最小值,最小值是2.【点睛】此题主要考查了二次根式的应用,根据题意结合a+b≥2 (a、b均为正实数)求出是解题关键.【变式10-1】(2019•太原一模)阅读与计算:请阅读以下材料,并完成相应的任务.古希腊的几何学家海伦在他的《度量》一书中给出了利用三角形的三边求三角形面积的“海伦公式”:如果一个三角形的三边长分别为a、b、c,设p=,则三角形的面积S=.我国南宋著名的数学家秦九韶,曾提出利用三角形的三边求面积的“秦九韶公式”(三斜求积术):如果。
二次根式综合题型

一、逆用 ( a ) 2 a(a 0) 进行因式分解 3、在实数范围内因式分解
1
(1)x -3;
2
(2) x 6 x 9
4 2
二、利用二次根式的性质进行化简、计算 4、根据下列条件,求字母 x 的取值范围:
2 (1) ( x 3) x 3 ; (2) x 2 2x x ; (3) x 2 2 x 1 =1-x ;
14. 分析: 第一个二次根式的被开方数的分子与分母都可以分解因式. 把它们分别分解因式 后,再利用二次根式的基本性质把式子化简,化简中应注意利用题中的隐含条件 3-a≥0 和
1-a>0。
3
3和 3 A. 3 和 18 B. C. a b和 ab 知识点四:二次根式有意义的条件 2、x 是怎样的实数时,下列各式在实数范围内有意义?
(1) x 2 - 3 2 x ; (2) x - 知识点五:二次根式的性质 ① a 0(a 0) 双重非负性; ③ ② ( a ) 2 a(a 0) ;
c 3 3 c ,求 abc 的值。
分析:
c3 3c
}有意义
被开方数非负
c 3 0 c 3 3 c 0
b 2a 3 a b 2 0
b 2a 3 0 a b 2 0
知识点六、分母有理化 把分母中的根号化去,叫做分母有理化;两个含有二次根式的代数式相乘,若它们的积 不含二次根式,则称这两个代数式互为有理化因式。 常用的有理化因式:
1, 1.5 , 2
n , m m , 等都不是最简二次根式。 a
。如:
ab3 ,
x3 x 2 ,
2 2 问: x y 是最简二次根式吗?
专题02 二次根式综合(压轴33题10个考点)(解析版)

专题02二次根式综合(压轴33题10个考点)一.二次根式的定义(共1小题)1.若是整数,则正整数n的最小值是51.【答案】51.【解答】解:∵204=4×51,∴,∴,∵是整数,且n是整数,∴n的最小值为:51.故答案为:51.二.二次根式有意义的条件(共3小题)2.使式子有意义的x的取值范围是()A.x≥﹣1B.﹣1≤x≤2C.x≤2D.﹣1<x<2【答案】B【解答】解:根据题意,得,解得,﹣1≤x≤2;故选:B.3.已知|2004﹣a|+=a,则a﹣20042=2005.【答案】2005.【解答】解:∵有意义,∴a﹣2005≥0,解得:a≥2005,∴|2004﹣a|+=a﹣2004+=a,故=2004,∴a﹣2005=20042,∴a﹣20042=a﹣(a﹣2005)=a﹣a+2005=2005.故答案为:2005.4.已知,则x2022y2023=﹣.【答案】.【解答】解:∵,即,解得:,∴x=2,∴,∵x2022y2023=(xy)2022•y,将x=2,代入,∴x2022y2023=(xy)2022•y=[2×(﹣)]2022×(﹣)=(﹣1)2022×(﹣)=﹣.故答案为:.三.二次根式的性质与化简(共8小题)5.已知x<1,则化简的结果是()A.x﹣1B.x+1C.﹣x﹣1D.1﹣x【答案】D【解答】解:==|x﹣1|∵x<1,∴原式=﹣(x﹣1)=1﹣x,故选:D.6.实数a,b表示的点在数轴上的位置如图,则将化简的结果是()A.4B.2a C.2b D.2a﹣2b【答案】A【解答】解:由数轴知:﹣2<a<﹣1,1<b<2,a<b,∴a+2>0,b﹣2<0,a﹣b<0.∴=|a+2|+|b﹣2|+|a﹣b|=a+2+2﹣b+b﹣a=4.故选:A.7.如图是一个按某种规律排列的数阵:根据数阵排列的规律,第n(n是整数,且n≥4)行从左向右数第(n﹣3)个数是(用含n的代数式表示)()A.B.C.D.【答案】C【解答】解:由图中规律知,前(n﹣1)行的数据个数为2+4+6+…+2(n﹣1)=n(n ﹣1),所以第n(n是整数,且n≥4)行从左向右数第(n﹣3)个数的被开方数是n(n﹣1)+n﹣3=n2﹣3,所以第n(n是整数,且n≥4)行从左向右数第(n﹣3)个数是.故选:C.8.已知T1===,T2===,T3===,…T n=,其中n为正整数.设S n=T1+T2+T3+…+T n,则S2021值是()A.2021B.2022C.2021D.2022【答案】A【解答】解:由T1、T2、T3…的规律可得,T1==1+(1﹣),T2==1+(﹣),T3==1+(﹣),……T2021==1+(﹣),所以S2021=T1+T2+T3+…+T2021=1+(1﹣)+1+(﹣)+1+(﹣)+…+1+(﹣)=(1+1+1+…+1)+(1﹣+﹣+﹣+…+﹣)=2021+(1﹣)=2021+=2021,故选:A.9.已知a≠0,b≠0且a<b,化简的结果是﹣a.【答案】﹣a.【解答】解:由题意:﹣a3b≥0,即ab≤0,∵a<b,∴a<0<b,所以原式=|a|=﹣a,故答案为:﹣a.10.已知|x+2|+|1﹣x|=9﹣﹣,则x+y的最小值为﹣3.【答案】﹣3.【解答】解:∵|x+2|+|1﹣x|=9﹣﹣,∴|x+2|+|x﹣1|+|y+1|+|y﹣5|=9,∵|x+2|+|x﹣1|可理解为在数轴上,数x的对应的点到﹣2和1两点的距离之和;|y+1|+|y ﹣5|可理解为在数轴上,数y的对应的点到﹣1和5两点的距离之和,∴当﹣2≤x≤1,|x+2|+|x﹣1|的最小值为3;当﹣1≤y≤5时,|y+1|+|y﹣5|的最小值为6,∴x的范围为﹣2≤x≤1,y的范围为﹣1≤y≤5,当x=﹣2,y=﹣1时,x+y的值最小,最小值为﹣3.故答案为﹣3.11.若,则m的取值范围是m≤4.【答案】见试题解答内容【解答】解:,得4﹣m≥0,解得m≤4,故答案为:m≤4.12.若x<2,化简|﹣x|的正确结果是2x+2或﹣4x+2.【答案】2x+2或﹣4x+2.【解答】解:当0≤x<2时,原式=|x﹣2|+3x=2﹣x+3x=2x+2;当x<0时,原式=|x﹣2|﹣3x=2﹣x﹣3x=﹣4x+2.故答案为:2x+2或﹣4x+2.四.二次根式的乘除法(共4小题)13.使式子成立的条件是()A.a≥5B.a>5C.0≤a≤5D.0≤a<5【答案】B【解答】解:由题意得:,解得:a>5.故选:B.14.“分母有理化”是我们常用的一种化简的方法,如:==7+ 4,除此之外,我们也可以用平方之后再开方的方式来化简一些有特点的无理数,如:对于﹣,设x=﹣,易知>,故x>0,由x2=(﹣)2=3++3﹣﹣2=2,解得x=,即﹣=.根据以上方法,化简+﹣后的结果为()A.5+3B.5+C.5﹣D.5﹣3【答案】D【解答】解:设x=﹣,且>,∴x<0,∴x2=6﹣3﹣2+6+3,∴x2=12﹣2×3=6,∴x=,∵=5﹣2,∴原式=5﹣2﹣=5﹣3,故选:D.15.若a,b为有理数且满足,则a+b=4.【答案】1.【解答】解:∵,∴=.∴a=3,b=1.∴a+b=3+1=4.故答案为:4.16.阅读下面的解题过程体会如何发现隐含条件并回答下面的问题化简:.解:隐含条件1﹣3x≥0,解得:.∴1﹣x>0.∴原式=(1﹣3x)﹣(1﹣x)=1﹣3x﹣1+x=﹣2x.【启发应用】(1)按照上面的解法,试化简.【类比迁移】(2)实数a,b在数轴上的位置如图所示,化简:.(3)已知a,b,c为A B C的三边长.化简:.【答案】(1)1;(2)﹣a﹣2b;(3)2a+2b+2c.【解答】解:(1)隐含条件2﹣x≥0,解得:x≤2,∴x﹣3<0,∴原式=(3﹣x)﹣(2﹣x)=3﹣x﹣2+x=1;(2)观察数轴得隐含条件:a<0,b>0,|a|>|b|,∴a+b<0,b﹣a>0,∴原式=﹣a﹣a﹣b﹣b+a=﹣a﹣2b;(3)由三角形的三边关系可得隐含条件:a+b+c>0,a﹣b<c,b﹣a<c,c﹣b<a,∴a﹣b﹣c<0,b﹣a﹣c<0,c﹣b﹣a<0,∴原式=(a+b+c)+(﹣a+b+c)+(﹣b+a+c)+(﹣c+b+a)=a+b+c﹣a+b+c﹣b+a+c﹣c+b+a=2a+2b+2c.五.分母有理化(共1小题)17.阅读材料:我们已经知道,形如的无理数的化简要借助平方差公式:例如:.下面我们来看看完全平方公式在无理数化简中的作用.问题提出:该如何化简?建立模型:形如的化简,只要我们找到两个数a,b,使a+b=m,ab=n,这样=m,,那么便有:(a>b),问题解决:化简:,解:首先把化为,这里m=7,n=12,由于4+3=7,4×3=12,即=7,∴.模型应用1:利用上述解决问题的方法化简下列各式:(1);(2);模型应用2:(3)在Rt△ABC中,∠C=90°,AB=4﹣,AC=,那么BC边的长为多少?(结果化成最简).【答案】(1)1+;(2)2﹣;(3)2﹣2.【解答】解:(1)这里m=6,n=5,由于1+5=6,1×5=5,即12+()2=6,1×=,所以:===1+;(2)首先把化为,这里m=13,n=40,由于5+8=13,5×8=40,即()2+()2=13,×=,所以====﹣=2﹣;(3)在Rt△ABC中,由勾股定理得,AC2+BC2=AB2,所以,所以,.六.同类二次根式(共1小题)18.已知最简二次根式与是同类二次根式,则a的值为()A.16B.0C.2D.不确定【答案】B【解答】解:∵=3,而最简二次根式与是同类二次根式,∴a+2=2,解得a=0.故选:B.七.二次根式的加减法(共1小题)19.若,则x﹣x2的值为﹣6.【答案】﹣6.【解答】解:由题意得,x﹣2≥0.∴x≥2.∴1﹣x<0.∴.∴x﹣1+=x.∴.∴x=3.∴x﹣x2=3﹣9=﹣6.故答案为:﹣6.八.二次根式的混合运算(共4小题)20.已知,,则2y﹣3x的平方根为±4.【答案】±4.【解答】解:∵,∴96﹣x≥0,∴x≤96,∴100﹣x+96﹣x=200,解得x=﹣2,∵,∴m+23≥0,m﹣2≥0,2﹣m≥0,解得m=2,∴y=5,∴±=±=±4,故答案为:±4.21.计算的结果是+.【答案】+.【解答】解:原式=[(﹣)(+)]2022×(+)=(2﹣3)2022×(+)=+.故答案为:+.22.已知a=,b=.(1)求a+b的值;(2)设m是a小数部分,n是b整数部分,求代数式4m2+4mn+n2的值.【答案】(1)2;(2)20.【解答】解:(1)a===﹣2,b===+2.a+b=﹣2++2=2,(2)∵2<<3,∴0<﹣2<1,4<+2<5,∴m=﹣2,n=4,∴4m2+4mn+n2=(2m+n)2=(2﹣4+4)2=20.23.先阅读下面的材料,再解答下列问题.∵,∴.特别地,,∴.这种变形叫做将分母有理化.利用上述思路方法计算下列各式:(1);(2).【答案】(1)2020;(2)1.【解答】解:(1)===2021﹣1=2020;(2)====1.九.二次根式的化简求值(共8小题)24.已知,则代数式x2﹣2x﹣6的值是()A.B.﹣10C.﹣2D.【答案】C【解答】解:∵,∴x﹣1=,∴x2﹣2x﹣6=(x﹣1)2﹣7=()2﹣7=5﹣7=﹣2,故选:C.25.已知,,则a与b的关系是()A.a=b B.ab=1C.ab=﹣1D.a+b=0【答案】D【解答】解:a===3﹣=﹣(﹣3),A.a=﹣b,故本选项不符合题意;B.ab=(3﹣)×(﹣3)=﹣(﹣3)2=﹣(5﹣6+3)=﹣5+6﹣3=﹣8+6,故本选项不符合题意;C.ab=﹣8+6,故本选项不符合题意;D.a+b=3﹣+﹣3=0,故本选项符合题意.故选:D.26.若x2+y2=1,则++的值为()A.0B.1C.2D.3【答案】D【解答】解:∵x2+y2=1,∴﹣1≤x≤1,﹣1≤y≤1,∵==,x+1≥0,y﹣2<0,(x+1)(y﹣2)≥0,∴x+1=0,∴x=﹣1,∴y=0,∴++=2+1+0=3.故选:D.27.若a=2+,b=2﹣,则=8.【答案】8.【解答】解:∵a=2+,b=2﹣,∴a2=(2+√5)2=4+4+5=9+4,b2=(2﹣)2=4﹣4+5=9﹣4,ab=(2+)(2﹣)=4﹣5=﹣1.﹣===8.故答案为:8.28.若m=,则m3﹣m2﹣2017m+2015=4030.【答案】见试题解答内容【解答】解:∵m====,∴原式=m2(m﹣1)﹣2017m+2015=(+1)2×﹣2017(+1)+2015=(2017+2)﹣2017﹣2017+2015=2017+2×2016﹣2017﹣2017+2015=4032﹣2=403029.已知a=2+,b=,则a2﹣3ab+b2的值为11.【答案】11.【解答】解:当a=2+,b=时,a2﹣3ab+b2,=﹣+,=,=,=11.30.某同学在解决问题:已知,求2a2﹣8a+1的值.他是这样分析与求解的:先将a进行分母有理化,过程如下,,∴,∴(a﹣2)2=3,a2﹣4a+4=3,∴a2﹣4a=﹣1,∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.请你根据上述分析过程,解决如下问题:(1)若,请将a进行分母有理化;(2)在(1)的条件下,求a2﹣2a的值;(3)在(1)的条件下,求2a3﹣4a2﹣1的值.【答案】(1);(2)1;(3).【解答】解:(1)a===;(2)∵,∴(a﹣1)2=2,(a﹣1)2=a2﹣2a+1,∴a2﹣2a+1=2,∴a2﹣2a=1;(3)根据(2)可知,a2﹣2a=1,∴2a3﹣4a2﹣1=2a(a2﹣2a)﹣1=2a﹣1,当a=时,原式=2()﹣1=2.31.小芳在解决问题:已知a=,求2a2﹣8a+1的值.他是这样分析与解的:a==2﹣,∴a=2﹣,∴(a﹣2)2=3,a2﹣4a+4=3,∴a2﹣4a=﹣1,∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.请你根据小芳的分析过程,解决如下问题:(1)计算:.(2)若a=.①化简a,求4a2﹣8a﹣1的值;②求a3﹣3a2+a+1的值.【答案】(1)9;(2)①a=+1,4a2﹣8a﹣1的值是3;②0.【解答】解:(1)=﹣1+++…+=﹣1+=﹣1+10=9;(2)①a====+1,∴a=+1,∴(a﹣1)2=()2=2,∴a2﹣2a+1=2,∴a2﹣2a=1,∴4a2﹣8a﹣1=4(a2﹣2a)﹣1=4×1﹣1=4﹣1=3;②由①知a2﹣2a=1,∴a3﹣3a2+a+1=a(a2﹣2a)﹣(a2﹣2a)﹣a+1=a×1﹣1﹣a+1=a﹣1﹣a+1=0.十.二次根式的应用(共2小题)32.俊俊和霞霞共同合作将一张长为,宽为1的矩形纸片进行裁剪(共裁剪三次),裁剪出来的图形刚好是4个等腰三角形(无纸张剩余).霞霞说:“有一个等腰三角形的腰长是1”;俊俊说:“有一个等腰三角形的腰长是﹣1”;那么另外两个等腰三角形的腰长可能是1或或2﹣.【答案】1或或2﹣.【解答】解:如图1方式裁剪,另两个等腰三角形腰长是或;如图2方式裁剪,另两个等腰三角形腰长都是1.故答案为:1或或2﹣.33.古希腊几何学家海伦通过证明发现:如果一个三角形的三边长分别为a,b,c.记,那么三角形的面积为,俗称海伦公式,若在△ABC中,AB=3,BC=6,AC=7,则用海伦公式求得△ABC的面积为.【答案】【解答】解:由题意可得:a=6,b=7,c=3,∴,∴===,故答案为:.。
二次根式知识点归纳及题型总结-精华版
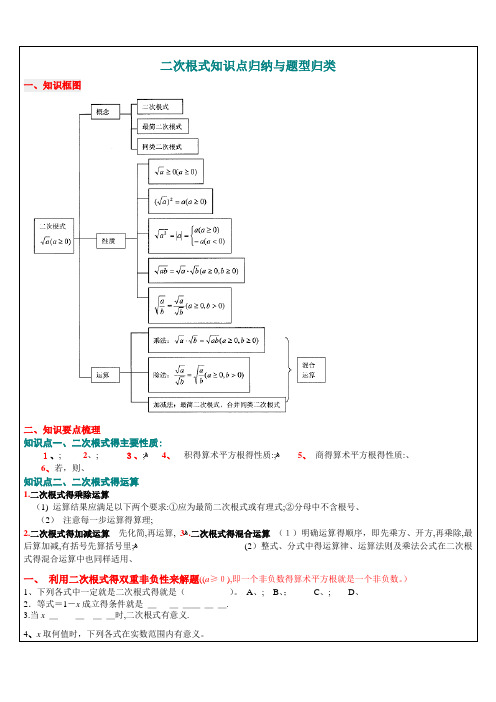
二次根式知识点归纳与题型归类一、知识框图二、知识要点梳理知识点一、二次根式得主要性质:1、; 2、; 3、;ﻫ4、积得算术平方根得性质:;ﻫ5、商得算术平方根得性质:、6、若,则、知识点二、二次根式得运算1.二次根式得乘除运算(1) 运算结果应满足以下两个要求:①应为最简二次根式或有理式;②分母中不含根号、(2)注意每一步运算得算理;2.二次根式得加减运算先化简,再运算, ﻫ3.二次根式得混合运算(1)明确运算得顺序,即先乘方、开方,再乘除,最后算加减,有括号先算括号里;ﻫ(2)整式、分式中得运算律、运算法则及乘法公式在二次根式得混合运算中也同样适用、一、利用二次根式得双重非负性来解题((a≥0),即一个非负数得算术平方根就是一个非负数。
)1、下列各式中一定就是二次根式得就是()。
A、; B、;C、; D、2.等式=1-x成立得条件就是_____________.3.当x____________时,二次根式有意义.4、x取何值时,下列各式在实数范围内有意义。
(1) (2) (3) ﻫ(4)若,则x得取值范围就是(5)若,则x得取值范围就是。
6、若有意义,则m能取得最小整数值就是 ;若就是一个正整数,则正整数m得最小值就是________.7、当x为何整数时,有最小整数值,这个最小整数值为。
8、若,则=_____________;若,则9.设m、n满足,则=。
10、若三角形得三边a、b、c满足=0,则第三边c得取值范围就是11、若,且时,则( ) A、B、ﻩC、D、二.利用二次根式得性质=|a|=(即一个数得平方得算术平方根等于这个数得绝对值)来解题1、已知=-x,则( ) A、x≤0 B、x≤-3 C、x≥-3 D、-3≤x≤02、.已知a<b,化简二次根式得正确结果就是()A. B. C.D.3、若化简|1-x|-得结果为2x-5则( ) A、x为任意实数B、1≤x≤4 C、x≥1 D、x≤44、已知a,b,c为三角形得三边,则=5、当-3<x<5时,化简= 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题:二次根式重难点综合题型
题型一:二次根式的性质
1.写出下列各式有意义时x 的取值范围.
(1)12--x ; (2) .
2.已知:,x y 为实数,且311+-+-<x x y , 化简:23816y y y ---+。
3.已知,a b , 求20152014a a -的值。
4.已知数a ,b ,c 在数轴上的位置如图所示:
化简:||)(|2|||22b b c c a a a ---++--.
题型二:二次根式的化简
1.判断下列各式是不是最简二次根式,如果不是,请化简成最简二次根式.
(1) (2) (3) (4)
2.已知2
31-=
a ,
2
31+=
b ,求值: (1)33ab b a - ; (2) 22b ab a ++。
3.化简下列二次根式
(1) 549549++- (2)
4.已知:625+=+b a ,625-=-b a ,求2015
2212⎪
⎪⎭
⎫ ⎝⎛--b a 的值。
题型三:二次根式的运算 1.计算下列各题: (1) (2)
(3) (4)
(5) (6)
2.计算:
2004
2003200320041
3
22312
21++
+++
+
a
1-42+x 3
8m -()x x --11131
+x 35
6356++-()
21341183122⨯-⨯;2
23b a b a a
b ⨯÷-⎪⎪⎭
⎫ ⎝⎛-+483814122223321825038a a a a a a -+(1110a b b +--).32
18)(8321(-+.
)21()21(20092008-+
※课后练习
1.若53+的小数部分是a ,5-3的小数部分是b ,求a +b 的
值。
2.已知411+=-+-y x x ,则xy 的平方根为______.
3.已知25-=x ,求4)25()549(2++-+x x 的值.
4.计算下列各题:
(1)
(2)
(3) (4)
5.已知,23,23-=+=y x
求(1)x 2-xy +y 2; (2)x 3y +xy 3的值.
6.已知△ABC 的三边长a ,b ,c 均为整数,且a 和b 满足
.09622=+-+-b b a 试求△ABC 的c 边的长.
7
.已知:11a a +=221
a a
+的值。
8.化简:
9.已知:x,y,z 满足关系式:
y x y x z y x z y x --+-+=-++--+20122012223,试求x ,y ,
z 的值。
10.求值:
2004
20031431321211++
++++++ x
x x x x 1399413+-a
a b b a a a 2129122+-+)
23(623
24b a a b b a ab b -⨯-÷2
310253b a
b a ÷-
⋅。
