对称性与守恒定律
物理学中的对称性与守恒定律

物理学中的对称性与守恒定律对称性和守恒定律是物理学中的基本概念,它们在理解和解释自然界中各种物理现象和规律中起着重要作用。
本文将探讨物理学中的对称性和守恒定律,并探讨它们之间的密切关系。
一、对称性在物理学中的意义对称性是物理学中的重要概念,它描述了物理系统在某些变换下保持不变的性质。
在物理学中,对称性可以分为时空对称性和内禀对称性两种。
1. 时空对称性时空对称性是指物理系统在时空变换下保持不变。
在相对论物理学中,洛伦兹变换是描述时空变换的数学工具。
根据洛伦兹变换的不同类型,物理系统可以表现出平移对称性、旋转对称性和洛伦兹对称性等。
平移对称性是指物理系统在空间位置上的平移不会改变其物理性质。
例如,一个均匀介质中的物理规律在空间中的任何位置都是相同的。
旋转对称性是指物理系统在空间方向的旋转下保持不变。
例如,地球的自转周期不会影响物理规律的成立。
洛伦兹对称性是指物理系统在洛伦兹变换下保持不变,包括时间和空间的坐标变换。
相对论物理学中的基本原理就是洛伦兹对称性。
2. 内禀对称性内禀对称性是指物理系统在内部变换下保持不变。
在粒子物理学中,内禀对称性描述了粒子的基本性质。
例如,电荷共轭对称性指粒子与其反粒子具有相同的物理性质。
对称性在物理学中具有广泛的应用。
它不仅可以用于解释物理定律的成因,还可以帮助物理学家发现新的规律和预测新的物理现象。
二、守恒定律与对称性的关系守恒定律是物理学中的基本定律,描述了物理系统在某些变换下某个物理量保持不变的规律。
守恒定律与对称性之间存在着密切的关系。
以能量守恒定律为例,它描述了物理系统的能量在各种变换下保持不变。
能量守恒定律与时间平移对称性密切相关,即物理规律在时间上的平移不变性保证了能量守恒。
动量守恒定律是另一个重要的守恒定律,它描述了物理系统的总动量在某些变换下保持不变。
动量守恒定律与空间平移对称性密切相关,即物理规律在空间上的平移不变性保证了动量守恒。
角动量守恒定律和电荷守恒定律等也与对称性有着密切的联系。
理论物理中对称性与守恒定律的关系

理论物理中对称性与守恒定律的关系在理论物理中,对称性与守恒定律是两个核心概念。
对称性描述了系统在某些变换下保持不变的性质,而守恒定律则说明了系统在各种变化中某些物理量的不变性。
这两个概念之间存在着密切的关系,对称性的存在导致了守恒定律的存在,反之亦然。
本文将深入探讨对称性与守恒定律的关系。
首先,让我们来了解对称性的概念。
对称性可以简单地理解为某种变换下系统保持不变的性质。
在物理学中,常见的对称性有平移对称性、旋转对称性、时间平移对称性和粒子对称性等。
平移对称性指的是系统在空间中的平移下保持不变,旋转对称性指的是系统在空间中的旋转下保持不变,时间平移对称性指的是系统在时间上的平移下保持不变,而粒子对称性指的是系统在粒子交换下保持不变。
对称性在物理学中起着非常重要的作用。
与对称性相关联的是守恒定律。
守恒定律描述了系统在各种变化中某些物理量守恒的性质。
守恒定律可以用数学表达式表示为:某一物理量的变化率等于该物理量进入与离开系统的流量之差。
根据对称性的不同,我们可以得到不同的守恒定律。
首先,根据时间平移对称性,我们可以得到能量守恒定律。
能量守恒定律指的是系统的能量在时间上保持不变。
这是因为系统的物理规律在时间上的不变性导致的。
无论系统中发生了怎样的能量转化,总能量的变化率始终为零,能量守恒得到维持。
其次,根据空间平移对称性,我们可以得到动量守恒定律。
动量守恒定律指的是系统的动量在空间上保持不变。
这是因为系统的物理规律在空间上的不变性导致的。
无论系统中的物体如何运动,总动量的变化率始终为零,动量守恒得到维持。
此外,根据空间旋转对称性,我们可以得到角动量守恒定律。
角动量守恒定律指的是系统的角动量在空间上保持不变。
这是因为空间旋转对称性导致的。
无论系统中的物体如何旋转,总角动量的变化率始终为零,角动量守恒得到维持。
最后,根据粒子对称性,我们可以得到电荷守恒定律。
电荷守恒定律指的是系统中的总电荷量在粒子交换下保持不变。
粒子物理学中的对称性与守恒定律

粒子物理学中的对称性与守恒定律粒子物理学是研究物质的最基本组成部分和相互作用的学科。
在这个领域中,对称性与守恒定律是非常重要的概念。
对称性指的是在某种变换下,系统的性质保持不变;而守恒定律则是指物理量在时间和空间上的变化率为零。
一、对称性在粒子物理中的重要性对称性是粒子物理学中一项基本原则。
根据量子力学和相对论的理论基础,我们知道,自然界的基本定律应该具有某种形式的对称性。
首先是空间对称性,即物理系统的性质在空间位置的变换下保持不变。
例如,相对论性量子场论中的拉格朗日量具有洛伦兹对称性,这意味着在任何洛伦兹变换下,物理定律保持不变。
其次是时间对称性,即物理系统的性质在时间演化的过程中保持不变。
例如,量子力学中的薛定谔方程描述的系统具有时间反演对称性,即系统在时间反演下的演化与正常的时间演化完全一致。
还有内禀对称性,即系统在某种内部变换下保持不变。
例如,电荷守恒定律是电荷在整个物理过程中都保持不变的内禀对称性。
二、粒子物理中的守恒定律在粒子物理学中,守恒定律描述了一系列重要的物理量在物理过程中的守恒。
这些守恒定律为粒子物理学的研究和实验提供了重要的基础。
首先是能量守恒定律。
能量是物理过程中最基本的物理量之一,根据能量守恒定律,能量在物理过程中总是守恒的。
例如,在粒子碰撞实验中,总能量守恒可以用来解释反应产物的能量分布。
其次是动量守恒定律。
动量是描述物体运动状态的物理量,根据动量守恒定律,系统中所有粒子的总动量在物理过程中保持不变。
例如,在高能碰撞实验中,通过测量反应产物的动量可以对碰撞发生前的粒子进行研究。
还有角动量守恒定律和电荷守恒定律。
角动量守恒定律描述了系统中所有粒子的总角动量在物理过程中保持不变,而电荷守恒定律描述了系统中电荷的总量保持不变。
这些守恒定律在研究物质的性质和相互作用时起着至关重要的作用。
三、对称性与守恒定律的关系对称性与守恒定律之间存在密切的关系。
根据诺特定理,守恒定律可以由系统的对称性得出。
对称性和守恒定律
空气阻力: f = –v,在时间反演下变为 f = v 不具有时间反演对称性
匀角速转动参照系 惯性离心力或科里奥利力 牛顿定律不成立
物理定律不具有匀速转动的对称性
傅科摆
物理定律不具有标度对称性
材料的强度并不恰好与其尺寸成比例
一只蚂蚁能够举起超过自身体重400倍的东西,如果将蚂蚁按 比例放大到人的尺度,举起同样比例的重物将会把它压垮
对称性的普遍定义 1951年,德国数学家威尔(H. Weyl)
一个系统经过一个操作(变换)变换到它的等价状态,则称 系统具有这种操作(变换)下的对称性,这个操作称为系统的 对称操作。
空间反演操作 (x, y, z)(-x, -y, -z)
反映操作
(x, y, z) (x, y, -z)
绕着z轴逆时针旋转/2 (x, y, z)(-y, x, z)
偎回月台泛来走开 林望明映舟客上篷 傍四孤碧渔仙烟一 水山寺泉浦亭花棹 绿观古寒满闲踏远 悠落林井飞伴径溪 悠日幽冷鸥鹤游流
标度变换对称性
分形
共性: 被研究对象通过某种方式与最初的状态等价 被研究的对象称为系统,系统可以处于不同的状态。 系统从一个状态变到另一个状态的过程,叫做变换或操作 两个状态观察不出任何区别,称这两个状态等价
据估计现在质子和中子数与光子数的比值大约是 1: 1010, 即不对称性是微乎其微的,只有 1/ 1010, 然而这对称性破缺的残 渣却构成了大千世界和人类本身.
对称性的破缺
星系,太阳,地球,人类.
这个对称性破缺是如何发生的 ? 大统一理论正企图解决,尚无结果
例3:生物界的不对称性: 生命的微观过程最显著的一个特征,是分子水平上的对称性破缺
生面体
Escher骑士图案
对称性与守恒定律

对称性与守恒律物理规律是分层次的,有的只对某些具体事物适用,如胡克定律只适用于弹性体;有的在一定范畴内成立,如牛顿定律适用于一切低速运动的宏观物体;有的如能量、动量守恒等守恒律,则在所有领域的自然界起作用。
后者属于自然界更深层次、最为基本的规律。
而守恒律和对称性有紧密联系。
了解对称性的概念、规律及其分析方法,对于深入地认识自然有重要意义。
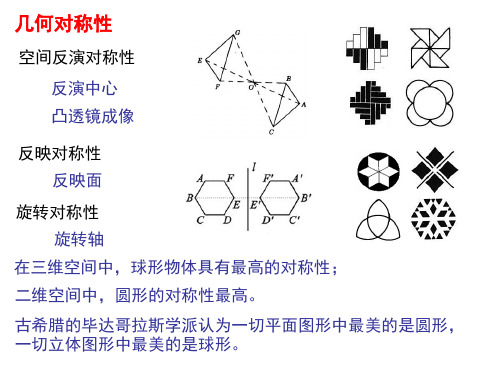
一、什么是对称性对称的概念日常生活中就有,如人体外部器官的左右对称,紫禁城建设布局的东西对称,不带任何标记的球的中心对称等。
对称性的定义如下。
若某个体系(研究对象)经某种操作(或称变换)后,其前后状态等价(相同),则称该体系对此操作具有对称性,相应的操作称为对称操作。
简言之,对称性就是某种变换下的不变性。
二、物理学中几种常见的(对称)变换1.空间变换1)平移:即对位矢作的变换,相应的对称性谓之平移对称性。
例如,一个不带任何标记的无限大平面,对沿平面的任意平移具有对称性,而当此平面上均匀布满方格时,则对沿平面的特定方位(如边长或对角线方位)平移某个长度的整数倍具有对称性。
2)转动:绕某定点或轴线的转动前述球的中心对称,就是指球对绕球心的任意旋转对称,通常就称之为球对称。
一圆柱体,对绕其中心轴旋转任一角度状态不变,即具有旋转轴对称……3)镜像反射(反演):俗称照镜子。
指对镜面作物像变换。
紫禁城建筑的东西对称,就是以天安门中轴面(南北竖直面)为镜面的镜像对称。
●物理矢量的镜面反射——极矢量和轴矢量按镜面反射时,矢量物像的方向之间的关系,物理矢量分两类。
一类,以位移为例,其镜像为,如图1(a)所示。
它们平行于镜面的分量方向相同,垂直于镜面的分量的方向相反,这类矢量叫极矢量。
,,等都是极矢量。
另一类矢量,如图1(b)中右侧所示一沿圆轨道运动的质点的角速度。
保持角速度方向与轨道旋向成右手关系的规定不变,则其镜像为左侧的。
和沿镜面的平行分量反向,而垂直分量方向相同。
这类矢量叫轴矢量,又称赝矢量。
量子力学中的对称性与守恒定律

量子力学中的对称性与守恒定律量子力学是描述微观世界的物理学理论,它主要研究微观粒子的行为和性质。
在量子力学中,对称性和守恒定律是十分重要的概念,它们不仅帮助我们理解微观世界的规律,还对于解释和预测自然现象都起到了关键作用。
本文将对量子力学中的对称性与守恒定律进行论述。
1. 对称性在量子力学中的作用对称性在物理学中具有重要的地位,它可以帮助我们理解自然界中的各种现象。
在量子力学中,对称性可以通过算符的变换来描述。
对称性的存在意味着系统在某些变换下保持不变,这些变换可以是平移、旋转、粒子交换等。
不同的对称性对应着不同的物理规律和守恒量。
2. 空间对称性与动量守恒定律空间平移对称性是量子力学中的重要对称性之一。
根据诺特定理,一个系统的平移不变性对应着动量的守恒,即动量守恒定律。
在量子力学中,动量被表示为动量算符,根据平移算符的性质,能量本征态同时也是动量本征态,从而推导出动量守恒的数学表达式。
3. 时间对称性与能量守恒定律时间平移对称性是量子力学中另一个重要的对称性。
根据诺特定理,一个系统的时间平移不变性对应着能量的守恒,即能量守恒定律。
在量子力学中,能量被表示为能量算符,根据时间平移算符的性质,能量本征态同时也是时间本征态,从而推导出能量守恒的数学表达式。
4. 粒子交换对称性与电荷守恒定律粒子交换对称性是量子力学中独特的对称性。
根据粒子交换的性质,不同种类的粒子在交换后会得到正负符号不同的波函数。
通过对称性的研究,我们可以得出守恒定律,例如电荷守恒定律。
在量子力学中,电荷被表示为电荷算符,根据粒子交换算符的性质,电荷守恒可以被推导出来。
5. 空间反演对称性与正负宇称守恒空间反演对称性是又一种重要的对称性。
根据空间反演的性质,物理过程在空间反演后会得到相反的结果。
通过对称性的研究,我们可以得出守恒定律,例如正负宇称守恒。
正负宇称守恒与粒子的手性和反粒子的存在有关,通过对称性的分析可以得到这一守恒定律的数学表达式。
对称性与物理学中的守恒定律
对称性与物理学中的守恒定律物理学中对称性与守恒定律是一对密不可分的概念。
对称性是自然界的一种基本现象,而守恒定律则是对称性的体现。
本文将介绍对称性与物理学中的守恒定律的基本概念及其在物理学中的应用。
对称与对称性对称是指一个物体在某个操作下仍能保持不变。
常见的对称有平移对称、旋转对称和镜像对称等。
以矩形为例,它有平移、旋转和镜像三种对称。
当你将矩形向一个方向平移一定距离时,它仍看起来一模一样;当你绕矩形中心旋转90度时,它也仍然不变;当你将矩形沿着某一直线对折时,它还是一样的。
在数学中,对称主要是通过变换来定义的。
例如,将平面上的点(x,y)绕原点旋转一个角度θ得到(x',y'),则(x,y)和(x',y')就是关于原点对称的。
物理学中的对称性是指物理现象在某种变换下仍然保持不变。
例如,物体在不同位置、不同时间、不同方向和不同状态下具有平移、时间、旋转和内禀对称性。
具体而言,平移对称意味着物理定律在位置的变换下不变;时间对称性要求物理现象在时间上前后对称;旋转对称性要求物理定律在空间旋转下不变;内禀对称性指的是物理现象在基本粒子的内部对称变换下保持不变。
对称性原理对称性原理是物理学中一个重要的基本原理。
其基本思想是,自然界的基本定律应该具有某些对称性,而这些对称性可以用来推导自然界的规律。
换言之,对称性原理是自然界中某些规律的先决条件。
在物理学中,对称性原理有多个方面。
首先,对称性原理要求物理定律在各种对称变换下不变。
例如,物体的质量在不同位置、不同方向和不同速度下应该保持不变。
这是牛顿运动定律中的一个例子。
更具体地说,在牛顿定律中,物体的运动状态不随时间、空间和速度的变化而改变。
其次,对称性原理还要求物理定律在内部对称变换下不变。
例如,在电动力学中,电场和磁场在某些线性旋转下保持不变。
最后,对称性原理还要求物理定律在粒子转换下不变。
例如,在核物理学中,电荷守恒原理要求在粒子转换时总电荷量不变。
物理中的对称性与守恒定律
物理中的对称性与守恒定律在物理学中,对称性与守恒定律是两个非常重要的概念,它们贯穿于整个物理学的各个领域,为我们解释世界的运行规律提供了重要的理论支撑。
对称性和守恒定律之间存在着密切的联系,它们相辅相成,相互促进,共同构成了物理学中的基本框架。
本文将从对称性和守恒定律的基本概念入手,探讨它们在物理学中的重要作用以及彼此之间的内在联系。
## 对称性的基本概念对称性在物理学中是一个非常重要的概念,它指的是系统在某种变换下保持不变的性质。
具体来说,对称性可以分为空间对称性、时间对称性和内禀对称性等多种类型。
在物理学中,对称性通常表现为物理定律在某种变换下保持不变,这种不变性为我们揭示了自然界中隐藏的规律和对称性。
空间对称性是指系统在空间变换下保持不变的性质。
例如,一个物理系统在进行平移、旋转或镜像变换后仍保持不变,那么我们就说这个系统具有相应的空间对称性。
空间对称性的存在为我们提供了研究物理系统的重要线索,帮助我们揭示物质世界的奥秘。
时间对称性是指系统在时间变换下保持不变的性质。
在经典力学中,时间是一个普遍的参量,物理定律在时间平移下保持不变,这就是时间对称性。
时间对称性的存在为我们提供了研究物理系统随时间演化的重要线索,帮助我们理解自然界中的时间规律。
内禀对称性是指系统在内部变换下保持不变的性质。
例如,电荷守恒定律要求电荷在物理过程中保持不变,这就是内禀对称性的体现。
内禀对称性揭示了物理系统内部的稳定性和规律性,为我们理解微观世界提供了重要线索。
## 守恒定律的基本概念守恒定律是物理学中的另一个重要概念,它描述了系统某些物理量在时间演化过程中保持不变的规律。
根据不同的物理量和系统,可以得到不同的守恒定律,如能量守恒定律、动量守恒定律、角动量守恒定律等。
能量守恒定律是物理学中最基本的守恒定律之一,它表明一个封闭系统中能量的总量在时间演化过程中保持不变。
能量可以在不同形式之间转化,但总能量守恒。
能量守恒定律揭示了自然界中能量转化的规律,为我们研究能量转换和利用提供了基本原则。
守恒定律和对称性
例1.贝纳德对流
T2 > T1
T1
液体
T2
均匀加热
例2.弱作用中宇称不守恒 宇称守恒——与微观粒子的镜象对称性相联系的守 恒定律。强作用下宇称守恒得到实验证实。
但对 和 粒子的衰变,它们质量相等,电荷相同,
寿命也一样。但它们衰变的产物却不相同,即
或 0 0
得:fab fba
空间平移 对称性
作用与反作用 等大反向
动量守恒 定律
例3.空间旋转对称性——角动量守恒定律 角动量守恒定律
质点系所受合外力矩为零时,其总角动量 为恒矢量。 来源于质点系内力矩的矢量和为零,
来源于质点间相互作用沿二者连线 思路: 空间旋转对称性-作用力与反作用力在同一直线上
角动量守恒定律
香莲碧水动风凉 水动风凉夏日长 长日夏凉风动水 凉风动水碧莲香 镜面对称
一. 物理学中的对称性
关于对称的基本概念
被研究的对象——体系
对体系的描述——状态
体系从一个状态到另一个状态的变化——“变换”或“操作”
变换前后体系状态相同——“等价”或“不变”
如果一个操作能使某体系从一个状态变换到另一 个与之等价的状态,即体系的状态在此操作下保持 不变,则该体系对这一操作对称,这一操作称为该 体系的一个对称操作。
重点:对称性概念, 时空对称性与力学中三个守恒定律的联系
难点:对称性原理,对称性方法
对称性的概念最初来源于生活:动物、植物、建筑、 文学艺术……
何其相似!
C60分子结构(巴基球)
截角正20面体,每个顶点 上一个C原子,构成笼状 32面体(20个六边形, 12个五边形)。1985年 发现(1996 诺贝尔化学) 开创有机化学新篇章。
对称性与守恒定律
对称性与守恒定律在物理学中,对称性与守恒定律是两个重要的概念。
对称性指的是物理系统在某种变换下保持不变的性质,而守恒定律则是指物理量在时间或空间上的改变保持不变的规律。
这两个概念之间有着密切的联系,深入理解它们对于解释和预测自然界的现象至关重要。
一、对称性对称性在物理学中具有重要作用,它揭示了自然界普遍存在的规律和原则。
在物理学中,我们常常研究的是物理系统在某种变换下的行为。
如果系统在这种变换下保持不变,我们就说它具有对称性。
最常见的对称性是空间对称性,即物理系统在空间变换下保持不变。
例如,我们在研究一个孤立的粒子时,发现它在不同的空间位置上的行为是相同的。
这表明粒子具有平移对称性。
此外,还有旋转对称性。
许多自然现象在旋转变换下保持不变,这意味着它们具有旋转对称性。
例如,地球的自转使得我们一天之内所经历的自然现象没有明显差异,这是因为地球具有旋转对称性。
时间对称性是另一个重要的对称性概念。
物理系统在时间变换下保持不变,意味着它们具有时间对称性。
通常,我们假设自然界在时间上是均匀的,这意味着物理法则在时间上保持不变。
二、守恒定律守恒定律是物理学中的核心概念之一。
它指出,在某些条件下,特定的物理量在时间或空间上的改变保持不变。
最经典的守恒定律是能量守恒定律。
能量是宇宙中最基本的物理量之一,它在物理系统中的总量是不变的。
虽然能量可以在不同形式之间转化,但总能量的大小保持不变。
此外,动量守恒定律也是非常重要的。
动量是物体运动的属性,它在某些条件下保持不变。
例如,在一个封闭系统中,如果没有外力的作用,总动量保持不变。
其他重要的守恒定律包括角动量守恒定律、电荷守恒定律、线性动量守恒定律等。
每一个守恒定律都对应着自然界中某种物理量的守恒规律。
三、对称性与守恒定律的关系对称性与守恒定律之间存在着密切的联系。
根据诺特定理的基本思想,对称性给出了守恒定律的表达形式。
当物理系统具有某种对称性时,就会出现一个与该对称性相对应的守恒量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 对称性与守恒定律* §7.1 守恒量的平均值和测量取值几率⒈ 力学量平均值随时间变化的方程在本征态中,如果测量力学量F ,则每时刻都可测得确定值。
而在任意状态(),x t ψ中测量,力学量F 一般不显含时间t ,则在每一时刻测量结果一般没有确定值。
但(),x t ψ可以按F 的本征态系n φ做完全展开,所以测量F 本征值的几率是确定的,有确定的分布。
这样,每一时刻在任意态(),x t ψ下,力学量F 有确定的平均值。
在定态下,不显含时间t 的力学量算符F 的平均值不随时间变化。
(),x t ψ:t 时刻的任意状态(归一化的)F ()()ˆ,,x t F x t ψψ=()()*ˆ,,x t F x t dx ψψ=⎰其中(),x t ψ和ˆF都可能是时间的函数,则F 也可以是时间的函数。
量子力学中,讨论力学量随时间的变化是通过讨论力学量的平均值随时间的变化来反映的。
ˆF Fψψ= dFdt ()ˆˆF F t tψψψψ∂∂=+∂∂ˆˆˆF F Ft t t ψψψψψψ⎛⎫∂∂∂=++ ⎪∂∂∂⎝⎭利用含时薛定谔方程 1ˆH tiψψ∂=∂ˆ11ˆˆˆˆF H F F H i i t ψψψψψψ∂=++∂ ˆ11ˆˆˆˆF H F FH i i tψψψψψψ∂=-++∂ 利用ˆH的厄密性ˆˆH Hψϕψϕ=ˆ11ˆˆˆˆFHF FH i i t ψψψψψψ∂=-++∂()ˆ1ˆˆˆˆFHF FH itψψψψ∂=-+∂ 1ˆˆ,F F H t i∂⎡⎤=+⎣⎦∂即1ˆˆ,dF FF H dt i t ∂⎡⎤=+⎣⎦∂ 力学量平均值随时间变化的方程。
⒉ 守恒量⑴ 定义:在任意状态下,力学量的平均值不随时间变化,即为与时间无关的常量。
数学:0dFdt= (F 与t 无关的常量)⑵ 力学量守恒的条件0F t∂=∂说明ˆF 不显含时间t (ˆ0F t ∂=∂)(ˆF 不显含t , ˆ0F t ∂=∂而ˆdF dt 不一定为0) 不特别声明,一般ˆ0F t∂=∂,如ˆr ,ˆp ,ˆL F F F F dF dx dy dz dt x y z t∂∂∂∂=+++∂∂∂∂ ˆˆ,0FH ⎡⎤=⎣⎦即ˆF 与ˆH 对易,也可以作为守恒量的定义⑶ 性质特点① 体系在任意状态下,平均值不随时间变化。
这是守恒量物理上的定义。
② 体系在任意状态下,测量力学量(不显含t )取值的几率分布不随时间变化。
证明:F 为守恒量,因为ˆˆ,0F H ⎡⎤=⎣⎦,所以ˆF 、ˆH 有共同完全本征函数系{}nφ,则有ˆn n nH E φφ=和ˆn n n F f φφ= 对任意态(),r t ψ(),r t ψ()()n n nc t r φ=∑()()(),n n c t r r t φψ=为了求()2n c t 随时间的变化()n dc t dt ()(),n d r r t dt φψ=()(),n r t r tψφ∂=∂ (1ˆH t i ψψ∂=∂) ()()1ˆ,n r Hr t iφψ=利用ˆH 的厄密性 ()()1ˆ,n H r r t iφψ=()()*,n n E r r t i φψ=()n n E c t i = 关于()n c t 的一阶微分方程,其解为:()n c t ()0n iE tn c e-⋅=⋅ ()()220n n c t c = 与t 无关。
∴()20n d c t dt=③ 问题:量子体系的守恒量一定取确定值吗?不一定(一定取确定的平均值) 量子体系的守恒量并不一定取确定值,即体系的状态并不一定就是某个守恒量的本征态。
若初始时刻,体系不处于守恒量F 的本征态,则此后任意时刻也不会处于F 的本征态,即守恒量不取确定值,违者违背性质②。
若初始时刻体系处于守恒量F 的本征态,则此后任何时刻它将处于F 的属于同一本征值的本征态中,否则也违背性质②。
这时守恒量的量子数称为好量子数,就是与能量同时有确定值的力学量的量子数。
⒊ 守恒定律举例说明 ˆF 不显含t ,则ˆ0F t∂=∂,ˆˆ,0F H ⎡⎤=⎣⎦⑴ 自由粒子的动量(守恒)ˆp i =-∇, ˆ0p t∂=∂, 2ˆˆ2p H μ=, 2ˆˆˆˆ,,02p p H p μ⎡⎤⎡⎤==⎢⎥⎣⎦⎣⎦,所以动量是守恒量 因为dp dt 1ˆˆ,0p H i ⎡⎤==⎣⎦,量子力学中的动量守恒定律⑵ 中心力场运动粒子的角动量(2ˆL ,ˆx L ,ˆy L ,ˆzL ) (守恒) ()()U r U r =,中心势场,对坐标原点各向同性ˆH()222U r μ=-∇+, 2ˆ0L t∂=∂ ,ˆ0i L t ∂=∂ 不显含时间 可以证明2ˆˆ,0L H⎡⎤=⎢⎥⎣⎦,即角动量是守恒量 物理理解:在绕原点转动变换下,如2r r r =一样,22∇=∇=∇∇也表现为一个标量,即不变化。
而势()U r 也不变化,于是ˆH在绕原点转动变换下保持不变,可以证明,这时轨道角动量L 和2L 是守恒量,即2ˆˆ,0L H⎡⎤=⎢⎥⎣⎦数学理解:如对2ˆL ,将2ˆL 与ˆH采用球坐标的表述。
球极坐标下:2∇2222222111sin sin sin r r r r r r θθθθθϕ∂∂∂∂∂⎛⎫⎛⎫=++ ⎪ ⎪∂∂∂∂∂⎝⎭⎝⎭22,21rr θϕ=∇+∇ 2ˆL 222211sin sin sin θθθθθϕ⎡⎤∂∂∂⎛⎫=-+ ⎪⎢⎥∂∂∂⎝⎭⎣⎦⇒ 2∇22222ˆ1L r r r r r ∂∂⎛⎫=-⎪∂∂⎝⎭ ∴ˆH()222,212r U r r θϕμ⎛⎫=-∇+∇+ ⎪⎝⎭()()22222ˆ2r L U r r μ⎡⎤⎢⎥=-∇++-⎢⎥⎣⎦()2222ˆ22rL U r rμμ=-∇++ 2ˆL 只对角变量作用,r 与,θϕ独立 2ˆˆ,0L H ⎡⎤=⎢⎥⎣⎦θ的函数与r 的函数对易,22ˆˆ,0L L ⎡⎤=⎢⎥⎣⎦2ˆL 与r 无关所以221ˆˆ,0d L L H dt i⎡⎤==⎢⎥⎣⎦同理i d L dt =1ˆˆ,0i L H i⎡⎤=⎣⎦,,,i x y z =即 量子力学中的角动量守恒定律如库仑场中的电子,氢原子⑶ 哈密顿不显含时间体系的能量(守恒)ˆ0H t∂=∂ ˆˆ,0H H ⎡⎤=⎣⎦,即能量是守恒量 所以1ˆˆ,0dH H H dt i⎡⎤==⎣⎦,即量子力学中的能量守恒定律 如一维无限深势阱的粒子,线性谐振子等等⑷ 哈密顿对空间反演不变时的宇称(守恒)已学过,宇称指波函数在空间反演(r r →-)下的奇偶性()()r r ψψ-=±,﹢偶宇称,﹣奇宇称把这种对波函数的空间反演运算用宇称算符表示。
宇称算符ˆP: 对波函数的空间反演运算 ()()ˆ,,Pr t r t ψψ=- 宇称本征值:()()2ˆˆˆ,,Pr t PP r t ψψ=()()ˆ,,P r t r t ψψ=-= 即2ˆP算符的本征值为1 2P =1 所以ˆP算符的本征值为±1, 1P =± 1 偶宇称 ˆP ψψ=-1 奇宇称ˆPψψ=-宇称守恒:证明:如果()()ˆˆHr H r =-,即哈密顿量在空间反演下保持不变,则体系宇称是守恒量即ˆˆ,0PH ⎡⎤=⎣⎦证明:()()ˆˆ,,PH r r t ψ⎡⎤=⎣⎦()()()()ˆˆˆˆ,,PH r r t H r P r t ψψ- ()()()()ˆˆˆ,,Hr r t H r P r t ψψ=--- ()()()()ˆˆˆˆ,,Hr P r t H r P r t ψψ=-=0 所以ˆˆ,0PH ⎡⎤=⎣⎦问题:①宇称守恒的状态,宇称一定有确定值(即处在宇称本征态)吗? 不一定。
(看初态) ②[例2.7.1] 粒子在势场()x U 中运动,求坐标算符和动量算符对时间的微商。
解 粒子的()x U p H +=μ22 ,将0=∂∂tx 代入(2.7.5)式,利用[]nk k n i p x δ =,,可得[]()[]⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡+==∑∑==3131222,21,212,1,1n k k n n p x e i p x i x U p x i H x i dt x d μμμ [][][]{}∑∑∑∑====+==313123131,,21,21n k k k n k n k n k n n k n p p x p x p e i p x e iμμ μδμp i p e i nk k n k n=∑∑==2213131(2.7.6)以μ乘上式两边,即有υμμ==dtx d p (2.7.7)这表明,经典力学的动量表达式的量子力学中以算符的形式出现,坐标算符对时间的微商就是速度算符υ。
同理,将0=∂∂tp 代入(2.7.5)式,并利用()[]()x U i x U p∇-=,(见习题2.2.7),即()()ˆˆHr H r =-[]()()[]()F x U x U p i x U p p i H p i dt p d=-∇==⎥⎦⎤⎢⎣⎡+==,12,1,12μ (2.7.8)式中F是作用力算符。
这表明,经典力学的运动方程在量子力学中将以算符的形式出现,动量算符对时间的微商正好等于力算符。
将式(2.7.7)和(2.7.8)式对()x ψ态求平均,即得坐标平均值x 与动量平均值p的运动方程式μp dt x d = , ()F x U dtp d =∇-= (2.7.9) 将(2.7.9)式与(2.7.10)式联立可得()F x U dtx d=∇-=22μ (2.7.10) (2.7.11)式称为厄任费斯特(Ehrenfest )方程,由于与年顿方程相似又称为“量子力学中的年顿方程”,但它与经典力学的年顿方程存在本质的区别:(1) 在经典力学中,22dtx d给出的是坐标x 的加速度;在量子力学中,由于每一时刻x一般没有确定值,22dtxd 给出的是坐标平均值的加速度。
(2) 在经典力学中,位于x 的粒子所受的力()x U∇-仅决定于该点的势场,而且受力的大小与粒子的运动状态无关;在量子力学中,起作用的是力的平均值()()()τψψd t x x U t x F ,,*∇-=⎰ (2.7.11)它是涉及整个势场的作用,而且与粒子所处的状态()t x ,ψ有关。
总之,经典力学中有关力学量之间的关系式,在量子力学中将以平均值或算符的形式出现。
2.7.2 守恒量及其性质1 守恒量的定义在任意态中,如果体系某一力学量的平均值F 对时间的微商为零,即()()()..,**c c d t x x i E t C nn n+=⎰τψψ()0..2=+=c c t c i E n n(2.7.17)这表明,守恒量F 取值的概率分布为()2t c n 不随时间而变。
