阴阳离子半径比与配位数的关系
配位数的确定

影响配位数的因素如下 : 1、中心原子的大小 2、中心原子的电荷 3、配体的性质
中心原子的大小
中心原子的最高配位数决定于它在周期表中的周次。 在周期表内,第1周期元素的最高配位数为2; 第2周期元素的最高配位数为4; 第3周期为6,以下为8、10。 最高配位数是指在配合物中,中心原子周围的最高 配位原子数,实际上一般可低于最高数。 在实际中第1周期元素原子的配位数为2,第2周期 不超过4。除个别例外,第3、4周期不超过6,第5、6 周期为8。 最常见的配位数为4和6,其次为2、5、8。配位数 为奇数的通常不如偶数的普遍。
配位数越大,结合能越低,晶体结构越稳定。
2.密堆积 如果晶体由完全相同的一种粒子组成,而粒子被看作小圆 球,则这些全同的小圆球最紧密的堆积称为密堆积。 密堆积特点:结合能低,晶体结构稳定;配位数最大为12。
(1)六角密积
(Be,Mg,Cd,Zn)
AB
第一层:每个球与6个球相切,有6个空隙,
如编号1,2,3,4,5,6。
中心原子的电荷
中心原子的电荷高,配位数就大。例如, 等电子系列的中心原子Ag+、Cd2+和In3+与Cl-分 别生成配位数为2、4和6的【AgCl2】-、 【CdCl4】2-和【InCl6】3-配离子。同一元素不 同氧化态的离子常具有不同的配位数,例如,二 价铂离子Pt2+的配位数为4,而4价铂离子配位 数Pt4+为6。
配位数的确定
高考备考
NaCl晶体中阴离子的配位数为6,而Cl-按面心立 方堆积的配位数是12。怎么都是配位数一会儿是6,一 会儿又是12,这怎么理解?
氯离子按面心立方堆积是没错,但那不是真正的 配位数,因为氯离子是同号离子,是相互斥的; 同理,钠离子也是按面心立方堆积的,这两种离 子形成的面心立方堆积都产生八面体空穴,彼此进入 对方八面体空穴中就对了,此时异号离子之间的接触 才算配位数,这样配位数就是真正的配位数,即6。 面心立方堆积如果是金属原子,则其配位数是12, 因为周围的原子都与该原子形成金属键的,这时也是 真正的配位数。
离子晶体中离子配位数的影响因素

离子晶体中离子配位数的影响因素[摘要]对离子晶体配位数的影响因素:几何因素、电荷因素和键性因素在教材的基础上作了适当展开介绍,着重通过定量数据推导了半径比和离子晶体配位数的关系,并从离子极化角度对键性因素作了分析,最后对晶体化学定律做了适当介绍[关键词]离子晶体半径比规则离子极化配位数人民教育出版社高中化学选修3第三章第四节《离子晶体》中通过氯化钠、氯化铯和氟化钙晶体模型的具体分析,得出了影响离子晶体结构(配位数)的三个因素:几何因素、电荷因素和键性因素。
然而对于几何因素仅仅是通过两个特定数值得出的结论,并没有给出具体的说明和定量的推导,更没有说明当半径比在怎样的范围内形成怎样的配位数,对于键性因素更是一笔带过。
本文将对几何因素对离子晶体配位数的影响作出定量讨论,同时也将对电荷因素和键性因素适当展开介绍一、几何因素——半径比规则由于离子键没有方向性和饱和性,离子在晶体中常常采取尽可能的密堆积形式。
由于阴离子的体积一般比阳离子大得多,故阴离子的堆积形式对离子晶体的结构起主导作用。
为使堆积紧密,较小的阳离子常处在阴离子堆积的空隙之中。
为了降低晶体体系的能量,应尽量使阳离子具有较大的配位数并使异号离子充分接触,同号离子尽可能不接触,因此一个阳离子周围配位的阴离子数(配位数)将受到阴阳离子半径比的限制。
阴阳离子的半径比对离子晶体结构(配位数)的影响叫做几何因素(或半径比规则)。
我们以最常见的AB型理想6:6配体晶体构型(即阴阳离子和阴阴离子恰好完全接触的情形)的某一层为例说明(如图1)设r-=1,则AB=BC=2r-=2;AC=2(r-+ r+)=2+2r+,因为ΔABC为等腰直角三角型,根据毕达哥拉斯定理:AC2=AB2+BC2,即22+22 =(2+2r+)2,解得r+=0.414也就是说,当r+/r-=0.414时,阴阳离子直接接触,阴阴离子也直接接触。
当r+/r-0.414时,则阴阴离子开始接触不良,阴阳离子却能紧靠在一起。
离子晶体结构

分数坐标:
Ti4+:
111
(0,0,0),( , , )
222
O2-:
1 1 11 1 1
( u ,u ,0 ) ,( 1 u ,1 u ,0 ) ,( u , u ,) ,( u , u ,)
2 2 22 2 2
u为一结构参数,金红石本身u = 0.31。
5、节约规则(鲍林第五规则 ) 在晶体中,本质上不同组成的结构单元的数目,趋向了最少。
2.4.2典型的离子晶体的结构 要求掌握的具体内容:
晶胞中离子的排列,离子的配位数,晶体常数与离子半径关系式,一个晶胞所占有正负离子的数目,质点所处 的空间坐标,空间格子类型以及同型结构的化合物等。
1.AB型化合物结构
MgF2, FeF2, VO2,CrO2, PbO2,WO2,MoO2等为金红石型。
3.A2B3型化合物结构
以aAlO为代表 刚玉型结构 23
O2-近似作六方最紧密堆积,配位数为4,堆积层垂直于三次轴,Al3+充填了O2-形成的八面体空隙数的2/3,每三 个相邻的八面体空隙有一个是有规则地空着;每个晶胞含4个Al3+和6个O2-。
22 2 2 22
50
0
75
25
0
50
25
75
0
50
(1,1,1),(3,3,1),(1,3,3),(3,1,3) 444 444 444 444
图2-54 -ZnS晶胞
Zn S
图2-55 a-ZnS晶胞
六方ZnS型(纤锌矿型)结构
2 S 2 : 000 ; 2 1 1 332
2 Zn 2 : 00 7 ; 2 1 3 8 338
配位类型与正负离子半径比的关系

配位类型与正负离子半径比的关系
配位类型和正离子半径与负离子半径比有关,该比值反映了位于配位
物周围的离子之间的电荷相互作用。
对于同一化合物中的不同配位类型,其正离子半径与负离子半径比可
能会有所不同。
一般来说,配位数越高,配位物中的配体越大,所需的正
离子半径就越大,以保持配离子间的相对稳定性。
因此,在配位化合物中,通常会发现配位数更高的离子(如Fe3+)具有更大的正离子半径和更小
的正离子半径与负离子半径比。
正离子半径与负离子半径比还与配位物的几何形状有关。
在某些情况下,配位物中的配体可能排列在某种非正几何形状中,例如姿态异构体或
八面体配位。
这些几何形状可能会导致正离子半径与负离子半径比的变化。
总的来说,正离子半径与负离子半径比的变化与配位类型和化合物的
几何形状有关,可以用于解释化学反应的趋势和性质。
材料科学基础 2.3决定离子晶体结构的基本因素

表1-4 正离子与O2-离子结合时常见的配位数
配位数 3 4 6 8 12
正离子 B 2+ 2+ 2+ 2+ 3+ 4+ 4+ 5+ Be ,Ni ,Zn ,Cu ,Al ,Ti ,Si ,P + 2+ 2+ 2+ 2+ 3+ 3+ 3+ 4+ 5+ 5+ Na , Mg ,Ca ,Fe ,Mn ,Al ,Fe ,Cr ,Ti ,Nb ,Ta 2+ 4+ 4+ 4+ 3+ Ca ,Zr ,Th ,U ,TR + + 2+ 3+ K ,Na ,Ba ,TR
1.3 决定离子晶体结构的基本因素
一、内在因素对晶体结构的影响 1.质点的相对大小 2.晶体中质点的堆积
3.配位数与配位多面体
4.离子极化
二、外在因素对晶体结构的影响──同质多晶与类质
同晶及晶型转变
一、内在因素对晶体结构的影响
1.质点的相对大小 2.晶体中质点的堆积 3.配位数与配位多面体 4.离子极化.
离子半径
每个离子周围存在的球形力场的半径即是离子半径。 离子晶体的正、负离子半径之和等于相邻两原子面间的
距离,可根据x-射线衍射测出,这时要确定正、负离子半径分
别为多少,还要再建立一个关系式,才能求解出正、负离子半 径的确切数据。
确定正、负离子半径的确切数据,有两种方法,其一是
哥希密特(Goldschmidt)从离子堆积的几何关系出发,建立 方程所计算的结果称为哥希密特离子半径(离子间的接触半 径)。其二是鲍林(Pauling)考虑了原子核及其它离子的电子 对核外电子的作用后,从有效核电荷的观点出发定义的一套质 点间相对大小的数据,称为鲍林离子半径。
晶体结构,配合物结构知识点与习题1-1
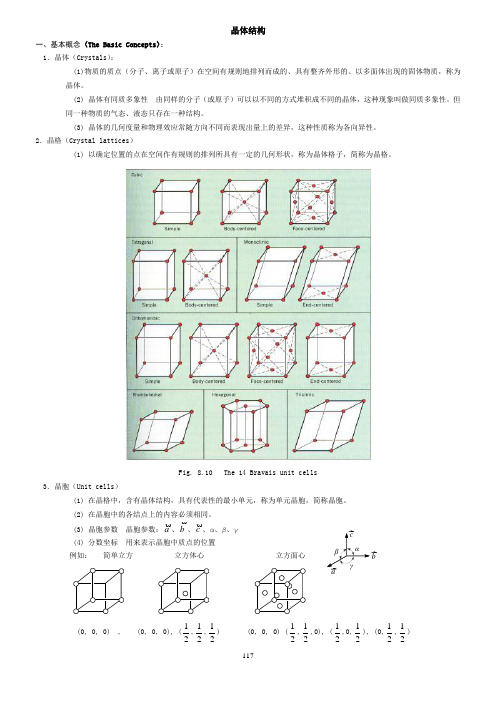
117晶体结构一、基本概念(The Basic Concepts ): 1.晶体(Crystals ):(1)物质的质点(分子、离子或原子)在空间有规则地排列而成的、具有整齐外形的、以多面体出现的固体物质,称为晶体。
(2) 晶体有同质多象性 由同样的分子(或原子)可以以不同的方式堆积成不同的晶体,这种现象叫做同质多象性。
但同一种物质的气态、液态只存在一种结构。
(3) 晶体的几何度量和物理效应常随方向不同而表现出量上的差异,这种性质称为各向异性。
2.晶格(Crystal lattices )(1) 以确定位置的点在空间作有规则的排列所具有一定的几何形状,称为晶体格子,简称为晶格。
Fig. 8.10 The 14 Bravais unit cells3.晶胞(Unit cells )(1) 在晶格中,含有晶体结构,具有代表性的最小单元,称为单元晶胞,简称晶胞。
(2) 在晶胞中的各结点上的内容必须相同。
(3) 晶胞参数 晶胞参数:a、b、c、α、β、γ (4) 分数坐标 用来表示晶胞中质点的位置例如: 简单立方 立方体心 立方面心(0, 0, 0) , (0, 0, 0), (21,21,21) (0, 0, 0) (21,21,0), (21,0,21), (0,21,21) αβγbc a118在分数坐标中,绝对不能出现1,因为1即0。
这说明晶胞是可以前后、左右、上下平移的。
等价点只需要一个坐标来表示即可,上述三个晶胞中所含的质点分别为1、2、4,所以分数坐标分别为1组、2组和4组。
(5) 晶面指数 晶面在三维空间坐标上的截距的倒数(h 、k 、l )来表示晶体中的晶面,称为晶面指数,如立方晶系中(100),(110),(111)面分别为(100) (110)(111)lFig. 8.12 Selected planes and their Miller indices for cubic system用X-ray 的衍射可以测量晶体中的面间距,2d ·sin θ = n ·λ。
材料物理化学习题指南

0,
,0 ,
Na+:00 ,
,0 0,
(2) 球体紧密堆积法: 离子晶体中负离子常按紧密堆积排列, 而正离子处于空 隙之中。例如 NaCl,Cl 按立方紧密堆积和 Na+处于全部八面体空隙之中。 (3) 配位多面体及其连接方式: 对结构比较复杂的硅酸盐晶体结构常使用配位 多面体和它们的连接方式来描述。例如 NaCl 结构是由 Na-Cl 八面体以共棱方式相连 而成。 表 2-1 用负离子堆积方式,列出典型晶体结构的分类。 硅酸盐晶体结构是按晶体中硅氧四面体在空间的排列方式分为孤岛状、组群状、链状、 层状和架状五类。这五类的[SiO4]四面体中,桥氧的数目也依次由 0 增加至 4,非桥氧数由 4 减至 0。硅离子是高电价低配位的阳离子,因此在硅酸盐晶体中,[SiO4]只能以共顶方式连 接,而不能以共棱或共面方式连接。表 2-2 列出硅酸盐晶体结构类型和实例。
例
题
1-1 作图阐明表示晶面符号的米氏指数。 解:图 1-2 的晶体中,晶面 XYZ 在三个结晶轴 上的截距依次为 。已知轴率为 a:b:c。
图 1-2 例题 1-1 附图
该晶面在结晶轴上的截距系数为 2a、3b、6c。根据米 氏指数的含意则:
因此,该晶面的晶面符号为(321) 。 1-2 在面心立方和体心立方中,最密排的平面的米氏符号是什么? 解:在面心立方堆积中,由(100) 、 (010)和(001)三个面的对角线所构 成的平面是最密排的面。因此,它的米氏符号为(111) 。 在体心立方堆积中,由(001)面的对角线和 c 轴构成的平面是最密排的面。因 此,它的米氏符号为(110)。 1-3 金属铝为面心立方结构,晶胞参数为 0.4049nm,求 d(200)和 d(220) 各为多少?(d(200)为(200)面之间的距离) 。 解:d(200)为(200)面之间的距离,根据米氏符号的定义,d(200)应 为 d(100) 。因为铝是立方结构,因此 d(100)即为晶胞参数 0.4049nm。所以 d(200)=0.2025nm。 同理,d(220)= d(110) 。在立方体中,d(110)为(001)面对角线的 1/2。
离子配位多面体及其连接规律

-0.732 6 八面体 对于ZnS晶体,Z+= Z -=2,正负离子配位数=4:4,静电键强度
正八面体 和正四面体连接时M-M间的距离
-1 8 立方体 与X-X距离相比
与M-X距离相比
共顶点 共棱 共面 共顶点 共棱 共面
1 12 密堆积结构 四面体
ρ 67
八面体
1.
配位数 配为多面体构型
-0.225 Si与O的配位数分别降到4:2。
离子电价规则(第二规则)
3
三角形
例如 NaCl晶体,Z+= Z -=1,正负离子配位数=6:6,静电键强度
-0.414 4 四面体 氧的剩余电价为2-=,不足再与一个S相连,所以在晶体中,SO42-是分立的离子基团。
2. 离子电价规则(第二规则)
在稳定的离子晶体结构中,每个负离子的电价数等
于或近似等于与其邻近的正负离子间的各静电强度的总
和,即
Z
i
Si
i
Zi vi
Z-为负离子的电荷,Zi 为正离子的电荷,vi为正离子的配 位数,Si为负离子与i正离子的静电键强度。
例如 NaCl晶体,Z+= Z -=1,正负离子配位数=6:6,
ρ
配位数 配为多面体构型
原则上这些多面体可以共顶点或共棱或共面连接,但共棱或共面会使处于多面体中心的离子相互间的距离缩短,使得同号离子间的排
斥能增加,降低晶体结构的稳定性。
Si与O的配位数分别降到4:2。
正负离子半径比只是影响离子晶体结构的一个因素, 在复杂多样的离子晶体中,还有其他因素影响其结构,如
离子配位多面体及其连接规律
ball-and-stick and combined polyhedral/ball-and-stick representation for [As6edral/ball-and-stick representation and ball and stick representation of double-sandwich polyoxomolybdate [As2Fe6Mo22O85(H2O)]14-
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
阴阳离子半径比与配位数的关系
(选自苏教版物质结构与性质 41页)
由上述表中数据可发现如下规律:
225.0≈-+r r 时 126
-=-+r r
414.0≈-+r r 时 12-=-
+r r
732.0≈-+r r 时 13-=-
+r r
因此,我们可以利用立体几何知识进行对上述问题的证明。
一.配位数为4的
-
+
r r 关系 (只讨论下限,在(二)中推导上限)
ZnS 阴离子堆积方式为面心立方堆积
如右图:小球代表阳离子,构成8个区域,阴离子填充4个区域,4个阴离
子与1个阳离子构成正四面体,阳离子位于中心。
当
-
+
r r 有最小值时,4个阴离子相切,阳离子与4个阴离子相切。
即证如下问题:4个球两两相切堆积,球心构成正四面体,4个球内部有一小球,且与各球相切,求
大
小r r ?(即
-
+
r r )
E 为BC 中点,取四面体ABCD 的剖面 AED
做AM ⊥面BCD ,M 在ED 上。
得剖面图。
小球圆心Q ,大球圆心A 、D
设a AD 22=,则a AM 3
3
4=
设x OM = -++==r r QD AQ
a a a AM AD DM 3
6
2)334(
)22(2222=-=-=
a x a x x a QD AQ 3
3
)362()334(
2222=⇒+=-⇒=
a AQ 3=∴
⎩
⎨⎧==-=-=a r a
r AQ r 2AD 2
1)23(大大小
1-2
62
2-3=
=
∴
大
小r r
当小球增大时
-
r r +
增大
二、配位数为6的
-
r r +
关系(只讨论下限,上限在(三)中讨论)
Nacl 类晶胞如右图
四个阴离子与1个阳离子球s 构成一个平面,且4个阴离子相邻的相切,且当
-
r r +
最小时,阳离子与四个球均相切
即正如下问题:四个大球如图示相切,一个小球与四个大球均相切,求
-
大小r r (
-
r r +)?
P 为小球圆心,设大球半径为a
a 22AC = a m AD 22
1
==
12a 1
1
2-
-
-=-==
+
r r r r 大小
当小球增大时
-
r r +
增大
三、配位数为8的
-
r r +
关系(只讨论下限,上限在(四)中讨论)
C s CL 类晶胞如右图
八个阴离子在正方体8个顶点,阳离子在正方体中心。
当八个阴离子有相切且阳离子与阴
离子均相切时-
r r +
最小
即证如下问题:球A 与球B 相切,球C 与球D 相切,球O 与ABCD 均相切(ABCD 为正
方体的对角面)求-
大小r r (
-
r r +)?
设大球半径为a ,a AC 32= a AO 3=
13a 1
13--
-=-==
+r r r r 大小 当小球增大时
-r r +
增大 四、配位数为12的
-
r r +
关系 C s F 类晶胞如右图
六个阴离子在正六边形的六个顶点,一个阳离子在正六边形中央(球心与中心重合)当阳离子与阴离子相切时,
-
r r +
最小 即证如下问题:如下图6个球球心连线构成正六边形,一个小球球心在正六边形中央,且与6个球均相切,求
外
中r r (
-
r r +)?
设外边球半径a ,a A 2B =a A 4D =a A 2O =
a a 1
12-=-==
+r r r r 外
中 由(一)(二)(三)(四)可发现阳阴离子半径比与晶胞类型的一些规律。
For personal use only in study and research; not for commercial use.
Nur für den persönlichen für Studien, Forschung, zu kommerziellen Zwecken verwendet werden.
Pour l 'étude et la recherche uniquement à des fins personnelles; pas à des fins commerciales.
толькодля людей, которые используются для обучения, исследований и не должны использоваться в коммерческих целях.
以下无正文
For personal use only in study and research; not for commercial use.
Nu r für den persönlichen für Studien, Forschung, zu kommerziellen Zwecken verwendet werden.
Pour l 'étude et la recherche uniquement à des fins personnelles; pas à des fins commerciales.
толькодля людей, которые используются для обучения, исследований и недолжны использоваться в коммерческих целях.
以下无正文。
