【配套K12】高考数学二轮复习 专题能力训练26 解答题专项训练 立体几何 文
【数学】高考数学二轮复习专题能力提升训练七立体几何

文档来源为:从网络收集整理.word版本可编辑.欢迎下载支持. 【关键字】数学杭州三维设计高考数学二轮复习:立体几何本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.有下列四个命题:1)过三点确定一个平面2)矩形是平面图形3)三条直线两两相交则确定一个平面4)两个相交平面把空间分成四个区域其中错误命题的序号是( )A.1)和2)B.1)和3)C.2)和4)D.2)和3)【答案】B2.下列命题中,正确的是( )A.直线l⊥平面α,平面β∥直线l,则α⊥βB.平面α⊥β,直线m⊥β,则m∥αC.直线l是平面α的一条斜线,且l⊂β,则α与β必不笔直D.一个平面内的两条直线与另一个平面内的两条直线分别平行,则这两个平面平行【答案】A3.如图,在平行六面体中,为与的交点.若,,则下列向量中与相等的向量是( )A.B.C.D.【答案】A4.设是两条不同的直线,是三个不同的平面,给出下列四个命题:①若,,则②若,,,则③若,,则④若,,则其中正确命题的序号是( )A.①和②B.②和③C.③和④D.①和④【答案】A5.三个平面可将空间分成个部分,则的最小最大值分别是( )A.4,7 B.6,C.4,8 D.6,8【答案】C6.下列命题中错误的是( )A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面βB.如果平面α不笔直于平面β,那么平面α内一定不存在直线笔直于平面βC.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γD.如果平面α⊥平面β,那么平面α内所有直线都笔直于平面β【答案】D7.下列正方体或正四面体中,P、Q、R、S分别是所在棱的中点,这四个点不共面的一个图是( )【答案】D8.已知向量与向量平行,则x,y的值分别是( )A.6和–10 B.–6和C.–6和–10 D.6和10【答案】A9.空间三条直线中的一条直线与其他两条都相交,那么由这三条直线最多可确定平面的个数是( )个文档来源为:从网络收集整理.word 版本可编辑.欢迎下载支持. A .1 B .C . 3D .4【答案】C10.底面是正三角形,且每个侧面是等腰三角形的三棱锥是( )A .一定是正三棱锥B .一定是正四面体C .不是斜三棱锥D .可能是斜三棱锥【答案】D11.三个不重合的平面可把空间分成n 部分,则n 的所有可能取值为( )A .4B . 4或C .4或6或8D . 4或6或7或8【答案】D12.利用斜二测画法得到的①三角形的直观图一定是三角形;②正方形的直观图一定是菱形;③等腰梯形的直观图可以是平行四边形;④菱形的直观图一定是菱形.以上结论正确的是( )A .①②B . ①C .③④D . ①②③④【答案】B第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.α、β是两个不同的平面,m 、n 是平面α及β之外的两条不同直线,给出四个论断:①m ⊥n ,② α⊥β,③n ⊥β,④ m ⊥α.以其中三个论断作为条件,余下一个作为结论,写出你认为正确的一个命题 【答案】①③④⇒②或②③④⇒①14.如图,在正方体ABCD —1111D C B A 中,M ,N 分别是棱CD 、1CC 的中点,则异面直线M A 1与DN 所成的角的大小是【答案】︒9015.一个几何体的三视图如图所示,则该几何体为 。
“立体几何”大题的常考题型探究(课件)2023年高考数学二轮复习(全国通用)

因为 ,所以 .由已知得 ,故 .又 ,所以 .因为 , , , , ,所以 .
提分秘籍 体积问题考查的本质就是点面距离,解题关键是抓住以下几种方法:
(1)等体积法(仅限三棱锥)转换顶点;
(2)顶点不变,延展或缩小底面,如四棱锥的高即同顶点的三棱锥的高,点 到平面 的距离可看作点 到平面 的距离;
设 ,则 , , .设平面 的法向量为 ,则 即
令 ,则 ,∴平面 的一个法向量为 , .∵直线的方向向量与平面的法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值,∴直线 与平面 所成角的正弦值等于, ,当且仅当 时取等号.
∴直线 与平面 所成角的正弦值的最大值为 .(法二:定义法)如图2, 平面 , , 平面 .
大题攻略03 平面与平面所成的角
例3 (2021年全国甲卷)已知直三棱柱 中,侧面 为正方形, , , 分别为 和 的中点, 为棱 上的点, .
(1)证明: .(2)当 为何值时,平面 与平面 所成的二面角的正弦值最小?
▶审题微“点”
切入点
(1)常规方法是几何法,不过用几何法较为复杂,根据题目条件建系是最优解法;(2)建系是常规方法,也是最优法
▶审题微“点”
切入点
(1)关键是在平面 内找一条直线与 平行,根据线面平行的判定定理即可证明;(2)将包装盒分割成几个规则的锥体和柱体求解
障碍点
(1)在平面 内找直线与 平行;(2)将不规则的几何体分割或补形成几个规则的几何体
隐蔽点
(1)平面 内与 平行的直线;(2)包装盒的高
[解析] (1)如图1所示,分别取 , 的中点 , ,连接 ,因为 , 为全等的正三角形,所以 , , .
2021届高考二轮复习数学专题训练:立体几何(2021-2021年全国卷高考题选)

2021-2021年高考全国卷数学之立体几何专题训练一.选择题(共13小题)A.2B.2C.3D.2 A.12B.18C.24D.54 A.64πB.48πC.36πD.32πA.B.C.D.A.E B.F C.G D.HA.6+4B.4+4C.6+2D.4+2 A.B.C.1D.A.8πB.4πC.2πD.πA.BM=EN,且直线BM,EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM,EN是异面直线D.BM≠EN,且直线BM,EN是异面直线A.B.C.D.A.2x+y﹣z+2=0B.2x+y+z﹣6=0C.2x+y+z﹣4=0D.2x+y﹣z﹣3=0 A.B.C.D.A.B.C.D.二.填空题(共10小题)三.解答题(共17小题)(1)证明:平面ACD⊥平面ABC;(2)Q为线段AD上一点,P为线段BC上一点,且BP=DQ=DA,求三棱锥Q﹣ABP 的体积.(1)证明:P A⊥平面PBC;(2)求二面角B﹣PC﹣E的余弦值.(1)证明:平面P AB⊥平面P AC;(2)设DO=,圆锥的侧面积为π,求三棱锥P﹣ABC的体积.(1)证明:AA1∥MN,且平面A1AMN⊥平面EB1C1F;(2)设O为△A1B1C1的中心.若AO∥平面EB1C1F,且AO=AB,求直线B1E与平面A1AMN所成角的正弦值.(1)证明:点C1在平面AEF内;(2)若AB=2,AD=1,AA1=3,求二面角A﹣EF﹣A1的正弦值.(1)当AB=BC时,EF⊥AC;(2)点C1在平面AEF内.(1)证明:AA1∥MN,且平面A1AMN⊥平面EB1C1F;(2)设O为△A1B1C1的中心.若AO=AB=6,AO∥平面EB1C1F,且∠MPN=,求四棱锥B﹣EB1C1F的体积.(1)证明:MN∥平面C1DE;(2)求点C到平面C1DE的距离.(1)证明:MN∥平面C1DE;(2)求二面角A﹣MA1﹣N的正弦值.(1)证明:BE⊥平面EB1C1;(2)若AE=A1E,求二面角B﹣EC﹣C1的正弦值.(1)证明:BE⊥平面EB1C1;(2)若AE=A1E,AB=3,求四棱锥E﹣BB1C1C的体积.(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图2中的二面角B﹣CG﹣A的大小.(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图2中的四边形ACGD的面积.(1)证明:PO⊥平面ABC;(2)若点M在棱BC上,且MC=2MB,求点C到平面POM的距离.(1)证明:平面AMD⊥平面BMC;(1)证明:平面PEF⊥平面ABFD;(2)求DP与平面ABFD所成角的正弦值.(1)证明:PO⊥平面ABC;(2)若点M在棱BC上,且二面角M﹣P A﹣C为30°,求PC与平面P AM所成角的正弦值.答案一.选择题(共13小题)1.【解答】解:由题意可知几何体是圆柱,底面周长16,高为:2,直观图以及侧面展开图如图:圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度:=2.故选:B.2.【解答】解:△ABC为等边三角形且面积为9,可得,解得AB=6,球心为O,三角形ABC的外心为O′,显然D在O′O的延长线与球的交点如图:O′C==,OO′==2,则三棱锥D﹣ABC高的最大值为:6,则三棱锥D﹣ABC体积的最大值为:=18.故选:B.3.【解答】解:由题意可知图形如图:⊙O1的面积为4π,可得O1A=2,则AO1=AB sin60°,,∴AB=BC=AC=OO1=2,外接球的半径为:R==4,球O的表面积:4×π×42=64π.故选:A.4.【解答】解:设正四棱锥的高为h,底面边长为a,侧面三角形底边上的高为h′,则依题意有:,因此有h′2﹣()2=ah′⇒4()2﹣2()﹣1=0⇒=(负值舍去);故选:C.5.【解答】解:根据几何体的三视图转换为直观图:如图所示:根据三视图和几何体的的对应关系的应用,这个多面体某条棱的一个端点在正视图中对应的点为M,在俯视图中对应的点为N,所以在侧视图中与点E对应.故选:A.6.【解答】解:由三视图可知,几何体的直观图是正方体的一个角,如图:P A=AB=AC=2,P A、AB、AC两两垂直,故PB=BC=PC=2,几何体的表面积为:3×=6+2,故选:C.7.【解答】解:由题意可知图形如图:△ABC是面积为的等边三角形,可得,∴AB=BC=AC=3,可得:AO1==,球O的表面积为16π,外接球的半径为:R;所以4πR2=16π,解得R=2,所以O到平面ABC的距离为:=1.故选:C.8.【解答】解:如图,由P A=PB=PC,△ABC是边长为2的正三角形,可知三棱锥P﹣ABC为正三棱锥,则顶点P在底面的射影O1为底面三角形的中心,连接BO1并延长,交AC于G,则AC⊥BG,又PO1⊥AC,PO1∩BG=O1,可得AC⊥平面PBG,则PB⊥AC,∵E,F分别是P A,AB的中点,∴EF∥PB,又∠CEF=90°,即EF⊥CE,∴PB⊥CE,得PB⊥平面P AC,∴正三棱锥P﹣ABC的三条侧棱两两互相垂直,把三棱锥补形为正方体,则正方体外接球即为三棱锥的外接球,其直径为D====.半径为,则球O的体积为.故选:D.9.【解答】解:∵点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,∴BM⊂平面BDE,EN⊂平面BDE,∵BM是△BDE中DE边上的中线,EN是△BDE中BD边上的中线,∴直线BM,EN是相交直线,设DE=a,则BD=,BE==,∴BM=a,EN==a,∴BM≠EN,故选:B.10.【解答】解:∵正三棱锥P﹣ABC的侧面都是直角三角形,E,F分别是AB,BC的中点,∴以P为原点,P A为x轴,PB为y轴,PC为z轴,建立空间直角坐标系,设P A=PB=PC=2,则A(2,0,0),B(0,2,0),C(0,0,2),E(1,1,0),F(0,1,1),=(0,2,0),=(1,1,0),=(0,1,1),设平面PEF的法向量=(x,y,z),则,取x=1,得=(1,﹣1,1),设PB与平面PEF所成角为θ,则sinθ===.∴PB与平面PEF所成角的正弦值为.故选:C.11.【解答】解:设与平面2x+y﹣z+4=0平行的平面方程为2x+y﹣z+k=0,代入点(1,﹣1,3),得2×1﹣1﹣3+k=0,解得k=2,则所求的平面方程为2x+y﹣z+2=0.故选:A.12.【解答】解以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,设正方体ABCD﹣A1B1C1D1棱长为2,则A(2,0,0),E(0,2,1),D(0,0,0),C(0,2,0),=(﹣2,2,1),=(0,﹣2,0),设异面直线AE与CD所成角为θ,则cosθ===,sinθ==,∴tanθ=.∴异面直线AE与CD所成角的正切值为.故选:C.13.【解答】解:正方体的所有棱中,实际上是3组平行的棱,每条棱所在直线与平面α所成的角都相等,如图:所示的正六边形平行的平面,并且正六边形时,α截此正方体所得截面面积的最大,此时正六边形的边长,α截此正方体所得截面最大值为:6×=.故选:A.二.填空题(共10小题)14.【解答】解:如图,∵A1、B1、C1分别为OA、OB、OC的中点,∴△A1B1C1∽△ABC,则,过O作OG⊥平面ABC,交平面A1B1C1于G1,则.∴==.故答案为:.15.【解答】解:∵长方体ABCD﹣A1B1C1D1,AB=AD=4,AA1=8,E、F、G为AB、A1B1、DD1的中点,H为A1D1上一点,则A1H=1,∴以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,F(4,2,8),H(3,0,8),E(4,2,0),G(0,0,4),=(﹣1,﹣2,0),=(﹣4,﹣2,4),设异面直线FH与EG所成角为θ,则cosθ===.故答案为:.16.【解答】解:由已知得BD=AB=,BC=2,因为D、E、F三点重合,所以AE=AD=,BF=BD=AB=,所以CE=CF=1,则在△BCF中,由余弦定理得cos∠FCB===﹣,故答案为:﹣.17.【解答】解:向量=(1,﹣1),=(m+1,2m﹣4),若⊥,则m=5,故答案为:5.18.【解答】解:因为圆锥内半径最大的球应该为该圆锥的内切球,如图,圆锥母线BS=3,底面半径BC=1,则其高SC==2,不妨设该内切球与母线BS切于点D,令OD=OC=r,由△SOD∽△SBC,则=,即=,解得r=,V=πr3=π,故答案为:π.19.【解答】解:∠ACB=90°,P为平面ABC外一点,PC=2,点P到∠ACB两边AC,BC的距离均为,过点P作PD⊥AC,交AC于D,作PE⊥BC,交BC于E,过P作PO⊥平面ABC,交平面ABC于O,连结OD,OC,则PD=PE=,∴由题意得CD=CE=OD=OE==1,∴PO===.∴P到平面ABC的距离为.故答案为:.20.【解答】解:该半正多面体共有8+8+8+2=26个面,设其棱长为x,则x+x+x=1,解得x=﹣1.故答案为:26,﹣1.21.【解答】解:该模型为长方体ABCD﹣A1B1C1D1,挖去四棱锥O﹣EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H,分别为所在棱的中点,AB=BC=6cm,AA1=4cm,∴该模型体积为:﹣V O﹣EFGH=6×6×4﹣=144﹣12=132(cm3),∵3D打印所用原料密度为0.9g/cm3,不考虑打印损耗,∴制作该模型所需原料的质量为:132×0.9=118.8(g).故答案为:118.8.22.【解答】解:∵平面α截球O的球面所得圆的面积为π,则圆的半径为1,该平面与球心的距离d=3,∴球半径R=.∴球的表面积S=4πR2=40π.故答案为:40π.23.【解答】解:圆锥的顶点为S,母线SA,SB互相垂直,△SAB的面积为8,可得:,解得SA=4,SA与圆锥底面所成角为30°.可得圆锥的底面半径为:2,圆锥的高为:2,则该圆锥的体积为:V==8π.故答案为:8π.三.解答题(共17小题)24.【解答】解:(1)证明:∵在平行四边形ABCM中,∠ACM=90°,∴AB⊥AC,又AB⊥DA.且AD∩AC=A,∴AB⊥面ADC,∵AB⊂面ABC,∴平面ACD⊥平面ABC;(2)∵AB=AC=3,∠ACM=90°,∴AD=AM=3,∴BP=DQ=DA=2,由(1)得DC⊥AB,又DC⊥CA,∴DC⊥面ABC,∴三棱锥Q﹣ABP的体积V==××==1.25.【解答】解:(1)不妨设圆O的半径为1,OA=OB=OC=1,AE=AD=2,,,,在△P AC中,P A2+PC2=AC2,故P A⊥PC,同理可得P A⊥PB,又PB∩PC=P,故P A⊥平面PBC;(2)建立如图所示的空间直角坐标系,则有,E(0,1,0),故,设平面PCE的法向量为,则由,得,取x=1,则,z=,所以平面PCE的法向量为,由(1)可知P A⊥平面PBC,不妨取平面PBC的法向量为,故,即二面角B﹣PC﹣E的余弦值为.26.【解答】解:(1)连接OA,OB,OC,△ABC是底面的内接正三角形,所以AB=BC=AC.O是圆锥底面的圆心,所以:OA=OB=OC,所以AP=BP=CP=OA2+OP2=OB2+OP2=OC2+OP2,所以△APB≌△BPC≌△APC,由于∠APC=90°,所以∠APB=∠BPC=90°,所以AP⊥BP,CP⊥BP,由于AP∩CP=P,所以BP⊥平面APC,由于BP⊂平面P AB,所以:平面P AB⊥平面P AC.(2)设圆锥的底面半径为r,圆锥的母线长为l,所以.由于圆锥的侧面积为π,所以,整理得(r2+3)(r2﹣1)=0,解得r=1.所以AB==.由于AP2+BP2=AB2,解得则:=.27.【解答】解:(1)证明:∵M,N分别为BC,B1C1的中点,底面为正三角形,∴B1N=BM,四边形BB1NM为矩形,A1N⊥B1C1,∴BB1∥MN,∵AA1∥BB1,∴AA1∥MN,∵MN⊥B1C1,A1N⊥B1C1,MN∩A1N=N,∴B1C1⊥平面A1AMN,∵B1C1⊂平面EB1C1F,∴平面A1AMN⊥平面EB1C1F,综上,AA1∥MN,且平面A1AMN⊥平面EB1C1F.(2)解:∵三棱柱上下底面平行,平面EB1C1F与上下底面分别交于B1C1,EF,∴EF∥B1C1∥BC,∵AO∥面EB1C1F,AO⊂面AMNA1,面AMNA1∩面EB1C1F=PN,∴AO∥PN,四边形APNO为平行四边形,∵O是正三角形的中心,AO=AB,∴A1N=3ON,AM=3AP,PN=BC=B1C1=3EF,由(1)知直线B1E在平面A1AMN内的投影为PN,直线B1E与平面A1AMN所成角即为等腰梯形EFC1B1中B1E与PN所成角,在等腰梯形EFC1B1中,令EF=1,过E作EH⊥B1C1于H,则PN=B1C1=EH=3,B1H=1,,sin∠B1EH==,∴直线B1E与平面A1AMN所成角的正弦值为.28.【解答】(1)证明:在AA1上取点M,使得A1M=2AM,连接EM,B1M,EC1,FC1,在长方体ABCD﹣A1B1C1D1中,有DD1∥AA1∥BB1,且DD1=AA1=BB1.又2DE=ED1,A1M=2AM,BF=2FB1,∴DE=AM=FB1.∴四边形B1F AM和四边形EDAM都是平行四边形.∴AF∥MB1,且AF=MB1,AD∥ME,且AD=ME.又在长方体ABCD﹣A1B1C1D1中,有AD∥B1C1,且AD=B1C1,∴B1C1∥ME且B1C1=ME,则四边形B1C1EM为平行四边形,∴EC1∥MB1,且EC1=MB1,又AF∥MB1,且AF=MB1,∴AF∥EC1,且AF=EC1,则四边形AFC1E为平行四边形,∴点C1在平面AEF内;(2)解:在长方体ABCD﹣A1B1C1D1中,以C1为坐标原点,分别以C1D1,C1B1,C1C所在直线为x,y,z轴建立空间直角坐标系.∵AB=2,AD=1,AA1=3,2DE=ED1,BF=2FB1,∴A(2,1,3),E(2,0,2),F(0,1,1),A1(2,1,0),则,,.设平面AEF的一个法向量为.则,取x1=1,得;设平面A1EF的一个法向量为.则,取x2=1,得.∴cos<>==.设二面角A﹣EF﹣A1为θ,则sinθ=.∴二面角A﹣EF﹣A1的正弦值为.29.【解答】解:(1)因为ABCD﹣A1B1C1D1是长方体,所以BB1⊥平面ABCD,而AC⊂平面ABCD,所以AC⊥BB1,因为ABCD﹣A1B1C1D1是长方体,且AB=BC,所以ABCD是正方形,所以AC⊥BD,又BD∩BB1=B.所以AC⊥平面BB1D1D,又因为点E,F分别在棱DD1,BB1上,所以EF⊂平面BB1D1D,所以EF⊥AC.(2)取AA1上靠近A1的三等分点M,连接D1M,C1F,MF,C1E.因为点E在DD1,且2DE=ED1,所以ED∥AM,且ED1=AM,所以四边形AED1M为平行四边形,所以D1M∥AE,且D1M=AE,又因为F在BB1上,且BF=2FB1,所以A1M∥FB1,且A1M=FB1,所以A1B1FM为平行四边形,所以FM∥A1B1,FM=A1B1,即FM∥C1D1,FM=C1D1,所以C1D1MF为平行四边形,所以D1M∥C1F,所以AE∥C1F,所以A,E,F,C1四点共面.所以点C1在平面AEF内.30.【解答】证明:(1)由题意知AA1∥BB1∥CC1,又∵侧面BB1C1C是矩形且M,N分别为BC,B1C1的中点,∴MN∥BB1,BB1⊥BC,∴MN∥AA1,MN⊥B1C1,又底面是正三角形,∴AM⊥BC,A1N⊥B1C1,又∵MN∩AM=M,∴B1C1⊥平面A1AMN,∵B1C1⊂平面EB1C1F,∴平面A1AMN⊥平面EB1C1F;解:(2)∵AO∥平面EB1C1F,AO⊂平面A1AMN,平面A1AMN∩平面EB1C1F=NP,∴AO∥NP,∵NO∥AP,∴AO=NP=6,∵O为△A1B1C1的中心,∴ON=A1C1sin60°=×6×=,∴ON=AP=,∴AM=3AP=3,过M作MH⊥NP,垂足为H,∵平面A1AMN⊥平面EB1C1F,平面A1AMN∩平面EB1C1F=NP,MH⊂平面A1AMN,∴MH⊥平面EB1C1F,∵在等边三角形中=,即EF===2,由(1)可知四边形EB1C1F为梯形,∵∠MPN=,∴MH=MP sin∠MPN==3,31.【解答】解法一:证明:(1)连结B1C,ME,∵M,E分别是BB1,BC的中点,∴ME∥B1C,又N为A1D的中点,∴ND=A1D,由题设知A1B1DC,∴B1C A1D,∴ME ND,∴四边形MNDE是平行四边形,MN∥ED,又MN⊄平面C1DE,∴MN∥平面C1DE.解:(2)过C作C1E的垂线,垂足为H,由已知可得DE⊥BC,DE⊥C1C,∴DE⊥平面C1CE,故DE⊥CH,∴CH⊥平面C1DE,故CH的长即为C到平面C1DE的距离,由已知可得CE=1,CC1=4,∴C1E=,故CH=,∴点C到平面C1DE的距离为.解法二:证明:(1)∵直四棱柱ABCD﹣A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.∴DD1⊥平面ABCD,DE⊥AD,以D为原点,DA为x轴,DE为y轴,DD1为z轴,建立空间直角坐标系,M(1,,2),N(1,0,2),D(0,0,0),E(0,,0),C1(﹣1,,4),=(0,﹣,0),=(﹣1,),=(0,),设平面C1DE的法向量=(x,y,z),则,取z=1,得=(4,0,1),∴MN∥平面C1DE.解:(2)C(﹣1,,0),=(﹣1,,0),平面C1DE的法向量=(4,0,1),∴点C到平面C1DE的距离:d===.32.【解答】(1)证明:如图,过N作NH⊥AD,则NH∥AA1,且,又MB∥AA1,MB=,∴四边形NMBH为平行四边形,则NM∥BH,由NH∥AA1,N为A1D中点,得H为AD中点,而E为BC中点,∴BE∥DH,BE=DH,则四边形BEDH为平行四边形,则BH∥DE,∴NM∥DE,∵NM⊄平面C1DE,DE⊂平面C1DE,∴MN∥平面C1DE;(2)解:以D为坐标原点,以垂直于DC得直线为x轴,以DC所在直线为y轴,以DD1所在直线为z轴建立空间直角坐标系,则N(,,2),M(,1,2),A1(,﹣1,4),,,设平面A1MN的一个法向量为,由,取x=,得,又平面MAA1的一个法向量为,∴cos<>===.∴二面角A﹣MA1﹣N的正弦值为.33.【解答】证明:(1)长方体ABCD﹣A1B1C1D1中,B1C1⊥平面ABA1B1,∴B1C1⊥BE,∵BE⊥EC1,∵B1C1∩EC1=C1,∴BE⊥平面EB1C1.解:(2)以C为坐标原点,建立如图所示的空间直角坐标系,设AE=A1E=1,则BE=EB1,∵BE⊥平面EB1C1,∴BE⊥EB1,∴BE2+EB12=2BE2==4,∴BE2=2,∵AE2+AB2=1+AB2=BE2=2,∴AB=1,则E(1,1,1),A(1,1,0),B1(0,1,2),C1(0,0,2),C(0,0,0),∵BC⊥EB1,∴EB1⊥面EBC,故取平面EBC的法向量为==(﹣1,0,1),设平面ECC1的法向量=(x,y,z),由,得,取x=1,得=(1,﹣1,0),∴cos<>==﹣,∴二面角B﹣EC﹣C1的正弦值为.34.【解答】解:(1)证明:由长方体ABCD﹣A1B1C1D1,可知B1C1⊥平面ABB1A1,BE⊂平面ABB1A1,∴B1C1⊥BE,∵BE⊥EC1,B1C1∩EC1=C1,∴BE⊥平面EB1C1;(2)由(1)知∠BEB1=90°,由题设可知Rt△ABE≌Rt△A1B1E,∴∠AEB=∠A1EB1=45°,∴AE=AB=3,AA1=2AE=6,∵在长方体ABCD﹣A1B1C1D1中,AA1∥平面BB1C1C,E∈AA1,AB⊥平面BB1C1C,∴E到平面BB1C1C的距离d=AB=3,∴四棱锥E﹣BB1C1C的体积V=×3×6×3=18.35.【解答】证明:(1)由已知得AD∥BE,CG∥BE,∴AD∥CG,∴AD,CG确定一个平面,∴A,C,G,D四点共面,由已知得AB⊥BE,AB⊥BC,∴AB⊥面BCGE,∵AB⊂平面ABC,∴平面ABC⊥平面BCGE.解:(2)作EH⊥BC,垂足为H,∵EH⊂平面BCGE,平面BCGE⊥平面ABC,∴EH⊥平面ABC,由已知,菱形BCGE的边长为2,∠EBC=60°,∴BH=1,EH=,以H为坐标原点,的方向为x轴正方向,建立如图所求的空间直角坐标系H﹣xyz,则A(﹣1,1,0),C(1,0,0),G(2,0,),=(1,0,),=(2,﹣1,0),设平面ACGD的法向量=(x,y,z),则,取x=3,得=(3,6,﹣),又平面BCGE的法向量为=(0,1,0),∴cos<>==,∴二面角B﹣CG﹣A的大小为30°.36.【解答】解:(1)证明:由已知可得AD∥BE,CG∥BE,即有AD∥CG,则AD,CG确定一个平面,从而A,C,G,D四点共面;由四边形ABED为矩形,可得AB⊥BE,由△ABC为直角三角形,可得AB⊥BC,又BC∩BE=B,可得AB⊥平面BCGE,AB⊂平面ABC,可得平面ABC⊥平面BCGE;(2)连接BG,AG,由AB⊥平面BCGE,可得AB⊥BG,在△BCG中,BC=CG=2,∠BCG=120°,可得BG=2BC sin60°=2,可得AG==,在△ACG中,AC=,CG=2,AG=,可得cos∠ACG==﹣,即有sin∠ACG=,则平行四边形ACGD的面积为2××=4.37.【解答】(1)证明:∵AB=BC=2,AC=4,∴AB2+BC2=AC2,即△ABC是直角三角形,又O为AC的中点,∴OA=OB=OC,∵P A=PB=PC,∴△POA≌△POB≌△POC,∴∠POA=∠POB=∠POC=90°,∴PO⊥AC,PO⊥OB,OB∩AC=O,∴PO⊥平面ABC;(2)解:由(1)得PO⊥平面ABC,PO=,在△COM中,OM==.=××=,S△COM==.设点C到平面POM的距离为d.由V P﹣OMC=V C﹣POM⇒,解得d=,∴点C到平面POM的距离为.38.【解答】(1)证明:矩形ABCD所在平面与半圆弦所在平面垂直,所以AD⊥半圆弦所在平面,CM⊂半圆弦所在平面,∴CM⊥AD,M是上异于C,D的点.∴CM⊥DM,DM∩AD=D,∴CM⊥平面AMD,CM⊂平面CMB,∴平面AMD⊥平面BMC;(2)解:存在P是AM的中点,理由:连接BD、AC交于O,取AM的中点P,连接OP,连接PD,PB,可得MC∥OP,MC⊄平面BDP,OP⊂平面BDP,所以MC∥平面PBD.39.【解答】(1)证明:由题意,点E、F分别是AD、BC的中点,则,,由于四边形ABCD为正方形,所以EF⊥BC.由于PF⊥BF,EF∩PF=F,则BF⊥平面PEF.又因为BF⊂平面ABFD,所以:平面PEF⊥平面ABFD.(2)在平面PEF中,过P作PH⊥EF于点H,连接DH,由于EF为面ABCD和面PEF的交线,PH⊥EF,则PH⊥面ABFD,故PH⊥DH.在三棱锥P﹣DEF中,可以利用等体积法求PH,因为DE∥BF且PF⊥BF,所以PF⊥DE,又因为△PDF≌△CDF,所以∠FPD=∠FCD=90°,所以PF⊥PD,由于DE∩PD=D,则PF⊥平面PDE,故V F﹣PDE=,因为BF∥DA且BF⊥面PEF,所以DA⊥面PEF,所以DE⊥EP.设正方形边长为2a,则PD=2a,DE=a在△PDE中,,所以,故V F﹣PDE=,又因为,所以PH==,所以在△PHD中,sin∠PDH==,即∠PDH为DP与平面ABFD所成角的正弦值为:.40.【解答】(1)证明:连接BO,∵AB=BC=2,O是AC的中点,∴BO⊥AC,且BO=2,又P A=PC=PB=AC=4,∴PO⊥AC,PO=2,则PB2=PO2+BO2,则PO⊥OB,∵OB∩AC=O,∴PO⊥平面ABC;(2)建立以O坐标原点,OB,OC,OP分别为x,y,z轴的空间直角坐标系如图:A(0,﹣2,0),P(0,0,2),C(0,2,0),B(2,0,0),=(﹣2,2,0),设=λ=(﹣2λ,2λ,0),0<λ<1则=﹣=(﹣2λ,2λ,0)﹣(﹣2,﹣2,0)=(2﹣2λ,2λ+2,0),则平面P AC的法向量为=(1,0,0),设平面MP A的法向量为=(x,y,z),则=(0,﹣2,﹣2),令z=1,则y=﹣,x=,即=(,﹣,1),∵二面角M﹣P A﹣C为30°,∴cos30°=||=,即=,解得λ=或λ=3(舍),则平面MP A的法向量=(2,﹣,1),=(0,2,﹣2),PC与平面P AM所成角的正弦值sinθ=|cos<,>|=||==.。
高考数学(文)二轮复习 大题专项强化练专题能力提升练(四) 立体几何

专题能力提升练(四) 立体几何一、选择题(每小题5分)1.已知某几何体的三视图如图所示,则该几何体的体积为( )A.83πB.163π C .8π D .16π 解析:该几何体是从一个圆柱里挖去一个圆锥所得,所以体积为V =π×22×2-13π×22×2=163π.答案:B2.某四棱锥的三视图如图所示,则最长的一条侧棱的长度是( )A.13 B .13 C .29 D.29解析:由题意可知四棱锥的底面是上、下底边长分别为2,4,高为3的直角梯形,棱锥的高为2,高所在的棱垂直于底面,所以侧棱最长为22+32+42=29.答案:D3.已知某棱锥的三视图如图所示,俯视图为正方形,则该棱锥外接球的体积是( )A.4π3B.8π3C.82π3D.162π3解析:该几何体是一个底面是边长为2的正方形、高为2的四棱锥,其中一条侧棱垂直于底面,它是长方体的一部分,与长方体具有相同的外接球.则原四棱锥的外接球半径r =122+2+4=2,故其体积为4π3×(2)3=82π3. 答案:C4.如图所示是一个几何体的三视图,则这个几何体外接球的表面积为( )A .8πB .16πC .32πD .64π解析:该几何体为一四棱锥,其直观图如图,它是三棱柱的一部分,四棱锥与三棱柱具有相同的外接球.三棱柱的底面为等腰直角三角形,所以其外接球的半径r =22+22=22,所以该几何体外接球的表面积为4πr 2=32π.答案:C5.下列结论正确的是( )A .过一点有且只有一个平面与已知平面垂直B .过一条直线有且只有一个平面与已知平面垂直C .过一点有且只有一条直线与已知直线垂直D .过一点有且只有一条直线与已知平面垂直解析:过一点如果有两条直线与已知平面垂直,根据直线与平面垂直的性质定理可知,这两条直线平行,矛盾,所以选项D 中的结论正确;过一点有无数个平面与已知平面垂直,选项A 中的结论不正确;当直线与平面垂直时,过该直线的任意平面即与已知平面垂直,选项B 中的结论不正确;在空间,过一点与已知直线垂直的直线有无数条,选项C 中的结论不正确.答案:D6.正四面体ABCD 中,AO ⊥平面BCD ,垂足为O ,设M 是线段AO 上一点,且∠BMC=90°,则AMMO的值为( )A .1B .2 C.12 D.23解析:如图,连接OB ,设正四面体的棱长为a ,则OB =33a ,MB =22a ,故OM =66a =12AO ,则AM MO=1.答案:A7.设l ,m 是两条不同的直线,α是一个平面,则下列说法正确的是( ) A .若l ⊥m ,m ⊂α,则l ⊥α B .若l ⊥α,l ∥m ,则m ⊥αC .若l ∥α,m ⊂α,则l ∥mD .若l ∥α,m ∥α,则l ∥m解析:选项A 中,一条直线与一个平面内的一条直线垂直,不能保证该直线与该平面垂直;两平行线中的一条与一个平面垂直,另一条也垂直于这个平面,选项B 中的说法正确;选项C 中,一条直线与一个平面平行,不能保证其平行于平面内的任意直线,选项C 中的说法不正确;平行于同一个平面的两条直线的位置关系不确定,选项D 中的说法不正确.答案:B8.已知三棱柱的三个侧面均垂直于底面,底面为正三角形,且侧棱长与底面边长之比为21,顶点都在一个球面上,若该球的表面积为16π3,则此三棱柱的侧面积为( )A. 3B.32C .8D .6解析:如图,根据球的表面积可得球的半径为r =43,设三棱柱的底面边长为x ,则⎝⎛⎭⎫432=x 2+⎝⎛⎭⎫33x 2,解得x =1,故该三棱柱的侧面积为3×1×2=6. 答案:D9.如图,在三棱柱ABC -A 1B 1C 1中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则BB 1与平面AB 1C 1所成角的大小为( )A.π6B.π4C.π3D.π2解析:分别取BC ,B 1C 1的中点D ,D 1,连接AD ,DD 1,AD 1. 显然DD 1⊥B 1C 1,AD 1⊥B 1C 1, 故B 1C 1⊥平面ADD 1,故平面AB 1C 1⊥平面ADD 1,故DD 1在平面AB 1C 1内的射影在AD 1上,∠AD 1D 即为直线DD 1与平面AB 1C 1所成的角. 在Rt △AD 1D 中,AD =3,DD 1=3,所以tan ∠AD 1D =33,所以∠AD 1D =π6.因为BB 1∥DD 1,所以直线BB 1与平面AB 1C 1所成角的大小为π6.答案:A10.正三角形ABC 的边长为23,将它沿高AD 翻折,使点B 与点C 间的距离为3,此时四面体ABCD 的外接球的半径为( )A.13B.132C .2 3 D.3解析:球心O 一定在与平面BCD 垂直且过底面正三角形中心O ′的直线上,也在平面ADO 中AD 的垂直平分线上,如图.OE =O ′D =3×32×23=1,DE =12AD =12×23×32=32,故所求外接球的半径r =12+⎝⎛⎭⎫322=132.答案:B二、填空题(每小题5分)11.如图所示是一个几何体的三视图,则该几何体的体积为__________.解析:由题可知该几何体由两个相同的半圆柱和一个长方体拼接而成,因此该几何体的体积V =1×2×4+π×12×2=8+2π.答案:8+2π12.如图,四棱锥P -ABCD 中,∠ABC =∠BAD =90°,BC =2AD ,△P AB 和△P AD 都是等边三角形,则异面直线CD 与PB 所成角的大小为__________.解析:如图,取BC 的中点E ,连接AE ,ED ,BD ,PE . 设BD ∩AE =O ,连接PO .设AB =a ,则OA =OB =22a . 又PB =P A =PD ,O 为BD 的中点,所以BD ⊥PO , 所以PO =a 2-⎝⎛⎭⎫22a 2=22a ,所以PO ⊥OA ,所以PO ⊥平面ABCD ,所以PO ⊥AE .由已知可得四边形ABED 为正方形,所以BD ⊥AE ,所以AE ⊥平面PBD ,所以AE ⊥PB .又CD ∥AE ,所以CD ⊥PB ,即异面直线CD 与PB 所成角的大小为90°.答案:90°13.(·池州二模)表面积为60π的球面上有四点S 、A 、B 、C ,且△ABC 是等边三角形,球心O 到平面ABC 的距离为3,若平面SAB ⊥平面ABC ,则棱锥S -ABC 体积的最大值为________.解析:∵表面积为60π的球,∴球的半径为15,设△ABC 的中点为D ,则OD =3,所以DA =23,则AB =6棱锥S -ABC 的底面积S =34×62=93为定值,欲使其体积最大,应有S 到平面ABC 的距离取最大值, 又平面SAB ⊥平面ABC ,∴S 在平面ABC 上的射影落在直线AB 上,而SO =15,点D 到直线AB 的距离为3, 则S 到平面ABC 的距离的最大值为33,∴V =13×93×33=27.答案:27 14.如图,边长为2的正方形ABCD 中,点E ,F 分别是边AB ,BC 的中点,将△AED ,△EBF ,△FCD 分别沿DE ,EF ,FD 折起,使A ,B ,C 三点重合于点A ′,若四面体A ′EFD 的四个顶点在同一个球面上,则该球的半径为__________.解析:易知四面体A ′EFD 的三条侧棱A ′E ,A ′F ,A ′D 两两垂直,且A ′E =1,A ′F =1,A ′D =2,我们把四面体A ′EFD 扩成棱长为1,1,2的一个长方体,则长方体的外接球即为四面体A ′EFD 的外接球,所以球的半径为r =1212+12+22=62.答案:6215.如图,在四棱锥P -ABCD 中,底面ABCD 为菱形,∠BAD =60°,Q 为AD 的中点.若平面P AD ⊥平面ABCD ,P A =PD =AD =2,点M 在线段PC 上,且PM =2MC ,则四棱锥P -ABCD 与三棱锥P -QBM 的体积之比是__________.解析:过点M 作MH ∥BC 交PB 于点H .∵平面P AD ⊥平面ABCD ,平面P AD ∩平面ABCD =AD ,PQ ⊥AD , ∴PQ ⊥平面ABCD .∵P A =PD =AD =AB =2,∠BAD =60°, ∴PQ =BQ = 3.∴V P -ABCD =13PQ ·S 菱形ABCD =13×3×2×3=2.又PQ ⊥BC ,BQ ⊥AD ,AD ∥BC , ∴BQ ⊥BC ,又QB ∩QP =Q ,∴BC ⊥平面PQB ,又MH ∥BC ,PM =2MC ,∴MH ⊥平面PQB ,MH BC =PM PC =23,∵BC =2,∴MH =43,∴V P -QBM =V M -PQB =13×12×3×3×43=23,∴V P -ABCD V P -QBM =3 1. 答案:31三、解答题(第16,17,18,19题每题12分,第20题13分,第21题14分)16.如图,已知三棱柱ABC -A ′B ′C ′的侧棱垂直于底面,AB =AC ,∠BAC =90°,点M ,N 分别为A ′B 和B ′C ′的中点.(1)证明:MN ∥平面AA ′C ′C ;(2)设AB =λAA ′,当λ为何值时,CN ⊥平面A ′MN ,试证明你的结论. 解:(1)取A ′B ′的中点E ,连接ME ,NE ,因为M ,N 分别为A ′B 和B ′C ′的中点,所以NE ∥A ′C ′,ME ∥AA ′.又ME ∩NE =E ,A ′C ′∩AA ′=A ′, 所以平面MNE ∥平面AA ′C ′C , 因为MN ⊂平面MNE , 所以MN ∥平面 AA ′C ′C .(2)连接BN ,设AA ′=a ,则AB =λAA ′=λa ,由题意知BC =2λa ,NC =BN =a 2+12λ2a 2,因为三棱柱ABC -A ′B ′C ′的侧棱垂直于底面, 所以平面A ′B ′C ′⊥平面BB ′C ′C ,因为AB =AC ,点N 是B ′C ′的中点,所以A ′N ⊥平面BB ′C ′C , 所以CN ⊥A ′N ,要使CN ⊥平面A ′MN , 只需CN ⊥BN 即可, 所以CN 2+BN 2=BC 2,即2⎝⎛⎭⎫a 2+12λ2a 2=2λ2a 2,所以λ=2, 则当λ=2时,CN ⊥平面A ′MN .17.如图,在四棱锥P -ABCD 中,底面ABCD 是直角梯形,AD ∥BC ,AB ⊥BC ,侧面P AB ⊥底面ABCD ,P A =AD =AB =1,BC =2.(1)证明:平面PBC ⊥平面PDC ;(2)若∠P AB =120°,求点B 到直线PC 的距离. 解:(1)延长BA ,CD 交于M 点,连接MP ,则BM =2,A 是BM 的中点,因为P A =12BM ,所以MP ⊥PB ,又因为侧面P AB ⊥底面ABCD ,AB ⊥BC , 所以BC ⊥平面PBM ,所以BC ⊥MP ,故MP ⊥平面PBC ,因为MP ⊂平面PCD ,所以平面PBC ⊥平面PCD .(2)过B 点作BN ⊥PC 于N ,则BN 为点B 到直线PC 的距离. 因为∠P AB =120°,P A =AD =AB =1,BC =2, 所以MP =1,PB =3,PC =7,因为BN ×PC =BC ×PB ,所以BN =237=2217.18.(·山东烟台期末)如图,在三棱柱ABC -A 1B 1C 1中,侧面ABB 1A 1,ACC 1A 1均为正方形,AB =AC =1,∠BAC =90°,点D 是棱B 1C 1的中点.(1)求证:A 1D ⊥平面BB 1C 1C ;(2)求证:AB 1∥平面A 1DC ; (3)求三棱锥C 1-A 1CD 的体积.解:(1)∵面ABB 1A 1,ACC 1A 1均为正方形, AA 1⊥A 1C 1,AA 1⊥A 1B 1,A 1C 1∩A 1B 1=A 1,A 1C 1,A 1B 1⊂平面A 1B 1C 1, ∴AA 1⊥平面A 1B 1C 1,∵AA 1∥CC 1,∴CC 1⊥平面A 1B 1C 1. ∵A 1D ⊂平面A 1B 1C 1,∴CC 1⊥A 1D , ∵三棱柱ABC -A 1B 1C 1,AB =AC =1, ∴A 1B 1=A 1C 1,∵D 是B 1C 1的中点,∴A 1D ⊥B 1C 1.∵CC 1∩B 1C 1=C 1,又CC 1,B 1C 1⊂平面BB 1C 1C , ∴A 1D ⊥平面BB 1C 1C .(2)连接AC 1交A 1C 于点O ,连接OD , ∵四边形ACC 1A 1为正方形,点O 为AC 1的中点,D 为B 1C 1的中点, ∴OD 为△AB 1C 1的中位线,∴AB 1∥OD , ∵OD ⊂平面A 1DC ,AB 1⊄平面A 1DC , ∴AB 1∥平面A 1DC .(3)由(1)CC 1⊥平面A 1B 1C 1,∴CC 1为三棱柱ABC -A 1B 1C 1的高, ∵A 1B 1=A 1C 1=1,∠B 1A 1C 1=90°, D 是B 1C 1的中点,S △A 1C 1D =12S △A 1B 1C 1=12×12×12=14,VC 1-A 1CD =VC -A 1C 1D =13S △A 1C 1D ·CC 1=13×14×1=112,即三棱锥C 1-A 1CD 的体积V =112.19.(·河北衡水二中期中)如图,在四棱锥P -ABCD 中,侧面P AD ⊥底面ABCD ,侧棱P A =PD =2,底面ABCD 为直角梯形,其中BC ∥AD ,AB ⊥AD ,AD =2AB =2BC =2,O 为AD 中点.(1)求证:PO ⊥平面ABCD ;(2)求异面直线PB 与CD 所成角的余弦值;(3)线段AD 上是否存在点Q ,使得它到平面PCD 的距离为32?若存在,求出AQQD的值;若不存在,请说明理由.解:(1)在△P AD 中,P A =PD ,O 为AD 中点,所以PO ⊥AD .又侧面P AD ⊥底面ABCD ,平面P AD ∩平面ABCD =AD ,PO ⊂平面P AD , 所以PO ⊥平面ABCD .(2)连接BO ,在直角梯形ABCD 中,BC ∥AD ,AD =2AB =2BC ,有OD ∥BC 且OD =BC ,所以四边形OBCD 是平行四边形, 所以OB ∥DC .由(1)知PO ⊥OB ,∠PBO 为锐角,所以∠PBO 是异面直线PB 与CD 所成的角. 因为AD =2AB =2BC =2,在Rt △AOB 中,AB =1,AO =1,所以OB =2,在Rt △POA 中,因为AP =2,AO =1,所以OP =1,在Rt △PBO 中,PB =3,所以cos ∠PBO =63,所以异面直线PB 与CD 所成的角的余弦值为63.(3)假设存在点Q ,使得它到平面PCD 的距离为32.设QD =x ,则S △DQC =12x ,由(2)得CD =OB =2, 在Rt △POC 中,PC =2,所以PC =CD =DP ,S △PCD =34×(2)2=32,由V P -DQC =V Q -PCD ,得x =32,所以存在点Q 满足题意,此时AQ QD =13.20.(·天津五区期末)已知四棱柱ABCD -A 1B 1C 1D 1的侧棱AA 1⊥底面ABCD ,ABCD 是等腰梯形,AB ∥DC ,AB =2,AD =1,∠ABC =60°,E ,F 分别为A 1C ,A 1B 1的中点.(1)求证:D 1E ∥平面BB 1C 1C ; (2)求证:BC ⊥A 1C ;(3)若A 1A =AB ,求直线DF 与平面A 1ADD 1所成角的正弦值.解:(1)连接D 1F ,EF ,B 1C ,因为EF 是△A 1CB 1的中位线,所以EF ∥CB 1. 因为AB ∥DC ,所以A 1B 1∥D 1C 1, 又AB =2AD =2,∠ABC =60°,可求D 1C 1=1,故D 1C 1=FB 1,所以四边形C 1D 1FB 1为平行四边形,所以D 1F ∥C 1B 1,又EF ∩D 1F =F ,CB 1∩C 1B 1=B 1, 所以平面D 1EF ∥平面BB 1C 1C ,又D 1E ⊂平面D 1EF , 所以D 1E ∥平面BB 1C 1C .(2)连接AC ,在等腰三角形ADC 中可求AC =3,又因为BC =1,AB =2,所以AC 2+BC 2=AB 2,所以BC ⊥AC . 又四棱柱是直四棱柱,故A 1A ⊥平面ABCD ,BC ⊂平面ABCD , 所以A 1A ⊥BC .因为A 1A ∩AC =A ,所以BC ⊥平面A 1AC ,A 1C ⊂平面A 1AC , 所以BC ⊥A 1C .(3)取A 1D 1的中点G ,连结FG ,由已知可知△A 1D 1F 为正三角形,故FG ⊥A 1D 1,又因为四棱柱是直四棱柱,所以平面A 1D 1F ⊥平面A 1ADD 1, 所以FG ⊥平面A 1ADD 1.连结DG ,则∠FDG 为直线DF 与平面A 1ADD 1所成的角.在Rt △FDG 中,FG =32,DG =172,故DF =5,所以sin ∠FDG =FG DF =325=1510.21.(·江西赣州期中)如图①,在四棱锥P -ABCD 中,P A ⊥底面ABCD ,面ABCD 为正方形,E 为侧棱PD 上一点,F 为AB 上一点.该四棱锥的正(主)视图和侧(左)视图如图②所示.(1)求四面体PBFC 的体积; (2)证明:AE ∥平面PFC ;(3)证明:平面PFC ⊥平面PCD .解:(1)由左视图可得F 为AB 的中点,∴△BFC 的面积为S =12×1×2=1.∵P A ⊥平面ABCD ,∴四面体PBFC 的体积为V P -BFC =13S △BFC ·P A =13×1×2=23.(2)取PC 中点Q ,连接EQ ,FQ . 由正(主)视图可得E 为PD 的中点,∴EQ ∥CD ,EQ =12CD .又AF ∥CD ,AF =12CD ,∴AF ∥EQ ,AF =EQ .∴四边形AFQE 为平行四边形, ∴AE ∥FQ .∵AE ⊄平面PFC ,FQ ⊂平面PFC , ∴直线AE ∥平面PFC .(3)∵P A⊥平面ABCD,∴P A⊥CD.∵平面ABCD为正方形,∴AD⊥CD.∴CD⊥平面P AD.∵AE⊂平面P AD,∴CD⊥AE.∵P A=AD,E为PD中点,∴AE⊥PD.∴AE⊥平面PCD.∵AE∥FQ,∴FQ⊥平面PCD.∵FQ⊂平面PFC,∴平面PFC⊥平面PCD.第11页共11页。
【配套K12】高考数学二轮专题复习 专题五 5.1 空间几何体的三视图、表面积与体积能力训练 新人教
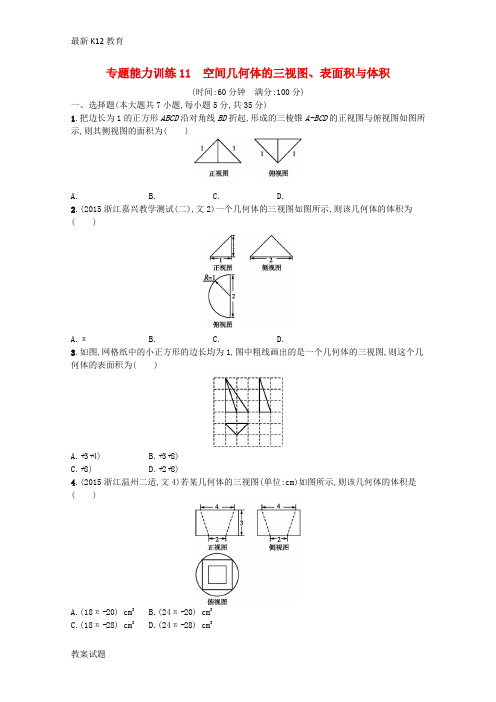
专题能力训练11 空间几何体的三视图、表面积与体积(时间:60分钟满分:100分)一、选择题(本大题共7小题,每小题5分,共35分)1.把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为()A. B. C. D.2.(2015浙江嘉兴教学测试(二),文2)一个几何体的三视图如图所示,则该几何体的体积为()A.πB.C.D.3.如图,网格纸中的小正方形的边长均为1,图中粗线画出的是一个几何体的三视图,则这个几何体的表面积为()A.+3+4)B.+3+8)C.+8)D.+2+8)4.(2015浙江温州二适,文4)若某几何体的三视图(单位:cm)如图所示,则该几何体的体积是()A.(18π-20) cm3B.(24π-20) cm3C.(18π-28) cm3D.(24π-28) cm35.正三棱锥的高和底面边长都等于6,则其外接球的表面积为()A.64πB.32πC.16πD.8π6.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为()A.6B.6C.4D.47.某几何体的三视图如图所示,则该几何体的表面积为()A.54B.60C.66D.72二、填空题(本大题共4小题,每小题5分,共20分)8.(2015浙江温州三适应,文11)下面是某几何体的三视图(单位:cm),则该几何体的表面积是cm2,体积为cm3.9.(2015浙江绍兴教学质量检查,文11)某几何体的三视图如图所示,则该几何体的最长棱长为,体积为.10.(2014浙江台州质检)已知正方形ABCD的边长为12,动点M(不在平面ABCD内)满足MA⊥MB,则三棱锥A-BCM的体积的取值范围为.11.已知直三棱柱ABC-A1B1C1中,∠BAC=90°,侧面BCC1B1的面积为2,则直三棱柱ABC-A1B1C1外接球表面积的最小值为.三、解答题(本大题共3小题,共45分.解答应写出必要的文字说明、证明过程或演算步骤)12.(本小题满分14分)(2014陕西,文17)四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.(1)求四面体ABCD的体积;(2)证明:四边形EFGH是矩形.13.(本小题满分15分)(2015课标全国Ⅰ,文18)如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.(1)证明:平面AEC⊥平面BED;(2)若∠ABC=120°,AE⊥EC,三棱锥E-ACD的体积为,求该三棱锥的侧面积.14.(本小题满分16分)如图,在Rt△ABC中,AB=BC=4,点E在线段AB上.过点E作EF∥BC交AC 于点F,将△AEF沿EF折起到△PEF的位置(点A与P重合),使得∠PEB=30°.(1)求证:EF⊥PB;(2)试问:当点E在何处时,四棱锥P-EFCB的侧面PEB的面积最大?并求此时四棱锥P-EFCB的体积.参考答案专题能力训练11空间几何体的三视图、表面积与体积1.D解析:由正视图与俯视图可得三棱锥A-BCD的一个侧面与底面垂直,其侧视图是直角三角形,且直角边长均为,所以侧视图的面积为S=.故选D.2.D解析:由题中所给的三视图可知,该几何体为一半圆锥,底面直径为2,半径为1,高为1,体积V=·π·12·1=.故选D.3.B解析:根据三视图可知该几何体是底面为直角三角形的三棱锥,其表面积S=×3+×2×3++3+8).故选B.4.D解析:由题中所给的三视图可知,该几何体为一个圆柱中间挖去了一个上、下底面为正方形且底面边长分别为4 cm和2 cm的棱台,由三视图可知,圆柱的底面半径为=2 cm,则该几何体的体积为V=π·(2)2·3-(42++22)·3=(24π-28) cm3.故选D.5.A解析:作PM⊥平面ABC于点M,则球心O在PM上,|PM|=6,连接AM,AO,则|OP|=|OA|=R.在Rt△OAM 中,|OM|=6-R,|OA|=R,又|AB|=6,且△ABC为等边三角形,故|AM|==2,则R2-(6-R)2=(2)2, 解得R=4,所以球的表面积S=4πR2=64π.6.B解析:如图所示的正方体ABCD-A1B1C1D1的棱长为4.取B1B的中点G,即三棱锥G-CC1D1为满足要求的几何体,其中最长棱为D1G,D1G==6.7.B解析:根据几何体的三视图可得该几何体的直观图为如图所示的ABC-DEF,故其表面积为S=S△DEF+S△ABC+S梯形ABED+S梯形CBEF+S矩形ACFD=×3×5+×3×4+×(5+2)×4+×(5+2)×5+3×5=60.故选B.8.14+24解析:由题中所给的三视图知,对应的几何体为如下图所示的三棱锥P-ABC,PC⊥平面ABC,PC=2,底面△ABC中,AC=5,AB=4,BC=3,所以AC2=AB2+BC2.所以AB⊥BC.所以PB⊥AB.在直角三角形PCB中,PB=,所以该几何体的表面积为×5×2+×3×2+×4×3+×4×=14+2,该几何体的体积为×4×3×2=4.9. 解析:由题中所给的三视图可知,该几何体是一个三棱锥,底面三角形是底边为2,高为1的等腰三角形,几何体的高为2,有一侧面与底面垂直,且该侧面是等腰三角形(如图).其最长的棱为PB=,体积为×2×1×2=.10.(0,144]解析:因为动点M(不在平面ABCD内)满足MA⊥MB,所以动点M的轨迹是以AB的中点为球心,以6为半径的一个球面去除与平面ABCD相交的部分.因V A-BCM=V M-ABC=×S△ABC×h≤×6=144,故三棱锥A-BCM的体积的取值范围为(0,144].11.4π解析:如图所示,设BC,B1C1的中点分别为E,F,则知三棱柱ABC-A1B1C1外接球的球心为线段EF的中点O,且BC·EF=2.设外接球的半径为R,则R2=BE2+OE2=×2BC·EF=1,当且仅当BC=EF=时取等号.故直三棱柱ABC-A1B1C1外接球表面积的最小值为4π×12=4π.12.(1)解:由该四面体的三视图可知,BD⊥DC,BD⊥AD,AD⊥DC,BD=DC=2,AD=1,∴AD⊥平面BDC.∴四面体体积V=×2×2×1=.(2)证明:∵BC∥平面EFGH,平面EFGH∩平面BDC=FG,平面EFGH∩平面ABC=EH,∴BC∥FG,BC∥EH.∴FG∥EH.同理EF∥AD,HG∥AD,∴EF∥HG.∴四边形EFGH是平行四边形.又∵AD⊥平面BDC,∴AD⊥BC.∴EF⊥FG.∴四边形EFGH是矩形.13.(1)证明:因为四边形ABCD为菱形,所以AC⊥BD.因为BE⊥平面ABCD,所以AC⊥BE.故AC⊥平面BED.又AC⊂平面AEC,所以平面AEC⊥平面BED.(2)解:设AB=x,在菱形ABCD中,由∠ABC=120°,可得AG=GC=x,GB=GD=.因为AE⊥EC,所以在Rt△AEC中,可得EG=x.由BE⊥平面ABCD,知△EBG为直角三角形,可得BE=x.由已知得,三棱锥E-ACD的体积V E-ACD=AC·GD·BE=x3=.故x=2.从而可得AE=EC=ED=.所以△EAC的面积为3,△EAD的面积与△ECD的面积均为.故三棱锥E-ACD的侧面积为3+2.14.(1)证明:∵EF∥BC,且BC⊥AB,∴EF⊥AB,即EF⊥BE,EF⊥PE.又BE∩PE=E,∴EF⊥平面PBE.又PB⊂平面PBE,∴EF⊥PB.(2)解:设BE=x,PE=y,则x+y=4.∴S△PEB=BE·PE·sin∠PEB=xy≤=1,当且仅当x=y=2时,S△PEB的面积最大.此时,BE=PE=2.由(1)知EF⊥平面PBE,∴平面PBE⊥平面EFCB.在平面PBE中,作PO⊥BE于O,则PO⊥平面EFCB.即PO为四棱锥P-EFCB的高.又PO=PE·sin 30°=2×=1,S EFCB=×(2+4)×2=6,∴V P-BCFE=×6×1=2.。
配套K12高考数学二轮复习 第一部分 专题四 立体几何专题跟踪训练16 文

小学+初中+高中+努力=大学 小学+初中+高中+努力=大学 专题跟踪训练(十六)
1.(2015·江苏卷)如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1.设AB1的中点为D,B1C∩BC1=E. 求证:(1)DE∥平面AA1C1C; (2)BC1⊥AB1. [证明] (1)由题意知,E为B1C的中点, 又D为AB1的中点,因此DE∥AC. 又因为DE⊄平面AA1C1C,AC⊂平面AA1C1C, 所以DE∥平面AA1C1C. (2)因为棱柱ABC-A1B1C1是直三棱柱, 所以CC1⊥平面ABC. 因为AC⊂平面ABC, 所以AC⊥CC1. 又因为AC⊥BC,CC1⊂平面BCC1B1,BC⊂平面BCC1B1,BC∩CC1=C, 所以AC⊥平面BCC1B1. 又因为BC1⊂平面BCC1B1,所以BC1⊥AC. 因为BC=CC1,所以矩形BCC1B1是正方形,因此BC1⊥B1C. 因为AC,B1C⊂平面B1AC,AC∩B1C=C, 所以BC1⊥平面B1AC. 又因为AB1⊂平面B1AC,所以BC1⊥AB1.
2.(2015·安徽卷)如图,三棱锥P-ABC中,PA⊥平面ABC,PA=1,AB=1,AC=2,∠BAC=60°. (1)求三棱锥P-ABC的体积; 小学+初中+高中+努力=大学 小学+初中+高中+努力=大学 (2)证明:在线段PC上存在点M,使得AC⊥BM,并求PMMC的值. [解] (1)由题设AB=1,AC=2,∠BAC=60°, 可得S△ABC=12·AB·AC·sin 60°=32. 由PA⊥平面ABC,可知PA是三棱锥P-ABC的高,又PA=1, 所以三棱锥P-ABC的体积V=13·S△ABC·PA=36.
(2)证明:如图,在平面ABC内,过点B作BN⊥AC,垂足为N.在平面PAC内,过点N作MN∥PA交PC于点M,连接BM. 由PA⊥平面ABC知PA⊥AC,所以MN⊥AC. 由于BN∩MN=N,故AC⊥平面MBN, 又BM⊂平面MBN,所以AC⊥BM.
高考数学二轮复习空间向量与立体几何专题训练(含解析)
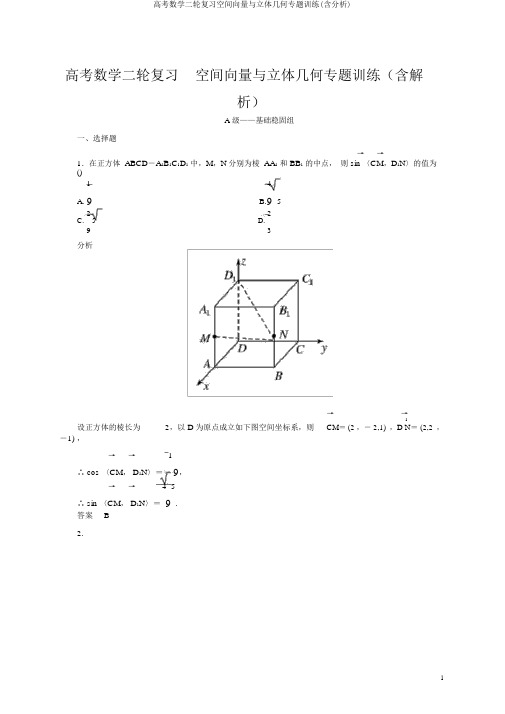
高考数学二轮复习空间向量与立体几何专题训练(含解析)A 级——基础稳固组一、选择题→ →1.在正方体ABCD-A1B1C1D1中,M,N分别为棱AA1和BB1的中点,则 sin 〈CM,D1N〉的值为()14A. 9B.9 522C. 5D.93分析→→设正方体的棱长为2,以D为原点成立如下图空间坐标系,则CM=(2,-2,1)1,,D N=(2,2-1) ,→ →1∴ cos 〈CM,D1N〉=-9,→ → 4 5∴ sin 〈CM,D1N〉=9 .答案B2.如图, 三棱锥 A - BCD 的棱长全相等, E 为 AD 的中点, 则直线 CE 与 BD 所成角的余弦值为 ()33A.B.62331C.D.62→→→→→→ 1→ 2 1→→→→→→1 1 分析设 AB = 1,则 CE · BD = ( AE - A C ) ·(AD - AB ) = 2AD - 2AD · AB -AC · AD + AC · AB = 2-21cos60°- cos60°+ cos60°= 4.→ →1→ → 4 3CE · BD∴ cos 〈CE , BD 〉= → → =3 = 6.应选 A.||| |CE BD2答案A3.如图,点 P 是单位正方体 ABCD - A B CD→ →中异于 A 的一个极点,则 AP · AB 的值为 ()1 1 1 1A . 0B . 1C .0或 1D .随意实数分析 →7 个向量: →→→→→→→ → → →AP 可为以下 AB , AC , AD ,AA 1, AB 1,AC 1, AD 1,此中一个与 AB 重合, AP · AB =| → | 2= 1;→,→1,→ 1与→垂直,这时 → · → = 0; → ,→1与→的夹角为45°,这时→·→= 2AB AD AD AA AB AP ABAC AB ABAP AB×1×cos π = 1,最后 →1· →= 3×1×cos ∠1= 3× 1 = 1,应选 C.4 ACABBAC3答案 C4.(201 3·山东卷 ) 已知三棱柱- 1 11的侧棱与底面垂直,体积为 9,底面是边长为3的正ABC ABC4三角形.若 P 为底面 A 1B 1C 1 的中心,则 PA 与平面 ABC 所成角的大小为 ()5ππ A. 12B. 3πD.πC.64分析如下图,设△ABC1 3 3ABC 的中心为 O , S= 2× 3× 3×sin60 °= 4 .3 39∴ VABC - A 1B 1C 1 =S ABC ×OP =4 × OP = 4,∴ OP = 3.32又 OA = 2 × 3× 3=1,OP ∴ tan ∠ OAP == 3,OAπ又 0<∠ OAP < 2 ,π∴∠ OAP = 3 .5.在正方体 ABCD - A 1B 1C 1D 1 中,点 E 为 BB 1 的中点,则平面 A 1ED 与平面 ABCD 所成的锐二面角的余弦值为 ()1 2 A. 2B. 332C. 3D. 2分析以 A 为坐标原点成立空间直角坐标系,如图.设棱长为 1,则 1(0,0,1) ,E 1, 0, 1, (0,1,0) ,A2 D→→1, 0,-1,112所以 AD =(0,1 ,- 1),AE =设平面 1 的一个法向量为 1=(1 , y , ) ,A EDn zy - z =0,y =2,则1所以 n = (1,2,2) .所以1- 2z = 0, z =2,1由于平面 ABCD 的一个法向量为 n = (0,0,1) ,2所以 |cos 〈n 1, n 2〉 | =223×1 = .3即平面 A ED 与平面 ABCD 所成的锐二面角的余弦值为23. 应选 B.1答案 B6. P 是二面角 α-AB - β 棱上的一点,分别在 α, β 平面上引射线PM ,PN ,假如∠ BPM =∠=45°,∠=60°,那么二面角 - -的大小为 ()A.60° B .70°C.80° D .90°分析不如设 PM= a, PN= b,作 ME⊥ AB于点 E, NF⊥AB于点 F,如图.由于∠ EPM=∠ FPN=45°,所以 PE=22a, PF=22b,→ →→ →→→所以 EM· FN=( PM-PE)·(PN- PF)→ → →→ →→→ →= PM· PN-PM· PF- PE· PN+ PE·PF2222=ab cos60°- a×2 b cos45°-2 ab cos45°+2 a×2 b abab ab ab=2-2-2+2=0.→→所以 EM⊥ FN,所以二面角α-AB-β 的大小为90°.答案D二、填空题7.已知a= (2 ,-1,1),b=(-1,4,-2),c=(11,5,λ).若向量 a,b,c 共面,则λ=________.分析由向量,,c 共面可得c=xa+(x,∈R) ,a b yb y11= 2x-y,x=7,故有 5=-x+ 4y,解得 y=3,λ =x-2y,λ=1.答案18.已知空间不共面四点,,,,→·→=→·→=→·→=0,且 |→| =|→|=|→|,→O A B COAOBOAOCOBOC OA OB OC AM →= MB,则 OM与平面 ABC所成角的正切值是________.分析由题意可知, OA , OB , OC 两两垂直,如图,成立空间直角坐标系O - xyz ,设 OA = OB = OC = 1,1 1则 A (1,0,0) , B (0,1,0) , C (0,0,1) , M 2 ,2, 0 ,→→ → 1 1故 AB = ( - 1,1,0) ,AC = ( - 1,0,1) , OM = 2,2,0 .设平面 ABC 的法向量为 n = ( x ,y , z ) ,→- x +y = 0,n ⊥AB ,则由得→ - x +z = 0,n ⊥AC ,令 x = 1,得平面 ABC 的一个法向量为 n = (1,1,1) .→1= 6故 cos 〈n , OM 〉=,2 33× 2→6 2 3sin 〈 n ,OM 〉=1-3 = 3 ,→→2sin 〈n , OM 〉tan 〈 n ,OM 〉= cos 〈 , →〉=2.nOM答案229.已知点 E , F 分别在正方体 ABCD - A 1B 1C 1D 1 的棱 BB 1, CC 1 上,且 B 1E = 2EB , CF = 2FC 1,则平面与平面所成的二面角的正切值为________.AEFABC分析如图,成立空间直角坐标系.设= 1,由已知条件得(1,0,0),E1, 1,1,F0, 1,2,DA A33→1AE=0, 1,3,→2AF=-1,1,3,设平面 AEF的法向量为n=( x,y, z),平面 AEF与平面→n· AE=0,由→n· AF=0,ABC所成的二面角为θ,1y+3z=0,得2-x+ y+3z=0.令 y=1,得 z=-3, x=-1,则 n=(-1,1,-3),平面 ABC的法向量为 m=(0,0,-1),cos θ= cos〈n,m〉=3,tanθ=2. 113答案2 3三、解答题10.如下图,四棱锥S- ABCD的底面是正方形,SD⊥平面 ABCD, SD= AD= a,点 E 是 SD上的点,且 DE=λa(0<λ≤1).(1)求证:对随意的λ∈(0,1],都有AC⊥BE;(2)若二面角 C- AE- D的大小为60°,求λ的值.解(1) 证明:如下图,成立空间直角坐标系D -xyz ,则 A ( a, 0,0) ,B ( a ,a, 0) ,C (0 ,a, 0) ,D (0,0,0) ,E (0,0 , λa ) ,∴→=(- ,0) ,→=( - ,- ,) ,ACaa, BEaa λa→ →对随意 λ∈ (0,1]都成立,∴ AC · BE =0即对随意的 λ∈ (0,1] ,都有 AC ⊥ BE .(2) 明显n = (0,1,0) 是平面的一个法向量,ADE设平面 ACE 的法向量为 m = ( x ,y , z ) ,→→- a, 0, λa ), ∵ AC = ( - a , a, 0) , AE =(→- ax + ay =0, x - y = 0, m · AC = 0, ∴ →即+= 0,∴-= 0.· = 0, -ax λazxλzm AE令 z = 1,则 x = y =λ,∴ m =( λ, λ, 1) .∵二面角 C - AE - D 的大小为 60°,∴ cos 〈n ,m 〉=n ·mλ1== ,| n || m |1+ 2λ222 ∵ λ∈ (0,1] ,∴ λ=.211.(2014 ·北京卷 ) 如图,正方形AMDE的边长为 2,B,C分别为AM,MD的中点.在五棱锥P-ABCDE中, F为棱 PE的中点,平面 ABF与棱 PD,PC分别交于点 G, H.(1)求证: AB∥ FG;(2) 若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长.解 (1) 证明:在正方形AMDE中,由于B是AM的中点,所以 AB∥ DE.又由于 AB?平面 PDE,所以 AB∥平面 PDE.由于 AB?平面 ABF,且平面 ABF∩平面 PDE= FG,所以 AB∥ FG.(2)由于 PA⊥底面 ABCDE,所以 PA⊥AB,PA⊥ AE.如图成立空间直角坐标系A- xyz,则 A(0,0,0),B(1,0,0), C(2,1,0), P(0,0,2), F(0,1,1)→., BC=(1,1,0)设平面 ABF的法向量为 n=( x,y, z),→x=0,n· AB=0,则即n ·→=0,y+ z=0. AF令 z=1,则 y=-1.所以 n=(0,-1,1).设直线 BC 与平面 ABF 所成角为 α,→1则 sin=|cos 〈,→〉 | = n ·BCα= .n BC→2| n || BC |π所以直线 BC 与平面 ABF 所成角的大小为 6 .设点 H 的坐标为 ( u ,v , w ) .→→由于点 H 在棱 PC 上,所以可设 PH = λPC (0< λ<1) ,即 ( u , v , w - 2) = λ(2,1 ,- 2) ,所以 u = 2λ , v = λ, w = 2- 2λ.由于 n 是平面 ABF 的法向量,→所以 n ·AH = 0,即 (0 ,- 1,1) ·(2 λ,λ, 2- 2λ) = 0,2解得 λ=3.所以点 H 的坐标为4 2 2, ,3 3 3 .所以 = 4 2 2 2 42+ + - =2.PH 3 3 3B 级——能力提升组1.(2014 ·江西卷 ) 如图,四棱锥 P - ABCD 中, ABCD 为矩形,平面 PAD ⊥平面 ABCD .(1) 求证: AB ⊥ PD ;(2) 若∠ BPC =90°, PB = 2,PC = 2,问 AB 为什么值时,四棱锥 P - ABCD 的体积最大?并求此时平面 PBC 与平面 DPC 夹角的余弦值.解 (1) 证明: ABCD 为矩形,故 AB ⊥ AD .又平面 PAD ⊥平面 ABCD ,平面 PAD ∩平面 ABCD = AD ,所以 AB ⊥平面 PAD ,故 AB ⊥ PD .故 PO⊥平面 ABCD, BC⊥平面 POG, BC⊥ PG,23266在 Rt △BPC中,PG=3,GC=3,BG=3,2242设 AB= m,则 OP=PG- OG=3- m,故四棱锥 P- ABCD的体积为142m2V=3·6· m·3- m=38-6m.由于-2=24-2228m-=6m-+,86m8m 6m3366P-ABCD的体积最大.此时,成立如下图的坐标系,各故当 m=,即 AB=时,四棱锥3366626266点的坐标为 O(0,0,0), B3,-3, 0, C3,3, 0,D 0,3, 0,P 0,0,3.→6266→故 PC=3,3,-3, BC=(0,6,0),→6.CD=-3,0,0设平面 BPC的法向量 n =( x, y, 1),16266→→3 x+3 y-3=0,则由 n ⊥ PC, n ⊥ BC,得116y=0,解得 x=1, y=0,n1=(1,0,1).21同理可求出平面=0,,1,DPC的法向量n2进而平面与平面夹角的余弦值为11| n·n |110cos θ12=5 .=| n1|| n2|=12·4+ 12.如图,在长方体ABCD- A1B1C1D1中, AA1= AD=1,E 为 CD的中点.(1)求证: B1E⊥ AD1;(2)在棱 AA1上能否存在一点 P,使得 DP∥平面 B1AE?若存在,求 AP的长;若不存在,说明原因;(3)若二面角 A- B1E-A1的大小为30°,求 AB的长.解 (1) 证明:以A 为原点,→,→,→x轴、y轴、z轴的正方向成立空间直角1的方向分别为AB AD AA1a1,1,0坐标系 ( 如图 ) ,设AB=a,则A(0,0,0), D(0,1,0), D(0,1,1), E2, B ( a, 0,1),→→a→→a,1,011-,1,- 11, AE=2.故 AD=(0,1,1),BE=2,AB=( a, 0,1)→→a∵ AD1· B1E=-2×0+1×1+(-1)×1=0,∴B1E⊥ AD1.(2)假定在棱 AA1上存在一点 P(0,0, z0)(0≤ z0≤1),使得 DP∥平面 B1AE.高考数学二轮复习空间向量与立体几何专题训练(含分析)→此时 DP = (0 ,- 1, z 0) .又设平面 B 1AE 的法向量 n = ( x , y , z ) .→→ax + z =0, ax由 n ⊥ AB ,n ⊥ AE ,得12+ y = 0. 取 x = 1,得平面 B 1AE 的一个法向量an = 1,- 2,- a .→a要使 DP ∥平面 B 1AE ,只需 n ⊥DP ,有 2- az 0= 0,1解得 z 0= 2. 又 DP ?平面 B 1AE ,1∴存在点P ,知足 DP ∥平面 B 1AE ,此时 AP = 2.(3) 连结 A 1D , B 1C ,由长方体 ABCD - A 1B 1C 1D 1 及 AA 1= AD = 1,得 AD 1⊥ A 1D .∵ B 1C ∥ A 1D ,∴ AD 1⊥ B 1C .又由 (1) 知 B 1E ⊥ AD 1,且 B 1C ∩ B 1E = B 1,∴ AD 1⊥平面 DCB 1A 1.→→.∴ AD 1是平面 A 1B 1E 的一个法向量,此时 AD 1= (0,1,1) → 设 AD 1与 n 所成的角为 θ ,a· →1- 2-aAD.则 cos θ= → =2| n || AD 1|21+ a+ a 24∵二面角- 1- 1 的大小为 30°,A B E A3a∴ |cos θ| =cos30°,即235a 2=2 ,21+ 4解得 a = 2,即 AB 的长为 2.。
高考数学二轮复习专题突破练26 圆锥曲线中的最值、范围、证明问题 (2)

专题突破练26圆锥曲线中的最值、范围、证明问题1.(2020山东潍坊一模,21)在平面直角坐标系xOy中,F1,F2分别为椭圆C:x 2a2+y2b2=1(a>b>0)的左、右焦点,A为椭圆的右顶点,点P为椭圆C上的动点(点P与椭圆C的左、右顶点不重合),当△PF1F2为等边三角形时,其面积为√3.(1)求椭圆C的方程;(2)如图,M为AP的中点,直线MO交直线x=-4于点D,过点O作OE∥AP交直线x=-4于点E,证明∠OEF1=∠ODF1.2.(2020百校联考高考百日冲刺金卷,19)已知△PF1F2中,F1(-1,0),F2(1,0),|PF1|=4,点Q在线段PF1上,且|PQ|=|QF2|.(1)求点Q的轨迹E的方程;(2)若点M,N在曲线E上,且M,N,F1三点共线,求△F2MN面积的最大值.3.(2020山东泰安一模,21)已知椭圆C :x 2a2+y 2b2=1(a>b>0)的左、右焦点分别为F 1,F 2,直线l :y=kx+m 与椭圆C 相交于P ,Q 两点;当直线l 经过椭圆C 的下顶点A 和右焦点F 2时,△F 1PQ 的周长为4√2,且l 与椭圆C 的另一个交点的横坐标为43. (1)求椭圆C 的方程;(2)点M 为△POQ 内一点,O 为坐标原点,满足MP⃗⃗⃗⃗⃗⃗ +MO ⃗⃗⃗⃗⃗⃗ +MQ ⃗⃗⃗⃗⃗⃗ =0,若点M 恰好在圆O :x 2+y 2=49上,求实数m 的取值范围.4.(2020山东聊城一模,20)已知椭圆C :x 2a2+y 2b2=1(a>b>0)的长轴长为4,右焦点为F ,且椭圆C 上的点到点F 的距离的最小值与最大值的积为1,圆O :x 2+y 2=1与x 轴交于A ,B 两点. (1)求椭圆C 的方程;(2)动直线l :y=kx+m 与椭圆C 交于P ,Q 两点,且直线l 与圆O 相切,求△APQ 的面积与△BPQ 的面积乘积的取值范围.5.(2019湖北恩施高三2月教学质量检测)已知抛物线C :y 2=2px (p>0)的焦点为F ,其准线l :x=-1与x 轴的交点为K ,过点K 的直线l 与抛物线C 交于A ,B 两点. (1)求抛物线C 的方程;(2)点A 关于x 轴的对称点为D ,证明:存在实数t ∈(0,1),使得KF ⃗⃗⃗⃗⃗ =t KB ⃗⃗⃗⃗⃗⃗ +(1-t )KD ⃗⃗⃗⃗⃗⃗ .6.(2020云南昆明高三“三诊一模”教学质量检测,21)椭圆规是画椭圆的一种工具,如图1所示,在十字形滑槽上各有一个活动滑标M ,N ,有一根旋杆将两个滑标连成一体,|MN|=4,D 为旋杆上的一点且在M ,N 两点之间,且|ND|=3|MD|,当滑标M 在滑槽EF 内作往复运动,滑标N 在滑槽GH 内随之运动时,将笔尖放置于D 处可画出椭圆,记该椭圆为C.如图2所示,设EF 与GH 交于点O ,以EF 所在的直线为x 轴,以GH 所在的直线为y 轴,建立平面直角坐标系.(1)求椭圆C 的方程;(2)设A 1,A 2是椭圆C 的左、右顶点,点P 为直线x=6上的动点,直线A 1P ,A 2P 分别交椭圆于Q ,R 两点,求四边形A 1QA 2R 面积的最大值.专题突破练26 圆锥曲线中的最值、范围、证明问题1.(1)解 设椭圆C 的半焦距为c ,因为△PF 1F 2是等边三角形,所以此时P 在上顶点或下顶点处,所以a=2c ,所以bc=√3.又由a 2=b 2+c 2,解得c 2=1,a 2=4,b 2=3,故椭圆的方程为x 24+y 23=1. (2)证明 由题意知A (2,0),设AP 的中点M (x 0,y 0),P (x 1,y 1),设直线AP 的方程为y=k (x-2)(k ≠0),将其代入椭圆方程整理得 (4k 2+3)x 2-16k 2x+16k 2-12=0, 所以x 1+2=16k24k 2+3,所以x 0=8k24k 2+3,y 0=k (x 0-2)=-6k 4k 2+3,即M 的坐标为(8k24k 2+3,-6k4k 2+3),从而k OM =-6k 4k 2+38k24k 2+3=-34k , 所以直线OM 的方程为y=-34k x,令x=-4,得D(-4,3k ),直线OE的方程为y=kx,令x=-4,得E(-4,-4k),由F1(-1,0),得k EF1=-4k-3=4k3,所以k OM·k EF1=-1,即OM⊥EF1,记垂足为H,因为k DF1=3k-3=-1k,k OE=k AP=k,所以OE⊥DF1,记垂足为G.在直角三角形EHO和直角三角形DGO中,∠ODF1和∠OEF1都与∠EOD互余,所以∠ODF1=∠OEF1.2.解(1)因为|PQ|=|QF2|,故|QF1|+|QF2|=|QF1|+|QP|=|PF1|=4>|F1F2|=2,故点Q的轨迹是以F1,F2为焦点,长轴长为4的椭圆(不包含长轴的端点).故点Q的轨迹E的方程为x24+y23=1(x≠±2).(2)直线MN过点F1(-1,0),设直线MN的方程为x=ky-1,M(x1,y1),N(x2,y2),联立{x=ky-1,x24+y23=1,消去x得(4+3k2)y2-6ky-9=0,∴{y1+y2=6k3k2+4,y1y2=-93k2+4,∴S△F2MN =12·|F1F2|·|y1-y2|=12√k2+13k2+4.令√k2+1=t,则t≥1,∴S△F2MN =123t+1t.令f(t)=3t+1t,则f'(t)=3-1t2,当t∈[1,+∞)时,f'(t)>0,f(t)=3t+1t 在[1,+∞)上单调递增.∴S△F2MN=123t+1t≤3,当t=1时取等号.即当k=0时,△F2MN面积的最大值为3.3.解(1)由题意知4a=4√2,∴a=√2,直线AF2的方程为y=bc(x-c).∵直线AF2与椭圆C的另一个交点的横坐标为43,∴{ y =b c (43-c),(43)22+y 2b 2=1,解得c=1或c=2(舍去).∴b 2=1, ∴椭圆C 的方程为x 22+y 2=1.(2)设P (x 1,y 1),Q (x 2,y 2), ∵MP ⃗⃗⃗⃗⃗⃗ +MO ⃗⃗⃗⃗⃗⃗ +MQ ⃗⃗⃗⃗⃗⃗ =0,∴点M 为△POQ 的重心, ∴M (x 1+x 23,y 1+y 23). ∵点M 在圆O :x 2+y 2=49上, ∴(x 1+x 2)2+(y 1+y 2)2=4, 由{y =kx +m ,x 22+y 2=1,得(1+2k 2)x 2+4kmx+2m 2-2=0,∴x 1+x 1=-4km 1+2k2,x 1x 2=2m 2-21+2k2,∴(x 1+x 2)2+(y 1+y 2)2=(-4km 1+2k2)2+[k (-4km 1+2k2)+2m]2=4,即16(1+k 2)k 2m 2(1+2k 2)2−16k 2m 21+2k2+4m 2=4.∴m 2=(1+2k 2)24k 2+1.由Δ>0得1+2k 2>m 2,∴1+2k 2>(1+2k 2)24k 2+1,解得k ≠0.∴m 2=(1+2k 2)24k 2+1=1+4k44k 2+1=1+44k 2+1k4>1, ∴m>1或m<-1.4.解 (1)设椭圆C 的焦距为2c ,则由已知得2a=4,(a-c )(a+c )=1,解得a=2,b=1,所以椭圆C 的方程为x 24+y 2=1.(2)由{y =kx +m ,x 24+y 2=1,得(1+4k 2)x 2+8kmx+4m 2-4=0,Δ=(8km )2-4(1+4k 2)(4m 2-4)=16(1+4k 2-m 2)>0. 设P (x 1,y 1),Q (x 2,y 2),则x 1+x 2=-8km 1+4k2,x 1x 2=4m 2-41+4k2,所以|PQ|=√1+k 2·√(x 1+x 2)2-4x 1x 2=√1+k 2·√(-8km 1+4k2)2-4·4m 2-41+4k2=√1+k 2·√16(1+4k 2-m 2)(1+4k 2)2.因为直线l 与O 相切,所以点O 到直线l 的距离d=√1+k =1,即1+k 2=m 2,所以Δ=48k 2,由Δ>0,得k 2>0. 又A ,B 两点到直线l 的距离分别为d 1=√1+k,d 2=√1+k.所以△APQ 的面积与△BPQ 的面积乘积为S △APQ ·S △BPQ=14(√1+k 2·√16(1+4k 2-m 2)(1+4k 2)2)2·√1+k·√1+k=4(1+4k 2-m 2)|k 2-m 2|(1+4k 2)2=4(1+4k 2-1-k 2)|k 2-1-k 2|(1+4k 2)2=12k2(1+4k 2)2=1216k 2+1k2+8. 因为k 2>0,所以16k 2+1k2+8≥16,116k 2+1k2+8∈(0,116],S △APQ ·S △BPQ ∈(0,34].因此△APQ 的面积与△BPQ 的面积乘积的取值范围为(0,34]. 5.(1)解 因为抛物线C :y 2=2px (p>0)的准线方程为直线l :x=-1,所以-p2=-1,解得p=2.所以抛物线C 的方程为y 2=4x.(2)证明 易知点K 的坐标为(-1,0),据此可设直线l 的方程为x=my-1,设A (x 1,y 1),B (x 2,y 2).联立{x =my -1,y 2=4x ,整理得y 2-4my+4=0,故{y 1+y 2=4m ,y 1y 2=4.因为点A 关于x 轴的对称点为D ,A (x 1,y 1),所以D (x 1,-y 1).则直线BD 的方程为y-y 2=y 2+y 1x 2-x 1(x-x 2),得y-y 2=y 2+y1(my 2-1)-(my 1-1)(x-x 2),得y-y 2=y 2+y1m (y 2-y 1)(x-x 2),即y-y 2=4y 2-y1x-y 224.令y=0,得0-y 2=4y 2-y1x-y 224,得x=y 224-y 2·y 2-y 14=y 22-y 22+y 1y 24=y 1y 24=44=1.所以直线BD 恒过定点(1,0). 所以点F (1,0)在直线BD 上,所以不妨令DF ⃗⃗⃗⃗⃗ =t DB ⃗⃗⃗⃗⃗⃗ (t ∈(0,1)). 因为KF ⃗⃗⃗⃗⃗ =KD ⃗⃗⃗⃗⃗⃗ +DF ⃗⃗⃗⃗⃗ ,所以KF ⃗⃗⃗⃗⃗ =KD ⃗⃗⃗⃗⃗⃗ +t DB ⃗⃗⃗⃗⃗⃗ , 所以KF ⃗⃗⃗⃗⃗ =KD ⃗⃗⃗⃗⃗⃗ +t (KB ⃗⃗⃗⃗⃗⃗ −KD ⃗⃗⃗⃗⃗⃗ ), 所以KF ⃗⃗⃗⃗⃗ =(1-t )KD ⃗⃗⃗⃗⃗⃗ +t KB⃗⃗⃗⃗⃗⃗ . 所以存在实数t ∈(0,1),使得KF ⃗⃗⃗⃗⃗ =t KB ⃗⃗⃗⃗⃗⃗ +(1-t )KD⃗⃗⃗⃗⃗⃗ ,命题得证. 6.解 (1)由|MN|=4,D 为旋杆上的一点,且在M ,N 两点之间,且|ND|=3|MD|,可得|MD|=1,|ND|=3,所以椭圆的长半轴a 为3,短半轴b 为1,所以椭圆的方程为x 29+y 2=1.(2)由对称性设P (6,t ),其中t>0,则直线A 1P 的方程为y=t9(x+3),直线A 2P 的方程为y=t3(x-3),设Q (x 1,y 1),R (x 2,y 2),由{x 29+y 2=1,y =t9(y +3),消x 可得(9+t 2)y 2-6ty=0,由于y A 1=0,所以y 1=6t 9+t2,由{x 29+y 2=1,y =t 3(x -3),消x 可得(1+t 2)y 2+2ty=0,由于y A 2=0,所以y 2=-2t1+t 2, 所以四边形A 1QA 2R 的面积为S=12|A 1A 2|·|y 1-y 2|=12·6·(6t 9+t 2+2t1+t 2) =24t (3+t 2)(9+t 2)(1+t 2)=24t 2+3t +4t t 2+3,由于t>0,设m=t 2+3t≥2√3,又y=m+4m 在[2√3,+∞)上单调递增,所以y=m+4m ≥8√33, 故S=24m+4m≤3√3.当且仅当m=2√3,即t=√3时,四边形A1QA2R的面积的最大值为3√3.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小初高试卷教案类
K12小学初中高中
专题能力训练26 解答题专项训练(立体几何)
1.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
(1)若PA=PD,求证:平面PQB⊥平面PAD;
(2)点M在线段上,PM=tPC,试确定实数t的值,使PA∥平面MQB.
2.
在斜三棱柱ABC-A1B1C1中,平面A1ACC1⊥平面ABC,AC⊥BC,A1B⊥C1C,AC=BC.
(1)求证:A1A⊥A1C;
(2)若A1A=A1C=2,求三棱锥B1-A1BC的体积.
小初高试卷教案类
K12小学初中高中
3.
如图,在四棱锥S-ABCD中,底面ABCD是矩形,AD=2AB,SA=SD,SA⊥AB,N是棱AD的中点.
(1)求证:AB∥平面SCD;
(2)求证:SN⊥平面ABCD;
(3)在棱SC上是否存在一点P,使得平面PBD⊥平面ABCD?若存在,求出的值;若不存在,说明理由.
4.
如图,在四棱锥P-ABCD中,O为AC与BD的交点,AB⊥平面PAD,△PAD是正三角形,DC∥
AB,DA=DC=2AB.
(1)若点E为棱PA上一点,且OE∥平面PBC,求的值;
(2)求证:平面PBC⊥平面PDC.
5.(2014江苏高考,16)如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥
AC,PA=6,BC=8,DF=5.
小初高试卷教案类
K12小学初中高中
求证:(1)直线PA∥平面DEF;
(2)平面BDE⊥平面ABC.
6.
如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2.
(1)求证:平面A1AC⊥平面AA1B;
(2)若点P为B1C1的中点,求三棱锥P-ABC与四棱锥P-AA1B1B的体积之比.
7.如图,已知在△SCD中,SD=3,CD=,cos∠SDC=-,SA=2AD,AB⊥SD交SC于点B,M为SB上一点,且
SM=2MB.将△SAB沿AB折起,使平面SAB⊥平面ABCD.
小初高试卷教案类
K12小学初中高中
(1)求证:AM∥平面SCD;
(2)求三棱锥S-CDM的体积.
答案与解析
专题能力训练26 解答题专项训练(立体几何)
1.证明:(1)连接BD,因为四边形ABCD为菱形,
且∠BAD=60°,所以△ABD为正三角形,
又Q为AD的中点,所以AD⊥BQ.
又因为PA=PD,所以AD⊥PQ.
又BQ∩PQ=Q,所以AD⊥平面PQB.
又AD⊂平面PAD,
所以平面PQB⊥平面PAD.
(2)因为PA∥平面MQB,连接AC交BQ于点N,连接MN.
由AQ∥BC可得,△ANQ∽△CNB,
所以.
因为PA∥平面MQB,PA⊂平面PAC,
平面PAC∩平面MQB=MN,所以PA∥MN.
因此,,即t的值为.
2.解:(1)因为平面A1ACC1⊥平面ABC,AC⊥BC,
所以BC⊥平面A1ACC1,所以A1A⊥BC.
因为A1B⊥C1C,A1A∥C1C,所以A1A⊥A1B.
又BC∩A1B=B,所以A1A⊥平面A1BC.
又A1C⊂平面A1BC,所以A1A⊥A1C.
(2)由已知及(1),△A1AC是等腰直角三角形,AA1=A1C=2,AC=2.
因为平面A1ACC1⊥平面ABC,
所以Rt△A1AC斜边上的高等于斜三棱柱ABC-A1B1C1的高,且等于.
在Rt△ABC中,AC=BC=2,S△ABC=AC·BC=4,
所以三棱柱ABC-A1B1C1的体积V=S△ABC·=4.
又三棱锥A1-ABC与三棱锥C-A1B1C1的体积相等,都等于V,
所以三棱锥B1-A1BC的体积V1=V-2×V=.
小初高试卷教案类
K12小学初中高中
3.解:(1)因为底面ABCD是矩形,所以AB∥CD.
又因为AB⊄平面SCD,CD⊂平面SCD,
所以AB∥平面SCD.
(2)因为AB⊥SA,AB⊥AD,SA∩AD=A,所以AB⊥平面SAD,
又因为SN⊂平面SAD,所以AB⊥SN.
因为SA=SD,且N为AD的中点,所以SN⊥AD.
又因为AB∩AD=A,所以SN⊥平面ABCD.
(3)存在点P,使得平面PBD⊥平面ABCD.理由如下:
如图,连接BD交NC于点F,
在平面SNC中过点F作FP∥SN交SC于点P,连接PD,PB.
因为SN⊥平面ABCD,所以FP⊥平面ABCD.
又因为FP⊂平面PBD,所以平面PBD⊥平面ABCD.
在矩形ABCD中,因为ND∥BC,所以.
在△SNC中,因为FP∥SN,所以.
则在棱SC上存在点P,使得平面PBD⊥平面ABCD,
此时.
4.(1)解:因为OE∥平面PBC,OE⊂平面PAC,平面PAC∩平面PBC=PC,所以OE∥PC,AO∶OC=AE∶
EP.
因为DC∥AB,DC=2AB,
所以AO∶OC=AB∶DC=1∶2.所以.
(2)证明:(方法一)取PC的中点F,连接FB,FD.
因为△PAD是正三角形,DA=DC,所以DP=DC.
因为F为PC的中点,所以DF⊥PC.
因为AB⊥平面PAD,
所以AB⊥PA,AB⊥AD,AB⊥PD.
因为DC∥AB,所以DC⊥DP,DC⊥DA.
设AB=a,在等腰直角三角形PCD中,DF=PF=a.
在Rt△PAB中,PB=a.
在直角梯形ABCD中,BD=BC=a.
因为BC=PB=a,点F为PC的中点,
所以PC⊥FB.
在Rt△PFB中,FB=a.
在△FDB中,由DF=a,FB=a,BD=a,
可知DF2+FB2=BD2,所以FB⊥DF.
由DF⊥PC,DF⊥FB,PC∩FB=F,PC,FB⊂平面PBC,
所以DF⊥平面PBC.
又DF⊂平面PCD,所以平面PBC^平面PDC.
(方法二)取PD,PC的中点,分别为M,F,连接AM,FB,MF,
小初高试卷教案类
K12小学初中高中
则MF∥DC,MF=DC.
因为DC∥AB,AB=DC,
所以MF∥AB,MF=AB,
即四边形ABFM为平行四边形,所以AM∥BF.
在正三角形PAD中,M为PD的中点,所以AM⊥PD.
因为AB⊥平面PAD,所以AB⊥AM.
又因为DC∥AB,所以DC⊥AM.
因为BF∥AM,所以BF⊥PD,BF⊥CD.
又因为PD∩DC=D,PD,DC⊂平面PCD,
所以BF⊥平面PCD.
因为BF⊂平面PBC,
所以平面PBC⊥平面PDC.
5.证明:(1)因为D,E分别为棱PC,AC的中点,
所以DE∥PA.
又因为PA⊄平面DEF,DE⊂平面DEF,
所以直线PA∥平面DEF.
(2)因为D,E,F分别为棱PC,AC,AB的中点,PA=6,BC=8,
所以DE∥PA,DE=PA=3,EF=BC=4.
又因为DF=5,故DF2=DE2+EF2,
所以∠DEF=90°,即DE⊥EF.
又PA⊥AC,DE∥PA,
所以DE⊥AC.
因为AC∩EF=E,AC⊂平面ABC,EF⊂平面ABC,
所以DE⊥平面ABC.
又DE⊂平面BDE,
所以平面BDE⊥平面ABC.
6.(1)证明:由题意得A1B⊥平面ABC,故A1B⊥AC.
又AB⊥AC,AB∩A1B=B,
∴AC⊥平面AA1B.
∵AC⊂平面A1AC,∴平面A1AC⊥平面AA1B.
(2)解:在三棱锥P-ABC中,因为AB⊥AC,
所以底面ABC是等腰直角三角形.
又因为点P到底面的距离h=A1B=2,
所以VP-ABC=S△ABC·h=AC·AB·h=.
由(1)可知AC⊥平面AA1B.
因为点P在B1C1的中点,
所以点P到平面AA1B1B距离h2等于点C1到平面AA1B1B的距离的一半,即h2=1.
·h2=AB·A1B·h2=×2×2×1=,
所以三棱锥P-ABC与四棱锥P-AA1B1B的体积之比为1∶1.
7.(1)证明:如图①,过点C作CO⊥SD交SD的延长线于点O,在BC上取点N使BN∶NC=1∶2,连
接AN.
小初高试卷教案类
K12小学初中高中
图①
在△SCD中,由CD=,cos∠SDC=-,得DO=1,CO=2,即SA=AO.
由AB⊥SD,得SB=BC.
又BN∶NC=1∶2,∴SN∶NC=2∶1.
又SA=2AD,∴AN∥CD.
如图②,连接MN,AN,由于SM∶MB=2∶1⇒MN∥SC.
又AN∥CD,AN∩MN=N,SC∩DC=C,
∴平面AMN∥平面SCD,∴AM∥平面SCD.
图②
(2)解:由AM∥平面SCD,知点M到平面SCD的距离等于点A到平面SCD的距离.
∵平面SAB⊥平面ABCD,SA⊥AB,
∴SA⊥平面ABCD.
所以VS-CDM=VM-SCD=VA-SCD=VS-ACD=×1×2×2=.
