高考数学专题训练试题7
高考数学基础知识专题提升训练7--- 集合的概念
高考数学基础知识专题提升训练集合的概念课程标准学科素养1．通过实例，了解集合的含义，理解元素与集合的属于关系．2．针对具体问题，能在自然语言和图形语言的基础上，用符号语言刻画集合.通过对集合概念的学习，提升“数学抽象”、“逻辑推理”的核心素养.[对应学生用书P1]知识点1 集合相关概念(1)元素：一般地，把研究对象统称为元素，常用小写的拉丁字母a，b，c…表示．(2)集合：把一些元素组成的总体叫做集合，简称集，常用大写拉丁字母A，B，C…表示．(3)集合相等：构成两个集合的元素是一样的．(4)集合中元素的特性：确定性、互异性和无序性．[微思考](1)本班所有的“帅哥”能否构成一个集合？(2)一个集合中可以有相同的元素吗？提示：(1)某班所有的“帅哥”不能构成集合，因为“帅哥”没有明确的标准．(2)根据集合元素的互异性可知，集合中不能有相同的元素．知识点2 元素与集合的关系及常用数集(1)如果a是集合A的元素，就说a属于集合A，记作a∈A；如果a不是集合A中的元素，就说a不属于集合A，记作a∉A.(2)数学中一些常用的数集及其记法名称自然数集正整数集整数集有理数集实数集符号N N*或N＋Z Q R [微体验]1．设集合A只含有一个元素a，则下列各式正确的是( )A．0∈A B．a∉AC．a∈A D．a＝A答案C2．用符号“∈”或“∉”填空．(1)1________N*；(2)－3________N；(3)13________Q；(4)π________Q；(5)－12________R.答案(1)∈(2)∉(3)∈(4)∉(5)∈知识点3 集合的表示方法(1)把集合的所有元素一一列举出来，并用花括号“{}”括起来表示集合的方法叫做列举法.(2)一般地，设A是一个集合，我们把集合A中所有具有共同特征P(x)的元素x所组成的集合表示为{x∈A|P(x)}，这种表示集合的方法称为描述法.[微体验]1．思考辨析(1)由1,1,2,3组成的集合可用列举法表示为{1,1,2,3}．( )(2)集合{(1,2)}中的元素是1和2.( )(3)集合A＝{x|x－1＝0}与集合B＝{1}表示同一个集合．( )答案(1)×(2)×(3)√2．方程x2＝4的解集用列举法表示为( )A．{(－2,2)} B．{－2,2}C．{－2} D．{2}B[由x2＝4得x＝±2，故用列举法可表示为{－2,2}．]3．集合A＝{x∈Z|－2＜x＜3}的元素个数为( )A．1 B．2C．3 D．4D[因为A＝{x∈Z|－2＜x＜3}，所以x的取值为－1，0,1,2，共4个．]][对应学生用书P2探究一集合的基本概念考察下列每组对象，能构成集合的是( )①中国各地最美的乡村；②直角坐标系中横、纵坐标相等的点；③不小于3的自然数；④2020年第32届奥运会所设比赛项目．A．③④B．②③④C．②③D．②④B[①中“最美”标准不明确，不符合确定性，②③④中的元素标准明确，均可构成集合．][方法总结]判断一组对象能否组成集合的标准及其关注点(1)标准：判断一组对象能否组成集合，关键看该组对象是否满足确定性．如果该组对象满足确定性，就可以组成集合；否则，不能组成集合．(2)关注点：利用集合的含义判断一组对象能否组成一个集合，应注意集合中元素的特性，即确定性、互异性和无序性．[跟踪训练1] 考察下列每组对象能否构成一个集合．(1)不超过20的非负数；(2)方程x2－9＝0在实数范围内的解；(3)某校2016年在校的所有高个子同学；(4)3的近似值的全体．解(1)对任意一个实数能判断出是不是“不超过20的非负数”，所以能构成集合；(2)能构成集合；(3)“高个子”无明确的标准，对于某个人算不算高个子无法客观地判断，因此不能构成一个集合；(4)“3的近似值”不明确精确到什么程度，因此很难判断一个数，如“2”，是不是它的近似值，所以不能构成集合．探究二元素与集合之间的关系(1)下列所给关系中正确的个数是( )①π∈R；②3∉Q；③0∈N*；④|－4|∉N*.A．1 B．2C．3 D．4(2)已知集合A含有三个元素2,4,6，且当a∈A，有6－a∈A，那么a为( )A．2 B．2或4C．4 D．0(1)B[根据各数集的意义可知，①②正确，③④错误．](2)B[集合A含有三个元素2,4,6，且当a∈A，有6－a∈A，a＝2∈A,6－a＝4∈A，所以a＝2，或者a＝4∈A，6－a＝2∈A，所以a＝4，综上所述，a＝2或4.故选B．] [方法总结]判断元素和集合关系的两种方法(1)直接法：①使用前提：集合中的元素是直接给出的．②判断方法：首先明确集合是由哪些元素构成，然后再判断该元素在已知集合中是否出现即可．(2)推理法：①使用前提：对于某些不便直接表示的集合．②判断方法：首先明确已知集合的元素具有什么特征，然后判断该元素是否满足集合中元素所具有的特征即可．[跟踪训练2] (1)已知集合A中元素满足2x＋a＞0，a∈R，若1∉A,2∈A，则( )A ．a ＞－4B ．a ≤－2C ．－4＜a ＜－2D ．－4＜a ≤－2 D [由题意可知⎩⎨⎧ 2×1＋a ≤0，2×2＋a ＞0，解得－4＜a ≤－2.](2)设集合D 是满足方程y ＝x 2的有序数对(x ，y )的集合，则－1____D ，(－1,1)____D . 解析因为集合D 中的元素是有序数对(x ，y )，而－1是数，所以－1∉D ，(－1,1)∈D . 答案∉∈探究三 列举法表示集合用列举法表示下列给定的集合．(1)不大于10的非负偶数组成的集合A ；(2)小于8的质数组成的集合B ；(3)方程2x 2－x －3＝0的实数根组成的集合C ；(4)一次函数y ＝x ＋3与y ＝－2x ＋6的图象的交点组成的集合D .解(1)不大于10的非负偶数有0,2,4,6,8,10，所以A ＝{0,2,4,6,8,10}．(2)小于8的质数有2,3,5,7，所以B ＝{2,3,5,7}．(3)方程2x 2－x －3＝0的实数根为－1，32，所以C ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫－1，32. (4)由⎩⎨⎧ y ＝x ＋3，y ＝－2x ＋6，得⎩⎨⎧ x ＝1，y ＝4.所以一次函数y ＝x ＋3与y ＝－2x ＋6的交点为(1,4)，所以D ＝{(1,4)}．[方法总结]列举法表示集合的步骤(1)分清元素：列举法表示集合，要分清是数集还是点集．(2)书写集合：列元素时要做到不重复、不遗漏．提醒：二元方程组的解集，函数的图象上的点形成的集合都是点的集合，一定要写成实数对的形式，元素与元素之间用“，”隔开，如{(2,3)，(5，－1)}．[跟踪训练3] 用列举法表示下列集合．(1)由book 中的字母组成的集合；(2)方程(x －2)2＋|y ＋1|＝0的解集．解(1)由book 中的字母组成的集合为{b ，o ，k }．(2)由方程(x －2)2＋|y ＋1|＝0可知，⎩⎨⎧ x －2＝0，y ＋1＝0，即⎩⎨⎧ x ＝2，y ＝－1.从而方程的解集为{(2，－1)}．探究四 描述法表示集合用描述法表示下列集合．(1)所有正偶数组成的集合；(2)不等式3x －2＞4的解集；(3)在平面直角坐标系中，第一、三象限内点的集合．解(1)正偶数都能被2整除，所以正偶数可以表示为x ＝2n ，(n ∈N *)的形式． 于是这个集合可以表示为{x |x ＝2n ，n ∈N *}．(2)由3x －2＞4，得x ＞2，故不等式的解集为{x |x ＞2}．(3)第一、三象限中的点(x ，y )满足xy ＞0，于是这个集合可以表示为{(x ，y )|xy ＞0}．[变式探究] 若将本例(3)改为“坐标平面内坐标轴上的点组成的集合”，如何用描述法表示？解坐标平面内，x轴上的点纵坐标为0，横坐标为任意实数；y轴上的点横坐标为0，纵坐标为任意实数．故坐标轴上的点满足xy＝0.用集合表示为{(x，y)|xy＝0}．[方法技巧]描述法表示集合的步骤(1)确定集合中元素的特征．(2)给出其满足的性质．(3)根据描述法的形式写出其满足的集合.[跟踪训练4] 用适当的方法表示下列集合．(1)由大于5，且小于9的所有正整数组成的集合；(2)使y＝2－xx有意义的实数x的集合；(3)抛物线y＝x2－2x与x轴的公共点的集合；(4)直线y＝x上去掉原点的点的集合．解(1)列举法：{6,7,8}．(2)描述法：{x|x≤2，且x≠0，x∈R}．(3)列举法：{(0,0)，(2,0)}．(4)描述法：{(x，y)|y＝x，x≠0}．[对应学生用书P4]1．集合中元素的三个特性(1)确定性：指的是作为一个集合中的元素，必须是确定的，即一个集合一旦确定，某一个元素属不属于这个集合就确定了．这个特性通常被用来判断涉及的总体是否构成集合．(2)互异性：集合中的元素必须是互异的，就是说，对于一个给定的集合，它的任何两个元素都是不同的．(3)无序性：集合与其中元素的排列顺序无关，如由元素a，b，c与由元素b，a，c 组成的集合是相等的集合．这个性质通常用来判断两个集合的关系．2．元素a与集合A之间只有两种关系：a∈A，a∉A.3．在用列举法表示集合时应注意(1)元素间用分隔号“，”；(2)元素不重复；(3)元素无顺序；(4)列举法可表示有限集，也可以表示无限集．若集合中的元素个数比较少，则用列举法比较简单；若集合中的元素较多或无限，但出现一定的规律性，在不发生误解的情况下，也可以用列举法表示．4．在用描述法表示集合时应注意(1)弄清元素所具有的形式(即代表元素是什么)，是数、还是有序实数对(点)、还是集合或其他形式；(2)当题目中用了其他字母来描述元素所具有的属性时，要去伪存真(元素具有怎样的属性)，而不能被表面的字母形式所迷惑．课时作业(一) 集合的概念[见课时作业(一)P]1351．下面有四个语句：①集合N*中最小的数是0；②－a∉N，则a∈N；③a∈N，b∈N，则a＋b的最小值是2；④x2＋1＝2x的解集中含有两个元素．其中正确语句的个数是( )A．0 B．1C．2 D．3A[N*是不含0的自然数，所以①错误；取a＝2，则－2∉N，2∉N，所以②错误；对于③，当a＝b＝0时，a＋b取得最小值0，而不是2，所以③错误；对于④，解集中只含有元素1，故④错误．]2．如果A＝{x|x＞－1}，那么( )A．－2∈A B．{0}∈AC．－3∈A D．0∈AD[∵0＞－1，故0∈A.]3．集合A＝{x||x|＜2，x∈Z}用列举法表示正确的是( )A．{－2，－1,0,1,2} B．{－2，－1,1,2}C．{－1,0,1} D．{－1,1}C[因为|x|＜2，x∈Z，所以－2＜x＜2，故用列举法表示为{－1,0,1}．]4．(多选题)下列集合中表示数集的是( )A．{0} B．{y|y2＝0}C．{x|x＝0} D．{x＝0}ABC[A，B，C中的元素都是数，且只有一个元素0，D中的元素是式子x＝0.故D不是数集，A，B，C是数集．]5．P (1,3)和集合A ＝{(x ，y )|y ＝x ＋2}之间的关系是________．解析集合A 是点集，P (1,3)的坐标满足集合A ，所以P ∈A .答案P ∈A6．用列举法表示集合A ＝{(x ，y )|(x ＋2)2＋|y －3|＝0，x ∈R ，y ∈R }＝________. 解析(x ＋2)2＋|y －3|＝0，只有x ＋2＝0与y －3＝0同时成立，即x ＝－2，y ＝3.集合A ＝{(－2,3)}．答案{(－2,3)}7．集合B ＝{1,3,4}，若a ∈B ，且8－a ∈B ，那么a 的值为________．解析当a ＝1时，8－a ＝7∉B 不满足题意．当a ＝3时，8－a ＝5∉B 不满足题意．当a ＝4时，8－a ＝4满足题意．所以a 的值为4.答案48．若两个集合A ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1，a ，b a ，B ＝{0，a 2，a ＋b }的元素相同，求a ＋b 的值．解依题意0∈A ，所以b ＝0.所以B ＝{0，a 2，a }，又1∈B ，且a ≠1.所以a 2＝1，所以a ＝－1，所以a ＋b ＝－1.9．用另一种方法表示下列集合．(1){绝对值不大于2的整数}；(2){能被3整除，且小于10的正数}；(3){x |x ＝|x |，x ＜5，且x ∈Z }；(4){(x ，y )|x ＋y ＝6，x ∈N *，y ∈N *}；(5){－3，－1,1,3,5}．解(1){－2，－1,0,1,2}．(2){3,6,9}．(3)∵x＝|x|，∴x≥0.又∵x∈Z，且x＜5，∴x＝0或1或2或3或4.∴集合可以表示为{0,1,2,3,4}．(4){(1,5)，(2,4)，(3,3)，(4,2)，(5,1)}．(5){x|x＝2k－1，－1≤k≤3，k∈Z}．1．已知x，y，z为非零实数，代数式x|x|＋y|y|＋z|z|＋|xyz|xyz的值所组成的集合是M，则下列判断正确的是( )A．0∉M B．2∈MC．－4∉M D．4∈MD[结合x，y，z的取值情况，可知当x＞0，y＞0，z＞0时，代数式的值为4，所以4∈M.]2．下列集合表示同一集合的是( )A．M＝{(3,2)}，N＝{(2,3)}B．M＝{3,2}，N＝{2,3}C．M＝{(x，y)|x＋y＝1}，N＝{y|x＋y＝1}D．M＝{2,3}，N＝{(2,3)}B[A中两个坐标不同，C，D中一个点集一个数集．]3．若集合A＝{x|ax2＋ax＋1＝0}中只有一个元素，则a＝( )A ．4B ．2C ．0D ．0或4A [当a ＝0时，1≠0，此时方程无解．当a ≠0时，Δ＝a 2－4a ＝0即a ＝4，此时满足A 中只有一个元素x ＝－12.]4．集合A ＝{1,4,9,16,25，…}，若m ∈A ，n ∈A ，则mΔn ∈A ，“Δ”是一种运算，则“Δ”可以是________．(①加法；②减法；③乘法；④除法)解析因为两个整数的平方的乘积必为一个整数的平方．所以③正确．答案③5．已知集合P ＝{x |x ＝2k ，k ∈Z }，M ＝{x |x ＝2k ＋1，k ∈Z }，a ∈P ，b ∈M ，设c ＝a ＋b ，则c 与集合M 有什么关系？解∵a ∈P ，b ∈M ，c ＝a ＋b ，∴设a ＝2k 1，k 1∈Z ，b ＝2k 2＋1，k 2∈Z .∴c ＝2k 1＋2k 2＋1＝2(k 1＋k 2)＋1.又k 1＋k 2∈Z ，∴c ∈M .6．(拓广探索)已知集合A 中的元素全为实数，且满足：若a ∈A ，则1＋a 1－a ∈A . (1)若a ＝2，求出A 中其他所有元素； (2)0是不是集合A 中的元素？请说明理由．解(1)由2∈A ，得1＋21－2＝－3∈A . 又由－3∈A ，得1－31＋3＝－12∈A .再由－12∈A ，得1－121＋12＝13∈A . 由13∈A ，得1＋131－13＝2∈A . 故A 中除2外，其他所有元素为－3，－12，13. (2)0不是集合A 中的元素．理由如下：若0∈A ，则1＋01－0＝1∈A ，而当1∈A 时，1＋a 1－a 不存在， 故0不是集合A 中的元素．。
高中数学--历年高考真题精选7(附答案)
高中数学--历年高考真题精选题号 一 二 三 总分 得分一 、选择题（本大题共10小题，每小题4分，共40分）1.给定两个命题p ，q ，若⌝p 是q 的必要而不充分条件，则p 是⌝q 的( )．A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件2.已知二次函数的图象如图所示，则它与轴所围图形的面积为A ．B ．C ．D ．3.在5(1)x +-6(1)x +的展开式中,含3x 的项的系数是(A) -5(B) 5(C) -10 (D) 104.为了迎接2010年广州亚运会，某大楼安装5个彩灯，他们闪亮的顺序不固定，每个彩灯彩灯闪亮只能是红橙黄绿蓝中的一种颜色，且这5个彩灯商量的颜色各不相同，记得这5个彩灯有序地闪亮一次为一个闪烁，而相邻两个闪烁的时间间隔均为5妙。
在每一个闪烁中，那么需要的时间至少是 A ．1205秒B ．1200秒C ．1195秒D ．1190秒 5.由直线12x =，x =2，曲线1y x =及x 轴所围图形的面积为（ ） A ．154B ．174 C ．1ln 22D ．2ln 26. ( 2x －3 )5的展开式中x 2项的系数为（A ）－2160（B ）－1080 （C ）1080（D ）21607.某地政府召集5家企业的负责人开会，其中甲企业有2人到会，其余4家企业各有1人到会，会上有3人发言，则这3人来自3家不同企业的可能情况的种数为【 】A ．14B ．16C ．20D ．488.下列函数中，满足“()()()f x y f x f y +=”的单调递增函数是（ ）（A ）()12f x x = （B ）()3f x x = （C ）()12xf x ⎛⎫= ⎪⎝⎭（D ）()3x f x =9.i 是虚数单位，()=-+113i i i (A) 1- (B) 1 (C) i - (D) i10.甲、乙两人从4门课程中各选修2门，则甲、乙所选的课程中恰有1门相同的选法有A.6种B.12种C.24种D.30种二 、填空题（本大题共8小题，每小题3分，共24分） 11.已知圆C 的圆心是直线1,(1x t y t=⎧⎨=+⎩为参数）与x 轴的交点，且圆C 与直线x+y+3=0相切，则圆C 的方程为12.明天上午李明要参加奥运志愿者活动，为了准时起床，他用甲、乙两个闹钟叫醒自己，假设甲闹钟准时响的概率是0.80，乙闹钟准时响的概率是0.90，则两个闹钟至少有一准时响的概率是 . 13.若函数f(x)=a x -x-a(a>0且a ≠1)有两个零点，则实数a 的取值范围是 .14.若变量x,y 满足约束条件 ,4,,y x x y y k ≤⎧⎪+≤⎨⎪≥⎩且 2z x y =+的最小值为-6，则k =_______.15.（几何证明选讲选做题）如图3，AB 是圆O 的直径，点C 在圆O 上，延长BC 到D 是BC=CD ，过C 作圆O 的切线交AD 于E 。
高考数学专题训练 (7)
专题训练71．已知集合{|{|12}M x y N x x ===+≤，且M 、N 都是全集I 的子集， 则右图韦恩图中阴影部分表示的集合为A．{|1}x x ≤≤B ．{|31}z z -≤≤C．{|3z z -≤< D．{|1x x <≤ 2．已知1sin()43πα+=，则sin cos αα的值为A ．718-B ．79-C ．718D ．793．已知等比数列{}n a 的前10项的积为32，则以下命题为真命题的是A ．数列{}n a 的各项均为正数B ．数列{}n a的项C ．数列{}n a 的公比必是正数D ．数列{}n a 中的首项和公比中必有一个4. 如果函数()cos 2y x φ＝3＋的图像关于点43π⎛⎫⎪⎝⎭，0中心对称， 那么||ϕ的最小值为 A6πB4πC3πD2π5．如图为一个算法的程序框图，则其输出结果是（ A ）A ．0B ．2012C ．2011D ．16．已知ABC ∆三边a ，b ，c 的长都是整数，且a b c ≤≤， 如果25=b ，则符合条件的三角形共有（ ）个 A ．124 B ．225 C ．300 D ．325 7．已知E ，F ，G ，H 是空间四点，命题甲：E ，F ，G ，H 四点不共面，命题乙：直线EF 和GH 不相交，则甲是乙成立的A ．必要不充分条件B ．充分不必要条件C ．充要条件D ．既不充分也不必要条件8．设双曲线)0,0(12222>>=-b a by ax 的离心率为3，且它的一条准线与抛物线x y 42=的准线重合，则此双曲线的方程为163)(22=-yxA . 1323)(22=-y xB .19648)(22=-yxC . 12412)(22=-yxD .9. 对于函数：①2)(+=x x f ；②2)2()(-=x x f ；③)2cos()(-=x x f .有如下两 个命题：命题甲：)2(+x f 是偶函数；命题乙：)(x f 在)2,(-∞上是减函数，在),2(+∞上是增函数.能使命题甲、乙均为真的所有函数的序号是)(A ①②. )(B ①③. )(C ②. )(D ③.10.在下列区间中，函数()43x f x e x =+-的零点所在的区间为 A.（14，12） B.（-14，0） C.（0，14） D.（12，34）11.设函数()sin(2)cos(2)44f x x x ππ=+++,则A.()y f x =在(0,)2π单调递增,其图象关于直线4x π=对称 B.()y f x =在(0,)2π单调递增,其图象关于直线2x π=对称 C.()y f x =在(0,)2π单调递减,其图象关于直线4x π=对称 D.()y f x =在(0,)2π单调递减,其图象关于直线2x π=对称12．设方程0)21(=-x x的实根为1x ，方程0log 2=+x x 的实根为2x ，方程01log 2=-xx 的实根为3x ，则 A ．321x x x << B ．312x x x << C ．321x x x <= D ．321x x x ==13．函数xx x y )2ln(2++-=的定义域为 .14．已知两个等比数列{}{},n n a b 满足11122(0),1,2a a a b a b a =>-=-=，333b a -=，若数列{}n a 唯一，则a = ．15．双曲线2221()4xy b N b-=∈的两个焦点为1F 、2F ，P 为双曲线上一点，15,OP PF <、12F F 、2PF 成等比数列， 则2______b = .16、如图，某几何体的正视图（主视图） 是平行四边形，侧视图（左视图）和俯视图 都是矩形，则该几何体的体积为 。
2023年高考数学模拟试题（七）参考答案
2023年高考数学模拟试题(七)参考答案 一㊁选择题1.A 2.C 3.A 4.B 5.C 6.C图17.B 提示:对于A :如图1,连接D C 1,交D 1C 于点O ,连接B 1O ,O N ,显然O 为D C 1的中点,又M ,N 分别为B B 1,C D 的中点,所以O N ʊC C 1且O N =12C C 1,B 1M ʊC C 1且B 1M =12C C 1,所以O N B 1M ,所以四边形O NM B 1为平行四边形,所以O B 1ʊMN ,又MN ⊄平面C B 1D 1,O B 1⊂平面C B 1D 1,所以MN ʊ平面C B 1D 1,故A 正确;图2对于B :如图2,连接B N ,则四边形A B N D 为三棱锥A 1 MN D 1在平面A B C D 上的正投影,因为S 梯形A B N D =12ˑ1+2ˑ2=3,故B 错误;对图3于C :如图3,取B C 的中点E ,连接A E ,E B 1,A B 1,显然әA B E ɸәB C N ,所以øA E B =øB N C ,又øN B C +øB N C =90ʎ,所以øN B C +øA E B =90ʎ,所以A E ʅB N ,由正方体A BCD A 1B 1C 1D 1,可得B B 1ʅ平面A B C D ,AE ⊂平面A B C D ,所以B B 1ʅA E ,又B B 1,B N ⊂平面MN B ,B B 1ɘB N =B ,所以A E ʅ平面MN B ,又A E ⊂平面A E B 1,所以平面A E B 1ʅ平面MN B ,故C 正图4确;对于D :如图4,若F 为棱A B 的中点,则MN =12+22+12=6,F N =2,F M =12+12=2,所以MN2=F N2+F M 2,即øM F N =90ʎ,即әF MN ,әMN B 均为直角三角形,且MN 是公共斜边,由直角三角形的性质可知MN 为三棱锥M N F B 的外接球的直径,故外接球的半径为R =12MN =62,所以三棱锥M N F B 的外接球的表面积S =4πR 2=6π,故D 正确㊂8.C 9.D10.D 提示:将f (x )=c o s (ωx +φ)的图像向左平移π3个单位长度,得到函数g (x )=c o s ωx +ωπ3+φ的图像,又函数g (x )为奇函数,故g (x )=-g (-x ),又函数g (x )的图像关于x =-π4对称,所以g (x )=g -π2-x,所以g -π2-x=-g (x ),所以函数g (x )的周期为π,所以ω=2πT =2,又函数g (x )为奇函数,所以2π3+φ=k π+π2,所以φ=k π-π6,又φ<π2,所以φ=-π6,所以f x =c o s 2x -π6,令2k π-πɤ2x -π6ɤ2k π,得k π-5π12ɤx ɤk π+π12,k ɪZ ,所以函数f x =c o s 2x -π6的单调递增区间为k π-5π12,k π+π12(k ɪZ ),当k =0时,函数f x =c o s 2x -π6的单调递增区间为-5π12,π12,当k =1时,函数f x =c o s 2x -π6 的单调递增区间为7π12,13π12 ,因为2π3,π ⊆7π12,13π12,所以函数f x =c o s 2x -π6 在区间2π3,π上为增函数,故A 正确;因为函数f x=c o s 2x -π6关于直线x =π12对称,所以f 12 =f π6-12 ,又函数f (x )在区间-5π12,π12上是增函数,所以f π6-12 >f (0),即f 12 >f (0),故C 正确;f π2=c o s π-π6 =-c o s π6=-32,故B 正确;因为π3>1,所以-π3<-1,结合函数f x=c o s 2x -π6在区间-5π12,π12上是增函数,可得f-π3<f (-1),又f -π3=-f (0),所以-f (0)<f (-1),即f (-1)+f (0)>0,故D 错误㊂11.C 提示:因为O 为F 1F 2的中点,则S әO P F 1=S әO P F 2=2S әO P Q ,即S әO P Q S әO P F 1=P QP F 1=12,所以P Q =12P F 1,所以Q 为线段P F 1的中点,由题图可知,直线O P 的方程为y =ba x ,因为P F 2ʅO P ,所以直线P F 2的方程为y =-abx -c,联立y =b ax ,y =-ab x -c,解得x =a 2c,y =a bc,即P 的坐标为a 2c ,a b c,因为点F 1-c ,0,所以点Q 的坐标为-b 22c ,a b 2c,又点Q 在直线y =-b a x上,则有a b 2c =b a ㊃b22c ,即b =a ,因此该双曲线的渐近线方程为y =ʃx ㊂12.D 提示:由f (x )+g '(x )=1,f (x )-g'(4-x )=1,得g '(x )=-g '(4-x ),则g (x )+C 1=g (4-x )+C 2(C 1与C 2为常数),令x =2,则g (2)+C 1=g (2)+C 2,所以C 1=C 2,则g (x )=g (4-x ),故g (x )的图像关于直线x =2对称,故②正确;因为g (x )为偶函数,则g (x )=g (-x ),g'(x )=-g'(-x ),则g '(x )为奇函数,故g '(x )=-g'(4-x )=g '(x -4),即g '(x +4)=g'(x ),则g '(x )是以4为周期的周期函数,由g '(x )=-g'(4-x ),令x =2,则g '(2)=-g'(2),即g '(2)=0,故g '(2022)=g '(2)=0,故①正确;由g '(x )=-g '(4-x ),令x =1,则g '(1)=-g'(3),即g '(1)+g '(3)=0,令x =0,则g '(0)=-g '(4)=0,即g '(4)=0,故g '(1)+g '(2)+g '(3)+g'(4)=0,则g '(4k +1)+g '(4k +2)+g'(4k +3)+g'(4k +4)=0(k ɪN ),由f (x )+g '(x )=1,即f (x )=1-g '(x ),得ð2022k =1f (k )=ð2022k =11-g '(k ) =2022-ð2022k =1g'(k )=2022-g '(1)+g '(2) =2022-g '(1),由于无法得出g '(1)的值,故③错误;ð2023k =1f (k )=ð2023k =11-g '(k )=2023-ð2023k =1g '(k )=2023-[g '(1)+g '(2)+g'(3)]=2023,故④正确㊂二、填空题13.91014.x =0㊂答案不唯一,y =33x -1也满足㊂15.[1,3) 提示:由题意知可设P (-2,m ),A (x 1,y 1),B (x 2,y 2),易知点A 处的斜率不为0,设点A 处的切线方程为y -y 1=k (x -x 1),联立y -y 1=k x -x 1 ,y 2=4x ,消去x得y 2-4k y +4y 1k-4x 1=0,由Δ=0得k =2y 1,所以A 处的切线方程为2x -y 1y +2x 1=0,因为切线过点P -2,m ,所以-4-y 1m +2x 1=0,同理可得点B 处的切线方程为-4-y 2m +2x 2=0,所以直线A B 的方程为-4-y m +2x =0,则直线A B 过定点N (2,0),由题意MH ʅA B ,即MH ʅHN ,故点H 的轨迹是以MN 为直径的圆,又点H 与点M 不重合,故点H 的轨迹是以MN 为直径的圆去掉点M ,其方程为(x -3)2+y 2=1(x ʂ4),又点F (1,0)在圆外,故F H 的最小值为F N =1,F H 的最大值为F M =3,故F H 的取值范围为[1,3)㊂16.[4e ,+ɕ) 提示:由已知得a >0,(a x -4)l n x <2l n a -a x l n 2⇒a x l n (2x )<2(l n a +2l n x )⇒a x l n (2x )2<l n (a x 2)⇒l n (2x )2x <l n (a x 2)a x2㊂令f (x )=l n xx ,所以f (2x )<f (a x 2),求导得f '(x )=1-l n x x2,所以f (x )在(0,e )上单调递增,在(e ,+ɕ)上单调递减,且当0<x <1时f (x )<0;当x >1时,f (x )>0㊂因为x ɪ12е,12,所以2x ɪ1е,1,所以f (2x )<0,由f (2x )<f (a x 2)及f (x )=l n x x 的图像可知,2x <a x 2恒成立,即a >2x 成立,而2xɪ(4,4e ),所以a ȡ4е㊂三、解答题17.(1)由s i n A +s i n C2=s i n 2B +3s i n A s i n C ,得s i n 2A +2s i n A s i n C +s i n 2C=s i n 2B +3s i n A s i nC ,即s i n 2A +s i n 2C -s i n 2B =s i n A s i nC ,由正弦定理得a 2+c 2-b 2=a c ,由余弦定理得c o s B =a 2+c 2-b 22a c=a c 2a c =12,又因为B ɪ0,π,所以B =π3㊂(2)已知6a =2b +3c ,由正弦定理得6s i n A =2s i n B +3s i n C ,所以6s i n A =2s i n π3+3s i n π3+A,展开整理化简得s i n A -π6=13㊂又因为A ɪ0,2π3,所以A -π6ɪ-π6,π2㊂所以c o s A -π6 =1-132=223㊂所以s i n A =s i n A -π6+π6 =s i n A -π6 c o s π6+c o s A -π6 s i nπ6=13ˑ32+223ˑ12=22+36㊂18.(1)延长B A ,C D 相交于点E ,连接S E ,则S E 为平面S C D 与平面S B A 的交线l ㊂由平面S A B ʅ平面A B C D ,B A ʅA D ,A D ⊂平面ABCD ,且平面S A B ɘ平面A B C D =A B ,所以A D ʅ平面S A B ㊂又A DʊB C ,所以B C ʅ平面S A B ㊂因为S E ⊂平面S A B ,所以B C ʅS E ,所以B C ʅl ㊂(2)由(1)知S A ʅA B ,A D ʅA B ,SA ʅA D ,以A 为坐标原点,A D ,AB ,A S 所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐图5标系A -x y z ,如图5所示,可得A (0,0,0),B (0,1,0),C (1,1,0),D 12,0,0,S (0,0,1),则B D ң=12,-1,0 ㊂设S Q ң=λS C (其中0<λ<1),则Q (λ,λ,1-λ),所以B Q ң=(λ,λ-1,1-λ)㊂设平面Q B D 的一个法向量为n =(x ,y ,z ),则n ㊃B D ң=12x -y =0,n ㊃B Q ң=λx +λ-1 y +1-λz =0,令x =2,得y =1,z =1-3λ1-λ,所以n =2,1,1-3λ1-λ ㊂因为S A ʅ平面B D C ,所以平面B D C 的一个法向量为m =0,0,1㊂所以c o s <m ,n >=m ㊃nm n=1-3λ1-λ5+1-3λ1-λ2㊃1=66,解得λ=12㊂所以存在Q 为S C 的中点时,使得二面角Q B D C 的余弦值为66㊂19.(1)根据表格数据可得, x =15(6+6.2+6.4+6.6+6.8)=6.4, y=15(50+45+45+40+35)=43,所以^b =ði =1nx i yi-n x yði =1nx2i-nx 2=1369-5ˑ6.4ˑ43205.2-5ˑ6.42=-17.5,^a = y -^b x=43-(-17.5)ˑ6.4=155,故经验回归方程为^y =-17.5x +155㊂(2)由题意知η的所有可能取值为0,1,2,3,4,5,6,7,8,由于顾客人数很多,可近似认为η服从二项分布,即η~B 8,12,P (η=k )=C k812k128-k=C k828,其中k ɪ{0,1,2,3,4,5,6,7,8}㊂故P (η=0)=C 0828=1256;P (η=1)=C 1828=132;P (η=2)=C 2828=764;P (η=3)=C 3828=732;P (η=4)=C 4828=35128;P (η=5)=C 5828=732;P (η=6)=C 6828=764;P (η=7)=C 7828=132;P (η=8)=C 8828=1256㊂所以η的分布列为表1:表1η12345678P1256132764732351287327641321256故E (η)=8ˑ12=4㊂20.(1)由题知A -2,0 ,设C x 0,y 0,则Dx 0-22,y 02,所以k A C ㊃k O D =y 0x 0+2㊃y 0x 0-2=1-14x 2x 20-4=-14㊂因为A C =5,所以点C 在圆(x +2)2+y 2=5上,又点C 在椭圆x 24+y 2=1上,所以点C x 0,y 0满足(x +2)2+y 2=5,x 24+y 2=1,消去y 整理得34x 2+4x =0,解得x 0=0,或x 0=-163<-2(舍去),又点C 在x 轴上方,所以C 0,1,所以直线A C 的斜率为12,故直线O D 的斜率为-12,所以直线A C 与直线O D 关于y 轴对称㊂设直线A C 的倾斜角θ,则c o s øP O M =c o s 2π2-θ=-co s 2θ=s i n 2θ-c o s 2θ=s i n 2θ-c o s 2θs i n 2θ+c o s 2θ=t a n 2θ-1t a n 2θ+1=-35㊂(2)由题意知,直线MN 的斜率存在㊂设直线MN 的斜率为k ,k >0,则直线MN :y =k x ,直线P Q :y =-14kx ㊂设M (x 1,y 1),N (x 2,y 2),联立y =k x ,x 24+y 2=1,消去y 整理得x 2=44k 2+1,所以MN2=1+k 2164k 2+1㊂同理P Q2=1+116k2114k2+1=416k 2+14k 2+1㊂所以|MN |2㊃|P Q |2=16(4k 2+4)(16k 2+1)(4k 2+1)2ɤ164k 2+4+16k 2+1224k 2+12=100㊂所以MN ㊃P Q ɤ10,当且仅当4k 2+4=16k 2+1,即k =12时,等号成立,所以P Q ㊃MN 的最大值为10㊂21.(1)当a =1时,f'(x )=(x +1)㊃(e x-1),令f '(x )>0,解得x >0或x <-1;令f '(x )<0,解得-1<x <0㊂故f (x )在区间(-ɕ,-1),(0,+ɕ)上单调递增,在区间(-1,0)上单调递减㊂所以f (x )的极大值是f (-1)=e -22e,极小值是f (0)=0㊂(2)求导得f '(x )=(x +1)(e x-a ),当x ɪ[0,2]时,e xɪ[1,e 2],且f (2)=2e 2-4a ,f (0)=0,对任意的x 1,x 2ɪ[0,2],恒有f (x 1)-f (x 2)ɤa +2e 2等价于f (x )m a x-f (x )m i n ɤa +2e 2㊂若a ɤ1,则e x-a ȡ0,故f '(x )ȡ0,所以f(x)在区间[0,2]上单调递增,故f(x)m a x -f(x)m i n=f(2)-f(0)=2e2-4aɤa+ 2e2,解得0ɤaɤ1㊂若aȡe2,则e x-aɤ0,故f'(x)ɤ0,所以f(x)在区间[0,2]上单调递减,故f(x)m a x -f(x)m i n=f(0)-f(2)=4a-2e2ɤa+ 2e2,解得e2ɤaɤ43e2㊂若1<a<e2,由f'(x)=(x+1)㊃(e x-a)>0,解得l n a<xɤ2,故f(x)在区间(l n a,2]上单调递增;由f'(x)=(x+1)㊃(e x-a)<0,解得0ɤx<l n a,故f(x)在区间[0,l n a)上单调递减㊂所以f(x)m i n=f(l n a)= -12a(l n a)2,f(x)m a x=f(2)或f(0)㊂又f(2)-f(0)=2e2-4a,当1<aɤe22时,f(2)-f(0)ȡ0,故f(x)m a x-f(x)m i n= f(2)-f(l n a)=2e2-4a+12a(l n a)2ɤa+2e2,解得0<aɤe10,又1<aɤe22,故1<aɤe22㊂当e22<a<e2时,f(2)-f(0)<0,故f(x)m a x-f(x)m i n=f(0)-f(l n a)=12a㊃(l n a)2ɤa+2e2,令h(a)=12a(l n a)2-a -2e2,则h'(a)=12(l n a)2+l n a-1,又l n aɪ(2-l n2,2),故h'(a)>0,即h(a)在区间e22,e2上单调递增,又h(e2)=-e2< 0,则12a(l n a)2ɤa+2e2恒成立㊂综上可得,0ɤaɤ43e2㊂22.(1)由M的参数方程可得(x-1)2+ (y-1)2=5,即x2+y2-2x-2y=3,所以ρ2-2ρc o sθ-2ρs i nθ=3㊂由题设知,直线l1:y=t a nα㊃x,故直线l1的极坐标方程为θ=αρɪR㊂又l2ʅl1,所以直线l2的极坐标方程为θ=α+π2,ρɪR,αɪ0,π2㊂(2)记ρ1=O A,ρ2=O B,ρ3= O C,ρ4=O D,联立直线l1与曲线M的极坐标方程得ρ2-2ρc o sα+s i nα-3=0,所以ρ1+ρ3=2c o sα+s i nα,ρ1ρ3=-3㊂同理联立直线l2与曲线M的极坐标方程得ρ2+ρ4=2(c o sα-s i nα),ρ2ρ4=-3㊂所以|A B|2+|B C|2+|C D|2+|D A|2 =2(ρ21+ρ22+ρ23+ρ24)=2{[(ρ1+ρ3)2-2ρ1ρ3]+[(ρ2+ρ4)2-2ρ2ρ4]}=2ˑ20=40㊂23.(1)由f(1)=1得a+b+c=1,因为3(a+b+c)=[(a)2+(b)2+(c)2](12 +12+12)=3,由柯西不等式得3= (a)2+(b)2+(c)212+12+12ȡ(a+b+c)2,当且仅当a=b=c=13时,等号成立,所以a+b+cɤ3㊂(2)由f xȡ2a x+b得a x2+ b-2a x+c-bȡ0,由题意知, a>0,Δ=(b-2a)2-4a c-bɤ0,则b2ɤ4a c-4a2,所以b2a2+c2ɤ4a c-4a2a2+c2=4ca-41+c2a2=4c a-1ca-12+2ca-1+2㊂因为4a c-4a2=4a c-aȡb2ȡ0,又a >0,所以cȡa,则c a-1ȡ0㊂令t=c a-1,则tȡ0,设g t=4tt2+2t+2tȡ0,当t=0时,g t=0;当t>0时,g t=4t+2t+2ɤ42t㊃2t+2=22-2,当且仅当t=2时,等号成立,所以b2a2+c2的最大值为22-2㊂(责任编辑王福华)。
押第7题 三角函数(新高考)(原卷版)--2023年新高考数学临考题号押题
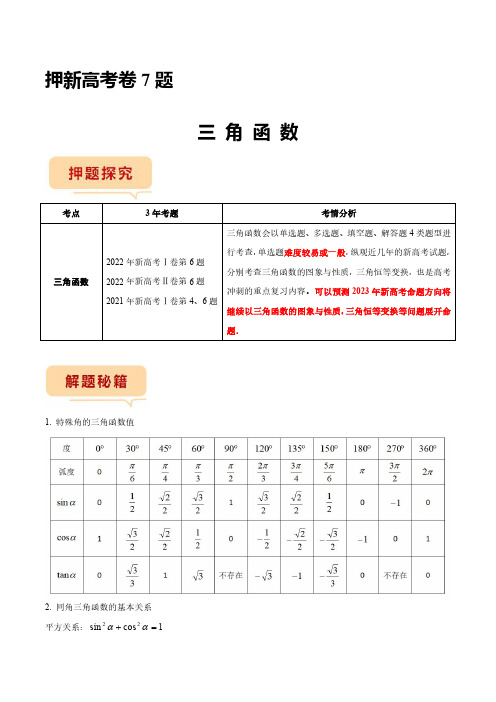
押新高考卷7题三角函数考点3年考题考情分析三角函数2022年新高考Ⅰ卷第6题2022年新高考Ⅱ卷第6题2021年新高考Ⅰ卷第4、6题三角函数会以单选题、多选题、填空题、解答题4类题型进行考查，单选题难度较易或一般，纵观近几年的新高考试题，分别考查三角函数的图象与性质，三角恒等变换，也是高考冲刺的重点复习内容。
可以预测2023年新高考命题方向将继续以三角函数的图象与性质，三角恒等变换等问题展开命题．1.特殊角的三角函数值2.同角三角函数的基本关系平方关系：1cos sin 22=+αα商数关系：αααcos sin tan =3.正弦的和差公式()βαβαβαsin cos cos sin sin +=+，()βαβαβαsin cos cos sin sin -=-4.余弦的和差公式()βαβαβαsin sin cos cos cos -=+，()βαβαβαsin sin cos cos cos +=-5.正切的和差公式()βαβαβαtan tan 1tan tan tan -+=+，()βαβαβαtan tan 1tan tan tan +-=-6.正弦的倍角公式⇒=αααcos sin 22sin ααα2sin 21cos sin =7.余弦的倍角公式()()αααααααsin cos sin cos sin cos 2cos 22-+=-=升幂公式：αα2sin 212cos -=，1cos 22cos 2-=αα降幂公式：22cos 1sin 2αα-=，22cos 1cos 2αα+=8.正切的倍角公式ααα2tan 1tan 22tan -=9.推导公式2)cos (sin )cos (sin 22=-++αααα10.辅助角公式x b x a y cos sin +=，)0(>a )sin(22ϕ++=⇒x b a y ，其中a b =ϕtan ，)2,2(ππϕ-∈1．（2022·新高考Ⅰ卷高考真题）记函数()sin (0)4f x x b πωω⎛⎫=++> ⎪⎝⎭的最小正周期为T ．若23T ππ<<，且()y f x =的图象关于点3,22π⎛⎫ ⎪⎝⎭中心对称，则2f π⎛⎫= ⎪⎝⎭（）A ．1B ．32C ．52D ．32．（2022·新高考Ⅱ卷高考真题）若sin()cos()22cos sin 4παβαβαβ⎛⎫+++=+ ⎪⎝⎭，则（）A ．()tan 1αβ-=B ．()tan 1αβ+=C ．()tan 1αβ-=-D ．()tan 1αβ+=-3．（2021·新高考Ⅰ卷高考真题）下列区间中，函数()7sin 6f x x π⎛⎫=- ⎪⎝⎭单调递增的区间是（）A ．0,2π⎛⎫ ⎪⎝⎭B ．,2ππ⎛⎫ ⎪⎝⎭C ．3,2ππ⎛⎫ ⎪⎝⎭D ．3,22ππ⎛⎫ ⎪⎝⎭4．（2021·新高考Ⅰ卷高考真题）若tan 2θ=-，则()sin 1sin 2sin cos θθθθ+=+（）A ．65-B ．25-C ．25D ．651．（2023·广东深圳·深圳中学统考模拟预测）已知1cos 23x =-，则22ππcos cos 66x x ⎛⎫⎛⎫-++ ⎪ ⎪⎝⎭⎝⎭的值为（）A ．916B ．56C ．1320D ．17242．（2023·重庆·统考模拟预测）已知角α，β满足1tan 3α=，()sin 2cos sin βαβα=+，则tan β=（）．A ．14B ．12C ．1D ．23．（2023·辽宁·新民市第一高级中学校联考一模）已知α，π0,2β⎛⎫∈ ⎪⎝⎭，且()()sin sin sin2αβαββ++-=，则（）A ．π2αβ+=B ．2παβ+=C ．2αβ=D ．αβ=4．（2023·浙江金华·模拟预测）已知函数π()sin cos (0)6f x x x ωωω⎛⎫=-+> ⎪⎝⎭在[0,π]上有且仅有2个零点，则ω的取值范围是（）A ．131,6⎡⎤⎢⎥⎣⎦B ．713,66⎡⎫⎪⎢⎣⎭C ．7,26⎡⎫⎪⎢⎣⎭D ．131,6⎡⎫⎪⎢⎣⎭5．（2023·广东广州·统考二模）已知函数()()sin 2f x x ϕ=+，若()π3f x f ⎛⎫ ⎪⎝⎭≤恒成立，且()ππ4f f ⎛⎫> ⎪⎝⎭，则()f x 的单调递增区间为（）A ．π2ππ,π63k k ⎡⎤++⎢⎥⎣⎦（k ∈Z ）B ．πππ,π63k k 轾犏-+犏臌（k ∈Z ）C ．πππ,π36k k ⎡⎤-+⎢⎥⎣⎦（k ∈Z ）D ．2πππ,π36k k ⎡⎤--⎢⎥⎣⎦（k ∈Z ）A ．49.25mC ．56.74m 11．（2023·河北邯郸·统考二模）已知函数个单位长度后，得到一个偶函数的图象，则函数A ．()ππZ 6k k +∈。
2020新课标高考数学(理)二轮总复习(课件+专题限时训练)专题7 高效解答客观题-2
专题限时训练建议用时：45分钟一、选择题1．命题“存在x0∈R,2x0≤0”的否定是()A．不存在x0∈R,2x0>0B．存在x0∈R,2x0>0C．对任意x∈R,2x≤0D．对任意x∈R,2x>0答案：D解析：本题主要考查全称命题与特称命题．由题意知,原命题的否定为“对任意x ∈R,2x>0”．2．下列命题中的假命题是()A．∀x∈R,e x>0B．∀x∈R,x2≥0C．∃x0∈R,sin x0＝2D．∃x0∈R,2x0>x20答案：C解析：本题考查命题真假的判定．∀x∈R,sin x≤1<2,所以C选项是假命题．3．(2019·中卫一模)命题“若a2＋b2＝0,则a＝0且b＝0”的逆否命题是() A．若a2＋b2≠0,则a≠0且b≠0”B．若a2＋b2≠0,则a≠0或b≠0”C．若a＝0且b＝0,则a2＋b2≠0D．若a≠0或b≠0,则a2＋b2≠0答案：D解析：命题“若a2＋b2＝0,则a＝0且b＝0”的逆否命题是“若a≠0或b≠0,则a2＋b2≠0”．4．已知p：x≤1；q：x2－x>0,则p是¬q的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案：B解析：本题考查充要条件的判定．依题意,¬q：x2－x≤0,即0≤x≤1；由x≤1不能得知0≤x≤1；反过来,由0≤x≤1可得x≤1.因此,p是¬q成立的必要不充分条件．5．(2019·绵阳模拟)已知命题p：∃x0∈R,使得lgcos x0＞0；命题q：∀x＜0,3x＞0,则下列命题为真命题的是()A．p∧q B．p∨¬qC．¬p∧¬q D．p∨q答案：D解析：命题p：∃x0∈R,使得lgcos x0＞0,∵－1≤cos x≤1,∴lgcos x≤0,∴命题p为假命题,命题q：∀x＜0,3x＞0,是真命题,∴p∧q为假命题,p∨¬q为假命题,¬p∧¬q为假命题,p∨q为真命题．6．若“0<x<1”是“(x－a)[x－(a＋2)]≤0”的充分不必要条件,则实数a的取值范围是()A．(－∞,0]∪[1,＋∞)B．(－1,0)C．[－1,0]D．(－∞,－1)∪(0,＋∞)答案：C解析：(x－a)[x－(a＋2)]≤0⇒a≤x≤a＋2,由集合的包含关系知⎩⎪⎨⎪⎧a ≤0，a ＋2≥1⇒a ∈[－1,0]． 7．已知命题p ：∀x >0,x ＋4x ≥4；命题q ：∃x 0∈(0,＋∞),2x 0＝12.则下列判断正确的是( )A ．p 是假命题B ．q 是真命题C ．p ∧¬q 是真命题D ．¬p ∧q 是真命题 答案：C解析：因为当x >0时,x ＋4x ≥2x ·4x ＝4,当且仅当x ＝2时等号成立,所以p 是真命题,当x 0>0时,2x 0>1,所以q 是假命题,所以p ∧¬q 是真命题,¬p ∧q 是假命题．8．若x ,y ∈R ,则x >y 的一个充分不必要条件是( )A ．|x |>|y |B ．x 2>y 2 C.x >yD ．x 3>y 3答案：C解析：本题考查充要条件的判断．由|x |>|y |,x 2>y 2未必能推出x >y ,排除A,B ；由x >y 可推出x >y ,反之,未必成立,而x 3>y 3是x >y 的充要条件．9．“a ≤－2”是“函数f (x )＝|x －a |在[－1,＋∞)上单调递增”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件答案：A解析：结合图象可知函数f (x )＝|x －a |在[a ,＋∞)上单调递增,易知当a ≤－2时,函数f (x )＝|x －a |在[－1,＋∞)上单调递增,但反之不一定成立．10．(2019·南昌二模)已知函数f (x )＝ax 2＋x ＋a ,命题p ：∃x 0∈R ,f (x 0)＝0,若p 为假命题,则实数a 的取值范围是( )A.⎣⎢⎡⎦⎥⎤－12，12B.⎝ ⎛⎭⎪⎫－12，12 C.⎝ ⎛⎭⎪⎫－∞，－12∪⎝ ⎛⎭⎪⎫12，＋∞ D.⎝ ⎛⎦⎥⎤－∞，－12∪⎣⎢⎡⎭⎪⎫12，＋∞ 答案：C解析：因为p 为假命题,所以¬p 为真命题,即∀x ∈R ,f (x )≠0,故Δ＝1－4a 2＜0,解得a >12或a <－12.11．下列命题正确的个数是( )①命题“∃x 0∈R ,x 20＋1>3x 0”的否定是“∀x ∈R ,x 2＋1≤3x ”；②“函数f (x )＝cos 2ax －sin 2ax 的最小正周期为π”是“a ＝1”的必要不充分条件；③x 2＋2x ≥ax 在x ∈[1,2]上恒成立⇔(x 2＋2x )min ≥(ax )max 在x ∈[1,2]上恒成立； ④“平面向量a 与b 的夹角是钝角”的充要条件是“a ·b <0”．A ．1B ．2C ．3D ．4答案：B解析：易知①正确；因为f (x )＝cos 2ax ,所以2π|2a |＝π,即a ＝±1,因此②正确；因为x 2＋2x ≥ax 在x ∈[1,2]上恒成立⇒a ≤x ＋2在x ∈[1,2]上恒成立⇒a ≤(x ＋2)min ,x ∈[1,2],因此③不正确；因为钝角不包含180°,而由a ·b ＜0时向量夹角包含180°,因此“平面向量a 与b 的夹角是钝角”的充要条件是“a ·b ＜0且a 与b 不反向”,故④不正确．12．(2019·珠海二模)“－1≤x ＋y ≤1且－1≤x －y ≤1”是“x 2＋y 2≤1”的( )A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既不充分也不必要条件答案：A解析：作出不等式组对应的平面区域如图．则“－1≤x＋y≤1且－1≤x－y≤1对应的区域在单位圆内,则“－1≤x＋y≤1且－1≤x－y≤1”是“x2＋y2≤1”的充分不必要条件．二、填空题13．已知命题p：∃x∈R,sin x>a,若¬p是真命题,则实数a的取值范围为__________．答案：a≥1解析：依题意得,∀x∈R,sin x≤a恒成立,于是有a≥1.14．(2019春·思明区校级月考)命题p：|x|＞1；命题q：x＜m,若¬p是¬q的充分不必要条件,则实数m的取值范围为__________．答案：(－∞,－1]解析：由|x|＞1得x＞1或x＜－1,若¬p是¬q的充分不必要条件,则q是p的充分不必要条件,即m≤1,即实数m的取值范围是(－∞,－1]．15．(2019春·西湖区校级月考)命题p：若直线与抛物线有且只有一个公共点,则直线与抛物线相切．命题p是__________(真,假)命题,命题p的否命题是__________(真,假)命题．答案：假真解析：当直线和抛物线的对称轴平行时,满足只有一个交点,但此时直线和抛物线是相交关系,即命题p是假命题．命题p的逆命题为：若直线与抛物线相切,则直线与抛物线有且只有一个公共点,正确．命题的否命题和逆命题互为逆否命题,则命题的否命题为真命题．16．已知命题p：∃x0∈R,mx20＋2≤0；命题q：∀x∈R,x2－2mx＋1>0,若p∨q为假命题,则实数m的取值范围是________．答案：[1,＋∞)解析：因为p∨q是假命题,所以命题p和q都是假命题．由命题p：∃x0∈R,mx20＋2≤0为假命题知,¬p：∀x∈R,mx2＋2＞0为真命题,所以m≥0.①由命题q：∀x∈R,x2－2mx＋1＞0为假命题知,¬q：∃x0∈R,x20－2mx0＋1≤0为真命题,所以Δ＝(－2m)2－4≥0⇒m2≥1⇒m≤－1或m≥1.②由①和②得m≥1.。
2024年高考数学复习大题全题型专练：专题07 解三角形(解析版)
专题7解三角形一、解答题1．（2022·全国·高考真题（理））记ABC 的内角,,A B C 的对边分别为,,a b c ，已知sin sin()sin sin()C A B B C A ．(1)证明：2222a b c ；(2)若255,cos 31a A ，求ABC 的周长．【答案】(1)见解析(2)14【解析】【分析】（1）利用两角差的正弦公式化简，再根据正弦定理和余弦定理化角为边，从而即可得证；（2）根据（1）的结论结合余弦定理求出bc ，从而可求得b c ，即可得解.(1)证明：因为 sin sin sin sin C A B B C A ，所以sin sin cos sin sin cos sin sin cos sin sin cos C A B C B A B C A B A C ，所以2222222222222a c b b c a a b c ac bc ab ac bc ab，即22222222222a c b a b c b c a ，所以2222a b c ；(2)解：因为255,cos 31a A，由（1）得2250b c ，由余弦定理可得2222cos a b c bc A ，则50502531bc ，所以312bc，故 2222503181b c b c bc ，所以9b c ，所以ABC 的周长为14a b c .2．（2022·全国·高考真题）记ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知cos sin 21sin 1cos 2A B A B．(1)若23C ，求B ；(2)求222a b c 的最小值．【答案】(1)π6；(2)5．【解析】【分析】（1）根据二倍角公式以及两角差的余弦公式可将cos sin 21sin 1cos 2A B A B 化成 cos sin A B B ，再结合π02B ，即可求出；（2）由（1）知，π2C B ，π22A B ，再利用正弦定理以及二倍角公式将222a b c 化成2224cos 5cos B B ，然后利用基本不等式即可解出．(1)因为2cos sin 22sin cos sin 1sin 1cos 22cos cos A B B B B A B B B ，即 1sin cos cos sin sin cos cos 2B A B A B A BC ，而π02B ，所以π6B ；(2)由（1）知，sin cos 0BC ，所以πππ,022C B ，而πsin cos sin 2B C C，所以π2C B ，即有π22A B ．所以222222222sin sin cos 21cos sin cos a b A B B B c C B2222222cos 11cos 24cos 555cos cos B B B BB ．当且仅当22cos 2B 时取等号，所以222a b c的最小值为5．3．（2022·浙江·高考真题）在ABC 中，角A ，B ，C 所对的边分别为a ，b ，c．已知34,cos 5a C ．(1)求sin A 的值；(2)若11b ，求ABC 的面积．【答案】(2)22．【解析】【分析】（1）先由平方关系求出sin C ，再根据正弦定理即可解出；（2）根据余弦定理的推论222cos 2a b c C ab以及4a 可解出a ，即可由三角形面积公式in 12s S ab C 求出面积．(1)由于3cos 5C ，0πC ，则4sin 5C．因为4a ，由正弦定理知4sin A C，则sin 45A C ．(2)因为4a ，由余弦定理，得2222221612111355cos 22225a a a abc C ab a a ，即26550a a ，解得5a ，而4sin 5C ，11b ，所以ABC 的面积114sin 51122225S ab C ．4．（2022·北京·高考真题）在ABC 中，sin 2C C．(1)求C ；(2)若6b ，且ABC 的面积为ABC 的周长．【答案】(1)6 (2)6+【解析】【分析】（1）利用二倍角的正弦公式化简可得cos C 的值，结合角C 的取值范围可求得角C 的值；（2）利用三角形的面积公式可求得a 的值，由余弦定理可求得c 的值，即可求得ABC 的周长.(1)解：因为 0,C ，则sin 0C2sin cos C C C ，可得cos 2C ，因此，6C .(2)解：由三角形的面积公式可得13sin 22ABC S ab C a，解得a .由余弦定理可得2222cos 48362612c a b ab C ，c所以，ABC 的周长为6a b c .5．（2022·全国·高考真题）记ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，分别以a ，b ，c 为边长的三个正三角形的面积依次为123,,S S S ，已知12313S S S B．(1)求ABC 的面积；(2)若sin sin A C，求b ．【答案】(2)12【解析】【分析】（1）先表示出123,,S S S ，再由123S S S2222a c b ，结合余弦定理及平方关系求得ac ，再由面积公式求解即可；（2）由正弦定理得22sin sin sin b ac B A C，即可求解.(1)由题意得22221231,,2S a S S，则222123S S S a b c 即2222a c b ，由余弦定理得222cos 2a c b B ac ，整理得cos 1ac B ，则cos 0B ，又1sin 3B ，则22cos 3B ，1cos 4ac B ，则12sin 28ABC S ac B ；(2)由正弦定理得：sin sin sin b a c B A C，则229sin sin sin sin sin 423b a c ac B A C A C ，则3sin 2b B ，31sin 22b B .6．（2022·全国·高考真题（文））记ABC 的内角A ，B ，C 的对边分别为a ，b ，c ﹐已知 sin sin sin sin C A B B C A ．(1)若2A B ，求C ；(2)证明：2222a b c 【答案】(1)5π8；(2)证明见解析．【解析】【分析】（1）根据题意可得， sin sin C C A ，再结合三角形内角和定理即可解出；（2）由题意利用两角差的正弦公式展开得 sin sin cos cos sin sin sin cos cos sin C A B A B B C A C A ，再根据正弦定理，余弦定理化简即可证出．(1)由2A B ， sin sin sin sin C A B B C A 可得， sin sin sin sin C B B C A ，而π02B ，所以 sin 0,1B ，即有 sin sin 0C C A ，而0π,0πC C A ，显然C C A ，所以，πC C A ，而2A B ，πA B C ，所以5π8C．(2)由 sin sin sin sin C A B B C A 可得，sin sin cos cos sin sin sin cos cos sin C A B A B B C A C A ，再由正弦定理可得，cos cos cos cos ac B bc A bc A ab C ，然后根据余弦定理可知，22222222222211112222a cb bc a b c a a b c ，化简得：2222a b c ，故原等式成立．7．（2022·上海·高考真题）如图，矩形ABCD 区域内，D 处有一棵古树，为保护古树，以D 为圆心，DA 为半径划定圆D 作为保护区域，已知30AB m ，15AD m ，点E 为AB 上的动点，点F 为CD 上的动点，满足EF 与圆D 相切.(1)若∠ADE 20 ，求EF 的长；(2)当点E 在AB 的什么位置时，梯形FEBC 的面积有最大值，最大面积为多少？（长度精确到0.1m ，面积精确到0.01m²）【答案】(1)23.3m(2)当8.7AE 时，梯形FEBC 的面积有最大值,最大值为255.14【解析】【分析】（1）设EF 与圆D 相切于对点H ，连接DH ，则DH EF ，15DH AD ，在直角HED △和直角FHD △中分别求出,EH HF ,从而得出答案.（2）先求出梯形AEFD 的面积的最小值，从而得出梯形FEBC 的面积的最大值.(1)设EF 与圆D 相切于对点H ，连接DH ，则DH EF ，15DH AD 则AE EH ，所以直角ADE 与直角HED △全等所以20ADE HDE在直角HED △中，tan 2015tan 20EH DH90250HDF ADE在直角FHD △中，tan 5015tan 50HF ADsin 20sin 5015tan 20tan 5015cos 20cos50EF EH HFsin 2050sin 20cos50cos 20sin 501515cos 20cos50cos 20cos50sin 70151523.3cos 20cos50cos50(2)设ADE ,902HDF ，则15tan AE ，15tan 902FH 115151515tan 15tan 90215tan 222tan 2EFD S EF DHV 11515tan 22ADE S AD AE V 所以梯形AEFD 的面积为215152251tan 30tan 2tan 2tan 222tan ADE DEF S S S22512253tan 4tan 42当且当13tan tan ，即tan 时取得等号，此时15tan 158.73AE即当tan 3 时，梯形AEFD 的面积取得最小值2则此时梯形FEBC 的面积有最大值1530255.142所以当8.7AE 时，梯形FEBC 的面积有最大值,最大值为255.148．（2022·全国·模拟预测）在 ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，其面积为S ，且 sin sin sin 6b a b c A B C S .(1)求角B 的大小；(2)若1a b ，2c b ，求cos A ，cos C 的值.【答案】(1)3(2)17，1114【解析】【分析】（1）由三角形的面积公式结合正弦余弦定理化简即可得到答案;（2）由余弦定理计算即可.(1)由in 12s S ab C ，又 sin sin sin 3sin b a b c A B C ab C ，由0b ，则 sin sin sin 3sin a b c A B C a C .由正弦定理得 3a b c a b c ac ，所以222a c b ac .由余弦定理得2221cos 222a cb ac B ac ac ，因为0B ，所以3B .(2)因为222a c b ac ，1a b ，2c b ，所以 2221212b b b b b ，解得7b ，所以8a ，5c .所以2222227581cos 2707b c a A bc ，22222287511cos 211214a b c C ab .9．（2022·全国·模拟预测）在ABC 中，角A B C ，，的对边长分别为a b c ，，，ABC 的面积为S ，且24cos cos tan S a B ab A B．(1)求角B 的大小；(2)若322AB BC ，，点D 在边AC 上，______，求BD 的长．请在①AD DC ；②DBC DBA ；③BD AC 这三个条件中选择一个，补充在上面的横线上，并完成解答．注：如果选择多个条件分别解答，按第一个解答计分．【答案】(1)π3B (2)答案不唯一，具体见解析【解析】【分析】（1）根据面积公式可得2cos cos cos c B a B b A ，利用正弦定理以及和角关系可得1cos 2B ，进而可求.（2）根据余弦定理可求出AC ，然后在ABD △和在DBC △中分别用余弦定理即可求①.根据面积公式即可求解②③.(1)因为24cos cos tan S a B ab A B ，所以214sin 2cos cos sin cos ac B a B ab A B B，所以22cos cos cos ac B a B ab A ，即2cos cos cos c B a B b A ．由正弦定理，得2sin cos sin cos sin cos C B A B B A ，所以 2sin cos sin sin C B A B C ．因为 0,πC ，所以sin 0C ，所以1cos 2B．又 0,πB ，所以π3B．(2)若选①．法一：在ABC 中，由余弦定理，得2222233π132cos 222cos 2234AC AB BC AB BC B ，所以ACAD DC 在ABD △中，由余弦定理，得2222cos AB BD DA BD DA ADB ，即2134cos 16BD BD ADB ．在DBC △中，由余弦定理，得2222cos BC BD DC BD DC CDB ，即2913cos 416BD CDB ．又πADB CDB ，所以cos cos 0ADB CDB ．所以29134248BD ，所以374BD ．法二：因为AD DC ，所以D 为AC 的中点，所以 12BD BA BC ，所以222124BD BA BC BA BC 19337422cos6044216．所以BD BD 若选②．在ABC 中，ABC ABD CBD S S S ，即1π1π1πsin sin sin 232626BA BC BA BD BD BC ，即1311131222222222BD BD ，解得BD 若选③．在ABC 中，由余弦定理，得2222cos AC AB BC AB BC B2233π13222cos 2234 ，所以AC ．因为1sin 2ABC S BA BC B △12ABC S BD AC △，BD 10．（2022·全国·模拟预测）在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，cos 2cos tan sin C A B C ，a b ．(1)求角B ；(2)若3a ，7b ，D 为AC 边的中点，求BCD △的面积．【答案】(1)23B (2)1538【解析】【分析】（1）根据同角三角函数的关系，结合两角和差的正余弦公式化简即可（2）由余弦定理可得5c ，再根据BCD △的面积为ABC 面积的一半，结合三角形的面积公式求解即可(1)由cos 2cos tan sin C A B C，有tan sin cos 2cos B C C A ，两边同乘cos B 得sin sin cos cos 2cos cos B C B C A B ，故 cos 2cos cos B C A B ，即cos 2cos cos A A B ．因为a b ，所以A 为锐角，cos 0A ，所以1cos 2B ．又因为 0,B ，所以23B ．(2)在ABC 中，由余弦定理2221cos 22a c b B ac ，即2949162c c ，故23400c c ，解得5c 或8c 舍）．故11235sin 223BCD ABC S S △△11．（2022·福建·三明一中模拟预测）已知ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，且22cos c b a C ．(1)求角A ；(2)若M 为BC 的中点，AM ABC 面积的最大值．【答案】(1)π3A 【解析】【分析】（1）解法一：根据正弦定理边化角求解即可；解法二：利用余弦定理将cos C 用边表示再化简即可；（2）解法一：根据基底向量的方法得1()2AM AB AC ，两边平方化简后可得2212b c bc ，再结合基本不等式与面积公式求面积最大值即可；解法二：设BM MC m ，再分别在ABM ，ACM △和ABC 中用余弦定理，结合cos cos 0AMB AMC 可得2212b c bc ，再结合基本不等式与面积公式求面积最大值即可(1)解法一：因为22cos c b a C ，由正弦定理得：sin 2sin 2sin cos C B A C ，所以sin 2sin()2sin cos C A C A C 2sin cos 2cos sin 2sin cos 2cos sin A C A C A C A C ，因为sin 0C ，所以12cos 1,cos 2A A，为0πA ，所以π3A ．解法二：因为22cos c b a C ，由余弦定理得：222222a b c c b a ab，整理得222bc b c a ，即222a b c bc ，又由余弦定理得2222cos a b c bc A所以12cos 1,cos 2A A，因为0πA ，所以π3A ．(2)解法一：因为M 为BC 的中点，所以1()2AM AB AC ，所以222124AM AB AB AC AC ，即22132cos 43c b bc ，即2212b c bc ，而222b c bc ，所以122bc bc 即4bc ，当且仅当2b c 时等号成立所以ABC 的面积为113sin 4222ABC S bc A △即ABC 解法二：设BM MC m ，在ABM 中，由余弦定理得2232cos c m AMB ，①在ACM △中，由余弦定理得2232cos b m AMC ，②因为πAMB AMC ，所以cos cos 0AMB AMC 所以①+②式得22262b c m ．③在ABC 中，由余弦定理得22242cos m b c bc A ，而π3A ，所以2224m b c bc ，④联立③④得：22222212b c b c bc ，即2212b c bc ，而222b c bc ，所以122bc bc ，即4bc ，当且仅当2b c 时等号成立．所以ABC 的面积为11sin 4222ABC S bc A △ABC 12．（2022·北京市第十二中学三模）ABC 的内角A 、B 、C 的对边分别为a 、b 、c ，已知cos sin a B A .(1)求角B 的大小；(2)从以下4个条件中选择2个作为已知条件，使三角形存在且唯一确定，并求ABC 的面积.条件①：3a ；条件②：b ；条件③：2cos 3C ；条件④：2c .【答案】(1)6B(2)答案不唯一，见解析【解析】【分析】（1）由正弦定理化简可得出tan B 的值，结合角B 的取值范围可求得角B 的值；（2）选①②，利用余弦定理可判断ABC 不唯一；选①③或②③或③④，利用三角形的内角和定理可判断ABC 唯一，利用正弦定理结合三角形的面积可判断ABC 的面积；选①④，直接判断ABC 唯一，再利用三角形的面积公式可求得ABC 的面积；选②④，利用余弦定理可判断ABC 唯一，再利用三角形的面积公式可求得ABC 的面积.(1)解：由cos sin a B A 及正弦定理可得sin cos sin A B A B ，A ∵、 0,B ，则sin 0A ，cos 0 B B ，tanB 6B .(2)解：若选①②，由余弦定理可得2222cos b a c ac B ，即210c ，解得 c ，此时，ABC 不唯一；若选①③，已知3a ，6B，21cos 32C ，且 0,C ，则25,36C ，所以，5,6B C，则ABC 唯一，sin C， sin sin sin cos cos sin 66A C B C C由正弦定理sin sin b a B A 可得 92sin sin 11a B b A，所以， 9211sin 32211ABC S ab C △；若选①④，已知3a ，6B，2c ，此时ABC 唯一，1322sin ABC S ac B；若选②③，已知b 6B ，21cos 32C，且 0,C ，则25,36C ，所以，5,6B C，则ABC 唯一，sin C， sin sin sin cos cos sin 66A CBC C 由正弦定理sin sin b c B C 可得sin 410sin 3b C c B ，所以，120385sin 29ABC S bc A △；若选②④，已知b 6B，2c ，由余弦定理可得2222cos b a c ac B ，可得240a ，0a ∵，解得a ABC 唯一，1sin2ABC S ac B △若选③④，已知6B ，2c ，231cos 322C，且 0,C ，则25,36C ，所以，5,6B C，则ABC 唯一，5sin 3C， 152sin sin sin cos cos sin 666A CBC C ，由正弦定理sin sin b c B C 可得sin sin 5c B b C ，1sin 210ABC S bc A △.13．（2022·内蒙古·海拉尔第二中学模拟预测（文））在ABC 中，角A ，B ，C 的对边分别为,,a b c ，且sin cos (cos )sin .232B BC C (1)当π3B，求sin sin C A 的值(2)求B 的最大值.【答案】(1)sin C +sin A =1(2)2π3【解析】【分析】（1）代入π3B ，解得313sin cos 223C C ，对sin sin C A 变形得到1sin sin sin cos 12C A C C ，求出答案；（2）对题干条件两边同乘以2cos2B ，变形得到sin sin sin C A B ，利用正弦定理得到a c ，利用余弦定理和基本不等式求出B 的最大值.(1)由题意得：ππsin coscos )sin 66C C ，1cos 2C C则π31sin sin sin sin sin cos sin cos 1322C A C C C C C C(2)sin cos cos )sin 22B B C C ，两边同乘以2cos 2B 得：22sin cos cos )2sin cos 222B B B C C ，即 sin 1cos cos )sin C B C B ，整理得：sin sin sin C A B ，由正弦定理得：3a cb ，由余弦定理得： 2222222cos 1226ac b ac a c b b B ac ac ac，因为 22143a c acb ，当且仅当ac 时等号成立，此时21cos 162b B ac ，由于 0,πB ，而cos y x 在 0,π上单调递减，故B 的最大值为2π314．（2022·广东·大埔县虎山中学模拟预测）在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，且222ab a b c ．(1)求角C ；(2)若△ABC 的面积534S ，且c △ABC 的周长．【答案】(1)π3(2)6【解析】【分析】（1）利用余弦定理求得cos C 的值，进而求得角C 的值；（2）依据题给条件得到关于a b ，的方程组，求得+a b 的值，进而求得△ABC 的周长．(1)因为222ab a b c ，由余弦定理，得到2221cos 22a b c C ab ，又0πC ，所以π3C ；(2)因为△ABC 的面积4S ，且c π3C所以有221sin 212S ab C ab a b ，联立22526ab a b ，则6a b ，所以△ABC 的周长为6a b c 15．（2022·四川·宜宾市叙州区第一中学校模拟预测（理））已知ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，tan tan tan 0B C B C ．(1)求角A 的大小；(2)若2B D D C ，2AD ，且AD 平分BAC ，求ABC 的面积．【答案】(1)60A (2)332【解析】【分析】（1）由两角和的正切公式化简后求解（2）由AD 是角平分线得到2c b ，再利用面积公式求解(1)tan tantan tan tan tan 0tan()1tan tan B C B C B C B C B C故tan A 60A ；(2)设BC 边的高为h ，所以11sin 22ABD S AB AD BAD BD h ，11sin 22ABC S AC AD DAC CD h 又AD 是角平分线，所以BAD DAC所以AB BD AC DC，即2c b ，又ABC ABD ACD S S S ，则111sin 602sin 302sin 30222bc c b ，解得b c ，133sin 6022ABC S bc △．16．（2022·全国·模拟预测）在ABC 中，角A ，B ，C 所对的边分别是a ，b ，c ，3a ，2b ，sin A m ．(1)若ABC 唯一确定，求m 的值；(2)设I 是ABC 的内切圆圆心，r 是ABC 内切圆半径，证明：当21c r 时，IC IA IB ．【答案】(1)1(2)证明见解析【解析】【分析】（1）若01m ，根据sin A m ，b a ，可知A 可以为锐角，也可以为钝角，ABC 有两种情况，若1m ，则三角形为直角三角形，ABC 有唯一解.（2）由21c r 可推导出ABC 为直角三角形，故可计算出,,IC IA IB 的值，即得证.(1)设AB 边上的高为c h ，则sin 20c h b A m ．当1m 时，由勾股定理，若A 为锐角，则c A 为钝角，则c ABC 存在两种情况，不能被唯一确定．当1m 时，ABC 为直角三角形，其中A 为直角顶点，c 可以唯一确定，即ABC 唯一确定，故m 的值为1．(2)当21c r 时，由余弦定理，22223cos 23a b c r r C ab ，故由同角三角函数的关系可得sin C所以ABC 的面积1sin 2S ab C另一方面， 132S a b c r r r3r r ，两边平方可得 213r r r r ，解得r ，21c r ABC 是以A 为直角顶点的直角三角形．因此有222112922IC，IC22211322IA 2IA ；22211322IB ，IB 所以有IC IA IB 成立．17．（2022·上海市光明中学模拟预测）已知在三角形ABC 中，2a b ，三角形的面积12S ．(1)若4b ，求 tan A B ；(2)若3sin 5C ，求sin sin A B ，．【答案】(1)(2)25sin 5A ，sin B 或6205sin 205A ，sin B 【解析】【分析】（1）根据面积公式及4b ，得到3sin 4C ，分C 为锐角和C 为钝角时，求出cos C ，进而求出tan C ，求出 tan A B ；（2）由面积公式求出b a ，分C 为锐角和C 为钝角，由余弦定理和正弦定理求出答案.(1)∵2113sin 2sin 16sin 12sin 224S ab C b C C C 而sin tan()tan(π)tan cos CA B C C C分情况讨论，当C 为锐角时，cos 0cos C C∴tan()A B当C 为钝角时，cos 0cos C Ctan()A B (2)22113sin 2sin 12225S ab C b C b ,因为0b ，所以b a分情况讨论，当C 为锐角时，4cos 0cos 5C C由余弦定理，222cos 366c a b ab C c由正弦定理，10sin sin sin sin sin sin 5a b c A A B C A B ，sin 5B当C 为钝角时，4cos 0cos 5C C ，由余弦定理，222cos 164c a b ab C c由正弦定理，sin sin sin sin a b c A A B C，sin B 18．（2022·辽宁·渤海大学附属高级中学模拟预测）ABC 的内角A 、B 、C 所对边的长分别为a 、b 、c，已知cos sin B b C ．(1)求C 的大小；(2)若ABC为锐角三角形且c 22a b 的取值范围．【答案】(1)3C(2)(5,6]【解析】【分析】（1）利用正弦定理边化角，再分析求解即可；（2）22224sin 4sin 3a b A A，再利用三角函数求值域即可.(1)cos sin B b C及正弦定理可得sin sin sin )B C B C A B Ccos sin B C B C ，所以sin sin cos B C B C ，因为B 、(0,)C ，则sin 0Bsin 0C C，则tan C 3C．(2)依题意，ABC为锐角三角形且c2sin sin sin a b c A B C ，所以2sin a A ，2sin 2sin()2sin 3b B A C A，所以222221cos 21cos 234sin 4sin 44322A A a b A A142cos 2222cos 222c 2cos 2222os 23A A A A A2c 42co os 242sin 246s 2cos 2sin 2A A A A A A，由于23A B ，所以022032A A，解得62A ，所以23A ，52666A ，所以푠� 2�∈12,1，所以2sin 2(1,2]6A ，所以2sin 24(5,6]6A．所以22a b 的取值范围是(5,6]．19．（2022·辽宁实验中学模拟预测）在① sin sin sin sin A C a b c B C ，② 2222cos 2a b c a c B a，③ sin cos 6a B C B b这三个条件中选一个，补充在下面问题中，并解答．已知ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且__________．(1)求B(2)若b ABC 的平分线交AC 于点D ，且5BD，求ABC 的面积．【答案】(1)=3B【解析】【分析】（1）若选条件①，先用正弦定理将角转化为边的关系，再利用余弦定理即可；若选条件②，先用余弦定理将边转化为角的关系，再利用正弦定理即可；若选条件③，先用三角形的内角之和为 ，再利用正弦定理即可；（2）利用角平分线的性质得到ABC ABD BCD S S S △△△，结合余弦定理和三角形的面积公式即可(1)选择条件①：根据正弦定理，可得：a c abc b c 可得：222a c b ac 根据余弦定理，可得：2221cos 22a cb B ac 0,,=3B B 选择条件②：根据余弦定理，可得：2cos (2)cos =cos 2abC a c B b C a根据正弦定理，可得：(2sin sin )cos sin cos A C B B C整理可得：2sin cos sin()sin A B B C A可得：1cos 2B 0,,=3B B选择条件③：易知：A B C可得：sin cos()6a A B b根据正弦定理，可得：sin sin cos(sin 6A A B B可得：1sin cos()sin 62B B B B整理可得：tan B 0,,=3B B(2)根据题意，可得：ABC ABD BCDS S S △△△可得：1143143sin sin sin 23256256ac a 整理可得：54a c ac 根据余弦定理，可得：2222cosb ac ac ABC可得：2213=a c ac ，即2()313a c ac 可得：225()482080ac ac 解得：4ac 或5225ac （舍）故1=sin 23ABC S ac △20．（2022·全国·南京外国语学校模拟预测）在ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，且5sin sin 35cos cos cos 2B C B C A ．(1)求角A 的大小；(2)若a 2bc 的最大值．【答案】(1)3A (2)【解析】【分析】（1）利用两角和的余弦公式、二倍角的余弦公式可得出关于cos A 的方程，结合1cos 1A 可求得cos A 的值，再结合角A 的取值范围可求得角A 的值；（2）由正弦定理结合三角恒等变换化简得出 2b c B ，结合正弦型函数的有界性可求得2b c 的最大值.(1)解：由已知可得 cos 25cos cos sin sin cos 25cos A B C B C A B C 2cos 25cos 2cos 5cos 13A A A A ，即22cos 5cos 20A A ，0A ∵，则1cos 1A ，解得1cos 2A ，因此，3A .(2)解：由正弦定理可得2sin sin sin b c aBC A，所以， 24sin 2sin 4sin 2sin 4sin 2sin 3b c B C B B A B B 4sin sin 5sin B B B B B B，其中 为锐角，且tan，因为3A ，则203B ，23B ，所以，当2B 时，即当2B 时，2b c 取得最大值。
2020高考终极训练试题 专题7 第1讲 坐标系与参数方程(大题)
第1讲坐标系与参数方程(大题)热点一极坐标与简单曲线的极坐标方程1.直角坐标与极坐标的互化把直角坐标系的原点作为极点，x轴的正半轴作为极轴，且在两种坐标系中取相同的长度单位.如图，设M是平面内的任意一点，它的直角坐标、极坐标分别为(x，y)和(ρ，θ)，则⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ，⎩⎪⎨⎪⎧ρ2＝x 2＋y 2，tan θ＝y x (x ≠0). 2.在与曲线的直角坐标方程进行互化时，一定要注意变量的范围，要注意转化的等价性. 例1 (2019·全国Ⅱ)在极坐标系中，O 为极点，点M (ρ0，θ0)(ρ0>0)在曲线C ：ρ＝4sin θ上，直线l 过点A (4,0)且与OM 垂直，垂足为P . (1)当θ0＝π3时，求ρ0及l 的极坐标方程；(2)当M 在C 上运动且P 在线段OM 上时，求P 点轨迹的极坐标方程.跟踪演练1 在平面直角坐标系xOy 中，已知直线l ：x ＋3y ＝53，以原点O 为极点，x 轴的正半轴为极轴建立极坐标系，圆C 的极坐标方程为ρ＝4sin θ.(1)求直线l 的极坐标方程和圆C 的直角坐标方程；(2)射线OP ：θ＝π6(ρ≥0)与圆C 的交点为O ，A ，与直线l 的交点为B ，求线段AB 的长.热点二 简单曲线的参数方程 1.直线的参数方程过定点M (x 0，y 0)，倾斜角为α的直线l 的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数).2.圆的参数方程圆心为点M (x 0，y 0)，半径为r 的圆的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋r cos θ，y ＝y 0＋r sin θ(θ为参数).3.圆锥曲线的参数方程(1)椭圆x 2a 2＋y 2b 2＝1(a >b >0)的参数方程为⎩⎪⎨⎪⎧x ＝a cos θ，y ＝b sin θ(θ为参数).(2)抛物线y 2＝2px (p >0)的参数方程为⎩⎪⎨⎪⎧x ＝2pt 2，y ＝2pt (t 为参数).4.(1)参数方程的实质是将曲线上每一点的横、纵坐标分别用同一个参数表示出来，所以有时处理曲线上与点的坐标有关的问题时，用参数方程求解非常方便；(2)充分利用直线、圆、椭圆等参数方程中参数的几何意义，在解题时能够事半功倍.例2 (2019·聊城模拟)在直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos θ，y ＝sin θ(θ为参数)，倾斜角为α的直线l 经过点P (0，2). (1)求曲线C 的普通方程和直线l 的参数方程；(2)若直线l 与曲线C 有两个不同的交点M ，N ，求|PM |＋|PN |的最大值.跟踪演练2 (2018·全国Ⅲ)在平面直角坐标系xOy 中，⊙O 的参数方程为⎩⎪⎨⎪⎧x ＝cos θ，y ＝sin θ(θ为参数)，过点(0，－2)且倾斜角为α的直线l 与⊙O 交于A ，B 两点. (1)求α的取值范围；(2)求AB 中点P 的轨迹的参数方程.热点三 极坐标方程与参数方程的综合应用解决与圆、圆锥曲线的参数方程有关的综合问题时，要注意普通方程与参数方程的互化公式，主要是通过互化解决与圆、圆锥曲线上动点有关的问题，如最值、范围等.例3 (2019·衡阳调研)在直角坐标系xOy 中，设P 为⊙O ：x 2＋y 2＝9上的动点，点D 为P 在x 轴上的投影，动点M 满足2DM →＝MP →，点M 的轨迹为曲线C .以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为ρsin ⎝⎛⎭⎫θ＋π6＝23，点A (ρ1,0)，B ⎝⎛⎭⎫ρ2，π2为直线l 上两点.(1)求曲线C 的参数方程；(2)是否存在M ，使得△MAB 的面积为8？若存在，有几个这样的点？若不存在，请说明理由.|AB |＝ρ21＋ρ22＝8. S △MAB ＝12|AB |d ≥43，∵8>43，故存在符合题意的点M ，且存在两个这样的点.跟踪演练3 (2019·烟台模拟)在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎨⎧x ＝1－32t ，y ＝－3＋12t (t 为参数)，以坐标原点为极点，x 轴的正半轴为极轴，建立极坐标系，曲线C 的极坐标方程为ρ＝222－cos 2θ.(1)求直线l 的普通方程及曲线C 的直角坐标方程；(2)设点P (1，－3)，直线l 与曲线C 相交于A ，B 两点，求1|P A |＋1|PB |的值.真题体验(2019·全国Ⅰ，理，22)在直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝1－t 21＋t 2，y ＝4t1＋t2(t 为参数).以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系，直线l 的极坐标方程为2ρcos θ＋3ρsin θ＋11＝0.(1)求C 和l 的直角坐标方程； (2)求C 上的点到l 距离的最小值.押题预测在平面直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为ρcos θ－2ρsin θ＋1＝0，曲线C 的参数方程为⎩⎨⎧x ＝2cos α，y ＝3sin α(α为参数).(1)求曲线C 上的点到直线l 的距离的最大值；(2)直线l 与曲线C 交于A ，B 两点，已知点M (1,1)，求|MA |·|MB |的值.A 组 专题通关1.(2019·贵州普通高等学校招生考试)在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝t cos α，y ＝t sin α(t 为参数，t ≥0)，在以O 为原点，x 轴正半轴为极轴的极坐标系中，曲线C 2，C 3的极坐标方程为ρ2－2ρcos θ－45＝0，ρ(cos θ＋sin θ)＝75.(1)判断C 2，C 3的位置关系，并说明理由；(2)若tan α＝34(0≤α≤π)，C 1分别与C 2，C 3交于M ，N 两点，求|MN |.2.(2019·全国Ⅲ)如图，在极坐标系Ox 中，A (2,0)，B ⎝⎛⎭⎫2，π4，C ⎝⎛⎭⎫2，3π4，D (2，π)，弧»»»AB C BC D ，，所在圆的圆心分别是(1,0)，⎝⎛⎭⎫1，π2，(1，π)，曲线M 1是弧»AB ，曲线M 2是弧»BC ，曲线M 3是弧».CD(1)分别写出M 1，M 2，M 3的极坐标方程；(2)曲线M 由M 1，M 2，M 3构成，若点P 在M 上，且|OP |＝3，求P 的极坐标.3.(2019·陕西八校联考)已知曲线C 的极坐标方程为ρ＝4cos θsin 2θ，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝t cos α，y ＝1＋t sin α(t 为参数，0≤α<π). (1)把曲线C 的极坐标方程化为直角坐标方程，并说明曲线C 的形状； (2)若直线l 经过点(1,0)，求直线l 被曲线C 截得的线段AB 的长.B 组 能力提高4.(2019·六安模拟)已知曲线E 的极坐标方程为ρ＝4tan θcos θ，倾斜角为α的直线l 过点P (2,2).(1)求曲线E 的直角坐标方程和直线l 的参数方程；(2)设l 1，l 2是过点P 且关于直线x ＝2对称的两条直线，l 1与E 交于A ，B 两点，l 2与E 交于C ，D 两点.求证：|P A |∶|PD |＝|PC |∶|PB |.5.在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎨⎧x ＝3cos α，y ＝3sin α(α为参数，α∈[0，π]).以O为极点，x 轴正半轴为极轴建立极坐标系，曲线C 2的极坐标方程为ρ2＝61－sin 2θ＋3cos 2θ.(1)求曲线C 1的极坐标方程；(2)设C 1与C 2的交点为M ，N ，求∠MON .数学核心素养练习一、数学抽象、直观想象素养1 数学抽象例1 (2019·全国Ⅱ)设函数f (x )的定义域为R ，满足f (x ＋1)＝2f (x )，且当x ∈(0,1]时，f (x )＝x (x －1).若对任意x ∈(－∞，m ]，都有f (x )≥－89，则m 的取值范围是( )A.⎝⎛⎦⎤－∞，94 B.⎝⎛⎦⎤－∞，73 C.⎝⎛⎦⎤－∞，52 D.⎝⎛⎦⎤－∞，831.如图表示的是一位骑自行车和一位骑摩托车的旅行者在相距80 km 的甲、乙两城间从甲城到乙城所行驶的路程与时间之间的函数关系，有人根据函数图象，提出了关于这两个旅行者的如下信息：①骑自行车者比骑摩托车者早出发3 h，晚到1 h；②骑自行车者是变速运动，骑摩托车者是匀速运动；③骑摩托车者在出发1.5 h后追上了骑自行车者；④骑摩托车者在出发1.5 h后与骑自行车者速度一样.其中，正确信息的序号是________.素养2直观想象例2(2019·全国Ⅲ)如图，点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，则()A.BM＝EN，且直线BM，EN是相交直线B.BM≠EN，且直线BM，EN是相交直线C.BM＝EN，且直线BM，EN是异面直线D.BM≠EN，且直线BM，EN是异面直线2.(2018·北京)某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为()A.1B.2C.3D.4二、逻辑推理、数学运算素养3逻辑推理例3(2019·全国Ⅱ)在“一带一路”知识测验后，甲、乙、丙三人对成绩进行预测.甲：我的成绩比乙高.乙：丙的成绩比我和甲的都高. 丙：我的成绩比乙高.成绩公布后，三人成绩互不相同且只有一个人预测正确，那么三人按成绩由高到低的次序为( )A.甲、乙、丙B.乙、甲、丙C.丙、乙、甲D.甲、丙、乙3.(2018·全国Ⅰ)已知双曲线C ：x 23－y 2＝1，O 为坐标原点，F 为C 的右焦点，过F 的直线与C 的两条渐近线的交点分别为M ，N .若△OMN 为直角三角形，则|MN |等于( ) A.32B.3C.2 3D.4 素养4 数学运算例4 (2019·全国Ⅰ)已知非零向量a ，b 满足|a |＝2|b |，且(a －b )⊥b ，则a 与b 的夹角为( ) A.π6 B.π3 C.2π3 D.5π64.(2018·全国Ⅲ)设a＝log0.20.3，b＝log20.3，则()A.a＋b<ab<0B.ab<a＋b<0C.a＋b<0<abD.ab<0<a＋b三、数学建模、数据分析素养5数学建模例5(2019·全国Ⅰ)古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是5－12⎝⎛⎭⎪⎫5－12≈0.618，称为黄金分割比例，著名的“断臂维纳斯”便是如此.此外，最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是5－12.若某人满足上述两个黄金分割比例，且腿长为105 cm，头顶至脖子下端的长度为26 cm，则其身高可能是()A.165 cmB.175 cmC.185 cmD.190 cm5.(2019·北京)李明自主创业，在网上经营一家水果店，销售的水果中有草莓、京白梨、西瓜、桃，价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量，李明对这四种水果进行促销：一次购买水果的总价达到120元，顾客就少付x元，每笔订单顾客网上支付成功后，李明会得到支付款的80%.(1)当x＝10时，顾客一次购买草莓和西瓜各1盒，需要支付________元；(2)在促销活动中，为保证李明每笔订单得到的金额均不低于促销前总价的七折，则x的最大值为________.素养6数据分析例6(2019·全国Ⅲ)为了解甲、乙两种离子在小鼠体内的残留程度，进行如下试验：将200只小鼠随机分成A，B两组，每组100只，其中A组小鼠给服甲离子溶液，B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图：记C为事件：“乙离子残留在体内的百分比不低于5.5”，根据直方图得到P(C)的估计值为0.70.(1)求乙离子残留百分比直方图中a，b的值；(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).6.某市一水电站的年发电量y (单位：亿千瓦时)与该市的年降雨量x (单位：毫米)有如下统计数据：(1)若从统计的5年中任取2年，求这2年的发电量都高于7.5 亿千瓦时的概率；(2)由表中数据求得线性回归方程为y ^＝0.004x ＋a ^，该水电站计划2019年的发电量不低于8.6 亿千瓦时，现由气象部门获悉2019年的降雨量约为1 800 毫米，请你预测2019年能否完成发电任务？回扣2复数、程序框图与平面向量1.复数的相关概念及运算法则(1)复数z＝a＋b i(a，b∈R)的分类①z是实数⇔b＝0；②z是虚数⇔b≠0；③z是纯虚数⇔a＝0且b≠0.(2)共轭复数复数z＝a＋b i(a，b∈R)的共轭复数z＝a－b i.(3)复数的模复数z＝a＋b i(a，b∈R)的模|z|＝a2＋b2.(4)复数相等的充要条件a＋b i＝c＋d i⇔a＝c且b＝d(a，b，c，d∈R).特别地，a ＋b i ＝0⇔a ＝0且b ＝0(a ，b ∈R ). (5)复数的运算法则加减法：(a ＋b i)±(c ＋d i)＝(a ±c )＋(b ±d )i ； 乘法：(a ＋b i)(c ＋d i)＝(ac －bd )＋(ad ＋bc )i ； 除法：(a ＋b i)÷(c ＋d i)＝ac ＋bd c 2＋d 2＋bc －adc 2＋d2i(c ＋d i ≠0).()其中a ，b ，c ，d ∈R2.复数的几个常见结论 (1)(1±i)2＝±2i. (2)1＋i 1－i ＝i ，1－i1＋i＝－i. (3)i 4n ＝1，i 4n ＋1＝i ，i 4n ＋2＝－1，i 4n ＋3＝－i ，i 4n ＋i 4n ＋1＋i 4n ＋2＋i 4n ＋3＝0(n ∈Z ). 3.程序框图的三种基本逻辑结构 (1)顺序结构. (2)条件结构. (3)循环结构. 4.平面向量基本定理如果e 1，e 2是同一平面内的两个不共线向量，那么对于这一平面内的任意向量a ，有且只有一对实数λ1，λ2，使a ＝λ1e 1＋λ2e 2.我们把不共线的向量e 1，e 2叫做表示这一平面内所有向量的一组基底. 5.向量a 与b 的夹角已知两个非零向量a 和b .作OA →＝a ，OB →＝b ，则∠AOB ＝θ(0°≤θ≤180°)叫做向量a 与b 的夹角.当θ＝0°时，a 与b 同向；当θ＝180°时，a 与b 反向.如果a 与b 的夹角是90°，我们说a 与b 垂直，记作a ⊥b . 6.平面向量的数量积(1)若a ，b 为非零向量，夹角为θ，则a·b ＝|a||b |cos θ. (2)设a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a·b ＝x 1x 2＋y 1y 2.(3)a ·b 的几何意义：数量积a ·b 等于a 的长度|a |与b 在a 的方向上的投影|b |cos θ的乘积. 7.两个非零向量平行、垂直的充要条件 若a ＝(x 1，y 1)，b ＝(x 2，y 2)，则 (1)a ∥b ⇔a ＝λb (b ≠0)⇔x 1y 2－x 2y 1＝0. (2)a ⊥b ⇔a·b ＝0⇔x 1x 2＋y 1y 2＝0. 8.利用数量积求长度(1)若a ＝(x ，y )，则|a |＝a·a ＝x 2＋y 2. (2)若A (x 1，y 1)，B (x 2，y 2)，则 |AB →|＝(x 2－x 1)2＋(y 2－y 1)2. 9.利用数量积求夹角设a ，b 为非零向量，若a ＝(x 1，y 1)，b ＝(x 2，y 2)，θ为a 与b 的夹角， 则cos θ＝a·b|a||b |＝x 1x 2＋y 1y 2x 21＋y 21 x 22＋y 22.10.三角形“四心”向量形式的充要条件设O 为△ABC 所在平面上一点，角A ，B ，C 所对的边长分别为a ，b ，c ，则 (1)O 为△ABC 的外心⇔|OA →|＝|OB →|＝|OC →|＝a 2sin A. (2)O 为△ABC 的重心⇔OA →＋OB →＋OC →＝0. (3)O 为△ABC 的垂心⇔OA →·OB →＝OB →·OC →＝OC →·OA →. (4)O 为△ABC 的内心⇔aOA →＋bOB →＋cOC →＝0.1.复数z为纯虚数的充要条件是a＝0且b≠0(z＝a＋b i，a，b∈R).还要注意巧妙运用参数问题和合理消参的技巧.2.复数的运算与多项式运算类似，要注意利用i2＝－1化简合并同类项.3.在解决含有循环结构的框图时，要弄清停止循环的条件.注意理解循环条件中“≥”与“>”的区别.4.解决程序框图问题时，要注意流程线的指向与其上文字“是”“否”的对应.5.在循环结构中，易错误判定循环体结束的条件，导致错求输出的结果.6.a·b>0是〈a，b〉为锐角的必要不充分条件；a·b<0是〈a，b〉为钝角的必要不充分条件.数学的核心素养引领复习一、数学抽象、直观想象素养1数学抽象通过由具体的实例概括一般性结论，看我们能否在综合的情境中学会抽象出数学问题，并在得到数学结论的基础上形成新的命题，以此考查数学抽象素养.例1(2019·全国Ⅱ)设函数f(x)的定义域为R，满足f(x＋1)＝2f(x)，且当x∈(0,1]时，f(x)＝x(x －1).若对任意x∈(－∞，m]，都有f(x)≥－89，则m的取值范围是()A.⎝⎛⎦⎤－∞，94 B.⎝⎛⎦⎤－∞，73C.⎝⎛⎦⎤－∞，52 D.⎝⎛⎦⎤－∞，83答案B解析当－1<x≤0时，0<x＋1≤1，则f(x)＝12f(x＋1)＝12(x＋1)x；当1<x≤2时，0<x－1≤1，则f(x)＝2f(x－1)＝2(x－1)(x－2)；当2<x≤3时，0<x－2≤1，则f(x)＝2f(x－1)＝22f(x－2)＝22(x－2)(x－3)，…，由此可得f(x)＝⎩⎪⎨⎪⎧…，12(x＋1)x，－1<x≤0，x(x－1)，0<x≤1，2(x－1)(x－2)，1<x≤2，22(x－2)(x－3)，2<x≤3，由此作出函数f(x)的图象，如图所示.由图可知当2<x≤3时，令22(x－2)·(x－3)＝－89，整理，得(3x－7)(3x－8)＝0，解得x＝73或x＝83，将这两个值标注在图中.要使对任意x∈(－∞，m]都有f(x)≥－89，必有m≤73，即实数m的取值范围是⎝⎛⎦⎤－∞，73，故选B.1.如图表示的是一位骑自行车和一位骑摩托车的旅行者在相距80 km的甲、乙两城间从甲城到乙城所行驶的路程与时间之间的函数关系，有人根据函数图象，提出了关于这两个旅行者的如下信息：①骑自行车者比骑摩托车者早出发3 h，晚到1 h；②骑自行车者是变速运动，骑摩托车者是匀速运动；③骑摩托车者在出发1.5 h后追上了骑自行车者；④骑摩托车者在出发1.5 h后与骑自行车者速度一样.其中，正确信息的序号是________.答案①②③解析看时间轴易知①正确；骑摩托车者行驶的路程与时间的函数图象是直线，所以是匀速运动，而骑自行车者行驶的路程与时间的函数图象是折线，所以是变速运动，因此②正确；两条曲线的交点的横坐标对应着4.5，故③正确，④错误.素养2直观想象通过空间图形与平面图形的观察以及图形与数量关系的分析，通过想象对复杂的数学问题进行直观表达，看我们能否运用图形和空间想象思考问题，感悟事物的本质，形成解决问题的思路，以此考查直观想象素养.例2(2019·全国Ⅲ)如图，点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，则()A.BM＝EN，且直线BM，EN是相交直线B.BM≠EN，且直线BM，EN是相交直线C.BM＝EN，且直线BM，EN是异面直线D.BM≠EN，且直线BM，EN是异面直线答案B解析取CD的中点O，连接ON，EO，因为△ECD为正三角形，所以EO⊥CD，又平面ECD⊥平面ABCD，平面ECD∩平面ABCD＝CD，所以EO⊥平面ABCD.设正方形ABCD的边长为2，则EO＝3，ON＝1，所以EN2＝EO2＋ON2＝4，得EN＝2.过M作CD的垂线，垂足为P，连接BP，则MP＝32，CP＝32，所以BM2＝MP2＋BP2＝⎝⎛⎭⎫322＋⎝⎛⎭⎫322＋22＝7，得BM＝7，所以BM≠EN.连接BD，BE，因为四边形ABCD为正方形，所以N为BD的中点，即EN，MB均在平面BDE内，所以直线BM，EN是相交直线.2.(2018·北京)某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为()A.1B.2C.3D.4答案C解析由三视图得到空间几何体，如图所示，则P A⊥平面ABCD，平面ABCD为直角梯形，P A＝AB＝AD＝2，BC＝1，所以P A⊥AD，P A⊥AB，P A⊥BC.又BC⊥AB，AB∩P A＝A，AB，P A⊂平面P AB，所以BC⊥平面P AB.又PB⊂平面P AB，所以BC⊥PB.在△PCD中，PD＝22，PC＝3，CD＝5，所以△PCD为锐角三角形.所以侧面中的直角三角形为△P AB，△P AD，△PBC，共3个.故选C.二、逻辑推理、数学运算素养3逻辑推理通过提出问题和论证命题的过程，看我们能否选择合适的论证方法和途径予以证明，并能用准确、严谨的数学语言表述论证过程，以此考查逻辑推理素养.例3(2019·全国Ⅱ)在“一带一路”知识测验后，甲、乙、丙三人对成绩进行预测.甲：我的成绩比乙高.乙：丙的成绩比我和甲的都高.丙：我的成绩比乙高.成绩公布后，三人成绩互不相同且只有一个人预测正确，那么三人按成绩由高到低的次序为( )A.甲、乙、丙B.乙、甲、丙C.丙、乙、甲D.甲、丙、乙答案 A解析 由于三人成绩互不相同且只有一个人预测正确.若甲预测正确，则乙、丙预测错误，于是三人按成绩由高到低的次序为甲、乙、丙；若甲预测错误，则甲、乙按成绩由高到低的次序为乙、甲，再假设丙预测正确，则乙、丙按成绩由高到低的次序为丙、乙，于是甲、乙、丙按成绩由高到低排序为丙、乙、甲，从而乙的预测也正确，与事实矛盾；若甲、丙预测错误，则可推出乙的预测也错误.综上所述，三人按成绩由高到低的次序为甲、乙、丙.3.(2018·全国Ⅰ)已知双曲线C ：x 23－y 2＝1，O 为坐标原点，F 为C 的右焦点，过F 的直线与C 的两条渐近线的交点分别为M ，N .若△OMN 为直角三角形，则|MN |等于( ) A.32 B.3 C.2 3 D.4 答案 B解析 由已知得双曲线的两条渐近线方程为y ＝±13x . 设两渐近线的夹角为2α，则有tan α＝13＝33， 所以α＝30°.所以∠MON ＝2α＝60°.又△OMN 为直角三角形，由于双曲线具有对称性，不妨设MN ⊥ON ，如图所示. 在Rt △ONF 中，|OF |＝2， 则|ON |＝ 3.则在Rt △OMN 中，|MN |＝|ON |·tan 2α＝3·tan 60°＝3.素养4 数学运算通过各类数学问题特别是综合性问题的处理，看我们能否做到明确运算对象，分析运算条件，选择运算法则，把握运算方向，设计运算程序，获取运算结果，以此考查数学运算素养.例4 (2019·全国Ⅰ)已知非零向量a ，b 满足|a |＝2|b |，且(a －b )⊥b ，则a 与b 的夹角为( ) A.π6 B.π3 C.2π3 D.5π6 答案 B解析 设a 与b 的夹角为α，∵(a －b )⊥b ，∴(a －b )·b ＝0，∴a ·b ＝b 2，∴|a |·|b |cos α＝|b |2，又|a |＝2|b |，∴cos α＝12，∵α∈[0，π]，∴α＝π3，故选B.4.(2018·全国Ⅲ)设a ＝log 0.20.3，b ＝log 20.3，则( ) A.a ＋b <ab <0 B.ab <a ＋b <0 C.a ＋b <0<ab D.ab <0<a ＋b答案 B解析 ∵a ＝log 0.20.3>log 0.21＝0， b ＝log 20.3<log 21＝0，∴ab <0.∵a ＋b ab ＝1a ＋1b＝log 0.30.2＋log 0.32＝log 0.30.4， ∴1＝log 0.30.3>log 0.30.4>log 0.31＝0， ∴0<a ＋b ab<1，∴ab <a ＋b <0.三、数学建模、数据分析素养5数学建模通过实际应用问题的处理，看我们是否能够运用数学语言清晰、准确地表达数学建模的过程和结果，以此考查数学建模素养.例5(2019·全国Ⅰ)古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是5－12⎝⎛⎭⎪⎫5－12≈0.618，称为黄金分割比例，著名的“断臂维纳斯”便是如此.此外，最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是5－12.若某人满足上述两个黄金分割比例，且腿长为105 cm，头顶至脖子下端的长度为26 cm，则其身高可能是()A.165 cmB.175 cmC.185 cmD.190 cm答案B解析若头顶至咽喉的长度为26 cm，则身高为26＋26÷0.618＋(26＋26÷0.618) ÷0.618≈178(cm)，此人头顶至脖子下端的长度为26 cm，即头顶至咽喉的长度小于26 cm，所以其身高小于178 cm，同理其身高也大于105÷0.618≈170(cm)，故其身高可能是175 cm，故选B.5.(2019·北京)李明自主创业，在网上经营一家水果店，销售的水果中有草莓、京白梨、西瓜、桃，价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量，李明对这四种水果进行促销：一次购买水果的总价达到120元，顾客就少付x元，每笔订单顾客网上支付成功后，李明会得到支付款的80%.(1)当x ＝10时，顾客一次购买草莓和西瓜各1盒，需要支付________元；(2)在促销活动中，为保证李明每笔订单得到的金额均不低于促销前总价的七折，则x 的最大值为________. 答案 130 15解析 (1)顾客一次购买草莓和西瓜各1盒，总价为60＋80＝140(元)，又140>120，所以优惠10元，顾客实际需要付款130元.(2)设顾客一次购买的水果总价为m 元，由题意知，当0<m <120时，x ＝0，当m ≥120时，(m －x )×80%≥m ×70%，得x ≤m 8对任意m ≥120恒成立，又m8≥15，所以x 的最大值为15.素养6 数据分析通过对概率与统计问题中大量数据的分析和加工，看我们能否获得数据提供的信息及其所呈现的规律，进而分析随机现象的本质特征，发现随机现象的统计规律，以此考查数据分析素养.例6 (2019·全国Ⅲ)为了解甲、乙两种离子在小鼠体内的残留程度，进行如下试验：将200只小鼠随机分成A ，B 两组，每组100只，其中A 组小鼠给服甲离子溶液，B 组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图：记C 为事件：“乙离子残留在体内的百分比不低于5.5”，根据直方图得到P (C )的估计值为0.70.(1)求乙离子残留百分比直方图中a ，b 的值；(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表). 解 (1)由已知得0.70＝a ＋0.20＋0.15，故a ＝0.35.b ＝1－0.05－0.15－0.70＝0.10.(2)甲离子残留百分比的平均值的估计值为2×0.15＋3×0.20＋4×0.30＋5×0.20＋6×0.10＋7×0.05＝4.05. 乙离子残留百分比的平均值的估计值为3×0.05＋4×0.10＋5×0.15＋6×0.35＋7×0.20＋8×0.15＝6.00.6.某市一水电站的年发电量y (单位：亿千瓦时)与该市的年降雨量x (单位：毫米)有如下统计数据：2013年 2014年 2015年 2016年 2017年 降雨量x (毫米) 1 500 1 400 1 900 1 600 2 100 发电量y (亿千瓦时)7.47.09.27.910.0(1)若从统计的5年中任取2年，求这2年的发电量都高于7.5 亿千瓦时的概率；(2)由表中数据求得线性回归方程为y ^＝0.004x ＋a ^，该水电站计划2019年的发电量不低于8.6 亿千瓦时，现由气象部门获悉2019年的降雨量约为1 800 毫米，请你预测2019年能否完成发电任务？解 (1)从统计的5年发电量中任取2年，基本事件为{7.4,7.0}，{7.4,9.2}，{7.4,7.9}，{7.4,10.0}，{7.0,9.2}，{7.0,7.9}，{7.0,10.0}，{9.2,7.9}，{9.2,10.0}，{7.9,10.0}，共10个；其中这2年的发电量都高于7.5 亿千瓦时的基本事件为{9.2,7.9}，{9.2,10.0}，{7.9,10.0}，共3个.所以这2年发电量都高于7.5 亿千瓦时的概率为P ＝310.(2)因为x ＝1 500＋1 400＋1 900＋1 600＋2 1005＝8 5005＝1 700， y ＝7.4＋7.0＋9.2＋7.9＋10.05＝41.55＝8.3. 又直线y ^＝0.004x ＋a ^过点(x ，y )，所以8.3＝0.004×1 700＋a ^， 解得a ^＝1.5， 所以y ^＝0.004x ＋1.5.当x ＝1 800时，y ^＝0.004×1 800＋1.5＝8.7>8.6， 所以预测该水电站2019年能完成发电任务.。
押题预测卷7丨决胜2024届高考数学押题预测7模拟试卷及答案
决胜2024年高考数学押题预测卷07数学（新高考九省联考题型）（考试时间：120分钟试卷满分：150分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。
答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答第Ⅰ卷时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其他答案标号。
写在本试卷上无效。
3．回答第Ⅱ卷时，将答案写在答题卡上。
写在本试卷上无效。
4．考试结束后，将本试卷和答题卡一并交回。
一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．抛物线24x y =-的准线方程是（）A.1y =B.1y =- C.2y = D.=2y -2．已知集合{}2R 230A x x x =∈--<，集合(){}2R log 21B x x =∈+<，则A B ⋂＝（）A.()3,2- B.()2,3- C.()2,0- D.()1,0-3．已知向量a ，b 满足3a = ，b = ()a ab ⊥+ ，则b 在a方向上的投影向量为（）A.3B.3-C.3a -D.a-r4．已知m，n表示两条不同直线，α表示平面，下列说法正确的是（）A.若//,//,m n αα则//m n B.若m α⊥，n α⊂，则m n ⊥C.若m α⊥，m n ⊥，则//n α D.若//m α，m n ⊥，则n α⊥5．设0x >，0y >，122y x+=，则1x y +的最小值为（）A.32B. C.32+ D.36．阿波罗尼斯（约公元前262年～约公元前190年），古希腊著名数学家﹐主要著作有《圆锥曲线论》、《论切触》等.尤其《圆锥曲线论》是一部经典巨著，代表了希腊几何的最高水平，此书集前人之大成，进一步提出了许多新的性质.其中也包括圆锥曲线的光学性质，光线从双曲线的一个焦点发出，通过双曲线的反射，反射光线的反向延长线经过其另一个焦点.已知双曲线C ：22221x y a b-=（0a >，0b >）的左、右焦点分别为1F ，2F ，其离心率e =，从2F 发出的光线经过双曲线C 的右支上一点E 的反射，反射光线为EP ，若反射光线与入射光线垂直，则21sin F F E ∠=（）A.56B.55C.45D.2557．若3sin cos θθ+=，则π1tan π8tan 8θθ⎛⎫+-⎪⎛⎫⎝⎭+ ⎪⎝⎭的值为（）A.7- B.14- C.17D.278．已知函数()()e 2,ln 2x f x x g x x x =+-=+-，若12,0x x ∃∈>R ，使得()()12f x g x =，则12x x 的最小值为（）A.e- B.1- C.1e- D.21e-二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9．已知复数z z-，下列说法正确的是（）A.若0z z -=，则z 为实数B.若220z z +=，则0z z ==C.若i 1z -=，则||z 的最大值为2D.若|i |||1z z -=+，则z z -为纯虚数10．已知,A B 分别为随机事件,A B 的对立事件，满足()()01,01P A P B <<<<，则下列叙述可以说明事件A ，B 为相互独立事件的是（）A.()()P B P B A =∣B.()()P B A P B A=∣∣C.()()()P A P B P A B += D.()()()P AB P AB P B A +=∣11．已知函数()f x ，()g x 的定义域均为R ，()f x 的图象关于点(2，0)对称，(0)(2)1g g ==，()()()()++-=g x y g x y g x f y ，则（）A.()f x 为偶函数B.()g x 为偶函数C.(1)(1)--=--+g x g x D.(1)(1)g x g x -=+三、填空题：本题共3小题，每小题5分，共15分.12．一组数据为3，5，1，6，8，2，记这组数据的上四分位数为n，则二项式2nx ⎛- ⎝展开式的常数项为__________．13.已知ABC 的内角C B A ,,的对边分别为c b a ,,，CD =是ACB ∠的角平分线,满足sin sin 1sin sin sin sin A b B B C b A c B +=++,若3CD =，ABC的面积为，则c 的值为__________．14.若正四棱锥的棱长均为2，则以所有棱的中点为顶点的十面体的体积为________，该十面体的外接球的表面积为________.四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15．为考察药物M对预防疾病A以及药物N对治疗疾病A的效果，科研团队进行了大量动物对照试验．根据100个简单随机样本的数据，得到如下列联表：（单位：只）药物M疾病A未患病患病合计未服用301545服用451055合计7525100（1）依据0.1α=的独立性检验，分析药物M对预防疾病A的有效性；（2）用频率估计概率，现从患病的动物中用随机抽样的方法每次选取1只，用药物N进行治疗．已知药物N的治愈率如下：对未服用过药物M的动物治愈率为12，对服用过药物M的动物治愈率为34．若共选取3次，每次选取的结果是相互独立的．记选取的3只动物中被治愈的动物个数为X，求X的分布列和数学期望．附：()()()()()22n ad bca b c d a c b dχ-=++++，n a b c d=+++.α0.1000.0500.0100.001 xα2.7063.841 6.63510.82816．如图，在四棱锥P ABCD -中，四边形ABCD 是菱形，平面ABCD ⊥平面PAD ，点M 在DP 上，且2,,120DM MP AD AP PAD ==∠=︒．（1）求证：BD ⊥平面ACM ；（2）若60ADC ∠=︒，求平面ACM 与平面ABP 夹角的余弦值．17．已知函数()21e 2xf x ax x x =--.（1）当1a =时，讨论函数()f x 的单调性；（2）若不等式2321()ln 2f x x x x x x ≤-+-在1,e ∞⎡⎫+⎪⎢⎣⎭上恒成立，求实数a 的取值范围.18．已知数列{}n a 的前n 项和为n S ，对任意正整数n ，总存在正数,,p q r ，使得1,n n n n a p S q r -==-恒成立；数列{}n b 的前n 项和为n T ，且对任意正整数,2n n n T nb =恒成立．(1)求常数,,p q r 的值；(2)证明数列{}n b 为等差数列；(3)若22b =，记311221222222422n n n n n n n n n nn b n b n b n b n b P a a a a a ---+++++=+++⋯++，是否存在正整数k ，使得对任意正整数,n n P k ≤恒成立，若存在，求正整数k 的最小值；若不存在，请说明理由．19．在平面直角坐标系xOy 中，已知椭圆Γ：22221(0)x y a b a b +=>>的离心率为3，直线l 与Γ相切，与圆O ：2223+=x y a 相交于A ，B 两点.当l 垂直于x 轴时，||AB =.（1）求Γ的方程；（2）对于给定的点集M ，N ，若M 中的每个点在N 中都存在距离最小的点，且所有最小距离的最大值存在，则记此最大值为,()d M N .（ⅰ）若M ，N 分别为线段AB 与圆O 上任意一点，P 为圆O 上一点，当PAB 的面积最大时，求,()d M N ；（ⅱ）若,()d M N ，(,)d N M 均存在，记两者中的较大者为(,)H M N .已知(,)H X Y ，(,)H Y Z ，(,)H X Z 均存在，证明：(,)(,)(,)≥+H X Z H Y Z H X Y .决胜2024年高考数学押题预测卷07数学（新高考九省联考题型）（考试时间：120分钟试卷满分：150分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。
广东省佛山市三水区2012高考数学 中低档题型专题训练(7)理
2012广东省理科数学大题（中低档题型）专题训练（七）1．已知函数)4sin(32sin )(2π++=x x x f 3cos )4cos(.2---x x π. (1)求函数f(x)的最小正周期和最值； (2)求函数f(x)的单调递减区间．【答案】解：(1))4sin(32sin )(2π++=x x x f 3cos )4cos(2---x x π32cos )4(sin 322--+=x x πxx 2cos 2sin 3-=)62sin(2π-=xππ==∴22T当2262πππ+=-k x 即)(3Z k k x ∈+=ππ时，f(x)取最大值2；当2262πππ-=-k x 即)(6Z k k x ∈-=ππ时，f(x)取最小值-2.(2)由≤-≤+6222πππx k )(232z k k ∈+ππ，得)(653z k k x k∈+≤≤+ππππ ∴单调递减区间为)](65,3[z k k k ∈++ππππ. 2． 本着健康、低碳的生活理念，租自行车骑游的人越来越多。
某自行车租车点的收费标准是每车每次租车时间不超过两小时免费，超过两小时的部分每小时收费标准为2元（不足1小时的部分按1小时计算）。
有甲乙两人相互独立来该租车点租车骑游（各租一车一次），设甲、乙不超过两小时还车的概率分别为2141，；两小时以上且不超过三小时还车的概率分别为4121，；两人租车时间都不会超过四小时。
（Ⅰ）求出甲、乙两人所付租车费用相同的概率；（Ⅱ）设甲、乙两人所付的租车费用之和为随机变量ξ，求ξ的分布列与数学期望ξE ； 【答案】解：（1）所付费用相同即为0,2,4元。
设付0元为8121411=⨯=P ，…………………2分付2元为8141212=⨯=P ， 付4元为16141413=⨯=P (4)分则所付费用相同的概率为165221=++=P P P P ……………6分 （2）设甲，乙两个所付的费用之和为ξ，ξ可为0,2,4,6,81(0)811115(2)4422161111115(4)4424241611113(6)442416111(8)4416P P P P P ξξξξξ====⋅+⋅===⋅+⋅+⋅===⋅+⋅===⋅=…………………10分分布列ξ0 24 6 8P18 516516 316 1165591784822E ξ=+++=…………………14分3. 如图6，四棱柱1111D C B A ABCD -的底面ABCD 是平行四边形，且1=AB ，2=BC ，060=∠ABC ，E 为BC 的中点，⊥1AA 平面ABCD ．⑴证明：平面⊥AE A 1平面DE A 1； ⑵若E A DE 1=，试求异面直线AE 与D A 1 所成角的余弦值．【答案】⑴依题意，CD AB BC EC BE ====21……1分，所以ABE ∆是正三角形，060=∠AEB ……2分，又00030)120180(21=-⨯=∠CED ……3分，所以090=∠AED ，AE DE ⊥……4分，因为⊥1AA 平面ABCD ，⊂DE 平面ABCD ，所以DE AA ⊥1……5分，因为A AE AA = 1，所以⊥DE 平面AE A 1……6分，因为⊂DE 平面DE A 1，所以平面⊥AE A 1平面DE A 1……7分．⑵取1BB 的中点F ，连接EF 、AF ……8分，连接C B 1，则D A C B EF 11////……9分，所以A E F ∠是异面直线AE 与D A 1所成的角……10分。
山西省朔州市重点中学2024届高三高考数学试题系列模拟卷(7)
山西省朔州市重点中学2024届高三高考数学试题系列模拟卷（7）注意事项:1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。
2．答题时请按要求用笔。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．设x ∈R ，则“327x <”是“||3x <”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件2．棱长为2的正方体1111ABCD A B C D -内有一个内切球O ，过正方体中两条异面直线AB ，11A D 的中点,P Q 作直线，则该直线被球面截在球内的线段的长为（ ）A ．2B 1CD ．1 3．若函数32()39f x x ax x =++-在3x =-时取得极值，则a =（ ）A ．2B ．3C ．4D ．54．设双曲线22221y x a b-=（0a >，0b >）的一条渐近线与抛物线213y x =+有且只有一个公共点，且椭圆22221x y a b +=的焦距为2，则双曲线的标准方程为（ ）A ．22143x y -= B ．22143y x -= C ．22123x y -= D ．22132y x -= 5．函数()[]()cos 2,2f x x x ππ=∈-的图象与函数()sin g x x =的图象的交点横坐标的和为（ ） A ．53π B ．2π C ．76π D ．π6．半正多面体(semiregular solid ) 亦称“阿基米德多面体”，是由边数不全相同的正多边形为面的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，是由正方体切截而成的，它由八个正三角形和六个正方形为面的半正多面体.如图所示，图中网格是边长为1的正方形，粗线部分是某二十四等边体的三视图，则该几何体的体积为（ ）A ．83B ．4C ．163D ．2037．已知等差数列{}n a 中，468a a +=则34567a a a a a ++++=（ ）A ．10B ．16C ．20D ．248．已知非零向量,a b 满足a b λ=，若,a b 夹角的余弦值为1930，且()()23a b a b -⊥+，则实数λ的值为（ ） A ．49- B ．23 C ．32或49- D ．32 9．若某几何体的三视图如图所示，则该几何体的表面积为（ ）A ．240B ．264C ．274D ．28210．已知i 是虚数单位，则(2)i i +=（ ）A ．12i +B ．12i -+C ．12i --D ．12i -11．定义在R 上的偶函数f （x ）满足f （x +2）＝f （x ），当x ∈[﹣3，﹣2]时，f （x ）＝﹣x ﹣2，则（ ） A ．66f sin f cos ππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭＞ B ．f （sin 3）＜f （cos 3） C ．4433f sin f cos ππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭＜ D ．f （2020）＞f （2019）12．在ABC ∆中，D 为BC 中点，且12AE ED =，若BE AB AC λμ=+，则λμ+=（ ） A ．1 B ．23- C ．13- D ．34- 二、填空题：本题共4小题，每小题5分，共20分。
专题07 不等式丨十年高考数学真题分项汇编(解析版)(共39页)
十年（2014－2023）年高考真题分项汇编—不等式目录题型一：不等式的性质及其应用.......................................1题型二：解不等式...................................................4题型三：基本不等式.................................................5题型四：简单的线性规划问题.........................................7题型五：不等式的综合问题 (34)题型一：不等式的性质及其应用一、选择题1．(2019·天津·理·第6题)已知5log 2a =，0.5og 2.l 0b =，0.20.5c =，则,,a b c 的大小关系为()A ．a c b <<B．a b c<<C．b c a<<D．c a b<<【答案】A解析：5511log 2log ,0,22a a ⎛⎫=<=∴∈ ⎪⎝⎭，110.5222log 2log 50.log 5log 42b --===>=，即2b >，11520.211220.5,,12222c c ⎛⎫⎛⎫⎛⎫==>=∴∈ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以a c b <<．2．(2019·全国Ⅰ·理·第3题)已知2log 0.2a =，0.22b =，0.30.2c =，则()A ．a b c <<B ．a c b<<C ．c a b <<D ．b c a<<【答案】答案：B解析：22log 0.2log 10a =<=，0.20221b =>=，0.300.20.21,(0,1)c c =<=∴∈，故a c b <<．3．(2014高考数学四川理科·第4题)若0,0a b c d >><<，则一定有()A．a b c d >B．a b c d <C．a b d c >D．a b d c<【答案】D解析：由1100c d d c <<⇒->->，又0a b >>，由不等式性质知：0a b d c ->->，所以a bd c<4．(2018年高考数学课标Ⅲ卷（理）·第12题)设0.2log 0.3a =，2log 0.3b =，则()A ．0a b ab +<<B．0ab a b <+<C ．0a b ab +<<D．0ab a b<<+【答案】B解析：一方面()0.2log 0.30,1a =∈，()2log 0.32,1b =∈--，所以0ab <0.31log 0.2a =，0.31log 2b =，所以()()0.30.311log 0.22log 0.40,1a b+=⨯=∈所以1101a b <+<即01a b ab +<<，而0ab <，所以0a b +<，所以1a ba b ab ab+<⇒+>综上可知0ab a b <+<，故选B ．5．(2014高考数学湖南理科·第8题)某市生产总值连续两年持续增加，第一年的增长率为p ，第二年的增长率为q ，则该市这两年生产总值的年平均增长率为()A．2q p +B．()()2111-++q p C．pqD．()()111-++q p 【答案】D解析：设两年的平均增长率为x ,则有()()()2111x p q +=++1x ⇒=-,故选D．6．(2017年高考数学山东理科·第7题)若0a b >>,且1ab =,则下列不等式成立的是()A．()21log 2a ba ab b +<<+B．()21log 2a b a b a b<+<+C．()21log 2a b a a b b +<+<D．()21log 2a ba b a b +<+<【答案】B【解析】221,01,1,log ()log 1,2aba b a b ><<∴<+>=12112log ()a ba ab a a b b b+>+>+⇒+>+,所以选B．二、填空题1．(2017年高考数学北京理科·第13题)能够说明“设,,a b c 是任意实数．若a b c >>,则a b c +>”是假命题的一组整数,,a b c 的值依次为_________________________．【答案】1,2,3---(答案不唯一)【解析】()123,1233->->--+-=->-出现矛盾,所以验证是假命题．三、多选题1．(2020年新高考全国Ⅰ卷(山东)·第11题)已知a >0，b >0，且a +b =1，则()A ．2212a b +≥B ．122a b->C ．22log log 2a b +≥-D +≤【答案】ABD解析：对于A ，()222221221a b a a a a +=+-=-+21211222a ⎛⎫⎪⎭+ ⎝≥-=，当且仅当12a b ==时，等号成立，故A 正确；对于B ，211a b a -=->-，所以11222a b-->=，故B 正确；对于C ，2222221log log log log log 224a b a b ab +⎛⎫+=≤==- ⎪⎝⎭，当且仅当12a b ==时，等号成立，故C 不正确；对于D ，因为2112a b =+≤++=，所以≤，当且仅当12a b ==时，等号成立，故D 正确；故选：ABD 2．(2020年新高考全国卷Ⅱ数学(海南)·第12题)已知a >0，b >0，且a +b =1，则()A ．2212a b +≥B ．122a b->C ．22log log 2a b +≥-D +≤【答案】ABD解析：对于A ，()222221221a b a a a a +=+-=-+21211222a ⎛⎫⎪⎭+ ⎝≥-=，当且仅当12a b ==时，等号成立，故A 正确；对于B ，211a b a -=->-，所以11222a b-->=，故B 正确；对于C ，2222221log log log log log 224a b a b ab +⎛⎫+=≤==- ⎪⎝⎭，当且仅当12a b ==时，等号成立，故C 不正确；对于D ，因为2112a b =+≤++=，所以≤，当且仅当12a b ==时，等号成立，故D 正确；故选：ABD一、选择题1．(2015高考数学北京理科·第7题)如图，函数()f x 的图象为折线ACB ，则不等式()()2log 1f x x +≥的解集是()()A．{}|10x x -<≤B．{}|11x x -≤≤C．{}|11x x -<≤D．{}|12x x -<≤【答案】C解析：如图所示，把函数2log y x =的图象向左平移一个单位得到2log (1)y x =+的图象1x =时两图象相交，不等式的解为11x -<≤，用集合表示解集，故选C．二、填空题1．(2015高考数学江苏文理·第7题)不等式422<-xx的解集为_______．【答案】(1,2).-解析：由题意得：2212x x x -<⇒-<<，解集为(1,2).-2．(2017年高考数学上海(文理科)·第7题)不等式11x x->的解集为________．【答案】(),0-∞【解析】111100x x x->⇒<⇒<,解集为(,0)-∞．一、填空题1．(2021高考天津·第13题)若0 , 0a b >>，则21a b a b ++的最小值为____________．【答案】解析： 0 , 0a b >>，212a b b a b b b ∴++≥+=+≥=，当且仅当21a a b =且2b b=，即a b ==所以21a b ab ++的最小值为故答案为：．2．(2020天津高考·第14题)已知0,0a b >>，且1ab =，则11822a b a b+++的最小值为_________．【答案】4【解析】0,0,0a b a b >>∴+> ，1ab =,11882222ab ab a b a b a b a b∴++=++++842a b a b +=+≥=+，当且仅当a b +=4时取等号，结合1ab =,解得22a b =-=，或22a b ==时，等号成立．故答案为：43．(2020江苏高考·第12题)已知22451(,)x y y x y R +=∈，则22x y +的最小值是_______．【答案】45【解析】22451x y y += ,0y ∴≠且42215y x y -=42222221144+5555y y x y y y y -∴+=+=≥=，当且仅当221455y y =，即2231,102x y ==时取等号．22x y ∴+的最小值为45．故答案为：45．4．(2019·天津·理·第13题)设0,0,25x y x y >>+=，则的最小值为．【答案】解析：524x y =+≥，=====即31xy=⎧⎨=⎩或232xy=⎧⎪⎨=⎪⎩时等号成立，因为2538<<5．(2019·上海·第7题)若x y R+∈、，且123yx+=，则yx的最大值为________.【答案】98【解析】法一：yxyx212213⋅≥+=，∴892232=⎪⎪⎭⎫⎝⎛≤xy；法二：由yx231-=，yyyyxy32)23(2+-=⋅-=(230<<y)，求二次最值89max=⎪⎭⎫⎝⎛xy. 6．(2019·江苏·第10题)在平面直角坐标系xOy中，P是曲线()4y x xx=+>0上一动点，则点P到直线x y+=的距离最小值是______.【答案】4【解析】法1：由已知，可设4(,0P x x xx+>，，所以42+4xxd===.当且仅当42xx=，即x=时取等号，故点P到直线的距离的最小值为4.法2：距离最小时，24'11yx-=-=，则x=，所以P,所以最小值为4.7．(2018年高考数学江苏卷·第13题)在ABC△中，角,,A B C所对的边分别为,,a b c，120ABC∠=︒，ABC∠的平分线交AC于点D，且1BD=，则4a c+的最小值为．【答案】9解析：由题意可知，ABC ABD BCDS S S∆∆∆=+，由角平分线性质和三角形面积公式得，111sin1201sin60+1sin60222ac a c=⨯⨯⨯⨯，化简得+ac a c=，111a c+=，因此1144(4)()5c aa c a ca c a c+=++=++≥，当且仅当=2=3c a时取等号，所以4a c+的最小值为9．8．(2018年高考数学天津(理)·第13题)已知,a b∈R，且360a b-+=，则128ab+的最小值为．【答案】14解析：由360a b -+=，得36a b =-，所以3633112222284ab b b ---+=+=⨯=≥，当且仅当363b b -=-，即1,3b a =-=-时等号成立，故128ab +的最小值为14．9．某公司一年购买某种货物400吨，每次都购买x 吨，运费为4万元／次，一年的总存储费用为4x 万元，要使一年的总运费与总存储费用之和最小，则x =吨．【答案】20解：某公司一年购买某种货物400吨，每次都购买x 吨，则需要购买400x次，运费为4万元/次，一年的总存储费用为4x 万元，一年的总运费与总存储费用之和为40044x x ⋅+万元，40044x x⋅+≥160，当16004x x=即x =20吨时，一年的总运费与总存储费用之和最小。
高考数学真题专题分类汇编专题七 平面向量(教师版)
专题七平面向量与解三角形真题卷题号考点考向2023新课标1卷3 向量的数量积向量数量积的坐标运算17 解三角形正、余弦定理解三角形2023新课标2卷13 向量的数量积利用向量数量积求模长17 解三角形解三角形的综合应用2022新高考1卷3 平面向量的线性运算向量的加减及数乘运算18 解三角形正弦定理变形、三角恒等变形2022新高考2卷4 向量的数量积向量数量积的坐标运算18 解三角形正余弦定理解三角形2021新高考1卷10 向量的坐标运算求向量的模、向量数量积的坐标运算19 解三角形正、余弦定理解三角形2021新高考2卷15 向量的数量积向量数量积的运算18 解三角形正弦定理解三角形、余弦定理判断三角形的形状2020新高考1卷7 向量的数量积求向量数量积的取值范围17 解三角形正、余弦定理解三角形2020新高考2卷3 向量的线性运算向量的加、减法运算17 解三角形正、余弦定理解三角形【2023年真题】1.（2023·新课标I 卷 第3题）已知向量(1,1)a = ，(1,1).b=− 若()()a b a b λµ+⊥+，则( ) A. 1λµ+=B.1λµ+=− C. 1λµ= D. 1λµ=−【答案】D 【解析】 【分析】本题考查向量的数量积运算，结合向量垂直，向量的数量积为0，为较易题. 【解答】解：22()()()()2(1)0a b a b a a b b λµλµλµλµ+⋅+=++⋅+=+=，所以1;λµ=−故选.D2. （2023·新课标II 卷 第13题）已知向量a ，b 满足||a b − |||2|a b a b +=− ，则||b = __________【答案】【解析】 【分析】本题考查向量模及向量数量积的运算，属于基础题． 将两等式分别平方，然后化简计算即可． 【解答】 解：将原式平方：化简可得：即23b =，故||b =3. （2023·新课标I 卷 第17题）已知在ABC 中，3A B C +=，2sin()sin .A C B −=(1)求sin A ；(2)设5AB =，求AB 边上的高.【答案】解：(1)3A B C +=，3C C π∴−=，解得.4C π=2sin()sin A C B ∴−=可化为2sin()sin()44A A πππ−=−−，即32sin()sin()44A A ππ−=−，A A A A=，整理得sin3cosA A=，将1cos sin3A A=代入22sin cos1A A+=，得210sin19A=，29sin10A∴=，sin A=(2)由(1)知sin A=，1cos sin3A A==4Cπ=，又sin sinAC ABB C=，sinsinAB BACC∴==AB∴边上的高sin 6.h AC A===【解析】本题考查了三角恒等变换与解三角形的相关知识，属于中等题.(1)根据题意，结合A B Cπ++=可直接求出C，再将C代入2sin()sinA C B−=进行恒等变换得sin3cosA A=，最后再结合同角三角函数的基本关系即可求解；(2)结合三角恒等变换、正弦定理，分别求出sin B和AC，即可得AB边上的高sinAC A的值.4.（2023·新课标II卷第17题）记ABC的内角A，B，C的对边分别为a，b，c，已知ABC，D为BC的中点，且 1.AD=(1)若3ADCπ∠=，求tan B；(2)若228b c+=，求b，.c【答案】解：(1)ABCS=，D为BC的中点，ADCS∴11sin122AD CD ADC CD⋅⋅∠=××=，解得2CD=，则 2.BD=过点A作AE CD⊥于点E，则在ADE中，AE=12DE=，∴在Rt AEB中，52BE BD DE=+=，tanAEBBE==(2) 在ABC 中，1()2AD AB AC =+，222222111||()(||||2)(2cos )444AD AB AC AB AC AB AC c b bc A ∴=+=++⋅=++ ，11(82cos )4bc A ∴=+，即cos 2bc A =−，又1sin 2ABC S bc A == ，sin bc A ∴，sintancos bc A Abc A ∴==23A π∴=，sin A =， 4.bc =再将4b c=代入228b c +=，即可解得 2.b c == 【解析】本题考查了解三角形的综合应用，属于中等题.(1)结合三角形面积和中点关系进行求解；(2)观察题目所给条件，结合中线的向量表示和三角形面积进行求解.【2022年真题】5.（2022·新高考I 卷 第3题）在ABC 中，点D 在边AB 上，2.BD DA =记CA m = ，CD n = ，则CB =( ) A. 32m n −B. 23m n −+C. 32m n +D. 23m n +【答案】B 【解析】 【分析】本题主要考查向量的加减及数乘运算，属于基础题. 【解答】解：2133CD CA CB =+ ，3223.CB CD CA m n =−=−+6.（2022·新高考II 卷 第4题）已知向量(3,4)a = ，(1,0)b = ，c a tb =+ ，若,,a c b c <>=<> ，则实数t =( ) A. 6− B. 5−C. 5D. 6【答案】C 【解析】 【分析】本题考查了向量的坐标运算和夹角运算，属于基础题。
新疆昌吉九中2024年下学期高三数学试题高考仿真考试试卷(七)
新疆昌吉九中2024年下学期高三数学试题高考仿真考试试卷（七）注意事项:1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。
2．答题时请按要求用笔。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．在等差数列{}n a 中，若244,8a a ==，则7a =（ ） A ．8B ．12C ．14D ．102．为实现国民经济新“三步走”的发展战略目标，国家加大了扶贫攻坚的力度．某地区在2015 年以前的年均脱贫率（脱离贫困的户数占当年贫困户总数的比）为70%．2015年开始，全面实施“精准扶贫”政策后，扶贫效果明显提高，其中2019年度实施的扶贫项目，各项目参加户数占比（参加该项目户数占 2019 年贫困户总数的比）及该项目的脱贫率见下表：那么2019年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的（ ） A ．2728倍 B ．4735倍 C ．4835倍 D ．75倍 3．已知(),A A A x y 是圆心为坐标原点O ，半径为1的圆上的任意一点，将射线OA 绕点O 逆时针旋转23π到OB 交圆于点(),B B B x y ，则2AB yy +的最大值为（ ）A ．3B ．2CD4．已知函数()2sin()(0,0)3f x x A ωωπ=->>，将函数()f x 的图象向左平移3π个单位长度，得到函数()g x 的图象，若函数()g x 的图象的一条对称轴是6x π=，则ω的最小值为A ．16B ．23C ．53D ．565．已知函数()()1xf x k xe =-，若对任意x ∈R ，都有()1f x <成立，则实数k 的取值范围是（ ）A ．(),1e -∞-B ．()1,e -+∞C ．(],0e -D ．(]1,1e -6．抛物线24y x =的焦点为F ，点(,)P x y 为该抛物线上的动点，若点(1,0)A -，则PFPA的最小值为（ ） A ．12B ．22C ．32D ．2237．已知函数2ln(2),1,()1,1,x x f x x x -⎧=⎨-+>⎩若()0f x ax a -+恒成立，则实数a 的取值范围是（ ） A ．1,12⎡⎤-⎢⎥⎣⎦B ．[0,1]C ．[1,)+∞D ．[0,2]8．已知实数集R ，集合{|13}A x x =<<，集合1|2B x y x ⎧⎫==⎨⎬-⎩⎭，则()R A C B ⋂=（ ） A ．{|12}x x <≤ B ．{|13}x x << C ．{|23}x x ≤<D ．{|12}x x <<9．已知命题p ：1m =“”是“直线0x my -=和直线0x my +=互相垂直”的充要条件；命题q ：对任意()2,∈=+a R f x x a 都有零点；则下列命题为真命题的是（ ）A ．()()p q ⌝∧⌝B ．()p q ∧⌝C ．p q ∨D ．p q ∧10．已知函22()(sin cos )2cos f x x x x =++，,44x ππ⎡⎤∈-⎢⎥⎣⎦，则()f x 的最小值为（ ） A ．22-B ．1C ．0D ．2-11．函数sin (3sin 4cos )y x x x =+()x R ∈的最大值为M ，最小正周期为T ，则有序数对(,)M T 为（ ） A ．(5,)πB ．(4,)πC ．(1,2)π-D ．(4,2)π12．已知复数z 满足(12)43i z i +=+，则z 的共轭复数是（ ） A ．2i -B ．2i +C ．12i +D ．12i -二、填空题：本题共4小题，每小题5分，共20分。
专题07 数列-2023年高考数学真题题源解密(新高考)(原卷版)
专题07 数列目录一览考向一等差数列}为等差数列，1．（2023•新高考Ⅰ•第7题）记S n为数列{a n}的前n项和，设甲：{a n}为等差数列；乙：{S nn 则（ ）A．甲是乙的充分条件但不是必要条件B．甲是乙的必要条件但不是充分条件C．甲是乙的充要条件D．甲既不是乙的充分条件也不是乙的必要条件考向二等比数列2．（2023•新高考Ⅱ•第8题）记S n为等比数列{a n}的前n项和，若S4＝﹣5，S6＝21S2，则S8＝（ ）A．120B．85C．﹣85D．﹣120考向三数列综合3．（2023•新高考Ⅰ•第20题）设等差数列{a n}的公差为d，且d＞1．令b n=S n，T n分别为数列n{a n}，{b n}的前n项和．（1）若3a2＝3a1+a3，S3+T3＝21，求{a n}的通项公式；（2）若{b n}为等差数列，且S99﹣T99＝99，求d．4．（2023•新高考Ⅱ•第18题）已知{a n}为等差数列，b n=a n−6，n为奇数2a n，n为偶数，记S n，T n为{a n}，{b n}的前n 项和，S4＝32，T3＝16．（1）求{a n}的通项公式；（2）证明：当n＞5时，T n＞S n．【命题意图】考查等差、等比数列的通项公式和前n 项和公式，考查等差、等比数列的性质；考查数列的求和方法，考查根据数列的递推公式求通项公式，考查数列和其他知识结合等综合知识．【考查要点】数列是高考考查热点之一，其中等差、等比数列的通项公式、求和公式，以及与等差、等比数列有关的错位相消求和及裂项相消求和，是考查的重点．作为数列综合题，常和充要条件、方程、不等式、函数等结合，涉及到恒成立，存在，最值，解不等式或者证明不等式等，对于基础能力和基础运算要求较高．【得分要点】1．解决等差、等比数列有关问题的几点注意(1)等差数列、等比数列公式和性质的灵活应用；(2)对于计算解答题注意基本量及方程思想的运用；(3)注重问题的转化，由非等差数列、非等比数列构造出新的等差数列或等比数列，以便利用相关公式和性质解题；(4)当题目中出现多个数列时，既要纵向考察单一数列的项与项之间的关系，又要横向考察各数列之间的内在联系.2．数列求和问题一般转化为等差数列或等比数列的前n 项和问题或已知公式的数列求和，不能转化的再根据数列通项公式的特点选择恰当的方法求解.,一般常见的求和方法有：（一）公式法②等比数列的前n 项和公式：③数列前项和重要公式：（2）（5）等差数列中，；n 1(21)n k k =-=∑()13521n ++++-= 2nm n m n S S S mnd +=++（6）等比数列中，.(二)分组求和法：把一个数列分成几个可以直接求和的数列.(三)裂项(相消)法：有时把一个数列的通项公式分成两项差的形式，相加过程消去中间项，只剩有限项再求和.(四)错位相减法：适用于一个等差数列和一个等比数列对应项相乘构成的数列求和.(1)适用条件：若{a n }是公差为d (d ≠0)的等差数列，{b n }是公比为q (q ≠1)的等比数列，求数列{a n b n }的前n 项和S n ；(2)基本步骤(3)注意事项：①在写出S n 与qS n 的表达式时，应特别注意将两式“错位对齐”，以便下一步准确写出S n－qS n ；②作差后，等式右边有第一项、中间n －1项的和式、最后一项三部分组成；③运算时，经常把b 2＋b 3＋…＋b n 这n －1项和看成n 项和，把－a n b n ＋1写成＋a n b n ＋1导致错误． (五)倒序相加法相加，就得到一个常数列的和，这一求和方法称为倒序相加法，等差数列前n 项和公式的推导便使用了此法. 用倒序相加法解题的关键，就是要能够找出首项和末项之间的关系，因为有时这种关系比较隐蔽.考向一 等差数列5．（2022•新高考Ⅱ）图1是中国古代建筑中的举架结构，AA ′，BB ′，CC ′，DD ′是桁，相邻桁的水平距离称为步，垂直距离称为举．图2是某古代建筑屋顶截面的示意图，其中DD 1，CC 1，BB 1，AA 1是举，OD 1，DC 1，CB 1，BA 1是相等的步，相邻桁的举步之比分别为＝0.5，＝k 1，＝k 2，＝k 3．已知k 1，k 2，k 3成公差为0.1的等差数列，且直线OA 的斜率为0.725，则k 3＝（ ）n m m n n m m n S S q S S q S +=+=+A．0.75B．0.8C．0.85D．0.9考向二数列递推公式6.（多选）（2021•新高考Ⅱ）设正整数n＝a0•20+a1•21+…+a k﹣1•2k﹣1+a k•2k，其中a i∈{0，1}，记ω（n）＝a0+a1+…+a k，则（ ）A．ω（2n）＝ω（n）B．ω（2n+3）＝ω（n）+1C．ω（8n+5）＝ω（4n+3）D．ω（2n﹣1）＝n考向三数列的求和7．（2021•新高考Ⅰ）某校学生在研究民间剪纸艺术时，发现剪纸时经常会沿纸的某条对称轴把纸对折．规格为20dm×12dm的长方形纸，对折1次共可以得到10dm×12dm，20dm×6dm两种规格的图形，它们的面积之和S1＝240dm2，对折2次共可以得到5dm×12dm，10dm×6dm，20dm×3dm三种规格的图形，它们的面积之和S2＝180dm2，以此类推．则对折4次共可以得到不同规格图形的种数为 ；如果对折n次，那么S k＝ dm2．考向四数列综合8．（2021•新高考Ⅱ）记S n是公差不为0的等差数列{a n}的前n项和，若a3＝S5，a2a4＝S4．（Ⅰ）求数列{a n}的通项公式a n；（Ⅱ）求使S n＞a n成立的n的最小值．9．（2021•新高考Ⅰ）已知数列{a n}满足a1＝1，a n+1＝（1）记b n＝a2n，写出b1，b2，并求数列{b n}的通项公式；（2）求{a n}的前20项和．10．（2022•新高考Ⅰ）记S n为数列{a n}的前n项和，已知a1＝1，{}是公差为的等差数列．（1）求{a n}的通项公式；（2）证明：++…+＜2．11．（2022•新高考Ⅱ）已知{a n}是等差数列，{b n}是公比为2的等比数列，且a2﹣b2＝a3﹣b3＝b4﹣a4．（1）证明：a1＝b1；（2）求集合{k|b k＝a m+a1，1≤m≤500}中元素的个数．重点考查等差、等比数列的概念、性质、通项公式和前n项和，考查错位相减、裂项相消等求和方法。
2014高考数学专题提升训练 训练7
常考问题7三角恒等变换与解三角形(建议用时：60分钟)1．(2013·济宁二模)在△ABC中，角A，B，C所对的边分别为a，b，c，且a＝1，B＝45°，S△ABC＝2，则b等于()．A．5 B．25 C.41 D．5 2解析∵S＝12ac sin B＝2，∴12×1×c×sin 45°＝2.∴c＝4 2.∴b2＝a2＋c2－2ac cos B＝1＋32－2×1×42×cos 45°.∴b2＝25，b＝5.答案 A2．(2013·北京东城区期末)在△ABC中，A，B，C为内角，且sin A cos A＝sin B cos B，则△ABC是()．A．等腰三角形B．直角三角形C．等腰直角三角形D．等腰或直角三角形解析由sin A cos A＝sin B cos B得sin 2A＝sin 2B＝sin(π－2B)，所以2A＝2B或2A＝π－2B，即A＝B或A＋B＝π2，所以△ABC为等腰或直角三角形．答案 D3．(2013·浙江卷)已知α∈R，sin α＋2cos α＝102，则tan 2α等于()．A.43 B.34C．－34D．－43解析∵sin α＋2cos α＝10 2，∴sin2α＋4sin α·cos α＋4cos2α＝5 2.化简，得4sin 2α＝－3cos 2α， ∴tan 2α＝sin 2αcos 2α＝－34. 答案 C4．在△ABC 中，内角A ，B ，C 所对的边分别是a ，b ，c .已知8b ＝5c ，C ＝2B ，则cos C 等于( )．A.725 B ．－725 C ．±725 D.2425解析 先用正弦定理求出角B 的余弦值，再求解． 由b sin B ＝csin C ，且8b ＝5c ，C ＝2B ， 所以5c sin 2B ＝8c sin B ，所以cos B ＝45. 所以cos C ＝cos 2B ＝2cos 2 B －1＝725. 答案 A5．已知tan β＝43，sin(α＋β)＝513，其中α，β∈(0，π)，则sin α的值为( )．A.6365 B.3365 C.1365D.6365或3365解析 依题意得sin β＝45，cos β＝35；注意到sin(α＋β)＝513<sin β，因此有α＋β>π2(否则，若α＋β≤π2，则有0<β<α＋β≤π2，0<sin β<sin(α＋β)，这与“sin(α＋β)<sin β”矛盾)，则cos(α＋β)＝－1213，sin α＝sin[(α＋β)－β]＝sin(α＋β)cos β－cos(α＋β)sin β＝6365. 答案 A6．(2013·衡水调研)在△ABC 中，内角A ，B ，C 的对边长分别为a ，b ，c ，已知a 2－c 2＝2b ，且sin A cos C ＝3cos A sin A ，求b ＝______.解析 在△ABC 中，sin A cos C ＝3cos A sin C ，则由正弦定理及余弦定理有a ·a 2＋b 2－c 22ab ＝3·b 2＋c 2－a 22bc ·c ，化简并整理得2(a 2－c 2)＝b 2.又由已知a 2－c 2＝2b ，则4b ＝b 2，解得b ＝4或b ＝0(舍)． 答案 47．若α，β∈⎝ ⎛⎭⎪⎫0，π2，cos ⎝ ⎛⎭⎪⎫α－β2＝32，sin ⎝ ⎛⎭⎪⎫α2－β＝－12，则cos (α＋β)＝________.解析 ∵α，β∈⎝ ⎛⎭⎪⎫0，π2，∴－π4<α－β2<π2，－π2<α2－β<π4，由cos ⎝ ⎛⎭⎪⎫α－β2＝32和sin ⎝ ⎛⎭⎪⎫α2－β＝－12得α－β2＝±π6，α2－β＝－π6，当α－β2＝－π6，α2－β＝－π6时，α＋β＝0，与α，β∈⎝ ⎛⎭⎪⎫0，π2矛盾；当α－β2＝π6，α2－β＝－π6时，α＝β＝π3，此时cos (α＋β)＝－12. 答案 －128．如图，嵩山上原有一条笔直的山路BC ，现在又新架设了一条索道AC ，小李在山脚B 处看索道AC ，发现张角∠ABC ＝120°；从B 处攀登400米到达D 处，回头看索道AC ，发现张角∠ADC ＝150°；从D 处再攀登800米方到达C 处，则索道AC 的长为______米．解析 如题图，在△ABD 中，BD ＝400米，∠ABD ＝120°.因为∠ADC ＝150°，所以∠ADB ＝30°.所以∠DAB ＝180°－120°－30°＝30°. 由正弦定理，可得BD sin ∠DAB ＝ADsin ∠ABD.所以400sin 30°＝AD sin 120°，得AD ＝4003(米)．在△ADC 中，DC ＝800米，∠ADC ＝150°，由余弦定理，可得AC 2＝AD 2＋CD 2－2×AD ×CD ×cos ∠ADC ＝(4003)2＋8002－2×4003×800×cos 150°＝4002×13，解得AC ＝40013(米)． 故索道AC 的长为40013米． 答案 400139．已知函数f (x )＝2cos ⎝ ⎛⎭⎪⎫ωx ＋π6(其中ω＞0，x ∈R )的最小正周期为10π.(1)求ω的值；(2)设α，β∈⎣⎢⎡⎦⎥⎤0，π2，f ⎝ ⎛⎭⎪⎫5α＋53π＝－65，f ⎝ ⎛⎭⎪⎫5β－56π＝1617，求cos(α＋β)的值．解 (1)由题意知f (x )＝2cos ⎝ ⎛⎭⎪⎫ωx ＋π6的最小正周期T ＝10π＝2πω，则ω＝15.(2)由(1)知f (x )＝2cos ⎝ ⎛⎭⎪⎫15x ＋π6，又α，β∈⎣⎢⎡⎦⎥⎤0，π2，f ⎝ ⎛⎭⎪⎫5α＋5π3＝－65，f ⎝ ⎛⎭⎪⎫5β－5π6＝1617，即cos ⎝ ⎛⎭⎪⎫α＋π2＝－35，cos β＝817，∴sin α＝35，cos α＝45，sin β＝1517， ∴cos(α＋β)＝cos αcos β－sin αsin β ＝45×817－35×1517＝－1385.10．(2013·新课标全国Ⅰ卷)如图，在△ABC 中，∠ABC ＝90°，AB ＝3，BC ＝1，P 为△ABC 内一点，∠BPC ＝90°.(1)若PB ＝12，求P A ；(2)若∠APB ＝150°，求tan ∠PBA . 解 (1)因为PB ＝12，所以∠CBP ＝60°，所以∠PBA ＝30°，由余弦定理，得 P A ＝PB 2＋BA 2－2PB ·BA ·cos ∠PBA ＝72.(2)设∠PBA ＝α，由已知得PB ＝sin α， 由正弦定理，得3sin 150°＝sin αsin (30°－α)，化简得3cos α＝4sin α，故tan α＝3 4.即tan∠PBA＝3 4.11．(2013·新课标全国Ⅱ卷)△ABC中内角A，B，C的对边分别为a，b，c，已知a＝b cos C＋c sin B.(1)求B；(2)若b＝2，求△ABC面积的最大值．解(1)由已知及正弦定理，得sin A＝sin B cos C＋sin C sin B，①又A＝π－(B＋C)，故sin A＝sin(B＋C)＝sin B cos C＋cos B sin C．②由①，②和C∈(0，π)得sin B＝cos B.又B∈(0，π)，所以B＝π4.(2)△ABC的面积S＝12ac sin B＝24ac.由已知及余弦定理，得4＝a2＋c2－2ac cos π4.又a2＋c2≥2ac，故ac≤42－2，当且仅当a＝c时，等号成立．因此△ABC面积的最大值为2＋1. 备课札记：。
高考数学函数专项复习押题密卷含参考解析 (7)
点
Q
x0
−t 2
+1 ,
y0
(t
R)
在函数
y
=
g
(
x)
的图像上移动，
（1）若点 P 的坐标为 (1, −1) ，点 Q 也在 y = f ( x) 图像上，求 t 的值．
（2）求函数 y = g ( x) 的解析式．
（3）当 t
0
，令
h(x)
=
log 1
2
1− x 2x +t
，求
当 y −1,0时， f '( y) 0 ，此时 f ( y) 单调递减，当 y (0,1时， f '( y) 0 ，
此时 f ( y) 单调递增，则 f (−1) = e−1 ， f (1) = e ， f ( y) 的最小值为 f (0) = 0 ，
因为对任意 x 1, e，总存在唯一的 y −1,1 ，使得 lnx + y2ey − a = 0 成立，
②若函数 f（x）＝ ，则
，都有
；
③若函数 f（x）＝loga|x| 2）>f（a＋1）；
在（0，＋∞）上单调递增，则 f（－
④若函数
(x∈ )，则函数 f(x)的最小值为-2.
其中真命题的序号是
三、解答题
15．已知动圆过定点 (0, 2) ，且在 x 轴上截得的弦长为 4 ，记动圆圆心的轨迹为
曲线 C . （1）求直线 x − 4 y + 2 = 0 与曲线 C 围成的区域面积；
F
(
x)
=
f
(
x)
+
g
(
x
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一部分 专题二 第1讲 等差数列、等比数列(限时60分钟，满分100分)一、选择题(本大题共6个小题，每小题6分，共36分) 1．(精选考题·北京高考)在等比数列{a n }中，a 1＝1，公比|q |≠1.若a m ＝a 1a 2a 3a 4a 5，则m ＝( )A ．9B ．10C ．11D ．12解析：由题知a m ＝|q |m －1＝a 1a 2a 3a 4a 5＝|q |10，所以m ＝11. 答案：C2．(精选考题·广元质检)已知数列{a n }满足a 1＝2，a n ＋1＝1＋a n1－a n(n ∈N *)，则连乘积a 1a 2a 3…aa 精选考题的值为( )A ．－6B ．3C ．2D ．1解析：∵a 1＝2，a n ＋1＝1＋a n 1－a n，∴a 2＝－3，a 3＝－12，a 4＝13，a 5＝2，∴数列{a n }的周期为4，且a 1a 2a 3a 4＝1，∴a 1a 2a 3a 4…aa 精选考题＝aa 精选考题＝a 1a 2＝2×(－3)＝－6. 答案：A3．设等差数列{a n }的前n 项和为S n ，若2a 8＝6＋a 11，则S 9＝( ) A ．54 B ．45C ．36D ．27解析：根据2a 8＝6＋a 11得2a 1＋14d ＝6＋a 1＋10d ，因此a 1＋4d ＝6，即a 5＝6.因此S 9＝9(a 1＋a 9)2＝9a 5＝54.答案：A4．已知各项不为0的等差数列{a n }，满足2a 3－a 27＋2a 11＝0，数列{b n }是等比数列，且b 7＝a 7，则b 6b 8＝( )A ．2B ．4C ．8D ．16 解析：因为a 3＋a 11＝2a 7，所以4a 7－a 27＝0，解得a 7＝4，所以b 6b 8＝b 27＝a 27＝16.答案：D5．(精选考题·福建高考)设等差数列{a n }的前n 项和为S n .若a 1＝－11，a 4＋a 6＝－6，则当S n 取最小值时，n 等于( )A ．6B ．7C ．8D ．9解析：设等差数列{a n }的公差为d ， ∵a 4＋a 6＝－6，∴a 5＝－3， ∴d ＝a 5－a 15－1＝2，∴a 6＝－1<0，a 7＝1>0，故当等差数列{a n }的前n 项和S n 取得最小值时，n 等于6. 答案：A6．(精选考题·陕西高考)对于数列{a n }，“a n ＋1>|a n |(n ＝1,2…)”是“{a n }为递增数列”的( )A ．必要不充分条件B ．充分不必要条件C ．充要条件D ．既不充分也不必要条件 解析：因为a n ＋1>|a n |⇒a n ＋1>a n ⇒{a n }为递增数列，但{a n }为递增数列⇒a n ＋1>a n 推不出a n ＋1>|a n |，故“a n ＋1>|a n |(n ＝1,2…)”是“{a n }为递增数列”的充分不必要条件．答案：B二、填空题(本大题共3个小题，每小题6分，共18分) 7．(精选考题·广东中山)在等比数列{a n }中，公比q ＝2，前精选考题项的和S 精选考题＝90，则a 2＋a 4＋a 6＋…＋a 精选考题＝________.解析：S 精选考题＝a 1(1－q 2010)1－q ＝a 1(1－22010)1－2＝90∴a 1＝9022010－1a 2＋a 4＋a 6＋…＋a 精选考题＝a 2[1－(q 2)1005]1－q 2＝2a 1(1－22010)1－4＝60 答案：608．已知等差数列{a n }的前n 项和为S n ，a 4＝15，S 5＝55，则过点P (3，a 3)，Q (10，a 10)的直线的斜率为________．解析：∵a 4＝15，S 5＝55.∴55＝5(a 1＋a 5)2＝5a 3，∴a 3＝11.∴公差d ＝a 4－a 3＝15－11＝4. a 10＝a 4＋6d ＝15＋24＝39. ∴P (3,11)，Q (10,39) k PQ ＝39－1110－3＝4.答案：49．已知两个等差数列{a n }和{b n }的前n 项和分别为A n 和B n ，且A nB n＝5n ＋63n ＋3，则使得a nb n 为整数的个数是________．解析：∵A nB n ＝n (a 1＋a n )2n (b 1＋b n )2＝a 1＋a n b 1＋b n ＝5n ＋63n ＋3，∴a n b n ＝2a n 2b n ＝a 1＋a 2n －1b 1＋b 2n －1＝5(2n －1)＋63(2n －1)＋3＝10n ＋582n ＋2＝5n ＋29n ＋1＝5＋24n ＋1. ∴要使a nb n ∈Z ，只要24n ＋1∈Z 即可，∴n ＋1为24的正约数，即2,3,4,6,8,12,24，共有7个． 答案：7三、解答题(本大题共3个小题，共46分)10．(本小题满分15分)(精选考题·浙江高考)设a 1，d 为实数，首项为a 1，公差为d 的等差数列{a n }的前n 项和为S n ，满足S 5S 6＋15＝0.(1)若S 5＝5，求S 6及a 1； (2)求d 的取值范围．解：(1)由题意知S 6＝－15S 5＝－3，a 6＝S 6－S 5＝－8，所以⎩⎨⎧5a 1＋10d ＝5，a 1＋5d ＝－8解得a 1＝7，所以S 6＝－3，a 1＝7.(2)因为S 5S 6＋15＝0，所以(5a 1＋10d )(6a 1＋15d )＋15＝0，即2a 21＋9da 1＋10d 2＋1＝0，故(4a 1＋9d )2＝d 2－8，所以d 2≥8. 故d 的取值范围为d ≤－22或d ≥2 2.11．(本小题满分15分)(精选考题·全国卷Ⅱ)已知{a n }是各项均为正数的等比数列，且a 1＋a 2＝2(1a 1＋1a 2)，a 3＋a 4＋a 5＝64(1a 3＋1a 4＋1a 5)．(1)求{a n }的通项公式；(2)设b n ＝(a n ＋1a n )2，求数列{b n }的前n 项和T n .解：(1)设公比为q ，则a n ＝a 1q n －1.由已知有 ⎩⎪⎨⎪⎧a 1＋a 1q ＝2(1a 1＋1a 1q )，a 1q 2＋a 1q 3＋a 1q 4＝64(1a 1q 2＋1a 1q 3＋1a 1q 4).化简得⎩⎨⎧a 21q ＝2，a 21q 6＝64.又a 1＞0，故q ＝2，a 1＝1.所以a n ＝2n －1. (2)由(1)知b n ＝(a n ＋1a n )2＝a 2n ＋1a 2n ＋2 ＝4n －1＋14n －1＋2.因此T n ＝(1＋4＋…＋4n －1)＋(1＋14＋…＋14n －1)＋2n ＝4n －14－1＋1－14n1－14＋2n ＝13(4n－41－n )＋2n ＋1. 12．(本小题满分16分)已知数列{a n }是等比数列，其前n 项和为S n ，a 1＋2a 2＝0，S 4－S 2＝18.(1)求数列{a n }的通项公式； (2)求数列{a n S n }的前n 项和；(3)求使不等式a n ≥116成立的n 的集合．解：(1)设等比数列{a n }的公比是q ，因为a 1＋2a 2＝0，且a 1≠0，所以q ＝a 2a 1＝－12.因为S 4－S 2＝18，所以a 1(1－q 4)1－q －a 1(1＋q )＝18，将q ＝－12代入上式，解得a 1＝1，所以a n ＝a 1qn －1＝(－12)n －1(n ∈N *)．(2)由于a n ＝(－12)n －1，S n ＝23[1－(－12)n]，∴a n S n ＝23[(－12)n －1＋(12)2n －1]，故a 1S 1＋a 2S 2＋…＋a n S n ＝89－49·(－12)n －49·(14)n. (3)a n ≥116⇔(－12)n －1≥116.显然当n 是偶数时，此不等式不成立．当n 是奇数时，(－12)n －1≥116⇔(12)n －1≥(12)4⇔n ≤5，但n 是正整数，所以n ＝1,3,5.综上，使原不等式成立的n 的集合为{1,3,5}．1．已知等差数列{a n }的前n 项和为S n ，且满足S 33－S 22＝1，则数列{a n }的公差是( )A.12 B ．1 C ．2 D ．3解析：由等差数列性质得S 3＝3a 2，所以S 33－S 22＝a 2－a 1＋a 22＝1，得a 2－a 1＝2.答案：C2．两个正数a 、b 的等差中项是52，一个等比中项是6，且a >b ，则椭圆x 2a 2＋y 2b2＝1的离心率e 等于( )A.32B.133C.53D.13解析：由已知得⎩⎨⎧a ＋b ＝5，ab ＝6，又a >b ，所以⎩⎨⎧a ＝3，b ＝2，c ＝a 2－b 2＝ 5.因此，离心率e ＝ca ＝53.答案：C3．(精选考题·辽宁高考)设{a n }是由正数组成的等比数列，S n 为其前n 项和．已知a 2a 4＝1，S 3＝7，则S 5＝( )A.152B.314C.334D.172解析：显然公比q ≠1，由题意得，⎩⎨⎧a 1q ·a 1q 3＝1a 1(1－q 3)1－q＝7，解得⎩⎪⎨⎪⎧a 1＝4q ＝12，∴S 5＝a 1(1－q 5)1－q ＝4(1－125)1－12＝314.答案：B2．(精选考题·广东高考)已知数列{a n }为等比数列，S n 是它的前n 项和．若a 2·a 3＝2a 1，且a 4与2a 7的等差中项为54，则S 5＝( )A ．35B ．33C ．31D ．29解析：设数列{a n }的公比为q ，a 2·a 3＝a 21·q 3＝a 1·a 4＝2a 1⇒a 4＝2，a 4＋2a 7＝a 4＋2a 4q 3＝2＋4q 3＝2×54⇒q ＝12，故a 1＝a 4q 3＝16，S 5＝a 1(1－q 5)1－q ＝31.答案：C5．(精选考题·山东高考)已知等差数列{a n }满足：a 3＝7，a 5＋a 7＝26.{a n }的前n 项和为S n .(1)求a n 及S n ； (2)令b n ＝1a 2n －1(n ∈N *)，求数列{b n }的前n 项和T n . 解：(1)设等差数列{a n }的首项为a 1，公差为d ， 由于a 3＝7，a 5＋a 7＝26， 所以a 1＋2d ＝7,2a 1＋10d ＝26， 解得a 1＝3，d ＝2.由于a n ＝a 1＋(n －1)d ，S n ＝n (a 1＋a n )2，所以a n ＝2n ＋1，S n ＝n (n ＋2)． (2)因为a n ＝2n ＋1，所以a 2n －1＝4n (n ＋1)，因此b n ＝14n (n ＋1)＝14(1n －1n ＋1)．故T n ＝b 1＋b 2＋…＋b n＝14(1－12＋12－13＋…＋1n －1n ＋1) ＝14(1－1n ＋1) ＝n 4(n ＋1)， 所以数列{b n }的前n 项和T n ＝n4(n ＋1).6．已知函数f (x )＝x 2－ax ＋b (a ，b ∈R)的图象经过坐标原点，且f ′(1)＝1，数列{a n }的前n 项和S n ＝f (n )(n ∈N *)(1)求数列{a n }的通项公式；(2)若数列{b n }满足a n ＋log 3n ＝log 3b n ，求数列{b n }的前n 项和． 解：(1)∵函数f (x )＝x 2－ax ＋b (a ，b ∈R)的图象经过坐标原点，∴f (0)＝b ＝0，∴f (x )＝x 2－ax ，由f ′(x )＝2x －a ，得f ′(1)＝2－a ＝1，∴a ＝1，第6页 共8页 ∴f (x )＝x 2－x ，∴S n ＝n 2－n ，∴当n ≥2时，a n ＝S n －S n －1＝n 2－n －[(n －1)2－(n －1)]＝2n －2，a 1＝S 1＝0，∴a n ＝2n －2(n ∈N *)．(2)由a n ＋log 3n ＝log 3b n 得：b n ＝n ·32n －2(n ∈N *)， 设{b n }的前n 项和为T n ，∴T n ＝b 1＋b 2＋b 3＋…＋b n＝30＋2·32＋3·34＋…＋n ·32n －2， ①∴9T n ＝32＋2·34＋3·36＋…＋n ·32n ， ②由②－①得：8T n ＝n ·32n －(1＋32＋34＋36＋…＋32n －2) ＝n ·32n －32n －18，∴T n ＝n ·32n 8－32n －164＝(8n －1)32n ＋164.。