七年级数学下册7.2.1 三角形的内角练习人教版.doc
最新版初中七年级数学题库 7.2.1 三角形的内角(含答案)
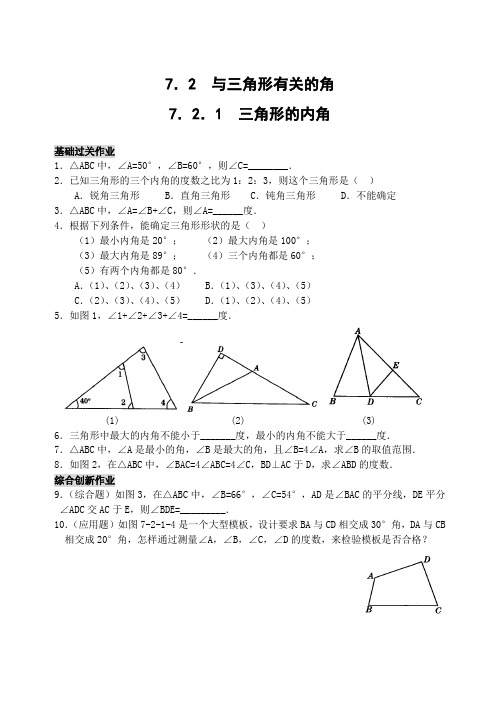
7.2 与三角形有关的角7.2.1 三角形的内角基础过关作业1.△ABC中,∠A=50°,∠B=60°,则∠C=________.2.已知三角形的三个内角的度数之比为1:2:3,则这个三角形是()A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定3.△ABC中,∠A=∠B+∠C,则∠A=______度.4.根据下列条件,能确定三角形形状的是()(1)最小内角是20°;(2)最大内角是100°;(3)最大内角是89°;(4)三个内角都是60°;(5)有两个内角都是80°.A.(1)、(2)、(3)、(4) B.(1)、(3)、(4)、(5)C.(2)、(3)、(4)、(5) D.(1)、(2)、(4)、(5)5.如图1,∠1+∠2+∠3+∠4=______度.(1) (2) (3)6.三角形中最大的内角不能小于_______度,最小的内角不能大于______度.7.△ABC中,∠A是最小的角,∠B是最大的角,且∠B=4∠A,求∠B的取值范围.8.如图2,在△ABC中,∠BAC=4∠ABC=4∠C,BD⊥AC于D,求∠ABD的度数.综合创新作业9.(综合题)如图3,在△ABC中,∠B=66°,∠C=54°,AD是∠BAC的平分线,DE平分∠ADC交AC于E,则∠BDE=_________.10.(应用题)如图7-2-1-4是一个大型模板,设计要求BA与CD相交成30°角,DA与CB 相交成20°角,怎样通过测量∠A,∠B,∠C,∠D的度数,来检验模板是否合格?11.(创新题)如图,△ABC 中,AD 是BC 上的高,AE 平分∠BAC ,∠B=75°,•∠C=45°,求∠DAE 与∠AEC 的度数.12.(2005年,福建厦门)如图,已知,在直角△ABC 中,∠C=90°,BD 平分∠ABC 且交AC 于D .(1)若∠BAC=30°,求证:AD=BD ;(2)若AP 平分∠BAC 且交BD 于P ,求∠BPA 的度数.13.(易错题)在△ABC 中,已知∠A=13∠B=15∠C ,求∠A 、∠B 、∠C 的度数.培优作业14.(探究题)(1)如图,在△ABC中,∠A=42°,∠ABC和∠ACB•的平分线相交于点D,求∠BDC的度数.(2)在(1)中去掉∠A=42°这个条件,请探究∠BDC和∠A之间的数量关系.15.(开放题)如图,在直角三角形ABC中,∠BAC=90°,作BC边上的高AD,•图中出现多少个直角三角形?又作△ABD中AB边上的高DD1,这时,图中共出现多少个直角三角形?按照同样的方法作下去,作出D1D2,D2D3,…,当作出D n-1D n时,图中共出现多少个直角三角形?数学世界推门与加水爱迪生成名以后,去拜访他的人很多,但客人们都感到爱迪生家的大门很重,推门很吃力.后来,一位朋友对他说:“你有没有办法让你家的大门开关起来省力一些?”爱迪生边笑边回答:“我家的大门做得非常合理,我让那个门与一个打水装置相连接,来访的客人,每次推开门都可以往水槽加20升水.”不仅如此,爱迪生还在想,如果每次推门能向水槽加入25升水的话,那么比原来少推12次门,水槽就可以装满了.你能算出爱迪生家水槽的容积吗?答案:1.70°2.B 点拨:设这个三角形的三个内角分别为x°、2x°、3x°,则x+2x+3x=180,解得x=30.∴3x=90.∴这个三角形是直角三角形,故选B.3.90 点拨:由三角形内角和定理知∠A+∠B+∠C=180°,又∠B+∠C=∠A,•∴∠A+∠A=180°,∴∠A=90°.4.C5.280 点拨:由三角形内角和定理知,∠1+∠2=180°-40°=140°,•∠3+•∠4=180°-40°=140°.∴∠1+∠2+∠3+∠4=140°×2=280°.6.60;607.解:设∠B=x,则∠A=14x.由三角形内角和定理,知∠C=180°-54x.而∠A≤∠C≤∠B.所以14x≤180°-54x≤x.•即80°≤x≤120°.8.解:设∠ABC=∠C=x°,则∠BAC=4x°.由三角形内角和定理得4x+x+x=180.解得x=30.∴∠BAC=4×30°=120°.∠BAD=180°-∠BAC=180°-120°=60°.∴∠ABD=90°-∠BAD=90°-60°=30°.点拨:∠ABD是Rt△BDA的一个锐角,若能求出另一个锐角∠DAB.就可运用直角三角形两锐角互余求得.9.132°点拨:因为∠BAC=180°-∠B-∠C=180°-66°-54°=60°,且AD•是∠BAC的平分线,所以∠BAD=∠DAC=30°.在△ABD中,∠ADB=180°-66°-30°=84°.在△ADC中,∠ADC=180°-54°-30°=96°.又DE平分∠ADC,所以∠ADE=48°.故∠BDE=∠ADB+∠ADE=84°+48°=132°.10.解:设计方案1:测量∠ABC,∠C,∠CDA,若180°-(∠ABC+∠C)=30°,180°-(∠C+∠CDA)=20°同时成立,则模板合格;否则不合格.设计方案2:测量∠ABC,∠C,∠DAB,若180°-(∠ABC+∠C)=30°,(∠BAD+∠ABC)-180°=20°同时成立,则模板合格;否则不合格.设计方案3:测量∠DAB,∠ABC,∠CDA,若(∠DAB+∠CDA)-180°=30°,(∠BAD+∠ABC)-180°=20°同时成立,则模板合格;否则不合格.设计方案4:测量∠DAB,∠C,∠CDA,若(∠DAB+∠CDA)-180°=30°,180°-(∠C+∠CDA)=20°同时成立,则模板合格;否则不合格.点拨:这是一道几何应用题,借助于三角形知识分析解决问题,•对形成用数学的意识解决实际问题是大有益处的.11.解法1:∵∠B+∠C+∠BAC=180°,∠B=75°,∠C=45°,∴∠BAC=60°.∵AE平分∠BAC,∴∠BAE=∠CAE=12∠BAC=12×60°=30°.∵AD是BC上的高,∴∠B+∠BAD=90°,∴∠BAD=90°-∠B=90°-75°=15°,∴∠DAE=∠BAE-∠BAD=30°-15°=15°.•在△AEC中,∠AEC=180°-∠C-∠CAE=180°-45°-30°=105°.解法2:同解法1,得出∠BAC=60°.∵AE平分∠BAC,∴∠EAC=12∠BAC=12×60°=30°.∵AD是BC上的高,∴∠C+∠CAD=90°,∴∠CAD=90°-45°=45°,∴∠DAE=∠CAD-•∠CAE=45°-30°=15°.∵∠AEC+∠C+∠EAC=180°,∴∠AEC+30°+45°=180°,•∴∠AEC=105°.答:∠DAE=15°,∠AEC=105°.点拨:本节知识多与角平分线的定义,余角的性质,平行线的性质,三角形高的定义综合应用,有时也结合方程组、不等式等代数知识综合应用.求角的度数的关键是把已知角放在三角形中,利用三角形内角和定理求解,或转化为与已知角有互余关系或互补关系求解,有些题目还可以转化为已知角的和或差来求解.12.(1)证明:∵∠BAC=30°,∠C=90°,∴∠ABC=60°.又∵BD平分∠ABC,∴∠ABD=30°.∴∠BAC=∠ABD,∴BD=AD.(2)解法1:∵∠C=90°,∴∠BAC+∠ABC=90°.∴12(∠BAC+∠ABC)=45°.∵BD平分∠ABC,AP平分∠BAC,∴∠BAP=12∠BAC,∠ABP=12∠ABC;即∠BAP+∠ABP=45°,∴∠APB=180°-45°=135°.解法2:∵∠C=90°,∴∠BAC+∠ABC=90°.∴12(∠BAC+∠ABC)=45°.∵BD平分∠ABC,AP平分∠BAC,∴∠DBC=12∠ABC,∠PAC=12∠BAC,∴∠DBC+∠PAD=45°.∴∠APB=∠PDA+∠PAD=∠DBC+∠C+∠PAD=∠DBC+∠PAD+∠C=45°+90°=135°.13.解:由∠A=13∠B=15∠C知,∠B=3∠A,∠C=5∠A.设∠A=x°,则∠B=3x°,∠C=5x°.由三角形内角和定理得x+3x+5x=180.解得x=20.∴3x=60,5x=100.∴∠A=20°,∠B=60°,∠C=100°.点拨:解此类题,一般设较小的角为未知数.14.解:(1)∵∠A=42°,∴∠ABC+∠ACB=180°-∠A=138°.∵BD、CD平分∠ABC、∠ACB的平分线.∴∠DBC=12∠ABC,∠DCB=12∠ACB.∴∠DBC+∠DCB=12(∠ABC+∠ACB)=12×138°=69°.∴∠BDC=180°-(∠DBC+∠DCB)=180°-69°=111°.(2)∠BDC=90°+12∠A.理由:∵BD、CD分别为∠ABC、∠ACB的平分线,∴∠DBC=12∠ABC,∠DCB=12∠ACB.∴∠DBC+∠DCB=12(∠ABC+∠ACB)=12(180°-∠A)=90°-12∠A.∴∠BDC=180°-(∠DBC+∠DCB)=180°-(90°-12∠A)=90°+12∠A.点拨:欲求∠BDC,只要求出∠DBC+∠DCB即可.15.解:作出BC边上的高AD时,图中出现3个直角三角形;作出△ABD中AB边上的高DD1时,图中出现5个直角三角形;作出D n-1D n时,图中共出现(2n+3)个直角三角形.数学世界答案:设原来推门x次可把水槽装满水,由题意,得20x=25(x-12).解得x=60.则水槽容积为20×60=1200(升).。
七年级数学下7.2.1三角形的内角

同学们,你们知道其中的道理吗? 三角形中可能有两个直角吗?
(1)一个三角形中最多有 (2)一个三角形中最多有
个直角?为什么? 个钝角?为什么?
(3)一个三角形中至少有
个锐角?为什么?
xo
xo
xo
x
o
xo
xo
150o
2xo
xo
在△ABC中,∠A=35°,∠ B=43 °, 则∠C= .
如图,某同学把一块三角形的玻璃 打碎成三片,现在他要到玻璃店去 配一块形状完全一 样的玻璃, 那么最省事的办法是 ( )
三角形的内角和
内角三兄弟之争
在一个直角三角形里住着三个内角,平 时,它们三兄弟非常团结。可是有一天,老 二突然不高兴,发起脾气来,它指着老大说: “你凭什么度数最大,我也要和你一样 大!”“不行啊!”老大说:“这是不可能 的,否则,我们这个家就再也围不起来 了……”“为什么?” 老二很纳闷。
同学们,你们知道其中的道理吗?
三角形的三个内角和是多少?
你有什么办法可以验证呢? 把三个角拼在一起试试看?
从刚才拼角的过程你 能想出证明的办法吗?
三角形的内角和等于1800.
证法1:延长BC到CD,在△ABC的外部,
以CA为一边,CE为另一边作∠1=∠A, 于是CE∥BA (内错角相等,两直线平行). ∴∠B=∠2 (两直线平行,同位角相等). A 又∵∠1+∠2+∠ACB=180° ∴∠A+∠B+∠ACB=180°
A、锐角△ C、钝角△ B、直角△ D、等腰△
如图∠A+∠B+∠C+∠D+∠E+∠F= ( )
A、180°
B、360°
C、540°
A F E B C
7.2.1 三角形的内角

7.2 与三角形有关的角7.2.1 三角形的内角基础过关作业1.△ABC中,∠A=50°,∠B=60°,则∠C=________.2.已知三角形的三个内角的度数之比为1:2:3,则这个三角形是()A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定3.△ABC中,∠A=∠B+∠C,则∠A=______度.4.根据下列条件,能确定三角形形状的是()(1)最小内角是20°;(2)最大内角是100°;(3)最大内角是89°;(4)三个内角都是60°;(5)有两个内角都是80°.A.(1)、(2)、(3)、(4) B.(1)、(3)、(4)、(5)C.(2)、(3)、(4)、(5) D.(1)、(2)、(4)、(5)5.如图1,∠1+∠2+∠3+∠4=______度.(1) (2) (3)6.三角形中最大的内角不能小于_______度,最小的内角不能大于______度.7.△ABC中,∠A是最小的角,∠B是最大的角,且∠B=4∠A,求∠B的取值范围.8.如图2,在△ABC中,∠BAC=4∠ABC=4∠C,BD⊥AC于D,求∠ABD的度数.综合创新作业9.(综合题)如图3,在△ABC中,∠B=66°,∠C=54°,AD是∠BAC的平分线,DE平分∠ADC交AC于E,则∠BDE=_________.10.(应用题)如图7-2-1-4是一个大型模板,设计要求BA与CD相交成30°角,DA与CB相交成20°角,怎样通过测量∠A,∠B,∠C,∠D的度数,来检验模板是否合格?11.(创新题)如图,△ABC中,AD是BC上的高,AE平分∠BAC,∠B=75°,•∠C=45°,求∠DAE与∠AEC的度数.12.(2005年,福建厦门)如图,已知,在直角△ABC 中,∠C=90°,BD 平分∠ABC 且交AC 于D . (1)若∠BAC=30°,求证:AD=BD ;(2)若AP 平分∠BAC 且交BD 于P ,求∠BPA 的度数.13.(易错题)在△ABC 中,已知∠A=13∠B=15∠C ,求∠A 、∠B 、∠C 的度数.培优作业14.(探究题)(1)如图,在△ABC 中,∠A=42°,∠ABC 和∠ACB•的平分线相交于点D ,求∠BDC 的度数.(2)在(1)中去掉∠A=42°这个条件,请探究∠BDC 和∠A 之间的数量关系.15.(开放题)如图,在直角三角形ABC中,∠BAC=90°,作BC边上的高AD,•图中出现多少个直角三角形?又作△ABD中AB边上的高DD1,这时,图中共出现多少个直角三角形?按照同样的方法作下去,作出D1D2,D2D3,…,当作出D n-1D n时,图中共出现多少个直角三角形?数学世界推门与加水爱迪生成名以后,去拜访他的人很多,但客人们都感到爱迪生家的大门很重,推门很吃力.后来,一位朋友对他说:“你有没有办法让你家的大门开关起来省力一些?”爱迪生边笑边回答:“我家的大门做得非常合理,我让那个门与一个打水装置相连接,来访的客人,每次推开门都可以往水槽加20升水.”不仅如此,爱迪生还在想,如果每次推门能向水槽加入25升水的话,那么比原来少推12次门,水槽就可以装满了.你能算出爱迪生家水槽的容积吗?答案:1.70°2.B 点拨:设这个三角形的三个内角分别为x°、2x°、3x°,则x+2x+3x=180,解得x=30.∴3x=90.∴这个三角形是直角三角形,故选B.3.90 点拨:由三角形内角和定理知∠A+∠B+∠C=180°,又∠B+∠C=∠A,•∴∠A+∠A=180°,∴∠A=90°.4.C5.280 点拨:由三角形内角和定理知,∠1+∠2=180°-40°=140°,•∠3+•∠4=180°-40°=140°.∴∠1+∠2+∠3+∠4=140°×2=280°.6.60;607.解:设∠B=x,则∠A=14x.由三角形内角和定理,知∠C=180°-54x.而∠A≤∠C≤∠B.所以14x≤180°-54x≤x.•即80°≤x≤120°.8.解:设∠ABC=∠C=x°,则∠BAC=4x°.由三角形内角和定理得4x+x+x=180.解得x=30.∴∠BAC=4×30°=120°.∠BAD=180°-∠BAC=180°-120°=60°.∴∠ABD=90°-∠BAD=90°-60°=30°.点拨:∠ABD是Rt△BDA的一个锐角,若能求出另一个锐角∠DAB.就可运用直角三角形两锐角互余求得.9.132°点拨:因为∠BAC=180°-∠B-∠C=180°-66°-54°=60°,且AD•是∠BAC的平分线,所以∠BAD=∠DAC=30°.在△ABD中,∠ADB=180°-66°-30°=84°.在△ADC中,∠ADC=180°-54°-30°=96°.又DE平分∠ADC,所以∠ADE=48°.故∠BDE=∠ADB+∠ADE=84°+48°=132°.10.解:设计方案1:测量∠ABC,∠C,∠CDA,若180°-(∠ABC+∠C)=30°,180°-(∠C+∠CDA)=20°同时成立,则模板合格;否则不合格.设计方案2:测量∠ABC,∠C,∠DAB,若180°-(∠ABC+∠C)=30°,(∠BAD+∠ABC)-180°=20°同时成立,则模板合格;否则不合格.设计方案3:测量∠DAB,∠ABC,∠CDA,若(∠DAB+∠CDA)-180°=30°,(∠BAD+∠ABC)-180°=20°同时成立,则模板合格;否则不合格.设计方案4:测量∠DAB,∠C,∠CDA,若(∠DAB+∠CDA)-180°=30°,180°-(∠C+∠CDA)=20°同时成立,则模板合格;否则不合格.点拨:这是一道几何应用题,借助于三角形知识分析解决问题,•对形成用数学的意识解决实际问题是大有益处的.11.解法1:∵∠B+∠C+∠BAC=180°,∠B=75°,∠C=45°,∴∠BAC=60°.∵AE平分∠BAC,∴∠BAE=∠CAE=12∠BAC=12×60°=30°.∵AD是BC上的高,∴∠B+∠BAD=90°,∴∠BAD=90°-∠B=90°-75°=15°,∴∠DAE=∠BAE-∠BAD=30°-15°=15°.•在△AEC中,∠AEC=180°-∠C-∠CAE=180°-45°-30°=105°.解法2:同解法1,得出∠BAC=60°.∵AE平分∠BAC,∴∠EAC=12∠BAC=12×60°=30°.∵AD是BC上的高,∴∠C+∠CAD=90°,∴∠CAD=90°-45°=45°,∴∠DAE=∠CAD-•∠CAE=45°-30°=15°.∵∠AEC+∠C+∠EAC=180°,∴∠AEC+30°+45°=180°,•∴∠AEC=105°.答:∠DAE=15°,∠AEC=105°.点拨:本节知识多与角平分线的定义,余角的性质,平行线的性质,三角形高的定义综合应用,有时也结合方程组、不等式等代数知识综合应用.求角的度数的关键是把已知角放在三角形中,利用三角形内角和定理求解,或转化为与已知角有互余关系或互补关系求解,有些题目还可以转化为已知角的和或差来求解.12.(1)证明:∵∠BAC=30°,∠C=90°,∴∠ABC=60°.又∵BD平分∠ABC,∴∠ABD=30°.∴∠BAC=∠ABD,∴BD=AD.(2)解法1:∵∠C=90°,∴∠BAC+∠ABC=90°.∴12(∠BAC+∠ABC)=45°.∵BD平分∠ABC,AP平分∠BAC,∴∠BAP=12∠BAC,∠ABP=12∠ABC;即∠BAP+∠ABP=45°,∴∠APB=180°-45°=135°.解法2:∵∠C=90°,∴∠BAC+∠ABC=90°.∴12(∠BAC+∠ABC)=45°.∵BD平分∠ABC,AP平分∠BAC,∴∠DBC=12∠ABC,∠PAC=12∠BAC,∴∠DBC+∠PAD=45°.∴∠APB=∠PDA+∠PAD=∠DBC+∠C+∠PAD=∠DBC+∠PAD+∠C=45°+90°=135°.13.解:由∠A=13∠B=15∠C知,∠B=3∠A,∠C=5∠A.设∠A=x°,则∠B=3x°,∠C=5x°.由三角形内角和定理得x+3x+5x=180.解得x=20.∴3x=60,5x=100.∴∠A=20°,∠B=60°,∠C=100°.点拨:解此类题,一般设较小的角为未知数.14.解:(1)∵∠A=42°,∴∠ABC+∠ACB=180°-∠A=138°.∵BD、CD平分∠ABC、∠ACB的平分线.∴∠DBC=12∠ABC,∠DCB=12∠ACB.∴∠DBC+∠DCB=12(∠ABC+∠ACB)=12×138°=69°.∴∠BDC=180°-(∠DBC+∠DCB)=180°-69°=111°.(2)∠BDC=90°+12∠A.理由:∵BD、CD分别为∠ABC、∠ACB的平分线,∴∠DBC=12∠ABC,∠DCB=12∠ACB.∴∠DBC+∠DCB=12(∠ABC+∠ACB)=12(180°-∠A)=90°-12∠A.∴∠BDC=180°-(∠DBC+∠DCB)=180°-(90°-12∠A)=90°+12∠A.点拨:欲求∠BDC,只要求出∠DBC+∠DCB即可.15.解:作出BC边上的高AD时,图中出现3个直角三角形;作出△ABD中AB边上的高DD1时,图中出现5个直角三角形;作出D n-1D n时,图中共出现(2n+3)个直角三角形.数学世界答案:设原来推门x次可把水槽装满水,由题意,得20x=25(x-12).解得x=60.则水槽容积为20×60=1200(升).。
七年级数学下册《三角形的内角和》典型例题(含答案)

《三角形的内角和》典型例题例1 三角形一个角是第二个角的23倍,第三个角比这两个角的和大30°,求这个三角形的三个角.例2 根据条件,判断ABC ∆的形状(锐角三角形、直角三角形、钝角三角形)(1)︒=∠︒=∠89,76B A(2)C B A ∠=∠+∠(3)C B A ∠=∠︒=∠2,30例3 在ABC ∆中,5:4:3::=∠∠∠C B A ,求ABC ∆各内角的度数.参考答案例1 分析:如果设第二个角是︒x ,则有第一个角是︒)23(x ,第三个角是︒++)3023(x x ,由三角形内角和等于180°可以列出方程,从而求出各个角. 解:设第二个角是︒x ,则第一个角是︒)23(x ,第三个角是︒++)3023(x x ,根据三角形三个内角和是180°,得︒=++++180)3023(23x x x x 解这个方程,得30=x 所以1053023,4523=++=x x x . 答:这个三角形第一个角是45°,第二个角是30°,第三个角是105°.说明:一般在三角形求内角问题时,我们首先应考虑应用三角形三个内角间的关系.例2 分析:三角形中如果有一个内角是钝角(或直角)那么这个三角形一定是钝角三角形(或直角三角形),但是如果有一个内角是锐角,那么它未必是锐角三角形,因为锐角三角形必须是三个内角均为锐角.可以根据三角形内角和定理确定各内角的度数,进而确定三角形的形状.解:(1)︒=︒-︒-︒=∠158976180C ,∴ABC ∆是锐角三角形.(2)∵在ABC ∆中,︒=∠+∠+∠180C B A又C B A ∠=∠+∠ ,∴︒=∠1802C ,︒=∠90C∴ABC ∆是直角三角形.(3)︒=︒-︒=∠+∠15030180C B ,又C B ∠=∠2 ,∴︒=∠1503C ,∴︒=∠50C ,∴︒=︒-︒=∠10050150B ∴ABC ∆是钝角三角形.例3 分析:告诉各内角之间的比例关系,求各内角,可以根据比例关系设未知量,比如本题可以设三个内角分别为3x ,4x ,5x ,这样只要求出x 的值,就可以得知三个内角的度数.要求x 的值可以根据三角形内角和定理列方程.解:设x A 3=∠,则x C x B 5,4=∠=∠∴︒=++180543x x x (三角形内角和定理)∴︒=15x ,∴︒=∠︒=∠︒=∠75,60,45C B A。
初中数学七年级下册第七章《三角形的内角》

新课标人教版初中数学七年级下册第七章《7.2.1三角形的内角》精品教案一.引课:以前在小学,我们就已接触了与三角形有关的知识,那三角形的内角和为多少度呢?(1800)同学们想知道为什么吗?(想).今天,老师将与大家一起研究和讨论“与三角形有关的角”第一节:“三角形的内角”(板书课题)。
二.正课:活动一:结论的证明1.动手操作,发现结论:师:请同学们观看幻灯片,各小组按要求亲自动手实验,你能得到什么结论?幻灯片(一):幻灯片一剪下内角,动手拼拼看,三个内角是否为180度。
生:动手实验,并将自己的做法展示给大家。
(实物投影)。
注:一名学生亲自演示,一名与师进行师生合作。
最后得出结论:三角形内角和等于180度。
(师板书)师:演示幻灯片(二):进一步从直观感性上确定结论的正确性。
2.数学证明,验证结论:师:同学们观察和总结的非常棒,但这只是实验,而观察与实验得到的结论不一定正确,可靠,这样就需要通进数学证明来验正结论是否正确,请同学们结合幻灯片(二),交流讨论说明结论为什么成立。
生:交流讨论。
师:将图画在黑板上,并巡视指导。
生:总结汇报,说明结论成立的理由。
师:同学们表达的十分准确,理由也很充分,但数学还需要书写规范的过程,接下师板演过程。
证明:延长BC ,过点C 做CD ∥AB。
有:∠1=∠A ∠B=∠2A BB幻灯片二因为:∠1+∠2+∠ACB=1800所以:∠A+∠B+∠ACB=18003.方法赏析,巩固结论。
师;同学们还有其他的方法吗?请大家观察幻灯片(三):生:在所给卡片上结合自己的能力仿照板书,选择完成证明过程。
师:有选择的展示汇报。
4.新知应用:幻灯片(四):幻灯片三幻灯片四5.跟踪小练:幻灯片(五):幻灯片五活动二:结论的应用。
1.自学指导,例题解析:师:同学们对“三角形内角和为1800”掌握已经非常牢固了,下面请同学们结合所学知识,按照自学指导完成例题的自学任务,比一比,谁理解的最好。
72与三角形有关的角-721三角形的内角教案人教新课标七年级下

7.2与三角形有关的角
7.2.1三角形的内角
教学目标
1 经历实验活动的过程,得出三角形的内角和定理,能用平行线的性质推出这一定理
2 能应用三角形内角和定理解决一些简单的实际问题
重点:三角形内角和定理
难点:三角形内角和定理的推理的过程
课前准备
每个学生准备好二个由硬纸片剪出的三角形
教学过程
一、做一做
1在所准备的三角形硬纸片上标出三个内角的编码
2 让学生动手把一个三角形的两个角剪下拼在第三个角的顶点处,用量角器量出BCD ∠的度数,可得到
180=∠+∠+∠ACB B A
3 剪下A ∠,按图(2)拼在一起,从而还可得到
180=∠+∠+∠ACB B A
图2
4 把B ∠和C ∠剪下按图(3)拼在一起,用量角器量一量MAN ∠的度数,会得到什么结果。
二想一想
如果我们不用剪、拼办法,可不可以用推理论证的方法来说明上面的结论的正确性呢? 已知ABC ∆,说明
180=∠+∠+∠C B A ,你有几种方法?结合图(1)、图(2)、图(3)
能不能用图(4)也可以说明这个结论成立
二、例题如图,C 岛在A 岛的北偏东 50方向,B 岛在A 岛的北偏东
80方向,C 岛在B 岛
的北偏西 40方向,从C 岛看A 、B 两岛的视角ACB 是多少度?
练习:课本P80,练习1,2
作业:P81
1,2,3,4,5
补充练习
1 三角形中最大的角是 70,那么这个三角形是锐角三角形( )
2 一个三角形中最多只有一个钝角或直角( )
3 一个等腰三角形一定是锐角三角形( )
4 一个三角形最少有一个角不大于 60( )。
7.2.1三角形的内角

∴ ∠ RPC= ∠ B(两直线平行,同位角相等) (两直线平行,同位角相等) ∠ QPB= ∠ C(两直线平行,同位角相等) (两直线平行,同位角相等) ∠ QPR= ∠ 1, ∠ A= ∠ 1 Q
∴ ∠ QPR= ∠ A 1 ∵ ∠ QPB+ ∠ QPR + ∠ RPC=180 ° (1平角 平角=180 ° ) 平角
E
A
B
C
试一试
☞
R
根据下面的图形,写出相应的证明 根据下面的图形 写出相应的证明. 写出相应的证明 A Q B P (1) Q M B
(3)
“行家” 行家” 行家 门道” 看“门道”
A
S
Q C
S
P T
N
R B P T C
N
M
C
A R
(2)
你还能想出其它证法吗? 你还能想出其它证法吗
证明:过点 作 证明:过点P作PQ ∥ AC交AB于Q点, 交 于 点 作PR ∥ AB交AC于R点。 交 于 点
想一想
三角形的三个内角和是多少? 三角形的三个内角和是多少?
1、度量法
1、度量法
90 +60 +30 =180
0
0
0
0
900+450+450=1800
740+370+690=1800
三角形的三个内角和等于180° 三角形的三个内角和等于180° 180
180° °
你有什么办法可以验证呢? 你有什么办法可以验证呢 把三个角拼在一起试试看? 把三个角拼在一起试试看?
北 北 D C E
.
40° °
A
.
80° ° 50° °
七年级数学下册三角形的内角和外角练习题

七年级数学下册三角形的内角和外角练习题1. 小明正在学习三角形的内角和外角,以下是一些练习题帮助他巩固理解和加深记忆。
题1:已知三角形ABC,∠A = 45°,∠B = 60°。
求∠C的度数。
题2:三角形DEF中,∠D = 75°,∠E = 45°。
求∠F的度数。
题3:三角形GHI中,∠G = 120°,∠H = 30°。
求∠I的度数。
题4:三角形JKL中,∠J = 65°,∠L = 45°。
求∠K的度数。
题5:三角形MNO中,∠M = 70°,∠O = 40°。
求∠N的度数。
题6:三角形PQR中,∠Q = 85°,∠R = 65°。
求∠P的度数。
题7:已知三角形STU,∠S = 55°,∠T = 95°。
求∠U的度数。
题8:已知三角形VWX,∠V = 75°,∠W = 30°。
求∠X的度数。
解答:题1:∠A + ∠B + ∠C = 180°(三角形内角和定理)45° + 60° + ∠C = 180°105° + ∠C = 180°∠C = 75°题2:∠D + ∠E + ∠F = 180°75° + 45° + ∠F = 180°120° + ∠F = 180°∠F = 60°题3:∠G + ∠H + ∠I = 180°120° + 30° + ∠I = 180°150° + ∠I = 180°∠I = 30°题4:∠J + ∠K + ∠L = 180°65° + ∠K + 45° = 180°110° + ∠K = 180°∠K = 70°题5:∠M + ∠N + ∠O = 180°70° + ∠N + 40° = 180°110° + ∠N = 180°∠N = 70°题6:∠P + ∠Q + ∠R = 180°∠P + 85° + 65° = 180°∠P + 150° = 180°∠P = 30°题7:∠S + ∠T + ∠U = 180°55° + 95° + ∠U = 180°150° + ∠U = 180°∠U = 30°题8:∠V + ∠W + ∠X = 180°75° + 30° + ∠X = 180°105° + ∠X = 180°∠X = 75°2. 通过以上练习题,小明巩固了对三角形内角和外角的理解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.2.1 三角形的内角
(检测时间50分钟满分100分)
班级________ 姓名_________ 得分______
一、选择题:(每小题3分,共21分)
1.如果三角形的三个内角的度数比是2:3:4,则它是( )
A.锐角三角形
B.钝角三角形;
C.直角三角形
D.钝角或直角三角形
2.下列说法正确的是( )
A.三角形的内角中最多有一个锐角;
B.三角形的内角中最多有两个锐角
C.三角形的内角中最多有一个直角;
D.三角形的内角都大于60°
3.已知三角形的一个内角是另一个内角的2
3
,是第三个内角的
4
5
,则这个三角形
各内角的度数分别为( )
A.60°,90°,75°
B.48°,72°,60°
C.48°,32°,38°
D.40°,50°,90°
4.已知△ABC中,∠A=2(∠B+∠C),则∠A的度数为( )
A.100°
B.120°
C.140°
D.160°
5.已知三角形两个内角的差等于第三个内角,则它是( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.等边三角形
6.设α,β,γ是某三角形的三个内角,则α+β,β+γ,α+γ中 ( )
A.有两个锐角、一个钝角
B.有两个钝角、一个锐角
C.至少有两个钝角
D.三个都可能是锐角
7.在△ABC中,∠A=1
2
∠B=
1
3
∠C,则此三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
二、填空题:(每小题3分,共15分)
1.三角形中,若最大内角等于最小内角的2倍,最大内角又比另一个内角大20°,则此三角形的最小内角的度数是________.
2.在△ABC中,若∠A+∠B=∠C,则此三角形为_______三角形;若∠A+∠B<∠C,则此三角形是_____三角形.
3.已知等腰三角形的两个内角的度数之比为1: 2, 则这个等
腰三角形的顶角为_______.
4.在△ABC中,∠B,∠C的平分线交于点O,若∠BOC=132°,则
∠A=_______度.
5.如图所示,已知∠1=20°,∠2=25,∠A=35°,则∠BDC的度
数为________.
三、基础训练:(每小题15分,共30分)
1.如图所示,在△ABC中,AD⊥BC于D,AE平分∠BAC(∠C>∠
B),
试说明∠EAD=1
2
(∠C-∠B).
2
1
D
A
D C
B A
2.在△ABC 中,已知∠B-∠A=5°,∠C-∠B=20°,求三角形各内角的度数.
四、提高训练:(共15分)
如图所示,已知∠1=∠2,∠3=∠4,∠C=32°,∠D=28°,求∠P 的度数.
4
3P
2
1D
C
B
A
五、探索发现:(共15分)
如图所示,将△ABC 沿EF 折叠,使点C 落到点C ′处,试探求∠1,∠2与∠C 的关系.
2
1
C 'F
E
C B
A
六、中考题与竞赛题:(共4分)
(2001·天津)如图所示,在△ABC 中,∠B=∠C,FD ⊥BC,DE ⊥AB, ∠AFD=158°, 则∠EDF=________度.
答案:
一、1.A 2.C 3.B 4.B 5.C 6.C 7.B
二、1.40° 2.直角 钝角 3.36°或90° 4.84 5.80° 三、1.解:∵AD ⊥BC,
∴∠BDA=90°,
∴∠BAD=90°-∠B, 又∵AE 平分∠BAC,
F
E
A
∴∠BAE=1
2
∠BAC=
1
2
(180°-∠B-∠C),
∴∠EAD=∠BAD-∠BAE
=90°-∠B-1
2
(180°-∠B-∠C)
=90°-∠B-90°+1
2
∠B+
1
2
∠C
=1
2
∠C-
1
2
∠B
=1
2
(∠C-∠B).
2.∠A=50°,∠B=55°,∠C=75.
四、∠P=30°
五、解:∵∠1=180°-2∠CEF,∠2=180°-2∠CFE,
∴∠1+∠2=360°-2(∠CEF+ ∠CFE)
=360°-2(180°-∠C)
=360°-360°+2∠C=2∠C.
六、68.。
