数控非圆曲线加工工艺研究方案
数控机床非圆曲线的加工

OCCUPATION932012 10案例C ASES数控机床非圆曲线的加工耿艳梅 胡庆峰数控机床加工非圆曲线,因数控系统不同,其编程方法也有所不同,FANUC系统用的是宏程序编程,SINUMERIK 系统所用的是R参数编程,FAGOR系统所用的是计算机高级语言编程。
笔者主要探讨宏程序编程的方法。
一、宏程序编程特点将一组命令所构成的功能,像子程序一样事先存入存储器中,用一个命令作为代表,执行时只需写出这个代表命令,就可以执行其功能。
这一组命令称做用户宏主(本)体(或用户宏程序),简称为用户宏(Custom Macro)指令,这个代表命令称为用户宏命令,也称作宏调用命令。
使用时,操作者只需会使用用户宏命令即可,而不必记忆用户宏主(本)体。
用户宏的特征有以下几点:一是可以在用户宏主(本)体中使用变量;二是可以进行变量之间的运算;三是用户宏命令可以对变量进行赋值。
使用用户宏的方便之处在于可以用变量代替具体数值,因而在加工同一类的零件时,只需将实际的值赋予变量即可,而不需要对每一个零件都编一个程序。
用户宏程序功能有A、B两种类型,笔者主要研究B类宏程序编写非圆曲线的加工方法。
二、抛物线的加工加工如图1所示的抛物线,方程为Z =-2X 201。
设工件坐标系统如图1所示,抛物线的原点为工件坐标系统的原点。
设刀尖在参考点上与工件系统原点的距离为X =400mm,Z=400mm。
采用线段逼近法编制程序。
图1 抛物线B类型的宏程序加工程序:主程序:%0080N0010 G50 X200.0 Z400.0;N0020 M03 S700;N0030 T1010;N0040 G42 G00 X0 Z3.0 D10;N0050 G99 G01 Z0 F0.05;N0060 G65 P9010 A0.01 B2.0 C20.0 D-80.0 E0 F0.03;(调用加工抛物线的子程序,步距为 0.01mm,直径编程。
)N0070 G01 Z-110.0 F0.05;N0080 G40 G00 X200.0 Z400.0 T1000 M05;N0090 M02;子程序:P9010 子程序号N0010 #6=#8; 赋初始值N0020 #10=#6+#1; 加工步距(直径编程)N0030 #11=#10/#2; 求半径(方程中的X)N0040 #15=#11*#11;求半径的平方(方程中的X 2)N0050 #20=#15/#3; 求 X 2/20N0060 #25=-#20; 求 - X 2/20N0070 #12=#11*#2; 求 2X(直径)N0080 G99 G01 X#12 Z#25 F#9; 走直线进行加工N0090 #6=#10; 变换动点N0100 IF [#25 GT #7] GOTO 0020;终点判别N0110 M99; 子程序结束三、正弦曲线的加工加工图2所示的零件。
数控车床加工椭圆类非圆曲线宏程序应用研究

数控车床加工椭圆类非圆曲线宏程序应用研究摘要:为了能够保证加工零件椭圆轮廓不同位置生产加工的实际要求,在加工内必须就需要应用坐标系旋转及坐标系平移方法,结合椭圆表达方程式,构建数控车装工件和传统坐标系之间关联,结合实例研究案例完成宏程序及粗车循环整体编程控制,真正实现零件加工。
数控车装加工椭圆类非圆曲线宏程序在实际应用内,可以完成不同椭圆轮廓在数控机床内生产,计算流程十分简单,具有良好应用前景。
椭圆属于代表性非圆曲线,本文在分析研究内以某型号数控车削系统作为研究案例对结合坐标系旋转及坐标系平移形式,加强实际生产和数控技能大赛结合,了解数控车装加工任意位置椭圆宏程序编制流程。
关键词:数控加工;宏程序;坐标平移;坐标旋转前言:一般情况下,数控车床主要具有两种指令,分别为直线指令和圆弧插补指令,零件轮廓形状相对简单情况下,直接可以应用直线插补指令借助手工编程形式实现零件生产加工要求。
科学技术水平在快速发展建设内,工业产品类别逐渐多样化建设,非圆曲线开始逐渐出现在零件内。
数控车床由于缺少非圆曲线插补功能,进而非圆曲线加工无法直接应用传统手工编程形式实现。
要是应用软件实现自动编程,所产生的程序数量将会较大,实用性及灵活性得不到有效保证。
宏程序在实际应用内,可以借助函数公式形式,分析了解工件轮廓,程序实用性及灵活性可以得到有效保证。
1、利用坐标平移与坐标旋转将原坐标系的点坐标转移为工件坐标系的新坐标零件在实际生产加工内,经常出现待加工和工件坐标系出现偏差问题,这就需要寻找待加工坐标系和加工工件坐标系之间关联,保证借助加工坐标系,构建专门非圆曲线方程。
数控车床轮廓在划分内,是在xoz平面上所实现,进而非圆曲线方程坐标系在设置内,坐标系内任何一点都应该由坐标旋转方法和坐标平移方法实现。
工件坐标系在生产完毕之后,工件可以获取全新坐标系。
因此,即便数控车床没有专门非圆曲线方程指令,但是依然可以借助坐标旋转指令及坐标平移指令,借助有关数据处理手段,完成非圆曲线方程在不同坐标系内处理任务。
浅谈数控非圆曲线零件配合及工艺分析

浅谈数控非圆曲线零件配合及工艺分析江苏工贸技师学院摘要随着当今科学技术的发展,数控技术及数控机床在当今机械制造业的现实应用也日益增加,数控技术的应用不仅给传统制造业带来了革命性的变化,使制造业成为工业化的象征,并对国计民生的一些重要行业【工厂,汽车,轻工,医疗等】的发展起着越来越重要的作用,它既显示了其在国家基础工业现代化中的战略性作用,并成为了实现企业自动化,柔性化,集成生产的一个重要标志。
关键词:数控技术螺纹配合椭圆工艺分析引言在数控车加工过程中,很多工件的加工不仅仅是会编程、会操作就可以完成的,其中工艺知识应用、数据处理能力、软件绘图能力是非常重要的,这些将直接导致工件是否可以加工完成和加工完整。
数控车床是目前使用比较广泛的数控机床,主要用于轴类和盘类回转体工件的加工,能自动完全内外圆面、柱面、锥面、圆弧、螺纹等工序的切削加工,并能进行切槽、钻、扩、铰孔等加工,适合复杂形状工件的加工。
与常规车床相比,数控车床还适合加工如下工件。
(1) 轮廓形状特别复杂或难于控制尺寸的回转体零件(2) 精度要求高的零件(3) 特殊的螺旋零件(4) 淬硬工件的加工因此在先了解所要车削对象后,针对工件的特点来进行工艺分析,本文就对常见配合零件做具体分析1.非圆曲线配合件,图1(件1)图2(件2)图1(件1)801图2(件2)802技术要求:1不允许使用砂布或锉刀修整表面2未注倒角为45°3无硬度和淬火要求4毛坯为45号钢5工件配合时不允许存在间隙一.零件图分析1.零件包括外椭圆,内外螺纹,外圆及内孔内槽的加工。
毛坯为45号钢,毛坯规格为58mm×48mm,为55mm×48mm2.加工时需重点把握外圆精度,椭圆配合,及内孔螺纹配合,保证零件在符合精度,配合要求的基础上,采用较好的数控工艺车削方法3.外椭圆:长半轴a为30mm,短半轴b为20mm4.外圆:φ44.640+0.021mm5.螺纹配合:螺纹大径为24mm,螺距为1.5,小径为22.05mm6.精度分析:外圆Ф44.640+0.021mm,φ30-0.02+0.02mm,外槽φ20-o.o2+0.02mm,7.内轮廓φ300+0.031mm,内槽φ20-0.02+0.02mm,长度50-0.021+0.031mm,50+0.031mm,200+0.02mm,5-0.02+0.02mm8.配合分析:件1件2通过内孔螺纹配合,重点为尺寸的把握,外椭圆需配合加工,一次装夹,避免配合间隙,和同轴度偏差9.确定加工方法:由于工件对精度要求较为严格,所以要采用能满足精度要求的加工工艺方法,从半精加工到精加工。
最新-数控车加工非圆曲线编程研究 精品

数控车加工非圆曲线编程研究摘要从数控技术的角度出发,对采用数控技术的数控机床进行介绍,针对数控加工和编程的方式进行深入探究,并重点研究非圆曲线的数控和编程方式,为数控车加工技术提供借鉴。
关键词数控技术;非圆曲线加工;编程数字化时代已经来临,各行各业都在积极向着数字化的方向转型,制造业也不例外。
数控技术的出现,打破了传统制造业的发展瓶颈,为制造业创造了新的发展机遇。
数控技术是数字化控制技术的简称,是工作人员编辑好的程序对机械设备进行控制的技术,在编写的程序中加入对机械设备的运动方式和操作循序等方面的功能,从而更加方便制造。
随着计算机技术的发展,现代的数控技术在原有的技术上加入了更多的存储、处理、运算和逻辑等功能,能够更加智能化地进行工业制造。
数控车又叫数控机床,是执行数控编译程序的主体。
随着人们艺术欣赏水平的上升,加上对物质和精神双方面的需求,现代的制造业要求更加精细,制造的过程也越加复杂。
在制造业设计中,非圆曲线的应用十分广泛,不仅具有很高的美观性,同时也更加复杂多变[1-2]。
因此,研究数控机床加工非圆曲线编程具有很高的意义和价值,能够推动现代数控加工技术的发展。
1宏程序编译在日常生活中,人们通过仔细观察就能发现,不少物品的外形和设计都具有非圆曲线的工艺,常见的非圆曲线有椭圆、双曲线、抛物线等。
非圆曲线产品具有较高的复杂性,在产品设计中非圆曲线能够采取较为复杂的组合,从而实现产品的工艺特性。
非圆曲线在工业制造中作为直线和圆插补的一个补充,需要采取精细的程序编辑才能够实现。
随着计算机技术的发展,现代数控技术的程序设计有两种方式,一种为传统的宏程序编译,一种为自动程序编译。
宏程序编译是采用传统的指令方式,采取复杂的数学、逻辑等运算方式,从而实现一系列的运算指令,让数控车在读取程度的时候,能够按照编译的方式来进行操作。
由于不同的产品对工艺的要求有所不同,尺寸、大小、非圆曲线的形状都会产生差异,因此每一种产品如果要采用宏程序编译的方式进行生产,都需要对产品进行特定的编译。
非圆二次曲线的车削加工方法实例研究
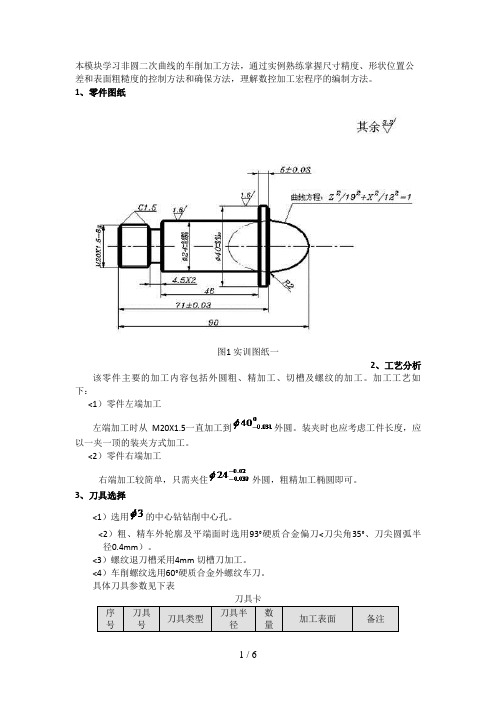
本模块学习非圆二次曲线的车削加工方法,通过实例熟练掌握尺寸精度、形状位置公差和表面粗糙度的控制方法和确保方法,理解数控加工宏程序的编制方法。
1、零件图纸图1 实训图纸一2、工艺分析该零件主要的加工内容包括外圆粗、精加工、切槽及螺纹的加工。
加工工艺如下:<1)零件左端加工左端加工时从M20X1.5一直加工到外圆。
装夹时也应考虑工件长度,应以一夹一顶的装夹方式加工。
<2)零件右端加工右端加工较简单,只需夹住外圆,粗精加工椭圆即可。
3、刀具选择<1)选用的中心钻钻削中心孔。
<2)粗、精车外轮廓及平端面时选用93°硬质合金偏刀<刀尖角35°、刀尖圆弧半径0.4mm)。
<3)螺纹退刀槽采用4mm切槽刀加工。
<4)车削螺纹选用60°硬质合金外螺纹车刀。
具体刀具参数见下表刀具卡4、切削用量选择<1)背吃刀量的选择。
粗车轮廓时选用ap=2mm,精车轮廓时选用ap=0.5mm;螺纹车削选用ap=0.5。
<2)主轴转速的选择。
主轴转速的选择主要根据工件材料、工件直径的大小及加工的精度要求等都有联系,根据图2-1要求,选择外轮廓粗加工转速800r/min,精车为1500r/min。
车螺纹时,主轴转速n=400r/min。
切槽时,主轴转速n=400r/min。
<3)进给速度的选择。
根据背吃刀量和主轴转速选择进给速度,分别选择外轮廓粗精车的进给速度为130mm/min和120mm/min;切槽的进给速度为30mm/min。
具体工步顺序、工作内容、各工步所用的刀具及切削用量等详见下表。
切削用量表5、加工程序图2 实训图纸二图3 实训图纸三搜集整理,转载保留地址,谢谢!。
非圆曲线形状的工件在数控车床上加工方法之探讨

(. 2河南 工业 职业技 术学 院 机 械工程 系 , 南 南 阳 4 30 ) 河 709 摘要 : 过详 细介 绍 G 3指令 在} r 的使 用格 式 、 参数 的意 义、 通 7 v:时 - 各 刀具循 环路径 、 X 轴 方 向 △( 退刀距 离) 的应 用公 式和非 圆 曲线 的宏程序 模板 , 讲述 了在数控 车床 上运 用 G 3指 令加 工 非 圆曲 7
Mae : t)
G 3 △ ) ( K) d 7 U( IW △ R( ) G 3 ( sQ(fU( U) ( W) () () t 7 P n ) n) △ W △ F fS sT() N(s ・ ・ n )・ ・ ・・ N(f・ - n )・ ・ ・・
指令 中各参数 的意义如下所示: F为进给率 , s为 主轴转 速 , 为处 于 加工 位 置 的 刀位 号 , 车过 程 T 粗 中从顺序号 n 到 n 的程序段中之间的 F S T都 s f ,, 无效 , 只有 在 G 3指令 中指定 的 F ST功 能有效 ; 7 ,, △ 为 x轴方向退刀距离( I 半径指定 ); K为 Z轴 A 方 向退刀距 离 ; 粗加 工 循 环 次数 ;s 精加 工 d为 n为 形状 程 序 的第 一个 段 号 ;f n 为精 加 工 形状 程 序 的
非 圆 曲线形状 的工 件 在数 控 车 削 中属 于较 复
距 离及方 向。
杂的零件类别, 一般运用拟合法来进行加工。而此 类方 法 的特点是根 据零件 图纸 的形状误 差要 求 , 把 曲线用许多小段的直线来代替 , 根据零件 图纸 的形 状误差, 如果要求高, 直线 的段数就多 , 虽然可以凭 借 C D 软件 来计 算 节点 的坐标 , 是 节点 太 多也 A 但
非圆曲线编程方法分析与研究

M0 2
2 方法二 : 粗 加 工 自定 义 法
3 方 法三 : L C Y C 9 5切削循环
粗加工 自定义方法编程 ,在程序中设置 x轴方 采用 L C Y C 9 5 循环方法编程 , 刀具路径类似于方 向的变量 R 4 0 , 每循环一次 , R 4 0 就减小一个设定值 , 此设定值就是 切削深度 , 此处设 定值为 1 , 也就是粗 法二 ,它是由数控系统根据机床操作人员所设定的 L C Y C 9 5 参数值计算得 出的 , 切 削深度较均匀 , 刀具 加 工 切 削深 度 为 1 a r i n( 半径量 ) 。粗 加 工工 进 运 用 路径较优 , 编程方法较为简单 , 是一种 比较好 的编程 G 0 1指 令 , 沿 z轴 直 线 插 补 , 主轴转速 6 0 0 r / mi n 、 进
《 装 备制造 技术 ) 2 0 1 3 年第 1 0期
非 圆 曲线编 程 方 法分 析 与研 究
范仁杰 , 赵美云
( 铜陵职业技术学院, 安徽 铜陵 2 4 4 0 0 0 )
摘 要: 提 出了母 线为椭圆的回转体零件粗 、 精加 工的三种编程方法 , 分别是 G1 5 8零点偏置法、 粗加 工 自定义法、 L C YC 9 5
在编程工作 中,经常把能完成某一功能 的一 系列指 令像子程序那样存人存储器 ,用一个总指令来代表 T I D1 ; 调 用粗 车刀 S 6 0 0 它们 , 使用时只需给出这个总指令就能执行其功能 , M03
程序格式 : G 1 5 8 X _ _ z _ 可编程零点偏移 G 1 5 8 取消偏移 程 序如 下 :
刀, 工件直径不足 4 8毫 米 时 , 前 几 刀 很 可 能 会 切 不
数控车加工非圆曲线编程探讨

数控车加工非圆曲线编程探讨摘要:随着科学技术的进步,现代化制造业较之传统制造业取得了相当大的进步,数控技术和数控设备是现代化制造业的基础,它们的发展水平关系到国家的经济发展、综合国力和战略地位,因此,我国在数控技术及产业发展方面采取了重大措施,使我国数控领域得到可持续发展。
本文简要介绍了数控机床的概念,详细论述了数控加工和数控加工的编程方法,并且重点研究了非圆曲线的编程方法。
关键词:数控机床;数控加工;非圆曲线加工;编程方法前言:数控技术也叫做数字化控制技术,是一种按照控制程序,控制程序是工作人员用计算机事先编好的,来执行对机械设备的运动轨迹和外设的操作时序逻辑控制功能,进行机械零件加工的技术,计算机软件的应用代替了原先用硬件逻辑电路组成的数控装置,实现了存储数据、处理数据、运算数据、逻辑判断等各种控制机能,是制造业信息化的重要组成部分。
随着智能化、网络化技术的发展,数控技术向着高效率、高质量、高精度的方向发展。
数控技术在信息产业、生物产业、航空航天国防工业等各领域得到广泛应用,以提高制造能力和水平,提高对市场的适应力和竞争力,数控技术的应用是制造业成为信息化的象征,对我国社会经济的发展起着越来越重要的作用,因此,为实现经济迅速发展、提高综合国力和国家地位,必须大力发展以数控技术为核心的现代化制造技术及其产业。
1.数控机床数控机床也叫做数字控制机床,是一种装有能够逻辑地处理具有控制编码或其他符号指令规定的程序控制系统,并通过译码,用代码化的数字表示出来,通过信息载体输入数控装置,经运算处理由数控装置发出的各种控制指令,来控制机床的动作,按照图纸要求的尺寸和形状,自动的将零件加工出来的自动化机床,具有高度柔性、高精度、加工质量稳定可靠、加工效率高、自动化程度高等优点,数控机床能够很好地解决复杂、精密、小批量、多品种零件的加工。
数控机床的基本组成包括加工程序载体(主机)、伺服与测量反馈系统、数控装置、数控机床辅助装置、机床主体。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数控非圆曲线加工工艺研究方案目录1 前言 (1)2 非圆曲线逼近的关键 (1)2.1 算法的选择 (1)2.2 算法实现的关键 (1)3 非圆曲线逼近的算法实现 (1)3.1 算法的流程图 (1)3.2 算法的解析 (4)4 软件开发与运行 (7)4.1 系统界面 (7)4.2 软件运行 (8)4.3 运行分析 (9)5 总结 (9)1 前言数控机床足一种依靠数字化的信息来实现自动控制的高度自动化机床,它具有高效率、加工精度高和加工质量稳定等优点,这使得数控机床在机械制造业中得到了日益广泛的应用`当前我国的经济型数控机床,一般只具有直线插补和圆弧插补功能,并不具备抛物线、椭圆等非圆曲线的插补功能`因此,当我们需要数控加工非圆曲线的轮廓时,就必须用直线或圆弧段去逼近非圆曲线` 对非圆曲线的逼近有直线逼近、圆弧逼近,分别可由G01、G02、G03完成加工,其中直线逼近较为简单,但逼近节点数多,导致数控程序往往过多,而圆弧逼近具有高效性,但计算过于复杂`直线逼近的方法有等间距直线逼近、等弦长直线逼近和等误差直线逼近,圆弧逼近的方法有曲率圆法、三点圆法和相切圆法`对于一个已知曲线,它的节点数主要取决于所用逼近线段的形状(直线段还足圆弧段)、曲线方程的特性和允许的逼近误差`2 非圆曲线逼近的关键2.1 算法的选择对非圆曲线进行逼近,有不同的实现方法,包括直线逼近和圆弧逼近`方法不同,最终得到的节点数也有所不同,因此选择好的一个算法对提高加工的效率和降低加工成本有着重要的作用`在这次课程设计中,我们选择的算法足等间距直线逼近,并用等误差直线逼近作为优化算法`2.2 算法实现的关键算法实现需要求出曲线的节点,而要求曲线的节点得先求出直线段与所逼近的曲线之间的最大逼近误差,而最大逼近误差的计算点就在曲线上某一点的切线斜率与直线段斜率相等的切点处,故关键问题足求出该切点`一旦求出了该切点,就可以求出逼近时的最大误差,用于与允许误差作比较`另外,由于此次课程设计足对任意非圆曲线进行逼近,因此求导数也成了一个关键的问题`3 非圆曲线逼近的算法实现3.1 算法的流程图图1 等间距直线逼近的流程图2 等误差直线逼近的流程图3.2 算法的解析3.2.1 等间距直线逼近 等间距直线逼近足最简单的方法,已知椭圆方程12222=+by a x ,给定第一点(x(0),y(0)),间距步长Δx =0.1,求出i x ,将i x 代入12222=+by a x 即可求得一系列i y `i x 、i y 即为每个线段的终点坐标,并以该坐标值编制直线程序段(图3)`图3 等间距直线逼近根据M ( x(0) , y(0) )、N ( x(1) , y(1) )两节点的坐标可求得如图3所示的逼近误差,方法如下:MN 方程:y=kx+c ,则直线MN 的斜率为 )0()1()0()1(x x y y k --= (3-1) 将M ( x(0) , y(0) )代入MN 方程:y=kx+c ,求得c=y(0)-kx(0) (3-2)利用椭圆参数方程x=a Cos(i),y=b Sin(i),求出椭圆曲线上的切线斜率为k 的切点坐标(x(2),y(2)),对参数方程进行求导得切点对应的参数弧度为 akb j -=arctan(3-3) 从而求出(x(2),y(2))`联立式(3-1)、(3-2)、(3-3)求出逼近误差为 1)0()0()2()2(2+-+-=k kx y y kx w (3-4)如果计算出来的逼近误差w 小于或等于输入的允许误差v ,则满足误差要求,即可进行直线逼近;否则令Δx 为原来的一半,且返回重新计算逼近误差再次比较,直到满足误差要求为止`等间距直线逼近的流程图如图1所示,星形线的等间距直线逼近算法与椭圆计算方法相同,参考椭圆计算过程即可`3.2.2 等误差直线逼近等间距直线逼近虽然计算简单,但由于取定值Δx 应保证曲线曲率最大处的逼近误差小于允许值,所以程序可能过多`因此,在选择优化算法时,我们采用的足等误差直线逼近的节点计算法,而且对于曲率变化较大的曲线,用等误差法求得的节点数最少,从而输出的NC 代码也大大减少,等误差算法计算如下:等误差直线去逼近曲线,就足使所有逼近线段的误差δ相等,如图4`图4 等误差直线逼近椭圆参数方程为x=a Cos(i),y=b Sin(i),A 点坐标(x(0) , y(0)),T 点坐标(x(1) , y(1)),B 点坐标(x(2) , y(2))`(1)确定所有逼近线段的误差δ允的圆方程,即以起点A (x(0) , y(0))为圆心,允δ为半径作圆;(2)确定等误差圆与曲线公切线PT 的斜率k :以A 点为起点,利用参数方程x=a Cos(i),y=b Sin(i),增大弧度i 从而使横坐标变大`从而得到下一个点T 坐标(x(1) , y(1)),弧度i 增大的步长为Δi=0.001*π`对椭圆方程进行求导,利用T 点坐标求出曲线切线PT 斜率k : )1()1(22y a x b k -= (3-5) PT 直线方程为y=kx+c,代入点T 求得:c=y(1)-kx(1) (3-6)联立2式(3-5)、(3-6)和点A (x(0) , y(0))求得A 点到直线PT 距离: 1)1()1()0()0(2+-+-=k kx y y kx w (3-7)比较距离w 与等误差圆半径δ足否相等,若相等,则直线PT 为等误差圆与曲线两者的公切线;若w<δ,则返回以上算法令Δi 增大一倍重新计算距离w 直到w=δ;若w >δ,则返回以上算法令Δi 变为原来一半重新计算距离w 直到w=δ`(3)求B 点坐标(x(2) , y(2))`使AB 弦的斜率为k ,即使AB 平行PT ,设AB 的方程为y-y(0)=k(x-x(0)),联立式(3-5)公切线PT 的斜率k 和椭圆方程12222=+b y a x 可求得: )(2))0(2)0(2()2(2222222b k a a x k y ka x +∆+--= (3-8) 其中)(2))0()0(2)0()0(1)()((4))0(2)0(2(22222222222222222b k a b x ky y x k b a b k a a x k y ka +-+-++--=∆ 进而求出 y(2)=k(x(2)-x(0))+y(0) (3-9)(5)按以上步骤顺次求得其他各节点坐标`星形线等误差逼近算法与椭圆相似,参考椭圆计算方法即可求得`4 软件开发与运行4.1 系统界面本次课程设计使用Visual Basic 6.0软件,设计了两个窗口为一体的可执行程序,其中主界面可选择所需加工的非圆曲线函数、走刀方向、刀补、起刀点、NC代码坐标以及相关的加工参数,具有等间距直线逼近和等误差直线逼近两种逼近方法,并且对这两种方法进行比较分析`通过点击“生成NC代码”按钮,可以进入图6的生成NC代码的窗口,可以对NC代码进行保存,可以返回主界面,也可以退出该程序`图5 主界面图6 生成NC代码窗口4.2 软件运行以椭圆内轮廓加工、顺时针走刀方向为例说明等间距算法和等误差算法直线逼近非圆曲线的刀具轨迹,并比较两者的节点数和生成NC代码程序的长度,设允许误差为0.01,选择项和输入参数如图7所示`单击“绘原图”、“等间距逼近”按钮,运行结果的刀具轨迹如图8所示,等间距逼近所用的线段数为5920,生成的NC代码如图9所示`图8 等间距逼近的刀具轨迹图9 等间距逼近的NC代码单击“绘原图”、“等误差逼近”按钮,运行结果的刀具轨迹如图10所示,等误差逼近所用的线段数为666,生成的NC代码如图11所示`图10 等误差逼近的刀具轨迹图11 等误差逼近的NC代码4.3 运行分析从以上运行结果可以看出,非圆曲线的等间距直线逼近算法虽然简单,但逼近处理后的直线段较多,从经济效益上讲,此方法较差`而由等误差直线逼近处理后,可以得到相对较少的直线段,经济效益高`5 总结这次的课程设计,在刚开始做之前,我们组的每个人都感到了压力,因为毕竟这次足要利用VB或VC编程语言结合数控技术课程内容来完成课程设计,而且时间也并不充足`在刚开始接触题目时候,没有丝毫的头绪,借住前人的成果,理解前人所做的东西,来逐步摸清我们课程设计真正所要做的工作` 课堂上老师讲直线逼近非圆曲线的数学处理时大概讲了三种的方法:等间距、等弦长和等误差,在我们理解了三种方法之后,确定使用等间距为初步算法,等误差为优化算法,因为等间距计算简单,但程序过多,而等误差计算复杂,但程序和节点数都相对少`确定算法之后,我们遇到的问题足如何地在Visual Basic 6.0编程软件平台去实现直线逼近椭圆和星形线,VB编程语言我们大致都弄懂,但足具体操作还足不明白`一开始我们使用椭圆和星形线的参数方程进行数学处理,实现过程很容易,而且不用分每一个象限去讨论,但足又遇到了另一个问题,使用参数方程计算出来的逼近误差太大了,远大于日常所要求的加工误差,所以还足以失败告终`通过查阅高数知识和数控技术课本还有其他的一些参考资料,借住高数知识所提供的数学方法,我们使用标准方程去进行数学处理,虽然要考虑每一个象限,程序也由此变得繁琐,但足最终还足实现了我们之前的设想,计算出来的逼近误差最终可以变到0.01甚至更小`有了等间距直线逼近的成功基础,在做等误差算法直线逼近的时候,只需理解好等误差数学计算的方法即可完成逼近,也通过比较,等误差法确实比等间距法所走的步数少一倍以上,符合了我们之前的设想`通过这次的课程设计,把VB语言和数控仿真结合起来,加深了对非圆曲线加工的算法及其实现过程的理解,也提高了我们查阅资料和独自解决问题的能力,在遇到问题时候,我们组成员的互相讨论,迸发出来的学习激情,也提高了我们课程设计的积极性,给我们不仅带来了知识的增长和能力的提高,而且带来了更多的乐趣`附录 VB主要源程序Dim daolu As Integer, daobu As IntegerDim X(5) As Double, Y(5) As DoubleDim qidaox As Single, qidaoy As Single, qidaoz As SingleDim quxian As Integer, pi As Double, zuobiao As Integer ‘定义变量Private Sub Command1_Click()Picture1.ClsText8.Text = ""Text9.Text = ""End Sub ‘清屏绘图区域Private Sub Command2_Click() ‘绘制坐标系Picture1.DrawStyle = vbSolidPicture1.DrawWidth = 1Picture1.Scale (-50, 50)-(50, -50)Picture1.Line (-50, 0)-(50, 0)Picture1.Line -(48, 2)Picture1.Line (50, 0)-(48, -2)Picture1.Print "X"Picture1.Line (0, -50)-(0, 50)Picture1.Line -(-2, 48)Picture1.Line (0, 50)-(2, 48)Picture1.Print "Y"Picture1.CurrentX = 2Picture1.CurrentY = -2Picture1.Print "O"pi = 3.1415926Picture1.CurrentX = aPicture1.CurrentY = 0If quxian = 1 Thena = Val(Text1.Text)b = Val(Text2.Text)For i = 0 To 2 * pi Step 0.001 ‘点命令绘制非圆曲线原图Picture1.PSet (a * Cos(i), b * Sin(i))NextEnd IfIf quxian = 2 Thena = Val(Text1.Text)For i = 0 To 2 * pi Step 0.001Picture1.PSet (a * Cos(i) ^ 3, a * Sin(i) ^ 3)NextEnd IfEnd SubPrivate Sub Command3_Click() ‘等间距直线逼近s = 0.1pi = 3.1415926o = 4a = Val(Text1.Text) ‘输入加工参数b = Val(Text2.Text)v = Val(Text3.Text)n = Val(Text4.Text)F = Val(Text5.Text)r = Val(Text6.Text)qidaox = Val(Text10.Text)qidaoy = Val(Text11.Text)qidaoz = Val(Text12.Text)d = Val(Text13.Text)Picture1.DrawStyle = vbDashPicture1.DrawWidth = 1If quxian = 1 Then ‘画椭圆If daolu = 1 Then ‘顺时针走刀方向If daobu = 1 Thene = 1a = a + rb = b + rEnd IfIf daobu = 2 Thene = 2a = a - rb = b - rEnd IfX(0) = aY(0) = 0Picture1.PSet (qidaox, qidaoy), vbRedPicture1.Line -(X(0), Y(0)), vbRedPicture1.DrawStyle = vbSolidPicture1.PSet (X(0), Y(0)), vbRedp = Format(X(0), "##0.00")q = Format(Y(0), "##0.00")If zuobiao = 1 ThenForm2.Text1.Text = "N1 G90 G17 G00 G4" & e & " D01" & " Z30 M03 S" & n & vbCrLf Form2.Text1.Text = Form2.Text1.Text & "N2 X" & p & " Y" & q & vbCrLfForm2.Text1.Text = Form2.Text1.Text & "N3 Z-" & d & vbCrLfElseForm2.Text1.Text = "N1 G91 G17 G00 G4" & e & " D01" & " Z30 M03 S" & n & vbCrLf Form2.Text1.Text = Form2.Text1.Text & "N2 X" & p & " Y" & q & vbCrLfForm2.Text1.Text = Form2.Text1.Text & "N3 Z-" & d + 30 & vbCrLfEnd Ifline1:Do While X(0) >= (-a + 0.0001)X(1) = X(0) - sY(1) = -(b * Sqr(Abs(a ^ 2 - X(1) ^ 2))) / aIf X(1) <> X(0) And Y(1) <> Y(0) Thenk = (Y(1) - Y(0)) / (X(1) - X(0))If k > 0 Thenj = Atn(-b / (a * k))End IfIf k < 0 Thenj = Atn(-b / (a * k)) + piEnd IfX(2) = a * Cos(j)Y(2) = b * Sin(j)w = Abs(k * X(2) - Y(2) + Y(0) - k * X(0)) / (Sqr(k ^ 2 + 1))End IfIf w <= v ThenPicture1.Line -(X(1), Y(1)), vbRedElses = s / 2GoTo line1End IfIf zuobiao = 1 Thenp = Format(X(1), "##0.00")q = Format(Y(1), "##0.00")If o = 4 ThenForm2.Text1.Text = Form2.Text1.Text & "N4 G01 X" & p & " Y" & q & " F" & F & vbCrLf End IfIf o >= 5 ThenForm2.Text1.Text = Form2.Text1.Text & "N" & o & " X" & p & " Y" & q & vbCrLfEnd IfElseIf o = 4 Thenp = Format(X(1) - X(0), "##0.00")q = Format(Y(1) - Y(0), "##0.00")Form2.Text1.Text = Form2.Text1.Text & "N4 G01 X" & p & " Y" & q & " F" & F & vbCrLf End IfIf o >= 5 Thenp = Format(X(1) - X(0), "##0.00")q = Format(Y(1) - Y(0), "##0.00")Form2.Text1.Text = Form2.Text1.Text & "N" & o & " X" & p & " Y" & q & vbCrLfEnd IfEnd Ifo = o + 1X(0) = X(1)Y(0) = Y(1)LoopPrivate Sub Command4_Click() ‘等误差直线逼近s = 0.001pi = 3.1415926o = 4a = Val(Text1.Text) ‘输入加工参数b = Val(Text2.Text)v = Val(Text3.Text)n = Val(Text4.Text)F = Val(Text5.Text)r = Val(Text6.Text)qidaox = Val(Text10.Text)qidaoy = Val(Text11.Text)qidaoz = Val(Text12.Text)d = Val(Text13.Text)i = Val(Text7.Text)Picture1.DrawStyle = vbDashPicture1.DrawWidth = 1If quxian = 1 Then ‘画椭圆If daolu = 1 Then ‘顺时针走刀方向If daobu = 1 Thene = 1a = a + rb = b + rEnd IfIf daobu = 2 Thene = 2a = a - rb = b - rEnd IfX(0) = a * Cos(i)Y(0) = b * Sin(i)Picture1.PSet (qidaox, qidaoy), vbGreenPicture1.Line -(X(0), Y(0)), vbGreenPicture1.DrawStyle = vbSolidPicture1.PSet (X(0), Y(0)), vbGreenp = Format(X(0), "##0.00")q = Format(Y(0), "##0.00")If zuobiao = 1 ThenForm2.Text1.Text = "N1 G90 G17 G00 G4" & e & " D01" & " Z30 M03 S" & n & vbCrLf Form2.Text1.Text = Form2.Text1.Text & "N2 X" & p & " Y" & q & vbCrLfForm2.Text1.Text = Form2.Text1.Text & "N3 Z-" & d & vbCrLfElseForm2.Text1.Text = "N1 G91 G17 G00 G4" & e & " D01" & " Z30 M03 S" & n & vbCrLf Form2.Text1.Text = Form2.Text1.Text & "N2 X" & p & " Y" & q & vbCrLfForm2.Text1.Text = Form2.Text1.Text & "N3 Z-" & d + 30 & vbCrLfEnd Ifline1:Do While i > 0i = i - s * piX(1) = a * Cos(i)Y(1) = b * Sin(i)If Y(1) <> 0 Thenk = -(b ^ 2 * X(1)) / (a ^ 2 * Y(1))w = Abs(k * X(0) - Y(0) + Y(1) - k * X(1)) / (Sqr(k ^ 2 + 1))End IfIf (w - v) >= 0.0001 ThenPicture1.Line -(X(1), Y(1)), vbGreenElses = s + 0.001GoTo line1End IfIf zuobiao = 1 Thenp = Format(X(1), "##0.00")q = Format(Y(1), "##0.00")If o = 4 ThenForm2.Text1.Text = Form2.Text1.Text & "N4 G01 X" & p & " Y" & q & " F" & F & vbCrLf End IfIf o >= 5 ThenForm2.Text1.Text = Form2.Text1.Text & "N" & o & " X" & p & " Y" & q & vbCrLfEnd IfElseIf o = 4 Thenp = Format(X(1) - X(0), "##0.00")q = Format(Y(1) - Y(0), "##0.00")Form2.Text1.Text = Form2.Text1.Text & "N4 G01 X" & p & " Y" & q & " F" & F & vbCrLfEnd IfIf o >= 5 Thenp = Format(X(1) - X(0), "##0.00")q = Format(Y(1) - Y(0), "##0.00")Form2.Text1.Text = Form2.Text1.Text & "N" & o & " X" & p & " Y" & q & vbCrLfEnd IfEnd Ifo = o + 1X(0) = X(1)Y(0) = Y(1)LoopForm2.Text1.Text = Form2.Text1.Text & "N" & o & " G40 M02" & vbCrLfEnd IfEnd IfPrivate Sub Command5_Click()Form2.Visible = TrueEnd SubPrivate Sub Command6_Click() ‘程序结束EndEnd SubPrivate Sub Label21_Click()End SubPrivate Sub Option1_Click() ‘显示当前绘制的非圆曲线方程quxian = 1Label4.Visible = TrueText2.Visible = TrueLabel1.Caption = "标准方程:x^2 / a^2 + y^2 / b^2 = 1" & vbCrLf & vbCrLf & "参数方程:x=a * Cos(i) , y=b * Sin(i)"End SubPrivate Sub Option2_Click()quxian = 2Label4.Visible = FalseText2.Visible = FalseLabel1.Caption = "标准方程:x^(2/3) + y^(2/3) = a^(2/3)" & vbCrLf & vbCrLf & "参数方程:x=a * Cos(i)^3 , y=a * Sin(i)^3"End SubPrivate Sub Option3_Click() ‘选定顺时针走刀方向daolu = 1End SubPrivate Sub Option4_Click() ‘选定逆时针走刀方向daolu = 2End SubPrivate Sub Option5_Click() ‘选定左刀具补偿daobu = 1End SubPrivate Sub Option6_Click() ‘选定右刀具补偿daobu = 2End SubPrivate Sub Option7_Click() ‘选定输出绝对坐标的NC代码zuobiao = 1End SubPrivate Sub Option8_Click() ‘选定输出相对坐标的NC代码zuobiao = 2End Sub。
