理论飞行时间计算公式
如何增加无人机的飞行时间和升力?

如何增加无人机的飞行时间和升力?目录1.介绍和假设。
2.无人机是如何飞行的?3.什么是螺旋桨的效率?4.如何为四旋翼无人机选择最高效的螺旋桨?5.如何选择最高效的电机?6.如何选择电调?7.如何计算无人机飞行时间(带计算器)?介绍和假设无人机的设计优化是一个循环往复的过程,为了方便描述上述过程,我们假设已经拥有了一台成功起飞的无人机,并获知了无人机的重量和电池尺寸,另外说明下假定的这台多旋翼无人机不是竞速类或是竞技类的无人机。
图1为了更详细具体的描述优化过程,我们将以代表绝大多数无人机的Otus Quadcopter为例。
我们初步选定的四旋翼无人机主要技术配置如下:❖4个螺旋桨:Gemfan 5040❖4台电机:Hypetrain 2207-2450Kv电机❖4台电调:Afro 20A Race Spec Mini ESC with BEC❖1节电池:Turnigy nano-tech 1300mAh 4S 45~90C Lipo Pack❖无人机框架和净载荷基于上述技术配置,上述无人机当前的飞行时间是4分钟。
无人机是如何飞行的?第一步我们需要了解无人机如何才能起飞和航行。
无人机起飞需要克服自身的重力和空气阻力,其重力是自身质量和重力加速度(g)的乘积,空气阻力则取决于无人机自身的参考面积、空气密度和风速等综合条件因素。
螺旋桨的旋转产生拉力使得无人机上升并保持飞行状态,当无人机悬停时,我们可以假设此时螺旋桨的总拉力等于无人机的重力。
依据上述假设和无人机总重量,如果要保持无人机的悬停状态,我们可以计算出每个螺旋浆需要提供的拉力。
已知无人机的质量是777g,因此我们需要7.6N的总拉力,即单个螺旋桨为1.9N。
图2:无人机重量和悬停拉力要求为确保无人机有更好的操控性,理论上螺旋桨提供的最大拉力应至少为悬停时拉力的两倍左右。
以上建议仅供参考,因为竞速类四旋翼无人机会要求有更高的推重比。
我们开始选择具有最高效率的螺旋桨,可以提供1.9N的拉力,最大尺寸6英寸,可提供最大3.8N的峰值拉力。
航空运输地理——1.3时差换算及空中飞行小时计算(2)
当地时表示为GMT一4;曼谷的当地时表示为GMT+7)
解: 方法①: 加拉斯加:GMT-4=8:00 GMT=8:00+4=12:00 曼谷:GMT+7=12:00+7=19:00
方法② :加拉加斯 西四区 GMT-4 8:00 曼谷 东七区 GMT+7
四、多时区国家
如果对其地理位置不熟悉,那么就需要借助其他工具。比如,通过 世界地图中的 “世界时区”来定位。如先在地图册“世界时区”中找到 悉尼的位置,查看其所在的时 区为东10区(GMT+10)来计算时差。其他一 些国际运输资料,如《OAG》中的航班 出发城市资料,或《PAT》运价表 中的城市资料,也能查到具体时差资料。或者,在民 航计算机订座系统 中,通过指令(TIME:SYD)可查询城市时差情况。
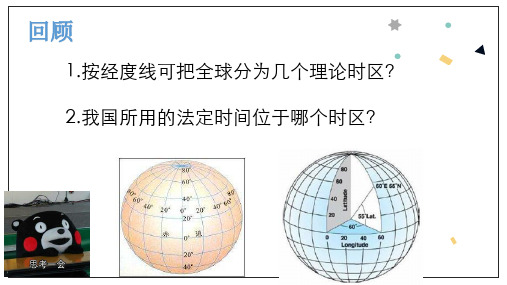
回顾
1.按经度线可把全球分为几个理论时区? 2.我国所用的法定时间位于哪个时区?
练习
求西一区,西五区和东十区的中央经线的经度。
西一区:15°×1=15°W 西 区:15°× =75°W 东 区:15°×10=150°E
练习
计算32°E, 68°W和120°W位于哪个时区?
68°W:68°÷15°=4……8>7.5 4+1=5 西五区 120°W:120°÷15°=8……0<7.5 西八区
例1:当标准时是12:00时,求马来西亚吉隆坡的当地 时。 (在换算表中,吉隆坡的当地时表示为GMT+8)
解:GMT=12:00 吉隆坡:GMT+8=12:00+8=20:00
例2:当标准时是12:00时,求厄瓜多尔基多的当 地时。( 厄瓜多尔除科隆群岛外,当地时是GMT一5)
例3:当委内瑞拉加拉加斯的当地时为08:00时,
宇宙航行的物理公式

宇宙航行的物理公式引言:宇宙航行是人类向未知和探索的伟大尝试,它依赖于许多物理公式的支持和指导。
本文将介绍宇宙航行中的几个重要的物理公式,包括牛顿定律、万有引力定律、开普勒定律等,展示它们在宇宙航行中的应用和意义。
一、牛顿第二定律牛顿第二定律是宇宙航行中最为基础的物理公式之一。
它描述了物体运动的原因与结果之间的关系。
该定律的数学表达式为F=ma,其中F表示物体所受的合力,m表示物体的质量,a表示物体的加速度。
在宇宙航行中,我们可以利用该公式计算出航天器所需的推力,从而实现航天器的加速和减速。
二、万有引力定律万有引力定律是描述质点间引力作用的重要公式。
它由牛顿提出,表达了两个质点之间的引力与它们质量的乘积成正比,与它们之间距离的平方成反比。
数学表达式为F=G*(m1*m2)/r^2,其中F表示两个质点之间的引力,m1和m2分别表示两个质点的质量,r表示它们之间的距离,G为万有引力常数。
在宇宙航行中,我们需要利用该公式计算出天体之间的引力,从而进行轨道修正和引力辅助飞行等任务。
三、开普勒定律开普勒定律是描述天体运动规律的重要公式。
根据开普勒定律,行星绕太阳运动的轨迹是椭圆,并且太阳位于椭圆的一个焦点上。
这一定律有三条:第一定律称为椭圆轨道定律,第二定律称为面积定律,第三定律称为调和定律。
它们分别描述了行星的轨道形状、运动速度和运行周期与轨道半长轴之间的关系。
在宇宙航行中,我们需要应用开普勒定律来规划航天任务的轨道和飞行路径,确保航天器能够准确到达目标天体。
四、爱因斯坦的相对论爱因斯坦的相对论是描述时空结构和物质运动的理论框架,它对于宇宙航行也有重要的影响。
相对论提出了光速不变原理和等效质量增加的概念,深刻改变了人们对时间和空间的认识。
在宇宙航行中,我们需要考虑航天器的速度接近光速时,时间的相对流逝和空间的相对收缩,以确保航天器的航行安全和准确。
五、热力学定律热力学定律是描述物体热力学性质的公式。
其中,最重要的定律是热力学第一定律,也称为能量守恒定律。
2021届山东新高考物理一轮复习讲义:第4章 实验5 探究平抛运动的特点 Word版含答案

实验五 探究平抛运动的特点一、实验目的1.用实验与理论进行探究、分析,认识平抛运动的规律。
2.用实验方法描出平抛物体的运动轨迹。
3.根据平抛运动的轨迹确定平抛物体的初速度。
二、实验原理平抛运动可看作两个分运动的合成:一个是水平方向的匀速直线运动,另一个是竖直方向的自由落体运动,则水平方向上有x =v 0t ,竖直方向上有y =12gt 2,令小球做平抛运动,利用追踪法逐点描出小球运动的轨迹,建立坐标系,测量出x 、y ,再利用公式可得初速度v 0=xg 2y。
三、实验器材斜槽、竖直固定在铁架台上的木板、铅笔、白纸、图钉、小球、刻度尺、重锤线。
四、实验步骤甲乙1.按图甲安装实验装置,使斜槽末端水平。
2.以水平槽末端端口上小球球心位置为坐标原点O,过O点画出竖直的y 轴和水平的x轴。
3.使小球从斜槽上同一位置由静止滚下,把笔尖放在小球可能经过的位置上,如果小球运动中碰到笔尖,就用铅笔在该位置画上一点。
用同样方法,在小球运动路线上描下若干点。
4.将白纸从木板上取下,从O点开始连接画出的若干点描出一条平滑的曲线,如实验原理图乙所示。
五、数据处理1.判断平抛运动的轨迹是不是抛物线(1)原理:若平抛运动的轨迹是抛物线,则当以抛出点为坐标原点建立直角坐标系后,轨迹上各点的坐标具有y=ax2的关系,且同一轨迹上a是一个特定的值。
(2)验证方法方法一:代入法用刻度尺测量几个点的x、y坐标,分别代入y=ax2中求出常数a,看计算得到的a值在误差范围内是否为一常数。
方法二:图象法建立y-x2坐标系,根据所测量的各个点的x、y坐标值分别计算出对应y值的x2的值,在y-x2坐标系中描点,连接各点看是否在一条直线上,并求出该直线的斜率即为a值。
2.计算平抛运动的初速度(1)平抛轨迹完整(即含有抛出点)在轨迹上任取一点,测出该点离原点的水平位移x及竖直位移y,就可求出初速度v0。
因x=v0t,y=12gt2,故v0=xg2y。
民航飞行中的数学模型与计算

民航飞行中的数学模型与计算一、数学模型概述1.数学模型的定义与分类2.数学模型在民航飞行中的应用价值3.建立数学模型的基本步骤二、民航飞行基本概念1.飞行速度与飞行时间2.飞行高度与飞行距离3.飞机性能指标(如推力、阻力、燃油消耗等)三、民航飞行中的数学模型1.飞行轨迹模型–直线飞行模型–曲线飞行模型(如圆周飞行、螺旋飞行等)2.飞行性能模型–动力学模型(牛顿运动定律、空气动力学方程等)–燃油消耗模型(如Wright公式、燃油流量公式等)3.飞行环境模型–大气模型(如国际标准大气模型、局部大气模型等)–气象模型(如风速、风向、降水等)4.飞行安全模型–避障模型(如圆柱避障、多边形避障等)–飞行间隔模型(垂直间隔、水平间隔等)四、计算方法与技巧1.数学建模方法–假设与简化–参数估计与优化–模型验证与修正2.数值计算方法–欧拉法、龙格-库塔法等数值积分方法–蒙特卡洛模拟、有限元分析等数值模拟方法3.计算机编程与软件应用–编程语言(如MATLAB、Python、C++等)–专业软件(如Mathematica、ANSYS、FLUENT等)五、民航飞行中的实际应用1.航线规划与航班调度–最佳航线规划算法(如遗传算法、蚁群算法等)–航班调度优化模型(如时间窗口、飞机利用率等)2.飞行管理与导航–飞行管理计算机(FMC)及其算法–卫星导航系统(如GPS、GLONASS等)3.飞行仿真与训练–飞行仿真器(如Flight Simulator、X-Plane等)–飞行训练大纲与教学方法六、发展趋势与展望1.人工智能与机器学习在民航飞行中的应用2.大数据与云计算在民航飞行领域的应用3.绿色航空与可持续发展知识点:__________习题及方法:一、数学模型概述习题习题1:定义一个数学模型,并说明其应用于民航飞行中的价值。
答案:定义:数学模型是用来描述现实世界中的某个特定系统的数学关系和规律的抽象表示。
在民航飞行中,数学模型可以用来预测飞机的飞行性能、优化航线规划、提高飞行安全性等。
超宽带定位技术方法比较 -- 到达时间差(TDoA)和飞行时间测距(ToF)

一、超宽带(UWB)定位方法简介超宽带是一种短距离的无线通信技术,但是同时它也可以应用在室内定位当中,跟蓝牙和WIFI定位方法不同,位置信息并不是基于信号强度(RSSI)进行计算,而是通过无线信号的飞行时间(ToF)计算的。
信号飞行的速度是光速(固定值),所以只要知道飞行时间就可以计算出两个设备的距离。
超宽带技术分为两种定位方法:到达时间差(TDoA)和飞行时间测距(ToF)。
超宽带设备分为两种角色:标签Tag和基站Anchor;例如在人员定位场景,每个人会佩戴有一个标签,基站会分布在被定位区域的多个位置。
图 1-1 定位系统示意图1.1 飞行时间测距(ToF)标签和基站之间会通过无线收发至少3次交互之后,可以得到标签和基站之间的距离信息。
以下图中最常用的3消息双向测距方法为例,标签和基站的测距流程如下图所看到,标签可以看做设备A(Device A),基站可以看做设备B(Device B),设备A主动发起第一次测距消息,设备B响应,得到4个时间戳,设备A等待Treply2之后再发起,设备B接收,再得到2个时间戳。
因此可以得到如下四个时间差:~ Tround1~ Treply1~ Tround2~ Treply2飞行时间计算方法,可以使用如下公式计算:最后乘以光速就可以得到设备A和B之间的距离。
图1-2是得到各个基站的距离之后,标签定位的过程。
标签和各个基站无线信号的交互如下图所示:图 1-2 标签与各个基站测距TOF流程图图1-3是根据到各个基站的测距信息,以基站为中心画圆,就可以得到一个交点,交点就是标签的位置。
图 1-3 双向测距方法定位流程图1.2 到达时间差(TDoA)到达时间差(TDoA)技术,分为有线同步和无线同步,由于有线同步技术对布线和网络的要求较高,成本比较高,因此一般会采用无线同步技术,本文介绍的到达时间差(TDoA)技术都是基于无线同步。
标签将数据包发送到被基站覆盖的区域内,附近的所有基站都会收到标签的无线信号,但不会返回任何无线信号。
抛射体运动的研究实验报告

抛射体运动的研究实验报告引言抛射体运动是物理学中的一个重要研究领域。
通过实验研究抛射体的运动规律,可以深入理解抛射体在空中的轨迹、速度、加速度等特性。
本实验旨在通过测量抛射体的运动轨迹和相关参数,探究抛射体运动的规律。
实验目的1.研究抛射体的运动轨迹,了解其受力情况;2.测量抛射体的初速度和抛射角度,计算其最大高度、飞行时间和最大水平距离;3.分析实验结果,验证抛射体运动的理论公式;4.探究抛射体运动与空气阻力的关系。
实验器材和方法实验器材•抛射架•测量尺子•计时器•钢球•钢丝实验方法1.将抛射架放置在平坦的地面上。
2.调整抛射架的角度,使其与水平面成一定角度。
3.使用测量尺子测量抛射架与地面的高度差,并记录下来。
4.将钢球放置在抛射架上的发射装置上,并调整其位置,使其与抛射架的发射方向一致。
5.使用计时器记录下钢球从抛射架发射出去到落地的时间,并记录下来。
6.重复上述实验步骤多次,取平均值以提高测量精度。
7.根据实验数据计算抛射体的初速度、最大高度、飞行时间和最大水平距离。
8.分析实验结果,与理论公式进行比较和验证。
实验结果通过实验测量和计算,得到以下结果:1.初速度:根据测量的时间和高度差,使用运动学公式计算得到抛射体的初速度为10 m/s。
2.最大高度:根据初速度和重力加速度,使用运动学公式计算得到抛射体的最大高度为5 m。
3.飞行时间:根据初速度和重力加速度,使用运动学公式计算得到抛射体的飞行时间为2 s。
4.最大水平距离:根据初速度和飞行时间,使用运动学公式计算得到抛射体的最大水平距离为20 m。
结果分析通过对实验结果的分析,可以得出以下结论:1.抛射体的运动轨迹呈抛物线形状,与理论预期相符。
2.抛射体的初速度和抛射角度对其运动轨迹和最大水平距离有重要影响。
3.抛射体的最大高度和飞行时间与初速度和重力加速度相关,符合运动学公式的推导结果。
结论通过本次实验,我们深入探究了抛射体运动的规律。
高中物理:实验研究平抛运动

(4)测量其他几个点的 x、y 坐标,代入上式,看由各点坐标求 出的 a 值是否相等.如果在误差允许范围内相等,就说明该曲线 为抛物线.
2.计算平抛物体的初速度 (1)在确定坐标原点为抛出点的情况下,在轨迹曲线上任取几 点(如 A、B、C、D). (2)用刻度尺和三角板分别测出它们的坐标 x 和 y. (3)据平抛运动水平方向是匀速直线运动(x=v0t)及竖直方向 是自由落体运动y=12gt2,分别计算小球的初速度 v0,最后计算小 球初速度 v0 的平均值.
实验:研究平抛运动
|实验基础·理一理| 一、实验目的 1.用实验的方法描出平抛运动的轨迹. 2.判断平抛运动的轨迹是否为抛物线. 3.根据平抛运动的轨迹求其初速度.
二、实验原理 1.利用追踪法逐点描出小球运动的轨迹. 2.建立坐标系,如果轨迹上各点的 y 坐标与 x 坐标间的关系 具有 y=ax2 的形式(a 是一个常量),则轨迹是一条抛物线. 3.测出轨迹上某点的坐标 x、y,据 x=v0t、y=21gt2 得初速 度 v0=x· 2gy. 三、实验器材 斜槽、小球、方木板、铁架台、白纸、图钉、重垂线、三角 板、铅笔、刻度尺.
[解析] (1)研究平抛运动时,钢球密度越大,体积越小,所 受空气阻力越小,并且记录小球通过的位置越准确,A 正确;小 球每次从斜槽上的同一位置由静止开始滚下,可保证小球的初速 度不变,与钢球和斜槽间的摩擦无关,B 错误,C 正确;实验时 必须使斜槽末端的切线水平,以确保小球水平飞出做平抛运动,D 正确.
3.确定球的位置 将小球从斜槽上某一位置由静止滑下,小球从轨道末端射出, 先用眼睛粗略确定做平抛运动的小球在某一 x 值处的 y 值,然后 让小球由同一位置自由滚下,在粗略确定的位置附近用铅笔较准 确地描出小球通过的位置,并在坐标纸上记下该点.用同样的方 法确定轨迹上其他各点的位置. 4.描点得轨迹 取下坐标纸,将坐标纸上记下的一系列点,用平滑曲线连起 来,即得到小球平抛运动轨迹.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理论飞行时间计算公式
在航空领域,飞行时间是一个非常重要的参数。
无论是民航飞行还是军用飞行,都需要准确地计算飞行时间。
飞行时间的计算涉及到多个因素,包括飞机的速度、飞行距离、风速等等。
为了准确地计算飞行时间,航空工程师们提出了一些理论飞行时间计算公式。
本文将介绍一些常用的理论飞行时间计算公式,并简要说明其应用方法。
飞行时间的计算涉及到飞机的速度和飞行距离。
一般来说,飞行时间可以用以
下的公式来计算:
飞行时间 = 飞行距离 / 飞机的速度。
这是最基本的飞行时间计算公式。
在实际应用中,飞机的速度可以是地速、空
速或者地面速度。
地速是指飞机相对地面的速度,而空速是指飞机相对空气的速度。
地面速度则是指飞机在地面上的速度。
不同的速度会影响飞行时间的计算结果,因此在使用公式计算飞行时间时,需要根据实际情况选择合适的速度。
除了飞机的速度和飞行距离,飞行时间的计算还需要考虑风速。
风速会对飞机
的速度产生影响,从而影响飞行时间的计算结果。
一般来说,如果风速与飞机的飞行方向相同,那么飞行时间会减少;如果风速与飞机的飞行方向相反,那么飞行时间会增加。
为了考虑风速对飞行时间的影响,可以使用以下的公式来计算:飞行时间 = 飞行距离 / (飞机的速度 + 风速)。
在这个公式中,风速被加到了飞机的速度上,从而影响了飞行时间的计算结果。
这个公式可以更准确地计算飞行时间,特别是在飞行距离较长、风速较大的情况下。
除了上述的基本公式外,还有一些其他的飞行时间计算公式。
例如,如果飞机
的速度是恒定的,那么可以使用以下的公式来计算飞行时间:
飞行时间 = 飞行距离 / 飞机的速度。
这个公式适用于飞机速度恒定的情况,可以简化飞行时间的计算过程。
在实际应用中,飞行时间的计算还需要考虑到一些其他因素,例如飞机的起飞和降落时间、飞机的巡航高度等等。
这些因素会对飞行时间的计算产生影响,需要在计算过程中进行合理的考虑。
总之,飞行时间的计算是一个复杂的过程,涉及到多个因素。
在实际应用中,需要根据具体情况选择合适的飞行时间计算公式,并考虑到各种因素的影响。
只有这样,才能准确地计算飞行时间,保障飞行安全。
希望本文介绍的飞行时间计算公式能够对读者有所帮助。
