34金属圆波导
合集下载
圆形波导的传输特性

0
类似TM波的方法可以得到:
Hz
H0J
m
(kc
r
)
cos
sin
m m
e
z
其中:H0 由激励条件确定, kc 由边界条件确定。
圆柱形波导中TE波的横向场分量由下式推到:
Et
j
kc2
(aˆz
t
Hz
)
Er
jm
kc2r
H0
J
m
(kc
r
)
sin m
cos
m
e
z
E
j
kc
H0
J
m
(kc
r
)
cos sin
因为 J0(x) J1(x) 所以 0n v1n
由边界条件,当 r a 时 Ez 0
Jm(kca) 0
可得: kc vmn a
vmn 为m 阶第一类Bessel函数的第 n 个根
圆柱形波导中TM波的横向场分量由下式推到:
Et
1 kc2
(t Ez )
Er
j
kc2
E0
J
m
(
kc
r
)
cos m sin m
e
z
E
j m
kc2
E0
J
m
(
kc
r
匀理想介质。
x
横截面的尺寸为 r a
z
特点:圆柱形波导结构对称,制作方便。
2. 传输波型及场分量的表达式
(1)TM波:
1 r
r
(r
Ez r
)
1 r2
2Ez
2
kc2 Ez
0
采用分离变量法求解,设 Ez (r,) R(r)()
圆波导

cTE
mn
2a
mn
cTM
mn
2a
mn
在所有的模式中,TE11模截止波长最长,其次为 TM01模,三种典型模式的截止波长分别为
cTE 3.4126a
11
cTM 2.6127 a
01
cTE 1.6398a
01
微波工程基础
5
第二章 规则金属波导之圆波导
圆波导中各模式截止波长的分布图
11
第二章 规则金属波导之圆波导
磁场有径向 和轴向分量
(3)低损耗的TE01模
波导内壁电流:
TE01模的场分布
圆波导三种模式的导体衰减曲线
J s n H a a z H z a H z
TE01 模是圆波导的高次模式,比它低的模式有 TE11 、TM01 、 TE21 ,它与TM11是简并模。它也是圆对称模故无极化简并。
方圆波导变换器
TE11模的截止波长最长,是圆波导中的最低次模,也是主模。圆 波导中模的场分布与矩形波导的模的场分布很相似,因此工程上容 易通过矩形波导的横截面逐渐过渡变为圆波导,从而构成方圆波导 变换器。 但由于圆波导中极化简并模的存在,所以很难实现单模传输,因 此圆波导不太适合于远距离传输场合。 微波工程基础
微波工程基础
7
第二章 规则金属波导之圆波导
极化简并
旋转
利用极化兼并现象制成极化衰减器、极化变换器等
微波工程基础
8
第二章 规则金属波导之圆波导
(c)传输功率 TEmn和TMmn模的传输功率分别为:
PTE mn
2 πa m 2 2 Z H ( 1 ) J TE mn m (kc a) 2 2 2 m kc k a 2
圆形波导的理论分析和特性
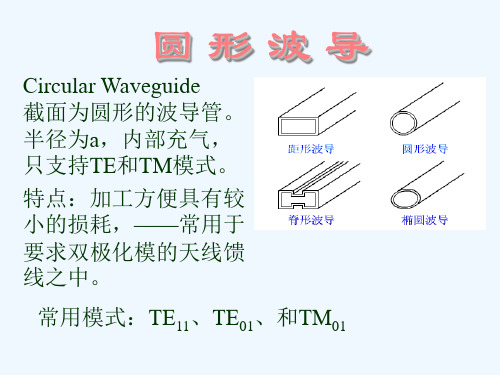
2 2 cmn
传播常数: mn k k 截至波长: cmn 截至频率 2 a u 'mn v
u 'mn k a
2
2
3.2 18
3.2 19 3.2 20
f cmn
cmn
u 'mn 2 a
其中贝塞尔函数最小根u11'=1.841对应TE11模。 c=3.41a;次低模为根u01=3.832, c=1.64a
圆形波导分析 – TM modes.(续四)
波导阻抗: Z TM Ef Er Hf H r w k
2 2 cmn 2
3.2 25
2
传播常数: mn k k 截至波长: cmn 截至频率 2 a u mn v
u mn k a
m 0 n 1
u m n co s m f j ( w t z ) jw m a 2 E mn J m ( r) e 2 si n m f u mn r a co s m f j ( w t z ) jw a ' u mn E mn J m ( r) e sin m f u mn a
3.2 26
3.2 27 3.2 28
f cmn
cmn
u mn 2 a
其中贝塞尔函数最小根 u01=2.405对应TM01模。 c=2.62a
圆形波导的特性
圆形波导模的传输条件是c> 或fc<f;传输特性 与矩形波导类似,为高通器件。 圆形波导存在两种模式简并现象: TE0n与TMm0的模兼并; 另一种是m非零的TEmn与TMmn模的极化简并。 圆形波导的基模—— 主模为TE11,其截止波长最长(TE11=3.41a) 次模为TM01,其截止波长最长(TM01=2.62a)
传播常数: mn k k 截至波长: cmn 截至频率 2 a u 'mn v
u 'mn k a
2
2
3.2 18
3.2 19 3.2 20
f cmn
cmn
u 'mn 2 a
其中贝塞尔函数最小根u11'=1.841对应TE11模。 c=3.41a;次低模为根u01=3.832, c=1.64a
圆形波导分析 – TM modes.(续四)
波导阻抗: Z TM Ef Er Hf H r w k
2 2 cmn 2
3.2 25
2
传播常数: mn k k 截至波长: cmn 截至频率 2 a u mn v
u mn k a
m 0 n 1
u m n co s m f j ( w t z ) jw m a 2 E mn J m ( r) e 2 si n m f u mn r a co s m f j ( w t z ) jw a ' u mn E mn J m ( r) e sin m f u mn a
3.2 26
3.2 27 3.2 28
f cmn
cmn
u mn 2 a
其中贝塞尔函数最小根 u01=2.405对应TM01模。 c=2.62a
圆形波导的特性
圆形波导模的传输条件是c> 或fc<f;传输特性 与矩形波导类似,为高通器件。 圆形波导存在两种模式简并现象: TE0n与TMm0的模兼并; 另一种是m非零的TEmn与TMmn模的极化简并。 圆形波导的基模—— 主模为TE11,其截止波长最长(TE11=3.41a) 次模为TM01,其截止波长最长(TM01=2.62a)
圆形波导
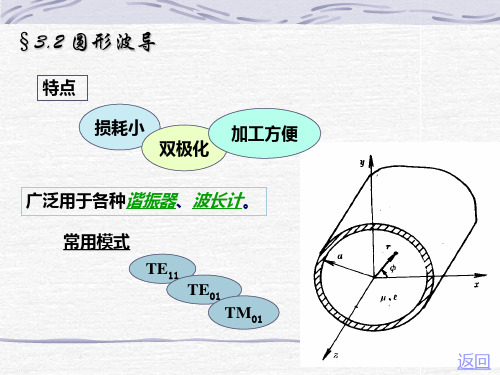
场沿圆周方向按正弦或余弦函数形式变化,波 型指数m表示场沿圆周分布的整波数。
TEmn导模的各参数:
波阻抗:
Z TE
Er H
E Hr
k
传播常数: mn
k2
k2 cmn
k
2
um n
2
a
截止波长: 截止频率:
cmn
2a
u m n
f cmn
k cmn
2
um n
2a
▪TE11模
u11 1.841对应本征值为最小值
bh k
传播常数: mn
k2
k2 cmn
k2
umn
2
a
截止波长:
cmn
2a
u mn
截止频率:
f cmn
k cmn
2
umn
2a
TM01模
u01 2.405 最小值 c 2.62a
圆波导中的 传输特性:
圆波导中传输条件 l c > l , f > fc
圆波导的主模是TE11模,cTE11 3.41a ; TM01模为次主模 cTE11 2.62a
必须为整数m
cos m () B1 cos m B2 sin m B sin m ,
m 0,1,2,...
由于圆波导结构具有轴对称性,场的极化方向具有不
确定性,使导波场在φ方向存在 cos m和sin m两
种可能的分布。它们独立存在,相互正交(两个线性 无关的独立成份),截止波长相同,构成同一波导的 极化简并模。
R(贝塞尔方程)的解为
R(r) A1J m (kc r) A2Ym (kc r) 式中 J m (k为crm) 阶贝塞尔函数,
第八章 金属波导

TE30
TE11 ,TM11 TE01 TE20
单模区(Ⅱ): a < < 2a 多模区(Ⅲ): < a
TE10
2b a
Ⅰ
2a
电磁场微波技术与天线
第8章 金属波导
说明: 截止区:
由于2a 是矩形波导中能出现的最长截止波长,因此,当工作 波长λ> 2a 时,电磁波就不能在波导中传播,故称为“截止区”。
单模传输条件
第8章 金属波导
a 1.8a,b / 2
由设计的波导尺寸实现单模传输。
截止波长相同时,传输TE10 模所要求的 a 边尺寸最小。同时 TE10 模的截止波长与 b 边尺寸无关,所以可尽量减小 b 的尺 寸以节省材料。但考虑波导的击穿和衰减问题,b 不能太小。
TE10 模和TE20 模之间的距离大于其他高阶模之间的距离, TE10 模波段最宽。 可以获得单方向极化波,这正是某些情况下所要求的。 对于一定比值a/b,在给定工作频率下TE10模具有最小的衰减。
同轴线没有电磁辐射,工作频带很宽。
电磁场微波技术与天线
2. 波导管
第8章 金属波导
矩形波导
波导是用金属管制作的导 波系统,电磁波在管内传播, 损耗很小,主要用于 3GHz ~ 30GHz 的频率范围。
电磁场微波技术与天线
圆波导
第8章 金属波导
8.1 导行电磁波概论
分析均匀波导系统时, 做如下假定:
第8章 金属波导
电磁场微波技术与天线
第8章 金属波导 导行电磁波 —— 被限制在某一特定区域内传播的电磁波 导波系统 —— 引导电磁波从一处定向传输到另一处的装置 常用的导波系统的分类 :
TEM传输线、金属波导管、表面波导。
第四章2-波导和空腔(矩、圆形波导、谐振腔)

xa
H0z (x, y) 0
y
y0
H0z (x, y) 0
y
yb
H0z (s) H0z (x, y) X (x)Y ( y)
Hz H0 cos kxx cos ky y expikzz
m
n
kx
, a
ky b ,
m, n
0, 1, 2, ...
TE波 边界条件:电磁场切向分量连续
z
s
zˆ
z
s
对偶性Es
1 2
kz2
s
Ez z
is
Hz
Hs
1 2 kz2
s
H z z
is
Ez
用纵向分量表示横向场
可区分TE和TM波
s
zˆ
z
Ez x
Hx
i ky 2 kz2
E0 sin kx x cos ky y exp ikz z
H y
i kx
2
k
2 z
E0 cos kx x sin ky y exp ikz z
其中kz
2
Ez x
i
H z y
TM波,H z 0
Ey
2
1
k
2 z
ikz
Ez y
i
H z x
第三章规则波导

ab
kc
( m a
)2
( n b
)2
kc1
c1
2 kc1
c2
2 kc2
( )2 a
(0 b
)2
kc2
( 0 )2 ( )2 ab
2)TM波
对TM波, Hz=0, Ez(x,y,z)=Eoz(x, y)e-jβz, 此时满足
2 ( x2
2 y 2
)Eoz (x,
y)
kc2 Eoz (x,
y)e jz
Ey
m0
n0
ju kc2
m a
m H mn sin( a
x) cos(n b
y)e jz
EZ 0
H X
m0 n0
j kc2
m a
m H mn sin( a
x) cos(n b
y)e jz
HY
m0 n0
j kc2
n b
m Hmn cos( a
x) sin( n b
y)e jz
h2
H z v
), Hu
j kc2
( h1
H z u
h2
Ez v
)
Ev
j kc2
( h2
Ez v
h1
H z u
)Hv
j kc2
( h2
H z v
h1
Ez u
)
E(x, y, z) Et (x, y, z) z Ez (x, y, z)
Eot ( x, y)e jz z Eoz (x, y) e jz
H
Z
(x,
y,
z)
m0
n0
H
mn
cos(mx a
2.3 圆形波导
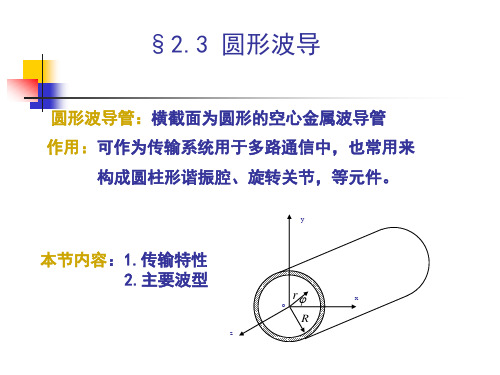
Eφ Hr
§2.3 圆形波导
TE01波的特点 : (1) 电磁场沿角向均无变化,具有轴对称性,不存
在极化简并,但它与 TM11模是简并的。
(2) 电场只有角向,电力线都是横截面内的同心圆。 (3) 在r=R的波导壁附近,Hr很小(因为J1(3.832)很小), 磁场只有Hz分量,故只有φ方向的管壁电流,而无纵 向电流。
(2-110) (2-131)
2 2 t H (r, ) Kc H (r, ) 0
一般意义上,柱坐标下,电场和磁场为 ˆ ˆ E(r, ) rEr (r, ) E (r, ) zEz (r, ) ˆ
ˆ ˆ H (r, ) rHr (r, ) H (r, ) zH z (r, ) ˆ
(3) 磁场仅有Hφ分量。因而管壁电流只有纵向分量。利用 TM01波的这种旋转对称性,可以制作雷达天线和馈电 波导间的旋转接头(图(2-26)。
§2.3 圆形波导
2.3.6 TE01波 截止波长 :
(c ) TE o 1.64 R
01
(2-144)
将m=0、n=1 代入TE波型的场方程,得到 TE01波的场方程, (2-145)式
§2.3 圆形波导
2.3.1 圆波导的TM波型 1.TM波型的场表达式
E z E0 J m ( K c r ) cos m sin m e j z
(2-123)
横向场
Et 2 t E z Kc
1 ˆ Ht z Et Z TM
或 者
j Et 2 t Ez Kc
E z E0 J m ( K c r ) cos m sin m e j z
极 化 简 并
(2-123) (2-132)
§2.3 圆形波导
TE01波的特点 : (1) 电磁场沿角向均无变化,具有轴对称性,不存
在极化简并,但它与 TM11模是简并的。
(2) 电场只有角向,电力线都是横截面内的同心圆。 (3) 在r=R的波导壁附近,Hr很小(因为J1(3.832)很小), 磁场只有Hz分量,故只有φ方向的管壁电流,而无纵 向电流。
(2-110) (2-131)
2 2 t H (r, ) Kc H (r, ) 0
一般意义上,柱坐标下,电场和磁场为 ˆ ˆ E(r, ) rEr (r, ) E (r, ) zEz (r, ) ˆ
ˆ ˆ H (r, ) rHr (r, ) H (r, ) zH z (r, ) ˆ
(3) 磁场仅有Hφ分量。因而管壁电流只有纵向分量。利用 TM01波的这种旋转对称性,可以制作雷达天线和馈电 波导间的旋转接头(图(2-26)。
§2.3 圆形波导
2.3.6 TE01波 截止波长 :
(c ) TE o 1.64 R
01
(2-144)
将m=0、n=1 代入TE波型的场方程,得到 TE01波的场方程, (2-145)式
§2.3 圆形波导
2.3.1 圆波导的TM波型 1.TM波型的场表达式
E z E0 J m ( K c r ) cos m sin m e j z
(2-123)
横向场
Et 2 t E z Kc
1 ˆ Ht z Et Z TM
或 者
j Et 2 t Ez Kc
E z E0 J m ( K c r ) cos m sin m e j z
极 化 简 并
(2-123) (2-132)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Zc
TEM D ln 2 d
或 Z c 60
D ln d
(3.5.7)
16
3.5.2 同轴线中的TE波和TM波
求解同轴线中的TE波和TM波的方法和圆波导中的求解思路相似,但在同轴线 中多了内导体的边界条件,因而它的解也变得更复杂。设代表同轴线中的Ez(TM 波)或Hz(TE波),有: r,, z R r e jkz z (3.5.8)
TE0i模的导行条件:J’=0,TM1i模的导行条件:J1=0
9
3.4.2 圆波导中的力线图
四类力线图:TEni(n≠0), TMni(n≠0) , TE0i, TM0i.
沿R方向
图3.14 适用与波导的假想的无界力线示意图 (a)TE1i以及TE12 (b)TM1i以及TM11 (c) TE2i以及TE22 (d)TM2i以及TM21
式中,Jn(u)是n阶贝塞尔函数,Nn(u)是诺埃曼函数。
图3.11 特殊函数曲线 (a)0阶、1阶、2阶贝塞尔函数 (b) 0阶、1阶、2阶贝塞尔导函数 (c) 0阶、1阶、2阶诺埃曼函数
2
下面列出若干对我们有用的贝塞尔函数和诺埃曼函数的性质:
J 0 0 1
J n 0 0
Nn 0
DJn kc r cos n e jk z
z
(3.4.12)
3
TE波 =Hz,常数D记作Hni,那么
在圆波导内壁r=R处,Hz所满足的边界条件为:
Hz Hni Jn kc r cos n e jkz z
H z r 0
rR
(3.4.13) (3.4.14)
2 n J n u cos u u 4 2 2 n N n (u ) sin u u 4 2
u 2 j (1) 4 2 H n u e u u 2 j (2) 4 2 H n u e u
10
图3.15 圆波导中TE02模和TM02模(横截面)
(a) TE02
(b)TM02
11
3.4.3 圆波导的色散方程
矩形波导中的kc可以分解为x和y分量,但是圆波导中的kc不能分解 成r和φ 分量。圆波导的色散方程同样是 (3.4.24) k2 k k2
z c
用圆波导的半径乘以色散方程两端,得
其中
C cos n
d 2R dR 2 2 u u ( u n )R 0 2 du du
2
(3.5.9)
令u=kcr,则R(u)满足圆柱坐标下的贝塞尔方程
为了在同轴线的边界条件下求解贝塞尔方程,介绍一下当u 曼函数、汉克尔函数的性质。 u ∞ 时,有
∞时贝塞尔函数、诺埃
17
n
n
第一类n阶汉克尔函数
H n(1) u J n (u ) jN n (u ) H n(2) u J n (u ) jN n (u )
第二类n阶汉克尔函数
Hn(1)(u) 和Hn(2)(u)分别表示内向收缩(向-r传播)和外向扩展(向+r传播)的柱面波。 同轴线存在着内外导体,可以想象在内外导体之间同时存在内向收缩和外向扩展的柱 面波。R(u)可写成第一和第二类汉克尔函数的线性组合,也可写成贝塞尔函数与诺埃 曼函数的线性组合,取后一种有
5
TM波 =Ez,常数D记作Eni,那么
Ez Eni J n kc r cos n e jkz z
在圆波导内壁r=R处,Ez所满足的边界条件为
(3.4.19)
Ez
J n kc R 0
r R
0
(3.4.20)
这是圆波导中TM波的导行条件。各阶贝赛尔函数的根uni与临界波数kc(ni)、 临界波长λ c(ni)的关系为
12
图3.16 圆波导的k图
图3.17 圆波导的kzR-kR图
13
3.5
同轴线与平行双线
同轴线与平行双线都是双导体系统,可以传输TEM波,其临界波数kc=0, 故在低端,同轴线可工作在较低的频率,直到直流;而在高端,同轴线工 作频率可高达几十吉赫兹(GHz),平行双线仅为几百兆赫兹(MHz),前 者主要受限于导体损耗,后者主要受限于辐射损耗。
kc称为临界波数,式(3.4.3)称为色散方程。
图3.10 圆波导的圆柱坐标系
1
采用分离变量法,令
求得:
(r,, z) R(r )( )e jk z
z
( ) C cos n 0
R u B1Jn u B2 Nn u
(3.4.5) (3.4.6) 单值性条件:n=1,2,„,0任意 (3.4.7)
c(ni)的值
jk z Er Eni J n kc r cos n kc jk E 2 z Eni J n kc r sin n kc r
kz H Er kz Hr E
(3.4.23)
n表示纵向点场Ez在0≤﹤2内沿变化的周期数,i表示纵向电场在0﹤r≤R范围 内零点的数目, 不包括r=0点。
3.5.1 同轴线中的TEM波
同轴线按其结构可分为两种:硬同轴线,其外导体 是一根铜管,内导体是一根铜棒、铜线或铜管, 硬铜轴线可以填充低损耗介质,如聚四氟乙烯, 也可以不填充介质;同轴电缆,内导体是单根 或多根导线,外导体由金属丝编织而成, 内导体之间充以低损耗介质如聚乙烯, 为了保护外导体再套一层介质保护。 同轴线的几何示意图如图3.18所示。
uni kc ni R 2 R c ni
园柱坐标系下横向电磁场与纵向电场的关系:
(3.4.21)
ET
jkz Ez 1 Ez ˆ ˆ r 2 k r r 1c ˆ ET HT z TM
(3.4.22)
6
表 3.2
TMni模的uni和λ
图3.18 同轴线几何示意图
14
同轴线是多导体系统,因为可以传输TEM波。TEM波的位函数ψ 满足二维 拉普拉斯方程,在圆柱坐标中二维拉普拉斯方程的具体形式为
1 = r r r r
2 T
2 1 =0 + 2 2 r
(3.5.1)
内外导体表面是两个等位面,分别记作1和2。设ψ 沿φ 方向无变化, 即 =0 ,则: 1 (3.5.2) r =0 r r r 设a是外导体的内表面的半径,在r=a处,=2;设b是内导体的外表面的 半径,在r=b处,ψ =ψ 1。ψ 1与ψ 2之差记作电压V,则:
3.4
波动方程
1 r r r r
金属圆波导(3.4.1)来自2 2 1 2 k 2 0 2 z r
圆柱坐标系如图3.10所示;k是自由空间波数;对于TE波,代表Hz分量,对 于TM波,代表Ez分量。R是圆波导的内壁的半径。
H z n 0
jkz H z 1 H z ˆ ˆ HT 2 r kc r r
ˆ ET TE HT z
(3.4.17)
4
表 3.1 TEni模的vni和λ
c(ni)的值
jk z Hr H ni J n kc r cos n e jkz z kc
由上式得:
(3.4.15) 这是圆波导中的TE波的导行条件。各阶贝塞尔函数的导函数的 根ni与临界波数kc(ni)和临界波长λ c(ni)的关系为
J n kc R 0
vni kc ni R 2 R cni
园柱坐标系下横向电磁场与纵向磁场的关系:
(3.4.16)
rR
Ez
r R
0
(3.4.2)
假设波沿+z方向传播,exp(-jkzz),对z的二次偏导数可用(-kz2) 取代,并 令: k 2 kz2 kc2 (3.4.3) 则
1 r r r r
2 2 1 kc 0 (3.4.4) 2 2 r
同轴线中的传输功率
1 V 2 * P= ET H T ds a 2s TEM ln( ) b
(3.5.5)
ˆ H zdl ˆ 同轴线内导体的电流 I= n
L
2V
a TEM ln( ) b
e jkz
(3.5.6)
同轴线的特性阻抗ZC
kR kc R k z R 或
2 2 2
k z R kR kc R
2 2
2
(3.4.25)
上两式对应了两种形式的k图。左式对应的k图,横坐标为kcR,纵 坐标为kzR。色散方程乘以R的好处是kcR只取一系列离散的值,如表 3.2和表3.1所示,这些值即为贝塞尔函数的根uni和贝塞尔导函数的根vni。 当给定工作频率和圆波导的半径后kR圆就完全确定了。若uni和vni落在 kR圆内,那么相应的模便是可以传播的模;若uni和vni落在kR圆外面, 与其相应得模便是截止的模。图3.17是与右式对应的图,横坐标为kR, 纵坐标为kzR。当kzR=0时,即临界状态时,kR=kcR=uni或kR=kcR =vni,图中的曲线为双曲线,但只画出了一半,每一条双曲线对应于 一个kcR的值。这些曲线以kzR=kR直线为渐近线。
7
H
E
图 3.12 圆波导TE11、TE01 、TM11和TM01模的力线图以及各种参数
8
TE11模 是圆波导中的最低模,c(ni)=3.41R最大。TE11模的电场具有一定的极化方向,任 意极化方向的电场,总可以分解成两个正交极化电场, 0=0,/2,如图3.13所示。 如果将这两个正交极化的TE11模看作两个模,他们对应着同一个临界波数kc(11), 这种现象称作极化简并。形成两个独立信道,频率再用。 TM01模 n=0,场沿向无变化,无极化简并现象。磁 ˆ H 可知电流只有z 场只有分量,由 J S n 分量。TM01模具有较强的纵向电场分量。 传导电流在圆波导的内壁,位移电流相 对集中在圆波导的中心,也是沿z方向。 图3.13 圆波导中的TE11模的极化简并 TE01模 n=0,场沿向无变化,无极化简并现象。波导壁附近的磁场只有z分量,壁电 流只有分量。TE01模的损耗比较小。 TM11模 不但有极化简并,而且有一般的模式简并。n≠0,有极化简并。TM11模和TE01模 的临界波数kc相等,故TE01和TM11模为简并模。事实上,TE0i和TM1i也是简并模。
