随机变量及其分布(答案)
随机变量及其分布期末练习题及答案

随机变量及其分布期末练习题及答案1.在事件A 发生的概率为p 的伯努利试验中,若以ξ记第r 次A 发生时的试验的次数,求ξ的分布。
[解] {}发生次试验次而第恰好出现了次试验中前A k r A k P k P 11-)(-==ξ),1,(,)1()1(11111 +=-=⋅-=-------r r k p p Cp p pC rk r r k r k r r k小结 求离散型随机变量的分布律时,首先应该搞清随机变量取可能值时所表示的随机事件,然后确定其分布列。
为验证所求分布是否正确,通常可计算一下所求得的“分布列”之和是否为1,若不是,则结果一定是错误的。
2.设随机变量X 的分布函数为⎪⎩⎪⎨⎧>≤≤<=.1,1;10.0,1)(2x x Ax x x F求(1)A 的值;(2)X 落在)21,1(-及)2,31(内的概率;(3)X 的概率密度函数。
[解] (1)有分布函数的右连续性, 在1=x 点处有1)01()1(=+==F A F ,即1=A (2)由分布函数的性质知,41)1()21())21,1((=--=-∈F F X P ;98311)31()2())2,31((2=⎪⎭⎫⎝⎛-=-=-∈F F X P ;(3)由于)(x F 最多除1=x 和0点外处处可导,且在1,0=x 处连续,若取 ⎩⎨⎧≤≤><=.10,2;10,0)(x x x x x f 或则0)(≥x f ,且对一切x 有⎰∞-=xdt t f x F )()(,从而)(x f 为随机变量X 的密度函数。
3.设),2(~2σN X ,且3.0)42(=<<X P ,求)0(<X P [解] 因为 )0(2)42(3.0Φ-⎪⎭⎫⎝⎛Φ=<<=σX P 所以 8.05.03.02=+=⎪⎭⎫⎝⎛Φσ于是 2.0212202)0(=⎪⎭⎫⎝⎛Φ-=⎪⎭⎫ ⎝⎛-Φ=⎪⎭⎫⎝⎛-<-=<σσσσX P X P4.一批鸡蛋,优良品种占三分之二,一般品种占三分之一,优良品种蛋重(单位:克))5,55(~21N X ,一般品种蛋重)5,45(~22N X 。
概率论与数理统计教程习题(第二章随机变量及其分布)(1)答案

概率论与数理统计练习题系 专业 班 姓名 学号第六章 随机变量数字特征一.填空题1. 若随机变量X 的概率函数为1.03.03.01.02.043211pX-,则=≤)2(X P ;=>)3(X P ;=>=)04(X X P .2. 若随机变量X 服从泊松分布)3(P ,则=≥)2(X P 8006.0413≈--e.3. 若随机变量X 的概率函数为).4,3,2,1(,2)(=⋅==-k c k X P k则=c1516. 4.设A ,B 为两个随机事件,且A 与B 相互独立,P (A )=,P (B )=,则()P AB =____________.() 5.设事件A 、B 互不相容,已知()0.4=P A ,()0.5=P B ,则()=P AB6. 盒中有4个棋子,其中2个白子,2个黑子,今有1人随机地从盒中取出2个棋子,则这2个棋子颜色相同的概率为____________.(13) 7.设随机变量X 服从[0,1]上的均匀分布,则()E X =____________.(12) 8.设随机变量X 服从参数为3的泊松分布,则概率密度函数为 __.(k 33(=,0,1,2k!P X k e k -==L )) 9.某种电器使用寿命X (单位:小时)服从参数为140000λ=的指数分布,则此种电器的平均使用寿命为____________小时.(40000)10在3男生2女生中任取3人,用X 表示取到女生人数,则X 的概率函数为11.若随机变量X 的概率密度为)(,1)(2+∞<<-∞+=x xa x f ,则=a π1;=>)0(X P ;==)0(X P 0 .12.若随机变量)1,1(~-U X ,则X 的概率密度为 1(1,1)()2x f x ⎧∈-⎪=⎨⎪⎩其它13.若随机变量)4(~e X ,则=≥)4(X P ;=<<)53(X P .14..设随机变量X 的可能取值为0,1,2,相应的概率分布为 , ,,则()E X =15.设X 为正态分布的随机变量,概率密度为2(1)8()x f x +-=,则2(21)E X -= 916.已知X ~B (n,p ),且E (X )=8,D (X )=,则n= 。
随机变量及其分布列习题(含解析)
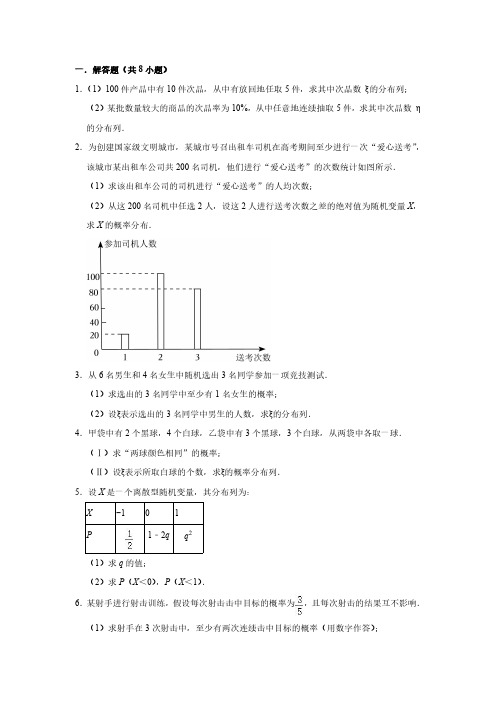
一.解答题(共8小题)1.(1)100件产品中有10件次品,从中有放回地任取5件,求其中次品数ξ的分布列;(2)某批数量较大的商品的次品率为10%,从中任意地连续抽取5件,求其中次品数η的分布列.2.为创建国家级文明城市,某城市号召出租车司机在高考期间至少进行一次“爱心送考”,该城市某出租车公司共200名司机,他们进行“爱心送考”的次数统计如图所示.(1)求该出租车公司的司机进行“爱心送考”的人均次数;(2)从这200名司机中任选2人,设这2人进行送考次数之差的绝对值为随机变量X,求X的概率分布.3.从6名男生和4名女生中随机选出3名同学参加一项竞技测试.(1)求选出的3名同学中至少有1名女生的概率;(2)设ξ表示选出的3名同学中男生的人数,求ξ的分布列.4.甲袋中有2个黑球,4个白球,乙袋中有3个黑球,3个白球,从两袋中各取一球.(Ⅰ)求“两球颜色相同”的概率;(Ⅱ)设ξ表示所取白球的个数,求ξ的概率分布列.5.设X是一个离散型随机变量,其分布列为:X−101P1﹣2q q2(1)求q的值;(2)求P(X<0),P(X<1).6.某射手进行射击训练,假设每次射击击中目标的概率为,且每次射击的结果互不影响.(1)求射手在3次射击中,至少有两次连续击中目标的概率(用数字作答);(2)求射手第3次击中目标时,恰好射击了4次的概率(用数字作答);(3)设随机变量ξ表示射手第3次击中目标时已射击的次数,求ξ的分布列.7.袋中有3个红球,4个黑球,从袋中任取4个球.(1)求红球个数X的分布列;(2)若取到一个红球得2分,取到一个黑球得1分,求得分不小于6分的概率.8.从5名男生和3名女生中任选2人去参加学校组织的“低碳杯”知识抢答赛,用ξ表示选出的女生的人数.(1)求随机变量ξ的分布列;(2)求事件“选出的2学生至少有一女生”的概率.参考答案与试题解析一.解答题(共8小题)1.(1)100件产品中有10件次品,从中有放回地任取5件,求其中次品数ξ的分布列;(2)某批数量较大的商品的次品率为10%,从中任意地连续抽取5件,求其中次品数η的分布列.【解答】解:(1)由题意知ξ的可能取值为0,1,2,3,4,5,每次取出次品的概率为:,相当于5次独立重复实验,ξ~B(5,),P(ξ=0)==0.59059,P(ξ=1)==0.32805,P(ξ=2)==0.07329,P(ξ=3)==0.0081,P(ξ=4)==0.00045,P(ξ=5)==0.00001,∴ξ的分布列为:ξ012345P0.590590.328050.07290.00810.000450.00001(2)由题意知η的可能取值为0,1,2,3,4,5,且η~B(5,0.1),∴η的分布列为:η012345P0.590590.328050.07290.00810.000450.000012.为创建国家级文明城市,某城市号召出租车司机在高考期间至少进行一次“爱心送考”,该城市某出租车公司共200名司机,他们进行“爱心送考”的次数统计如图所示.(1)求该出租车公司的司机进行“爱心送考”的人均次数;(2)从这200名司机中任选2人,设这2人进行送考次数之差的绝对值为随机变量X,求X的概率分布.【解答】解:(1)由统计图得200名司机中送考1次的有20人,送考2次的有100人,送考3次的有80人,∴该出租车公司的司机进行“爱心送考”的人均次数为;(2)从该公司任选两名司机,记“这两人中﹣人送考1次,另一人送考2次”为事件A,“这两人中一人送考2次,另一人送考3次“为事件B,“这两人中﹣人送考1次,另一人送考3次”为事件C,“这两人送考次数相同”为事件D,由题意知X的所有可能取值为0,1,2,,,,所以X的分布列为:X012P3.从6名男生和4名女生中随机选出3名同学参加一项竞技测试.(1)求选出的3名同学中至少有1名女生的概率;(2)设ξ表示选出的3名同学中男生的人数,求ξ的分布列.【解答】解:(1)由意可知,选出的3名同学全是男生的概率为=,∴选出的3名同学中至少有1名女生的概率为P=1﹣=.(2)根据题意,ξ的可能取值为0,1,2,3,P(ξ=0)==,P(ξ=1)==,P(ξ=2)==,P(ξ=3)==,∴ξ的分布列为:ξ0123P4.甲袋中有2个黑球,4个白球,乙袋中有3个黑球,3个白球,从两袋中各取一球.(Ⅰ)求“两球颜色相同”的概率;(Ⅱ)设ξ表示所取白球的个数,求ξ的概率分布列.【解答】解:(I)从甲中取出黑球的概率为,取出白球的概率为,从乙中取出黑球的概率为,取出白球的概率为,故“两球颜色相同”的概率P=.(II)由题意可得,ξ所有可能取值为0,1,2,P(ξ=0)==,P(ξ=1)=,P(ξ=2)=,故ξ的分布列为:ξ012P5.设X是一个离散型随机变量,其分布列为:X−101P1﹣2q q2(1)求q的值;(2)求P(X<0),P(X<1).【解答】解:(1)依题意,得,解得或(舍去),所以.(2)由(1)得,,所以,.6.某射手进行射击训练,假设每次射击击中目标的概率为,且每次射击的结果互不影响.(1)求射手在3次射击中,至少有两次连续击中目标的概率(用数字作答);(2)求射手第3次击中目标时,恰好射击了4次的概率(用数字作答);(3)设随机变量ξ表示射手第3次击中目标时已射击的次数,求ξ的分布列.【解答】解:(1)设事件该射手第i次射击,击中目标为A i,i=1,2,3,则,所以,事件射手在3次射击中,至少有两次连续击中目标可表示为,因为事件,,A1A2A3互斥,所以又事件A1,A2,A3相互独立,所以==;(2)事件射手第3次击中目标时,恰好射击了4次等于事件前3次中恰好击中两次目标且第四次击中目标,又各次击中目标的概率为,所以前3次中恰有两次击中目标的概率为,第四次击中目标的概率为,所以事件射手第3次击中目标时,恰好射击了4次的概率;(3)由已知ξ的取值有3,4,5,⋅⋅⋅,n,⋅⋅⋅,又,,,⋅⋅⋅,,所以随机变量ξ的分布列为:ξ345…n…P……7.袋中有3个红球,4个黑球,从袋中任取4个球.(1)求红球个数X的分布列;(2)若取到一个红球得2分,取到一个黑球得1分,求得分不小于6分的概率.【解答】解:(1)由题意可得,X可能取值为0,1,2,3,P(X=0)=,P(X=1)=,P(X=2)=,P(X=3)=,故X的分布列为:X0123P(2)设得分为Y,则得分Y可以取4,5,6,7,分别对应4个黑球,3黑1红,2黑2红,1黑3红四种情况,P(Y≥6)=P(Y=6)+P(Y=7)=,故得分不小于6分的概率为.8.从5名男生和3名女生中任选2人去参加学校组织的“低碳杯”知识抢答赛,用ξ表示选出的女生的人数.(1)求随机变量ξ的分布列;(2)求事件“选出的2学生至少有一女生”的概率.【解答】解:(1)由题意得ξ的可能取值为0,1,2,P(ξ=0)==,P(ξ=1)==,P(ξ=2)==,∴随机变量ξ的分布列为:ξ012P(2)事件“选出的2学生至少有一女生”的概率为:P=P(ξ=1)+P(ξ=2)==.。
第二章 随机变量及其分布 作业及其答案

第二章 随机变量及其分布18.[十七] 设随机变量X 的分布函数为⎪⎩⎪⎨⎧≥<≤<=.,1,1,ln ,1,0)(e x e x x x x F X ,求(1)P (X<2), P {0<X ≤3}, P (2<X<25);(2)求概率密度f X (x ). 解:(1)P (X ≤2)=F X (2)= ln2, P (0<X ≤3)= F X (3)-F X (0)=1,45ln 2ln 25ln )2()25(252(=-=-=<<X X F F X P (2)⎪⎩⎪⎨⎧<<==其它,0,1,1)(')(e x x x F x f24.[二十二] 设K 在(0,5)上服从均匀分布,求方程02442=+++K xK x 有实根的概率∵ K 的分布密度为:⎪⎩⎪⎨⎧<<-=其他50051)(K K f要方程有根,就是要K 满足(4K )2-4×4× (K+2)≥0。
解不等式,得K ≥2时,方程有实根。
∴53051)()2(5522=+==≥⎰⎰⎰∞+∞+dx dx dx x f K P 25.[二十三] 设X ~N (3.22)(1)求P (2<X ≤5),P (-4)<X ≤10),P {|X|>2},P (X>3)∵ 若X ~N (μ,σ2),则P (α<X ≤β)=φ-⎪⎭⎫ ⎝⎛-σμβφ⎪⎭⎫ ⎝⎛-σμα ∴P (2<X ≤5) =φ-⎪⎭⎫ ⎝⎛-235φ⎪⎭⎫ ⎝⎛-232=φ(1)-φ(-0.5) =0.8413-0.3085=0.5328P (-4<X ≤10) =φ-⎪⎭⎫ ⎝⎛-2310φ⎪⎭⎫ ⎝⎛--234=φ(3.5)-φ(-3.5) =0.9998-0.0002=0.9996P (|X |>2)=1-P (|X |<2)= 1-P (-2< P <2 )=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--Φ-⎪⎭⎫ ⎝⎛-Φ-2322321 =1-φ(-0.5) +φ(-2.5) =1-0.3085+0.0062=0.6977P (X >3)=1-P (X ≤3)=1-φ⎪⎭⎫⎝⎛-233=1-0.5=0.5(2)决定C 使得P (X > C )=P (X ≤C )∵P (X > C )=1-P (X ≤C )= P (X ≤C )得 P (X ≤C )=21=0.5 又P (X ≤C )=φ023,5.023=-=⎪⎭⎫ ⎝⎛-C C 查表可得∴ C =3 28.[二十六] 一工厂生产的电子管的寿命X (以小时计)服从参数为μ=160,σ(未知)的正态分布,若要求P (120<X ≤200==0.80,允许σ最大为多少?∵ P (120<X ≤200)=80.04040160120160200=⎪⎭⎫ ⎝⎛-Φ-⎪⎭⎫ ⎝⎛Φ=⎪⎭⎫ ⎝⎛-Φ-⎪⎭⎫ ⎝⎛-Φσσσσ 又对标准正态分布有φ(-x )=1-φ(x )∴ 上式变为80.040140≥⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛Φ--⎪⎭⎫ ⎝⎛Φσσ 解出9.040:40≥⎪⎭⎫ ⎝⎛Φ⎪⎭⎫ ⎝⎛Φσσ便得 再查表,得25.31281.140281.140=≤≥σσ 31.[二十八] 设随机变量X 在(0,1)上服从均匀分布 (1)求Y=e X 的分布密度∵ X 的分布密度为:⎩⎨⎧<<=为其他x x x f 0101)(Y=g (X ) =e X 是单调增函数 又 X=h (Y )=lnY ,反函数存在且α = min [g (0), g (1)]=min (1, e )=1=βmax [g (0), g (1)]=max (1, e )= e∴ Y 的分布密度为:⎪⎩⎪⎨⎧<<⋅=⋅=为其他y e y yy h y h f y ψ0111|)('|)]([)((2)求Y=-2lnX 的概率密度。
(必考题)高中数学选修三第二单元《随机变量及其分布》测试(有答案解析)

一、选择题1.现有一条零件生产线,每个零件达到优等品的概率都为p .某检验员从该生产线上随机抽检50个零件,设其中优等品零件的个数为X .若()8D X =,(20)P X =(30)P X <=,则p =( ) A .0.16B .0.2C .0.8D .0.842.已知随机变量X 的分布列则对于任意01a b c <<<<,()E X 的取值范围是( )A .10,3⎛⎫ ⎪⎝⎭B .1,13⎛⎫ ⎪⎝⎭C .()0,1D .1,3⎛+∞⎫ ⎪⎝⎭3.假定男女出生率相等,某个家庭有两个小孩,已知该家庭至少有一个女孩,则两个小孩都是女孩的概率是( ) A .12B .13C .14D .164.随机变量ξ的分布列如表所示,若1()3E X =-,则(31)D X +=( )A .4B .5C .6D .75.设01p <<,随机变量ξ的分布列是则当p 在()0,1内增大时( )A .()E ξ减小,()D ξ减小B .()E ξ减小,()D ξ增大C .()E ξ增大,()D ξ减小D .()E ξ增大,()D ξ增大6.从1,2,3,4,5,6,7,8,9中不放回地依次取2个数,事件A 为“第一次取到的是奇数”,B 为“第二次取到的是3的整数倍”,则(|)P B A =( ) A .38B .1340C .1345D .347.已知随机变量~X N ()22,σ,(0)0.84P X=,则(04)P X <<=( )A .0.16B .0.32C .0.66D .0.688.袋中有大小完全相同的2个红球和2个黑球,不放回地依次摸出两球,设“第一次摸得黑球”为事件A ,“摸得的两球不同色”为事件B ,则概率()|P B A 为( ) A .14B .23C .13D .129.随机变量X 服从正态分布()()()210,12810X N P X m P X n σ->==,,≤≤,则12m n+的最小值为( )A .3+B .6+C .3+D .6+10.甲、乙、丙、丁四名同学报名参加假期社区服务活动,社区服务活动共有关怀老人、环境监测、教育咨询、交通宣传等四个项目,每人限报其中一项,记事件A 为4名同学所报项目各不相同”,事件B 为“只有甲同学一人报关怀老人项目”,则(|)P B A =( ) A .14B .34C .29D .5911.某班组织由甲、乙、丙等5名同学参加的演讲比赛,现采用抽签法决定演讲顺序,在“学生甲不是第一个出场,学生乙不是最后一个出场”的前提下,学生丙第一个出场的概率为( ) A .313B .413C .14D .1512.10张奖券中有3张是有奖的,某人从中依次抽取两张.则在第一次抽到中奖券的条件下,第二次也抽到中奖券的概率是( ) A .27B .29C .310D .15二、填空题13.游乐场某游戏设备是一个圆盘,圆盘被分成红色和绿色两个区域,圆盘上有一个可以绕中心旋转的指针,且指针受电子程序控制,前后两次停在相同区域的概率为14,停在不同区域的概率为34,某游客连续转动指针三次,记指针停在绿色区域的次数为X ,若开始时指针停在红色区域,则()E X =______.14.由“0,1,2”组成的三位数密码中,若用A 表示“第二位数字是2”的事件,用B 表示“第一位数字是2”的事件,则(|)P A B =__________.15.一个家庭有两个小孩,假设生男生女是等可能的,已知这个家庭有一个是女孩的条件下,这时另一个也是女孩的概率是________. 16.下列说法中,正确的有_______.①回归直线ˆˆˆy bx a =+恒过点(),x y ,且至少过一个样本点;②根据22⨯列列联表中的数据计算得出2 6.635K ≥,而()26.6350.01P K ≥≈,则有99%的把握认为两个分类变量有关系;③2K 是用来判断两个分类变量是否相关的随机变量,当2K 的值很小时可以推断两个变量不相关;④某项测量结果ξ服从正态分布()21,N a,则(5)0.81P ξ≤=,则(3)0.19P ξ≤-=.17.已知某随机变量X 的分布列如下(,p q R ∈):且X 的数学期望()12E X =,那么X 的方差()D X =__________. 18.(1)10件产品,其中3件是次品,任取2件,若ξ表示取到次品的个数,则()E ξ=_______;(2)设随机变量ξ的分布列为()P k ξ==21C ()()33k k n kn -,k =0,1,2,…,n ,且()24E ξ=,则()D ξ= _______;(3)设袋中有两个红球一个黑球,除颜色不同,其他均相同,现有放回地抽取,每次抽取一个,记下颜色后放回袋中,连续摸三次,X 表示三次中红球被摸中的次数(每个小球被抽取的概率相同,每次抽取相互独立),则方差()D X =______.三、解答题19.已知某射手射中固定靶的概率为34,射中移动靶的概率为23,每次射中固定靶、移动靶分别得1分、2分,脱靶均得0分,每次射击的结果相互独立,该射手进行3次打靶射击:向固定靶射击1次,向移动靶射击2次.(1)求“该射手射中固定靶且恰好射中移动靶1次”的概率; (2)求该射手的总得分X 的分布列和数学期望.20.某校拟举办“成语大赛”,高一(1)班的甲、乙两名同学在本班参加“成语大赛”选拔测试,在相同的测试条件下,两人5次测试的成绩(单位:分)的茎叶图如图所示.(1)你认为选派谁参赛更好?并说明理由;(2)若从甲、乙两人5次的成绩中各随机抽取1次进行分析,设抽到的2次成绩中,90分以上的次数为X ,求随机变量X 的分布列和数学期望()E X .21.在某校举行的数学竞赛中,全体参赛学生的竞赛成绩ξ近似服从正态分布()70,100N .已知成绩在90分以上(含90分)的学生有12名.(1)此次参赛的学生总数约为多少人?(2)若该校计划奖励竞赛成绩排在前50名的学生,则设奖的分数线约为多少分? 说明:对任何一个正态分布()2~,X Nμσ来说,通过1X Z μσ-=转化为标准正态分布()~0,1Z N ,从而查标准正态分布表得到()()1P X X Z <=Φ. 参考数据:可供查阅的(部分)标准正态分布表()Z Φ Z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 1.2 0.8849 0.869 0.8888 0.8907 0.8925 0.8944 0.8962 0.8980 0.8997 0.9015 1.3 0.9032 0.9049 0.9066 0.9082 0.9099 0.9115 0.9131 0.9147 0.9162 0.9177 1.4 0.9192 0.9207 0.9222 0.9236 0.9251 0.9265 0.9279 0.9292 0.9306 0.9319 1.9 0.9713 0.9719 0.9726 0.9732 0.9738 0.9744 0.9750 0.9756 0.9762 0.9767 2.0 0.9772 0.9778 0.9783 0.9788 0.9793 0.9798 0.9803 0.9808 0.9812 0.9817 2.10.98210.98260.98300.98340.98380.98420.98460.98500.98540.985722.为了解学生寒假期间学习情况,学校对某班男、女学生学习时间进行调查,学习时间按整小时统计,调查结果绘制成折线图如下:(1)已知该校有400名学生,试估计全校学生中,每天学习不足4小时的人数; (2)若从学习时间不少于4小时的学生中选取4人,设选取的男生人数为X ,求随机变量X 的分布列及均值E (X );(3)试比较男生学习时间的方差21s 与女生学习时间的方差22s 的大小.(只需写出结论) 23.为检测某种抗病毒疫苗的免疫效果,某药物研究所科研人员随机选取100只小白鼠,并将该疫苗首次注射到这些小白鼠体内.独立环境下试验一段时间后检测这些小白鼠的某项医学指标值并制成如下的频率分布直方图(以小白鼠医学指标值在各个区间上的频率代替其概率):(1)根据频率分布直方图,估计100只小白鼠该项医学指标平均值x (同一组数据用该组数据区间的中点值表示);(2)若认为小白鼠的该项医学指标值X 服从正态分布()2,N μσ,且首次注射疫苗的小白鼠该项医学指标值不低于14.77时,则认定其体内已经产生抗体;进一步研究还发现,对第一次注射疫苗的100只小白鼠中没有产生抗体的那一部分群体进行第二次注射疫苗,约有10只小白鼠又产生了抗体.这里μ近似为小白鼠医学指标平均值x ,2σ近似为样本方差2s .经计算得2 6.92s =,假设两次注射疫苗相互独立,求一只小白鼠注射疫苗后产生抗体的概率p (精确到0.01). 附:参考数据与公式6.92 2.63≈,若()2~,X N μσ,则①()0.6827P X μσμσ-<≤+=;②()220.9545P X μσμσ-<≤+=;③()330.9973P X μσμσ-<≤+=. 24.甲、乙两人进行乒乓球比赛,规定比赛进行到有一人比对方多赢2局或打满6局时比赛结束.设甲、乙在每局比赛中获胜的概率均为12,各局比赛相互独立,用X 表示比赛结束时的比赛局数(1)求比赛结束时甲只获胜一局的概率; (2)求X 的分布列和数学期望.25.现有编号为1,2,3的三只小球和编号为1,2,3的三个盒子,将三只小球逐个随机地放入三个盒子中,每只球的放置相互独立. (1)求恰有一个空盒的概率;(2)求三只小球在三个不同盒子中,且每只球编号与所在盒子编号不同的概率; (3)记录所有至少有一只球的盒子,以X 表示这些盒子编号的最小值,求()E X . 26.某学校为了了解学生暑假期间学习数学的情况,抽取了人数相等的甲、乙两班进行调查,甲班同学每天学习数学的平均时间的频率分布直方图(将时间分成[0,1),[1,2),[2,3),[3,4),[4,5),[5,6]共6组)和乙班同学每天学习数学的平均时间的频数分布表如图所示(单位:小时).(1)从甲班每天学习数学的平均时间在[0,2)的人中随机选出3人,求3人中恰有1人学习数学的平均时间在[0,1)范围内的概率;(2)从甲、乙两个班每天学习数学平均时间不小于5个小时的学生中随机抽取4人进一步了解其他情况,设4人中乙班学生的人数为ξ,求ξ的分布列和数学期望.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】由(20)(30)p X P X =<=求出的范围,再由方差公式求出值.【详解】∵(20)(30)p X P X =<=,∴2020303030205050(1)(1)C p p C p p -<-,化简得1p p -<,即12p >,又()850(1)D X p p ==-,解得0.2p =或0.8p =,∴0.8p =,故选C . 【点睛】 本题考查概率公式与方差公式,掌握这两个公式是解题的关键,本题属于基础题.2.B解析:B 【分析】由题易得222()E X a b c =++,结合题中条件再由基本不等式可得2222()133a b c a b c ++++>=,即1()3E X >;再由2222()2()12()1a b c a b c ab bc ca ab bc ca ++=++-++=-++<,即()1E X <,最后得出()E X 的取值范围. 【详解】由随机变量的期望定义可得出222()E X a b c =++, 因为01a b c <<<<,且1a b c ++=,所以222222222a b aba c acbc bc ⎧+>⎪+>⎨⎪+>⎩,三式相加并化简可得222a b c ab bc ac ++>++,故2222222222()2222()3()a b c a b c ac bc ab a b c ac bc ab a b c ++=+++++=+++++<++,即2222()133a b c a b c ++++>=,所以2()1()33a b c E X ++>=,又因为2()()2()12()1E X a b c ab bc ca ab bc ca =++-++=-++<,所以1()13E X <<. 故选:B . 【点睛】本题考查随机变量的期望,考查基本不等式的应用,考查逻辑思维能力和运算求解能力,属于常考题.3.B解析:B 【分析】记事件A 为“至少有一个女孩”,事件B 为“另一个也是女孩”,分别求出A 、B 的结果个数,问题是求在事件A 发生的情况下,事件B 发生的概率,即求(|)P B A ,由条件概率公式求解即可. 【详解】解:一个家庭中有两个小孩只有4种可能:{男,男},{男,女},{女,男},{女,女}.记事件A 为“至少有一个女孩”,事件B 为“另一个也是女孩”,则{A =(男,女),(女,男),(女,女)},{B =(男,女),(女,男),(女,女)},{AB =(女,女)}.于是可知3()4P A =,1()4P AB =. 问题是求在事件A 发生的情况下,事件B 发生的概率,即求(|)P B A ,由条件概率公式,得()114334P B A ==.故选:B . 【点睛】本题的考点是条件概率与独立事件,主要考查条件概率的计算公式:()()()P AB P B A P A =,等可能事件的概率的求解公式:()mP M n=(其中n 为试验的所有结果,m 为基本事件的结果).4.B解析:B 【分析】 由于()13E X =-,利用随机变量的分布列列式,求出a 和b ,由此可求出()D X ,再由()(319)X D D X +=,即可求出结果.根据题意,可知:112a b ++=,则12a b +=, ()13E X =-,即:1123b -+=-,解得:16b =,13a ∴=,()22211111151013233369X D ⎛⎫⎛⎫⎛⎫∴=-+⨯++⨯++⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则()59959(31)D D X X ==⨯+=, ∴5(31)D X +=.故选:B. 【点睛】本题考查离散型随机变量的方差的求法,以及离散型随机变量的分布列、数学期望等知识,考查运算求解能力.5.B解析:B 【分析】根据题意计算随机变量ξ的分布列和方差,再判断p 在(0,1)内增大时,()E ξ、()D ξ的单调性即可. 【详解】解:设01p <<,随机变量ξ的分布列是1131()01222222p p E p ξ-=⨯+⨯+⨯=-, 方差是22231311311()(0)(1)(2)222222222p p D p p p ξ-=-+⨯+-+⨯+-+⨯ 21144p p =-++ 215(2)44p =--+,当p 在(0,1)内增大时,()E ξ减小,()D ξ增大.故选:B . 【点睛】本题考查了离散型随机变量的数学期望与方差的计算问题,也考查了运算求解能力.6.B【分析】由条件概率的定义()(|)()P A B P B A P A =,分别计算(),()P A B P A 即得解.【详解】 由题意5()9P A = 事件AB 为“第一次取到的是奇数且第二次取到的是3的整数倍”:若第一次取到的为3或9,第二次有2种情况;若第一次取到的为1,5,7,第二次有3种情况,故共有223313⨯+⨯=个事件1313()9872P A B ==⨯由条件概率的定义:()13(|)()40P A B P B A P A ==故选:B 【点睛】本题考查了条件概率的计算,考查了学生概念理解,分类讨论,数学运算的能力,属于中档题.7.D解析:D 【分析】先由对称性求出(X 4)P ≥,再利用(04)12(4)P X P X <<=-≥即得解. 【详解】由于随机变量~X N ()22,σ,关于2X =对称,故(4)(0)1(0)10.840.16P X P X P X ≥=≤=-≥=-= (04)12(4)10.320.68P X P X ∴<<=-≥=-=故选:D 【点睛】本题考查了正态分布在给定区间的概率,考查了学生概念理解,数形结合,数学运算的能力,属于基础题.8.B解析:B 【分析】根据题目可知,求出事件A 的概率,事件AB 同时发生的概率,利用条件概率公式求得()|P B A ,即可求解出答案.【详解】依题意,()1214C 1C 2P A ==,()11221143C C 1C C 3P AB ==,则条件概率()()()123|132P AB P B A P A ===.故答案选B . 【点睛】本题主要考查了利用条件概率的公式计算事件的概率,解题时要理清思路,注意()P AB 的求解.9.D解析:D 【分析】利用正态密度曲线的对称性得出12m n +=,再将代数式22m n +与12m n +相乘,展开后可利用基本不等式求出12m n+的最小值. 【详解】 由于()210,XN σ,由正态密度曲线的对称性可知,()()128P X P X m >=<=,所以,()()188102P X P X <+≤≤=,即12m n +=,221m n ∴+=, 由基本不等式可得()1212422266m n m n m n m n n m ⎛⎫+=++=++≥ ⎪⎝⎭6=, 当且仅当()420,0m n m n n m=>>,即当n =时,等号成立, 因此,12m n +的最小值为6+,故选D. 【点睛】本题考查正态密度概率以及利用基本不等式求最值,解题关键在于利用正态密度曲线的对称性得出定值,以及对所求代数式进行配凑,以便利用基本不等式求最值,考查计算能力,属于中等题.10.A解析:A 【分析】确定事件AB ,利用古典概型的概率公式计算出()P AB 和()P A ,再利用条件概型的概率公式可计算出()P B A 的值. 【详解】事件AB 为“4名同学所报项目各不相同且只有甲同学一人报关怀老人项目”,则()3344A P AB =,()4444A P A =,()()()3434444144P AB A P B A P A A ∴==⋅=,故选A. 【点睛】本题考查条件概型概率的计算,考查条件概率公式的理解和应用,考查运算能力,属于中等题.11.A解析:A 【分析】根据条件概率的计算公式,分别求解公式各个部分的概率,从而求得结果. 【详解】设事件A 为“学生甲不是第一个出场,学生乙不是最后一个出场”;事件B 为“学生丙第一个出场”则()41134333555578A C C A P A A A +==,()1333555518C A P AB A A == 则()()()1837813P AB P B A P A === 本题正确选项:A 【点睛】本题考查条件概率的求解,关键是能够利用排列组合的知识求解出公式各个构成部分的概率.12.B解析:B 【分析】根据第一次抽完的情况下重新计算总共样本数和满足条件样本数,再由古典概型求得概率. 【详解】在第一次抽中奖后,剩下9张奖券,且只有2张是有奖的,所以根据古典概型可知,第二次中奖的概率为29P =.选B. 【点睛】事件A 发生的条件下,事件B 发生的概率称为“事件A 发生的条件下,事件B 发生的条件概率”,记为(|)P B A ;条件概率常有两种处理方法: (1)条件概率公式:()(|)()P AB P B A P A =. (2)缩小样本空间,即在事件A 发生后的己知事实情况下,用新的样本空间的样本总数和满足特征的样本总数来计算事件B 发生的概率.二、填空题13.【分析】依题意画出数形图即可求出的分布列即可求出数学期望;【详解】解:该游客转动指针三次的结果的树形图如下:则的分布列如下:0 1 2 3 故故答案为:【点睛】本题考查概率的计算随机解析:27 16【分析】依题意画出数形图,即可求出X的分布列,即可求出数学期望;【详解】解:该游客转动指针三次的结果的树形图如下:则X的分布列如下:X0123P 16421643964364故()01236464646416 E X=⨯+⨯+⨯+⨯=.故答案为:27 16【点睛】本题考查概率的计算,随机变量的分布列和数学期望,解答的关键是画出树形图. 14.【分析】利用古典摡型的概率计算公式分别求得结合条件概率的计算公式即可求解【详解】由012组成的三位数密码共有个基本事件又由用A表示第二位数字是2的事件用B表示第一位数字是2的事件可得所以故答案为:【解析:1 3【分析】利用古典摡型的概率计算公式,分别求得(),()P B P A B,结合条件概率的计算公式,即【详解】由“0,1,2”组成的三位数密码,共有33327⨯⨯=个基本事件,又由用A表示“第二位数字是2”的事件,用B表示“第一位数字是2”的事件,可得33131 (),()273279P B P A B⨯====,所以1()19 (|)1()33P A BP A BP B===.故答案为:1 3 .【点睛】本题主要考查了条件概率的计算与求解,其中解答中熟记条件概率的计算公式,准确运算时解答得关键,属于基础题.15.【分析】利用列举法求出已知这个家庭有一个是女孩的条件下基本事件总数n=3这时另一个也是女孩包含的基本事件个数m=1由此能求出已知这个家庭有一个是女孩的条件下这时另一个也是女孩的概率【详解】一个家庭有解析:1 3【分析】利用列举法求出已知这个家庭有一个是女孩的条件下,基本事件总数n=3,这时另一个也是女孩包含的基本事件个数m=1,由此能求出已知这个家庭有一个是女孩的条件下,这时另一个也是女孩的概率.【详解】一个家庭有两个小孩,假设生男生女是等可能的,基本事件有: {男,男},{男,女},{女,男},{女,女},已知这个家庭有一个女孩的条件下,基本事件总数n=3 ,这时另一个也是女孩包含的基本事件个数m=1,∴已知这个家庭有一个女孩的条件下,这时另一个也是女孩的概率是13mpn==,故答案为:1 3【点睛】本题主要考查了条件概率,可以列举在某条件发生的情况下,所有事件的个数及所研究事件的个数,利用古典概型求解,属于中档题.16.②④【分析】由回归直线的性质判断①;由独立性检验的性质判断②③;由正态分布的特点判断④【详解】回归直线恒过点但不一定要过样本点故①错误;由得有99的把握认为两个分类变量有关系故②正确;的值很小解析:②④ 【分析】由回归直线的性质判断①;由独立性检验的性质判断②③;由正态分布的特点判断④. 【详解】回归直线ˆˆˆybx a =+恒过点(),x y ,但不一定要过样本点,故①错误; 由2 6.635K ≥,得有99%的把握认为两个分类变量有关系,故②正确;2K 的值很小时,只能说两个变量的相关程度低,不能说明两个变量不相关,故③错误;(5)0.81P ξ≤=,(5)(3)10.810.19P P ξξ∴>=<-=-=,故④正确;故答案为:②④ 【点睛】本题主要考查了正态分布求指定区间的概率等,属于中等题.17.【解析】根据题意可得解得故的方差解析:34【解析】根据题意可得112p q p q +=⎧⎪⎨-=⎪⎩,解得34p =,14q =,故X 的方差()22131131124244D X ⎛⎫⎛⎫=-⨯+--⨯= ⎪ ⎪⎝⎭⎝⎭.18.8【解析】(1)由题意得随机变量的可能取值为012所以(2)由题意可知所以解得所以(3)每次取球时取到红球的概率为黑球的概率为所以服从二项分布即所以解析:358 23 【解析】(1)由题意得,随机变量ξ的可能取值为0,1,2,()27210C 70C 15P ξ===,()1P ξ=1173210C C 7C 15==, ()23210C 12C 15P ξ===,所以()77130121515155E ξ=⨯+⨯+⨯=. (2)由题意可知2,3B n ξ⎛⎫ ⎪⎝⎭~,所以()2243n E ξ==,解得36n =,所以()D ξ= 22361833⎛⎫⨯⨯-= ⎪⎝⎭.(3)每次取球时,取到红球的概率为23、黑球的概率为13,所以X 服从二项分布,即23,3X B ⎛⎫~ ⎪⎝⎭,所以()22231333D X ⎛⎫=⨯⨯-= ⎪⎝⎭.三、解答题19.(1)13;(2)分布列答案见解析,数学期望:4112. 【分析】(1)记“该射手射中固定靶且恰好射中移动靶1次”为事件D ,得到D ABC BC A =+,结合互斥事件和相互独立事件的概率计算公式,即可求解;(2)随机变量X 的可能取值为0,1,2,3,4,5,根据互斥事件和相互独立事件的概率计算公式,求得相应的概率,得出分布列,利用期望的公式,即可求解. 【详解】(1)记“该射手射中固定靶且恰好射中移动靶1次”为事件D , 则()34P A =,()()23P B P C ==, D ABC BC A =+,其中ABC C AB +互斥,,,,,A B C B C 相互独立,从而()()()()322114336P ABC P A P B P C ⎛⎫==⨯-= ⎪⎝⎭, 则()()()()13P D P ABC ABC P ABC P ABC =+=+=, 所以该射手射中固定靶且恰好射中移动靶1次的概率为13. (2)随机变量X 的可能取值为0,1,2,3,4,5, 则()()()()()3221011143336P X P ABC P A P B P C ⎛⎫⎛⎫⎛⎫====---=⎪⎪⎪⎝⎭⎝⎭⎝⎭, ()()()()()3111143312P X P ABC P A P B P C ====⨯⨯=,1211121(2)()()()()()()()4334339P X P ABC ABC P A P B P C P A P B P C ==+=+=⨯⨯+⨯⨯=,()()()()()()()()321312134334333P X P ABC ABC P A P B P C P A P B P C ==+=+=⨯⨯+⨯⨯=()()()()()122144339P X P ABC P A P B P C ====⨯⨯=,3221(5)()()()()4333P X P ABC P A P B P C ====⨯⨯=,该射手的总得分X 的分布列为随机变量X 的数学期望()012345.3612939312E X =⨯+⨯+⨯+⨯+⨯+⨯= 【点睛】求随机变量X 的期望与方差的方法及步骤: 理解随机变量X 的意义,写出X 可能的全部值; 求X 取每个值对应的概率,写出随机变量的分布列; 由期望和方差的计算公式,求得数学期望()(),E X D X ;若随机变量X 的分布列为特殊分布列(如:两点分布、二项分布、超几何分布),可利用特殊分布列的期望和方差的公式求解.20.(1)选派乙参赛更好,理由见解析;(2)分布列见解析,()25E X =. 【分析】(1)计算出甲、乙两人5次测试的成绩的平均分与方差,由此可得出结论;(2)由题意可知,随机变量X 的取值有0、1、2,计算出随机变量X 在不同取值下的概率,可得出随机变量X 的分布列,进而可计算得出()E X . 【详解】(1)甲5次测试成绩的平均分为555876889236955x ++++==甲,方差为22222213693693693693695704555876889255555525s ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-+-=⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦甲,乙5次测试成绩的平均分为658287859541455x ++++==乙,方差为22222214144144144144142444658285879555555525s ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-+-=⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦乙,所以,x x <甲乙,22s s >甲乙,因此,选派乙参赛更好;(2)由题意可知,随机变量X 的可能取值有0、1、2,()24160525P X ⎛⎫=== ⎪⎝⎭,()148125525P X ==⨯⨯=,()2112525P X ⎛⎫=== ⎪⎝⎭, 所以,随机变量X 的分布列如下表所示:因此,()0122525255E X =⨯+⨯+⨯=. 【点睛】思路点睛:求解随机变量分布列的基本步骤如下:(1)明确随机变量的可能取值,并确定随机变量服从何种概率分布; (2)求出每一个随机变量取值的概率;(3)列成表格,对于抽样问题,要特别注意放回与不放回的区别,一般地,不放回抽样由排列、组合数公式求随机变量在不同取值下的概率,放回抽样由分步乘法计数原理求随机变量在不同取值下的概率. 21.(1)526(人);(2)83分. 【分析】(1)由题意知9070(90)(2)10P ξ-⎛⎫<=Φ=Φ ⎪⎝⎭,则(90)1(90)P P ξξ=-<可求,结合对应人数可得总人数;(2)假定设奖的分数线为x 分,由题意知7050()10.095110526x P x ξ-⎛⎫=-Φ== ⎪⎝⎭,查表得x 值.【详解】 (1)由题意知9070(90)1(90)11(2)10.97720.022810P P ξξ-⎛⎫=-<=-Φ=-Φ=-= ⎪⎝⎭,故此次参赛的学生总数约为125260.0228≈(人).(2)假定设奖的分数线为x 分,由题意知7050()1()10.095110526x P x P x ξξ-⎛⎫=-<=-Φ== ⎪⎝⎭, 即700.904910x -⎛⎫Φ=⎪⎝⎭,查表得70 1.3110x -=, 解得83.1x =,故设奖的分数线约为83分.【点睛】本题关键在于正确理解正态分布概率计算公式及运用. 22.(1)240人;(2)分布列见解析,2;(3)2212s s >. 【分析】(1)由折线图分析可得20名学生中有12名学生每天学习不足4小时,把频率当概率可以估计校400名学生中天学习不足4小时的人数;(2)学习时间不少于4本的学生共8人,其中男学生人数为4人,故X 的取值为0,1,2,3,4;利用组合知识,由古典概型公式计算可得X =0,1,2,3,4的概率,进而可得随机变量X 的分布列;(3)根据折线图,看出男生、女生的学习时间的集中与分散程度,根据方差的实际意义可得答案. 【详解】(1)由折线图可得共抽取了20人,其中男生中学习时间不足4小时的有8人,女生中学习时间不足4小时的有4人.故可估计全校学生中每天学习时间不足4小时的人数为400×1220=240. (2)学习时间不少于4小时的学生共8人,其中男生人数为4, 故X 的所有可能取值为0,1,2,3,4. 由题意可得P (X=0)=4448170C C =,P (X=1)=1344481687035C C C ==, P (X=2)=22444836187035C C C ==, P (X=3)=3144481687035C C C ==, P (X=4)=4448170C C =.∴均值E (X )=0×170+1×835+2×1835+3×835+4×170=2.(3)由折线图可得2212s s >. 【点睛】方法点睛:本题考查了折线统计图和超几何分布,考查了离散型随机变量分布列和数学期望的计算,求解离散型随机变量分布列的步骤是: 首先确定随机变量X 的所有可能取值;计算X 取得每一个值的概率,可通过所有概率和为1来检验是否正确; 进行列表,画出分布列的表格;最后扣题,根据题意求数学期望或者其它. 23.(1)17.4;(2)0.94. 【分析】(1)利用每一个小矩形的面积乘以对应的底边中点的横坐标之和即为x ;(2)先计算第一次注射疫苗后产生抗体的概率()()14.77P x P x μσ≥=≥-,即可计算第一次注射疫苗后100只小白鼠中产生抗体的数量,加上第二次注射疫苗10只小白鼠又产生了抗体,可以得出两次注射疫苗产生抗体的总数,即可求概率. 【详解】(1)0.021220.061420.141620.181820.05202x =⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯0.032220.0224217.4+⨯⨯+⨯⨯= (2)17.40 2.6314.77μσ-=-=∴()10.68270.68270.84142P x μσ-≥-=+= 记事件A 表示首先注射疫苗后产生抗体,则()()()14.770.8414P A P x P x μσ=≥=≥-=,因此100只小鼠首先注射疫苗后有1000.841484⨯≈只产生抗体,有1008416-=只没有产生抗体.故注射疫苗后产生抗体的概率84100.94100P +==. 【点睛】 结论点睛:频率分布直方图的相关公式以及数字特征的计算, ①直方图中各个小长方形的面积之和为1; ②直方图中每组样本的频数为频率乘以总数; ③最高的小矩形底边中点横坐标即是众数; ④中位数的左边和右边小长方形面积之和相等;⑤平均数是频率分布直方图的重心,等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和. 24.(1)18;(2)分布列见解析,()72E X =.【分析】(1)先分析出甲只获胜一局的所有情况,然后根据对应的情况去计算概率;(2)先分析X 的可能取值,然后根据取值列出对应的比赛获胜情况,由此计算出对应的概率,可得X 的分布列,根据分布列可计算出数学期望.【详解】(1)因为比赛结束时甲只获胜一局,所以一共比赛了4局,且甲在第1局或第2局赢了,当甲在第1局赢了,则乙在后面3局都赢了,此事件的概率为:31112216⎛⎫⋅= ⎪⎝⎭,当甲在第2局赢了,则乙在第1,3,4局赢了,此事件的概率为:2111122216⎛⎫⋅⋅= ⎪⎝⎭,记“比赛结束时甲只获胜一局”为事件A ,则()112168P A =⨯=; (2)根据条件可知:X 可取2,4,6,当2X =时,包含甲或乙前2局连胜,此时2种情况:{甲,甲},{乙,乙};当4X =时,包含甲或乙前2局赢了1局,后2局都没赢,此时4种情况:{甲,乙,乙,乙},{乙,甲,乙,乙},{乙,甲,甲,甲},{甲,乙,甲,甲}(大括号中,按顺序为各局的获胜者);()2112222P X ⎛⎫==⋅= ⎪⎝⎭,()4114424P X ⎛⎫==⋅= ⎪⎝⎭,()()()161244P X P X P X ==-=-==, 所以X 的分布列为:所以()2462442E X =⨯+⨯+⨯=. 【点睛】思路点睛:求离散型随机变量X 的数学期望的一般步骤: (1)先分析X 的可取值,根据可取值求解出对应的概率; (2)根据(1)中概率值,得到X 的分布列;(3)结合(2)中分布列,根据期望的计算公式求解出X 的数学期望. 25.(1)23;(2)227;(3)43. 【分析】(1)方法一:将三个小球放在盒子的基本事件全部写出来,写出满足条件的基本事件,用满足条件的个数除以总的个数计算其概率; 方法二:用排列组合数表示;(2)方法一:将三个小球放在盒子的基本事件全部写出来,写出满足条件的基本事件,用满足条件的个数除以总的个数计算其概率;方法二:用排列组合数表示;(3)方法一:将三个小球放在盒子的基本事件全部写出来,写出满足条件的基本事件,用满足条件的个数除以总的个数计算其概率;方法二:用排列组合数表示;【详解】解:方法一:记三个球分别为①,②,③,试验的全部基本事件如下表:共27种.根据古典概型公式()182 273P A==.(2)记“三只小球在三个不同盒子中,且每只球的编号与所在盒子编号不同”为事件B,事件B包含的基本事件数有2种.根据古典概型公式2 ()27 P B=.(3)X的可能取值为1,2,3.。
随机变量及其分布_真题(含答案与解析)-交互

随机变量及其分布(总分102, 做题时间90分钟)一、单项选择题(每题的备选项中,只有1个最符合题意)1.下列关于“右偏分布”的表述错误的是( )。
SSS_SINGLE_SELA 右偏分布是正态分布的形式之一B 符合右偏分布的随机变量大量取值在左边,少量分布在右边C 符合右偏分布的随机变量少量取值在左边,大量分布在右边D 随机变量的分布很散分值: 1答案:B[解析] 对数正态分布的特点之一就是“右偏分布”,符合右偏分布的随机变量的取值大量在左边,少量取值在右边,并且很分散。
2.对于产品的某个质量特性X的不合格品率,在计算之前需要知道的条件有( )。
SSS_SINGLE_SELA产品质量特性X的分布,在过程受控情况下X的分布常为正态分布(μ,σ2),这是稳定过程的概括B 某个公认标准对产品特性的要求C 企业对产品下达的任务书D X低于下规范限的概率和X高于上规范限的概率分值: 1答案:A[解析] 产品某个质量特性X的不合格品率的计算要知道两件事:①质量特性X 的分布,在过程受控情况下,X的分布常为正态分布N(μ,σ2),这是稳定过程的概括;②产品的规格限,包括上规格限TU 和下规格限TL。
3.设某二项分布的均值等于3,方差等于2.7,则二项分布参数P=( )。
SSS_SINGLE_SELA 0.1B 0.3C 0.7D 0.9分值: 1答案:A[解析] 此二项分布记为b(n,p),则E(X)=np,Var(X)=np(1-p),根据题意,代入数据可得np=3,np(1-p)=2.7,所以p=0.1。
4.对下列常见密度函数所对应的方差的形式正确的一项是( )。
SSS_SINGLE_SELA 两点分布b(1,的方差:np(1-B 超几何分布h(n,N,的方差:n(N-/(N-1)•(M/(1-(M/)C均匀分布U(a,的方差:(b+ 2/12D对数正态分布LN(μ,σ2)的方差:分值: 1答案:B[解析] A项两点分布的方差为p(1-p);C项均匀分布的方差为(b-a)2/12;D项对数正态分布的方差为。
概率论与数理统计教程习题(第二章随机变量及其分布)答案

15.设X为正态分布的随机变量,概率密度为 ,则 9
16.已知X~B(n,p),且E(X)=8,D(X)=4.8,则n=。
17.设随机变量X的密度函数为 ,则 0
二、单项选择题
1.甲、乙、丙三人射击的命中率分别为0.5、0.6、0.7,则三人都未命中的概率为(D)
解:设同一时刻被使用的供水设备的套数为 则 (二项分布).
于是, ,( 0,1,2,3,4,5),即
.,Biblioteka ,.3.若某型号电子元件的使用寿命 (单位: ),(1)写出概率密度 ;(2)求概率 ;(3)求这样的5个独立使用的元件在15000小时后至多有两个能使用的概率。.
解:(1)随机变量 的概率密度为
C.1/3D.1/2
4.设随机变量X的概率密度为 ,则X服从(A)
A.正态分布B.指数分布
C.泊松分布D.均匀分布
5.设随机变量 ,且 ,则参数 的值分别为(B)
A.4和0.6B.6和0.4
C. 8和0.3D.3和0.8
6.设随机变量X的概率密度为 则 ( B )
A. B.
C. D.
7. 设 为随机变量且 , 为常数,则下列各式中不正确的是( D )
(2)
(3)用 表示5个这样独立使用的元件在15000小时后仍能使用的个数,
则 服从二项分布 .于是
4.甲、乙两台自动机床,生产同一种标准件,生产2000只所出的次品数分别用X、Y来表示,经过一段时间的考察,X、Y的分布律分别为:
X
0
1
2
3
P
0.6
0.2
0.1
(完整版)概率论与数理统计及其应用课后答案(浙大版)第2章随机变量及其分布

第2章 随机变量及其分布1,解:显然,Y 是一个离散型的随机变量,Y 取k 表明第k 个人是A 型血而前1-k 个人都不是A 型血,因此有116.04.0)4.01(4.0}{--⨯=-⨯==k k k Y P , (Λ,3,2,1=k )上式就是随机变量Y 的分布律(这是一个几何分布)。
2,解:X 只能取值0,1,2。
设以)3,2,1(=i A i 记第i 个阀门没有打开这一事件。
则)}(){()}({}0{3121321A A A A P A A A P X P ⋃=⋃==)()()()()()()(}{}{}{32131213213121A P A P A P A P A P A P A P A A A P A A P A A P -+=-+= 072.0)8.01()8.01()8.01(322=---+-=,类似有512.08.0)()}({}2{3321321=====A A A P A A A P X P ,416.0}2{}0{1}1{==-=-==X P X P X P ,综上所述,可得分布律为3,解:根据题意,随机变量X 服从二项分布B(15, 0.2),分布律为15,2,1,0,8.02.0)(1515Λ=⨯⨯==-k C k X P k k k 。
(1),2501.08.02.0)3(123315=⨯⨯==C X P(2)8329.0)0()1(1)2(==-=-=≥X P X P X P ;(3)6129.0)3()2()1()31(==+=+==≤≤X P X P X P X P ;(4))2()3()4()5(1)5(=-=-=-=-=>X P X P X P X P X P0611.0)0()1(==-=-X P X P4,解:对于][5/3G 系统,当至少有3个元件正常工作时,系统正常工作。
而系统中正常工作的元件个数X 服从二项分布B(5, 0.9),所以系统正常工作的概率为99144.01.09.0)(535553=⨯⨯==∑∑=-=k k k k k Ck X P5,解:根据题意,次品数X 服从二项分布B(8000, 0.001),所以∑=-⨯=≤=<6080008000999.0001.0)6()7(k k k kC X P X P3134.0!8!)001.08000(6860001.08000==⨯≈∑∑=-=⨯-k k k k k e k e (查表得)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
概率论与数理统计练习题系 专业 班 姓名 学号第二章 随机变量及其分布(一)一.选择题:1.设X 是离散型随机变量,以下可以作为X 的概率分布是 [ B ](A )1234111124816Xx x x x p (B ) 123411112488X x x x x p (C )1234111123412Xx x x x p(D ) 1234111123412X x x x x p -2.设随机变量ξ的分布列为 01230.10.30.40.2X p )(x F 为其分布函数,则)2(F = [ C ](A ) (B ) (C ) (D )1 二、填空题:1.设随机变量X 的概率分布为0120.20.5X p a ,则a =2.某产品15件,其中有次品2件。
现从中任取3件,则抽得次品数X 的概率分布为313315660105()C P X C ===,12213315361105()C C P x C ===,2121331532105()C C P x C === 3.设射手每次击中目标的概率为,连续射击10次,则击中目标次数X 的概率分布为1010070301210()(.)(.)(,,,,)k k kP X k C k -===三、计算题:1.同时掷两颗骰子,设随机变量X 为“两颗骰子点数之和”求: (1)X 的概率分布; (2)(3)P X ≤; (3)(12)P X > 解:(1)1236()P X ==, 2336()P X ==, 3436()P X ==, 4536()P X ==, 5636()P X ==, 6736()P X ==, 5836()P X ==, 4936()P X ==31036()P X ==, 21136()P X ==, 11236()P X == 所以 X 的概率分布列:X 2 3 4 5 6 7 8 9 10 11 12 P 136 236 336 436 536 636 536 436 336 236 136(2)3336()P X ≤= (3) P(X>12)=02.产品有一、二、三等品及废品四种,其中一、二、三等品及废品率分别为60%,10%,20%及10%,任取一个产品检查其质量,试用随机变量X 描述检查结果。
解:设X=1、2、3及4分别表示一、二、三等品及废品X 1 2 3 4P3.已知随机变量X 只能取1-,0,1,2四个值,相应概率依次为1357,,,24816c c c c,试确定常数c ,并计算(1)P X < 解:由于1()X k ==∑,即1357124816c c c c+++= 所以3716C =110()()()P X P X P X <==-+= 8412373737=+=4.一袋中装有5只球编号1,2,3,4,5。
在袋中同时取3只,以X 表示取出的3只球中最大号码,写出随机变量X 的分布律和分布函数。
解:X 的可能取值为3、4、5。
随机变量X 的分布律为:3511310()P X C ===,23353410()C P X C ===,24356510()C P X C ===X 分布函数为030134044515.().x x F x x x <⎧⎪≤<⎪=⎨≤<⎪⎪≥⎩5.设随机变量~(2,),~(3,)X B P Y B P ,若5{1}9P X ≥=,求{1}P Y ≥ 解:由于0225{1}1(1)1(0)1(1)9P X P X P X C p p ≥=-<=-==--= 所以13p =30311819{1}1(1)1(0)111332727P Y P Y P Y C ⎛⎫⎛⎫≥=-<=-==--=-= ⎪⎪⎝⎭⎝⎭概率论与数理统计练习题系 专业 班 姓名 学号第二章 随机变量及其分布(二)一、选择题:1.设连续性随机变量X 的密度函数为201()0x x f x <<⎧=⎨⎩其他,则下列等式成立的是 [ A ](A )(1)1P X ≥-= (B)11()22P X ==(C)11()22P X <= (D)11()22P X >= 2.设连续性随机变量X 的密度函数为ln [1,]()0[1,]x x b f x x b ∈⎧=⎨∉⎩,则常数b = [ A ](A )e (B )1e + (C )1e - (D )2e3.设2~(,)X N μσ,要使~(0,1)Y N ,则 [ C ] (A )XY μσ=+ (B )Y X σμ=+ (C )X Y μσ-=(D )Y X σμ=-4.设~(0,1)X N,22()0)x x x edt x --∞Φ=≥(,则下列等式不成立的是 [ C ](A )()1()x x Φ=-Φ- (B )(0)0.5Φ= (C )()()x x Φ-=Φ (D )(||)2()1P x a a <=Φ- 5.X 服从参数19λ=的指数分布,则(39)P X <<= [ C ] (A )1(1)()3F F - (B)11)9e (C1e(D )993x e dx -⎰ 二、填空题:1.设连续性随机变量X 的密度函数为201()0Ax x f x ⎧≤≤=⎨⎩其他,则常数A = 32.设随机变量2~(2,)X N σ,已知(24)0.4P X ≤≤=,则(0)P X ≤= 三、计算题:1.设~(1,4),X U 求(5)P X ≤和(0 2.5)P X ≤≤ 解:(5)P X ≤= 1 (0 2.5)P X ≤≤=252511105413..|.x dx ==-⎰2.设随机变量X 的密度函数为01()120xx f x ax b x ≤<⎧⎪=+≤≤⎨⎪⎩其他,且37(0)28P X <≤=求:(1)常数,a b (2)13()22P X << (3)X 的分布函数()F x 解:(1) 由归一性120113122()()af x dx xdx ax b dx b +∞-∞=++=++=⎰⎰⎰又 312013157(0)()22828a b P X xdx ax b <≤=++=++=⎰⎰ 解得 12,a b =-=由此 得 01()2120x x f x x x ≤<⎧⎪=-+≤≤⎨⎪⎩其他(2)312112133()(2)0.75224P X xdx x <≤=+-+==⎰⎰(3)X 的分布函数110001()(2)1212xxx tdt x F x tdt t dtx x <⎧⎪≤<⎪⎪=⎨⎪+-+≤<⎪≥⎪⎩⎰⎰⎰22000.5010.5211212x x x x x x x <⎧⎪≤<⎪=⎨-+-≤<⎪⎪≥⎩3.设某种电子元件的使用寿命X (单位:h )服从参数1600λ=的指数分布,现某种仪器使用三个该电子元件,且它们工作时相互独立,求: (1)一个元件时间在200h 以上的概率;(2)三个元件中至少有两个使用时间在200h 以上的概率。
解:(1)1160032001200600()xP X e dx e --+∞>==⎰ (2)设Y 表示“三个元件中使用时间在200h 以上元件的个数”223()()()P Y P Y P Y ≥==+=1112223133333132()()()C e e e ee -----=-+=-概率论与数理统计练习题系 专业 班 姓名 学号第二章 随机变量及其分布(三)1.已知X 的概率分辨为21012320.132iX p a a a a a-- ,试求:(1)常数a ; (2)21Y X =-的概率分布。
解:由于201321.a a a a a +++++=,所以01.a = 则X 的概率分布列为:2101230.20.10.30.10.10.2iX p --(2)21Y X =-的概率分布为: 即22101230201030101021301038......i X P Y X --=--21103803020302 (i)Y X P =--2.设随机变量X 在(0,1)服从均匀分布,求: (1)XY e =的概率密度; (2)2ln Y X =-的概率密度。
解:(1)当y <1时,0()Y F y =,当y ≧ e 时,1()Y F y =当1y e ≤<时, ()()()(ln )XY F y P Y y P e y P X y =≤=≤=≤即 0111()ln Y y F y yy e y e<⎧⎪=≤<⎨⎪≥⎩所以 110()Y y e yf y ⎧<<⎪=⎨⎪⎩其他(2)当y ≧0时,0()Y F y =,0()f y = 当y > 0时,22()()(ln )()y Y F y P Y y P X y P X e-=≤=-≤=≥2211()y y P X ee--=-<=-212()()ydF y f y e dy -==即 200102()yy f y e y -<⎧⎪=⎨≥⎪⎩3.设~(0,1)X N ,求: (1)221Y X =+的概率密度; (2)||Y X =的概率密度。
解:(1)221212()()()()Y y F y P Y y P X y P X -=≤=-≤=≤(P X =≤≤21=Φ- (y > 1)2()()Y dF y f y dy ϕ==2122y -⎝⎭--==即12011()y y f y y --<⎧⎪=>(2) 21()()()()()F y P Y y P X y P y X y y =≤=≤=-≤≤=Φ- (y > 0)22222()y ydFf ydy--===(y > 0)即2200()yyf yy-<⎧=>4.设随机变量X的概率密度为22()xxf xππ⎧<<⎪=⎨⎪⎩其他,求sinY X=的概率密度。
解:()()(sin)(arcsin arcsin) YF y P Y y P X y P X y X yπ=≤=≤=≤⋃≥-1(arcsin)(arcsin)X XF y F yπ+--()()(arcsin)(arcsin)(YY X XdF yf y f y f ydyπ==--⋅2222arcsin(arcsin)(y yπππ-=-⋅=即01()Yyf y<<=⎩其他。
