宁夏育才中学2014-2015学年高二数学下学期期末考试试题 理(无答案)
宁夏育才中学2014-2015学年高一上学期第一次月考地理试题

宁夏育才中学2014-2015学年高一上学期第一次月考地理试题试卷说明:本试卷分两部分,第一卷为选择题,第二卷为非选择题一、选择题(共35题,每小题1分,共35分)1.目前人类认识的天体系统从小到大的排列,正确的是 ( )A.总星系-银河系-太阳系-地月系 B.地月系-太阳系-银河系-总星系C.总星系-太阳系-银河系-地月系 D.地月系-银河系-太阳系-总星系2.所谓地球是太阳系中一颗既普通又特殊的行星,其特殊性体现在()A. 是太阳系中体积、质量最大的行星B. 是八大行星中质量最小的行星C. 既有公转运动又有自转运动D.是太阳系中唯一存在生命的行星3.下列有关太阳外部圈层与其活动的组合正确的()A.日冕层——黑子B.色球层——耀斑C.光球层——日珥D.光球层——太阳风4.据监测,上一次太阳活动高峰发生在2001年3月。
根据太阳活动的周期,下次太阳活动的高峰时间大约是:A.2007年前后 B.2012年前后 C.2010年前后 D.2017年前后2007年10月24日18:05(北京时间),中国自己设计的“嫦娥一号”月球探测卫星发射升空,开始了太空旅行。
阅读太阳直射点周年变化示意图,回答5题。
5.当“嫦娥一号”发射时,太阳直射点A. 位于①-②之间,并向②点移动B. 位于②-③之间,并向③点移动C. 位于③-④之间,并向④点移动D. 位于④-⑤之间,并向⑤点移动6.图中能正确反映地球自转方向的是A.a和bB.a和cC.b和cD.c和d据美联社报道:2005年9月7日13时40分(西五区时间),地球朝向太阳一面的所有地区,高频无线电通讯几乎全部中断。
据此回答7题。
7.造成这一现象的主要原因是()A.地球大气层中的臭氧层空洞扩大使太阳辐射增强B.太阳耀斑爆发引起地球大气层的电离层扰动C.太阳黑子增多造成地球磁场紊乱D.太阳等天体对地球引力加强8.属于因地球公转运动而产生的地理现象是( )A.昼夜交替 B.地方时的产生 C.昼夜形成 D.四季的形成据《信息时报》报道,位于北回归线上的广州出现“头上有烈日,脚下无人影”的有趣景象。
宁夏育才中学勤行学区2014第一学期第十八周周测(数学)
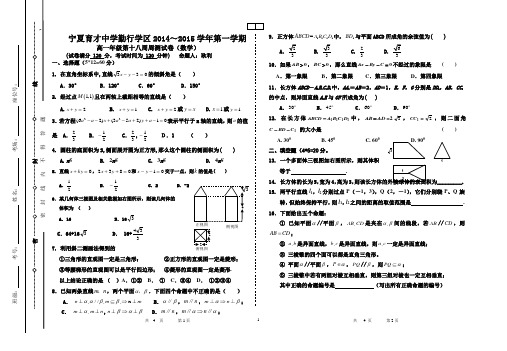
密班级: 考号: 姓名: 考场: 座位号:密封 线 内 不 得 答 题俯视图侧视图13题311213题图1宁夏育才中学勤行学区2014~2015学年第一学期高一年级第十八周周测试卷(数学)(试卷满分 120 分,考试时间为 120 分钟) 命题人:耿利一、选择题(5*12=60分)1. 在直角坐标系中,直线033=--y x 的倾斜角是( )A .30°B .120°C .60°D .150°2. 经过点()1,1M 且在两轴上截距相等的直线是( ) A.2x y +=B. 1x y +=C. 2x y +=或y x =D.1x =或1y =3.若方程22(62)(352)10a a x a a y a --+-++-=表示平行于x 轴的直线,则a 的值是 A .23B .12-C .23,12-D.1 ( )4. 圆柱的底面积为S,侧面展开图为正方形,那么这个圆柱的侧面积为( ) A.S π B. S π2C. S π3D. S π45. 直线0=+ky x ,0832=++y x 和01=--y x 交于一点,则k 的值是( ) A .21 B.21- C. 2 D. -26.某几何体三视图及相关数据如右图所示,则该几何体的 体积为 ( )A .16B .163C .64+163D . 16+334 7. 利用斜二测画法得到的①三角形的直观图一定是三角形; ②正方形的直观图一定是菱形; ③等腰梯形的直观图可以是平行四边形; ④菱形的直观图一定是菱形.以上结论正确的是 ( )A .①② B . ① C .③④ D . ①②③④8.已知两条直线m n ,,两个平面αβ,.下面四个命题中不正确...的是( ) A . ,//,,n m m ααββ⊥⊆⇒⊥n B .αβ∥,m n ∥,m n αβ⇒⊥⊥; C . ,α⊥m mn ⊥,βαβ⊥⇒⊥n D .m n ∥,m n αα⇒∥∥;9. 正方体ABCD -1111A B C D 中,1BD 与平面ABCD 所成角的余弦值为( )A 2310.如果0>AB ,0>BC ,那么直线0=--C By Ax 不经过的象限是 ( )A .第一象限B .第二象限C .第三象限D .第四象限11.长方体ABCD -A 1B 1C 1D 1中,AA 1=AB =2,AD =1,E ,F ,G 分别是DD 1,AB ,CC 1的中点,则异面直线A 1E 与GF 所成角为( )A . 30B . 45C . 60D . 9012. 在长方体1111D C B A ABCD -中,AD AB ==23,1CC =2,则二面角1C BD C -- 的大小是( )A. 300B. 450C. 600D. 900 二、填空题(4*5=20分。
宁夏育才中学2014-2015学年高二上学期期中考试物理试卷(解析版)

宁夏育才中学2014-2015学年高二上学期期中考试物理试卷(解析版)第I卷(选择题)1.下列关于匀强电场中场强和电势差的关系,正确的说法是( )A.任意两点之间的电势差,等于场强和这两点间距离的乘积B.在任何方向上,若两点间距离相等,则它们之间的电势差就相等C.沿着电场线的方向,任何相等距离上的电势降低量必定相等D.电势降落的方向必定是电场强度的方向【答案】C【解析】试题分析:匀强电场中任意两点的电势差等于场强和这两点沿电场方向距离的乘积,A错误;同理,在任何方向上,沿电场方向距离相等的两点,它们之间的电势差相等,B错误;根据U=Ed,知沿着电场线的方向,任何相等距离上的电势降低量必定相等,C正确;电势降落最快的方向必定是电场强度的方向,D错误。
考点:本题考查匀强电场的电场强度。
2.电场中有一点P,下列说法正确的是()A.若放在P点的试探电荷的电量减半,则P点的场强减半B.若P点没有试探电荷,则P点的场强为零C.P点的场强越大,则同一电荷在P点受到的电场力越大D.P点的场强方向为试探电荷在该点的受力方向【答案】C【解析】试题分析:电场强度由电场自身性质决定,与是否放入的试探电荷及试探电荷的电荷量无关,AB错误;由F=Eq,P点的场强越大,则同一电荷在P点受到的电场力越大,C正确;P点的场强方向为正的试探电荷在该点的受力方向,D错误。
考点:本题考查电场的电场强度。
3.如图所示的直线是真空中某电场中的一条电场线,A、B是这条直线上的两点。
一电子以速度v A经过A点向B点运动,经过一段时间后,电子以速度v B经过B点,且v B与v A方向相A.A点的场强一定大于B点的场强B.A点的电势一定低于B点的电势C.电子在A点的动能一定小于它在B点的动能D.电子在A点的电势能一定小于它在B点的电势能【答案】B【解析】试题分析:无法判断A、B两点所在位置电场线的疏密,无法判断A、B两点电场强度的大小,A错误;由题意知电子由A运动到B的过程中,电场力做负功,则电势能增加,D错误;即电子所受电场力沿BA方向,电场强度方向为AB方向,沿电场方向电势降低,则A点的电势一定低于B点的电势,B正确;电子在AB两点的速度大小关系无法判断,则电子在AB两点的动能大小无法判断,C错误。
高二下学期期末考试数学试卷(含参考答案)

高中二年级学业水平考试数学(测试时间120分钟,满分150分)第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)已知i 是虚数单位,若复数))((R a i a i ∈+-的实部与虚部相等,则=a (A )2-(B )1- (C )1 (D )2(2)若集合{}0,1,2A =,{}24,B x x x N =≤∈,则AB =(A ){}20≤≤x x(B ){}22≤≤-x x (C ){0,1,2} (D ){1,2}(3)已知直线a ,b 分别在两个不同的平面α,β内.则“直线a 和直线b 没有公共点”是“平面α和平面β平行”的(A )充分不必要条件(B )必要不充分条件 (C )充要条件(D )既不充分也不必要条件(4)若()1sin 3πα-=,且2παπ≤≤,则sin 2α的值为(A )9-(B )9-(C )9(D )9(5)在区间[]1,4-上随机选取一个数x ,则1≤x 的概率为 (A )23 (B )15 (C )52 (D )14(6)已知抛物线2y x =的焦点是椭圆22213x y a +=的一个焦点,则椭圆的离心率为(A )37(B )13(C )14 (D )17(7)以下函数,在区间[3,5]内存在零点的是(A )3()35f x x x =--+ (B )()24x f x =-图2俯视图侧视图主视图(C )()2ln(2)3f x x x =-- (D )1()2f x x=-+ (8)已知(2,1),(1,1)a b ==,a 与b 的夹角为θ,则cos θ=(A)10 (B)10 (C)5 (D)5(9)在图1的程序框图中,若输入的x 值为2,则输出的y 值为(A )0 (B )12 (C )1- (D )32- (10)某几何体的三视图如图2所示,则该几何体的侧面积是(A )76 (B )70 (C )64 (D )62 (11)设2()3,()ln(3)xf x eg x x =-=+,则不等式(())(())11f g x g f x -≤的解集为(A )[5,1]- (B )(3,1]- (C )[1,5]- (D )(3,5]-(12) 已知函数()f x =3231ax x -+,若()f x 存在唯一的零点0x ,且00x <,则a 的取值范围为(A )∞(-,-2) (B )1∞(-,-) (C )(1,+)∞ (D )(2,)+∞第Ⅱ卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须做答.第(22)题~第(24)题为选考题,考生根据要求做答.二、填空题(本大题共4小题,每小题5分,共20分,请把正确的答案填写在答题卡相应的横线上.(13)函数()cos f x x x =+的最小正周期为 .(14)已知实数y x ,满足不等式组⎪⎩⎪⎨⎧≤-≥+≤-3322y x y x x y ,则y x -2的最小值为 .(15)已知直线l :0x y a -+=,点()2,0A -,()2,0B . 若直线l 上存在点P 满足AP BP ⊥,则实数a 的取值范围为 .(16)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知2,b =3B π=,且△ABC 的面DC 1B 1CBA积S =a c += .三、解答题:本大题必做题5小题,选做题2小题,共70分.解答应写出文字说明,证明过程或演算步骤.(17)(本小题满分12分)已知等差数列{}n a 满足141,4a a ==;数列{}n b 满足12b a =,25b a =,数列{}n n b a -为等比数列. (Ⅰ)求数列{}n a 和{}n b 的通项公式; (Ⅱ)求数列{}n b 的前n 项和n S . (18)(本小题满分12分)某地区以“绿色出行”为宗旨开展“共享单车”业务.该地区某高级中学一兴趣小组由9名高二级学生和6名高一级学生组成,现采用分层抽样的方法抽取5人,组成一个体验小组去市场体验“共享单车”的使用.问:(Ⅰ)应从该兴趣小组中抽取高一级和高二级的学生各多少人;(Ⅱ)已知该地区有X ,Y 两种型号的“共享单车”,在市场体验中,该体验小组的高二级学生都租X 型车,高一级学生都租Y 型车.如果从组内随机抽取2人,求抽取的2人中至少有1人在市场体验过程中租X 型车的概率.(19)(本小题满分12分)如图3,已知四棱锥11A CBB C -的底面为矩形,D 为1AC 的中点,AC ⊥平面BCC 1B 1. (Ⅰ)证明:AB//平面CDB 1; (Ⅱ)若AC=BC=1,BB 1(1)求BD 的长;(2)求三棱锥C-DB 1C 1的体积. 图3 (20)(本小题满分12分)已知过点(0,1)A 的动直线l 与圆C :224230x y x y +---=交于M ,N 两点. (Ⅰ)设线段MN 的中点为P ,求点P 的轨迹方程; (Ⅱ)若2OM ON ⋅=-,求直线l 的方程. (21)(本小题满分12分)已知函数()ln f x x x =.(Ⅰ)求函数()f x 的极值;(Ⅱ)若对任意1,x e e⎡⎤∈⎢⎥⎣⎦,都有()213022f x x ax +++≤成立,求实数a 的取值范围. 请考生在(22)、(23)两题中任选一题作答,如果多做,则按所做的第一题记分. (22)(本小题满分10分)选修4-4:坐标系与参数方程将圆221x y +=上每一点的纵坐标不变,横坐标变为原来的14,得曲线C . (Ⅰ)写出C 的参数方程;(Ⅱ)设直线l :410x y ++=与C 的交点为P 1,P 2,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求过线段P 1 P 2的中点且与l 垂直的直线的极坐标方程. (23)(本小题满分10分)选修4-5:不等式选讲设函数()|2|||f x x x a =-+-. (Ⅰ)若2a =-,解不等式5)(≥x f ;(Ⅱ)如果当x R ∈时,()3f x a ≥-,求a 的取值范围.数学参考答案及评分说明一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数.一、选择题:部分解析:(10)依题意知,该几何体是底面为直角梯形的直棱柱,故其侧面积为42+44+245=64⨯⨯⨯⨯.(11)(())(())11f g x g f x -≤即22(3)3211450x x x x +--≤⇒+-≤51x ⇒-≤≤,注意到30x +>,即3x >-,故31x -<≤.(12)当0a =时,函数2()31f x x =-+有两个零点,不符合题意,故0a ≠,2'()363(2)f x ax x x ax =-=-,令'()0f x =得0x =或2x a =,由题意知,0a >,且2()0f a>,解得2a >.二、填空题:(15)问题转化为求直线l 与圆2222x y +=有公共点时,a 的取值范围,数形结合易得a -≤.(16)由余弦定理得2222cos 4b a c ac B =+-=,即224a c ac +-=,1sin 24S ac B ac ===得4ac =,故2()164a c a c +=⇒+= 三、解答题:(17)解:(Ⅰ)由数列{}n a 是等差数列且141,4a a ==∴公差4113a a d -==, ------------------------------------------------------------------------------1分 ∴1(1)n a a n d n =+-=,------------------------------------------------------------------------------3分 ∵12b a ==2,25b a ==5,∴11221,3,b a b a -=-= ∴数列{}n n b a -的公比22113b a q b a -==-,-----------------------------------------------------------5分∴1111()3n n n n b a b a q ---=-=,∴13n n b n -=+;-------------------------------------------------------------------------------------------7分 (Ⅱ)由13n n b n -=+得21(12)(1333)n n S n -=++++++++--------------------------------------------------------9分(1)31231n n n +-=+- 3(1)12n n n ++-=------------------------------------------------------------------------------------ 12分 (18)解:(Ⅰ)依题意知,应从该兴趣小组中抽取的高一学生人数为56=29+6⨯, ------2分 高二学生的人数为:59=39+6⨯; -------------------------------------------------------------------4分 (Ⅱ)解法1:记抽取的2名高一学生为12,a a ,3名高二的学生为123,,b b b ,------------5分 则从体验小组5人中任取2人的所有可能为:12111213(,),(,),(,),(,)a a a b a b a b ,(a 2,b 1), (a 2,b 2), (a 2,b 3), (b 1,b 2), (b 1,b 3), (b 2,b 3),共10种可能; ----------------------------------------------------------8分 其中至少有1人在市场体验过程中租X 型车的有:111213(,),(,),(,)a b a b a b ,212223121323(,),(,),(,),(,),(,),(,)a b a b a b b b b b b b 共9种,------------------------------------------10分故所求的概率910P =.-----------------------------------------------------------------------------------------12分 【解法:2:记抽取的2名高一学生为12,a a ,3名高二的学生为123,,b b b ,------------------------5分 则从体验小组5人中任取2人的所有可能为:12111213(,),(,),(,),(,)a a a b a b a b ,EABCB 1C 1D212223121323(,),(,),(,),(,),(,),(,)a b a b a b b b b b b b 共10种可能;--------------------------------------8分其中所抽的2人都不租X 型车的有:12(,)a a 一种,-------------------------------------------------9分 故所求的概率1911010P =-=. ---------------------------------------------------------------------------12分 (19)解:(Ⅰ)证明:连结1BC 交1B C 于E ,连结DE , ------------------------------------------1分 ∵D 、E 分别为1AC 和1BC 的中点,∴DE//AB,---------------------------------- --------------------2分 又∵DE ⊂平面1CDB ,AB ⊄平面1CDB ,∴AB//平面CDB 1;---------------------------------------------4分 (Ⅱ)(1)∵AC ⊥平面BCC 1B 1,BC ⊂平面11BCC B , ∴BC AC ⊥, 又∵1BC CC ⊥,1ACCC C =,∴BC ⊥平面1ACC , ∵CD ⊂平面1ACC ,∴BC CD ⊥,----------------------------------------------------------------------------------------------------6分 在Rt BCD ∆,∵BC=1,1112CD AC ===, ∴BD =分【注:以上加灰色底纹的条件不写不扣分!】 (2)解法1:∵BC ⊥平面1ACC ,BC//B 1C 1∴11B C ⊥平面1CC A ,-----------------------------------------------------------------------------------------10分 ∴111111113C DB C B CDC CDC V V S B C --∆==⋅111134=⨯⨯=. ---------------------------------12分 【解法2:取1CC 中点F,连结DF ,∵DF 为△1ACC 的中位线,∴DF//AC,-------------------------------------------------------------------9分 ∵AC ⊥平面11CBB C ,从而可得DF ⊥平面11CBB C ,----------------------------------------------10分∴11111113C DB C D CB C CB C V V S DF --∆==⋅1111322=⨯⨯=. --------------------------------12分 (20)解法(Ⅰ)将224230x y x y +---=化为标准方程得:222(2)(1)x y -+-=, ----------------------------------------------------------------------------1分可知圆心C 的坐标为(2,1),半径r =设点P 的坐标为(,)x y ,则(2,1),(,1)CP x y AP x y =--=-,---------------------------------------2分 依题意知CP AP ⊥,∴0CP AP ⋅=(2)(1)(1)0x x y y ⇒-+--=整理得:222210x y x y +--+=, ------------------------------------------------------------------------4分∵点A 在圆C 内部, ∴直线l 始终与圆C 相交,∴点P 的轨迹方程为222210x y x y +--+=.----------------------------------------------------------6分 (Ⅱ)设1122(,),(,)M x y N x y ,若直线l 与x 轴垂直,则l 的方程为0x =,代入224230x y x y +---=得2230y y --=,解得1y =-或3y =,不妨设121,3y y =-=,则3OM ON ⋅=-,不符合题设, ------------------------------------------------7分 设直线l 的斜率为k ,则l 的方程为1y kx =+,由224230,1.x y x y y kx ⎧+---=⎨=+⎩消去y 得:22(1)440k x x +--=, --------------------------------8分 216(2)0k ∆=+>,则12122244,11x x x x k k+==-++,------------------------------------------------------------------------9分 由2OM ON ⋅=-得212121212(1)()12x x y y k x x k x x +=++++=-,∴22244(1)1211kk k k-+++=-++2410k k ⇒-+=,解得:2k =±分∴当2OM ON ⋅=-时,直线l 的方程为(21y x =++或(21y x =-+. --------------12分 (21)解:(Ⅰ)函数()f x 的定义域为(0,)+∞, ∵()ln 1f x x '=+,令'()0f x =得1x e=,-------------------------------------------------------------2分 当10x e <<时'()0f x <,当1x e>时,'()0f x >, ∴函数()f x 在1(0,)e 上单调递减,在1(,)e+∞上单调递增,----------------------------------------4分∴函数()f x 无极大值, 当1x e =时,函数()f x 在(0,)+∞有极小值,11()()f x f e e==-极小,--------------------------5分 (Ⅱ)当1,x e e ⎡⎤∈⎢⎥⎣⎦时,由()213022f x x ax +++≤,得3ln 22x a x x ≤---,--------------6分 记()3ln 22x g x x x =---,1,x e e ⎡⎤∈⎢⎥⎣⎦, 则()()()2231113222x x g x x x x +-'=--+=-, 当∈x 1,1e ⎛⎫ ⎪⎝⎭时,得'()0g x >,当∈x ()1,e 时, '()0g x <∴()g x 在1,1e ⎛⎫ ⎪⎝⎭上单调递增,在()1,e 上单调递减,---------------------------------------------------9分又113122e g e e ⎛⎫=-- ⎪⎝⎭,()3122e g e e=---, ∵012)()1(<-+=-e e e g e g ,∴()1g g e e ⎛⎫< ⎪⎝⎭,-------------------------------------------------10分故()g x 在1,e e ⎡⎤⎢⎥⎣⎦上的最小值为1g e ⎛⎫ ⎪⎝⎭,故只需1a g e ⎛⎫≤ ⎪⎝⎭,即实数a 的取值范围是13,122e e ⎛⎤-∞-- ⎥⎝⎦.------------------------------------------------------------12分 选做题:(22)解:(Ⅰ)由坐标变换公式1',4'.x x y y ⎧=⎪⎨⎪=⎩ 得4','x x y y ==-------------------------------------2分 代入221x y +=中得2216''1x y +=,--------------------------------------------------------------------3分故曲线C 的参数方程为1cos ,4sin .x y θθ⎧=⎪⎨⎪=⎩(θ为参数);----------------------------------------------------5分 (Ⅱ)由题知,121(,0),(0,1)4P P --,--------------------------------------------------------------------6分 故线段P 1 P 2中点11(,)82M --,---------------------------------------------------------------------------7分∵直线l 的斜率4k =-∴线段P 1 P 2的中垂线斜率为14,故线段P 1 P 2的中垂线的方程为111()248y x +=+------------------------------------------------------8分即832150x y --=,将cos ,sin x y ρθρθ==代入得其极坐标方程为8cos 32sin 150ρθρθ--=----------------------------------------------------------10分 (23)解:(Ⅰ)当a =-2时,f (x )=|x -2|+|x +2|, ①当2x ≤-时,原不等式化为:25,x -≥解得52x ≤-,从而52x ≤-;-------------------------1分 ②当22x -<≤时,原不等式化为:45≥,无解;---------------------------------------------------2分 ③当2x >时,原不等式化为:25,x ≥解得52x ≥,从而52x ≥;----------------------------------3分 综上得不等式的解集为⎭⎬⎫⎩⎨⎧≥-≤2525x x x 或.----------------------------------------------------------------5分(Ⅱ)当x R ∈时,|2||||2()||2|x x a x x a a -+-≥---=- ---------------------------------------7分 所以当x R ∈时,()3f x a ≥-等价于|2|3a a -≥------(*) 当2a ≥时,(*)等价于23,a a -≥-解得52a ≥,从而52a ≥;----------------------------------8分 当2a <时,(*)等价于23,a a -≥-无解;------------------------------------------------------------9分 故所求a 的取值范围为5[,+2∞). --------------------------------------------------------------------------10分。
2021-2022学年宁夏青铜峡市高二年级下册学期期末考试数学(理)试题 【含答案】

2021-2022学年第二学期高二年级数学(理)期末卷一、选择题(本大题共12道小题,每小题5分,共60分)1. 已知集合,,则(){}2320M x x x =-+≤∣{0}N x x =>∣A. B. N M ⊆M N⊆C. D. M N ⋂=∅M N R= 【答案】B 【解析】【分析】先运用一元二次不等式的解法,求得集合M ,再运用集合间的包含关系,集合的交集、并集运算可得选项.【详解】因为,解不等式得,且,{}2320M x x x =-+≤∣{12}M x x =≤≤∣{0}N x x =>∣所以,,.M N ⊆{}12M N x x ⋂=≤≤≠∅{}M N x x ⋃=>故选:B.【点睛】本题考查了集合的交集、并集运算,集合的包含关系,意在考查学生的计算能力和应用能力,属于基础题.2. 命题“,”的否定是( )00x ∃>001ln 1x x <-A. ,B. ,0x ∀≤1ln 1x x <-0x ∀>1ln 1x x ≥-C. ,D. ,0x ∀≤1ln 1x x≥-0x ∀>1ln 1x x<-【答案】B 【解析】【分析】利用特称命题的否定可得出结论.【详解】由特称命题的否定可知,命题“,”的否定是“,”.00x ∃>001ln 1x x <-0x ∀>1ln 1x x ≥-故选:B.3. 已知向量,若,则()()()1,2,2,a b m ==-a b ⊥m =A. 1B.C. 4D. 1-4-【答案】A 【解析】【分析】根据向量垂直的坐标公式求解即可【详解】因为,故,故a b ⊥ ()1220m ⨯-+=1m =故选:A4. 某学校高一、高二、高三3个年级共有1080名学生,其中高一年级学生540名,高二年级学生360名,为了解学生身体状况,现采用分层随机抽样方法进行调查,在抽取的样本中高二学生有32人,则该样本中高三学生人数为( )A. 54 B. 48C. 32D. 16【答案】D 【解析】【分析】先求得样本容量,再根据分层抽样的比例,即可求得答案.【详解】由题意可知,抽取的样本容量为 ,32108096360⨯=则样本中高三学生有 人,108054036096161080--⨯=故选:D5. 设为虚数单位,若,则它的共轭复数对应的点位于( )i 1i34i i z -=+-z A. 第一象限 B. 第二象限C. 第三象限D. 第四象限【答案】A 【解析】【分析】根据复数的除法与模长公式可得,再根据共轭复数的定义与几何意义判定即可4i z =-【详解】∵,∴,1i (1i)i|34i |54i i i i --=+-=+=-⋅z 4i z =+则在复平面内对应的点的坐标为,位于第一象限.z ()4,1故选:A.6. 若幂函数没有零点,则实数m 的值为()()()223265m f x m m x -=-+A. 1B. 1或2C. 2D. 0【答案】A 【解析】【分析】根据幂函数的定义求得的值,在分别检验对应函数是否有零点即可得出答案.m 【详解】解:由幂函数,()()223265m f x m m x -=-+可得,解得或2,22651m m -+=1m =当时,,令,无解,符合题意,1m =()1f x x =10x =当时,,令,则,不符题意,2m =()f x x =()0f x x ==0x =所以.1m =故选:A.7. 为了得到函数的图象,只要把的图象( )sin 3 4y x π⎛⎫=- ⎪⎝⎭sin y x =A. 向右平移个单位长度,然后纵坐标不变,横坐标伸长为原来的倍4π3B. 向左平移个单位长度,然后纵坐标不变,横坐标缩短为原来的倍4π13C. 纵坐标不变,横坐标缩短为原来的倍,再向右平移个单位长度134πD. 纵坐标不变,横坐标缩短为原来的倍,再向右平移个单位长度1312π【答案】D 【解析】【分析】先化,再由三角函数的图象变换原则,即可得出结果. sin 3i 312s n 4x y x ππ⎡⎤⎛⎫- ⎪⎢⎥⎝⎭⎛⎫=-=⎭⎣ ⎪⎦⎝【详解】,纵坐标不变,横坐标缩短为原来的倍,可得;sin y x =13 sin3y x =再向右平移个单位,可得.12πsin 312sin 34y x x ππ⎡⎤⎛⎫- ⎪⎢⎥⎝⎭⎣⎛⎫==- ⎪⎝⎭⎦故选:D.A. B. C. D.【答案】C 【解析】【分析】根据函数的奇偶性排除AB ,再根据趋近于时的值判断即可x +∞()()x f x f x ---==-()3x x f x +.()()()()220225054222log 42f f f f =⨯+==-==故选:D .11. 四棱锥的外接球O 的半径为2,平面ABCD ,底面ABCD 为矩形,,P ABCD -PA ⊥2PA AB ==则平面PAD 截球O 所得的截面面积为( )A. B. C. D. 4π3π2ππ【答案】B 【解析】【分析】根据外接球的球心到所有顶点距离相等,故可得球心为的中点,即可根据截面的性质求解O PC 截面圆半径.【详解】由题意可知,球心为的中点,因为,所以平面O PC ,,CD AD CD PA AD PA A ⊥⊥= CD ⊥,为的中点,故到平面的距离为,故截面圆的半径为,截面面积为PAD O PC O PAD 112CD =221=3-()2π3=3π故选:B12. 已知,,,则,,的大小关系为( )ln 33a =1e b =ln 55c =a b c A. B. a b c >>c a b >>C. D. b c a >>b a c>>【答案】D 【解析】【分析】构造函数,利用导数确定其单调性,由单调性比较大小可得.ln ()xf x x =【详解】设,则,时,,是减函数,ln ()x f x x =21ln ()xf x x -'=e x >()0f x '<()f x 又,所以,即,e 35<<(e)(3)(5)f f f >>1ln 3ln 5e 35>>故选:D .二、填空题(本大题共4道小题,每小题5分,共20分)13. 从10件产品(其中次品3件)中,一件一件不放回地任意取出4件,则4件中恰有1件次品的概率为______.【答案】##0.512【解析】【分析】用计数原理计算出基本事件总数,并确定4件中恰有1件次品的事件数,利用古典概型及其概率计算公式求解.【详解】解:一件一件不放回地抽取4件,可以看成一次抽取4件,故共有种可能的结果,事件A 含410C 有种结果.∴.1337C C ⨯()1337410C C 1C 2P A ⨯==故答案为:.1214. 当时,的值有正也有负,则实数a 的取值范围是______.11x -≤≤21y ax a =++【答案】113a -<<-【解析】【分析】设,根据可求出结果.()21f x ax a =++(1)(1)0f f -⋅<【详解】设,()21f x ax a =++依题意可得,所以,(1)(1)0f f -⋅<(21)(21)0a a a a -++++<所以,得.(1)(31)0a a ++<113a -<<-故答案为:113a -<<-15. 边长为的等边三角形中,设,则___________.3ABC ,,AB c BC a CA b === a b b c c a ⋅+⋅+⋅= 【答案】##-4.592-【解析】【分析】利用平面向量的数量积的定义求解.【详解】解:在边长为的等边三角形中,因为,3ABC ,,AB c BC a CA b ===所以,a b b c c a ⋅+⋅+⋅,33cos12033cos12033cos120=⨯⨯+⨯⨯+⨯⨯ ,92=-故答案为:92-16. 的内角,的对边分别为 ,若,则的面积为ABC ,,A B C ,,a b c 1,sin sin ,234A B C a π===ABC _______【答案】33【解析】【分析】由正弦定理可以化简,利用面积公式求出的面积.1sin sin 4B C =ABC 【详解】由正弦定理得,4343sin sin ,sin sin sin 3sin 3a a b B B c C C A A ====所以,从而.164sin sin 33bc B C ==13sin 23ABC S bc A ==△【点睛】本题考查了正弦定理、面积公式,正确使用公式是解题的关键.三、解答题17. 已知.()231sin 2cos ,22f x x x x R =--∈⑴化简并求函数的最小正周期⑵求函数的最大值,并求使取得最大值的的集合()f x ()f x x 【答案】(1),最小正周期()sin(2)16f x x π=--T π=(2)max ,,()03x x x k k Z f x ππ⎧⎫∈=+∈=⎨⎬⎩⎭【解析】【分析】(1)由倍角公式,将函数化简,然后得其最小正周期;()f x (2)由(1)得知函数,根据正弦函数的性质,求得的最值以及此时的取值.()f x x 【详解】(1)由题()23131sin 2cos sin 2cos 21sin 2122226f x x x x x x π⎛⎫=--=--=-- ⎪⎝⎭所以函数的最小正周期22T ππ==(2)由(1)可知,当是,即时,函数取最大值,最大22,62x k k Zπππ-=+∈,3x k k Zππ=+∈()f x 值为1-1=0,所以,当max ,,()03x x x k k Z f x ππ⎧⎫∈=+∈=⎨⎬⎩⎭【点睛】被踢考查了三角函数的性质,解题的关键是利用三角恒等变化对函数进行化简,再利用性质,属于基础题.18. 的内角A ,B ,C 的对边分别为a ,b ,c ,已知.ABC cos cos 2cos a C c A b B +=(1)求B ;(2)若,的面积为,求的周长.23b =ABC 23ABC 【答案】(1);(2)3B π=623+【解析】【分析】(1)根据正弦定理以及两角和的正弦公式即可求出,进而求出;1cos 2B =B (2)根据余弦定理可得到,再根据三角形面积公式得到 ,即可求出()2312a b ab +-=8ab =,进而求出的周长.6a b +=ABC 【详解】解:(1),cos cos 2cos a C c A b B += 由正弦定理得:,sin cos sin cos 2sin cos A C C A B B +=整理得:,()sin 2sin cos sin A C B B B+==∵在中,,ABC 0B π<<∴,sin 0B ≠即,2cos 1B =∴,1cos 2B =参考公式:((11n i i n i x b ==-=∑∑(1)在给定的坐标系中画出表中数据的散点图;y(2),()12345 3.54x =+++=,42154i i x==∑4152.5ii i x y ==∑252.54 3.5 3.50.7544 3.5b -⨯⨯∴==-⨯(3)20.73 1.05 3.15ˆy=⨯+= 2223 3.150.1ˆˆ5ey y ∴=-=-=-当代入回归直线方程,得(小时)10x =0.710 1.058.05y =⨯+=加工10个零件大约需要8.05个小时∴【点睛】本题考查线性回归直线,考查学生的运算能力,属于基础题.21. 2022年6月5日神舟十四号发射升空,神舟十四号任务期间,将全面完成以天和核心舱、问天实验舱和梦天实验舱为基本构型的太空空间站建造等多项科研任务,并将继续开展天宫课堂.某校“航空航天”社团针对学生是否有兴趣收看天宫课堂进行了一项调查,获得了如下数据:感兴趣不感兴趣合计男生人数29332女生人数21728合计501060(1)是否有95%的把握认为“是否有兴趣收看天宫课堂与性别有关”?(2)从不感兴趣的10人中随机抽取两人做进一步宣传,设抽到的女生人数为X ,求X 的概率分布.参考公式:独立性检验统计量,其中.()()()()()22n ad bc a b c d a c b d χ-=++++n a b c d =+++临界值表:20()P x χ≥0.150.100.050.0250.0100.0050.0010x 2.072 2.706 3.841 5.0246.6357.87910.828【答案】(1)没有95%的把握认为“是否有兴趣收看天宫课堂与性别有关”(2)答案见解析【解析】【分析】(Ⅰ)求出,从而没有的把握认为“是否有兴趣收看天宫课堂与性别有2 2.625 3.841K ≈<95%关”;(Ⅱ)从不感兴趣的女生人数的可能取值为0,1,2,分别求出相应的概率,由此能求出的分布X X 列和数学期望.【小问1详解】解:提出假设:是否有兴趣收看天宫课堂与性别无关0H 根据列联表中的数据,可以求得()226029732121 2.625501032288χ⨯-⨯===⨯⨯⨯因为.而,()2 3.8410.05P χ≥= 2.625 3.841<所以没有95%的把握认为“是否有兴趣收看天宫课堂与性别有关” .【小问2详解】解:依题意,随机变量X 的可能取值为0,1,2,()()()211373221010272107170,1,2151155C C C P X P X P X C C C C =========随机变量X 的概率分布表如下:X012P 11571571522. 已知,的导数是.()ln x f x x =()f x ()f x '(1)求在的切线方程;()f x x e =(2)求在上的最大值.()f x ()0,∞+【答案】(1);(2).1y e =()max 1f x e =【解析】【分析】(1)根据导数的几何意义,求得在的切线斜率,根据点斜式即可得解;x e =(2)根据导数在研究函数中的应用,求得可得单调性,根据单调性即可求得最值.【详解】(1)由题意得, ;()'21ln x f x x -=0x >;∴()'0f e =又()1f e e=在处的切线方程为;∴()f x x e =1y e =(2)令得;令得()'0f x >0<<x e ()'0f x <>x e 于是在单调递增;在单调递减()f x ()0,e (),e +∞.∴()()max 1f x f e e ==。
高二下学期期末数学试卷及答案

高二下学期期末数学试卷一、单项选择1、设,若直线与线段相交,则的取值范围是( )A .B .C .D .2、已知点A (2,-3),B (-3,-2),直线l 方程为kx+y-k-1=0,且与线段AB 相交,求直线l的斜率k 的取值范围为( )A或 B C D 3、直线与曲线有两个不同的交点,则实数的k 的取值范围是( ) A .B .C .D .4、已知圆,直线l :,若圆上恰有4个点到直线l 的距离都等于1,则b 的取值范围为 A .B .C .D .5、若直线被圆截得弦长为,则) A . B . C6、设△ABC 的一个顶点是A (3,-1),∠B,∠C 的平分线方程分别是x=0,y=x ,则直线BC 的方程是( ) A .B .C .D .7、已知圆:,则过点(1,2)作该圆的切线方程为( )A .x+4y-4=0B .2x+y-5=0C .x=2D .x+y-3=0 8、阿波罗尼斯(约公元前262-190年)证明过这样一个命题:平面内到两定点距离之比为常数的点的轨迹是圆,后人将这个圆称为阿氏圆.若平面内两定点A 、B 间4k ≤-220(0,0)ax by a b -+=>>222410x y x y ++-+=494(0,1)k k k >≠的距离为,动点P、A、B不共线时,三角形PAB面积的最大值是()ABD9、若圆上有个点到直线的距离为1,则等于()A.2 B.1 C.4 D.310、圆的一条切线与圆相交于,两点,为坐标原点,则()AB.C.2 D11、已知直线与圆相交,则的取值范围是()A. B. C.D.12、古希腊数学家阿波罗尼奥斯的著作《圆锥曲线论》中给出了圆的另一种定义:平面内,到两个定点、距离之比是常数的点的轨迹是圆.若两定点、的距离为3,动点满足,则点的轨迹围成区域的面积为().A.B.C.D.13、已知直线l1:(k-3)x+(4-k)y+1=0与l2:2(k-3)x-2y+3=0平行,则k的值是()A.1或3 B.1或5 C.3或5 D.1或214、我国古代数学巨著《九章算术》中,有如下问题:“今有女子善织,日自倍,五日织五尺,问日织几何?”这个问题用今天的白话叙述为:“有一位善于织布的女子,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这位女子每天分别织布多少?”根据上面的已知条件可求得该女子第4天所织布的尺数为( )A.B C D15、在等比数列中,,前项和为,若数列也是等比数列,则等于()A.B.C.D.16、设数列满足,记数列的前项之积为,则2P22:(5)(1)4C x y-++=n4320x y+-=n 221x y+=224x y+=()11,A x y()22,B x y O1212x x y y+=2-:cos sin1()l x yααα+=∈R222:(0)C x y r r+=>r 01r<≤01r<<1r≥1r>)0(>>ba{}na21=a n n S{}1na+nS 122n+-3n2n31n-( ) A .B .C .D .17、已知公比不为的等比数列满足,若,则( )A .9B .10C .11D .12 18、设等差数列的前项和为,已知,,则( )A .B .C .D .19、在等差数列中,若,是方程的两根,则的前11项的和为( )A .22B .-33C .-11D .1120、已知数列满足,数列前项和为,则( )ABCD21、已知数列满足,,是数列的前项和,则( )A .B .C .数列是等差数列 D .数列是等比数列22、已知等数差数列中,是它的前项和,若且,则当最大时的值为( )A .9B .10 C .11 D .1823、已知正项等比数列{a n }满足:a 7=a 6+2a 5,若存在两项a m 、a n ,使得a m a n =16a 12 )1{}n a 15514620a a a a +=210m a =m ={}n a nnS ()()201920212017201720171201912000a a a -++-=()()20192021202020202020-1+201912038a a a +-=4036S =2019202020214036{}n a 2*1222...2()n n a a a n n N +++=∈n nS 12310...S S S S ⋅⋅⋅⋅={}n a n S n 180S >190S <n S nABCD .不存在24、的内角,,所对的边分别是,,.已知,则的最小值为( ) A . B .C .D .25、已知,,为的三个内角,,的对边,向量,,若,且,则角( )A .B .C .D .二、填空题26、点到直线的距离的最大值为________.27、已知点和圆,过点 作圆的切线有两条,则实数的取值范围是______28、已知直线l :x+y-6=0,过直线上一点P 作圆x 2+y 2=4的切线,切点分别为A ,B ,则四边形PAOB 面积的最小值为______,此时四边形PAOB 外接圆的方程为______. 29、已知实数满足,则的取值范围为________.30、已知实数x ,y 满足6x+8y-1=0,则的最小值为______.31、等比数列的前n 项和为32、若等差数列满足,则数列的前项和取得最大值时_________ 33、已知数列满足,则数列的最大值为________.34、已知数列中,,是数列的前项和,且对任意的,都有,则=_____35、已知首项与公比相等的等比数列中,若,,满足,则()1,2P 222:20C x y kx y k ++++=P C k {}n a n S {}n a 7897100,a a a a a ++>+<{}n a n n S =n {}n a 11a =n S {}n a n *,r t N ∈n a的最小值为_____.36、在锐角三角形中,角的对边分别为,若,则的最小值是_______.37、在锐角中,角,,所对应的边分别为,,.则________;若,则的最小值为________. 38、若△ABC 的内角,则的最小值是 . 39、已知分别是的内角的对边,,,则周长的最小值为_____。
宁夏灵武一中2014-2015学年高二数学上学期期中试题 理 新人教A版

灵武一中2014—2015学年第一学期高二期中数学(理)试卷一、选择题:(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,将答案填在答题纸上). 1.命题“若p ,则q ”的逆命题是 ( )A .若q ,则pB .若⌝p ,则⌝ qC .若q ⌝,则p ⌝D .若p ,则q ⌝ 2.下列命题是真命题的为( ) A .若11x y=,则x y = B .若21x =,则1x = C .若x y =x y .若x y <,则22x y =3.给出命题:“若220x y +=,则0x y ==”,在它的逆命题、否命题、逆否命题中,真命题的个数是( )A .0个B .1个C .2个D .3个4.已知点B 是点A (2,-3,5)关于平面xoy 的对称点,则点B 的坐标为A.(2,3,5)B. (-2,-3,5)C. (2,-3,-5)D. (-2,-3,-5) 5.已知椭圆的两个焦点为(1,0-),(1,0),椭圆的长半轴长为2,则椭圆方程为( )A .2214x y +=B .2214y x += C .22134x y D .22143x y += 6.抛物线212x y =的准线方程是( ) A.12x =-B. 12x =C. 18y =-D.18y = 7.双曲线2213x y 的焦点坐标是( )A .()2,0B .(0,2 C .()2,0± D .()0,2±8.若平面α、β的法向量分别为()()1,5,2,3,1,4m n =-=-,则 ( ) A.αβ⊥ B.//αβ C.,αβ 相交但不垂直 D.以上均不正确9.从椭圆短轴的一个端点看两焦点的视角是1200,则这个椭圆的离心率e=( ) A.32 B.12 C.33D.1310.已知直线a 和两个平面,αβ,给出下列两个命题:命题p :若//a α,,a β⊥则αβ⊥; 命题q :若//a α, //a β,则//αβ; 那么下列判断正确的是( )A. p 为假B.q ⌝为假 C. p ∧q 为真 D. p ∨q 为真11.已知对k R ∈,直线10y kx --=与椭圆2215x y m+=恒有公共点,则实数m 的取值范围是( )A .(0, 1)B .(0,5)C .[1,5)D .[1,5)∪(5,+∞)12.已知a b >,椭圆1C 的方程为22221x y a b+=,双曲线2C 的方程为22221x y a b -=, 1C 与2C 的离心率之积为32,则2C 的渐近线方程为( ) A.20x y ±= B.20x y ±= C.20x y ±= D.20x y ±=二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知向量错误!未找到引用源。
宁夏育才中学2014-2015学年高一上学期第一次月考英语试题

宁夏育才中学2014-2015学年高一上学期第一次月考英语试题第一部分:听力(共两节,满分20分)第一节(每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
所完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What does the man think of the soup?A. TastyB. DeliciousC. Healthy2. What can we know about the woman?A. She doesn’t think the chicken is good.B. She thinks the dinner was great.C. She thinks the roast beef was dry.3. What does the woman mean?A. She would like to go out for dinner.B. She does not want to go to the concert.C. She is bored with concerts.4. Where does this conversation probably take place?A. In a restaurant.B. In a post office.C. In a shop5. How many books can Angela borrow at most today?A. TwoB. ThreeC. Four.第二节(每小题1分,满分15分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标出试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各个小题将给出5秒钟的作答时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宁夏育才中学2014~2015学年第二学期高二年级期末考试数学(理科)试卷
(试卷满分150分,考试时间为120分钟)
试卷说明:本试卷分两部分,第一卷为选择题,第二卷为非选择题
第一卷选择题部分
一、选择题(每小题5分,共60分,每小题只有一个正确答案)
1.若集合
{}21|21|3,0,
3x A x x B x x ⎧+⎫
=-<=<⎨⎬-⎩⎭则A∩B 是(A)11232x x x ⎧⎫
-<<-<<⎨⎬
⎩
⎭或(B)
{}23x x <<(C)122x x ⎧⎫
-<<⎨⎬⎩⎭(D)112x x ⎧⎫
-<<-⎨⎬
⎩
⎭2.“a 和b 都不是偶数”的否定形式是
(
)
A.a 和b 至少有一个是偶数B.a 和b 至多有一个是偶数C.a 是偶数,b 不是偶数
D.a 和b 都是偶数
3.设命题甲:|1|2x ->,命题乙:3x >,则甲是乙的(
).
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
4.已知极坐标平面内的点
P
关于极点的对称点的极坐标与直角坐标分别为(
)
,(1,
3),(1,-
3),(-1,
3),(-1,-3)5.下列命题中的假命题是A.∀x R ∈,1
2
0x ->2x-1>0B.∀*x N ∈,2(1)0
x ->C.∃x R ∈,lg 1x < D.∃x R ∈,tan 2
x =6.将一枚均匀骰子掷两次,下列选项可作为此次试验的随机变量的是()
A.第一次出现的点数B.第二次出现的点数C.两次出现点数之和
D.两次出现相同点的种数
7.采用简单随机抽样从个体为6的总体中抽取一个容量为3的样本,则对于总体中指定的个体a ,前两次没被抽到,第三次恰好被抽到的概率为()
A.
1
2
B.
13
C.
15
D.
16
8.设~(100.8)X B ,,则(21)D X +等于()A.1.6
B.3.2
C.6.4
D.12.8
9.设随机变量X 的分布列如下表,且 1.6EX =,则a b -=(
)X 0123P
0.1
a
b
0.1
A.0.2B.0.1C.0.2-D.0.4
-10.袋中装有10个红球、5个黑球.每次随机抽取1个球后,若取得黑球则另换1个红球放回袋中,直到取到红球为止.若抽取的次数为ξ,则表示“放回5个红球”事件的是(
)
A.ξ=4
B.ξ=5
C.ξ=6
D.ξ≤5
11.一袋中有5个白球,3个红球,现从袋中往外取球,每次任取一个记下颜色后放回,直到红球出现10次时停止,设停止时共取了ξ次球,则P (ξ
=12)=(
)
A.C
B.C 9
·
3
8
C.C 9
D.C 9
12.在15个村庄中有7个村庄交通不方便,现从中任意选10个村庄,用X 表示这10个村庄中交通不方便的村庄数,下列概率中等于C 74
C 8
6
C 15
10的是(
)
A.P (X =2)
B.P (X ≤2)
C.P (X =4)
D.P (X ≤4)
第二卷非选择题部分
二.填空题(每小题5分,共20分.)13.设X~N(5,1),求P(6<X<7)=。
14.设全集},1|{},0)3(|{,-<
=<+==x x B x x x A R U 则右图中阴影部分表示的集合为
___.
15.对于x R ∈,不等式
1028
x x +--≥的解集为________
16.某射手射击1次,击中目标的概率是0.9,他连续射击4次,且各次射击是否击中目标相互之间没有影响,有下列结论:①他第3次击中目标的概率是0.9;
②他恰好击中目标3次的概率是0.93×0.1;③他至少击中目标1次的概率是41(0.1)-.其中正确结论的序号是
(写出所有正确结论的序号).
三.解答题.(6个小题,共70分)
17、(10分)已知直线01:=-+y x l 与抛物线2
x y =交与A,B 两点,求线段AB 的长和点M (-1,2)到A,B 两点的距离之积。
18.(12分)设.|4||12|)(--+=x x x f (1)解不等式2)(≥x f ;(2)求函数)(x f 的最小值。
19.(12分)在含有2件次品的10件产品中,任取3件,求:(1)渠道的次品书X 的分布列及数学期望(2)至少取到1件次品的概率。
20.(12分)某射手每次射击击中目标的概率是5
4
,求这名射手在10次射击中,(1)恰有8次击中目标的概率;(2)至少有8次击中目标的概率。
21.(12分)一张储蓄卡的密码共有8位数字,每位数字都可从0~9中任选一个。
某人在银行自动提款机上取钱时,忘记了密码的最后一位数字,求:(1)任意按最后一位数字,不超过2次就按对的概率:
(2)如果他记得密码的最后一位是偶数,不超过2次就按对的概率。
22.(12分)通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列
联表:
男女总计
看营养说明503080
不看营养说明102030
总计6050110
(1)从这50名女生中按是否看营养说明采取分层抽样的方法抽取一个容量为5的样本,则样本中看与不看营养说明的女生各有多少名?
(2)从(1)中的5名女生样本中随机选取两名作深度访谈,求选到看与不看营养说明的女生各一名的概率;
(3)根据以上列联表,问有多大把握认为“性别与在购买食物时是否看营养说明”有关?
参考公式:K2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
,其中n=a+b+c+d.
参考数据:
P(K2≥k
)0.100.050.0250.0100.005
k
2.706
3.841 5.024 6.6357.879。
