北京邮电大学《通信原理》课程讲义-模拟调制系统(2)
大学课程通信原理第5章-模拟调制系统课件

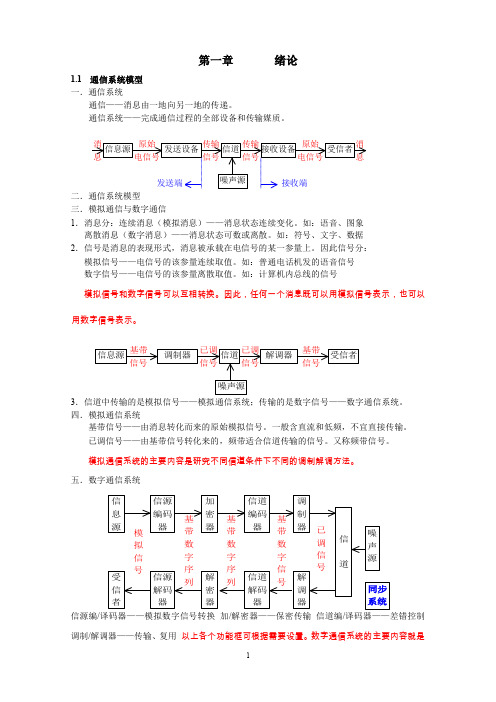
调制信号:原始基带信号
模拟调制:调制信号取值连续 数字调制:调制信号取值离散
正弦波模拟调制
载波:携带调制信号的信号
正弦波调制:正弦型信号作为载波 脉冲调制:脉冲串作为载波
正弦波数字调制 脉冲模拟调制 脉冲数字调制
2
1 调制的定义和分类(2)
正弦波模拟调制
调制信号:模拟信号:m(t)
0 0
A 2
M
c
M
c
已调信号的频谱是调制信号频谱的线性搬移。
线性调制
4
2.1 幅度调制的原理(2)
幅度调制器的一般模型
mt
ht
sm t
ht H
cos ct
sm t m t cos ct h t
Sm
1 2
M
c
M
c
H
m t ,ht 不同
双边带调幅(DSB) 标准调幅(AM)
载波分量
DSB分量
m ' t
sAM t
m0
S AM
m0
c
c
1 2
M
'
c
M
'
c
where m ' t M ' .
12
2.1 幅度调制的原理(8)
调幅系数
m ' t
AM
max 1 m0
已调信号的包络与调 制信号成比例变化.
m't
sAM t
m0
m0 m '(t )
sAM t m0 m '(t)
单边带调幅(SSB)
残留边带调幅(VSB) 5
常规调幅AM:H(ω)为全通网络,m(t) 有直流成 分。
北邮通信原理讲义
线性 时移 频移 比例
a
n 1
n f n (t )
a
n 1
N
n
Fn ( w)
f (t t 0 ) f (t ) e jw0t
f (at )
F ( w) e jwt0 F ( w w0 )
1 F ( w a) a
2f (w)
对偶 复共轭 微 分 时域
F (t )
f * (t )
S f ( w)dw S f ( f )df
பைடு நூலகம்
5.无限周期信号的平均功率和功率谱密度 功率谱密度 S f ( w) 2
n
| C
n
| 2 ( w nwT ) , 平均功率 P
n
| C
n
|2
Cn 为各个频率点的幅度,|Cn|2 为 nwT 分量的平均功率 四.信号通过线性系统 1.系统的传递函数 以冲激函数 δ (t)作为激励,通过系统后
信噪比
信号平均功率 噪声平均功率
二.数字通信系统性能指标 1. 速度指标 码元速率 RBN:每秒传送码元的数目。单位:B 信息速率 Rb:每秒传送的信息 量。单位:b/s, bps Rb = RBN log2 N (bit/s) 2. 质量指标 误码率 P B:码元被错误接收的概率。 误信率 Pb:传输每比特信息发生错误接收的概率。
第二章
2.1 确知信号的频谱分析 一.付立叶变换
随机信号分析
任一信号有两种表示方法:时域表示法 f (t ) :信号的大小随时间的变化。
频域表示法 F ( w) :信号的振幅和相位随频率成分的变化。两种表示法互相对应,记做:
f (t ) F (w) 。变换式为: f (t )
通信原理--模拟调制系统 ppt课件

– 线性调制:AM、DSB、SSB、VSB – 非线性调制:PM、FM调制
数字调制:ASK、FSK、PSK
第二章 模拟线性调制
调制的作用
– 信号与信道匹配 – 频分多路复用 – 电波辐射 – 频率分配 – 可减小干扰
第二章 模拟线性调制
模拟调制
以模拟信号为调制信号,对连续的正 (余)弦波进行调制。
下边带
上边带
调幅信号的平均功率为:
PAMsA 2M(t)
功
A0 f(t)2cos2ct
率 特
A02cos2ctf 2(t)cos2ct2A0f(t)cos2ct
性 分
因为 f (t ) 0
c os2ct
11
2
c
os2ct
析
cos2ct 0
PAM A 20 2 f22(t)PcPf
•常规调幅信号的功率由载波功率Pc和边带功率Pf组成; •边带功率与调制信号有关,是有用功率:
若 AM1 ,调制效率最大值为1/3。
常规调幅调制效率低,载波分量不携带信息 却占用大部分功率!
改进方案----抑制载波双边带调制
例题与习题
例2-1:已知一个AM广播电台输出功率是50kW,采用单频余弦信 号进行调制,调幅指数为0.707。
(1)试计算调制效率和载波功率;
(2)如果天线用50Ω的电阻负载表示,求载波信号的峰值幅度。
弦波,也可以是非正弦波。 – 已调信号 :载波受调制后称为已调信号。 – 解调(检波) :调制的逆过程,其作用是将已调
信号中的调制信号恢复出来。
信号、传输方式、调制方式的分类
电信号
– 基带信号 (携带有用信息的信号,未调制) – 频带信号 (基带信号经过某种调制)
2通信原讲义理模拟调制系统

• (D)调制在接收端,解调在发射端
• 3.在模拟无线通信的系统中,下列哪种说法是正确的。。
• (A)基带信号一定是正弦波。
• (B)基带信号一定是方波。
• (C)载波信号一定是正弦波。
• (D)载波信号一定是方波。
2.3 非线性调制系统
一、调频信号与调相信号
s(t)A(t)co(st)[]
瞬时幅度
2通信原理模拟调制系统
精品jing
易水寒江雪敬奉
基本概念
• 1、基带信号 • 2、调制的作用:易于辐射/频率资源充分使
用/多路复用/改善信噪比 • 3、模拟调制:以模拟信号为调制信号,对
连续的正(余)弦载波进行调制,即载波 的参数随着调制信号的作用而变化,此调 制称为模拟调制。 • 4、模拟调制 幅度调制 AM,DSB,SSB,VSB
300π 500 π
二、常规双边带调制系统
1、常规双边带调制(AM)信号的时域表达式及波形
调制信号f(t),其平均值为0,即f(t)=0;
调制后表达式:s A( M t) [A 0 f(t)c ]o c t sc ) (
f( t) c1 ot) 0 s c ( t ,) ( 0 c4 ot) 0 s c , ( 0 0
-w0
w0
3W0 4w0
w
作业
• 1、Page38, 2.1题,2.3
1、 在通信系统中,模拟线性调制是指
。
• (A)调幅 角
(B)调频
(C)调相
(D)调
• 2.下列有关通信系统中的调制、解调说法哪种是正确的。
• (A)调制、解调都在发射端
• B)调制、解调都在接收端
• (C)调制在发射端,解调在接收端
通信原理模拟调制系统

通信原理模拟调制系统一、模拟调制系统的基本原理模拟调制系统的基本原理是将数字信号通过调制技术转换为模拟信号,然后通过信道传输,并在接收端使用解调技术将模拟信号还原为数字信号。
模拟调制系统由三个基本组成部分组成,分别是源编码器、调制器和信道。
源编码器将输入的数字信号进行编码处理,调制器将编码后的数字信号转换为模拟信号,并通过信道传输,接收端的解调器将模拟信号还原为数字信号。
二、常用的调制技术1.幅度调制(AM)幅度调制是一种常用的调制技术,通过改变载波信号的幅度来传输数字信号。
具体实现时,将载波信号与数据信号相乘,得到一个幅度变化的信号,然后通过信道传输。
发射端的解调器使用包络检测器将幅度调制信号解调为原始数据。
2.频率调制(FM)频率调制是一种将数字信号转换为模拟信号的调制技术。
频率调制有两种常用的方式,即调频调制(FM)和相位调制(PM)。
在调频调制中,数字信号的变化会导致载波信号频率的变化,而振幅保持不变。
接收端的解调器使用频率解调器将模拟信号还原为数字信号。
3.相位调制(PM)相位调制也是一种将数字信号转换为模拟信号的调制技术。
在相位调制中,数字信号的变化会导致载波信号相位的变化,而频率和振幅保持不变。
接收端的解调器使用相位解调器将模拟信号还原为数字信号。
三、调制解调器调制解调器是模拟调制系统中的关键设备,用于实现数字信号与模拟信号的相互转换。
调制解调器在发射端将数字信号转换为模拟信号,并通过信道传输。
在接收端,调制解调器将模拟信号还原为数字信号,以便进行解码和处理。
四、模拟调制系统的应用模拟调制系统广泛应用于音频和视频信号的传输。
在电视广播中,模拟调制系统被用于将图像和声音信号转化为模拟信号,然后通过无线或有线信道传输。
在手机通信中,模拟调制系统被用于将语音信号转化为模拟信号,然后通过无线信道传输。
总结:模拟调制系统是一种将数字信号转换为模拟信号的技术,常用于音频和视频信号的传输。
它包括源编码器、调制器和信道等组成部分,并通过调制解调器实现数字信号与模拟信号的相互转换。
北京邮电大学《通信原理》课程讲义-模拟信号的传输

在给定输入信号概率密度p(x)及量化级数M,如
何进行最佳量化,使量化噪声的平均功率最小,
量化信噪比最大?
2006-6-16
北京邮电大学信息工程学院 Jrlin@
21
模拟信号的量化
2. 均匀量化器(线性量化器)
量化间隔Δk相等,即Δk =Δ
量化范围(-V,V)及量化级数M时
信息源
调制器
信道
解调器
信宿
模拟 信息源
抽样、量化 和编码
数字 通信系统
译码和低 通滤波
m(t) 模拟随机信号
{sk} 数字随机序列
{sk}
m(t)
数字随机序列 模拟随机信号
数字通信
2006-6-16
北京邮电大学信息工程学院 Jrlin@
5
模拟信号数字化的基本原理
抽样 量化 编码
– 抽样、量化、编码
• 模拟信号的抽样 • 模拟信号的量化 • 脉冲编码调制PCM
2006-6-16
北京邮电大学信息工程学院 Jrlin@
7
模拟信号的抽样
抽样定理:
一个频带限制在(0, fH) 赫内的时间连续信号m(t), 如果以Ts≤1/(2fH)秒的间隔对它进行等间隔(均匀) 抽样,则m(t)将被所得到的抽样值完全确定。
北京邮电大学信息工程学院 Jrlin@
18
模拟信号的量化
1. 标量量化的基本原理 标量量化(一维量化):每个样值独立地进行量化
x∈{xk-1, xk}时, y=Q( x)=yk k =1,2,…, M, M为量化级数
量化误差 eq = x − yk = x − Q(x)
m(t )
mS (t)
m~ S (t) 低通滤 m~(t)
(通信原理课件)第5章模拟调制系统

数字调制技术与模拟调制技术的对比
模拟信号
频率范围宽广,传输距离有限,信号易受噪声和干扰。
数字信号
信号质量稳定,传输距离远,可以进行纠错和加密处理。
模拟调制系统的应用场景
1 广播电视
2 电信网络
3 药物反应分析
模拟广播电视、卫星传输等 是模拟调制系统最典型的应 用场景。
手机号码的拨叫、语音通信 等都是通过模拟调制信号进 行传输的。
2
调制指数
反映基带信号对载波相位影响程度的实数。
3
调制解调
用相位调制解调器进行信号的解调,得到原始的基带信号。
相位调制电路实现
移相调制电路
加上一个可调的移相网络来实现相 位调制电路,具有较广泛的应用。
频率鉴别器
在解调中进行频率鉴别器,将相位 调制信号转化为幅度调制信号。
锁相环电路
利用反馈来使输出信号的相位与设 定相位保持一致,实现恒定的相位 调制。
模拟调制系统
在通信原理中,模拟调制系统是通信系统的基础。本次演示将介绍模拟调制 的各种技术和应用场景,并展示其未来的发展趋势。
模拟调制系统概述
定义
模拟调制系统,指通过调制信号的幅度、频率或相位,将基带信号转换为通信信号的一种系 统。
作用
模拟调制系统可以将语音、图像等信息转化为高频信号,方便远距通信,具有广泛的应用。
直接调频电路
使用直接的变容二极管调制电路进行频率调制,未 使用任何电感元件,在射频前端应用较广。
电容调制电路
通过改变电容的大小来调制载波频率,调制范围相 对较小,但制造相对简单。
相位锁定环电路
使用恒振幅恒频率的信号进行相位锁定,能够获得 较高的调制精度。
相位调制原理
《通信原理》课件第三章 模拟调制系统

解调较AM复杂(相干载波提取困难)。
3、单边带调幅(SSB)
▪ 双边带抑制载波调幅方式中,不含固定载波分量,因而可 以有效地利用发射机的功率传递信息。但它是双边带信号, 所占带宽仍为调制信号最高角频率的两倍。
▪ 而从有效传输信息的角度看,只要传送一个边带就够了, 只传送一个边带的调幅信号称为单边调幅,可以选择上边 带也可以采用下边带。
(1)频域表达
S VSB( ) SDSB( ) HVSB( )
1 2
H VSB (
) F(
c
)
F(
c
)
③② ①
HVSB(ω)
| SDSB( ) |
c
0
① ②③
残留部分上边带滤波器
①下边带全通区
| SDSB( ) |
c
②下边带抑制区
③上边带抑制区
① ②③
| SDSB( ) |
c
HVSB(ω)
0
F( )
f ( t )e jt dt
f ( t )costdt j f ( t ) sin tdt
可见 F( ) F( ),F( )和F( )是共轭对称的,
或者说 F( )和 F( )是关于轴 0对称的。
| F( )|
A
A0 A / 2
c
1 2
F(
c
)
| S AM ( )|
A0 A / 2
Pf PAM
f 2(t ) A02 f 2 ( t )
若f (t)
Am cos(mt m ) — 单频余弦,则 f 2 (t)
1 2
Am2, AM
1 2
Am2
A02
1 2
Am2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
sVSB ( t ) = ⎡ m ( t ) cos ω c t ⎤ ∗ h ( t ) ⎣ ⎦
sVSB ( t )
×
SVSB ( ω ) =
mα ( t )
LPF
mo ( t )
m α ( t ) = sVSB ( t ) cos ω c t
H ( ω ) 的截止特性在载频ω c 左右 具有互补对称特性。
−ω H
ωH
9
4.2随机调制信号的率谱密度
随机调制信号的功率谱密度特 性
为 R M (τ 假 设 消 息 随 机 过 程 M (t )是 一 均 值 为 零 , 自 相 关 函 数
)↔
PM ( ω ) 的 广 义 平 稳 随 机 过 程 .
E (t ) = ⎡ A + m ( t ) + n c ( t ) ⎤ + n s2 ( t ) ⎣ ⎦ ns ( t ) ψ ( t ) = arctg A + m ( t ) + nc ( t )
2
~ 包络检波器输出
14
4.4 线性调制系统的抗噪声性能(5)
大信噪比情况: A + m ( t )
s m (t )
+
s1 (t )
包络检波器
m 0 (t )
s (t ) = A d cos ω c t
s (t ) = s
1
ˆ = m (t ) cos ω c t ∓ m (t ) sin ω c t + = m (t ) +
m
(t ) + s (t )
[
A ]cos ω
d
2 d
c
ˆ t ∓ m (t ) sin ω c t
2 2 2 σn = σn = σn ,
i c s
i .e . ni2 ( t ) = nc2 ( t ) = ns2 ( t )
( B ~ BPF带宽/已调信号带宽 ) 调制制度增益:
N i = ni2 ( t ) = N 0 B
2 sm ( t ) Si 输入信噪比: = 2 N i ni ( t ) 2 S o mo ( t ) 输出信噪比: = 2 N o no ( t )
13
■
G =1
4.4 线性调制系统的抗噪声性能(4)
AM系统的性能
s A M ( t ) = ⎡ A + m ( t ) ⎤ cos ω c t , ⎣ ⎦
ni ( t ) = nc ( t ) cos ω c t − ns ( t ) sin ω c t
2 A2 m (t ) Si = + 2 2
2
A
d
cos ω c t
m
0
(t ) = ≈ ≈
[m ( t ) +
A A
d
Ad]
m (t )
+
ˆ [m ( t ) ]
2
+
A
d
+ m (t )
7
4.2.4 残留边带(VSB)
残留边带(VSB)信号
m (t)
×
h(t ) cos ω c t
HVSB ( ω )
sVSB ( t )
m ( t ) ∼ 无直流分量 h ( t ) ∼ 残留边带滤波器
s D SB ( t ) = M ( t ) cos ( ω c t )
Ps D SB ( ω ) = 1 ⎡ PM ( ω + ω c ) + PM ( ω − ω c ) ⎤ ⎦ 4⎣
s A M ( t ) = ⎡ A + M ( t ) ⎤ cos ( ω c t ) ⎣ ⎦ 1 Ps ( ω ) = ⎡ δ ( ω + ω c ) + δ ( ω − ω c ) ⎣
SSB调制系统的性能 (B=W )
■
1 1 ˆ sUSB ( t ) = m ( t ) cos ωc t − m ( t ) sin ωc t 2 2 2 2 1 2 ˆ S i = sUSB ( t ) = ⎡ m ( t ) cos ω c t ⎤ + ⎡ m ( t ) sin ω c t ⎤ ⎦ ⎣ ⎦ 4 ⎣
Mα ( ω ) = 1 ⎡ SVSB ( ω − ωc ) + SVSB ( ω + ω c ) ⎤ ⎦ 2⎣
cos ( ω c t )
Mα ( ω ) =
1 1 ⎡ M ( ω − 2ω c ) + M ( ω ) ⎤ H ( ω − ω c ) + ⎡ M ( ω ) + M ( ω + 2ω c ) ⎤ H ( ω + ω c ) ⎦ ⎦ 4⎣ 4⎣
×
SSB信号的产生
滤波法:频域 相移法:时域
−π 2
ˆ m (t)
m(t)
cos ωc t
−π 2
+ +/-
∑
sSSB ( t )
sin ω c t
×
SSB信号的解调——相干解调
m α ( t ) = s SSB ( t ) cos ( ω c t )
=
s SSB ( t )
×
mα ( t )
LPF
= ⎡ A + m ( t )⎤ 1 + ⎣ ⎦ A + m (t )
2 nc ( t )
⎡ nc ( t ) ⎤ ≈ ⎡ A + m ( t )⎤ ⎢1 + ⎥ ⎣ ⎦ A + m (t ) ⎥ ⎢ ⎣ ⎦
= A + m ( t ) + nc ( t )
有用信号 噪声
2 So m ( t ) = No N0 B
10
4.4 线性调制系统的抗噪声性能(1)
性能分析模型
sm ( t ) n(t )
+
BPF
sm ( t ) ni ( t )
解调器
mo (t ) no ( t )
■
ni ( t ) = nc ( t ) cos ω c t − ns ( t ) sin ω c t = V ( t ) cos ⎡ω c t + θ ( t ) ⎤ ⎣ ⎦
1 nc ( t ) 2
1 2 So = m ( t ) = m ( t ) 4 1 2 1 2 1 2 N o = no ( t ) = nc ( t ) = ni ( t ) = N 0W 4 4 2
2 o
■
Si m2 ( t ) So = = N 0W N o 2 N 0W
12
G=2
4.4 线性调制系统的抗噪声性能(3)
s
频谱: 带
m
ˆ ( t ) = A c R e [m ( t ) ∓ j m ( t ) ]e
Hilbert
{
j 2πfc t
}
]
⎯ ˆ 下边带取“+”,上边带取“-”。 m(t ) ←⎯ ⎯ → m(t )
S
m
Ac M (ω + ω c ) sgn(ω + ω c ) + M (ω − ω c ) sgn(ω − ω c )
cos ( 2.3单边带(SSB)(3)
sLSB ( t ) = 1 1 ˆ m ( t ) cos ω c t + m ( t ) sin ω c t 2 2 1 1 ˆ sUSB ( t ) = m ( t ) cos ω c t − m ( t ) sin ω c t 2 2
no ( t ) = ⎡ nc ( t ) cos ω c t − ns ( t ) sin ω c t ⎤ cos ω c t ⎣ ⎦
2 S o = mo ( t ) =
LPF
=
1 2 m (t) 16 1 1 N o = nc2 ( t ) = N 0W 4 4
1 nc ( t ) 2
Si m2 ( t ) So = = N 0W N o 4 N 0W
AM
4
+ PM ( ω + ω c ) + PM ( ω − ω c ) ⎤ ⎦
⎧PM (ω-ωc ) + PM (ω +ωc ) ω ≤ ωc ⎪ PSL(ω) = ⎨ ω > ωc ⎪0 ω > ωc ⎩
⎧0 ω ≤ ωc ⎪ Psu (ω) = ⎨ ⎪PM (ω-ωc ) + PM (ω + ωc ) ⎩
mo ( t )
cos ( ωc t )
1 1 1 ˆ m ( t ) + m ( t ) cos 2ω c t ∓ m ( t ) sin 2ω c t 4 4 4 1 mo (t ) = m (t ) 4
3
4.2.3 SSB(书上符号)
已调信号:
s
m
ˆ ( t ) = A c m ( t ) cos ω c t ∓ A c m ( t ) sin ω c t
E (t ) =
2
ni ( t ) , nc ( t ) ,
x
ns ( t )
1时 ,
⎡ A + m ( t ) + n c ( t ) ⎤ + n s2 ( t ) ⎣ ⎦
≈
⎡ A + m ( t ) ⎤ + 2 ⎡ A + m ( t ) ⎤ nc ( t ) ⎣ ⎦ ⎣ ⎦
2
1+ x ≈ 1+ x 2
LPF
M o (ω ) =
1 M (ω ) ⎡ H ( ω + ωc ) + H ( ω − ωc ) ⎤ ⎣ ⎦ 4
