二次函数与图形面积问题
二次函数与图形面积问题
二次函数与图形面积问题1、阅读材料：如图1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部的线段的长度叫△ABC的“铅垂高”（h）.我们可行出生种计算三角形面积的新方示：y=a(x-1)2+4 ，即三角形面积等于水平宽与铅垂高乘积的一半.解答下列问题:如图2，抛物线顶点C（1，4），交x轴于点A（3，0），交y轴于点B.（1）求抛物线和直线AB的解析式；（2）求△ABC的铅垂高CD及S △ ABC（3）设点P是抛物线（在第一象限内）上的一个动点，是否存在一点P，使a=-1 ，且S△PAB=9/8 S△CAB若存在，求出P点的坐标；若不存在，请说明理由.2、如图,已知抛物线y=ax2+bx+c经过点A（2,3）,B（6,1）,C（0,-2）．（1）求此抛物线的解析式,并用配方法把解析式化为顶点式；（2）点P是抛物线对称轴上的动点,当AP⊥CP时,求点P的坐标；（3）设直线BC与x轴交于点D,点H是抛物线与x轴的一个交点,点E（t,n）是抛物线上的动点,四边形OEDC的面积为S．当S取何值时,满足条件的点E只有一个?当S取何值时,满足条件的点E有两个?3、如图，已知平面直角坐标系xOy中，点A（m，6），B（n，1）为两动点，其中0＜m＜3，连接OA，OB，OA⊥OB。
（1）求证：mn=-6；（2）当S△AOB=10时，抛物线经过A，B两点且以y轴为对称轴，求抛物线对应的二次函数的关系式；（3）在（2）的条件下，设直线AB交y轴于点F，过点F作直线l交抛物线于P，Q两点，问是否存在直线l，使S△POF：S△QOF=1：3？若存在，求出直线l对应的函数关系式；若不存在，请说明理由。
4、如图1，在平面直角坐标系中，点A的坐标为（1，2），点B的坐标为（3，1），二次函数y=x2的图象记为抛物线l1。
（1）平移抛物线l1，使平移后的抛物线过点A，但不过点B，写出平移后的一个抛物线的函数表达式：______ （任写一个即可）；（2）平移抛物线l1，使平移后的抛物线过A，B两点，记为抛物线l2，如图2，求抛物线l2的函数表达式；（3）设抛物线l2的顶点为C，K为y轴上一点，若S△ABK=S△ABC，求点K的坐标；（4）请在图3上用尺规作图的方式探究抛物线l2上是否存在点P，使△ABP为等腰三角形，若存在，请判断点P共有几个可能的位置（保留作图痕迹）；若不存在，请说明理由。
二次函数与图形面积问题
M点的坐标
如图，已知抛物线y=x2-1 与 X轴交于A、B两点，与 y轴交于点C（3）
在X 轴上方的抛物线上是否存在一点M，过M作MG 垂直于X轴于点G，
使以A、M、G三点为顶点的三角形与 △PCA相似．若存在，请求出
M点的坐标
2.在平面直角坐标系中，△ABC是直角三角 形,∠ACB=90,AC=BC,OA=1，OC=4，抛物线 y=x2+bx+c经过A， B两点，抛物线的顶点为D．（1）求b,c的值；
如图，已知抛物线 y=ax2+bx+c(a≠0)的顶点坐标为Q （2，-1），且 与 Y轴交于点C(0,3) ，与X 轴交于A、B两点（点A在点B的右侧），点 P是该抛物线上一动点，从点C沿抛物线向点A运动（点P与A不重合 ），过点P作PD∥ Y轴，交AC于点D． (2)当△ADP是直角三角形时， 求点P的坐标；
二次函数与图形面积问题
1.如图，已知抛物线y=x2-1 与 X轴交于A、B
两点，与 y轴交于点C．
（1）求A、B、C三点的坐标;
解：（1）当y=0,得：x2-1=0, 解得：x=1或x=-1 令x=0得，y=-1 所以A(-1,0) B(1,0) C(0,-1)
如图，已知抛物线y=x2-1 与 X轴交于A、B两点，与
y轴交于点C． （2）过点A作AP∥CB交抛物线于点P， 求四边形ACBP的面积;
如图，已知抛物线y=x2-1 与 X轴交于A、B两点，与 y轴交于点C（3）
在X 轴上方的抛物线上是否存在一点M，过M作MG 垂直于X轴于点G，
使以A、M、G三点为顶点的三角形与 △PCA相似．若存在，请求出
《第1课时 二次函数与图形面积》基础训练
《第1课时二次函数与图形面积》基础训练知识点1 求二次函数的最值1. 已知二次函数y=2x2-3x+c的最小值为，则c的值为（）A. -4B. 3C. 4D. 52.（1）当x= 时，二次函数y=-x2+2x有最值，为；（2）当x= 时，二次函数y=2x2-2x+3有最值，为；知识点2 利用二次函数求几何图形面积的最值3. 如图，假设篱笆（虚线部分）的长度为16m，则所围成矩形ABCD的最大面积是（）4. 如图，用长8m的铝合金条制成使窗户的透光面积最大的矩形窗框，那么这个窗户的最大透光面积是（）A.B.C.D.5. 如图，已知ABCD的周长为8cm，∠B=30°，若边长AB=cm.（1）ABCD的面积y（cm2）与（cm）之间的函数解析式为，自变量的取值范围是（2）当取时，y的值最大，最大值为6. （沈阳中考）如图，一块矩形土地ABCD由篱笆围着，并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900m（篱笆的厚度忽略不计），当AB= m时，矩形土地ABCD的面积最大.7. 已知直角三角形两条直角边的和等于20，两条直角边各为多少时，这个直角三角形的面积最大最大值是多少8. 某高中学校为高一新生设计的学生单人桌的抽屉部分是长方体形，抽屉底面周长为180cm，高为20cm.请通过计算说明，当底面的宽为何值时，抽屉的体积y最大最大为多少（材质及其厚度等暂忽略不计）参考答案1. C2.（1）1 大 1 （2）小3. C4. C5.（1）（2） 2 26. 1507. 解：当x=10时，面积y取最大值，=50.8 .解：当底面的宽为45cm时，抽屉的体积最大，最大为40 500cm3.。
二次函数应用 图形面积问题
二次函数应用图形面积问题
1、在创建文明城市的活动中，政府想借助如图所示的直角墙角（两边足够长），用30m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB x
200m，求AB的
=m．（Ⅰ）若花园的面积是2
长；（Ⅱ）当AB的长是多少时，花园面积最大？最大面积是多少？
2、如图，在足够大的空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园
a=，所ABCD，其中AD MN，已知矩形菜园的一边靠墙，另三边一共用了200米木栏．（1）若30
围成的矩形菜园的面积为1800平方米，求所利用旧墙AD的长；（2）求矩形菜园ABCD面积的最大值．
3、某养鸡专业户用篱笆及一面墙（该墙可用最大长度为36米）围成一个矩形场地ABCD来供鸡室外活动，该场地中间隔有一道与AB平行的篱笆()
EF，如图，BE、EF上各留有1米宽的门（门不需要篱笆），该养鸡专业户共用篱笆58米，设该矩形的一边AB长x米，AD AB
>，矩形ABCD的面积为s 平方米．（1）求出S与x的函数关系式，直接写出自变量x的取值范围；
（2）若矩形ABCD的面积为252平方米，求AB的长．
4、如图，有长为24m的篱笆，一面利用墙（墙的最大可用长度a为10m）围成中间隔有一道篱笆的矩形
花圃，设花圃的宽AB为xm，面积为Sm2．（1）求S与x的函数表达式．（2）如果要围成面积为45m2的花圃，AB的长是多少米？（3）能围成面积为50m2的花圃吗？若能，请说明围法；若不能请说明理由．。
二次函数与面积例题
二次函数与面积例题常用求面积方法：①直接法求三角形面积．如图所示，△ABC中AD为边BC上的高，则S△ABC＝1/2BC·AD．②补全法求三角形面积．如图所示，S△ABC＝S矩形BDFE－ S△ABE － S△ACF－ S△BCD．③分割法求三角形面积．如图所示，S△ABC＝S△ABD＋S△ACD＝AD·BF＋AD·CE＝AD·(BF＋CE)．④平移法求三角形面积．如图所示，过点A作AD∥BC，则S△ABC＝S△BCD．当一个三角形（或其他多边形）的形状或大小发生变化时，产生面积变化．选择合适的方法，利用已知条件求出变化过程中该三角形（或其他多边形）的面积．典型例题1．如图，已知抛物线y＝ax2＋bx＋3与x轴交于A、B两点，过点A 的直线l与抛物线交于点C，其中A点的坐标是（1，0），C点坐标是（4，3）．（1）求抛物线的解析式；（2）在（1）中抛物线的对称轴上是否存在点D，使△BCD的周长最小？若存在，求出点D的坐标，若不存在，请说明理由；（3）若点E是（1）中抛物线上的一个动点，且位于直线AC的下方，试求△ACE的最大面积及E点的坐标．典型例题如图，抛物线与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C。
（1）填空:点A的坐标是________；点B的坐标是_________ （2）若点P为抛物线上一个动点（不含点C），当△ACB的面积时，求点P的坐标；（3）设点D为抛物线的对称轴上的任意一点，当△ACD的面积等于△ACB的面积时，求点D的坐标。
解答分析：（1）因为点A和点B在x轴上，所以纵坐标为0，令y=0，代入抛物线解析式，可以得到一个关于x的一元二次方程，解方程即可得出A 和B的横坐标。
∵y=0时，-3/8x²-3/4x+3=0∴x1=-4，x2=2∴A（-4.0）B（2,0）（2）△ACB的面积可以以AB为底，CO为高求出来，因为△ABP与△ACB 的底相同，如果想要面积相等，则必须高相等。
专题：二次函数与几何图形综合——图形面积问题(后附答案)【精品】
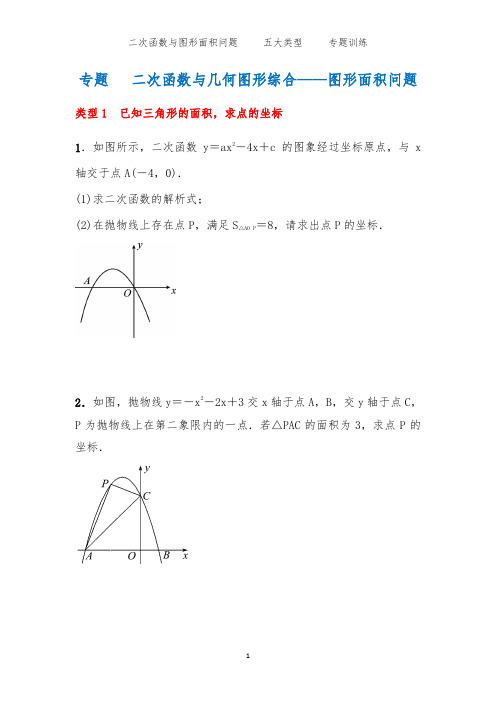
专题二次函数与几何图形综合——图形面积问题类型1 已知三角形的面积，求点的坐标
1．如图所示，二次函数y＝ax2－4x＋c的图象经过坐标原点，与x 轴交于点A(－4，0)．
(1)求二次函数的解析式；
(2)在抛物线上存在点P，满足S△AO P＝8，请求出点P的坐标．
2．如图，抛物线y＝－x2－2x＋3交x轴于点A，B，交y轴于点C，P为抛物线上在第二象限内的一点．若△PAC的面积为3，求点P的坐标．
类型2 已知三角形面积之间的数量关系，求点的坐标
3．如图是二次函数y＝(x＋m)2＋k的图象，其顶点坐标为M(1，－4)．(1)求出图象与x轴的交点A，B的坐标；
(2)在二次函数的图象上是否存在点P，使S△PAB＝5
4
S△MAB？若存在，求出点P的坐标；若不存在，请说明理由．
类型3 求三角形面积的最值
4．如图，直线l：y＝－3x＋3与x轴、y轴分别相交于A，B两点，抛物线y＝ax2－2ax＋a＋4(a＜0)经过点B.
(1)求该抛物线的函数解析式；
(2)已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM，BM.设点M的横坐标为m，△ABM的面积为S，求S关于m的函数解析式，并求出S的最大值．。
二次函数与图形面积问题
实际问题与二次函数
生活是数学的源泉， 我们是学习数学的主人.
，顶点坐标是
. ( b ,4acb2) 2a 4a
当a>0时，
开口向向上，有最 低 点，函数有最 小 值，是
4ac b2 4a
.
当a<0时，开口向 向下 ，有最 高 点，函数有最 大 值
，是
4ac b2 4a
。
温故知新
3.二次函数y=2(x-3)2+5的对称轴是 直线_x__=__3____, 顶点坐标是 (3 ，5) 。当x= 3 时，y有最 小 值 是5 .
点P从点A开始沿AB边向点B以2厘米／秒的速度移动， 点Q从点B开始沿BC边向点C以1厘米／秒的速度 A
移动，如果P,Q分别从A,B同时出发，
几秒后Δ PBQ的面积最大？
最大面积是多少？
P
C
Q
B
快乐展示
解：根据题意，设经过x秒后Δ PBQ的面积y最大，则
A 2 P x ,P B 8 2 x ,Q x B
过程
一 温故知新 二 学习目标 三 自主学习 四 合作探究 五 快乐展示 六 归纳小结
温故知新
温故知新
1.二次函数y=a(x-h)2+k的图象是一条 抛物线 ，
它的对称轴是 直线x=h ，顶点坐标是 (h，k) .
2.二次函数的一般式是 ya2xbxc，它的图像的对
称轴是
二次函数应用几何图形的最大面积问题教学课件
求解极值点
通过求导数并令其为0，找到函 数的极值点。
确定最大面积
根据极值点和单调性，确定几 何图形的最大面积对应的点。
05
练习题与答案解析
练习题
01
02
03
题目1
一个矩形ABCD的面积为 12，其中AB=2，求BC的 最大值。
题目2
一个直角三角形ABC的面 积为6，其中∠C=90°， AC=3，求BC的最大值。
详细描述
首先设定三角形的底和高为二次函数 的变量，然后根据二次函数的性质， 找到使面积最大的底和高的值。
利用二次函数求圆形面积的最大值
总结词
通过设定圆的半径为二次函数的变量 ，利用二次函数的性质求圆的最大面 积。
详细描述
首先设定圆的半径为二次函数的变量 ，然后根据二次函数的性质，找到使 面积最大的半径的值。
02
几何图形可以由二次函数图像与x 轴、y轴的交点确定，进而形成三 角形、矩形、平行四边形等。
二次函数的最值与几何图形面积的关系
二次函数的最值出现在顶点处，此时 对应的x值为函数的零点或对称轴。
几何图形面积的最大值或最小值出现 在二次函数最值处，可以通过求导数 或配方法找到最值点。Βιβλιοθήκη 02常见几何图形面积公式
题目3
一个等腰三角形ABC的面 积为10，其中AB=AC， ∠B=45°，求BC的最大值 。
答案解析
解析1
设BC=x，则矩形的面积可以表 示为2x=12，解得x=6。由于AB 已经给定为2，所以BC的最大值
为6。
解析2
设BC=x，则直角三角形的面积 可以表示为1/2×3x=6，解得 x=4。由于AC已经给定为3，所
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
生活是数学的源泉，
我们是学习数学的主人.
过程
一 二 三
温故知新 学习目标 自主学习
四
五
合作探究 快乐展示 归纳小结
六
温故知新
温故知新
1.二次函数y=a(x-h)2+k的图象是一条 抛物线 ， 它的对称轴是 直线x=h ，顶点坐标是 (h，k) .
2 y ax bx c ，它的图像的对 2.二次函数的一般式是
谢谢
福清西山学校初三数学组
用长为12cm的铁丝围成一个矩形，设矩形一边 典例：
x
6－ x
∵ a＝－1<0, ∴ y有最大值 当x＝3cm时， y最大值＝9 cm2 ∴ 6－x= 3cm
答：矩形的两边都是3cm，即为正方形时，矩形的面积最大。
合作探究
如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二 道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S平方米。 (1)求S与x的函数关系式及自变量的取值范围； (2)当x取何值时所围成的花圃面积最大，最大值是多少？ (3)若墙的最大可用长度为8米，则求围成花圃的最大面积。 解： (1) AB为x米,篱笆长为 24米 (3) ∵ ∵墙的可用长度为 8米 A D ∴ 0<24 － 4x ≤8 即 4≤x<6 ∴ BC为（24－4x）米 ∴ S＝ x（时， 24－S 4x ） ∵当 x>3 随 X的增大而减小， B C 2＋24 x （0<x<6） ＝－ 4x ∴当 x=4 时， S有最大值为32 2 4ac b b ∴当 x＝ S最大值 ＝ 32m2， 4m 时， 3 时， (2)当 x＝ S最大值 ＝ ＝36（平方米） 4 a 2a 即围成花圃的最大面积为32m2
P
∵ a＝－1<0, ∴ y有最大值 最大面积是 4 cm2
C
Q
B
∴当P、Q同时运动2秒后Δ PBQ的面积y最大,
归纳小结
归纳小结
对自己说,你有什么收获? 对老师说,你有什么疑惑? 对同学说,你有什么温馨提示?
作业
作业： 1、教科书P52页 第4,5题；
2、《名校课堂》P47页，P48页第11题。
称轴是
b 直线 x 2a
，顶点坐标是
b 4ac b 2 ( , ) . 2a 4a
当a>0时，
4ac b 2 4a
开口向 向上 ，有最 低 点，函数有最 小 值，是
4ac b 2 4a
.
当a<0时，开口向 向下 ，有最 高 点，函数有最 大 值 Nhomakorabea，是
。
温故知新
x=3 3.二次函数y=2(x-3)2+5的对称轴是 直线_________, 顶点坐标是 (3 ，5) 。当x= 3 时，y有最 小 值 是 5 . 4.二次函数y=-3(x+4)2-1的对称轴是 直线x=-4 ， 顶点坐标是 (-4 ，-1) 。当x= -4 时，函数有 最 大 值，是 -1 。 5.二次函数y=2x2-8x+9的对称轴是 直线x=2 , 顶点坐标是 (2 ，1) .当x= 2 时，函数有最 小 值，是 1 。
25 2. 形面积之和的最小值是______cm 2
快乐展示
能力提升
5、如图在ΔABC中，AB=8cm,BC=6cm，∠B＝90° 点P从点A开始沿AB边向点B以2厘米／秒的速度移动， A 点Q从点B开始沿BC边向点C以1厘米／秒的速度 移动，如果P,Q分别从A,B同时出发，
几秒后Δ PBQ的面积最大？
1、问题1中是通过什么方法来求出小球在运动中 的最大高度？
答：通过公式法来求出的。
2.归纳：一般地，当a>0(a<0)时，抛物线y=ax2+bx+c的
低 的顶点是最______(
4ac b 2 4a 数y=ax2+bx+c有最大（小）值________.
b 高 点,当x=________ 2a _____) 时，二次函
最大面积是多少？
P
C
Q
B
快乐展示
解：根据题意，设经过x秒后Δ PBQ的面积y最大，则
AP 2 x, PB 8 2 x, QB x 1 则 y (8 2 x) x （0<x<4） 2
A
x2 4x
( x 2 4 x 4 4) ( x 2) 2 4
4 (1) 0 302 s 225 4 (1)
当l 15时， S取最大值为 225
3.当场地面积S最大时，该场地是什么图形？ 答：正方形
合作探究
合作探究
长为xcm,面积为ycm2,问何时矩形的面积最大？ 解： ∵周长为12cm, 一边长为xcm , ∴ 另一边为（6－x）cm ∴ y ＝x（6－x） （0< x<6） ＝－x2＋6x ＝－（x2 -6x +9 -9） ＝－(x－3) 2＋9
构建快乐课堂 塑造美丽心灵
二次函数与图形面积
福清西山学校
初三数学组
学习目标
学习目标
学习目标
1、会用函数的知识求图形面积的最值问题.
2、能根据实际问题构建二次函数模型.
学习重难点
重点：掌握用二次函数求最值来解决实际应用问题. 难点： 将实际问题转化为数学问题.
自主学习
自主学习
阅读教材P49“问题”，解决下面问题。
快乐展示
快乐展示
《名校课堂》P47
4、如图，利用一面墙(墙的长度不超过 45 m)，用80 m长的篱笆围一个矩形场地 .当AD=______ 20 m时，矩形场地的面积最 大，最大值为______. 800m2
6.将一根长为20 cm的铁丝剪成两段，并以每一段铁
丝的长度为周长各做成一个正方形，则这两个正方
自主学习
阅读教材P49-P50“探究1”，解决下面问题。
1.“探究1”中，场地面积S与边长l之间是什么关系？ 你能写出它们的关系式吗？ 2 答：二次函数的关系。S l (30 l ),即S l 30l (0 l 30) 2.当l取何值时，S最大？
30 l 15, 2 (1)