天津理工概率论练习册答案
概率论与数理统计练习册答案(1-4)全解

概率论与数理统计练习册答案(1-4单元)第一单元 A 卷1解(1)有两种可能性30 30 10,50 10 10 P=2112525331035712024C CC CC ?==(2)用对立事件做 P=111532310314C C CC创-=2解: 由题意产品的合格率为96%合格产品中的一等品率为75%则出厂产品的一等品率P=96%*75%=72%所以在该厂产品中任取一件是一等品的概率为72%。
3解: 乙选手输掉一分有两种情况:第一种是乙第一次回球就失误,所以P1=0.3;第二种是乙第二次回球才失误,所以P2=0.7*0.6*0.5=0.21; 因此乙选手输掉一分的概率P=P1+P2=0.51。
4. 解: P(AUBUC)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC) =1/4+1/4+1/4-1/6-1/6=5/12则A 、B 、C 全不发生的概率为1-P(AUBUC)=1-5/12=7/12。
5解:令事件B 为被射中事件A 1表示甲射中乙没中 事件A 2表示乙射中甲没中 事件A 3表示俩人都中 则P (13()A A B+)=13()()()P A B P A B P B +=1133112233()()()()()()()()()()P B A P A P B A P A P B A P A P B A P A P B A P A ? ?? =0.60.60.50.40.50.60.5?? =0.757.解:设A i 为第一次抽到的新球个数。
B 为3只球为新球。
P (A 0)=0396315C C C ,P (A 1)=1296315C CCP (A 2)=2196315C C C ´,P (A 3)=3096315C C C ´P (0A B )=31539CC,P (1A B )=31538CCP (2A B )=31537CC,P (3A B )=31536CCP (B )=P (0A B )´P (A 0)+P (1A B )´P (A 1)+P (2AB )´P (A 2)+P (3AB )´P (A 3)=0.089四.1.证明重要公式:P(A-B)=P(A)P - (AB);(或P(AB)=P(A) -P(AB));2.设P(A)=0.7,P(A -B)=0.3,求P(AB ) 解:1.证明:因为A=A B ÈAB所以P (AB )= P (AB AB È)= P (AB )+P (AB )P - (AB ÇAB)又因为ABÇAB=Æ所以P (A )= P (AB )+P (AB )所以P (AB )= P (A )- P (AB )即P (A -B )=P (A )-P (AB ) 2.由1可得,P (AB )= P (A )-P (A -B )=0.4 所以P(AB )=1-P(AB)=0.6(画图可帮助解题)五.解:设事件A 为取到白球球分放在箱子中一共有四种情况:I. 一只箱子中没球,另一只箱子中4个球:P (A )=1/2*2/4=1/4 II. 一只箱子中1只白球,另一只箱子中其他三只球:P (A )=1/2+1/2*1/3=7/12III. 一只箱子中一只黑球,另一只箱子中其他三只球:P (A )=1/2*2/3=1/3IV.一只箱子中2只白球,另一只箱子中两只黑球:P (A )=1/2B 卷三、计算题1、① P=C 110C 4924/C 206=0.52 先从10双中取1双,再从剩下的9双中取4双,最后从4双中取每双中的一只② P=1-C 61026/C 620=0.653 考虑对立面,即没有两只能够配成对,先从10双中取6双,再从6双取每双的一只2解:由P(B|A )=)()(A P A B P =1.0)(A B P =0.4得()A B P =0.04,又由)(A B P =P(B)-P(AB)=0.75-P(AB)=0.04 故 P (AB )=0.713、解:记“甲获胜”为事件A,“乙获胜”为事件B 由题意得P(A)=23211151515()()()()...()()6666666n n -++++ P(B)= 223315151515()()()()()()...()()66666666n n++++两式相比得()5()6P A P B =故65(),()1111P A P B ==4解:若采用第一种 设A 为“不产出废品”P(A )=97%⨯96%⨯95%=0.88464若采用第二种 设B 为“不产出废品” P(B)=93%⨯93%=0.8649P(A)>P(B) 应采用第一种 5 P (A 0)=121211221122()()nnn n m n m nm n m n ?++++121212121112211221122()()()P m n nm m n n m A m n m nm n m nm n m n +=??++++++ 1212211221122()()()P m m m m A m n m nm n m n =?++++ )|(0A B P =0)|(1A B P =211)|(2=A B P P(B)=)(0A P )|(0A B P +)|()()|()(2211A A A A B P P B P P +=121221112222()()m m m n m n m n m n ++++6.解:设1A 表示取出的一只元件为正品,2A 表示取出的为次品。
12-13-1概率统计期中试卷(理工)答案(可编辑修改word版)

1A天津工业大学(2012—2013 学年第一学期)学 院《概率论与数理统计》(理工类)期中试卷 (2012/11)特别提示:请考生在密封线左侧的指定位置按照要求填写个人 装信息,若写在其它处视为作弊。
本试卷共有 8 页,共八道大题,请 订封 线线核对后做答,若有疑问请与监考教师联系。
专业班级装 密 订 封 线线一.填空题(本题满分 28 分)学1.设 A , B 是两个事件, P ( A ) = 0.5 , P (B ) = 0.4 , P ( A B ) = 0.3 号,则 P ( A BP (B A 2. 某系统连接方式如图,4 个独立工作的元件 A k 可靠的概率为p k (k = 1,2,3,4) .装 密 订 封 A 线线姓 名A 33. 一袋中装有 7 只球,其中 3 只白球、4 只红球,现从袋中依次取出 3 只球,取到的白球的数目为 X ,则 X 的分布律在有放回在不放回情形下为2⎧ 2( y -1), 1 < y < 4⎪9⎨ ⎪⎩ 0,⎧ 0, ⎪0.3, 0 ≤ x < 1 x < 0 ⎪⎨ ⎪0.8, 1 ≤ x < 2 ⎪⎩ 1x ≥ 2 2X p k0 0.31 0.52 0.2⎧Ax, 0 < x <1 4. 设随机变量 X 的概率密度 f X (x ) = ⎨ ⎩ 0, 他他 ,则常数 A =2 ,Y = 3X +1的概率密度 f Y (y ) ) = .5. 设随机变量 X 的分布律为则 X 的分布函数为 F X (x ) = .6. 设随机变量 X ~ π((泊松分布),且 P ( X = 0) = e -2 ,则常数 λ = 2 ,概率 P ( X ≤ 2) = 5e -2 .7. 设随机变量 X ~ U (1, 6) ( 均匀分布), 则 X 的概率密度函数为, 关于 t 的二次方程 t 2 - Xt +1 = 0 有实根的概率为0.8 .8. 设随机变量 X 的概率密度函数为f (x ) =-( x +3)2 e4, -∞ < x < +∞则Y = X + 3~ N (0,1) (写出分布类型及参数);而概率 P (Y > -2) = 0.9772 (已知Φ(2) = 0.9772 ).f X (x ) = ⎪5 ⎧1 ,⎨ ⎪⎩0, 1 < x < 6 他他 213i二.(本题满分 10 分)设某厂有甲乙丙三条流水线生产同一种 学 产品,产量分别占 15%,80%,5%;次品率分别为 0.02,0.01 和 0.03; 院三条流水线的产品混放在同一库房。
概率论·课后答案(绝对详解)

i习题一3 设,,B A 为二事件,化简下列事件:B B B A B BA B A B A B A =⋃=⋃⋃=⋃⋃)()())()(1(B B A B B A A A B A B A =⋃⋃⋃=⋃⋃)())()(2(4 电话号码由5个数字组成,每个数字可能是从0到9这10个数字中的任一个,求电话号码由5个不同数字组成的概率。
3024.010302410427210678910445==⋅=⋅⋅⋅⋅=p5 n 张奖券中有m 张有奖的,k 个人购买,每人一张,求其中至少有一人中奖的概率。
答案:.1k n k mn C C --6 从5双不同的鞋子中任取4只,这4只鞋子中“至少有两只配成一双”的概率是多少?解;将这五双靴子分别编号分组},,,,{};,,,,{5432154321b b b b b B a a a a a A ==,则C 表示:“至少有两只配成一双”;从5双不同的鞋子中任取4只,其可能选法有.45C不能配对只能是:一组中选i 只,另一组中选4-i 只,且编号不同,其可能选法为)0,1,2,3,4(;455=--i C C i i i41045341523251235451)(1)(C C C C C C C C C C P C P ++++-=-= 2113218177224161247720104060401011234789105453245224551=-=⋅⋅-=⋅++++-=⋅⋅⋅⋅⋅⋅⋅+⋅+⋅⋅+⋅⋅+-= 7在[—1,1]上任取一点,求该点到原点的距离不超过51的概率。
答案:518在长度为a 的线段内任取两点,将其分成三段,求它们可以构成三角形的概率。
,0,0a y a x <<<<且a y x <+<0,又41222,,=⎪⎪⎪⎩⎪⎪⎪⎨⎧<<>+⇒⎪⎩⎪⎨⎧--<---<--->+P ay a x a y x y x a x y y x a y x y x a y x 9在区间)1,0(内任取两个数,求这两个数的积小于41的概率。
天津理工大学概率论与数理统计考题库

3、设X 的密度函数为⎩⎨⎧≤≤=其它0102)(x x x f ,求)(X E 、)(X D 解:∫∫===+∞∞−10232d 2d )()(x x x x xf X E ∫∫===+∞∞−1032221d 2d )()(x x x x f x X E 故181)32(21))(()()(222=−=−=X E X E X D 5、设连续型随机变量X 的分布函数⎪⎩⎪⎨⎧>≤≤−+−<=1 ,111 ,arcsin 1 ,0)(x x x b a x X F 求a 、b 、)(X E 、)(X D .解:∵X 为连续型随机变量,∴)(x F 为连续函数.∴0),1()1(2=−⇒−=−−b a F F π∴1),1()1(2=+⇒=+b a F F π可解得;21=a ,π1=b .X 的概率密度⎪⎩⎪⎨⎧<−=′=其它,01,11)()(2x x x F x f π∫∫−+∞∞−−==112d 1d )()(x x x x x xf X E π=0∫∫−=−==−102211222d 12d 1)()(x x x x x x X E X D πππ令t x sin =,则21d sin 2)(202==∫ππt t XD 11、设随机变量),(Y X 的密度函数为⎩⎨⎧<<<<=其它00,102),(x y x y x f 求)(XY E .解:y x xy y x y x xyf XY E G xOy d d 2d d ),()(∫∫∫∫==G :10<<<x y =41d d d 2102100==∫∫∫x xx y y x x x .15、设区域G 为122≤+y x ,二维随机变量),(Y X 服从G 上的均匀分布,判断X 、Y的相关性、独立性.解:显然,二维随机变量),(Y X 的概率密度函数为⎪⎩⎪⎨⎧∉∈=Gy x G y x y x f ),( ,0),( ,1),(π所以⎪⎩⎪⎨⎧<==∫∫−−−∞+∞−其它 ,0 1 ,d 1d ),()(2211x x X x y y y x f x f π⎪⎩⎪⎨⎧<−=其它,0 1 ,122x x π)(y f Y ⎪⎩⎪⎨⎧<−=其它,0 1 ,122y y π因此0d 12d )()(112=−==∫∫−+∞∞−x x x x x xf X E π同样可得0)(=Y E 又0d d 1d d ),()(===∫∫∫∫y x xy y x y x xyf XY E GxOy π所以0)()()(),cov(=−=Y E X E XY E Y X 故X 、Y 不相关,但由于),()()(y x f y f x f Y X ≠所以X 与Y 不相互独立.16、设随机变量X 和Y 的联合分布律为XY1−011−8181810810811818181验证Y X ,不相关,但Y X ,不相互独立.证:因为0831083)1()(0831083)1()(=×++×−==×++×−=Y E X E 08111081)1(10811)1(081)1()1()(=××++×−×++××−++×−×−=XY E 所以0)()()(),cov(=−=Y E X E XY E Y X 故Y X ,不相关.又83 ,8311==••p p ,8111=p 所以1111p p p ≠••故Y X ,不相互独立.17、设随机变量),(Y X 具有概率密度⎪⎩⎪⎨⎧≤≤≤≤+=其它020,20)(81),(y x y x y x f 求XY Y X Y E X E ρ),,cov(),(),(.解:67d )(d 81d d ),()(2020=+==∫∫∫∫y y x x x y x y x xf X E xOy由y x ,的“对称性”可得67)(=Y E .又34d )(d 81d d ),()(2020∫∫∫∫=+==xOyy y x xy x y x y x xyf XY E 所以361)()()(),cov(−=−=Y E X E XY E Y X .又35d )(d 81d d ),()(2020222=+==∫∫∫∫y y x x x y x y x f x X E xOy由y x ,的“对称性”可得35)(2=Y E 所以.3611)( ,3611))(()()(22==−=Y D X E X E X D 故.111)()(),cov(−==Y D X D Y X XYρ2、设总体X 服从指数分布,0()0,x e x f x λλ−⎧>=⎨⎩其他,n X X X ⋯,,21是来自X 的样本,(1)求未知参数λ的矩估计;(2)求λ的极大似然估计.解:(1)由于1()E X λ=,令11X X λλ=⇒=,故λ的矩估计为1ˆX λ=(2)似然函数112(,,,)ni i x n n L x x x e λλ=−∑=⋯111ln ln ln 0n ii ni n i ii L n x d L n n x d xλλλλλ====−=−=⇒=∑∑∑故λ的极大似然估计仍为1X 。
概率论课后习题答案pdf

概率论课后习题答案pdf概率论课后习题答案pdf概率论是数学中的一门重要学科,研究的是随机事件发生的规律性。
在学习概率论的过程中,课后习题是巩固知识、提高应用能力的重要途径。
然而,对于一些复杂的概率题目,学生可能会遇到困惑和难以解答的情况。
因此,提供一份概率论课后习题答案pdf对于学生来说是非常有益的。
一、基础概率题1. 一个标准的扑克牌中,红桃和黑桃的数量各有多少张?答案:扑克牌一共有52张,其中红桃和黑桃各有13张。
2. 从一副标准扑克牌中,随机抽取两张牌,求两张牌都是红桃的概率。
答案:首先,从52张牌中抽取第一张红桃的概率为13/52。
然后,从剩下的51张牌中抽取第二张红桃的概率为12/51。
因此,两张牌都是红桃的概率为(13/52) * (12/51) = 1/17。
二、条件概率题1. 一家电子产品公司生产的手机中,10%的手机存在质量问题。
现在从该公司生产的手机中随机选择一个,发现该手机存在质量问题。
求该手机是该公司生产的概率。
答案:设事件A表示选择的手机存在质量问题,事件B表示该手机是该公司生产的。
根据条件概率的定义,我们需要求解P(B|A)。
根据题意,P(A) = 0.1,即选择的手机存在质量问题的概率为0.1。
又因为只有该公司生产的手机存在质量问题,所以P(A|B) = 1。
根据条件概率的公式,有P(B|A) = P(A|B) * P(B) / P(A) = 1 * P(B) / 0.1 = 10 * P(B)。
由于概率的取值范围在0到1之间,所以P(B)的取值范围也在0到0.1之间。
因此,该手机是该公司生产的概率为10 * P(B),其中0 <= P(B) <= 0.1。
三、随机变量题1. 设随机变量X表示一次抛掷一枚骰子的结果,求X的期望。
答案:一枚骰子的结果有1、2、3、4、5、6六种可能,每种可能出现的概率为1/6。
根据期望的定义,期望E(X) = (1/6) * 1 + (1/6) * 2 + (1/6) * 3 + (1/6) * 4 + (1/6) * 5 + (1/6) * 6 = 3.5。
概率统计练习册答案

概率统计练习册答案第一章 概率论的基本概念一、选择题1.将一枚硬币连抛两次,则此随机试验的样本空间为( ) A .{(正,正),(反,反),(一正一反)} B.{(反,正),(正,反),(正,正),(反,反)} C .{一次正面,两次正面,没有正面} D.{先得正面,先得反面}2.设A ,B 为任意两个事件,则事件(AUB)(Ω-AB)表示( ) A .必然事件 B .A 与B 恰有一个发生 C .不可能事件 D .A 与B 不同时发生3.设A ,B 为随机事件,则下列各式中正确的是( ). A.P(AB)=P(A)P(B)B.P(A-B)=P(A)-P(B)C.)()(B A P B A P -=D.P(A+B)=P(A)+P(B)4.设A,B 为随机事件,则下列各式中不能恒成立的是( ). A.P(A -B)=P(A)-P(AB) B.P(AB)=P(B)P(A|B),其中P(B)>0C.P(A+B)=P(A)+P(B)D.P(A)+P(A )=15.若φ≠AB ,则下列各式中错误的是( ). A .0)(≥AB P B.1)(≤AB P C.P(A+B)=P(A)+P(B)D.P(A-B)≤P(A)6.若φ≠AB ,则( ).A. A,B 为对立事件B.B A =C.φ=B AD.P(A-B)≤P(A)7.若,B A ⊂则下面答案错误的是( ).A. ()B P A P ≤)(B. ()0A -B P ≥C.B 未发生A 可能发生D.B 发生A 可能不发生 8.下列关于概率的不等式,不正确的是( ). A.)}(),(min{)(B P A P AB P ≤B..1)(,<Ω≠A P A 则若C.1212(){}n n P A A A P A A A ≤+++L LD.∑==≤ni i ni i A P A P 11)(}{Y9.(1,2,,)i A i n =L 为一列随机事件,且12()0n P A A A >L ,则下列叙述中错误的是( ).A.若诸i A 两两互斥,则∑∑===ni i n i i A P A P 11)()(B.若诸i A 相互独立,则11()1(1())nni i i i P A P A ===--∑∏C.若诸i A 相互独立,则11()()nni i i i P A P A ===∏UD.)|()|()|()()(1231211-=Λ=n n ni i A A P A A P A A P A P A P X10.袋中有a 个白球,b 个黑球,从中任取一个,则取得白球的概率是( ).A.21B.ba +1C.ba a+ D.ba b + 11.今有十张电影票,其中只有两张座号在第一排,现采取抽签方式发放给10名同学,则( )A.先抽者有更大可能抽到第一排座票B.后抽者更可能获得第一排座票C.各人抽签结果与抽签顺序无关D.抽签结果受以抽签顺序的严重制约12.将n 个小球随机放到)(N n N ≤个盒子中去,不限定盒子的容量,则每个盒子中至多有1个球的概率是( ).A.!!N n B. n Nn !C. nn N Nn C !⋅ D.Nn 13.设有r 个人,365≤r ,并设每个人的生日在一年365天中的每一天的可能性为均等的,则此r 个人中至少有某两个人生日相同的概率为( ).A.r r P 3651365-B. rr r C 365!365⋅C. 365!1r -D. rr 365!1-14.设100件产品中有5件是不合格品,今从中随机抽取2件,设=1A {第一次抽的是不合格品},=2A {第二次抽的是不合格品},则下列叙述中错误的是( ). A.05.0)(1=A PB.)(2A P 的值不依赖于抽取方式(有放回及不放回)C.)()(21A P A P =D.)(21A A P 不依赖于抽取方式15.设A,B,C 是三个相互独立的事件,且,1)(0<<C P 则下列给定的四对 事件中,不独立的是( ). A.C AUB 与B. B A -与CC. C AC 与D. C AB 与16.10张奖券中含有3张中奖的奖券,现有三人每人购买1张,则恰有一个中奖的概率为( ).A.4021 B.407 C. 3.0 D. 3.07.02310⋅⋅C 17.当事件A 与B 同时发生时,事件C 也随之发生,则( ).A.1)()()(-+≤B P A P C PB.1)()()(-+≥B P A P C PC.P(C)=P(AB)D.()()P C P A B =U18.设,1)()|(,1)(0,1)(0=+<<<<B A P B A P B P A P 且则( ). A. A 与B 不相容B. A 与B 相容C. A 与B 不独立D. A 与B 独立19.设事件A,B 是互不相容的,且()0,()0P A P B >>,则下列结论正确的 是( ). A.P(A|B)=0B.(|)()P A B P A =C.()()()P AB P A P B =D.P(B|A)>020.已知P(A)=P ,P(B)=q 且φ=AB ,则A 与B 恰有一个发生的概率为( ).A.q p +B. q p +-1C. q p -+1D. pq q p 2-+21.设在一次试验中事件A 发生的概率为P ,现重复进行n 次独立试验 则事件A 至多发生一次的概率为( ). A.n p -1 B.n pC. n p )1(1--D. 1(1)(1)n n p np p --+-22.一袋中有两个黑球和若干个白球,现有放回地摸球4次,若至少摸 到一个白球的概率为8180,则袋中白球数是( ). A.2B.4C.6D.823.同时掷3枚均匀硬币,则恰有2枚正面朝上的概率为( ). A.0.5B.0.25C.0.125D.0.37524.四人独立地破译一份密码,已知各人能译出的概率分别为61,31,41,51则密码最终能被译出的概率为( ).A.1B.21C.52 D. 32 25.已知11()()(),()0,()(),416P A P B P C P AB P AC P BC ======则事件A,B,C 全不发生的概率为( ).A. 81B. 83C. 85D.87 26.甲,乙两人独立地对同一目标射击一次,其命中率分别为0.6和0.5,则目标被击中的概率为( ).A. 0.5B. 0.8C. 0.55D. 0.627.接上题,若现已知目标被击中,则它是甲射中的概率为( ). A.43 B.65C.32D.116 28.三个箱子,第一箱中有4个黑球1个白球,第二箱中有3个黑球3个白球,第三个箱中有3个黑球5个白球,现随机取一个箱子,再从这个箱中取出一个球,则取到白球的概率是( ).A.12053 B.199 C.12067 D.1910 29.有三类箱子,箱中装有黑、白两种颜色的小球,各类箱子中黑球、白球数目之比为,2:3,2:1,1:4已知这三类箱子数目之比为1:3:2,现随机取一个箱子,再从中随机取出一个球,则取到白球的概率为( ). A.135 B.4519 C.157 D.3019 30.接上题,若已知取到的是一只白球,则此球是来自第二类箱子的概率为( ).A.21 B. 31C.75 D.71 31.今有100枚贰分硬币,其中有一枚为“残币”中华人民共和国其两面都印成了国徽.现从这100枚硬币中随机取出一枚后,将它连续抛掷10次,结果全是“国徽”面朝上,则这枚硬币恰为那枚“残币”的概率为( ).A.1001 B. 10099C.1010212+D.10102992+ 32.玻璃杯成箱出售,每箱20只,假设各箱含0,1,2只残品的概率分别是0.8,0.1,0.1,一顾客欲购一箱玻璃杯,在购买时,售货员随意取一箱,而顾客随机察看1只,若无残次品,则买下该箱玻璃杯,否则退回,如果顾客确实买下该箱,则此箱中确实没有残次品的概率为( ).A.0.94B.0.14C.160/197D.420418419C C C + 二、填空题1. E :将一枚均匀的硬币抛三次,观察结果:其样本空间=Ω . 2.某商场出售电器设备,以事件A 表示“出售74 Cm 长虹电视机”,以事件B 表示“出售74 Cm 康佳电视机”,则只出售一种品牌的电视机可以表示为 ;至少出售一种品牌的电视机可以表示为 ;两种品牌的电视机都出售可以表示为 .3.设A ,B ,C 表示三个随机事件,试通过A ,B ,C 表示随机事件A 发生而B ,C 都不发生为 ;随机事件A ,B ,C 不多于一个发生 .4.设P (A )=0.4,P (A+B )=0.7,若事件A 与B 互斥,则P (B )= ;若事件A 与B 独立,则P (B )= .5.已知随机事件A 的概率P (A )=0.5,随机事件B 的概率P (B )=0.6及条件概率P (B|A )=0.8,则P (AUB )=6.设随机事件A 、B 及和事件AUB 的概率分别是0.4,0.3和0.6,则P (AB )= .7.设A 、B 为随机事件,P (A )=0.7,P (A-B )=0.3,则P (AB )= .8.已知81)()(,0)(,41)()()(======BC p AC p AB p C p B p A p ,则C B A ,,全不发生的概率为 .9.已知A 、B 两事件满足条件P (AB )=P (AB ),且P (A )=p,则P (B )= .10.设A 、B是任意两个随机事件,则{()()()()}P A B A B A B A B ++++= .11.设两两相互独立的三事件A 、B和C 满足条件:φ=ABC ,21)()()(<==C p B p A p ,且已知Y Y 169)(=C B A p ,则______)(=A p . 12.一批产品共有10个正品和2个次品,任意抽取两次,每次抽一个,抽出后不再放回,则第二次抽出的是次品的概率为 .13.袋中有50个乒乓球,其中20个是黄球,30个是白球,今有两人依次随机地从袋中各取一球,取后不放回,则第二个人取得黄球的概率是 .14.将C 、C 、E 、E 、I 、N 、S 这7个字母随机地排成一行,恰好排成SCIENCE 的概率为 .15.设工厂A 和工厂B 的产品的次品率分别为1%和2%,现从由A和B 的产品分别占60%和40%的一批产品中随机抽取一件,发现是次品,则该次品属于A 生产的概率是 .16.设10件产品有4件不合格品,从中任取两件,已知所取两件产品中有一件是不合格品,则另一件也是不合格品的概率是 .17.甲、乙两人独立地对同一目标射击一次,其命中率分别为0.6和0.5.现已知目标被命中,则它是甲射中的概率是 .18.假设一批产品中一、二、三等品各占60%,30%,10%,从中随意取出一件,结果不是三等品,则取到的是一等品的概率是 .19.一种零件的加工由三道工序组成,第一道工序的废品率为1p ,第二道工序的废品率为2p ,第三道工序的废品率为3p ,则该零件的成品率为 .20.做一系列独立试验,每次试验成功的概率为p ,则在第n 次成功之前恰有m 次失败的概率是 .第二章 随机变量及其分布一、选择题1.设A,B 为随机事件,,0)(=AB P 则( ).A..φ=ABB.AB 未必是不可能事件C.A 与B 对立D.P(A)=0或P(B)=02.设随机变量X 服从参数为λ的泊松分布,且},2{}1{===X P X P 则}2{>X P 的值为( ).A.2-eB.251e-C.241e-D.221e-. 3.设X 服从]5,1[上的均匀分布,则( ). A.4}{ab b X a P -=≤≤ B.43}63{=<<X P C.1}40{=<<X PD.21}31{=≤<-X P4.设),4,(~μN X 则( ). A.)1,0(~4N X μ- B.21}0{=≤X P C.)1(1}2{Φ-=>-μX PD.0≥μ5.设随机变量X 的密度函数为⎩⎨⎧<<=其他,010,2)(x x x f ,以Y 表示对X 的三次独立重复观察中事件}21{≤X 出现的次数,则( ).A .由于X 是连续型随机变量,则其函数Y 也必是连续型的B .Y 是随机变量,但既不是连续型的,也不是离散型的C .649}2{==y P D.)21,3(~B Y6.设=≥=≥}1{,95}1{),,3(~),,2(~Y P X P p B Y p B X 则若( ). A.2719 B.91C.31D.278 7.设随机变量X 的概率密度函数为(),23X f x Y X =-+则的密度函数为( ).A.13()22X y f ---B.13()22X y f --C.13()22X y f +--D.13()22X y f +- 8.连续型随机变量X 的密度函数)(x f 必满足条件( ). A.1)(0≤≤x fB.)(x f 为偶函数C.)(x f 单调不减D.()1f x dx +∞-∞=⎰9.若)1,1(~N X ,记其密度函数为)(x f ,分布函数为)(x F ,则( ). A.{0}{0}P X P X ≤=≥ B.)(1)(x F x F --= C.{1}{1}P X P X ≤=≥D.)()(x f x f -=10.设)5,(~),4,(~22μμN Y N X ,记},5{},4{21+≥=-≤=μμY P P X P P 则( ).A.21P P =B.21P P <C.21P P >D.1P ,2P 大小无法确定11.设),,(~2σμN X 则随着σ的增大,}|{|σμ<-X P 将( ). A.单调增大B.单调减少C.保持不变.D.增减不定12.设随机变量X 的概率密度函数为(),()(),()f x f x f x F x =-是X 的分布函数,则对任意实数a 有( ).A.⎰-=-adx x f a F 0)(1)( B.⎰-=-adx x f a F 0)(21)(C.)()(a F a F =-D.1)(2)(-=-a F a F13.设X 的密度函数为3,01()20,x x f x ⎧≤≤⎪=⎨⎪⎩其他,则1{}4P X >为( ). A.78B.1432xdx ⎰ C.14312xdx -∞-⎰D.3214.设~(1,4),(0.5)0.6915,(1.5)0.9332,{||2}X N P X Φ=Φ=>则为( ). A.0.2417B.0.3753C.0.3830D.0.866415.设X 服从参数为91的指数分布,则=<<}93{X P ( ). A.)93()99(F F -B.)11(913ee -C.ee 113-D.⎰-939dx e x16.设X 服从参数λ的指数分布,则下列叙述中错误的是( ).A.⎩⎨⎧≤>-=-0,00,1)(x x e x F x λB.对任意的x e x X P x λ-=>>}{,0有C.对任意的}{}|{,0,0t X P s X t s X P t s >=>+>>>有D.λ为任意实数17.设),,(~2σμN X 则下列叙述中错误的是( ). A.)1,0(~2N X σμ- B.)()(σμ-Φ=x x FC.{(,)}()()a b P X a b μμσσ--∈=Φ-Φ D.)0(,1)(2}|{|>-Φ=≤-k k k X P σμ18.设随机变量X 服从(1,6)上的均匀分布,则方程012=++Xx x 有实根的概率是( ).A.0.7B.0.8C.0.6D.0.519.设=<=<<}0{,3.0}42{),,2(~2X P X P N X 则σ( ). A .0.2B.0.3C.0.6D.0.820.设随机变量X服从正态分布2(,)N μσ,则随σ的增大,概率{||}P X μσ-<( ).A.单调增大 B.单调减少 C.保持不变 D.增减不定二、填空题1.随机变量X 的分布函数)(x F 是事件 的概率. 2.已知随机变量X 只能取-1,0,1,2四个数值,其相应的概率依次是cc c c 161,81,41,21,则=c3.当a 的值为 时,Λ,2,1,)32()(===k a k X p k 才能成为随机变量X的分布列.4.一实习生用一台机器接连独立地制造3个相同的零件,第i 个零件不合格的概率)3,2,1(11=+=i i p i ,以X 表示3个零件中合格品的个数,则________)2(==X p .5.已知X 的概率分布为⎪⎪⎭⎫ ⎝⎛-4.06.011,则X的分布函数=)(x F .6.随机变量X 服从参数为λ的泊松分布,则X 的分布列为 .7.设随机变量X 的概率密度为⎪⎪⎪⎩⎪⎪⎪⎨⎧∈∈=其它,0]6,3[,92]1,0[,31)(x x x f ,若k 使得{}32=≥k X p则k 的取值范围是 . 8.设离散型随机变量X 的分布函数为:⎪⎪⎪⎩⎪⎪⎪⎨⎧≥+<≤-<≤--<=2,21,3211,1,0)(x b a x a x a x x F且21)2(==X p ,则_______,________a b ==.9.设]5,1[~U X ,当5121<<<x x 时,)(21x X x p <<= . 10.设随机变量),(~2σμN X,则X的分布密度=)(x f .若σμ-=X Y ,则Y 的分布密度=)(y f .11.设)4,3(~N X ,则}{=<<-72X p .12.若随机变量),2(~2σN X ,且30.0)42(=≤<X p ,则_________)0(=≤X p . 13.设)2,3(~2N X,若)()(c X p c X p ≥=<,则=c .14.设某批电子元件的寿命),(~2σμN X ,若160=μ,欲使80.0)200120(=≤<X p ,允许最大的σ= .15.若随机变量X的分布列为⎪⎪⎭⎫ ⎝⎛-5.05.011,则12+=X Y 的分布列为 .16.设随机变量X服从参数为(2,p)的二项分布,随机变量Y服从参数为(3,p)的二项分布,若P{X≥1}=5/9,则P{Y≥1}= .17.设随机变量X服从(0,2)上的均匀分布,则随机变量Y=2X 在(0,4)内的概率密度为()Y f y = .18.设随机变量X服从正态分布2(,)(0)N μσσ>,且二次方程240y y X ++=无实根的概率为1/2,则μ= .第三章 多维随机变量及其分布一、选择题1.X,Y 相互独立,且都服从]1,0[上的均匀分布,则服从均匀分布的是( ).A.(X,Y)B.XYC.X+YD.X -Y2.设X,Y 独立同分布,11{1}{1},{1}{1},22P X P Y P X P Y =-==-=====则( ).A.X =YB.0}{==Y X PC.21}{==Y X P D.1}{==Y X P3.设)(1x F 与)(2x F 分别是随机变量X 与Y 的分布函数,为使)()(21x bF x aF -是某个随机变量的分布函数,则b a ,的值可取为( ).A.52,53-==b aB.32,32==b aC.23,21=-=b aD.23,21-==b a4.设随机变量i X 的分布为12101~(1,2){0}1,111424i X i X X -⎛⎫ ⎪===⎪⎝⎭且P 则12{}P X X ==( ).A.0B.41C.21D.15.下列叙述中错误的是( ). A.联合分布决定边缘分布B.边缘分布不能决定决定联合分布C.两个随机变量各自的联合分布不同,但边缘分布可能相同D.边缘分布之积即为联合分布6.设随机变量(X,Y) 的联合分布为:则b a ,应满足( ).A .1=+b a 33D.23,21-==b a7.接上题,若X ,Y 相互独立,则( ). A.91,92==b aB.92,91==b aC.31,31==b aD.31,32=-=b a8.同时掷两颗质体均匀的骰子,分别以X,Y 表示第1颗和第2颗骰子出现的点数,则( ).A.1{,},,1,2,636P X i Y j i j ====L B.361}{==Y X P C.21}{=≠Y X P D.21}{=≤Y X P9.设(X,Y)的联合概率密度函数为⎩⎨⎧≤≤≤≤=其他,y x y x y x f 010,10,6),(2,则下1 23 1 1/6 1/9 1/18X Y面错误的是( ).A.1}0{=≥X PB.{0}0P X ≤=C.X,Y 不独立D.随机点(X,Y)落在{(,)|01,01}D x y x y =≤≤≤≤内的概率为1 10.接上题,设G 为一平面区域,则下列结论中错误的是( ). A.{(,)}(,)GP X Y G f x y dxdy ∈=⎰⎰B.2{(,)}6GP X Y G x ydxdy ∈=⎰⎰C.1200{}6x P X Y dx x ydy ≥=⎰⎰D.⎰⎰≥=≥yx dxdy y x f Y X P ),()}{(11.设(X,Y)的联合概率密度为(,)0,(,)(,)0,h x y x y Df x y ≠∈⎧=⎨⎩其他,若{(,)|2}G x y y x =≥为一平面区域,则下列叙述错误的是( ).A.{,)(,)GP X Y G f x y dxdy ∈=⎰⎰B.⎰⎰-=≤-Gdxdy y x f X Y P ),(1}02{C.⎰⎰=≥-Gdxdy y x h X Y P ),(}02{D.⎰⎰=≥DG dxdy y x h X Y P I ),(}2{12.设(X,Y)服从平面区域G 上的均匀分布,若D 也是平面上某个区域,并以G S 与D S 分别表示区域G 和D 的面积,则下列叙述中错误的是( ).A.{(,)}DGS P X Y D S ∈=B.0}),{(=∉G Y X PC.GDG S S D Y X P I -=∉1}),{(D.{(,)}1P X Y G ∈=13.设系统π是由两个相互独立的子系统1π与2π连接而成的;连接方式分别为:(1)串联;(2)并联;(3)备用(当系统1π损坏时,系统2π开始工作,令21,X X 分别表示21ππ和的寿命,令321,,X X X 分别表示三种连接方式下总系统的寿命,则错误的是( ). A.211X X Y += B.},m ax {212X X Y = C.213X X Y +=D.},m in{211X X Y =14.设二维随机变量(X,Y)在矩形}10,20|),{(≤≤≤≤=y x y x G 上服从均匀分布.记.2,12,0;,1,0⎩⎨⎧>≤=⎩⎨⎧>≤=YX YX V Y X Y X U 则==}{V U P ( ).A.0B.41C.21D.4315.设(X,Y)服从二维正态分布),,,,(222121ρσσμμN ,则以下错误的是( ).A.),(~211σμN X B ),(~221σμN X C.若0=ρ,则X,Y 独立 D.若随机变量),(~),,(~222211σμσμN T N S 则(,)S T 不一定服从二维正态分布16.若),(~),,(~222211σμσμN Y N X ,且X,Y 相互独立,则( ). A.))(,(~22121σσμμ+++N Y XB.),(~222121σσμμ---N Y XC.)4,2(~2222121σσμμ+--N Y XD.)2,2(~2222121σσμμ+--N Y X 17.设X ,Y 相互独立,且都服从标准正态分布(0,1) N ,令,22Y X Z +=则Z 服从的分布是( ).A .N (0,2)分布 B.单位圆上的均匀分布 C.参数为1的瑞利分布 D.N (0,1)分布18.设随机变量4321,,,X X X X 独立同分布,{0}0.6,i P X =={1}0.4i P X ==(1,2,3,4)i =,记1234X X D X X =,则==}0{D P ( ).A.0.1344B.0.7312C.0.8656D.0.383019.已知~(3,1)X N -,~(2,1)Y N ,且,X Y 相互独立,记27,Z X Y =-+~Z 则( ).A.)5,0(NB.)12,0(NC.)54,0(ND.)2,1(-N20.已知sin(),0,,(,)~(,)40,C x y x y X Y f x y π⎧+≤≤⎪=⎨⎪⎩其他则C 的值为( ). A.21B.22C.12-D.12+ 21.设⎪⎩⎪⎨⎧≤≤≤≤+=其他,020,10,31),(~),(2y x xy x y x f Y X ,则}1{≥+Y X P =( ) A.7265 B.727 C.721 D.727122.为使⎩⎨⎧≥=+-其他,00,,),()32(y x Ae y x f y x 为二维随机向量(X,Y)的联合密度,则A 必为( ).A.0B.6C.10D.1623.若两个随机变量X,Y 相互独立,则它们的连续函数)(X g 和)(Y h 所确定的随机变量( ).A.不一定相互独立B.一定不独立C.也是相互独立D.绝大多数情况下相独立 24.在长为a 的线段上随机地选取两点,则被分成的三条短线能够组成三角形的概率为( ).A.21B.31C.41D.5125.设X 服从0—1分布,6.0=p ,Y 服从2=λ的泊松分布,且X,Y 独立,则Y X +( ).A.服从泊松分布B.仍是离散型随机变量C.为二维随机向量D.取值为0的概率为0 26.设相互独立的随机变量X,Y 均服从]1,0[上的均匀分布,令,Y X Z +=则( ).A.Z 也服从]1,0[上的均匀分布B.0}{==Y X PC.Z 服从]2,0[上的均匀分布D.)1,0(~N Z27.设X,Y 独立,且X 服从]2,0[上的均匀分布,Y 服从2=λ的指数分布,则=≤}{Y X P ( ).A.)1(414--e B.414e - C.43414+-e D.21 28.设⎪⎩⎪⎨⎧≤≤≤≤=其他,010,20,23),(~),(2y x xy y x f Y X ,则(X,Y)在以(0,0),(0,2),(2,1)为顶点的三角形内取值的概率为( ).A. 0.4B.0.5C.0.6D.0.8 29.随机变量X,Y 独立,且分别服从参数为1λ和2λ的指数分布,则=≥≥--},{1211λλY X P ( ).A.1-eB.2-eC.11--eD.21--e 30.设22[(5)8(5)(3)25(3)](,)~(,)x x y y X Y f x y Ae-+++-+-=,则A 为( ).A.3π B.π3 C.π2 D.2π 31.设某经理到达办公室的时间均匀分布在8点12点,他的秘书到达办公室的时间均匀分布在7点到9点.设二人到达的时间相互独立,则他们到达办公室的时间相差不超过5分钟的概率为( ).A.481 B.21C.121D.24132.设12,,,n X X X L 相独立且都服从),(2σμN ,则( ).A.12n X X X ===LB.2121()~(,)n X X X N n nσμ+++LC.)34,32(~3221+++σμN XD.),0(~222121σσ--N X X33.设(,)0,(,)(,)~(,)0,g x y x y GX Y f x y ≠∈⎧=⎨⎩其它,D 为一平面区域,记G,D 的面积为,,D G S S ,则{(,)}P x y D ∈=( ).A.G DS S B.GG D S S I C.⎰⎰D dxdy y x f ),( D.⎰⎰Ddxdy y x g ),( 二、填空题1.),(Y X 是二维连续型随机变量,用),(Y X 的联合分布函数),(y x F 表示下列概率:(1);____________________),(=<≤≤c Y b X a p (2);____________________),(=<<b Y a X p (3);____________________)0(=≤<a Y p (4).____________________),(=<≥b Y a X p2.随机变量),(Y X 的分布率如下表,则βα,应满足的条件是 .XY1 2311/6 1/9 1/182 1/2αβ3.设平面区域D 由曲线xy 1=及直线2,1,0e x x y ===所围成,二维随机变量),(Y X 在区域D 上服从均匀分布,则),(Y X 的联合分布密度函数为 .4.设),,,,(~),(222121ρσσμμN Y X ,则YX ,相互独立当且仅当=ρ .5.设相互独立的随机变量X 、Y 具有同一分布律,且X 的分布律为 P (X=0)=1/2,P (X=1)=1/2,则随机变量Z=max{X,Y}的分布律为 .6.设随机变量321,,X X X 相互独立且服从两点分布⎪⎪⎭⎫ ⎝⎛2.08.010,则∑==31i i X X 服从 分布 .7.设X 和Y 是两个随机变量,且P{X ≥0,Y ≥0}=3/7,P{X ≥0}=P{Y ≥0}=4/7,则P{max (X ,Y )≥0}= .8.设某班车起点站上车人数X 服从参数为(0)λλ>的泊松分布,每位乘客在中途下车的概率为p(0<p<1),且中途下车与否相互独立.以Y 表示在中途下车的人数,则在发车时有n 个乘客的条件下,中途有m 人下车的概率为 ;二为随机变量(X ,Y )的概率分布为 .9.假设一设备开机后无故障工作的时间X 服从参数为1/5的指数分布,设备定时开机,出现故障时自动关机,而在无故障时工作2小时便关机,则该设备每次开机无故障工作的时间Y的分布函数 .10.设两个随机变量X与Y独立同分布,且P(X=-1)=P(Y=-1)=1/2,P(X=1)=P(Y=1)=1/2,则P(X=Y)= ;P(X+Y=0)= ;P(XY=1)= .第四章 随机变量的数字特征一、选择题1.X 为随机变量,()1,()3E X D X =-=,则2[3()20]E X +=( ). A. 18 B.9 C.30 D. 32 2. 设二维随机向量(X,Y)的概率密度函数为(),0,0(,)0,x y e x y f x y -+⎧<<+∞<<+∞=⎨⎩其它,则()E XY =( ).A. 0B.1/2C.2D. 13. (X,Y)是二维随机向量,与0Cov不等价的是( ).YX(=,)A. EYD+=(X+)YXYEX=)E⋅( B. DYDXC. DY-)( D. X与Y独立=YDXD+X4. X,Y独立,且方差均存在,则=X2(YD( ).-)3A.DYDX94+ D.4- C. DY2- B. DYDX9DX32+DX3DY5. 若X,Y独立,则( ).A. DYXYDX- B. DY=)(=D⋅D9YDXX)3(-C. 0{=}+=bE D. 1aXPY{[=][]}--EYEXYX6.若0)Cov,则下列结论中正确的是( ).YX,(=A. X,Y独立B. ()=⋅D XY DX DYC. DYDXYD-=(-)DXXX( D. DYD+Y+)=7.X,Y为两个随机变量,且,0YEXE则X,Y( ).-EYX)]-)([(=A. 独立B. 不独立C. 相关D. 不相关8.设,XD+=+则以下结论正确的是( ).YDX)(DYA. X,Y不相关B. X,Y独立C. 1ρ= D.xyρ=-1xy9.下式中恒成立的是( ).A. EYD+X-)(Y=XYDXE⋅EX=)( B. DYC. (,)+DXXD=Cov X aX b aDX+= D. 1)1(+10.下式中错误的是( ).A. ),(2)(Y X Cov DY DX Y X D ++=+B. (,)()Cov X Y E XY EX EY =-⋅C. ])([21),(DY DX Y X D Y X Cov --+=D. ),(694)32(Y X Cov DY DX Y X D -+=- 11.下式中错误的是( ).A. 22)(EX DX EX +=B.DX X D 2)32(=+C. b EY b Y E +=+3)3(D. 0)(=EX D 12.设X 服从二项分布, 2.4, 1.44EX DX ==,则二项分布的参数为( ).A. 4.0,6==p nB. 1.0,6==p nC. 3.0,8==p nD. 1.0,24==p n 13. 设X 是一随机变量,0,,2>==σσμDX EX ,则对任何常数c,必有( ). A.222)(C EX c X E -=- B.22)()(μ-=-X E c X EC. DX c X E <-2)(D. 22)(σ≥-c X E 14.()~(,),()D X X B n pE X =则( ). A. n B. p -1 C. p D. p-1115.随机变量X的概率分布律为1{},1,2,,,P X k k n n===L ()D X 则=( ). A.)1(1212+n B. )1(1212-n C. 2)1(12+n D. 2)1(121-n 16. 随机变量⎪⎩⎪⎨⎧≤>=-0,00,101)(~10x x e x f X x,则)12(+X E =( ).A.1104+ B. 41014⨯+ C. 21 D. 20 17.设X 与Y 相互独立,均服从同一正态分布,数学期望为0,方差为1,则(X ,Y )的概率密度为( ).A.22()21(,)2xy f x y eπ+-= B.22()2(,)2xy f x y π+-=C. 2()2(,)2x y f x y π+-=D. 2241(,)2x y f x y eπ+-=18.X 服从]2,0[上的均匀分布,则DX=( ).A. 21B. 31C.61D. 12119.,),1,0(~3X Y N X =则EY=( ).A. 2B.n 43 C. 0 D. n 3220. 若12,~(0,1),1,2,i Y X X X N i =+=则( ).A. EY=0B. DY=2C.~(0,1)Y ND.~(0,2)Y N21. 设2(,),(,)X b n p Y N μσ::,则( ). A.2()(1)D X Y np p σ+=-+ B.()E X Y np μ+=+ C.22222()E X Y n p μ+=+ D.2()(1)D XY np p σ=-22.将n 只球放入到M 只盒子中去,设每只球落在各个盒中是等可能的,设X 表示有球的盒子数,则EX 值为( ). A. ])11(1[nMM -- B.M n B. ])1(1[n MM - D. nM n ! 23. 已知X 服从参数为`λ的泊松分布,且[(1)(2)]1E X X --=,则λ为( ).A. 1B.-2C.21D.41 24. 设1X ,2X ,3X 相互独立,其中1X 服从]6,0[上的均匀分布,2X 服从正态分布)2,0(2N ,3X 服从参数为3的泊松分布,记12323Y X X X =-+,则DY=( ).A. 14B.46C.20D. 9 25. 设X 服从参数为1的指数分布,则2()X E X e -+=( ).A. 1B.0C. 13D.4326. 设X 为随机变量,}3|{|,,2σμσμ≥-==X P DX EX 则满足( ). A. 91≤ B. 31≤ C. 91≥ D. 31≥ 27. 设X,Y 独立同分布,记,,Y X V Y X U +=-=则U 与V 满足( ). A. 不独立 B. 独立 C.相关系数不为0 D. 相关系数为028. 设随机变量1210,,X X X L 相互独立,且1,2(1,2,,10)i i EX DX i ===L ,则下列不等式正确的是( ).A. 21011}1{-=-≥<-∑εεi i X P B. 21011}1{-=-≥<-∑εεi i X PC. 2101201}10{-=-≥<-∑εεi i X P D. 2101201}10{-=-≤<-∑εεi i X P29. 利用正态分布有关结论,⎰∞+∞---+-dx e x x x 2)2(22)44(21π=( ).A. 1B.0C.2D. -1 30.设(X,Y )服从区域},0:),{(a y x y x D ≤≤=上的均匀分布,则||Y X E - 的值为( ).A. 0B.a 21C. a 31D. a 41 31. 下列叙述中正确的是( ). A. 1)(=-DX EXX D B.~(0,1)N DXC. 22)(EX EX =D. 22)(EX DX EX +=32.某班有n 名同学,班长将领来的学生证随机地发给每个人,设X 表示恰好领到自己学生证的人数,则EX 为( ). A. 1 B.2n C.2)1(+n n D. nn 1- 33.设X 服从区间]2,1[-上的均匀分布,1,00,()0,1,0X X DY Y X -<⎧⎪===⎨⎪>⎩则.A.32 B. 31 C. 98D. 1 34.某种产品表面上的疵点数服从泊松分布,平均每件上有1个疵点,若规定疵点数不超过1的为一等品,价值10元;疵点数大于1不多于3的为二等品,价值8元;3个以上者为废品,则产品的废品率为( ). A.e 38 B. e 381- C. e 251- D. e25 35. 接上题,任取一件产品,设其价值为X, 则EX 为( ). A.e 376 B. e316C. 9D. 6 36. 设⎩⎨⎧<<=其他,010,2)(~x x x f X ,以Y 表示对X 的三次独立重复观察中“21≤X ”出现的次数,则DY=( ).A . 169 B. 916 C. 43 D. 3437. 设(X,Y)为连续型随机向量,其联合密度为),(y x f ,两个边缘概 率密度分别为()X f x 与()Y f y ,则下式中错误的是( ). A. ()X EX xf x dx +∞-∞=⎰ B. ⎰⎰+∞∞-+∞∞-=dxdy y x xf EX ),( C. ⎰⎰+∞∞-+∞∞-=dxdy y x f y EY ),(22D. ()()()X Y E XY xyf x f y dxdy +∞+∞-∞-∞=⎰⎰二、填空题1.随机变量X 服从参数为λ的泊松分布,且2)(=X D ,则{}==1X p .2.已知离散型随机变量X 可能取到的值为:-1,0,1,且2()0.1,()0.9E X E X ==,则X的概率密度是 .3.设随机变量2~(,)X N μσ,则X 的概率密度()f x =EX = ;DX = .若σμ-=X Y ,则Y 的概率密度()f y =EY = ;DY = .4.随机变量~(,4)X N μ,且5)(2=X E ,则X 的概率密度函数(24)0.3,p X <<=为 .5.若随机变量X服从均值为3,方差为2σ的正态分布,且(24)0.3,P X <<=则(2)P X <= .6.已知随机变量X 的分布律为:X0 1 2 3 4p 1/31/61/61/12 1/4则()E X = ,()D X = ,(21)E X -+= . 7.设4,9,0.5,(23)_____________XY DX DY D X Y ρ===-=则.8.抛掷n 颗骰子,骰子的每一面出现是等可能的,则出现的点数之和的方差为 .9.设随机变量X 和Y 独立,并分别服从正态分布(2,25)N 和(3,49)N ,求随机变量435Z X Y =-+的概率密度函数为 . 10.设X 表示10次独立重复射击命中目标的次数,每次击中目标的概率为0.4,则2X 的数学期望E (2X )= .11.已知离散型随机变量X 服从参数为2的泊松分布,则随机变量Z=3X-2的数学期望E (Z )= .第五章 大数定理及中心极限定理一、选择题1. 已知的iX 密度为()(1,2,,100)if x i =L ,且它们相互独立,则对任何实数x , 概率∑=≤1001}{i ix XP 的值为( ).A. 无法计算B. 100110011001[()]i i i i x xf x dx dx ==≤∑⎰⎰L L CC. 可以用中心极限定理计算出近似值D. 不可以用中心极限定理计算出近似值 2. 设X 为随机变量,}3|{|,,2σμσμ≥-==X P DX EX 则满足( ).A.91≤B.31≤ C. 91≥ D.31≥3. 设随机变量1X ,210,,X X L 相互独立,且1,2(1,2,,10)i i EX DX i ===L ,则( )A.21011}1{-=-≥<-∑εεi i X P B.21011}1{-=-≥<-∑εεi i X PC.2101201}10{-=-≥<-∑εεi i X PD.2101201}10{-=-≤<-∑εεi i X P4. 设对目标独立地发射400发炮弹,已知每发炮弹的命中率为0.2由中心极限定理,则命中 60发~100发的概率可近似为( ). A. (2.5)Φ B.2(1.5)1Φ- C.2(2.5)1Φ- D. 1(2.5)-Φ5. 设1X ,2,,nX X L 独立同分布,2,,1,2,,,ii EXDX i n μσ===L 当30≥n 时,下列结 论中错误的是( ).A. ∑=ni iX 1近似服从2(,)N n n μσ分布B.1nii Xn n μσ=-∑(0,1)N 分布C.21X X +服从)2,2(2σμN 分布D. ∑=ni iX 1不近似服从(0,1)N 分布6. 设12,,X X L 为相互独立具有相同分布的随机变量序列,且()1,2,iX i =L 服从参数为2的指数分布,则下面的哪一正确? ( ) A.()1lim ;n i i n X n P x x n =→∞⎧⎫-⎪⎪⎪≤=Φ⎨⎬⎪⎪⎪⎪⎩⎭∑B.()12lim ;n i i n X n P x x n =→∞⎧⎫-⎪⎪⎪≤=Φ⎨⎬⎪⎪⎪⎪⎩⎭∑C. ()12lim ;2n i i n X P x x n =→∞⎧⎫-⎪⎪⎪≤=Φ⎨⎬⎪⎪⎪⎪⎩⎭∑D. ()12lim ;2n i i n X P x x n =→∞⎧⎫-⎪⎪⎪≤=Φ⎨⎬⎪⎪⎪⎪⎩⎭∑其中()x Φ是标准正态分布的分布函数.二、填空题1、设nμ是n 次独立重复试验中事件A 出现的次数,pq p A P -==1,)(,则对任意区间],[b a 有⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≤-<∞→b npqnp a P nn μlim = . 2、设nμ是n 次独立重复试验中事件A 出现的次数,p是事件A 在每次试验中发生的概率,则对于任意的0>ε,均有⎭⎬⎫⎩⎨⎧>-∞→εμ||lim p nP nn = .3、一颗骰子连续掷4次,点数总和记为X ,估计)1810(<<X p = .4、已知生男孩的概率为0.515,求在10000个新生婴儿中女孩不少于男孩的概率= .第六章 样本及抽样分布一、选择题1. 设12,,,nX X X L 是来自总体X 的简单随机样本,则12,,,nX X X L 必然满足( )A.独立但分布不同;B.分布相同但不相互独立; C 独立同分布; D.不能确定2.下列关于“统计量”的描述中,不正确的是( ).A .统计量为随机变量 B. 统计量是样本的函数C. 统计量表达式中不含有参数D. 估计量是统计量3. 设总体均值为μ,方差为2σ,n 为样本容量,下式中错误的是( ). A.)(=-μX E B.2()D X nσμ-=C.1)(22=σS E D.~(0,1)/X N nσ4. 下列叙述中,仅在正态总体之下才成立的是( ). A. 22211()()nnii i i XX X n X ==-=-∑∑ B.2S X 与相互独立 C.22])ˆ([)ˆ()ˆ(θθθθθ-+=-E D E D.221[()]n i i E X n μσ=-=∑5. 下列关于统计学“四大分布”的判断中,错误的是( ). A. 若12~(,),F F n n 则211~(,)F n n FB .若2~(),~(1,)T t n TF n 则 C .若)1(~),1,0(~22x XN X 则D .在正态总体下2212()~(1)ni i Xx n μσ=--∑6. 设2,iiX S 表示来自总体2(,)iiN μσ的容量为in 的样本均值和样本方差)2,1(=i ,且两总体相互独立,则下列不正确的是( ).A.2221122212~(1,1)S F n n S σσ-- B.12221212(~(0,1)X X N n n σσ+C.)(~/11111n t n S X μ- D.2222222(1)~(1)n S x n σ--7. 设总体服从参数为θ1的指数分布,若X 为样本均值,n 为样本容量,则下式中错误的是( ).A.θ=X EB. 2DX nθ=C. ()22(1)n E X nθ+=D. ()221θ=X E8. 设12,,,nX X X L 是来自总体的样本,则211()1ni i X X n =--∑是( ).A.样本矩B. 二阶原点矩C. 二阶中心矩D.统计量9.12,,,nX X X L 是来自正态总体)1,0(N 的样本,2,SX 分别为样本均值与样本方差,则( ).A. )1,0(~N X B. ~(0,1)nX N C. 221~()nii Xx n =∑D.~(1)Xt n S-10. 在总体)4,12(~N X 中抽取一容量为5的简单随机样本,,,,,54321X X X X X 则}15),,,,{m ax (54321>X X X X X P 为( ).A. )5.1(1Φ-B. 5)]5.1(1[Φ- C. 5)]5.1([1Φ-D. 5)]5.1([Φ11.上题样本均值与总体均值差的绝对值小于1的概率为( ).A.1)5.0(2-Φ B.1)25(2-Φ C.1)45(2-ΦD. 1)5.2(2-Φ12. 给定一组样本观测值129,,,X X X L 且得∑∑====91291,285,45i ii iX X 则样本方差2S 的观测值为( ).A. 7.5B.60C.320 D.26513. 设X 服从)(n t 分布,aX P =>}|{|λ,则}{λ-<X P 为( ).A.a 21 B.a2 C. a+21D. a 211-14. 设12,,nX X X L ,是来自总体)1,0(N 的简单随机样本,则∑=-ni iX X12)(服从分布为( ).A .)(2n x B.)1(2-n xC.),0(2n N D.)1,0(nN15. 设12,,,nx x x L 是来自正态总体2(0,2)N 的简单随机样本,若298762543221)()()2(X X X X c X X X b X X a Y ++++++++=服从2x 分布,则c b a ,,的值分别为( ). A. 161,121,81 B. 161,121,201 C. 31,31,31 D.41,31,2116. 在天平上重复称量一重为a 的物品,假设各次称量结果相互独立且同服从2(,0.2)N a 分布,以nX 表示n 次称量结果的算术平均,则为了使n a X P n,95.0}1.0{≥<-值最小应取作( ).A. 20B. 17C. 15D. 1617. 设随机变量X 和Y 相互独立,且都服从正态分布2(0,3)N ,设921,,,X X X Λ和921,,,Y Y Y Λ分别是来自两总体的简单随机样本,则统计量91921ii ii XU Y===∑∑服从分布是( ).A. )9(t B. )8(t C.)81,0(ND.)9,0(N二、填空题1.在数理统计中,称为样本.2.我们通常所说的样本称为简单随机样本,它具有的两个特点是 . 3.设随机变量nX XX ,,,21Λ相互独立且服从相同的分布,2,σμ==DX EX ,令∑==ni iX n X 11,则EX =;.DX =4.设nX XX ,,,21Λ是来自总体的一个样本,样本均值_______________=X ,则样本标准差___________=S ;样本方差_________________2=S;样本的k 阶原点矩为 ;样本的k 阶中心矩为 . 5.),,,(1021X XX Λ是来自总体)3.0,0(~2N X 的一个样本,则=⎭⎬⎫⎩⎨⎧≥∑=101244.1i i X P .6.设nX XX ,,,21Λ是来自(0—1)分布)}1{,1}0{(p X P p X P ==-==的简单随机样本,X 是样本均值,则=)(X E.=)(X D. 7.设),,,(21n X X X Λ是来自总体的一个样本,),,,()()2()1(n X X X Λ是顺序统计量,则经验分布函数为=)(x F n ⎪⎩⎪⎨⎧_______________________8.设),,,(21nX X X Λ是来自总体的一个样本,称 为统计量; 9.已知样本1621,,,X X X Λ取自正态分布总体)1,2(N ,X 为样本均值,已知5.0}{=≥λX P ,则=λ .10.设总体),(~2σμN X ,X 是样本均值,2nS 是样本方差,n 为样本容量,则常用的随机变量22)1(σnSn -服从 分布. 11.设nX XX ,,,21Λ为来自正态总体),(~2σμN X 的一个简单随机样本,则样本均值∑==ni iX n X 11服从 ,又若ia 为常数),2,1,0(n i a i Λ=≠,则∑=ni iiX a 1服从 .12.设10=n 时,样本的一组观测值为)7,4,8,5,4,5,3,4,6,4(,则样本均值为 ,样本方差为 .第七章 参数估计一、选择题1. 设总体X 在),(ρμρμ+-上服从均匀分布,则参数μ的矩估计量为( ). (A )X 1 (B )∑=-ni iX n 111 (C )∑=-ni i X n 1211 (D )X2. 设总体),(~2σμN X ,nX X ,,1Λ为抽取样本,则∑=-n i iX X n 12)(1是( ).)(A μ的无偏估计)(B 2σ的无偏估计)(C μ的矩估计)(D 2σ的矩估计3. 设X 在[0,a]上服从均匀分布,0>a 是未知参数,对于容量为n 的样本nX X ,,1Λ,a 的最大似然估计为( ) (A )},,,m ax {21n X X X Λ(B )∑=ni i X n 11(C )},,,m in{},,,m ax {2121n n X X X X XX ΛΛ- (D )∑=+ni iX n 111;4. 设总体X 在[a,b]上服从均匀分布,nX XX ,,,21Λ是来自X 的一个样本,则a 的最大似然估计为( ) (A )},,,m ax {21n X X X Λ (B )X(C )},,,m in{21n X X X Λ(D )1X Xn-5. 设总体分布为),(2σμN ,2,σμ为未知参数,则2σ的最大似然估计量为( ). (A )∑=-ni i X X n 12)(1 (B )∑=--ni i X X n 12)(11 (C )∑=-ni i X n 12)(1μ (D )∑=--ni i X n 12)(11μ6. 设总体分布为),(2σμN ,μ已知,则2σ的最大似然。
(完整版)12-13-1概率统计期中试卷(理工)答案
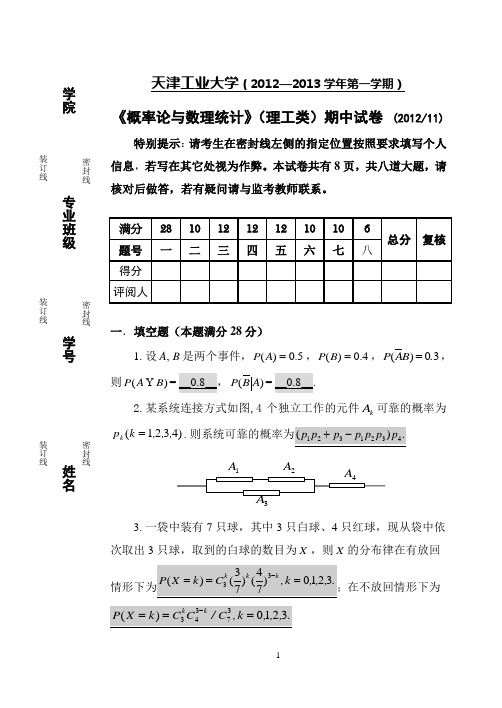
1天津工业大学(2012—2013学年第一学期)《概率论与数理统计》(理工类)期中试卷 (2012/11)特别提示:请考生在密封线左侧的指定位置按照要求填写个人信息,若写在其它处视为作弊。
本试卷共有8页,共八道大题,请核对后做答,若有疑问请与监考教师联系。
一.填空题(本题满分28分)1.设B A ,是两个事件,5.0)(=A P ,4.0)(=B P ,30)(.B A P =,则)(B A P Y )(A B P2.某系统连接方式如图,4个独立工作的元件k A 可靠的概率为)4321(,,,k p k =.3.一袋中装有7只球,其中3只白球、4只红球,现从袋中依次取出3只球,取到的白球的数目为X ,则X 的分布律在有放回在不放回情形下为 -----------------------密封线----------------------------------------密封线---------------------------------------密封线----------------------------------------------学院专业班级学号姓名----------------------装订线----------------------------------------装订线----------------------------------------装订线---------------------------------------------24.设随机变量X 的概率密度⎩⎨⎧<<=0 10 )(其它,x ,Ax x f X ,则常数A13+=X Y 的概率密度=)(y f Y5.设随机变量X 的分布律为则X 的分布函数为=)(x F X.6.设随机变量)(λ~X π(泊松分布),且20)(-==e X P ,则常数λ≤)2(X P7.设随机变量)61(,U ~X (均匀分布),则X的概率密度函数为t 的二次方程012=+-Xt t 有实根的概率为8.设随机变量X 的概率密度函数为2(3)4(),x f xx +-=-∞<<+∞则23+=X Y ;而概率)2(->Y P 知9772.0)2(=Φ).3二.(本题满分10分)设某厂有甲乙丙三条流水线生产同一种产品,产量分别占15%,80%,5%;次品率分别为0.02,0.01和0.03;三条流水线的产品混放在同一库房。
天津理工大学概率论与数理统计第二章习题答案详解

第2章一维随机变量 习题2一. 填空题:1.设 离 散 型 随 机 变 量 ξ 的 分 布 函 数 是 (){}x P x F ≤=ξ, 则 用 F (x) 表 示 概 {}0x P =ξ = __________。
解:()()000--x F x F2.设 随 机 变 量 ξ 的 分 布 函 数 为 ()()+∞<<∞-+=x arctgx x F π121 则 P{ 0<ξ<1} = ____14_____。
解: P{ 0<ξ<1} = =-)0(F )1(F 143.设 ξ 服 从 参 数 为 λ 的 泊 松 分 布 , 且 已 知 P{ ξ = 2 } = P{ ξ = 3 },则 P{ ξ = 3 }= ___2783e - 或 3.375e -3____。
4.设 某 离 散 型 随 机 变 量 ξ 的 分 布 律 是 {}⋅⋅⋅===,2,1,0,!k k C k P Kλξ,常 数 λ>0, 则 C 的 值 应 是 ___ e -λ_____。
解:{}λλλλξ-∞=∞=∞==⇒=⇒=⇒=⇒==∑∑∑e C Ce k C k Ck P KK KK K 11!1!105 设 随 机 变 量 ξ 的 分 布 律 是 {}4,3,2,1,21=⎪⎭⎫⎝⎛==k A k P kξ则⎭⎬⎫⎩⎨⎧<<2521ξP = 0.8 。
解:()A A k P k 161516181412141=⎪⎭⎫ ⎝⎛+++==∑=ξ 令15161A = 得 A =1615()()212521=+==⎪⎭⎫ ⎝⎛<<ξξξp p P 8.041211516=⎥⎦⎤⎢⎣⎡+=6.若 定 义 分 布 函 数 (){}x P x F ≤=ξ, 则 函 数 F(x)是 某 一 随 机 变 量 ξ 的 分 布 函 数 的 充 要 条 件 是F ( x ) 单 调 不 减 , 函 数 F (x) 右 连 续 , 且 F (- ∞ ) = 0 , F ( + ∞ ) = 17. 随机变量) ,a (N ~2σξ,记{}σ<-ξ=σa P )(g ,则随着σ的增大,g()σ之值 保 持 不 变 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 随机变量 习题一第一章 随机变量 习题一第一章 随机变量 习题一1、写出下列随机试验的样本空间(1)同时掷三颗骰子,记录三颗骰子点数之和Ω= {}1843,,, (2)生产产品直到有10件正品为止,记录生产产品的总件数Ω= {} ,,1110 (3)对某工厂出厂的产品进行检验,合格的记上“正品”,不合格的记上“次品”,如连续查出2个次品就停止,或检查4个产品就停止检查,记录检查的结果。
用“0”表示次品,用“1”表示正品。
Ω={111111101101011110111010110001100101010010000,,,,,,,,,,,}(4)在单位圆内任意取一点,记录它的坐标Ω= }|),{(122<+y x y x(5)将一尺长的木棍折成三段,观察各段的长度Ω=},,,|),,{(1000=++>>>z y x z y x z y x其中z y x ,,分别表示第一、二、三段的长度(6 ) .10只产品中有3只次品 ,每次从其中取一只(取后不放回) ,直到将3只次品都取出 , 写出抽取次数的基本空间U =“在 ( 6 ) 中 ,改写有放回抽取” 写出抽取次数的基本空间U =解: ( 1 ) U = { e3 , e4 ,… e10 。
}其 中 ei 表 示 “ 抽 取 i 次 ” 的 事 件 。
i = 3、 4、 …、 10( 2 ) U = { e3 , e4 ,… }其 中 ei 表 示 “ 抽 取 i 次 ” 的 事 件 。
i = 3、 4、 …2、互不相容事件与对立事件的区别何在?说出下列各对事件的关系(1)δ<-||a x 与δ≥-||a x 互不相容 (2)20>x 与20≤x 对立事件(3)20>x 与18<x 互不相容 (4)20>x 与22≤x 相容事件(5)20个产品全是合格品与20个产品中只有一个废品 互不相容(6)20个产品全是合格品与20个产品中至少有一个废品 对立事件解: 互不相容:φ=AB ; 对立事件 : φ=AB )1( 且 Ω=⋃B A3、设A,B,C 为三事件,用A,B,C 的运算关系表示下列各事件(1)A 发生,B 与C 不发生 - C B A (2)A 与B 都发生,而C 不发生 - C AB(3)A,B,C 中至少有一个发生 -C B A ⋃⋃ (4)A,B,C 都发生 -ABC(5)A,B,C 都不发生 - C B A (6)A,B,C 中不多于一个发生 -⋃⋃(7)A,B,C 中不多于两个发生-C B A ⋃⋃(8)A,B,C 中至少有两个发生-BC AC AB ⋃⋃4、盒内装有10个球,分别编有1- 10的号码,现从中任取一球,设事件A 表示“取到的球的号码为偶数”,事件B 表示“取到的球的号码为奇数”,事件C 表示“取到的球的号码小于5”,试说明下列运算分别表示什么事件.(1)B A 必然事件 (2)AB 不可能事件 (3)C 取到的球的号码不小于5 (4)C A 1或2或3或4或6或8或10(5)AC 2或4 (6)C A 5或7或9 (7)C B 6或8或10 (8)BC 2或4或5或6或7或8或9或105、指出下列命题中哪些成立,哪些不成立. (1)B B A B A = 成立 (2)B A B A = 不成立 (3)C B A C B A = 不成立 (4)φ=))((B A AB 成立 (5)若B A ⊂,则AB A = 成立(6)若φ=AB ,且A C ⊂,则φ=BC 成立 (7)若B A ⊂,则A B ⊂ 成立 (8)若A B ⊂,则A B A = 成立7、设一个工人生产了四个零件,i A 表示事件“他生产的第i 个零件是正品”),,,(4321=i ,用1A ,2A ,3A ,4A 的运算关系表达下列事件.(1)没有一个产品是次品; (1) 43211A A A A B =(2)至少有一个产品是次品;(2) 432143212A A A A A A A A B =⋃⋃⋃=(3)只有一个产品是次品;(3) 43214321432143213A A A A A A A A A A A A A A A A B ⋃⋃⋃=(4)至少有三个产品不是次品 4)432143214321432143214A A A A A A A A A A A A A A A A A A A A B ⋃⋃⋃⋃=8. 设 E 、F 、G 是三个随机事件,试利用事件的运算性质化简下列各式 : (1)()()F E F E (2) ()()()E F F E (3)()()G F F E 解 :(1) 原式 ()()()()E F F F E F E E E ==(2) 原式 ()()()()E F F E F F E F E F E ===(3) 原式 ()()()()()G E F G F F F G E F E ==9、设B A ,是两事件且7060.)(,.)(==B P A P ,问(1)在什么条件下)(AB P 取到最大 值,最大值是多少?(2)在什么条件下)(AB P 取到最小值,最小值是多少? 解: (1)6.0)(,=⊂AB P B A (2)3.0)(,==⋃AB P S B A 10. 设 事 件 A , B , C 分 别 表 示 开 关 a , b , c 闭 合 , D 表 示 灯 亮 , 则可用事件A ,B ,C 表示:(1) D = AB C ;(2) D = ()C B A 。
11、设A,B,C 是三事件,且81041======)(,)()(,)()()(AC P BC P AB P C P B P A P , 求A,B,C 至少有一个发生的概率.解:)()()()()()()()(ABC P BC P AC P AB P C P B P A P C B A P +---++=⋃⋃8500810414141=+---++= ABC AB ⊃ 0)()(0=<≤AB P ABC P 0)(=∴ABC P12. (1)设事件 A , B 的概率分别为 51 与 41,且 A 与 B 互 斥,则 )(B A P = 51 . (2).一个盒中有8只红球,3只白球,9只蓝球 ,如果随机地无放回地摸3只球 ,则取到的3 只 都 是 红 球 的 事 件 的 概 率 等 于 ___14285____。
(3) 一 袋中有4只白球,2只黑球,另一只袋中有3只白球和5只黑球,如果 从每只袋中各摸一只球 ,则摸到的一只是白球,一只是黑球的事件的概 率等于 ___1324___。
(4) .设 A1 , A2 , A3 是随机试验E 的三个相互独立的事件,已知P(A1) = α , P(A2) = β,P(A3) = γ ,则A1 , A2 , A3 至少有一个 发生的概率是 1- (1- α)(1- β)(1- γ) .(5) .一个盒中有8只红球,3只白球,9只蓝球,如果随机地无放回地摸3只球,则摸到的没有一只是白球的事件的概率等于 __3457____。
13、在1500个产品中有400个次品,1100个正品,任取200个,求(1)恰有90个次品的概率; (2)至少有2个次品的概率.解: 2001500110110090400)1(C C C P =⎥⎦⎤⎢⎣⎡+-=2000150019911001400200150020011001)2(C C C C C P 14、两射手同时射击同一目标,甲击中的概率为0.9,乙击中的概率为0.8,两射手同时击中的概率为0.72,二人各击中一枪,只要有一人击中即认为“中”的, 求“中”的概率.解:=A “甲中” =B “乙中”98.072.08.09.0)()()()(=-+=-+=⋃AB P B P A P B A P15、8封信随机地投入8个信箱(有的信箱可能没有信),问每个信箱恰有一封信的概 率是多少?解: 888!)(=A P16、房间里有4个人,问至少有两个人的生日在同一个月的概率是多少? 解:设所求事件=A “至少有两个人的生日在同一个月的”=“任何两个人的生日都不在同一个月”427.0121)(1)(,12)(44124412=-=-==A A P A P A A P17、将3个球随机地放入4个杯子中去,问杯子中球的最大个数分别为1,2,3的概 率各是多少?解:3个球放入4个杯子中去共有34种放法,设i B 表示杯子中球的最大个数为n 的事件),,(321=n ,1B 表示每只杯子最多只能放一个球,共有34A 种方法,故8343341==A B P )(;2B 表示有一只杯子中放2个球,先在3个球中任取2只放入4个杯子中的任意一只,共有423⨯C 种方法,剩下的一个球可以放入剩下的3只杯子中的任一只,有3种放法,故2B 包含的基本事件数为363423=⨯⨯C ,于是16943632==)(B P ;3B 表示有一只杯子中放3个球,共有4种方法,故1614433==)(B P . 18. 设 一 个 质 点 等 可 能 地 落 在 xoy 平 面 上 的 三 角 形 域 D 内( 其 中 D 是 x = 0 ,y = 0 , x + y = 2所 围 成 的 ) , 设 事 件 A 为:质 点 落 在 直 线 y = 1 的 下 侧 , 求 P(A) 。
y21 o 2 x D 143222121211=⨯⨯+==)()(D D A P19、(1)已知504030.)(,.)(,.)(===B A P B P A P ,求)|(B A B P(2)已知213141===)|(,)|(,)(B A P A B P A P ,求)(B A P解: (1)250.)|(=⋃B A B P(2)31=⋃)(B A P20、一批产品共100个,其中有次品5个,每次从中任取一个,取后不放回, 设i A ( i =1,2,3,)表示第i 次抽到的是次品,求: ()99412=A A P ,()999512=A A P ,()99512=A A P ()999412=A A P ,()983213=A A A P , ()9894213=A A A P 21、市场上供应的灯泡中,甲厂产品占70%,乙厂占30%,甲厂产品的合格率为95%,乙厂的合格率是80%。
若用事件A 、A 分别表示甲、乙两厂产品,B 表示合格品。
试写出有关事件的概率.(1)=)(A P 70%(2)=)(A P 30% (3)=)|(A B P 95% (4)=)|(A B P 80% (5)=)|(A B P 5% (6)=)|(A B P 20%22、袋中有10个球,9个是白球,1个是红球,10个人依次从袋中各取一球,每人取一球后,不再放回袋中,问第一人,第二人,……,最后一人取得红球的概 率各是多少?解: 解:设i A 第i 个人取得红球的事件),,,(1021 =i , 则i A 为第i 个人取得白球的事件, 显然101)(1=A P ,)(212121212φ==⋃=A A A A A A A A A 10191109)|()()()(121212=⨯=⋅==∴A A P A P A A P A P 同理101!10!9)()(1092110===A A A A P A P 23、某种动物由出生活到20年以上的概率为0.8,活25年以上的概率为0.4,问现 年20岁的这种动物活支25岁以上的概率是多少?解:设A 为{由出生活到20岁}的事件,B 为{由出生活到25岁}的事件则所求事件的概率为)()()|(A P AB P A B P = B AB A B =∴⊂218040====..)()()()()|(A P B P A P AB P A B P 24、十个考签中四个难的,三人参加抽签,(不放回)甲先、乙次、丙最后,记事件 A,B,C 分别表示甲、乙、丙各抽到难签,求)(),(),(),(ABC P B A P AB P A P . 解:152)(,104)(==AB P A P 154)(=B A P 301)(=ABC P 25. 设 0< P(C) <1 ,试 证 :对 于 两 个 互 不 相 容 的 事 件 A ,B ,恒 有P { ( A B )∣C} = P{A ∣C} + P{B ∣C}证:()[]()[]()C P C B A P C B A P +=+ ()()C P BC AC P +=()()()C P BC P AC P += ()()C B P C A P += 26、设事件A 与B 互斥,且10<<)(B P ,证明)()()|(B P A P B A P -=1. 证明:由于φ=AB ,故B A B B A A =⋃=)()1)(()(1)()()()|(≠-==∴B P B P A P B P B A P B A P27、一批零件为100个,次品率为10%,每次从中任取一个,不再放回,求第三次才 能取得正品的概率是多少?解:设i A 为{第i 次取到正品},)3,2,1(=i 由于次品率为10%,故100个零件约有90个正品,次品10个,设A 为{第三次抽到正品},即第一次第二次都取得次品,第三次才取得正品,则由一般乘法公式得)|()|()()()(213121321A A A P A A P A P A A A P A P ==0083.0989099910010=⨯⨯= 28、设每100个男人中有5个色盲者,而每10000个女人中有25个色盲者,今在3000 个男人和 2000个女人中任意抽查一人, 求 这 个 人 是 色 盲 者 的 概 率。
