九年级数学下册第三章三视图与表面展开图阶段性测试十四课件(新版)浙教版
2020浙教版九年级数学下 三视图与表面展开图全章测试

【文库独家】三视图与表面展开图全章测试一、选择题1.平行投影中的光线是( )A.平行的B.聚成一点的C.不平行的D.向四面八方发散2.正方形在太阳光下的投影不可能是( )A.正方形B.一条线段C.矩形D.三角形3.如图1,将一块正方形纸片沿对角线折叠一次,然后在得到的三角形的三个角上各挖去一个圆洞,最后将正方形纸片展开,得到的图案是( )4.由一些完全相同的小立方块搭成的几何体的三视图如图所示,那么搭成这个几何体所用的小立方块的个数是( )第4题图A.8 B.7 C.6 D.5 5.如图是某几何体的三视图及相关数据,则判断正确的是( )第5题图A.a>c B.b>cC.4a2+b2=c2D.a2+b2=c26.若干个正方体形状的积木摆成如图所示的塔形,平放于桌面上,上面正方体的下底四个顶点是下面相邻正方体的上底各边中点,最下面的正方体棱长为1,如果塔形露在外面的面积超过7,则正方体的个数至少是( )A.2 B.3 C.4 D.5二、填空题7.一个圆柱的俯视图是______,左视图是______.8.如果某物体的三视图如图所示,那么该物体的形状是______.第8题图9.一空间几何体的三视图如图所示,则这个几何体的表面积是______cm2.第9题图10.如图,水平放置的长方体的底面是边长为2和4的矩形,它的左视图的面积为6,则长方体的体积等于______.三、解答题11.楼房、旗杆在路灯下的影子如图所示.试确定路灯灯炮的位置,再作出小树在路灯下的影子.(不写作法,保留作图痕迹)12.画出图中的九块小立方块搭成几何体的主视图、左视图和俯视图.13.如图是由几个小立方块所搭几何体的俯视图,小正方形中的数字表示该位置小立方块的个数,请画出这个几何体的主视图和左视图.14.如图是一个几何体的主视图和俯视图,求该几何体的体积( 取3.14).图形并求这两种圆柱的表面积.答案与提示1.A . 2.D . 3.A . 4.A . 5.D . 6.B .7.圆;矩形. 8.三棱柱. 9.48π. 10.24.11.如图:12.如图:13.如图:14.体积为π×102×32+30×25×40≈40 048(cm 3).15.第一种:高为a ,表面积为;π221b ab S += 第二种:高为b ,表面积为⋅+=π222a ab S。
2019-2020学年浙教版九年级数学下学期第三章 三视图与表面展开图单元测试题(含答案)

浙教版九年级数学下第三章三视图与表面展开图单元检测第Ⅰ卷(选择题)一.选择题(共10小题,3*10=30)1.如图是由四个相同的小正方体组成的几何体,则这个几何体的主视图是()A B C D2.某时刻两根木棒在同一平面内的影子如图所示,此时,第三根木棒的影子表示正确的是()3.一个几何体的三视图如图所示,这个几何体的侧面积为()A.2π cm2B.4π cm2C.8π cm2D.16π cm24.小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为()A.上午12时B.上午10时C.上午9时30分D.上午8时5.如图,一个空心圆柱体,其主视图正确的是()A B C D6.下列命题正确的是()A.三视图是中心投影B.三视图等价于投影C.球的三视图均是半径相等的圆D.阳光从矩形窗子里照射到地面上,得到的投影仍是矩形7.如图,某厂生产横截面直径为7 cm的圆柱形罐头,需将“蘑菇罐头”字样贴在罐头侧面.为了获得较佳视觉效果,字样在罐头侧面所形成的弧的度数为90°,则“蘑菇罐头”字样的长度为()A.π4cm B.7π4cm C.7π2cm D.7π cm8.如图是由几个相同的小正方体搭成的几何体的三种视图,则搭成这个几何体的小正方体的个数有()A.3个B.4个C.5个D.6个9.如图,从一块直径为24 cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上.将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是() A.12 cm B.6 cm C.3 2 cm D.2 3 cm10.如图,夜晚,小亮从A经过路灯C的正下方沿直线走到点B,他的影子y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图象大致为()第Ⅱ卷(非选择题)二.填空题(共6小题,4*6=24)11.有一个圆柱,它的高等于12 cm,底面半径等于3 cm,如图9所示,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,则它沿圆柱侧面爬行的最短路程是_______ cm(π取3).12.为了在平面上表示空间物体,人们常用数学上的“投影”方法,即把物体从不同的方向投射到平面上,然后通过这些平面的投影图形去想象空间立体图形.这是人类征服空间所表现出的伟大智慧!如图是某一物体的三个方向的影像图.它相当于光线从正面、侧面和上面照射时,该物体留下的影子,那么这个几何体可能是____________.13.如图11所示是由几个相同的小正方体搭成的几何体的三种视图,则搭成这个几何体的小正方体的个数是__________.14.一个几何体的三视图如图所示(其中标注的a,b,c为相应的边长),则这个几何体的体积是___________.15.如图13是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是___________.16.如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),计算出这个立体图形的表面积是___________mm2.三.解答题(共6小题,46分)17.(8分)画出如图所示物体的三视图.18.(8分)如图,已知圆锥底面半径r=10 cm,母线长为40 cm.(1)求它的侧面展开图的圆心角和面积;(2)若一甲虫从点A出发沿着圆锥侧面绕行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是多少?为什么?19.(10分)一位同学想利用有关知识测旗杆的高度,如图,他在某一时刻测得高为0.5 m 的小木棒的影子长为0.3 m,但当他马上测量旗杆的影长时,因旗杆靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,他先测得留在墙上的影子CD=1.0 m,又测地面部分的影长BC=3.0 m,你能根据上述数据帮他测出旗杆的高度吗?20.(10分)如图,有一直径是 2 m的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形BAC.(1)求AB的长;(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面圆的半径为多少米.21.(10分)如图,不透明圆锥体DEC放在水平面上,在A处灯光照射下形成影子.设BP过圆锥底面的圆心,已知圆锥的高为2 3 m,底面半径为2 m,BE=4 m.(1)求∠B的度数;(2)若∠ACP=2∠B,求光源A距水平面的高度.(答案用含根号的式子表示)22.(10分)如图是一粮仓,其顶部是一圆锥,底部是一圆柱.(1)画出粮仓的三视图;(2)若圆柱的底面圆的半径为1 m,高为2 m,求圆柱的侧面积;(3)假设粮食最多只能装到与圆柱同样高,则最多可以存放多少立方米的粮食?23.(10分)为了加强视力保护意识,小明想在长为4.3米,宽为3.2米的书房里挂一张测试距离为5米的视力表.在一次课题学习课上,小明向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲、乙、丙三位同学设计的方案新颖,构思巧妙.(1)甲生的方案:如图1,将视力表挂在墙ABEF和墙ADGF的夹角处,被测试人站立在对角线AC上,问:甲生的设计方案是否可行?请说明理由;(2)乙生的方案:如图2,将视力表挂在墙CDGH上,在墙ABEF上挂一面足够大的平面镜,根据平面镜成像原理可计算得到:测试线应画在距离墙ABEF________米处;(3)丙生的方案:如图3,根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表.图中的△ADF∽△ABC,如果大视力表中“E”的长是3.5cm,那么小视力表中相应的“E”的长是多少cm?参考答案 1-5 CDBDB 6-10 CBBCA 11.1512. 一个倒立的圆锥 13. 5 14. abc_ 15. 左视图 16. 20017. 解:如答图所示.18. 解:(1)nπ×40180=2π×10,解得n =90.∴圆锥侧面展开图的圆心角为90°,圆锥侧面展开图的面积为π×10×40=400π(cm 2);(2)如图,由圆锥的侧面展开图可见,甲虫从A 点出发沿着圆锥侧面绕行到母线SA 的中点B 所走的最短路线是线段AB 的长.在Rt △ASB 中,SA =40 cm ,SB =20 cm ,∴AB =20 5 cm.∴甲虫走的最短路线的长度是20 5 cm.19. 解:作DE⊥AB于点E,那么四边形BCDE是矩形,∴BE=CD=1.0 m,DE=BC=3.0 m,∴AEDE=0.50.3,∴AE=5(m),∴AB=AE+BE=6(m)20. 解:(1)如图,连结BC.∵∠BAC=90°,∴BC为⊙O的直径,即BC= 2 m,∴AB=22BC=1(m);(2)设所得圆锥的底面圆的半径为r(m),由题意,得2πr=90×π×1180,解得r=14.答:圆锥的底面圆的半径为14m.21. 解:(1)在Rt△DOB中,OB=BE+OE=4+2=6(m),∴tanB=DOBO=236=33.∴∠B=30°(2)过点A作AF⊥BP,垂足为点F.∵∠B=30°,∴∠ACP=2∠B=60°.又∠ACP =∠B+∠BAC,∴∠B=∠BAC.∴AC=BC=BE+CE=8(m).在Rt△ACF中,AF=AC·sin∠ACF=8sin60°=43(m).故光源离水平面的高度为4 3 m22. 解:(1)粮仓的三视图如图所示:(2)S圆柱侧=2π·1×2=4π m2(3)V=π×12×2=2π(m3),即最多可存放2π m3的粮食23. 解:(1)甲生的方案可行.理由如下:根据勾股定理得AC2=AD2+CD2=3.22+4.32,∵3.22+4.32>52,∴AC2>52,即AC>5,∴甲生的方案可行;(2)设测试线应画在距离墙ABEFx米处,根据平面镜成像可得x+3.2=5,解得x=1.8,∴测试线应画在距离墙ABEF1.8米处;(3)∵△ADF∽△ABC,∴FDBC=ADAB,即FD3.5=35,∴FD=2.1(cm).答:小视力表中相应“E”的长是2.1cm.。
浙教版数学九年级下册第3章三视图与表面展开检测题参考答案(1).docx

第3章 三视图与表面展开图检测题参考答案1.A 解析:平行光线所形成的投影称为平行投影.2.B3.A 解析:注意太阳光线的投影是平行投影.4.D 解析:跟物体的摆放位置有关.5.C 解析:由于正方体的主视图是个正方形,而竖着的圆柱体的主视图是个长方形,因此只有C 的图形符合这个条件.故选C .6. B 解析:几何体①的主视图是矩形,几何体②的主视图是三角形,几何体③的主视图是矩形,几何体④的主视图是圆,所以几何体①与几何体③的主视图相同.7.B 解析:图形的形状首先应与主视图一致,然后再根据各个位置的立方体的个数进行判断.8.B 解析:根据题意,太阳是从东方升起,故影子指向的方向为西方.然后依次为西北-北-东北-东,由分析可得先后顺序为④①③②.故选B .9. D 解析:依据俯视图和左视图,可知这个正棱柱为正五棱柱,再借助俯视图,可知它的主视图应为选项D.10. B 解析:结合三视图,这个几何体中,底层有3+1=4(个)小正方体,第二层有1个小正方体,因此小正方体的个数为4+1=5.11. 中间的某处上方 12.1564m 解析:由题意可知, m ,人的身高 m ,则,得.又,则 ,解得AC =38.故.13. 4 解析:观察三视图容易得出左前方有2个小立方块,左后方有1个小立方块,右前方有1个小立方块,所以共有4个小立方块.14. π 解析:通过观察三视图可知此几何体是圆锥,它的底面直径是2,高是3,所以这个几何体的体积是π×12×3=π.15.28 解析:由几何体可知其主视图有4个正方形,左视图有5个正方形,俯视图有5个正方形,故需要涂色的面积为4×2+5×2+5×2=28(平方米).16.3 解析:由主视图和左视图可以画出俯视图如图所示,可知正六边形的边长为2,故3.17.18 解析:当取最大时,俯视图中各个位置小正方体的个数如图所示,可知共有18个.18.③19.解:如图所示.20. 解:(1)符合这个零件的几何体是直三棱柱.(2)如图,△是正三角形,⊥,23,∴,)(cm2).21.解:由主视图可以看出,左列立方体最多为2个,右列立方体最多为3个,故x和2的最大值为2,1和y的最大值为3,从而x=1或x=2,y=3 .22. 解:最大值为12个,最小值为7个,俯视图分别如图所示.23. 解:该几何体的三种视图如图所示.2222=++=S a a a a2(334)20,或表222=⨯-⨯=S a a a562520.表24. 解:示意图如图所示.其中米,米,由,得米.所以(米).又,即,所以(米).25. 解:(1)如图所示,连接A与建筑物的顶点B、C,发现在一条直线上,即视线被BM挡住了,所以在A点不能看到后面那座高大的建筑物.(2)已知203m, m,m,当恰好被挡住时,三点在一条直线上,此时由,得,解得3.所以当点与点的距离大于103m时,才能看到后面的楼.26.分析:在探究题中,由直三棱柱的三视图得到CQ=5 dm,又AB=BC=4 dm,根据勾股定理求出BQ==3(dm).根据直棱柱的体积公式:直棱柱体积V液=底面积S△BCQ×高AB,求出液体的体积.在Rt△BCQ中,根据锐角三角函数可求出∠BCQ的度数.由CQ∥BE得到α=∠BCQ,从而求出α的度数.在拓展题中,无论怎样旋转,液体的体积是不变的,由此可以确定y与x的函数关系式.在延伸题中,结合α=60°通过计算得出容器内的液体分为两部分.在每部分中分别计算求出容器内液体的体积,再求出溢出容器的液体的体积后,最后判定结论是否正确.解:探究(1)CQ∥BE;3.(2)V液=×3×4×4=24(dm3).(3)在Rt△BCQ中,tan∠BCQ=.∵CQ∥BE,∴α=∠BCQ=37°.拓展当容器向左旋转时,如图①,0°≤α≤37°.∵液体体积不变,∴(x+y)×4×4=24,∴y=-x+3.当容器向右旋转时,如图②,同理得y=.当液面恰好到达容器口沿,即点Q与点B′重合时,如图③,由BB′=4 dm,且×PB×BB′×4=24,得PB=3 dm,由tan∠PB′B=,得∠PB′B=37°,∴α=∠B′PB=53°.此时37°≤α≤53°.延伸当α=60°时,如图④所示,FN∥EB,GB′∥EB.过点G作GH⊥BB′于点H.在Rt△B′GH中,GH=MB=2 dm,∠GB′B=30°,∴HB′= dm.∴MG=BH=(4-)dm<MN.此时容器内液体形成两层液面,液体的形状分别是以Rt△NFM和直角梯形MBB′G为底面的直棱柱.∵S△NFM+S梯形MBB′G=××1+×(4-+4)×2=(dm2).∴V溢出=24-4×=(dm3)>4 dm3.∴溢出容器的液体可以达到4 dm3.点拨:(1)根据立体图形的三视图解计算题时,要注意根据三视图中的数据,找出立体图形中的相应数据.(2)常应用解直角三角形的知识求线段的长度和角的度数.初中数学试卷。
九年级数学下册第三章三视图与表面展开图阶段性测试十四新版浙教版

解:(1)∵正方体有 6 个表面,12 条棱, 要展成一个平面图形必须 5 条棱连接, ∴要剪 12-5=7 条棱, 4×(7×2)=4×14=56(cm). 答:这个平面图形的周长是 56 cm; (2)如图, 这个平面图形的最大周长是 8a+4b+2c.
(第15题答图) (第15题图)
阶段性测试(十四)
精彩练习 九年级 数学
第三章 三视图与表面展开图
阶段性测试(十四)
考查范围:三视图与表面展开图(3.1~3.4)
一
选择题
(每小题5分,共30分)
1.一个几何体的三视图如图所示,这个几何体是( B ) A.球 B.圆柱 C.圆锥 D.立方体 (第1题图) 2.将一个无盖立方体形状盒子的表面沿某些棱剪开,展开后不能得到的平面图形是( C )
解:(1)正六棱柱 (2)图略
(第13题图)
1 3 2 (3) ×5×5× ×6×2+5×5×6≈280(cm ) 2 2
2
答:制作一个纸盒所需纸板的面积约为 280 cm .
阶段性测试(十四)
第7 页
14. (9 分)如图 1 是我们常用的一次性纸杯, 下面我们来研究一次性纸杯的制作方法之一. 如 图 2,取一个半径为 18 cm 的圆形纸板,再裁下一个半径为 6 cm 的同心圆纸板,沿半径 OA,OB 及 CD,AB 剪下,由 AB,CD 及线段 AC 和 BD 的部分即可围成纸杯侧面,然后在扇 形 OCD 中再截去一个面积最大的圆形纸板. (1)若∠AOB=60°,利用图 3 求裁去的面积最大的圆形纸板半径. (2)(1)中的圆形纸板足够做纸杯的底面, 但要进行简单的剪裁, 至此, 纸杯也就制成了, 通过以上数据,请你计算一次性纸杯的高,并回答它最接近于哪一个整数值. 解:(1)∵原型纸板与 OC、OD、弧 CD 相切时面积最大, 如图设纸板的圆心为 M,作 MF⊥OC, 设 MF=x,则 OM=6-x, 在 Rt△MFO 中,∠MOF=30°, (第14题图) 则 OM=2MF,即 6-x=2x,解得 x=2. ∴裁去的面积最大的圆形纸板半径为 2 cm.
九年级数学下册 第三章 投影与三视图 3.4 简单几何体的表面展开图(第1课时)a课件 (新版)浙教版

全面积 侧面积+底面积
注: 实心几何体的全面积=表面积
体积 底面积×侧棱长(高)
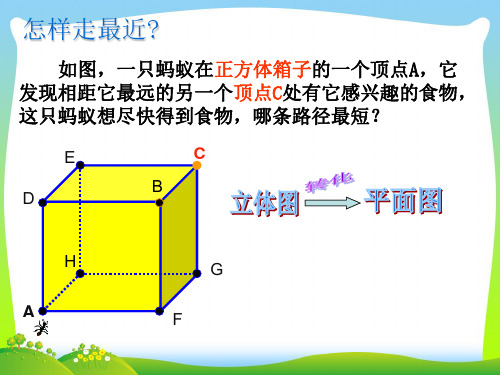
在一个边长 为4m的立方体的 房间里,一只蜘蛛 在A处,一只苍蝇 在G处,蜘蛛要想 尽快吃到苍蝇,爬 行的最短路程是多 少?
H E
G F
D
A 4m
C B
H´
H E 4m
D A
G´´
G
AG 82 42 4 5cm
思考: 课本P80,探究怎样利用表面展开图和两点间线段最 短的原理解决节前图的著名迷题。
. . . A
A
A
A
B
. . . B
B
B
C
AB=5 AB=5
AB 52 1.82 5.31
编后语
折叠课件作用 ①向学习者提示的各种教学信息; ②用于对学习过程进行诊断、评价、处方和学习引导的各种信息和信息处理; ③为了提高学习积极性,制造学习动机,用于强化学习刺激的学习评价信息; ④用于更新学习数据、实现学习过程控制的教学策略和学习过程的控制方法。 对于课件理论、技术上都刚起步的老师来说,POWERPOINT是个最佳的选择。因为操作上非常简单,大部分人半天就可以基本掌握。所以,就可以花
你能在 立方体的表 面展开图中 找到相对面 吗?
E ABCD F
如图是一个正方体纸盒的展开图,图中的6 个正方形中分别已填入了-1、7、 2 、a、b、 c,使展开图沿虚线折叠成正方体后相对面 上的两个数互为相反数,求:
a ___2,b _-_7_, c __1__
a
c 7 -1
b2
路程 62 (4 5)2 117cm
最短路程 117 cm
浙教版九年级数学下册第三章《 3.4简单几何体的表面展开图》公开课课件(共21张PPT)
12 3456
一三二型
12 345
6
12 345
6
12 345 6
二个三型
126 345
例1
请分别用1,2,3,4,5,6中的同一个数字 表示立方体和它的展开图中各对对应的面.
2 5 1 34
6
56 45 61
32 13 24
让思维更活跃一点!
如图是一个正方体纸盒的展开图,图中的6个 正方形中分别已填入了-1、7、2 、a、b、c,使展 开图折叠成正方体后相对面上的两个数互为相反
• 17、儿童是中心,教育的措施便围绕他们而组织起来。2021/7/302021/7/302021/7/302021/7/30
• 2、Our destiny offers not only the cup of despair, but the chalice of opportunity. (Richard Nixon, American President )命运给予我们的不是失望之酒,而是机会之杯。二〇二一年六月十七日2021年6月17日星期四 • 3、Patience is bitter, but its fruit is sweet. (Jean Jacques Rousseau , French thinker)忍耐是痛苦的,但它的果实是甜蜜的。10:516.17.202110:516.17.202110:5110:51:196.17.202110:516.17.2021 • 4、All that you do, do with your might; things done by halves are never done right. ----R.H. Stoddard, American poet做一切事都应尽力而为,半途而废永远不行6.17.20216.17.202110:5110:5110:51:1910:51:19 • 5、You have to believe in yourself. That's the secret of success. ----Charles Chaplin人必须相信自己,这是成功的秘诀。-Thursday, June 17, 2021June 21Thursday, June 17, 20216/17/2021
201X年秋九年级数学下册第三章三视图与表面展开图3.4简单几何体的表面展开图3课件新版浙教版

简单几何体的表面展开图(3)
第4 页
10.如图所示,现有一圆心角为 90°.半径为 80 cm 的扇形铁片,用它恰好围成一个圆锥形
的量筒,用其他铁片再做一个圆形盖子把量筒底面密封(接缝都忽略不计). 求:(1)该圆锥盖子的半径为多少 cm? (2)制作这个密封量筒,共用铁片多少 cm2?(结果保留π)
考虑展开图的圆心角是否相等,由于滤纸围成的圆锥形只有最外层侧面紧贴漏斗内壁,
故只考虑该滤纸圆锥最外层的侧面和漏斗内壁圆锥侧面的关系.将圆形滤纸片按图示的
步骤折成四层且每层为14圆,则围成的圆锥形的侧面积=1-2×41S
1 滤纸圆=2S
, 滤纸圆
精选ppt
8
简单几何体的表面展开图(3)
第9 页
∴它的侧面展开图是半圆,其圆心角为 180°,如将漏斗内壁构成的圆锥侧面也抽象地 180°
A.60π cm2
B.65π cm2
C.120π cm2
D.130π cm2 (第5题图)
6.若一个圆锥的侧面展开图是半径为 18 cm,圆心角为 240°的扇形,则这个圆锥的底面半
径长是( C )
【2020】九年级数学下册 第3章 三视图与表面展开图阶段性测试(十四)练习 (新版)浙教版

11.如图所示,在一次数学活动课上,张明用17个边长为1的小立方体搭成了一个几何体,然后他请王亮用其他同样的小立方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要__19__个小立方体,王亮所搭几何体的表面积为__48__.
A. B. C. D.
4.如图是按1∶10的比例画出的一个几何体的三视图,则该几何体的侧面积是(D)
A.200 cm2B.600 cm2
C.100π cm2D.200π cm2
第4题图
第5题图
5.如图所示,是由若干个相同的小立方体搭成的几何体俯视图和左视图.则小立方体的个数可能是(D)
A.5或6B.5或7
第8题图
第9题图
9.已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的表面积为__48+12 __.
10.如图所示,小军、小珠之间的距离为2.7 m,他们在同一盏路灯下的影长分别为1.8 m,1.5 m,已知小军、小珠的身高分别为1.8 m,1.5 m,则路灯的高为__3__ m.
第10题图
(1)若∠AOB=60°,利用图3求裁去的面积最大的圆形纸板半径.
(2)(1)中的圆形纸板足够做纸杯的底面,但要进行简单的剪裁,至此,纸杯也就制成了,通过以上数据,请你计算一次性纸杯的高,并回答它最接近于哪一个整数值.
第14题图
解:(1)∵原型纸板与OC、OD、弧CD相切时面积最大,
第14题答图
如图设纸板的圆心为M,作MF⊥OC,
【2020】九年级数学下册 第3章 三视图与表面展开图阶段性测试(十四)练习 (新版)浙教版
编 辑:__________________
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在太阳光下的影子恰好落到里程碑 E 处,他自己的影子恰好落在路灯 CD 的底部 C 处.晚
自习放学时,站在上午同一个地方,发现在路灯 CD 的灯光下自己的影子恰好落在里程
碑 E 处.
(1)在图中画出小明的位置(用线段 FG 表示),并画出光线,标明太阳光、灯光;
(2)若上午上学时候高 1 米的木棒的影子为 2 米,小明身高为 1.5 米,
1.8 m,1.5 m,则路灯的高为___3___ m.
(第10题图)
11.如图所示,在一次数学活动课上,张明用 17 个边长为 1 的小立
方体搭成了一个几何体,然后他请王亮用其他同样的小立方体在
旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几
何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),
(第6题图)
A.
B.
C. D.
二
填空题 (每小题5分,共25分)
7.如图是由若干个棱长为 1 的小立方体组合而成的一个几何体的三视图,则这个几何体的
表面积是___2_2__.
8.如图所示,一个几何体的三视图分别是两个矩形,一个扇形,则这个几何体表面积的大
小为_1_2_+__1_5_π__.
(第7题图)
(第14题图)
∴裁去的面积最大的圆形纸板半径为 2 cm.
阶段性测试(十四)
第8 页
(2)∵∠AOB=60°, ∴弧 AB 的长为1201π80×18=12π , 设杯子顶的半径为 r,
则 2π r=12π ,故 r=6,
杯子顶部的半径为 6 cm,
同理可得杯子底边的半径为 2 cm.
∴杯子的高为 (18-6)2-(6-2)2≈11.31(cm). ∴杯子的高最接近整数 11
精彩练习 九年级 数学
第三章 三视图与表面展开图
阶段性测试(十四)
考查范围:三视图与表面展开图(3.1~3.4)
一
选择题
(每小题5分,共30分)
1.一个几何体的三视图如图所示,这个几何体是( B )
A.球
B.圆柱
C.圆锥
D.立方体
(第1题图)
2.将一个无盖立方体形状盒子的表面沿某些棱剪开,展开后不能得到的平面图形是( C )
阶段性测试(十四)
第9 页
15.(10 分)(1)如图 1,一个正方体纸盒的棱长为 4 厘米,将它的一些棱剪开展成一个平面 图形,求这个平面图形的周长. (2)如图 2,一个长方体纸盒的长、宽、高分别是 a 厘米、b 厘米、c 厘米(a>b>c)将它 的一些棱剪开展成一个平面图形,求这个平面图形的最大周长,并画出周长最大的平面 图形. 解:(1)∵正方体有 6 个表面,12 条棱,
(2)(1)中的圆形纸板足够做纸杯的底面,但要进行简单的剪裁,至此,纸杯也就制成了,
通过以上数据,请你计算一次性纸杯的高,并回答它最接近于哪一个整数值.
解:(1)∵原型纸板与 OC、OD、弧 CD 相切时面积最大,
如图设纸板的圆心为 M,作 MF⊥OC,
设 MF=x,则 OM=6-x,
在 Rt△MFO 中,∠MOF=30°, 则 OM=2MF,即 6-x=2x,解得 x=2.
要展成一个平面图形必须 5 条棱连接,
∴要剪 12-5=7 条棱,
(第15题图)
4×(7×2)=4×14=56(cm).
答:这个平面图形的周长是 56 cm;
(2)如图,
这个平面图形的最大周长是 8a+4b+2c.
(第15题答图)
阶段性测试(十四)
第 10 页
16.(10 分)如图所示,公路旁有两个高度相等的路灯 AB,CD.小明上午上学时发现路灯 AB
B.600 cm2 D.200π cm2
(第4题图)
5.如图所示,是由若干个相同的小立方体搭成的几何体俯视图和左视图.
则小立方体的个数可能是( D )
A.5 或 6 C.4 或 5 或 6
B.5 或 7 D.5 或 6 或 7
(第5题图)
6.如图所示,圆柱体中挖去一个小圆柱,那么这个几何体的主视图和俯视图分别为( B )
(第11题图)
那么王亮至少还需要___1_9__个小立方体,王亮所搭几何体的表面积为__4__8__.
三
解答题 (5个小题,共45分)
12.(7 分)画出如图所示立体图形的三视图.
解:如图所示.
(第12题图)
(第12题答图)
13.(9 分)如图是一个包装纸盒的三视图(单位: cm).
(1)该包装纸盒的几何形状是________;
(2)画出该纸盒的平面展开图;
(3)计算制作一个纸盒所需纸板的面积(精确到个位).
(第13题图)
解:(1)正六棱柱 (2)图略 (3)21×5×5× 23×6×2+5×5×6≈280(cm2)
答:制作一个纸盒所需纸板的面积约为 280 cm2如图 1 是我们常用的一次性纸杯,下面我们来研究一次性纸杯的制作方法之一.如
(第8题图)
(第9题图)
9.已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的表面积为 ___4_8_+__1_2___3___.
阶段性测试(十四)
第5 页
10.如图所示,小军、小珠之间的距离为 2.7 m,他们在同一盏路灯
下的影长分别为 1.8 m,1.5 m,已知小军、小珠的身高分别为
A.
B.
C.
D.
3.如图是由几个大小相同的小立方体搭成的几何体的俯视图,小正方形中的数字表示该位
置上小立方体的个数,则该几何体的左视图是( D )
A. (第3题图)
B.
C.
D.
阶段性测试(十四)
第3 页
4.如图是按 1∶10 的比例画出的一个几何体的三视图,则该几何体
的侧面积是( D )
A.200 cm2 C.100π cm2
他离里程碑 E 恰好 5 米,求路灯高.
解:(1)如图所示.
(第16题图)
(2)∵上午上学时候高 1 米的木棒的影子为 2 米,小明身高为 1.5 米,
∴小明的影长 CF 为 3 米,∵GF⊥AC,DC⊥AC,∴GF∥CD,∴△EGF∽△EDC,
图 2,取一个半径为 18 cm 的圆形纸板,再裁下一个半径为 6 cm 的同心圆纸板,沿半径
OA,OB 及 CD,AB 剪下,由 AB,CD 及线段 AC 和 BD 的部分即可围成纸杯侧面,然后在扇
形 OCD 中再截去一个面积最大的圆形纸板.
(1)若∠AOB=60°,利用图 3 求裁去的面积最大的圆形纸板半径.
