浙教版数学九年级下册全册优质课件
合集下载
浙教版九年级下册数学《相交两圆的性质定理》PPT课件
RT
r
O1
O2
r
R
T O2 O1
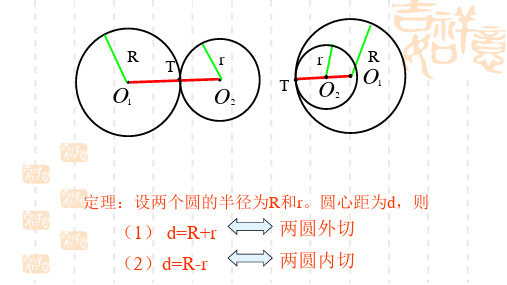
定理:设两个圆的半径为R和r。圆心距为d,则
(1) d=R+r
两圆外切
(2)d=R-r
两圆内切
T. . . 01 02
. T. .
01
02
A
A
定理:相切两圆的连心线必经过切点。
定理:如果两圆相切,那么其中任一个圆的过 两圆切点的切线,也必是另一个圆的切线。
两圆相切添两圆的公共切线
圆和圆的 五种位置关系
Rr
O1
O2
外离
O1O2>R+r
Rr
O1
O2
外切
O1O2=R+r
Rr O1 O2
相交
R-r<O1O2<R+r
R
O1
r
O2
内切
O1O2=R-r
R
O1
r
O2
内含
0≤O1O2<R-r
R r
O1O2
同心圆 (一种特殊的内含)
O1O2=0
相交两圆的性质定理
相交两圆的连心线垂直平分公共弦
已知:⊙01、⊙02 的半径分别为 r 和 R,( R>r ) 0102 >R+r,
两圆的内公线长 d 2 (R r)2
A
O1
O2
B E
公切线与连心线的夹角为∠ 0201E,再 用三角函数计算
BM C
O1 .
A . O2
如图 ,⊙O1与⊙O2 外切于A ,它们的半
径分别为
R 和r ,直线BC是⊙O1与⊙O2
A
O
O
2
1
r
O1
O2
r
R
T O2 O1
定理:设两个圆的半径为R和r。圆心距为d,则
(1) d=R+r
两圆外切
(2)d=R-r
两圆内切
T. . . 01 02
. T. .
01
02
A
A
定理:相切两圆的连心线必经过切点。
定理:如果两圆相切,那么其中任一个圆的过 两圆切点的切线,也必是另一个圆的切线。
两圆相切添两圆的公共切线
圆和圆的 五种位置关系
Rr
O1
O2
外离
O1O2>R+r
Rr
O1
O2
外切
O1O2=R+r
Rr O1 O2
相交
R-r<O1O2<R+r
R
O1
r
O2
内切
O1O2=R-r
R
O1
r
O2
内含
0≤O1O2<R-r
R r
O1O2
同心圆 (一种特殊的内含)
O1O2=0
相交两圆的性质定理
相交两圆的连心线垂直平分公共弦
已知:⊙01、⊙02 的半径分别为 r 和 R,( R>r ) 0102 >R+r,
两圆的内公线长 d 2 (R r)2
A
O1
O2
B E
公切线与连心线的夹角为∠ 0201E,再 用三角函数计算
BM C
O1 .
A . O2
如图 ,⊙O1与⊙O2 外切于A ,它们的半
径分别为
R 和r ,直线BC是⊙O1与⊙O2
A
O
O
2
1
浙教版数学九年级下册全册优质课件【完整版】

若AC=5呢?
A
C
取宝物比赛
10m
10m
(1)
1m
5m
(2)
B
∠A的对边
sinA
斜边
斜边
∠A的对边 cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
下课了!
锐角三角函数
B
∠A的对边
sinA
斜边
斜边
∠A的对边 cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
cos 60 a 1
2a 2
60°
tan 60 3a 3 a
设两条直角边长为a,则斜边长= a2 a2 2a
sin 45 a 2 2a 2
cos 45 a 2
45°
2a 2
tan 45 a 1 a
仔细观察,说说你发现 30°、45°、60°角的正弦值、余这弦值张和表正有切哪值些如下规表律:?
你想知道小明怎样 算出的吗?
?
1.65米
30°
10米
例3 (1)如图,在Rt△ABC中, ∠C=90°,AB= 6 ,BC= 3 。求∠A的度 数。
(2)如图,已3知圆锥的高AO等于圆锥的底面半
新浙教版九年级数学下册第一章《解直角三角形》优质公开课课件.ppt

1.3.1解直角三角形
第1课时 解直角三角形
1.(4分)△ABC中,a,b,c分别是∠A,∠B,∠C的对边,如
果a2+b2=c2,那么下列结论正确的是 (A )
A.c sinA=a B.b cosB=c C.a tanA=b D.c tanB=b
2.(4分)如图是教学用的直角三角形,边AC=30 cm,∠C=90°,
10 ,则
6.(4分)在△ABC中,∠C=90°,a=35,c=35 2 ,则∠A=
_4_5__°,b=_3__5_.
7.(4分)如图所示,AB是伸缩式的遮阳棚,CD是窗户,要想在 夏至的正午时刻阳光刚好不能射入窗户,则AB的长度是__3__ 米.(假设夏至的正午时刻阳光与地平面的夹角为60°)
8.(12分)在Rt△ABC中,∠C=90°. (1)已知a=4,b=8,求c的长; (2)已知b=10,∠B=60°,求a,c的长; (3)已知c=20,∠A=60°,求a,b的长.
=4,∴AC
=BC·sinB=4×sin60°=2 3 ,∴△ABC的周长=AB+AC +BC=6+2 3
14.(10分)一副直角三角板如图放置,点C在FD的延长线上, AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC= 12 2,试求CD的长.
解:过点B作BM⊥FD于点M.在△ACB中,∠ACB=90°,∠A= 45°,AC=12 2,∴BC=AC=12 2.
tan∠BAC= 33,则边BC的长为 ( C)
A.30 3 cm C.10 3 cm
B.20 3 cm D.5 3 cm
,第2题图)
3.(4分)已知:在△ABC中,AB=AC,∠BAC=120°,AD为
BC边上的高,则下列结论中,正确的是 ( B )
第1课时 解直角三角形
1.(4分)△ABC中,a,b,c分别是∠A,∠B,∠C的对边,如
果a2+b2=c2,那么下列结论正确的是 (A )
A.c sinA=a B.b cosB=c C.a tanA=b D.c tanB=b
2.(4分)如图是教学用的直角三角形,边AC=30 cm,∠C=90°,
10 ,则
6.(4分)在△ABC中,∠C=90°,a=35,c=35 2 ,则∠A=
_4_5__°,b=_3__5_.
7.(4分)如图所示,AB是伸缩式的遮阳棚,CD是窗户,要想在 夏至的正午时刻阳光刚好不能射入窗户,则AB的长度是__3__ 米.(假设夏至的正午时刻阳光与地平面的夹角为60°)
8.(12分)在Rt△ABC中,∠C=90°. (1)已知a=4,b=8,求c的长; (2)已知b=10,∠B=60°,求a,c的长; (3)已知c=20,∠A=60°,求a,b的长.
=4,∴AC
=BC·sinB=4×sin60°=2 3 ,∴△ABC的周长=AB+AC +BC=6+2 3
14.(10分)一副直角三角板如图放置,点C在FD的延长线上, AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC= 12 2,试求CD的长.
解:过点B作BM⊥FD于点M.在△ACB中,∠ACB=90°,∠A= 45°,AC=12 2,∴BC=AC=12 2.
tan∠BAC= 33,则边BC的长为 ( C)
A.30 3 cm C.10 3 cm
B.20 3 cm D.5 3 cm
,第2题图)
3.(4分)已知:在△ABC中,AB=AC,∠BAC=120°,AD为
BC边上的高,则下列结论中,正确的是 ( B )
浙教版九年级数学下册课件 2.3 三角形的内切圆

2 如图,点O是△ABC的内心,若∠ACB=70°,则 ∠AOB=( ) A.140° B.135° C.125° D.110°
(来自《典中点》)
知2-练
3 下列说法错误的是( ) A.三角形有且只有一个内切圆 B.等腰三角形的内心一定在它的底边的高上 C.三角形的内心不一定都在三角形的内部 D.若I是△ABC的内心,则AI平分∠BAC
(来自《典中点》)
总结
知2-讲
因为三角形的内心是三角形三条角平分线的交 点,所以三角形的内心与任一顶点的连线平分三角 形的内角.
(来自《点拨》)
13 三角形内切圆的圆心是( ) A.三个内角平分线的交点 B.三边中垂线的交点 C.三条中线的交点 D.三条高线的交点
知2-练
(来自《典中点》)
知2-练
知1-讲
见切点,连半径,结合等腰三角形、等边三角形的 性质求出半径长.
(来自《点拨》)
知1-讲
例2 已知:如图, ⊙O是△ABC的内切圆,切点分别为D, E,F.设△ABC的周长为l,求证: AE+BC= 1 l. 2
证明:∵⊙O是△ABC的内切圆,E,F为切点,
∴AE=AF(根据什么?).
A
同理,BD=BF,CD=CE.
理解三角形内切圆的概念要注意以下三点: ①与各边相切; ②在三角形内部; ③圆心叫做三角形的内心.
知1-讲
例1 如图,等边三角形ABC的边长为3 cm,求△ABC
的内切圆⊙O的半径.
解:如图,设⊙O切AB于点D,连结OA,OB,OD.
∵ ⊙O是△ABC的内切圆,
∴AO,BO 是∠BAC, ∠ABC,
(来自《典中点》)
1. 三角形的内切圆中“切”是指三角形的三边与圆的 位置关系.
(来自《典中点》)
知2-练
3 下列说法错误的是( ) A.三角形有且只有一个内切圆 B.等腰三角形的内心一定在它的底边的高上 C.三角形的内心不一定都在三角形的内部 D.若I是△ABC的内心,则AI平分∠BAC
(来自《典中点》)
总结
知2-讲
因为三角形的内心是三角形三条角平分线的交 点,所以三角形的内心与任一顶点的连线平分三角 形的内角.
(来自《点拨》)
13 三角形内切圆的圆心是( ) A.三个内角平分线的交点 B.三边中垂线的交点 C.三条中线的交点 D.三条高线的交点
知2-练
(来自《典中点》)
知2-练
知1-讲
见切点,连半径,结合等腰三角形、等边三角形的 性质求出半径长.
(来自《点拨》)
知1-讲
例2 已知:如图, ⊙O是△ABC的内切圆,切点分别为D, E,F.设△ABC的周长为l,求证: AE+BC= 1 l. 2
证明:∵⊙O是△ABC的内切圆,E,F为切点,
∴AE=AF(根据什么?).
A
同理,BD=BF,CD=CE.
理解三角形内切圆的概念要注意以下三点: ①与各边相切; ②在三角形内部; ③圆心叫做三角形的内心.
知1-讲
例1 如图,等边三角形ABC的边长为3 cm,求△ABC
的内切圆⊙O的半径.
解:如图,设⊙O切AB于点D,连结OA,OB,OD.
∵ ⊙O是△ABC的内切圆,
∴AO,BO 是∠BAC, ∠ABC,
(来自《典中点》)
1. 三角形的内切圆中“切”是指三角形的三边与圆的 位置关系.
新浙教版九年级数学下册第一章《锐角三角函数(1)》精品课件1.ppt
• 10、人的志向通常和他们的能力成正比例。2021/1/142021/1/142021/1/141/14/2021 6:41:13 PM • 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2021/1/142021/1/142021/1/14Jan-2114-Jan-21 • 12、越是无能的人,越喜欢挑剔别人的错儿。2021/1/142021/1/142021/1/14Thursday, January 14, 2021 • 13、志不立,天下无可成之事。2021/1/142021/1/142021/1/142021/1/141/14/2021
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
边之比 定义 表示 公式
B
∠A的对边a 正弦函数
斜边c
∠A的
对边 ∠A的邻边b
a
斜边c
余弦函数
sinA cosA
sssiiinnn
AAA
===
aaa ccc
cccooosss
AAA
===
bbb ccc
A
∠ A的邻边b
C
∠A的对边a ∠A的邻边b
正切函数
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
边之比 定义 表示 公式
B
∠A的对边a 正弦函数
斜边c
∠A的
对边 ∠A的邻边b
a
斜边c
余弦函数
sinA cosA
sssiiinnn
AAA
===
aaa ccc
cccooosss
AAA
===
bbb ccc
A
∠ A的邻边b
C
∠A的对边a ∠A的邻边b
正切函数
浙教版数学九年级(下)PPT资料优秀版

观察上表,你获得什么启示? 实验次数越多,频率越接近概率
120° 17202°° 120°
P=1/10000000
如我果们某 知让运道动,如任员意图投抛一一的次枚篮转均投匀盘中的的硬自概币率由,”正为面转0.朝动上”一的概次率,是停0.止转动后,指针落在红
观(1)察该上运色表动,区员你投获域5得次什的篮么,必概启有示率4?次是投中1. /3,以下是实验的方法:
80
25
160
58
240
78
320
110
400
130
频率
(4)根据上面的表格,在下图中画出频率分布折线图
0 80 160 240 320 400
(5)议一议:频率与概率有什么区别和联系?随着重复实验 次数的不断增加,频率的变化趋势如何?
通过大量重复的实验,用一个事件发生的频率来估 计这一事件发生的概率
计如约果需 某麦运色种动多员的少投一k小g次? 篮奶投中牛的概,据率为统0. 计,平均出生1千万头牛才会有1头是白色的, 如果某运由动员此投一估次篮计投中出的概生率为一0. 头奶牛为白色的概率为多少?
P=1/10000000
例1.在同样条件下对某种小麦种子进行发芽实验,统计发芽 种子数,获得如下频数分布表:
(3)若要销售这批西装2000件,为了方便购买次品西装的顾客前
来调换,至少应该进多少件西装?
概率是理论性的东西,频率是实践性的 东西,理论应该联系实际,因此我们可 以通过大量重复的实验,用一个事件发 生的频率来估计这一事件发生的概率
概率是理论性的东西,频率是实践性的 东西,理论应该联系实际,因此我们可 以通过大量重复的实验,用一个事件发 生的频率来估计这一事件发生的概率
浙教版九年级数学(全一册)课件第2章 直线与圆的位置关系 切线的性质与判定

★应用格式 OA为⊙O的半径 BC ⊥ OA于A
BC为⊙O的切线
新课讲解
B
O
A
C
新课讲解 判一判: 下列各直线是不是圆的切线?如果不是,请说明为什么?
O.
A l
(1)
(1)不是,因为没
有垂直.
O.
O
A
l
B
(2)
A
l
(3)
(2),(3)不是,因为没有经过半径的
外端点A.
注意:在此定理中,“经过半径的外端”和“垂直于 这条半径”,两个条件缺一不可,否则就不是圆的切线.
分析:根据切线的判定定理,要 证明AC是⊙O的切线,只要证明
A
E
F
由点O向AC所作的垂线段OF是
⊙O的半径就可以了,而OE是 B
O
C
⊙O的半径,因此只需要证明
OF=OE.
新课讲解
证明:连结OE ,OA, 过O 作OF ⊥AC.
∵⊙O 与AB 相切于E , ∴OE ⊥ AB.
又∵△ABC 中,AB =AC ,
的直径为6. 求证:直线AB是⊙O的切线.
作垂直 O
AC B
AC B
对比思考
新课讲解
2 切线的性质定理
思考:如图,如果直线l是⊙O 的切线,点A为切点,那么OA 与l垂直吗?
★切线性质 圆的切线垂直于经过切点的半径.
★应用格式 ∵直线l是⊙O 的切线,A是切点, ∴直线l ⊥OA.
O
A
l
新课讲解
性 质 有1个公共点
有切线时常用辅助线 添加方法: 见切线,连切点,得垂直.
d=r
情景引入
砂轮上打磨工件时飞出的火星
1 切线的判定定理
浙教版初中数学九年级下册(1.1 锐角三角函数2)课件(共25张PPT)
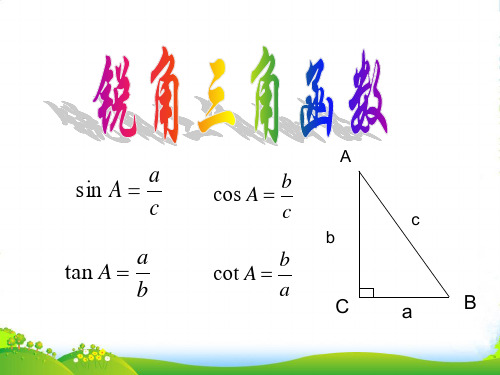
B
A
∠ A的邻边b
∠A的对边a 正弦函数
斜边c
∠A的
对边 a
∠A的邻边b 斜边c
余弦函数
C
∠A的对边a ∠A的邻边b
正切函数
sinA cosA tanA
ssssiiiinnnn ccccoooossss ttttaaaannnn
AAAA AAAA AAAA
==== ==== ====
aaaaccccbbbaaaabbbbcccc
BC
比值 A B 是一个确定的值.
与点B在角的边上的位置无关.
Do you know
三角函数的由来
“三角学”一词,是由希腊文三角形与测量二字构成 的,原意是三角形的测量,也就是解三角形.后来范围 逐渐扩大,成为研究三角函数及其应用的一个数学分支.
三角测量在我国出现的很早.据记载,早在公元前 两千年,大禹就利用三角形的边角关系,来进行对山川 地势的测量.
sin A a c
tan A a b
A
cos A b c
b
cot A b a
C
c
a
B
从最简单的做起---波利亚
探索园地
•
【量一量】你的那块不 等腰的三角尺中,
30°角所对的直角边
与斜边的长分别是多少?
它们的比等于多少?
如果改成是测量 这块等腰的三角 尺呢?还有刚才
的结论吗?
• 【想一想】老师上课时 用的那块不等腰的三角
∠A的邻边b ∠A的对边a 余切函数
cotA
ccccooootttt AAAA ==== bbbbaaaa
这四个函数统称为锐角A的三角函数.
例:求出如图所示的Rt△ABC 中你会求∠A的四个三角函数值 A 吗?∠B的呢?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾斜 角,铅直高度与梯子的比,水平 宽度与梯子的比,铅直高度与水 平宽度的比,都发生了什么变化?
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
越大 梯子越陡——倾斜角_____ 越大 倾斜角越大——铅直高度与梯子的比_____ 越小 倾斜角越大——水平宽度与梯子的比_____
倾斜角越大——铅直高度与水平宽度
A
C
取宝物比赛
10m
10m
(1)
1m
5m
(2)
B
∠A的对边
sinA 斜边
斜边 ∠A的对边
cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
下课了!
锐角三角函数
B
∠A的对边
sinA 斜边
斜边 ∠A的对边
cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
活 动 1
B
AC 1 BC 和 AB1 , AC
B1C 1 和 有什么关系? AC 1
A C C1
(3)如果改变B在梯子上的位置 呢?
想一想
B
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系? (2)
BC AB B1C 1 AC 和 AB1 , AB
AC 1 和 AB1 ,
BC AC
B1C 1 和 AC 1 有什么关系?
浙教版九年级下册
数 学
全册优质课件
取宝物比赛10m来自10m(1)1m
5m
(2)
梯子在上升变陡的过程中,倾斜 角,铅直高度与梯子的比,水平宽 度与梯子的比,铅直高度与水平宽 度的比,都发生了什么变化?
铅 直 高 度
倾斜角
水平宽度
梯子在上升变陡的过程中,倾斜 角,铅直高度与梯子的比,水平宽 度与梯子的比,铅直高度与水平宽 度的比,都发生了什么变化?
A C C1
(3)如果改变B在梯子上的位置 呢?
B
∠A的对边
sinA 斜边
斜边 ∠A的对边
cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
牛 刀 小 试
B
例1 如图,在Rt△ABC中,∠C=90° AB=5,BC=3, 求∠A, ∠B的正弦, 余弦和正切. 观察以上计算结果,你发现了什么? 若AC=5,BC=3呢? 若AC=5呢?
cos 60
tan 60
a 1 2a 2
3a 3 a
60°
设两条直角边长为a,则斜边长= a2 a2 2a
a sin 45 2a a cos 45 2a
2 2 2 2
45°
a tan 45 1 a
仔细观察,说说你发现 这张表有哪些规律? 30°、45°、60°角的正弦值、余弦值和正切值如下表: 锐角a 30° 三角函数 sin a
两块三角尺中有几个不同的锐 角?分别求出这几个锐角的正 弦值、余弦值和正切值. 60° 30° 45° 45°
设30°所对的直角边长为a,那么斜边长为2a 另一条直角边长=
sin 30
a 1 2a 2
30°
cos30
tan 30
3a 3 2a 2
a 3 3 3a
3a 3 sin 60 2a 2
BC B1C 1 AC (2) AB 和 AB1 , AB
B
和
AC 1 AB1
,
BC AC
B1C 1 和 AC 1有什么关系?
A C C1
(3)如果改变B在梯子上的位置 呢?
想一想
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系? (2)
BC AB B1C 1 AC 和 AB1 , AB
你想知道小明怎样 算出的吗?
?
30°
1.65米
10米
例3 (1)如图,在Rt△ABC中, ∠C=90°,AB=6 ,BC=3 。求∠A的度 数。 (2)如图,已知圆锥的高 AO等于圆锥的底面半 3 径OB的 倍,求α. A
B
6 3
(2)
O
A
C
B
(1)
例4 如图,在Rt△ABC中,∠ACB=90度,CD⊥AB于D , 已知∠B=30度,计算 tan ACD sin BCD的值。
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系? (2)
BC AB B1C 1 和 AB1
,
AC AB
和
AC 1 BC AB1 , AC
B
B1C 1 和 AC 1有什么关系?
A C C1
(3)如果改变B在梯子上的位置 呢?
想一想
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系?
越大 的比_____
铅 直 高 度 水平宽度
想一想
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系?
BC B1C 1 AB和 AB1
(2)
B
,
B1C 1 和 有什么关系? AC 1
AC AC 1 BC 和 , AB AB1 AC
A C C1
(3)如果改变B在梯子上的位置 呢?
想一想
A
D
B
C
例5
3 , AC 2 3, 如图,在△ABC中,∠A=30度, tanB 2
C
AC 2 3
求AB。 解:过点C作CD⊥AB于点D ∠A=30度,
1 CD 1 CD 2 3 3 sin A 2 AC 2
A
3 AD 3 AD 2 3 3 cos A 2 AC 2 CD 3 BD 3 2 2 tan B 3 BD 2
3 1 2 2
2
2
cos45 tan 45 ( 2) sin 45
2 2 1 2 2
=0
=1
例2 操场里有一个旗杆,老师让小明去测量旗杆
高度,小明站在离旗杆底部10米远处,目测旗杆的顶 部,视线与水平线的夹角为30度,并已知目高为1.65 米.然后他很快就算出旗杆的高度了。
1 2
45°
2 2
60°
3 2
cos a
tan a
3 2
3 3
2 2
1 2
1
3
例1 求下列各式的值:
(1)cos260°+sin260°
(3)tan450.sin450-4sin300.cos450+cos2300
cos45 tan 45 ( 2) sin 45
解: (1) cos260°+sin260°
水平宽度
梯子在上升变陡的过程中,倾斜 角,铅直高度与梯子的比,水平 宽度与梯子的比,铅直高度与水 平宽度的比,都发生了什么变化?
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
越大 梯子越陡——倾斜角_____ 越大 倾斜角越大——铅直高度与梯子的比_____ 越小 倾斜角越大——水平宽度与梯子的比_____
倾斜角越大——铅直高度与水平宽度
A
C
取宝物比赛
10m
10m
(1)
1m
5m
(2)
B
∠A的对边
sinA 斜边
斜边 ∠A的对边
cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
下课了!
锐角三角函数
B
∠A的对边
sinA 斜边
斜边 ∠A的对边
cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
活 动 1
B
AC 1 BC 和 AB1 , AC
B1C 1 和 有什么关系? AC 1
A C C1
(3)如果改变B在梯子上的位置 呢?
想一想
B
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系? (2)
BC AB B1C 1 AC 和 AB1 , AB
AC 1 和 AB1 ,
BC AC
B1C 1 和 AC 1 有什么关系?
浙教版九年级下册
数 学
全册优质课件
取宝物比赛10m来自10m(1)1m
5m
(2)
梯子在上升变陡的过程中,倾斜 角,铅直高度与梯子的比,水平宽 度与梯子的比,铅直高度与水平宽 度的比,都发生了什么变化?
铅 直 高 度
倾斜角
水平宽度
梯子在上升变陡的过程中,倾斜 角,铅直高度与梯子的比,水平宽 度与梯子的比,铅直高度与水平宽 度的比,都发生了什么变化?
A C C1
(3)如果改变B在梯子上的位置 呢?
B
∠A的对边
sinA 斜边
斜边 ∠A的对边
cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
牛 刀 小 试
B
例1 如图,在Rt△ABC中,∠C=90° AB=5,BC=3, 求∠A, ∠B的正弦, 余弦和正切. 观察以上计算结果,你发现了什么? 若AC=5,BC=3呢? 若AC=5呢?
cos 60
tan 60
a 1 2a 2
3a 3 a
60°
设两条直角边长为a,则斜边长= a2 a2 2a
a sin 45 2a a cos 45 2a
2 2 2 2
45°
a tan 45 1 a
仔细观察,说说你发现 这张表有哪些规律? 30°、45°、60°角的正弦值、余弦值和正切值如下表: 锐角a 30° 三角函数 sin a
两块三角尺中有几个不同的锐 角?分别求出这几个锐角的正 弦值、余弦值和正切值. 60° 30° 45° 45°
设30°所对的直角边长为a,那么斜边长为2a 另一条直角边长=
sin 30
a 1 2a 2
30°
cos30
tan 30
3a 3 2a 2
a 3 3 3a
3a 3 sin 60 2a 2
BC B1C 1 AC (2) AB 和 AB1 , AB
B
和
AC 1 AB1
,
BC AC
B1C 1 和 AC 1有什么关系?
A C C1
(3)如果改变B在梯子上的位置 呢?
想一想
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系? (2)
BC AB B1C 1 AC 和 AB1 , AB
你想知道小明怎样 算出的吗?
?
30°
1.65米
10米
例3 (1)如图,在Rt△ABC中, ∠C=90°,AB=6 ,BC=3 。求∠A的度 数。 (2)如图,已知圆锥的高 AO等于圆锥的底面半 3 径OB的 倍,求α. A
B
6 3
(2)
O
A
C
B
(1)
例4 如图,在Rt△ABC中,∠ACB=90度,CD⊥AB于D , 已知∠B=30度,计算 tan ACD sin BCD的值。
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系? (2)
BC AB B1C 1 和 AB1
,
AC AB
和
AC 1 BC AB1 , AC
B
B1C 1 和 AC 1有什么关系?
A C C1
(3)如果改变B在梯子上的位置 呢?
想一想
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系?
越大 的比_____
铅 直 高 度 水平宽度
想一想
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系?
BC B1C 1 AB和 AB1
(2)
B
,
B1C 1 和 有什么关系? AC 1
AC AC 1 BC 和 , AB AB1 AC
A C C1
(3)如果改变B在梯子上的位置 呢?
想一想
A
D
B
C
例5
3 , AC 2 3, 如图,在△ABC中,∠A=30度, tanB 2
C
AC 2 3
求AB。 解:过点C作CD⊥AB于点D ∠A=30度,
1 CD 1 CD 2 3 3 sin A 2 AC 2
A
3 AD 3 AD 2 3 3 cos A 2 AC 2 CD 3 BD 3 2 2 tan B 3 BD 2
3 1 2 2
2
2
cos45 tan 45 ( 2) sin 45
2 2 1 2 2
=0
=1
例2 操场里有一个旗杆,老师让小明去测量旗杆
高度,小明站在离旗杆底部10米远处,目测旗杆的顶 部,视线与水平线的夹角为30度,并已知目高为1.65 米.然后他很快就算出旗杆的高度了。
1 2
45°
2 2
60°
3 2
cos a
tan a
3 2
3 3
2 2
1 2
1
3
例1 求下列各式的值:
(1)cos260°+sin260°
(3)tan450.sin450-4sin300.cos450+cos2300
cos45 tan 45 ( 2) sin 45
解: (1) cos260°+sin260°
