因动点产生的面积问题
专题04 因动点产生的面积问题(原卷版)

(2)如图(3),在Rt△CDE的运动过程中,当CE经过点B时,求BC的长.
(3)在Rt△CDE的运动过程中,设AC=h,△OAB与△CDE的重叠部分的面积为S,请写出S与h之间的函数关系式,并求出面积S的最大值.
13.如图,在平面直角坐标系 中,已知抛物线 与直线 都经过 、 两点,该抛物线的顶点为C.
(1)求此抛物线和直线 的解析式;
(2)设直线 与该抛物线的对称轴交于点E,在射线 上是否存在一点M,过M作x轴的垂线交抛物线于点N,使点M、N、C、E是平行四边形的四个顶点?若存在,求点M的坐标;若不存在,请说明理由;
(3)M是直线OC上方抛物线C2上的一个动点,连接MO,MC,M运动到什么位置时,△MOC面积最大?并求出最大面积.
15.如图,抛物线 交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且 ,求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
A. B. C. D.
5.如图,点A是直线y=﹣x上的动点,点B是x轴上的动点,若AB=2,则△AOB面积的最大值为( )
A.2B. +1C. -1D.2
6.如图,已知 ,以 为圆心, 长为半径作 , 是 上一个动点,直线 交 轴于 点,则 面积的最大值是( )
A. B. C. D.
7.如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=﹣x2+6x上一点,且在x轴上方,则△BCD面积的最大值为__________
中考数学压轴题:由动点引出的几种面积问题

中考数学压轴题:由动点引出的几种面积问题动点题是近年来中考的一个热点问题也是难点问题,而因动点产生的面积问题是这类题目考查的重点。
解这类题目要掌握几个基本图形及思路,而后“以静制动”、“转化求解”。
即把动态问题变为静态问题,变为我们所熟知的模型来解。
基本方法:铅锤法!即利用“铅垂高、水平宽”求三角形面积.类型一、一次函数由动点问题引出的面积问题【分析】(1)Rt△AOH中利用勾股定理即可求得菱形的边长;(2)根据(1)即可求得OC的长,则C的坐标即可求得,利用待定系数法即可求得直线AC的解析式;(3)根据S△ABC=S△AMB+SBMC求得M到直线BC的距离为h,然后分成P在AM上和在MC上两种情况讨论,利用三角形的面积公式求解.【点评】本题考查了待定系数法求一次函数的解析式以及菱形的性质,根据三角形的面积关系求得M到直线BC的距离h是关键.类型二、二次函数由动点问题引出的面积问题【分析】(2)过点P作PE∥y轴交x轴于点E,交直线AC于点F,过点C作CQ∥y轴交x轴于点Q,设点P的坐标为(x,﹣x^2﹣2x+3)(﹣2<x<1),则点E的坐标为(x,0),点F的坐标为(x,﹣x+1),进而可得出PF的值,由点C的坐标可得出点Q 的坐标,进而可得出AQ的值,利用三角形的面积公式可得出S△APC=﹣1.5x^2﹣1.5x+3,再利用二次函数的性质,即可解决最值问题;【点评】本题考查了待定系数法求一次函数解析式、待定系数法求二次函数解析式、二次函数图像上点的坐标特征、一次函数图像上点的坐标特征、二次函数的性质、三角形的面积以及周长,解题的关键是:(1)根据点的坐标,利用待定系数法求出抛物线及直线AC的函数关系式;(2)利用三角形的面积公式找出S△APC=﹣1.5x^2﹣1.5x+3;(3)利用二次函数图像的对称性结合两点之间线段最短找出点M的位置.类型三、利用相似三角形求解由动点问题引出的面积问题【分析】(1)利用待定系数法即可;(2)①分别用t表示PE、PQ、EQ,用△PQE∽△QNC表示NC及QN,列出矩形PQNM面积与t的函数关系式问题可解;②由①利用线段中点坐标分别等于两个端点横纵坐标平均分的数量关系,表示点M坐标,分别讨论M、N、Q在抛物线上时的情况,并分别求出t值.【点评】本题是代数几何综合题,考查了二次函数、一次函数、三角形相似和矩形的有关性质,解答时应注意数形结合和分类讨论的数学思想.类型四、利用转化思想解决由动点问题引出的面积问题【分析】(1)根据待定系数法,可得函数解析式,根据自变量与函数值的对应关系,可得答案;(2)根据勾股定理,可得BC的长,根据等角的正切值相等,可得HO的长,根据待定系数法,可得BE的解析式,根据解方程组,可得E点坐标;(3)由题意△PMN是等腰直角三角形,得PM=PN=1,设M(a,a^2+3a﹣4)则N(a+1,a^2+3a+1)或(a+1,a^2+3a﹣5),代入抛物线的解析式即可求解.【点评】本题考查二次函数的有关知识、一次函数、直角三角形等知识,掌握两个函数的交点问题转化为方程组的解的问题是解题的关键,还要记住一个结论斜边为定值时直角边相等时面积最大.。
因动点产生的面积问题

例21:2011年四川省南充市中考第22题抛物线y=ax2+bx+c与x轴的交点为A(m﹣4,0)和B(m,0),与直线y=﹣x+p相交于点A和点C(2m﹣4,m﹣6).(1)求抛物线的解析式;(2)若点P在抛物线上,且以点P和A,C以及另一点Q为顶点的平行四边形ACQP面积为12,求点P,Q 的坐标;(3)在(2)条件下,若点M是x轴下方抛物线上的动点,当△PQM的面积最大时,请求出△PQM的最大面积及点M的坐标.解答:解:(1)∵点A(m﹣4,0)和C(2m﹣4,m﹣6)在直线y=﹣x+p上∴,解得:,∴A(﹣1,0),B(3,0),C(2,﹣3),设抛物线y=ax2+bx+c=a(x﹣3)(x+1),∵C(2,﹣3),代入得:﹣3=a(2﹣3)(2+1),∴a=1∴抛物线解析式为:y=x2﹣2x﹣3,答:抛物线解析式为y=x2﹣2x﹣3.(2)解:AC=3,AC所在直线的解析式为:y=﹣x﹣1,∠BAC=45°,∵平行四边形ACQP的面积为12,∴平行四边形ACQP中AC边上的高为=2,过点D作DK⊥AC与PQ所在直线相交于点K,DK=2,∴DN=4,∵ACPQ,PQ所在直线在直线ACD的两侧,可能各有一条,∴PQ的解析式或为y=﹣x+3或y=﹣x﹣5,∴,解得:或,,方程无解,即P1(3,0),P2(﹣2,5),∵ACPQ是平行四边形,A(﹣1,0),C(2,﹣3),∴当P(3,0)时,Q(6,﹣3),当P(﹣2,5)时,Q(1,2),∴满足条件的P,Q点是P1(3,0),Q1(6,﹣3)或P2(﹣2,5),Q2(1,2)答:点P,Q的坐标是P1(3,0),Q1(6,﹣3)或P2(﹣2,5),Q2(1,2).(3)解:设M(t,t2﹣2t﹣3),(﹣1<t<3),过点M作y轴的平行线,交PQ所在直线雨点T,则T(t,﹣t+3),MT=(﹣t+3)﹣(t2﹣2t﹣3)=﹣t2+t+6,过点M作MS⊥PQ所在直线于点S,MS=MT=(﹣t2+t+6)=﹣(t﹣)2+,∴当t=时,M(,﹣),△PQM中PQ边上高的最大值为,答:△PQM 的最大面积是,,点M 的坐标是(,﹣).点评:本题主要考查对用待定系数法求二次函数的解析式,二次函数的最值,平行四边形的性质,解二元一次方程组等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键,此题是一个综合性比较强的题目,有一定的难度.例22:2010年广东省湛江市中考第28题如图,在平面直角坐标系中,点B 的坐标为(-3,-4),线段OB 绕原点逆时针旋转后与x 轴的正半轴重合,点B 的对应点为点A .(1)直接写出点A 的坐标,并求出经过A 、O 、B 三点的抛物线的解析式;(2)在抛物线的对称轴上是否存在点C ,使BC +OC 的值最小?若存在,求出点C 的坐标;若不存在,请说明理由;(3)点P 是抛物线上的一个动点,且在x 轴的上方,当点P 运动到什么位置时,△PAB 的面积最大?求出此时点P 的坐标和△PAB 的最大面积.解:(1)A(5,0) ………1分由抛物线经过点O ,可设抛物线的解析式为bx ax y +=2…2分⎩⎨⎧=-=+4390525b a b a 解得⎪⎪⎩⎪⎪⎨⎧=-=6561b a …………………………4分 ∴抛物线的解析式为x x y 65612+-=…………………………5分 (2)如图,由(1)得抛物线的对称轴是直线25=x ,点O 、A 关于直线25=x 对称,连接AB 交直线25=x 于点C ,则点C 使BC+OC 的值最小………………………6分设直线AB 的解析式为b kx y +=,得⎩⎨⎧-=+-=+4305b k b k ,解得⎪⎪⎩⎪⎪⎨⎧-==2521b k∴直线的解析式为2521-=x y ………………………8分把25=x 代入2521-=x y ,得45-=y ,∴点C 的坐标为)45,25(-………………9分(3)如图,过点P 作y 轴的平行线交AB 于点D ,设点P 的横坐标为x ,得)6561,(2x x x P +-, )2521,(-x x D ………………10分∴PAD PBD PAB S S S ∆∆∆+==)(21B A x x PD -∙=))((21B A D p x x y y --=[])3(5)2521()6561(212--⨯⎥⎦⎤⎢⎣⎡--+-x x x =1034322++-x x =332)1(322+--x ∴当1=x 时,PAB S ∆的最大值为332………………12分 把1=x 代入x x y 65612+-=,得32=y ,∴此时点P 的坐标为)32,1(………………13分例23:2012年广东省广州市中考数学模拟第25题平面直角坐标系中,平行四边形ABOC 如图放置,点A 、C 的坐标分别为(0,3)、(1-,0),将此平行四边形绕点0顺时针旋转90°,得到平行四边形'''A B OC 。
因动点产生的面积问题

80因动点产生的面积问题★林广姗所谓的因动点产生的面积问题就是解决一个会移动的点在坐标系中的位置转变所形成的几何面积问题。
在往年真题中我们可以看到中考命题组特别喜爱动点面积相结合的问题,因动点产生的面积问题大多以函数为背景,充分结合函数、方程、转化及数形结合等思想进行展开,而学生对知识点多且题型复杂的动点问题也是又爱又恨。
在数学教学中,教师可以从哪些方向带着学生不慌不忙延伸拆解每一道题,让学生动脑生趣,不再害怕此类问题。
引言:在中考中,数学要如何和他人拉开距离,保持领先?那么我们就要教会学生破解压轴题,而作我们首要突破的热点压轴题则是动点问题,其中因动点产生的面积问题则是学生们最怕见到的压轴题类型。
如何让学生对动点产生兴趣?高效利用每一道真题,延伸派生,让学生一题多思。
接下来笔者将会对两道中考真题进行思路点拨和延伸,旨在与大家交流研讨。
一、思路建立阶段面积是平面图形中的一个重要的概念,关联着平面图形中的要素边与角,因点的运动而产生的面积问题,是一次函数图象与二次函数图象相结合的形式,经常出现的面积问题有规则图形(如直角三角形、平行四边形、特殊平行四边形的面积)以及不规则图形的面积计算,求解不规则几何图形的面积是中考压轴常考的题型,此类题目运算量较大,要根据不同题目的动点问题思考解的可变性和多可能性。
求解动点相关面积问题经常用到下列与面积有关的方法:平面几何的割与补、等积变形、等比转化等数学思想方法。
解决与面积相关的动点存在性题目,出现频率较高的题型和使用较多的解题策略有两种:一是据图形确定存在性,再列出方程,求解并检验方程的根.二是先认为关系存在,然后列出方程,再据方程的反推假设是否成立.而教师对真题进行延展派生时,可通过以下几个方面进行延展: (1)在原图中加一或多条辅助线,构成新图形,再求解新平面几何图形的面积;(2)改变面积比例求对应点坐标;(3)改变动点活动范围,例如当动点跑出函数外时;(4)求构成特殊图形时特殊点的坐标,例如直角三角形、等腰三角形、等边三角形、平行四边形、特殊的平行四边形等。
因动点产生的面积问题

因动点产生的面积问题例1:如图所示,将两张长为8,宽为2的矩形纸片交叉,使重叠部分呈一个菱形,求菱形面积的最大值。
例2:在平面直角坐标系中,O为坐标原点,△AOB为正三角形,A在第一象限上,点B的坐标为(2,0),点P是线段OB的三等分点.(1)求经过A、O两点的直线AO的解析式;(2)过点P作PC⊥AB,PD⊥AO,垂足分别为C、D,求PC+PD的值;(3)在(2)的条件下,点E在x轴的负半轴上,作直线CE交AO于点F,且△ACF和△EOF的面积相等,求直线CE的解析式.一、面积比定值问题已知:抛物线y=ax 2+bx+c 经过点O (0,0),A (7,4),且对称轴l 与x 轴交于点B (5,0)。
(1)求抛物线的表达式。
(2)如图,点E 、F 分别是y 轴、对称轴l 上的点,且四边形EOBF 是矩形,点C (5,25)是BF 上一点,将△BOC 沿着直线OC 翻折,B 点与线段EF 上的D 点重合,求D 点的坐标。
(3)在(2)的条件下,点G 是对称轴l 上的点,直线DG 交CO 于点H ,S △DOH :S △DHC =1:4,求G 点坐标。
例.如图,在平面直角坐标系XOY 中,已知点A 的坐标为(a ,3)(其中a >4),射线OA 与反比例函数y=x 12的图象交于点P ,点B 、C 分别在函数y=x 12的图象上,且AB ∥x 轴,AC ∥y 轴;(1)当点P 横坐标为6,求直线AO 的表达式;(2)联结BO ,当AB=BO 时,求点A 坐标;(3)联结BP 、CP ,试猜想:ACP ABP △S △S 的值是否随a 的变化而变化?如果不变,求出ACPABP △S △S 的值;如果变化,请说明理由.例:如图,在平面直角坐标系中,已知点A (m ,0),点B (4,0)、C (4,m ),其中m <0,点D 是y 轴正半轴上的一点,且OD=AB ,分别连接AD 、AC 、DB 和DC .(1)请直接写出D 点的坐标(用含m 的整式表示);(2)判断△DAC 的形状并说明理由;(3)是否存在实数m 的值,使得m S S ABCDACB 36-=∆四边形?若存在,请求出m 的值不存在,请说明理由.二、等面积求定点坐标问题例2.如图,在平面直角坐标系XOY 中,直线1+=mx y 与反比例函数y =xk (k >0)相交于点A 、B ,点C 在x 轴正半轴上,点D (2,-3),连结OA 、OD 、DC 、AC ,四边形AODC 为菱形.(1)求k 和m 的值.(2)当x 取何值时,反比例函数值不小于一次函数值.(3)设点P 是y 轴上一动点,且△OAP 的面积等于菱形OACD 的面积,求点P 的坐标.例:如图,在平面直角坐标系中,已知四边形ABCD 为菱形,且A (0,3)、 B (-4,0).(1)求经过点C 的反比例函数的解析式;(2)设P 是(1)中所求函数图象上一点,以P 、O 、A 顶点的三角形的面积与△COD 的面积相等.求点P 的坐标.例:如图,在平面直角坐标系中,点A 是反比例函数y 1=xk (k ≠0)图象上一点,AB ⊥x 轴于B 点,一次函数y 2=ax+b (a ≠0)的图象交y 轴于D (0,-2),交x 轴于C 点,并与反比例函数的图象交于A ,E 两点,连接OA ,若△AOD 的面积为4,且C 为OB 的中点.若点Q 在反比例函数图象上,且QAB S ∆=BAC S ∆4,求点Q 的坐标.三、面积极值问题例3:如图,在平面直角坐标系中,二次函数c bx ax y ++=2的图象经过矩形OABC的顶点A ,B ,与x 轴交于点E ,F ,且B ,E 两点的坐标分别为B (2,23),E (-1,0).(1)求二次函数的解析式;(2)若直线BE 与抛物线的对称轴交点为P ,M 是线段CB 上的一个动点(点M 与点B ,C 不重合),过点M 作MN ∥BE 交x 轴于点N ,连接PM ,PN ,设CM 的长为t ,△PMN 的面积为S ,求S 与t 的函数关系式,并求出S 的最大值;例:如图,二次函数c bx ax y ++=2的图象与x 轴的交点为A 、D (A 在D 的右侧),与y 轴的交点为C ,且A (4,0).C (0,-3),对称轴是直线x=l .(1)求二次函数的解析式;(2)若M 是第四象限抛物线上一动点,且横坐标为m ,设四边形OCMA 的面积为s .请写出s 与m 之间的函数关系式,并求出当m 为何值时,四边形OCMA 的面积最大;例:已知:在矩形AOBC 中,OB=4,OA=3.分别以OB ,OA 所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是边BC 上的一个动点(不与B ,C 重合),过F 点的反比例函数y=xk (k >0)的图象与AC 边交于点E . (1)求证:△AOE 与△BOF 的面积相等;(2)记ECF OEF S S S ∆∆-=,求当k 为何值时,S 有最大值,最大值为多少?例:如图1,已知二次函数c bx ax y ++=2的图象经过A (-3,0),B (1,0),C (0,3)三点,其顶点为D ,对称轴是直线l ,l 与x 轴交于点H ,(1)求二次函数的表达式;(2)如图2,若E 是线段AD 上的一个动点(E 与A 、D 不重合),过E 点作平行于y 轴的直线交抛物线与点F ,交x 轴与点G ,设点E 的横坐标为m ,△ADF 的面积为S ,①求S 与m 的函数表达式;②S 是否存在最大值?若存在,求出最大值及此时点E 的坐标;若不存在,请说明理由.例:如图,已知O为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).(1)求点B的坐标;(2)若二次函数c+=2的图象经过A、B、O三点,求此二次函数的解析y+axbx式;(3)在(2)中的二次函数图象的OB段(不包括点O、B)上,是否存在一点C,使得四边形ABCO的面积最大?若存在,求出这个最大值及此时点C的坐标;若不存在,请说明理由.四、重叠面积问题例4.如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x 轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.线段AE上有一动点P(不与A 重合),从A点开始沿AE方向匀速运动,到达点E时停止.运动的速度为每秒2个单位长度,设运动的时间为t秒,过P点作AE的垂线交AD于点Q,以PQ 为边向上作正方形PQMN,正方形PQMN与矩形ABCO重叠部分(阴影部分)面积为S(平方单位).(1)求D、E两点的坐标.(2)当重叠部分为五边形时,求S与t之间的函数关系式并直接写出t的取值范围.(3)在(2)的条件下,当t为何值时,S有最大值?最大值是多少?例.在矩形OABC 中,OA=4,AB=2,以点O 为坐标原点,OA 所在的直线为x 轴,建立直角坐标系.将矩形OABC 绕点O 逆时针旋转至矩形ODEF .(1)如图1,当∠AOD=60°时,△OCF 的形状是(2)如图2,当点E 落在y 轴的正半轴上,试求CE 的长度和点D 的坐标;(3)如图3,在图2的基础上再沿y 轴的负半轴向下平移,平移速度是每秒1个单位长度.①求经过几秒,直线DE 经过点A ;②设两矩形重叠部分的面积为S ,运动时间为t ,写出重叠部分面积S 与时间t 之间的函数关系式.例.如图,在平面直角坐标系中,点A 、点C 同时从点O 出发,分别以每秒2个单位、1个单位的速度向x 轴、y 轴的正半轴方向运动,以OA 、OC 为边作矩形OABC .以M (4,0),N (9,0)为斜边端点作直角△PMN,点P 在第一象限,且tan∠PMN=21,当点A 出发时,△PMN 同时以每秒0.5个单位的速度沿x 轴向右平移.设点A 运动的时间为t 秒,矩形OABC 与△PMN 重叠部分的面积为S .(1)求运动前点P 的坐标;(2)求S 与t 的函数关系式,并写出自变量t 的取值范围;(3)若在运动过程中,要使对角线AC 上始终存在点Q ,满足∠OQM=90°,请直接写出符合条件的t 的值或t 的取值范围.五、动点经过面积问题例5.如图,已知直线y =−21x+1交坐标轴于A 、B 点,以线段AB 为边向上作正方形ABCD ,过点A 、D 、C 的抛物线与直线的另一个交点为E .(1)求点C 、D 的坐标(2)求抛物线的解析式(3)若抛物线与正方形沿射线AB 下滑,直至点C 落在x 轴上时停止,求抛物线上C 、E 两点间的抛物线所扫过的面积.六、面积转化等值问题例6.已知:二次函数c x ax y +-=22的图象与x 于A 、B ,(A 在点B 的左侧),与y 轴交于点C ,对称轴是直线x=1,平移一个单位后经过坐标原点O.(1)求这个二次函数的解析式;(2)直线y =−31x+1交y 轴于D 点,E 为抛物线顶点.若∠DBC=α,∠CBE=β,求βα-的值;(3)在(2)问的前提下,P 为抛物线对称轴上一点,且满足PA=PC ,在y 轴右侧的抛物线上是否存在点M ,使得△BDM 的面积等于PA 2?若存在,求出点M 的坐标;若不存在,请说明理由.七、划分面积求动点坐标问题例7.如图,二次函数c bx ax y ++=2的图象与x 轴、y 轴分别交于A (-1,0)、B (5,0)、C (0,4)三点,顶点为点D .(1)求二次函数的解析式,并求出顶点坐标;(2)x 轴上方的抛物线是否存在异于B 、C 的点P ,过点P 作x 轴的垂线,垂足为点M ,使直线BC 平分△PMB 的面积?如果存在,请求出点P 的坐标;如果不存在,请说明理由;(3)抛物线的对称轴上是否存在点Q ,使AQ 等于点B 到直线AQ 的距离?如果存在,请直接写出点Q 的坐标;如果不存在,请说明理由.例.如图,已知直线y=x 与二次函数bx x y +=2的图象交于点A 、O ,(O 是坐标原点),点B 为二次函数图象的顶点,OA=32.(1)求b 的值及过B 、A 两点的一次函数的解析式;(2)抛物线的对称轴与x 轴交于C ,点P 在线段OA 上,Q 在抛物线上,且PQ ∥x 轴,若以O 、C 、P 、Q 为顶点的四边形是平行四边形时,求点Q 的坐标;(3)若点P 在线段OA 上,Q 在抛物线上,且PQ ∥x 轴,PQ 将△AOB 的面积二等分时,求点P 的坐标.例.如图,已知二次函数c bx ax y ++=2(a ≠0)的图象与x 轴交于点A (1,0),与x 轴交于另一点C ,与y 轴交于点B (0,3),对称轴是直线x=-1,顶点是M .(1)直接写出二次函数的解析式:;(2)点P 是抛物线上的动点,点D 是对称轴上的动点,当以P 、D 、B 、C 为顶点的四边形是平行四边形时,请直接写出此时点D 的坐标:;(3)过原点的直线l 平分△MBC 的面积,求l 的解析式.八、求面积问题例8:如图,在平面直角坐标系中,点A ,C 分别在x 轴,y 轴上,四边形ABCO 为矩形,AB=16,点D 与点A 关于y 轴对称,tan ∠ACB=34,点E 、F 分别是线段AD 、AC 上的动点,(点E 不与点A ,D 重合),且∠CEF=∠ACB .(1)求AC 的长和点D 的坐标;(2)求证:EC EF =DCAE (3)当△EFC 为等腰三角形时,求△AEC 的面积.。
动点产生的面积问题

运动变化题是随着图形的某一元素的运动变化,导致问题的结论改变或者保持不变的几何题,它揭示了“运动”与“静止”、“一般”与“特殊”的内在联系.解题的关键是分清几何元素运动的方向和捷径,注意在运动过程中哪些是变量,哪些不是变量,通常要根据几何元素所处的不同位置加以分类讨论,同时,综合运用勾股定理、方程和函数等知识,本节课的内容涉及三角形、特殊的四边形的面积问题.本节主要是在函数背景下求三角形或四边形的面积问题,较复杂的题目可以采取“割补”的思想构造较简单的图形进行求解.动点产生的面积问题内容分析知识结构模块一:面积计算的问题知识精讲【例1】 如图,已知直线l :22y x =-+与x 轴、y 轴分别交于点B 、C ,将直线y=x向上平移1个单位长度得到直线P A ,点Q 是直线P A 与y 轴的交点,求四边形PQOB 的面积. 【难度】★★ 【答案】 【解析】【例2】 如图,已知直线AB :2y x =+与直线OA :13y x =交于点A ,与直线OB :3y x =交于点B 两点.求△AOB 的面积. 【难度】★★ 【答案】 【解析】例题解析【例3】 如图,已知直线3y x =+的图像与x 轴、y 轴分别交于A 、B 两点,直线l 经过原点,与线段AB 交于点C ,把△AOB 的面积分为2:1两部分,求直线l 的解析式. 【难度】★★ 【答案】 【解析】【例4】 如图,已知,在矩形ABCD 中,AB =10,BC =12,四边形EFGH 的三个顶点E 、F 、H 分别在矩形ABCD 边AB 、BC 、DA 上,AE =2.(1)如图1,当四边形EFGH 为正方形时,求△GFC 的面积;(2)如图2,当四边形EFGH 为菱形,且BF =a 时,求△GFC 的面积.(用含a 的代数式表示)【难度】★★★ 【答案】 【解析】A B CDE F 图1GHABCDE F 图2GH【例5】 如图1,正方形ABCD 的边长为2,点A (0, 1)和点D 在y 轴正半轴上,点B 、C 在第一象限,一次函数y =kx +2的图像l 交AD 、CD 分别于E 、F . (1)若△DEF 与△BCF 的面积比为1∶2,求k 的值; (2)联结BE ,当BE 平分∠FBA 时,求k 的值. 【难度】★★★ 【答案】 【解析】【例6】 如图,在平面直角坐标系中,函数y =2x +12的图像分别交x 轴、y 轴于A 、B 两点,过点A 的直线交y 轴正半轴于点M ,且点M 为线段OB 的中点. (1)求直线AM 的表达式;(2)试在直线AM 上找一点P ,使得S △ABP =S △AOB ,请求出点P 的坐标; (3)若点H 为坐标平面内任意一点,是否存在点H ,使以A 、B 、M 、H 为顶点的四边形是等腰梯形?若存在,请直接写出点H 的坐标;若不存在,请说明理由. 【难度】★★★ 【答案】 【解析】【例7】 如图1,已知直角坐标平面内点A (2, 0),P 是函数y =x (x >0)图像上一点,PQ ⊥AP 交y 轴正半轴于点Q . (1)试证明:AP =PQ ;(2)设点P 的横坐标为a ,点Q 的纵坐标为b ,那么b 关于a 的函数关系式是_______;(3)当S △AOQ =23S △APQ 时,求点P 的坐标.【难度】★★★ 【答案】 【解析】本节主要研究点在运动的背景下,产生的面积与动点之间的关系,关键点是找出决定这个面积变化的几个量是怎样变化的,重点在于思维能力的培养,难度较大.模块二:与面积相关的函数解析式知识精讲【例8】 如图,矩形ABCD 中,AB =1,AD =2,M 是CD 的中点,点P 在矩形的边上沿A B C M →→→运动,试写出△APM 的面积y 与点P 经过的路程x 之间的函数关系,写出定义域,并画出函数图像. 【难度】★★ 【答案】 【解析】【例9】 如图,在梯形ABCD 中,AD //BC ,AB =CD =AD =5cm ,BC =11cm ,点P 从点D 出发沿DA 边以每秒1cm 的速度移动,点Q 从点B 出发沿BC 边以每秒2cm 的速度移动(当点P 到达点A 时,点P 与点Q 同时停止移动),假设点P 移动的时间为x (秒),四边形ABQP 的面积为y (cm 2). (1)求y 关于x 的函数解析式,并写出它的定义域;(2)在移动的过程中,求四边形ABQP 的面积与四边形QCDP 的面积相等时x 的值;(3)在移动过程中,是否存在x 使得PQ =AB ,若存在,求出所有的x 的值;若不存在,请说明理由. 【难度】★★ 【答案】 【解析】例题解析BAB CDMP【例10】已知:如图1,在线段AE的同侧作正方形ABCD和正方形BEFG(BE<AB),连结EG并延长交DC于点M,作MN⊥AB,垂足为N,MN交BD于P.设正方形ABCD的边长为1.(1)证明:△CMG≌△NBP;(2)设BE=x,四边形MGBN的面积为y,求y关于x的函数解析式,并写出定义域;(3)如果按照题设方法作出的四边形BGMP是菱形,求BE的长.【难度】★★★【答案】【解析】【例11】已知:在梯形ABCD中,AD//BC,∠B=90°,AB=BC=4,点E在边AB 上,CE=CD.(1)如图1,当∠BCD为锐角时,设AD=x,△CDE的面积为y,求y与x之间的函数解析式,并写出函数的定义域;(2)当CD=5时,求△CDE的面积.【难度】★★★【答案】【解析】AB CDEA BCDEFGPMN【例12】 如图1,四边形OABC 是矩形,点A 、C 的坐标分别为(3,0),(0,1),点D是线段BC 上的动点(与端点B 、C 不重合),过点D 作直线12y x m =-+交折线OAB 于点E .(1)当点E 恰为AB 中点时,求m 的值;(2)当点E 在线段OA 上,记△ODE 的面积为y ,求y 与m 的函数关系式并写出定义域;(3)当点E 在线段OA 上时,若矩形OABC 关于直线DE 的对称图形为四边形O 1A 1B 1C 1,试判断四边形O 1A 1B 1C 1与矩形OABC 的重叠部分的面积是否发生变化,若不变,写出该重叠部分的面积;若改变,写出重叠部分面积S 关于m 的函数关系式. 【难度】★★★ 【答案】 【解析】【例13】 如图1,在正方形ABCD 中,点E 在边AB 上(点E 与点A 、B 不重合),过点E 作FG ⊥DE ,FG 与边BC 相交于点F ,与边DA 的延长线相交于点G . (1)当E 是AB 中点时,求证AG =BF ;(2)当E 在边AB 上移动时,观察BF 、AG 、AE 之间具有怎样的数量关系?并证明你所得到的结论;(3)联结DF ,如果正方形的边长为2,设AE =x ,△DFG 的面积为y ,求y 与x 之间的函数解析式,并写出函数的定义域.【难度】★★★ 【答案】 【解析】xA BCD EFG【例14】 如图1,梯形ABCD 中,AD //BC ,∠B =90°,AD =18,BC =21.点P 从点A 出发沿AD 以每秒1个单位的速度向点D 匀速运动,点Q 从点C 沿CB 以每秒2个单位的速度向点B 匀速运动.点P 、Q 同时出发,其中一个点到达终点时两点停止运动,设运动的时间为t 秒.(1)当AB =10时,设A 、B 、Q 、P 四点构成的图形的面积为S ,求S 关于t 的函数关系式,并写出定义域;(2)设E 、F 为AB 、CD 的中点,求四边形PEQF 是平行四边形时t 的值.【难度】★★★ 【答案】【解析】【例15】 如图1,在菱形ABCD 中,∠B =45°,AB =4.左右作平行移动的正方形EFGH 的两个顶点F 、G 始终在边BC 上.当点G 到边BC 中点时,点E 恰好在边AB 上.(1)如图1,求正方形EFGH 的边长;(2)设点B 与点F 的距离为x ,在正方形EFGH 作平行移动的过程中,正方形EFGH 与菱形ABCD 重叠部分的面积为y ,求y 与x 的函数解析式,并写出它的定义域;(3)联结FH 、HC ,当△FHC 是等腰三角形时,求BF 的长. 【难度】★★★ 【答案】 【解析】ABCDE PAQ 图1备用图HAB C DEF G【例16】 如图1,在平面直角坐标系中,O 为坐标原点,四边形OABC 是矩形.A (0,4),C (5, 0),点D 是y 轴正半轴上一点,将四边形OABC 沿着过点D 的直线翻折,使得点O 落在线段AB 上的点E 处.过点E 作y 轴的平行线与x 轴交于点N .折痕与直线EN 交于点M ,联结DE 、OM . 设OD =t ,MN =s . (1)试判断四边形EDOM 的形状,并证明;(2)当点D 在线段OA 上时,求s 关于t 的函数解析式,并写出函数的定义域; (3)用含t 的代数式表示四边形EDOM 与矩形OABC 重叠部分的面积.【难度】★★★ 【答案】 【解析】【例17】 已知:如图1,梯形ABCD 中,AD //BC ,∠A =90°,∠C =45°,AB =AD =4.E 是直线AD 上一点,联结BE ,过点E 作EF ⊥BE 交直线CD 于点F .联结BF .(1)若点E 是线段AD 上一点(与点A 、D 不重合),(如图1所示) ①求证:BE =EF ;②设DE =x ,△BEF 的面积为y ,求y 关于x 的函数解析式,并写出此函数的定义域;(2)直线AD 上是否存在一点E ,使△BEF 是△ABE 面积的3倍,若存在,直接写出DE 的长,若不存在,请说明理由.【难度】★★★ 【答案】 【解析】AB DEFABCD图1备用图备用图ABCD【例18】如图,已知正方形ABCD的边长为3,菱形EFGH的三个顶点E、G、H分别在正方形的边AB、CD、DA上,AH=1,联结CF.(1)当DG=1时,求证菱形EFGH为正方形;(2)设DG=x,△FCG的面积为y,写出y关于x的函数解析式,并指出x的取值范围;(3)当DGGHE的度数.【难度】★★★【答案】【解析】A BCDEFGH【例19】已知:如图,四边形OABC的四个顶点坐标分别为O(0,0),A(8,0),B(4,4),C(0,4),直线l:y=x+m保持与四边形OABC的边交于点M、N(M 在折线AOC上,N在折线ABC上).设四边形OABC在l右下方部分的面积为S1,在l左上方部分的面积为S2,记S=S1-S2(S≥0).(1)求∠OAB的大小;(2)当M、N重合时,求l的解析式;(3)当m≤0时,线段AB上是否存在点N,使得S=0?若存在,求m的值;若不存在,请说明理由;(4)求S与m的函数关系式.【难度】★★★【答案】【解析】x【例20】 在边长为4的正方形ABCD 中,点O 是对角线AC 的中点,P 是对角线AC上一动点,过点P 作PF ⊥CD 于点F ,作PE ⊥PB 交直线CD 于点E ,设P A =x ,PCE S y =△.(1)求证:DF =EF ;(2)当点P 在线段AO 上时,求y 关于x 的函数关系式及自变量x 的取值范围;(3)点P 在运动过程中能否使△PEC 为等腰三角形?如果能,请直接写出P A 的长;如果不能,请简单说明理由. 【难度】★★★ 【答案】 【解析】【习题1】 如图,直线443y x =-+与y 轴交于点A ,与直线4455y x =+交于点B ,且直线4455y x =+与x 轴交于点C ,求△ABC 【难度】★★ 【答案】 【解析】随堂检测ABCD E F P O【习题2】已知直线2y x=-+与x轴、y轴分别交于A点和B点,另一条直线(0)y kx b k=+≠经过点C(1,0),且把△AOB分成两部分.若△AOB被分成的两部分面积比为1:5,求k和b的值.【难度】★★★【答案】【解析】【习题3】直线364y x=-+与坐标轴分别交与点A、B两点,点P、Q同时从O点出发,同时到达A点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿O B A→→运动.(1)直接写出A、B两点的坐标;(2)设点Q的运动时间为t秒,△OPQ的面积为S,求出S与t之间的函数关系;(3)当485S=时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标.【难度】★★★【答案】【解析】【习题4】 如图,已知:过点A (8,0)、B (0,y =交于点C ,平行于y 轴的直线l 从原点O 出发,以每秒1个单位长度的速度沿x 轴向右平移,到C 点时停止;l 分别交线段BC 、OC 于点D 、E ,以DE 为边向左侧作等边△DEF ,设△DEF 与△BCO 重叠部分的面积为S (平方单位),直线l 的运动时间为t (秒).(1) 写出点C 的坐标和t 的取值范围; (2) 求s 与t 的函数关系式. 【难度】★★★ 【答案】 【解析】【作业1】 如图,已知直线P A :(0)y x n n =+>与直线PB :2()y x m m n =-+>交于点P .(1)用m 、n 表示出A 、B 、P 点的坐标;(2)若点Q 是直线P A 与y 轴的交点,且四边形PQOB 的面积56,AB=2,试求点P 的坐标,并写出直线P A 与PB 的解析式. 【难度】★★ 【答案】 【解析】课后作业【作业2】 如图所示,直线y kx b =+的截距为6,该直线分别交x 轴、y 轴于E 、F ,点E 的坐标为(-4,0). (1)求直线y kx b =+的表达式;(2)若点P (x ,y )是该直线第二象限上的一个动点,P A ⊥x 轴,PB ⊥y 轴,垂足分别为点A 、B ,试求四边形OAPB 的面积S 与x 的函数关系式,并写出自变量x 的取值范围. 【难度】★★★ 【答案】 【解析】【作业3】 如图,已知:直角梯形ABCD 中,AB ∥CD ,∠A =90°,AB =6,AD =4,DC =3,点P 从点A 出发,沿ADCB 方向移动,动点Q 从点A 出发,在AB 边上移动,设点P 移动的路程为x ,点Q 移动的路程为y ,线段PQ 平分梯形ABCD 的周长. (1) 求y 关于x 的函数解析式,并写出x 和y 的取值范围;(2) 当P 不在BC 边上时,线段PQ 能否平分ABCD 的面积?若能,求出此时x 的值;若不能,说明理由. 【难度】★★★ 【答案】 【解析】ABCDP Q【作业4】如图,在平面直角坐标系中,两个函数162y x y x==-+,的图像交于点A,动点P从点O开始在线段O向点A方向以每秒1个单位的速度运动,作PQ∥x 轴交直线BC于点Q,以PQ为一边向下作正方形PAMN,设它与△ABO重叠部分的面积为S.(1)求点A的坐标;(2)试求出点P在线段OA上运动时,S与运动的时间t(秒)的关系式.【难度】★★★【答案】【解析】。
由动点引出的几种面积问题(含答案)
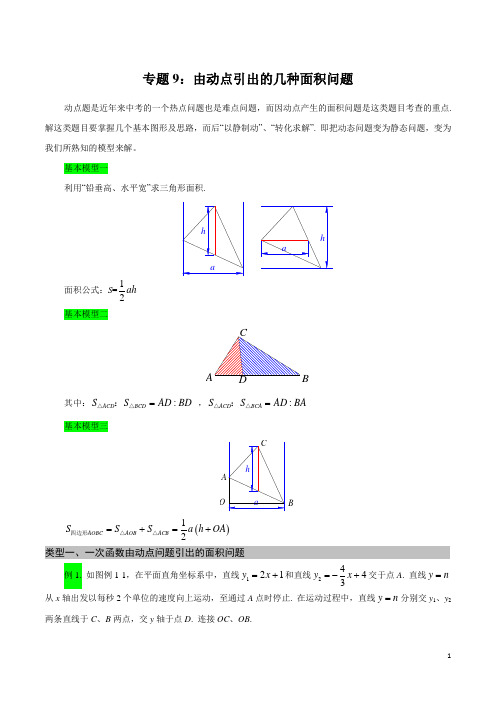
专题9:由动点引出的几种面积问题动点题是近年来中考的一个热点问题也是难点问题,而因动点产生的面积问题是这类题目考查的重点. 解这类题目要掌握几个基本图形及思路,而后“以静制动”、“转化求解”. 即把动态问题变为静态问题,变为我们所熟知的模型来解。
基本模型一利用“铅垂高、水平宽”求三角形面积.面积公式:S =12ah 基本模型二CABD其中::ACD BCD S S AD BD =△△: ,:ACD BCA S S AD BA =△△: 基本模型三OB()12AOB ACB AOBC S S S a h OA =+=+△△四边形 类型一、一次函数由动点问题引出的面积问题例1. 如图例1-1,在平面直角坐标系中,直线121y x =+和直线2443y x =-+交于点A . 直线y n =从x 轴出发以每秒2个单位的速度向上运动,至通过A 点时停止. 在运动过程中,直线y n =分别交y 1、y 2两条直线于C 、B 两点,交y 轴于点D . 连接OC 、OB .(1)设运动时间为t (s ),求t 的取值范围.(2)求出△OBC 的面积S 与t 的函数关系式,并求出S 的最大值及此时n 的值.y=n类型二、二次函数由动点问题引出的面积问题例2. 如图例2-1,二次函数y =ax 2+bx +c 的图像与x 轴的交点为A 、D (A 在D 的右侧),与y 轴的交点为C ,且A (4,0),C (0,-3),对称轴是直线x =1. (1)求二次函数的解析式;(2)若M 是第四象限抛物线上一动点,且横坐标为m ,设四边形OCMA 的面积为S .请写出S 与m 之间的函数关系式,并求出当m 为何值时,四边形OCMA 的面积最大.图例2-1图例2-2类型三、反比例函数由动点问题引出的面积问题例3. 如图例3-1,直线y=2x+6与反比例函数kyx(k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.(1)求m的值和反比例函数的表达式;(2)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?图例3-1类型四、利用三角函数求解由动点问题引出的面积问题例4. 如图例4-1,在矩形OABC中,点O为原点,边OA的长度为8,对角线AC=10,抛物线y =-49x 2+bx +c 经过点A 、C ,与AB 交于点D .(1)求抛物线的解析式;(2)点P 为线段BC 上一个动点(不与点C 重合),点Q 为线段AC 上一个动点,AQ =CP ,连接PQ ,设CP =m ,△CPQ 的面积为S . 求S 关于m 的函数表达式并求出S 最大时的m 值.图例4-1.类型五、由动点问题引出的面积存在性问题例5. 如图例5-1,在平面直角坐标系中,△ABC 是等腰直角三角形,∠BAC =90°,A (1,0),B (0,2),C (3,1)抛物线2122y x bx =+-的图象过C 点,交y 轴于点D . (1)在后面的横线上直接写出点D 的坐标及b 的值: ,b = ;(2)平移该抛物线的对称轴所在直线l ,设l 与x 轴交于点G (x ,0),当OG 等于多少时,恰好将△ABC的面积分为相等的两部分?AOxyBCGF H E图例5-1 图例5-2类型六、利用转化思想解决由动点问题引出的面积问题如图例6-1,在平面直角坐标系中,抛物线24 5y ax x c=++与直线2255y x=--交于A、B两点,已知点B的横坐标是4,直线2255y x=--与x、y轴的交点分别为A、C,点P是抛物线上一个动点.(1)求抛物线的解析式;(2)若点P在直线2255y x=--上方,求△P AC的最大面积.OxyPACBGEH 图例6-1专题9:由动点引出的几种面积问题动点题是近年来中考的一个热点问题也是难点问题,而因动点产生的面积问题是这类题目考查的重点. 解这类题目要掌握几个基本图形及思路,而后“以静制动”、“转化求解”. 即把动态问题变为静态问题,变为我们所熟知的模型来解。
1.4因动点产生的面积问题

1.4 因动点产生的面积问题例1(2015年河南省中考第23题)如图1,边长为8的正方形ABCD的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上A、C两点间的一个动点(含端点),过点P作PF⊥BC于点F.点D、E的坐标分别为(0, 6)、(-4, 0),联结PD、PE、DE.(1)直接写出抛物线的解析式;(2)小明探究点P的位置发现:当点P与点A或点C重合时,PD与PF的差为定值.进而猜想:对于任意一点P,PD与PF的差为定值.请你判断该猜想是否正确,并说明理由;(3)小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”,则存在多个“好点”,且使△PDE的周长最小的点P也是一个“好点”.请直接写出所有“好点”的个数,并求出△PDE周长最小时“好点”的坐标.图1 备用图例2(2014年昆明市中考第23题)如图1,在平面直角坐标系中,抛物线y=ax2+bx-3(a≠0)与x轴交于A(-2, 0)、B(4, 0)两点,与y轴交于点C.(1)求抛物线的解析式;(2)点P从点A出发,在线段AB上以每秒3个单位长度的速度向点B运动,同时点Q从点B出发,在线段BC上以每秒1个单位长度的速度向点C运动.其中一个点到达终点时,另一个点也停止运动.当△PBQ存在时,求运动多少秒时△PBQ的面积最大,最大面积是多少?(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK∶S△PBQ=5∶2,求点K的坐标.例3(2013年苏州市中考第29题)如图1,已知抛物线212y x bx c =++(b 、c 是常数,且c <0)与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴的负半轴交于点C ,点A 的坐标为(-1,0).(1)b =______,点B 的横坐标为_______(上述结果均用含c 的代数式表示);(2)连结BC ,过点A 作直线AE //BC ,与抛物线交于点E .点D 是x 轴上一点,坐标为(2,0),当C 、D 、E 三点在同一直线上时,求抛物线的解析式;(3)在(2)的条件下,点P 是x 轴下方的抛物线上的一动点,连结PB 、PC .设△PBC 的面积为S . ①求S 的取值范围;②若△PBC 的面积S 为正整数,则这样的△PBC 共有_____个.例 4(2011年南通市中考第28题)如图1,直线l 经过点A (1,0),且与双曲线my x =(x >0)交于点B (2,1).过点(,1)P p p -(p >1)作x 轴的平行线分别交曲线m y x =(x >0)和my x=-(x <0)于M 、N 两点. (1)求m 的值及直线l 的解析式;(2)若点P 在直线y =2上,求证:△PMB ∽△PNA ;(3)是否存在实数p ,使得S △AMN =4S △AMP ?若存在,请求出所有满足条件的p 的值;若不存在,请说明理由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
因动点产生的面积问题1.如图1,四边形OABC 是矩形,点A 、C 的坐标分别为(3,0),(0,1).点D 是线段BC 上的动点(与端点B 、C 不重合),过点D 作直线12y x b =-+交折线OAB 于点E . (1)记△ODE 的面积为S ,求S 与b 的函数关系式;(2)当点E 在线段OA 上时,若矩形OABC 关于直线DE 的对称图形为四边形O 1A 1B 1C 1,试探究四边形O 1A 1B 1C 1与矩形OABC 的重叠部分的面积是否发生变化?若不变,求出重叠部分的面积;若改变,请说明理由.图12. 如图1,已知直角梯形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =AB =2,OC =3,过点B 作BD ⊥BC ,交OA 于点D .将∠DBC 绕点B 按顺时针方向旋转,角的两边分别交y 轴的正半轴、x 轴的正半轴于E 和F .(1)求经过点A 、B 、C 三点的抛物线的解析式;(2)当BE 经过(1)中抛物线的顶点时,求CF 的长;(3)连结EF ,设△BEF 与△BFC 的面积之差为S ,问当CF 为何值时S 最小,并求出最小值.图13.如图1,在△ABC 中,∠C =90°,A C =3,BC =4,CD 是斜边AB 上的高,点E 在斜边AB 上,过点E 作直线与△ABC 的直角边相交于点F ,设AE =x ,△AEF 的面积为y .(1)求线段AD 的长;(2)若EF ⊥AB ,当点E 在斜边AB 上移动时,①求y 与x 的函数关系式(写出自变量x 的取值范围); ②当x 取何值时,y 有最大值?并求出最大值.(3)若点F 在直角边AC 上(点F 与A 、C 不重合),点E 在斜边AB 上移动,试问,是否存在直线EF 将△ABC 的周长和面积同时平分?若存在直线EF ,求出x 的值;若不存在直线EF ,请说明理由.图1 备用图4. 如图1,已知:抛物线y=x2+bx-3与x轴相交于A、B两点,与y轴相交于点C,并且OA = OC.(1)求这条抛物线的解析式;(2)过点C作CE // x轴,交抛物线于点E,设抛物线的顶点为点D,试判断△CDE的形状,并说明理由;(3)设点M在抛物线的对称轴l上,且△MCD的面积等于△CDE的面积,请写出点M的坐标(无需写出解题步骤).图15.如图1,在平面直角坐标系xOy中,直角梯形OABC的顶点O为坐标原点,顶点A、C分别在x轴、y 轴的正半轴上,CB∥OA,OC=4,BC=3,OA=5,点D在边OC上,CD=3,过点D作DB的垂线DE,交x轴于点E.(1)求点E的坐标;(2)二次函数y=-x2+bx+c的图像经过点B和点E.①求二次函数的解析式和它的对称轴;②如果点M在它的对称轴上且位于x轴上方,满足S△CEM=2S△ABM,求点M的坐标.图16.如图1,直线l经过点A(1,0),且与双曲线myx=(x>0)交于点B(2,1).过点(,1)P p p-(p>1)作x轴的平行线分别交曲线myx=(x>0)和myx=-(x<0)于M、N两点.(1)求m的值及直线l的解析式;(2)若点P在直线y=2上,求证:△PMB∽△PNA;(3)是否存在实数p,使得S△AMN=4S△AMP?若存在,请求出所有满足条件的p的值;若不存在,请说明理由.图1因动点产生的面积问题1.(2010年广州市中考第25题)如图1,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1).点D是线段BC上的动点(与端点B、C不重合),过点D作直线12y x b=-+交折线OAB于点E.(1)记△ODE的面积为S,求S与b的函数关系式;(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,试探究四边形O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化?若不变,求出重叠部分的面积;若改变,请说明理由.图1思路点拨1.数形结合,用b表示线段OE、CD、AE、BE的长.2.求△ODE的面积,要分两种情况.当E在OA上时,OE边对应的高等于OC;当E在AB边上时,要利用割补法求△ODE的面积.3.第(2)题中的重叠部分是邻边相等的平行四边形.4.图形翻折、旋转等运动中,计算菱形的边长一般用勾股定理.满分解答(1)①如图2,当E在OA上时,32b<<,由12y x b=-+可知,点E的坐标为(2b,0),OE=2b.此时S=S△ODE=112122OE OC b b⋅=⨯⨯=.②如图3,当E在AB上时,3522b<≤,把y=1代入12y x b=-+可知,点D的坐标为(2b-2,1),CD=2b-2,BD=5-2b.把x=3代入12y x b=-+可知,点E的坐标为3(3,)2b-,AE=32b-,BE=5 2b-.此时S=S矩形OABC-S△OAE-S△BDE-S△OCD=1315133()()(52)1(22)22222b b b b-⨯-----⨯⨯-252b b=-+.(2)如图4,因为四边形O1A1B1C1与矩形OABC关于直线DE对称,因此DM=DN,那么重叠部分是邻边相等的平行四边形,即四边形DMEN是菱形.作DH⊥OA,垂足为H.由于CD=2b-2,OE=2b,所以EH=2.设菱形DMEN的边长为m.在Rt△DNH中,DH=1,NH=2-m,DN=m,所以12+(2-m)2=m2.解得54m=.所以重叠部分菱形DMEN的面积为54.图2 图3 图4考点伸展把本题中的矩形OABC 绕着它的对称中心旋转,如果重叠部分的形状是菱形(如图5),那么这个菱形的最小面积为1,如图6所示;最大面积为53,如图7所示.图5 图6 图72. 2010年湖州市中考第24题如图1,已知直角梯形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =AB =2,OC =3,过点B 作BD ⊥BC ,交OA 于点D .将∠DBC 绕点B 按顺时针方向旋转,角的两边分别交y 轴的正半轴、x 轴的正半轴于E 和F .(1)求经过点A 、B 、C 三点的抛物线的解析式;(2)当BE 经过(1)中抛物线的顶点时,求CF 的长;(3)连结EF ,设△BEF 与△BFC 的面积之差为S ,问当CF 为何值时S 最小,并求出最小值.图1 图2思路点拨1.过点B 向坐标轴作垂线,图形中就构造出丰富的余角,从而构造出相似三角形.本题中因为点B 的坐标特殊,因此构造出全等三角形.2.用CF 表示△BEF 与△BFC 的面积之差,首先要判断△BEF 是等腰直角三角形,这样△BEF 的面积就转化为求BF 2的问题.满分解答(1)根据题意可得A (0,2),B (2,2),C (3,0).设抛物线的解析式为y =ax 2+bx +c ,那么2,422,930.c a b c a b c =⎧⎪++=⎨⎪++=⎩解得23a =-,43b =,2c =.所以抛物线的解析式为224233y x x =-++.(2)由224233y x x =-++228(1)33x =--+,得抛物线的顶点G 的坐标为(81,3).如图2,过点B 作x 轴的垂线,垂足为M ,过点E 作y 轴的垂线,交BM 于N .因为∠BEN 与∠FBM 都是∠EBN 的余角,所以∠BEN =∠FBM .又因为BM =EN =2,所以△BMF ≌△ENB .因此BE =BF ,BN =FM .当BE 经过抛物线的顶点G 时,842()2(2)33BN yG yB =-=-=.此时47133CF FM NC =+=+=.(3)设CF 的长为a .在Rt △BFM 中,2222222(1)25BF BM FM a a a =+=+-=-+.因为△BEF 是等腰直角三角形,所以22115222BEF S BF a a ∆==-+. 因此22151522222BEF BFC S S S a a a a a ∆∆=-=-+-=-+211(2)22a =-+.所以当CF =2时,S 取得最小值,最小值为12.考点伸展:图2是一个典型图,在这个图形中,△BMC ≌△BAD ,△BFC ≌△BED ,△BFM ≌△BEA≌△ENB ,△BEF 与△BDC 、△BAM 都是等腰直角三角形.如果把本题中的条件“角的两边分别交y 轴的正半轴、x 轴的正半轴于E 和F ”改为“角的两边分别交y 轴、x 轴于E 和F ”,那么上述结论依然成立(如图3,图4).图3 图43. 如图1,在△ABC 中,∠C =90°,A C =3,BC =4,CD 是斜边AB 上的高,点E 在斜边AB 上,过点E 作直线与△ABC 的直角边相交于点F ,设AE =x ,△AEF 的面积为y .(1)求线段AD 的长;(2)若EF ⊥AB ,当点E 在斜边AB 上移动时, ①求y 与x 的函数关系式(写出自变量x 的取值范围);②当x 取何值时,y 有最大值?并求出最大值. (3)若点F 在直角边AC 上(点F 与A 、C 不重合),点E 在斜边AB 上移动,试问,是否存在直线EF 将△ABC 的周长和面积同时平分?若存在直线EF ,求出x 的值;若不存在直线EF ,请说明理由.图1 备用图思路点拨1.第(1)题求得的AD 的长,就是第(2)题分类讨论x 的临界点. 2.第(2)题要按照点F 的位置分两种情况讨论.3.第(3)题的一般策略是:先假定平分周长,再列关于面积的方程,根据方程的解的情况作出判断.满分解答(1) 在Rt △ABC 中, AC =3,BC =4,所以AB =5.在Rt △ACD 中,39cos 355AD AC A ==⨯=. (2) ①如图2,当F 在AC 上时,905x <<.在Rt △AEF 中,4tan 3EF AE A x ==.所以21223y AE EF x =⋅=.如图3,当F 在BC 上时,955x <≤.在Rt △BEF 中,3tan (5)4EF BE B x ==-.所以21315288y AE EF x x =⋅=-+.②当905x <<时,223y x =的最大值为5425; 当955x <≤时,231588y x x =-+23575)8232x =--+(的最大值为7532.因此,当52x =时,y 的最大值为7532.图2 图3 图4 (3)△ABC 的周长等于12,面积等于6.先假设EF 平分△ABC 的周长,那么AE =x ,AF =6-x ,x 的变化范围为3<x ≤5.因此1142sin (6)(6)2255AEF S AE AF A x x x x ∆=⋅⋅=-⨯=--.解方程2(6)35x x --=,得3x =±为3x =+3<x ≤5范围内(如图4),因此存在直线EF 将△ABC 的周长和面积同时平分. 考点伸展如果把第(3)题的条件“点F 在直角边AC 上”改为“点F 在直角边BC 上”,那么就不存在直线EF 将△ABC 的周长和面积同时平分.先假设EF 平分△ABC 的周长,那么AE =x ,BE =5-x ,BF =x +1.因此21133sin (5)(1)(45)22510BEF S BE BF B x x x x ∆=⋅⋅=-+⨯=---. 解方程23(45)310x x ---=.整理,得2450x x -+=.此方程无实数根. 4.如图1,已知:抛物线y =x 2+bx -3与x 轴相交于A 、B 两点,与y 轴相交于点C ,并且OA = OC .(1)求这条抛物线的解析式;(2)过点C 作CE // x 轴,交抛物线于点E ,设抛物线的顶点为点D ,试判断△CDE 的形状,并说明理由;(3)设点M 在抛物线的对称轴l 上,且△MCD 的面积等于△CDE 的面积,请写出点M 的坐标(无需写出解题步骤).思路点拨 1.求抛物线的解析式,关键是求点A 的坐标,根据已知条件,数形结合. 2.判断△CDE 的形状是等腰直角三角形,可以方便第(3)求解点M 的坐标.满分解答(1)因为抛物线y =x 2+bx -3与y 轴交于点C (0,-3),OA =OC ,所以点A 的坐标为(-3,0). 将A (-3,0)代入y =x 2+bx -3,解得b =2.因此抛物线的解析式为y =x 2+2x -3.(2)由y =x 2+2x -3=(x +1) 2-4,得顶点D 的坐标为(-1,-4) .因为CE // x 轴所以点C 与点E 关于抛物线的对称轴对称.因此CE =2,DE =DC .由两点间的距离公式,求得DC DE 2+DC 2=CE 2.所以△CDE 是等腰直角三角形.(3)M 1(-1,-2),M 2(-1,-6).考点伸展第(3)题的解题思路是这样的:如图2,如图3,因为△MCD 与△CDE 是同底的两个三角形,如果面积相等,那么过点E 作CD 的平行线,与抛物线的对称轴的交点就是要探求的点M .再根据对称性,另一个符合条件的点M 在点D 的下方,这两个点M 关于点D 对称.还有更简单的几何说理方法:因为△CDE 是等腰直角三角形,对于点D 上方的点M ,四边形CDEM 是正方形,容易得到点M 的坐标为(-1,-2).再根据对称性,得到另一个点M 的坐标为(-1,-6).图2 图35.如图1,在平面直角坐标系xOy 中,直角梯形OABC 的顶点O 为坐标原点,顶点A 、C 分别在x 轴、y 轴的正半轴上,CB ∥OA ,OC =4,BC =3,OA =5,点D 在边OC 上,CD =3,过点D 作DB 的垂线DE ,交x 轴于点E .(1)求点E 的坐标;(2)二次函数y =-x 2+bx +c 的图像经过点B 和点E .①求二次函数的解析式和它的对称轴;②如果点M 在它的对称轴上且位于x 轴上方,满足S △CEM =2S △ABM ,求点M 的坐标.图1思路点拨1.这三道题目步步为赢,错一道题目,就要影响下一道的计算.2.点M 在抛物线的对称轴上且位于x 轴上方,要分两种情况讨论,分别为点M 在线段FB 和FB 的延长线上.因为用点M 的纵坐标表示△ABM 的底边长,因点M 的位置不同而不同.满分解答(1)因为BC ∥OA ,所以BC ⊥CD .因为CD =CB =3,所以△BCD 是等腰直角三角形.因此∠BCD =45°.又因为BC ⊥CD ,所以∠ODE =45°.所以△ODE 是等腰直角三角形,OE =OD =1.所以点E 的坐标是(1,0). (2)①因为抛物线y =-x 2+bx +c 经过点B (3,4)和点E (1,0),所以934,10.b c b c -++=⎧⎨-++=⎩ 解得6,5.b c =⎧⎨=-⎩所以二次函数的解析式为y =-x 2+6x -5,抛物线的对称轴为直线x =3.②如图2,如图3,设抛物线的对称轴与x 轴交于点F ,点M 的坐标为(3,t ).CEM MEF COE OFMC S S S S ∆∆∆=--梯形111(4)321442222tt t =+⨯-⨯⨯-⨯⨯=+.(ⅰ)如图2,当点M 位于线段BF 上时,t t S ABM -=⨯-=∆42)4(21.解方程)4(242t t -=+,得58=t .此时点M 的坐标为(3,58).(ⅱ)如图3,当点M 位于线段FB 延长线上时,42)4(21-=⨯-=∆t t S ABM .解方程)4(242-=+t t,得8=t .此时点M 的坐标为(3,8).图2 图3考点伸展对于图2,还有几个典型结论:此时,C 、M 、A 三点在同一条直线上;△CEM 的周长最小.可以求得直线AC 的解析式为445y x =-+,当x =3时,85y =.因此点M (3,58)在直线AC 上.因为点A 、E 关于抛物线的对称轴对称,所以ME +MC =MA +MC .当A 、M 、C 三点共线时,ME +MC 最小,△CEM的周长最小.6.如图1,直线l 经过点A (1,0),且与双曲线my x=(x >0)交于点B (2,1).过点(,1)P p p -(p >1)作x 轴的平行线分别交曲线m y x =(x >0)和my x=-(x <0)于M 、N 两点.(1)求m 的值及直线l 的解析式;(2)若点P 在直线y =2上,求证:△PMB ∽△PNA ;(3)是否存在实数p ,使得S △AMN =4S △AMP ?若存在,请求出所有满足条件的p 的值;若不存在,请说明理由.思路点拨1.第(2)题准确画图,点的位置关系尽在图形中.2.第(3)题把S △AMN =4S △AMP 转化为MN =4MP ,按照点M 与线段NP 的位置关系分两种情况讨论. 满分解答(1)因为点B (2,1)在双曲线m y x=上,所以m =2.设直线l 的解析式为y kx b =+,代入点A (1,0)和点B (2,1),得0,2 1.k b k b +=⎧⎨+=⎩ 解得1,1.k b =⎧⎨=-⎩ 所以直线l 的解析式为1y x =-. (2)由点(,1)P p p -(p >1)的坐标可知,点P 在直线1y x =-上x 轴的上方.如图2,当y =2时,点P 的坐标为(3,2).此时点M 的坐标为(1,2),点N 的坐标为(-1,2). 由P (3,2)、M (1,2)、B (2,1)三点的位置关系,可知△PMB 为等腰直角三角形. 由P (3,2)、N (-1,2)、A (1,0)三点的位置关系,可知△PNA 为等腰直角三角形. 所以△PMB ∽△PNA .图2 图3 图4(3)△AMN 和△AMP 是两个同高的三角形,底边MN 和MP 在同一条直线上.当S △AMN =4S △AMP 时,MN =4MP .①如图3,当M 在NP 上时,x M -x N =4(x P -x M ).因此222()4(1)x x x x ⎛⎫⎛⎫--=-- ⎪ ⎪⎝⎭⎝⎭.解得x =或x =P 在x 轴下方,舍去).此时p②如图4,当M 在NP 的延长线上时,x M -x N =4(x M -x P ).因此222()4(1)x x x x ⎛⎫⎛⎫--=-- ⎪ ⎪⎝⎭⎝⎭.解得x =x P 在x 轴下方,舍去).此时p = 考点伸展在本题情景下,△AMN 能否成为直角三角形?情形一,如图5,∠AMN =90°,此时点M 的坐标为(1,2),点P 的坐标为(3,2). 情形二,如图6,∠MAN =90°,此时斜边MN 上的中线等于斜边的一半. 不存在∠ANM =90°的情况.图5 图6。
