专题04 因动点产生的面积问题(原卷版)
因动点产生的面积问题

例21:2011年四川省南充市中考第22题抛物线y=ax2+bx+c与x轴的交点为A(m﹣4,0)和B(m,0),与直线y=﹣x+p相交于点A和点C(2m﹣4,m﹣6).(1)求抛物线的解析式;(2)若点P在抛物线上,且以点P和A,C以及另一点Q为顶点的平行四边形ACQP面积为12,求点P,Q 的坐标;(3)在(2)条件下,若点M是x轴下方抛物线上的动点,当△PQM的面积最大时,请求出△PQM的最大面积及点M的坐标.解答:解:(1)∵点A(m﹣4,0)和C(2m﹣4,m﹣6)在直线y=﹣x+p上∴,解得:,∴A(﹣1,0),B(3,0),C(2,﹣3),设抛物线y=ax2+bx+c=a(x﹣3)(x+1),∵C(2,﹣3),代入得:﹣3=a(2﹣3)(2+1),∴a=1∴抛物线解析式为:y=x2﹣2x﹣3,答:抛物线解析式为y=x2﹣2x﹣3.(2)解:AC=3,AC所在直线的解析式为:y=﹣x﹣1,∠BAC=45°,∵平行四边形ACQP的面积为12,∴平行四边形ACQP中AC边上的高为=2,过点D作DK⊥AC与PQ所在直线相交于点K,DK=2,∴DN=4,∵ACPQ,PQ所在直线在直线ACD的两侧,可能各有一条,∴PQ的解析式或为y=﹣x+3或y=﹣x﹣5,∴,解得:或,,方程无解,即P1(3,0),P2(﹣2,5),∵ACPQ是平行四边形,A(﹣1,0),C(2,﹣3),∴当P(3,0)时,Q(6,﹣3),当P(﹣2,5)时,Q(1,2),∴满足条件的P,Q点是P1(3,0),Q1(6,﹣3)或P2(﹣2,5),Q2(1,2)答:点P,Q的坐标是P1(3,0),Q1(6,﹣3)或P2(﹣2,5),Q2(1,2).(3)解:设M(t,t2﹣2t﹣3),(﹣1<t<3),过点M作y轴的平行线,交PQ所在直线雨点T,则T(t,﹣t+3),MT=(﹣t+3)﹣(t2﹣2t﹣3)=﹣t2+t+6,过点M作MS⊥PQ所在直线于点S,MS=MT=(﹣t2+t+6)=﹣(t﹣)2+,∴当t=时,M(,﹣),△PQM中PQ边上高的最大值为,答:△PQM 的最大面积是,,点M 的坐标是(,﹣).点评:本题主要考查对用待定系数法求二次函数的解析式,二次函数的最值,平行四边形的性质,解二元一次方程组等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键,此题是一个综合性比较强的题目,有一定的难度.例22:2010年广东省湛江市中考第28题如图,在平面直角坐标系中,点B 的坐标为(-3,-4),线段OB 绕原点逆时针旋转后与x 轴的正半轴重合,点B 的对应点为点A .(1)直接写出点A 的坐标,并求出经过A 、O 、B 三点的抛物线的解析式;(2)在抛物线的对称轴上是否存在点C ,使BC +OC 的值最小?若存在,求出点C 的坐标;若不存在,请说明理由;(3)点P 是抛物线上的一个动点,且在x 轴的上方,当点P 运动到什么位置时,△PAB 的面积最大?求出此时点P 的坐标和△PAB 的最大面积.解:(1)A(5,0) ………1分由抛物线经过点O ,可设抛物线的解析式为bx ax y +=2…2分⎩⎨⎧=-=+4390525b a b a 解得⎪⎪⎩⎪⎪⎨⎧=-=6561b a …………………………4分 ∴抛物线的解析式为x x y 65612+-=…………………………5分 (2)如图,由(1)得抛物线的对称轴是直线25=x ,点O 、A 关于直线25=x 对称,连接AB 交直线25=x 于点C ,则点C 使BC+OC 的值最小………………………6分设直线AB 的解析式为b kx y +=,得⎩⎨⎧-=+-=+4305b k b k ,解得⎪⎪⎩⎪⎪⎨⎧-==2521b k∴直线的解析式为2521-=x y ………………………8分把25=x 代入2521-=x y ,得45-=y ,∴点C 的坐标为)45,25(-………………9分(3)如图,过点P 作y 轴的平行线交AB 于点D ,设点P 的横坐标为x ,得)6561,(2x x x P +-, )2521,(-x x D ………………10分∴PAD PBD PAB S S S ∆∆∆+==)(21B A x x PD -∙=))((21B A D p x x y y --=[])3(5)2521()6561(212--⨯⎥⎦⎤⎢⎣⎡--+-x x x =1034322++-x x =332)1(322+--x ∴当1=x 时,PAB S ∆的最大值为332………………12分 把1=x 代入x x y 65612+-=,得32=y ,∴此时点P 的坐标为)32,1(………………13分例23:2012年广东省广州市中考数学模拟第25题平面直角坐标系中,平行四边形ABOC 如图放置,点A 、C 的坐标分别为(0,3)、(1-,0),将此平行四边形绕点0顺时针旋转90°,得到平行四边形'''A B OC 。
(完整版)汇编《因动点产生的面积问题》含答案

例1如图1,边长为8的正方形ABCD的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上A、C两点间的一个动点(含端点),过点P作PF⊥BC于点F.点D、E的坐标分别为(0, 6)、(-4, 0),联结PD、PE、DE.(1)直接写出抛物线的解析式;(2)小明探究点P的位置发现:当点P与点A或点C重合时,PD与PF的差为定值.进而猜想:对于任意一点P,PD与PF的差为定值.请你判断该猜想是否正确,并说明理由;(3)小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”,则存在多个“好点”,且使△PDE的周长最小的点P也是一个“好点”.请直接写出所有“好点”的个数,并求出△PDE周长最小时“好点”的坐标.图1 备用图如图1,边长为8的正方形ABCD 的两边在坐标轴上,以点C 为顶点的抛物线经过点A ,点P 是抛物线上A 、C 两点间的一个动点(含端点),过点P 作PF ⊥BC 于点F .点D 、E 的坐标分别为(0, 6)、(-4, 0),联结PD 、PE 、DE .(1)直接写出抛物线的解析式;(2)小明探究点P 的位置发现:当点P 与点A 或点C 重合时,PD 与PF 的差为定值.进而猜想:对于任意一点P ,PD 与PF 的差为定值.请你判断该猜想是否正确,并说明理由;(3)小明进一步探究得出结论:若将“使△PDE 的面积为整数” 的点P 记作“好点”,则存在多个“好点”,且使△PDE 的周长最小的点P 也是一个“好点”.请直接写出所有“好点”的个数,并求出△PDE 周长最小时“好点”的坐标.图1 备用图动感体验请打开几何画板文件名“15河南23”,拖动点P 在A 、C 两点间的抛物线上运动,观察S 随P 变化的图像,可以体验到,“使△PDE 的面积为整数” 的点P 共有11个.思路点拨1.第(2)题通过计算进行说理.设点P 的坐标,用两点间的距离公式表示PD 、PF 的长.2.第(3)题用第(2)题的结论,把△PDE 的周长最小值转化为求PE +PF 的最小值.满分解答(1)抛物线的解析式为2188y x =-+.(2)小明的判断正确,对于任意一点P ,PD -PF =2.说理如下: 设点P 的坐标为21(,8)8x x -+,那么PF =y F -y P =218x .而FD 2=22222222111+(86)+(2)(2)888x x x x x -+-=-=+,所以FD =2128x +. 因此PD -PF =2为定值. (3)“好点”共有11个.在△PDE 中,DE 为定值,因此周长的最小值取决于FD +PE 的最小值.而PD +PE =(PF +2)+PE =(PF +PE )+2,因此当P 、E 、F 三点共线时,△PDE 的周长最小(如图2).此时EF ⊥x 轴,点P 的横坐标为-4.所以△PDE 周长最小时,“好点”P 的坐标为(-4, 6).图2 图3考点伸展第(3)题的11个“好点”是这样求的:如图3,联结OP ,那么S △PDE =S △POD +S △POE -S △DOE . 因为S △POD =1()32P OD x x ⋅-=-,S △POE =2111624P OE y x ⋅=-+,S △DOE =12,所以 S △PDE =21316124x x --+-=21344x x --+=21(6)134x -++. 因此S 是x 的二次函数,抛物线的开口向下,对称轴为直线x =-6. 如图4,当-8≤x ≤0时,4≤S ≤13.所以面积的值为整数的个数为10.当S =12时,方程21(6)13124x -++=的两个解-8, -4都在-8≤x ≤0范围内. 所以“使△PDE 的面积为整数” 的 “好点”P 共有11个.图4例2如图1,在平面直角坐标系中,抛物线y=ax2+bx-3(a≠0)与x轴交于A(-2, 0)、B(4, 0)两点,与y轴交于点C.(1)求抛物线的解析式;(2)点P从点A出发,在线段AB上以每秒3个单位长度的速度向点B运动,同时点Q从点B出发,在线段BC上以每秒1个单位长度的速度向点C运动.其中一个点到达终点时,另一个点也停止运动.当△PBQ存在时,求运动多少秒时△PBQ的面积最大,最大面积是多少?(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK∶S△PBQ=5∶2,求点K的坐标.图1如图1,在平面直角坐标系中,抛物线y =ax 2+bx -3(a ≠0)与x 轴交于A (-2, 0)、B (4, 0)两点,与y 轴交于点C .(1)求抛物线的解析式;(2)点P 从点A 出发,在线段AB 上以每秒3个单位长度的速度向点B 运动,同时点Q 从点B 出发,在线段BC 上以每秒1个单位长度的速度向点C 运动.其中一个点到达终点时,另一个点也停止运动.当△PBQ 存在时,求运动多少秒时△PBQ 的面积最大,最大面积是多少?(3)当△PBQ 的面积最大时,在BC 下方的抛物线上存在点K ,使S △CBK ∶S △PBQ =5∶2,求点K 的坐标.图1动感体验请打开几何画板文件名“14昆明23”,拖动点P 从A 向B 运动,可以体验到,当P 运动到AB 的中点时,△PBQ 的面积最大.双击按钮“△PBQ 面积最大”,再拖动点K 在BC 下方的抛物线上运动,观察度量值,可以体验到,有两个时刻面积比为2.5.思路点拨1.△PBQ 的面积可以表示为t 的二次函数,求二次函数的最小值. 2.△PBQ 与△PBC 是同高三角形,△PBC 与△CBK 是同底三角形,把△CBK 与△PBQ 的比转化为△CBK 与△PBC 的比.满分解答(1)因为抛物线与x 轴交于A (-2, 0)、B (4, 0)两点,所以y =a(x +2)(x -4).所以-8a =-3.解得38a =.所以抛物线的解析式为3(2)(4)8y x x =+-233384x x =--.(2)如图2,过点Q 作QH ⊥x 轴,垂足为H .在Rt △BCO 中,OB =4,OC =3,所以BC =5,sin B =35.在Rt △BQH 中,BQ =t ,所以QH =BQ sin B =35t .所以S △PBQ =211399(63)(1)2251010BP QH t t t ⋅=-⨯=--+.因为0≤t≤2,所以当t=1时,△PBQ的面积最大,最大面积是910。
初三压轴题专项----因动点产生的面积问题

因动点产生的面积问题
教学目标
对中考可能出现的压轴题类型进行模块复习
教学内容
常见解法:
1.观察要求的图形是什么形状,各点坐标是否知道;
2.是否有一条边与x轴、y轴平行或重合,是否为规那么的图形,如是,直接用公式计算;
3.割,大多应用于四边形或多边形;
4.补,即用作差法求面积。实在没有方法就做高形成梯形,再做差。
2.如图,:抛物线 与 轴相交于 、 两点,与 轴相交于点 ,并且 = .
〔1〕求这条抛物线的解析式;
〔2〕过点 作 ∥ 轴,交抛物线于点 ,设抛物线的顶点为点 ,试判断△ 的形状,并说明理由;
〔3〕设点 在抛物线的对称轴 上,且△ 的面积等于△ 的面积,请写出点 的坐标〔无需写出解题步骤〕.
3.:抛物线 经过点 , ,且对称轴 与 轴交于点 .
〔1〕求抛物线的表达式;
〔2〕如图,点 、 分别是 轴、对称轴 上的点,且四边形 是矩形,点 是 上一点,将 沿着直线 翻折, 点与线段 上的 点重合,求 点的坐标;
〔3〕在〔2〕的条件下,点 是对称轴 上的点,直线 交 于点 , ,求 点坐标.
Байду номын сангаас家庭作业:
1.如图,在直角坐标平面内,点 的坐标为〔3,0〕,第一象限内的点 在直线 上,∠ =45度.
〔1〕求点 的坐标;
〔2〕如果二次函数的图像经过 、 、 三点,求这个二次函数的解析式,并写出它的图像的顶点坐标 ;
〔3〕如果将第〔2〕小题中的二次函数的图像向上或向下平移,使它的顶点落在直线 上的点 处,求△ 与△ 的面积之比.
1.如图,在平面直角坐标系 中,直角梯形 的顶点 为坐标原点,顶点 、 分别在 轴、 轴的正半轴上, ∥ , =4, =3, =5,点 在边 上, =3,过点 作 的垂线 ,交 轴于点 .
二次函数-因动点产生的面积问题典型例题.doc

二次函数-因动点产生的面积问题例1、如图1,己知抛物线y = -x2-}-bx + c(力、Q是常数,且c<0)与”轴交于人〃两点(点/在点〃的左侧),与y轴的负半轴交于点G点力的坐标为(-1,0).(1) ______ b=______________________,点〃的横坐标为(上述结果均用含c的代数式表示);(2)连结饥;过点/作直线力伤/应;与抛物线交于点仅点〃是/轴上一点,坐标为(2, 0),当C、〃、E三点在同一直线上时,求抛物线的解析式;(3)在(2)的条件下,点P是x轴下方的抛物线上的一动点,连结刖、PC.设比的面积为S.①求S的取值范围;②若的面积S为正整数,则这样的△/犹共有___________ 个.思路点拨1. 用c表示方以后,把抛物线的一般式改写为两点式,会发现OB=2OC.2. 当C、D、£、三点共线时,'EHAs'COB、'EHLS'COD.3. 求△观面积的取值范圉,要分两种情况计算,户在%上方或下方.4. 求得了S的取值范围,然后罗列P从M经过C运动到〃的过程中,面积的正整数值,再数一数个数•注意排除点久C.〃三个时刻的值.满分解答(1)b=c +丄,点〃的横坐标为— 2c.过点E作EHLx轴于〃.由于当AE//BC时,AH=2EIL所以x + l = (x+l)Cx+2c).因此x = l — 2c.所以E(l-2c,l-c).当C 、D 、F 三点在同一直线上时,—.所以 I =Z£.DH DO -2c-1 2整理,得2<?+3c —2 = 0.解得c=~2或0 =丄(舍去).2(3)①当P 在力下方时,过点P 作x 轴的垂线交氏于F.直线〃C'的解析式为y = ^x-2.131 1设 —- — tn -2),那么, FP = —nr +2m.2222所以S MB 卜+ S^pct-=丄FP{X B —X C ) = 2FP — —m 2+ 4m = —(m — 2)2 + 4 •2因此当P 在氏下方时,的最大值为4.当P 在比上方时,因为SHABC=5、所以S\PBC<5・ 综上所述,0VSV5.②若△/沆、的而积S 为止整数,则这样的△/沉共有11个. 考点伸展点P 沿抛物线从力经过C 到达〃的过程中,的面积为整数,依次为(5), 4, 3, 2, 3, 4, 3, 2, 1, (0).当戶在兀下方,S=4时,点P 在氏的中点的正下方,尸是应'的中点. 例2、如图1,在平面直角坐标系中放置一直角三角板,其顶点为水0, 1)、〃(2, 0)、0(0, 0),将此三 角板绕原点0逆时针旋转90° ,得到三角形/ B' 0.(1) 一抛物线经过点川、B, B,求该抛物线的解析式;(2) 设点"是第一象限内抛物线上的一个动点,是否存在点",使四边形/行A' 〃的面积是△彳夕0而积的4倍?若存在,请求出点戶的坐标;若不存在,请说明理由;(3) 在(2)的条件下,试指出四边形PB* 〃是哪种形状的四边形?并写出它的两条性质.2, 1, (0), 1,图1思路点拨1. 四边形丹'A9〃的面积是△才B' 0面积的4倍,可以转化为四边形丹'防的面积是△才B' 0面积的3倍.2. 联结四边形/为'必可以分割为两个三角形.3. 过点向无轴作垂线,四边形丹'血也可以分割为一个直角梯形和一个直角三角形.满分解答(1) 防绕着原点0逆时针旋转90°,点彳、B'的坐标分别为(一1, 0)、(0, 2).因为抛物线与x轴交于A1 (-1, 0)、凤2, 0),设解析式为尸=臼匕+1)匕一2),代入B r (0, 2),得&=1.所以该抛物线的解析式为y=-d+l)d-2) =-/+x+2・(2) o— 1.如果S四边形w A f g=4 S^A r g 0=4,那么S四边形曲加=3 S^A f ff o=3.如图2,作刃丄防,垂足为设点"的坐标为匕,—x+x+i).1 1 9 1 . 1 9 =-DO^O-^ PD) = -x(2-x2+x+2) = --x3 +-x2 + 2x .1 | 1 3S、PDB =—DB X PD=-(2-X)(-X2 + x + 2) = 一一兀2 + 2 .解方程一,+2/+2 = 3,得 K = Z =1.所以点戶的坐标为(1, 2).(3)如图3,四边形"F A r〃是等腰梯形,它的性质有:等腰梯形的对角线相等;等腰梯形同以底上的两个内角相等;等腰梯形是轴对称图形,对称轴是经过两底中点的直线. 考点伸展第(2)题求四边形加的面积,也可以如图4那样分割图形,这样运算过程更简单.S、PB ()=运 B'O ・心= — x2x = x-&PBO — — BO • yp — — x 2(—+ 兀 + 2) — —+ 无 + 2 • 21 2所以 % 边形阳池=Sp&o += —x + 2x+2 •甚至我们可以更大胆地根据抛物线的对称性直接得到点P : 作OB'关于抛物线的对称轴对称的△从加,那么点F 的坐标为(1, 2).而矩形励’0〃与△才OB'、△尿沪是等底等高的,所以四边形防'A f3的面积是△才ff 0面积的 4倍.因此点疋就是要探求的点尢所以%边 形PBAD图2图3=—x 2 + 2兀+2 •2图4S 梯形PBOD例3、如图1,在平面直角坐标系屮,直线y = -x+\与抛物线y= ax + bx — 3交于弭、〃两点,点力在/ 轴上,点〃的纵坐标为3.点P 是直线力〃下方的抛物线上的一动点(不与点/、〃重合),过点"作/轴 的垂线交直线力〃于点C,作皿丄血/于点〃.(1) 求曰、b 及sin^ACP 的值; (2) 设点P 的横坐标为饥① 用含刃的代数式表示线段刃的长,并求出线段刃长的最大值;② 连结/为,线段/乞把△/%矽分成两个三角形,是否存在适合的/〃的值,使这两个三角形的面积比为9 : 10?若存在,直接写出/〃的值;若不存在,请说明理由・思路点拨1. 第(1)题由于GV/y 轴,把z/m 转化为它的同位角.2. 第(2)题中,PD=PCskZACP,第(1)题已经做好了铺垫.3.与△"伪是同底边&、的两个三角形,面积比等于对应高〃V 与射的比.4. 两个三角形的面积比为9 : 10,要分两种情况讨论. 满分解答(1) 设直线 y = -x + 1 与 y 轴交于点 那么 71(-2, 0), 〃(4,3), MO,1).2在Rt △肋0屮,04=2, OE=\,所以AE =亦.所以sin ZAEO = 迈・5将力(一2,0)、8(4,3)分别代入尸/+&—3,得.⑵由"巧心尹一3),帥了+1),因为PG7%,所以ZACP=ZAEO.因此sin4。
2018年人教版中考压轴题汇编《因动点产生的面积问题》含答案

1.6 因动点产生的面积问题例1 2017年河南省中考第23题如图1,边长为8的正方形ABCD的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上A、C两点间的一个动点(含端点),过点P作PF⊥BC于点F.点D、E 的坐标分别为(0, 6)、(-4, 0),联结PD、PE、DE.(1)直接写出抛物线的解析式;(2)小明探究点P的位置发现:当点P与点A或点C重合时,PD与PF的差为定值.进而猜想:对于任意一点P,PD与PF的差为定值.请你判断该猜想是否正确,并说明理由;(3)小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”,则存在多个“好点”,且使△PDE的周长最小的点P也是一个“好点”.请直接写出所有“好点”的个数,并求出△PDE周长最小时“好点”的坐标.图1 备用图例2 2017年昆明市中考第23题如图1,在平面直角坐标系中,抛物线y =ax 2+bx -3(a ≠0)与x 轴交于A (-2, 0)、B (4, 0)两点,与y 轴交于点C .(1)求抛物线的解析式;(2)点P 从点A 出发,在线段AB 上以每秒3个单位长度的速度向点B 运动,同时点Q 从点B 出发,在线段BC 上以每秒1个单位长度的速度向点C 运动.其中一个点到达终点时,另一个点也停止运动.当△PBQ 存在时,求运动多少秒时△PBQ 的面积最大,最大面积是多少?(3)当△PBQ 的面积最大时,在BC 下方的抛物线上存在点K ,使S △CBK ∶S △PBQ =5∶2,求点K 的坐标.图1例3 2017年苏州市中考第29题如图1,已知抛物线212y x bx c =++(b 、c 是常数,且c <0)与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴的负半轴交于点C ,点A 的坐标为(-1,0).(1)b=______,点B的横坐标为_______(上述结果均用含c的代数式表示);(2)连结BC,过点A作直线AE//BC,与抛物线交于点E.点D是x轴上一点,坐标为(2,0),当C、D、E三点在同一直线上时,求抛物线的解析式;(3)在(2)的条件下,点P是x轴下方的抛物线上的一动点,连结PB、PC.设△PBC 的面积为S.①求S的取值范围;②若△PBC的面积S为正整数,则这样的△PBC共有_____个.图1例4 2017年菏泽市中考第21题如图1,在平面直角坐标系中放置一直角三角板,其顶点为A(0, 1)、B(2, 0)、O(0, 0),将此三角板绕原点O逆时针旋转90°,得到三角形A′B′O.(1)一抛物线经过点A′、B′、B,求该抛物线的解析式;(2)设点P是第一象限内抛物线上的一个动点,是否存在点P,使四边形PB′A′B的面积是△A′B′O面积的4倍?若存在,请求出点P的坐标;若不存在,请说明理由;(3)在(2)的条件下,试指出四边形PB′A′B是哪种形状的四边形?并写出它的两条性质.图1例 5 2017年河南省中考第23题如图1,在平面直角坐标系中,直线112y x=+与抛物线y=ax2+bx-3交于A、B两点,点A在x轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上的一动点(不与点A、B重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.(1)求a、b及sin∠ACP的值;(2)设点P的横坐标为m.①用含m的代数式表示线段PD的长,并求出线段PD长的最大值;②连结PB,线段PC把△PDB分成两个三角形,是否存在适合的m的值,使这两个三角形的面积比为9∶10?若存在,直接写出m的值;若不存在,请说明理由.图1例 6 2017年南通市中考第28题如图1,直线l经过点A(1,0),且与双曲线myx=(x>0)交于点B(2,1).过点(,1)P p p-(p>1)作x轴的平行线分别交曲线myx=(x>0)和myx=-(x<0)于M、N两点.(1)求m的值及直线l的解析式;(2)若点P在直线y=2上,求证:△PMB∽△PNA;(3)是否存在实数p,使得S△AMN=4S△AMP?若存在,请求出所有满足条件的p的值;若不存在,请说明理由.图1例7 2017年广州市中考第25题如图1,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1).点D是线段BC上的动点(与端点B、C不重合),过点D作直线12y x b=-+交折线OAB于点E.(1)记△ODE的面积为S,求S与b的函数关系式;(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,试探究四边形O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化?若不变,求出重叠部分的面积;若改变,请说明理由.图11.6 因动点产生的面积问题答案例1 2017年河南省中考第23题如图1,边长为8的正方形ABCD的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上A、C两点间的一个动点(含端点),过点P作PF⊥BC于点F.点D、E 的坐标分别为(0, 6)、(-4, 0),联结PD、PE、DE.(1)直接写出抛物线的解析式;(2)小明探究点P的位置发现:当点P与点A或点C重合时,PD与PF的差为定值.进而猜想:对于任意一点P,PD与PF的差为定值.请你判断该猜想是否正确,并说明理由;(3)小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”,则存在多个“好点”,且使△PDE 的周长最小的点P 也是一个“好点”.请直接写出所有“好点”的个数,并求出△PDE 周长最小时“好点”的坐标.图1 备用图动感体验请打开几何画板文件名“15河南23”,拖动点P 在A 、C 两点间的抛物线上运动,观察S 随P 变化的图像,可以体验到,“使△PDE 的面积为整数” 的点P 共有11个. 思路点拨1.第(2)题通过计算进行说理.设点P 的坐标,用两点间的距离公式表示PD 、PF 的长.2.第(3)题用第(2)题的结论,把△PDE 的周长最小值转化为求PE +PF 的最小值. 满分解答(1)抛物线的解析式为2188y x =-+.(2)小明的判断正确,对于任意一点P ,PD -PF =2.说理如下:设点P 的坐标为21(,8)8x x -+,那么PF =y F -y P =218x .而FD 2=22222222111+(86)+(2)(2)888x x x x x -+-=-=+,所以FD =2128x +. 因此PD -PF =2为定值.(3)“好点”共有11个.在△PDE 中,DE 为定值,因此周长的最小值取决于FD +PE 的最小值.而PD +PE =(PF +2)+PE =(PF +PE )+2,因此当P 、E 、F 三点共线时,△PDE 的周长最小(如图2).此时EF ⊥x 轴,点P 的横坐标为-4.所以△PDE 周长最小时,“好点”P 的坐标为(-4, 6).图2 图3考点伸展第(3)题的11个“好点”是这样求的:如图3,联结OP ,那么S △PDE =S △POD +S △POE -S △DOE .因为S △POD =1()32P OD x x ⋅-=-,S △POE =2111624P OE y x ⋅=-+,S △DOE =12,所以 S △PDE =21316124x x --+-=21344x x --+=21(6)134x -++. 因此S 是x 的二次函数,抛物线的开口向下,对称轴为直线x =-6.如图4,当-8≤x ≤0时,4≤S ≤13.所以面积的值为整数的个数为10.当S =12时,方程21(6)13124x -++=的两个解-8, -4都在-8≤x ≤0范围内. 所以“使△PDE 的面积为整数” 的 “好点”P 共有11个.图4例2 2017年昆明市中考第23题如图1,在平面直角坐标系中,抛物线y =ax 2+bx -3(a ≠0)与x 轴交于A (-2, 0)、B (4, 0)两点,与y 轴交于点C .(1)求抛物线的解析式;(2)点P 从点A 出发,在线段AB 上以每秒3个单位长度的速度向点B 运动,同时点Q 从点B 出发,在线段BC 上以每秒1个单位长度的速度向点C 运动.其中一个点到达终点时,另一个点也停止运动.当△PBQ 存在时,求运动多少秒时△PBQ 的面积最大,最大面积是多少?(3)当△PBQ 的面积最大时,在BC 下方的抛物线上存在点K ,使S △CBK ∶S △PBQ =5∶2,求点K 的坐标.图1动感体验请打开几何画板文件名“14昆明23”,拖动点P 从A 向B 运动,可以体验到,当P 运动到AB 的中点时,△PBQ 的面积最大.双击按钮“△PBQ 面积最大”,再拖动点K 在BC 下方的抛物线上运动,观察度量值,可以体验到,有两个时刻面积比为2.5.思路点拨1.△PBQ 的面积可以表示为t 的二次函数,求二次函数的最小值.2.△PBQ 与△PBC 是同高三角形,△PBC 与△CBK 是同底三角形,把△CBK 与△PBQ 的比转化为△CBK 与△PBC 的比.满分解答(1)因为抛物线与x 轴交于A (-2, 0)、B (4, 0)两点,所以y =a(x +2)(x -4).所以-8a =-3.解得38a =. 所以抛物线的解析式为3(2)(4)8y x x =+-233384x x =--. (2)如图2,过点Q 作QH ⊥x 轴,垂足为H .在Rt △BCO 中,OB =4,OC =3,所以BC =5,sin B =35. 在Rt △BQH 中,BQ =t ,所以QH =BQ sin B =35t . 所以S △PBQ =211399(63)(1)2251010BP QH t t t ⋅=-⨯=--+. 因为0≤t ≤2,所以当t =1时,△PBQ 的面积最大,最大面积是910。
由动点引出的几种面积问题(含答案)
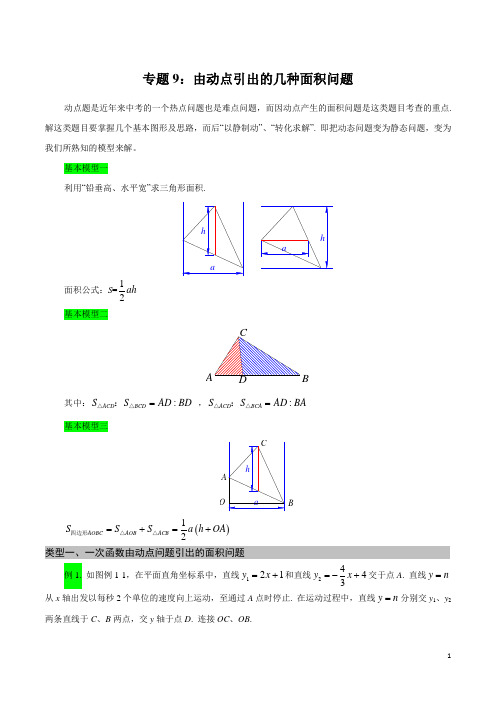
专题9:由动点引出的几种面积问题动点题是近年来中考的一个热点问题也是难点问题,而因动点产生的面积问题是这类题目考查的重点. 解这类题目要掌握几个基本图形及思路,而后“以静制动”、“转化求解”. 即把动态问题变为静态问题,变为我们所熟知的模型来解。
基本模型一利用“铅垂高、水平宽”求三角形面积.面积公式:S =12ah 基本模型二CABD其中::ACD BCD S S AD BD =△△: ,:ACD BCA S S AD BA =△△: 基本模型三OB()12AOB ACB AOBC S S S a h OA =+=+△△四边形 类型一、一次函数由动点问题引出的面积问题例1. 如图例1-1,在平面直角坐标系中,直线121y x =+和直线2443y x =-+交于点A . 直线y n =从x 轴出发以每秒2个单位的速度向上运动,至通过A 点时停止. 在运动过程中,直线y n =分别交y 1、y 2两条直线于C 、B 两点,交y 轴于点D . 连接OC 、OB .(1)设运动时间为t (s ),求t 的取值范围.(2)求出△OBC 的面积S 与t 的函数关系式,并求出S 的最大值及此时n 的值.y=n类型二、二次函数由动点问题引出的面积问题例2. 如图例2-1,二次函数y =ax 2+bx +c 的图像与x 轴的交点为A 、D (A 在D 的右侧),与y 轴的交点为C ,且A (4,0),C (0,-3),对称轴是直线x =1. (1)求二次函数的解析式;(2)若M 是第四象限抛物线上一动点,且横坐标为m ,设四边形OCMA 的面积为S .请写出S 与m 之间的函数关系式,并求出当m 为何值时,四边形OCMA 的面积最大.图例2-1图例2-2类型三、反比例函数由动点问题引出的面积问题例3. 如图例3-1,直线y=2x+6与反比例函数kyx(k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.(1)求m的值和反比例函数的表达式;(2)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?图例3-1类型四、利用三角函数求解由动点问题引出的面积问题例4. 如图例4-1,在矩形OABC中,点O为原点,边OA的长度为8,对角线AC=10,抛物线y =-49x 2+bx +c 经过点A 、C ,与AB 交于点D .(1)求抛物线的解析式;(2)点P 为线段BC 上一个动点(不与点C 重合),点Q 为线段AC 上一个动点,AQ =CP ,连接PQ ,设CP =m ,△CPQ 的面积为S . 求S 关于m 的函数表达式并求出S 最大时的m 值.图例4-1.类型五、由动点问题引出的面积存在性问题例5. 如图例5-1,在平面直角坐标系中,△ABC 是等腰直角三角形,∠BAC =90°,A (1,0),B (0,2),C (3,1)抛物线2122y x bx =+-的图象过C 点,交y 轴于点D . (1)在后面的横线上直接写出点D 的坐标及b 的值: ,b = ;(2)平移该抛物线的对称轴所在直线l ,设l 与x 轴交于点G (x ,0),当OG 等于多少时,恰好将△ABC的面积分为相等的两部分?AOxyBCGF H E图例5-1 图例5-2类型六、利用转化思想解决由动点问题引出的面积问题如图例6-1,在平面直角坐标系中,抛物线24 5y ax x c=++与直线2255y x=--交于A、B两点,已知点B的横坐标是4,直线2255y x=--与x、y轴的交点分别为A、C,点P是抛物线上一个动点.(1)求抛物线的解析式;(2)若点P在直线2255y x=--上方,求△P AC的最大面积.OxyPACBGEH 图例6-1专题9:由动点引出的几种面积问题动点题是近年来中考的一个热点问题也是难点问题,而因动点产生的面积问题是这类题目考查的重点. 解这类题目要掌握几个基本图形及思路,而后“以静制动”、“转化求解”. 即把动态问题变为静态问题,变为我们所熟知的模型来解。
由动点产生的面积问题

因动点产生的面积问题1.(南通)如图,已知直线l 经过点A (1,0),与双曲线my x =(x >0)交于点B (2,1).过点P (p ,p ﹣1)(p >1)作x 轴的平行线分别交双曲线m y x =(x >0)和my x=-(x <0)于点M 、N .(1)求m 的值和直线l 的解析式;(2)若点P 在直线y =2上,求证:△PMB ∽△PNA ;(3)是否存在实数p ,使得S △AMN =4S △AMP ?若存在,请求出所有满足条件的p 的值;若不存在,请说明理由.2.当点P运动2秒时,另一动点Q也从A出发沿A→B的路线运动,且在AB上以每秒1cm的速度匀速运动,(当P、Q中的某一点到达终点,则两点都停止运动.)过Q作直线QN,使QN∥PM,设点Q运动的时间为t秒(0≤t≤8),直线PM与QN截平行四边形ABCD所得图形的面积为S(cm2).(1)求S关于t的函数关系式;(2)求S的最大值.⑴略解:①当P、Q同时在AB边上运动时,0≤t≤6.AQ=t,AP=t+2, AF=t,QF=t,AG=(t+2), 由三角函数PG=(t+2),FG=AG-AF=(t+2)-t=1.S =·(QF+PG)·FG=[t+(t+2)]·1=t+.②当6<t≤8时,S=S平行四边形ABCD-S△AQF-S△GCP.易求S平行四边形ABCD=16,S△AQF=AF·QF=t2.而S△CGP=PC·PG,PC=4-BP=4-(t+2-8)=10-t.由比例式可得∴PG=(10-t).∴S△CGP=PC·PG=(10-t)·(10-t)=(10-t)2.∴S=16-t2-(10-t)2=(6<t≤8⑵分析:求面积的最大值时,应用函数的增减性求.若题中分多种情况,那么每一种情况都要分别求出最大值,然后综合起来得出一个结论.此题分两种情况,那么就分别求出0≤t≤6和6<t≤8时的最大值. 0≤t≤6时,是一次函数,应用一次函数的性质,由于一次项系数是正数,面积S随t的增大而增大.当6<t≤8时,是二次函数,应用配方法或公式法求最值.略解:由于所以t=6时,S=;由于S=(6<t≤8,所以t=8时,S最大=6.综上所述, 当t=8时,S最大=6.3.如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l 与菱形OABC的两边分别交于点M、N(点M在点N的上方).1.求A、B两点的坐标;2.设△OMN的面积为S,直线l运动时间为t秒(0≤t≤6),试求S与t的函数表达式;3.在题(2)的条件下,t为何值时,S的面积最大?最大面积是多少?1.分析:由菱形的性质、三角函数易求A、B两点的坐标.解:∵四边形OABC为菱形,点C的坐标为(4,0),∴OA=AB=BC=CO=4.如图①,过点A作AD⊥OC于D.∵∠AOC=60°,∴OD=2,AD=.∴A(2, ),B(6, ).2.分析:直线l在运动过程中,随时间t的变化,△MON的形状也不断变化,因此,首先要把所有情况画出相应的图形,每一种图形都要相应写出自变量的取值范围。
因动点产生的面积问题

1
例题 5 如图平面直角坐标系中,O 是坐标原点,抛物线y = ������ 2 − 4������ + ������与������轴
交于 A、B 两点(点 A 在点 B 的左侧) ,与������轴的负半轴交于点 C,且OB = OC。 1) 求该抛物线的解析式及点 B 的坐标; 2) P 是线段 OB 上的一点,过点 P 作PD ⊥ ������轴,与抛物线交于 D 点,直线 BC 能 否把∆������������������分成面积之比为2: 3的两部分?如能, 请求出点 P 的坐标; 如不能, 请说明理由。
������
Hale Waihona Puke 例题 3 如图,已知直线y = 2 ������与双曲线 y = ������ (k > 0)交于 A、B 两点,且点 A
的横坐标为 4. 1) 求 K 的值; 2) 若双曲线上的一点 C 的纵坐标为 8,求 AOC 的面积; 3) 过原点 O 的另一条直线交双曲线与 P、Q 两点(P 点在第一象限) ,若由 A、 B、P、Q 为顶点组成的四边形面积为 24,求点 P 的坐标。
第五篇因动点产生的面积问题 例题 1 如图已知一次函数y = ax − a(a ≠ 0)的图像是直线l,点 E 是直线l与y轴的
交点。 1) 证明:当a取不等于 0 的实数时,直线l都经过x轴上的一个定点 P,并求这个 定点 P 的坐标; 2) 在x轴上找出点 Q,使 S∆PQE=2S∆OPE ,求出点 Q 的坐标。
例题 2 如图,点 P、点 Q 分别在x轴、y轴上。
1) 已知点 P(3,0) ,Q(0,4) ,点 M 在线段 PQ 上,直线 OM 把∆POQ 分成两 个三角形,且这两个三角形的面积的比是 2:1,求直线 MO 的函数解析式; 2) 如图,已知 P(m,0) ,Q(0,n) (m>0,n>0),反比例函数y = ������ 的图像与线 段 PQ 交于 C、D 两点,若 S∆POC=S∆COD=S∆DOQ 求 n 的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)如图(3),在Rt△CDE的运动过程中,当CE经过点B时,求BC的长.
(3)在Rt△CDE的运动过程中,设AC=h,△OAB与△CDE的重叠部分的面积为S,请写出S与h之间的函数关系式,并求出面积S的最大值.
13.如图,在平面直角坐标系 中,已知抛物线 与直线 都经过 、 两点,该抛物线的顶点为C.
(1)求此抛物线和直线 的解析式;
(2)设直线 与该抛物线的对称轴交于点E,在射线 上是否存在一点M,过M作x轴的垂线交抛物线于点N,使点M、N、C、E是平行四边形的四个顶点?若存在,求点M的坐标;若不存在,请说明理由;
(3)M是直线OC上方抛物线C2上的一个动点,连接MO,MC,M运动到什么位置时,△MOC面积最大?并求出最大面积.
15.如图,抛物线 交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且 ,求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
A. B. C. D.
5.如图,点A是直线y=﹣x上的动点,点B是x轴上的动点,若AB=2,则△AOB面积的最大值为( )
A.2B. +1C. -1D.2
6.如图,已知 ,以 为圆心, 长为半径作 , 是 上一个动点,直线 交 轴于 点,则 面积的最大值是( )
A. B. C. D.
7.如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=﹣x2+6x上一点,且在x轴上方,则△BCD面积的最大值为__________
A. B.
C. D.
3.如图,已知直线 与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是()
A.8B.12C. D.
4.如图,在等腰直角三角形 中, , , 是 边上的高,正方形 的边 在高 上, , 两点分别在 , 上.将正方形 以每秒 的速度沿射线 方向匀速运动,当点 与点 重合时停止运动.设运动时间为 ,正方形 与 重叠部分的面积为 ,则能反映 与 的函数关系的图象()
18.已知抛物线y=ax2+bx+3(a≠0)经过A(3,0),B(4,1)两点,且与y轴交于点C.
(1)求抛物线y=ax2+bx+3(a≠0)的函数关系式及点C的坐标;
(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点P,使△PAB是以AB为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(1)求a、b及sin∠ACP的值;
(2)设点P的横坐标为m.
①用含m的代数式表示线段PD的长,并求出线段PD长的最大值;
②连结PB,线段PC把△PDB分成两个三角形,是否存在适合的m的值,使这两个三角形的面积比为9∶10?若存在,直接写出m的值;若不存在,请说明理由.
【例4】如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,动点P从点A出发,沿AB以每秒2个单位长度的速度向终点B运动.过点P作PD⊥AC于点D(点P不与点A、B重合),作∠DPQ=60°,边PQ交射线DC于点Q.设点P的运动时间为t秒.
16.如图,抛物线 的图象过点 .
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在一点P,使得△PAC的周长最小,若存在,请求出点P的坐标及△PAC的周长;若不存在,请说明理由;
(3)在(2)的条件下,在x轴上方的抛物线上是否存在点M(不与C点重合),使得 ?若存在,请求出点M的坐标;若不存在,请说明理由.
(1)求该抛物线的解析式及点E的坐标;
(2)若D点运动的时间为t,△CED的面积为S,求S关于t的函数关系式,并求出△CED的面积的最大值.
12.如图1,抛物线 与 轴交于 两点,与 轴交于点 ,连结AC,若
(1)求抛物线的解析式;
(2)抛物线对称轴上有一动点P,当 时,求出点 的坐标;
(3)如图2所示,连结 , 是线段 上(不与 、 重合)的一个动点.过点 作直线 ,交抛物线于点 ,连结 、 ,设点 的横坐标为.当t为何值时, 的面积最大?最大面积为多少?
(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求点E的坐标.
19.如图,抛物线y=ax2+bx(a>0)过点E(8,0),矩形ABCD的边AB在线段OE上(点A在点B的左侧),点C、D在抛物线上,∠BAD的平分线AM交BC于点M,点N是CD的中点,已知OA=2,且OA:AD=1:3.
如图5,同底三角形的面积比等于高的比.
如图6,同高三角形的面积比等于底的比.
图4图5图6
【典例分析】
【例1】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(-1,0),B(4,0)两点,与y轴交于点C(0,2).点M(m,n)是抛物线上一动点,位于对称轴的左侧,并且不在坐标轴上.过点M作x轴的平行线交y轴于点Q,交抛物线于另一点E,直线BM交y轴于点F.
17.如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(-1,0)、B(4,0)、C(0,2)三点.
(1)求该二次函数的解析式;
(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;
(3)点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若△PEB、△CEF的面积分别为S1、S2,求S1-S2的最大值.
(1)求B点坐标;
(2)设运动时间为t秒。
①当t为何值时,四边形OAMN的面积是梯形OABC面积的一半;
②当t为何值时,四边形OAMN的面积最小,并求出最小面积。
③若另有一动点P,在点M、N运动的同时,也从点A出发沿AO运动。在②的条件下,PM+PN的长度也刚好最小,求动点P的速度。
10.如图,(图1,图2),四边形ABCD是边长为4的正方形,点E在线段BC上,∠AEF=90°,且EF交正方形外角平分线CP于点F,交BC的延长线于点N, FN⊥BC.
【变式训练】
1.如图,利用一个直角墙角修建一个梯形储料场ABCD,其中∠C=120°.若新建墙BC与CD总长为12m,则该梯形储料场ABCD的最大面积是()
A.18m2B. m2C. m2D. m2
2.如图,正方形 的边长为 ,动点 , 同时从点 出发,在正方形的边上,分别按 , 的方向,都以 的速度运动,到达点 运动终止,连接 ,设运动时间为 , 的面积为 ,则下列图象中能大致表示 与 的函数关系的是( )
8.如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE,那么DE长的最小值是______________.
9.已知直角梯形OABC在如图所示的平面直角坐标系中,AB∥OC,AB=10,OC=22,BC=15,动点M从A点出发,以每秒一个单位长度的速度沿AB向点B运动,同时动点N从C点出发,以每秒2个单位长度的速度沿CO向O点运动。当其中一个动点运动到终点时,两个动点都停止运动。
(1)用含t的代数式表示线段DC的长;
(2)当点Q与点C重合时,求t的值;
(3)设△PDQ与△ABC重叠部分图形的面积为S,求S与t之间的函数关系式;
(4)当线段PQ的垂直平分线经过△ABC一边中点时,直接写出t的值.
【例5】如图,直线l经过点A(1,0),且与双曲线 (x>0)交于点B(2,1).过点 (p>1)作x轴的平行线分别交曲线 (x>0)和 (x<0)于M、N两点.
备战2020中考数学之解密压轴解答题命题规律
专题04 因动点产生的面积问题
【类型综述】
面积是平面几何中一个重要的概念,关联着平面图形中的重要元素边与角,由动点而生成的面积问题,是抛物线与直线形结合的觉形式,常见的面积问题有规则的图形的面积(如直角三角形、平行四边形、菱形、矩形的面积计算问题)以及不规则的图形的面积计算,解决不规则的图形的面积问题是中考压轴题常考的题型,此类问题计算量较大。有时也要根据题目的动点问题产生解的不确定性或多样性。解决这类问题常用到以下与面积相关的知识:图形的割补、等积变形、等比转化等数学方法.面积的存在性问题常见的题型和解题策略有两类:一是先根据几何法确定存在性,再列方程求解,后检验方程的根.二是先假设关系存在,再列方程,后根据方程的解验证假设是否正确.
(1)若点E是BC的中点(如图1),AE与EF相等吗?
(2)点E在BC间运动时(如图2),设BE=x,△ECF的面积为y.
①求y与x的函数关系式;
②当x取何值时,y有最大值,并求出这个最大值.
11.如图,已知抛物线y=﹣ x2 +bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
(3)设点P是直线 下方抛物线上的一动点,当 面积最大时,求点P的坐标,并求 面积的最大值.
14.如图,抛物线C1:y=x2﹣2x与抛物线C2:y=ax2+bx开口大小相同、方向相反,它们相交于O,C两点,且分别与x轴的正半轴交于点B,点A,OA=2OB.
(1)求抛物线C2的解析式;
(2)在抛物线C2的对称轴上是否存在点P,使PA+PC的值最小?若存在,求出点P的坐标,若不存在,说明理由;
【方法揭秘】
解决动点产生的面积问题,常用到的知识和方法,如下:
如图1,如果三角形的某一条边与坐标轴平行,计算这样“规则”的三角形的面积,直接用面积公式.
