高等数学(同济第六版)课件 第三章 1.中值定理
同济大学数学系《高等数学》(第6版)上册笔记和课后习题(含考研真题)详解-微分中值定理与导数的应用(

在带有佩亚诺型余项的泰勒公式中,如果取 x0=0,则有带有佩亚诺型余项的麦克劳林 公式:
。 如 果 存 在 正 实数 M 使得 区 间 ( -r, r ) 里 的任意 x 都 有
,如果当 n 趋向于无穷大时,
,则
,那么 。
可得近似公式:
。
5 / 84
圣才电子书 十万种考研考证电子书、题库视频学习平台
四、函数的单调性 微分中值定理,强调了函数值与导数之间的关系。这部分主要介绍如何通过函数的导数 来判定函数的单调性或凹凸性等性质。 1.单调性的判定 【定理】设函数 y=f(x)在[a,b]上连续,在(a,b)内可导。 (1)如果在(a,b)内 f'(x)>0,那么函数 y=f(x)在[a,b]上单调增加; (2)如果在(a,b)内 f'(x)<0,那么函数 y=f(x)在[a,b]上单调减少; 如果把这个判定法中的闭区间换成其他各种区间(包括无穷区间),那么结论也成立。 这是函数单调性判定的一个最基本也是最重要的法则。
2 / 84
圣才电子书 十万种考研考证电子书、题库视频学习平台
那么在(a,b)内至少有一点 ε,使等式
成立。
拉格朗日中值公式是柯西中值公式的特殊形式。
二、洛必达法则 洛必达法则在求函数极限过程中,有重要作用,在考研试题中也经常出现。一般,洛必 达法则针对 或 形式的极限公式。下面我们主要介绍相关定理及引入一些例题,方便读 者更进一步理解洛必达法则的应用。 1.x→a 【定理】设 (1)当 x→a 时,函数 f(x)及 F(x)都趋于零; (2)在点 a 的某去心邻域内,f'(x)及 F'(x)都存在且 F'(x)≠0;
(3)Biblioteka 存在(或为无穷大),那么
。
关于高等数学同济第六版上册期末复习重点

关于高等数学同济第六版上册期末复习重点标准化管理部编码-[99968T-6889628-J68568-1689N]第一章:1、极限(夹逼准则)2、连续(学会用定义证明一个函数连续,判断间断点类型)第二章:1、导数(学会用定义证明一个函数是否可导)注:连续不一定可导,可导一定连续2、求导法则(背)3、求导公式也可以是微分公式第三章:1、微分中值定理(一定要熟悉并灵活运用--第一节)2、洛必达法则3、泰勒公式拉格朗日中值定理4、曲线凹凸性、极值(高中学过,不需要过多复习)5、曲率公式曲率半径第四章、第五章:积分不定积分:1、两类换元法 2、分部积分法(注意加C )定积分: 1、定义 2、反常积分第六章:定积分的应用主要有几类:极坐标、求做功、求面积、求体积、求弧长第七章:向量问题不会有很难1、方向余弦2、向量积3、空间直线(两直线的夹角、线面夹角、求直线方程) 3、空间平面4、空间旋转面(柱面)第一章函数与极限1、函数的有界性在定义域内有f(x)≥K1则函数f(x)在定义域上有下界,K1 为下界;如果有f(x)≤K2,则有上界,K2称为上界。
函数f(x)在定义域内有界的充分必要条件是在定义域内既有上界又有下界。
2、数列的极限定理(极限的唯一性)数列{xn}不能同时收敛于两个不同的极限。
定理(收敛数列的有界性)如果数列{xn}收敛,那么数列 {xn}一定有界。
如果数列{xn}无界,那么数列{xn}一定发散;但如果数列{xn}有界,却不能断定数列{xn}一定收敛,例如数列 1,-1,1,-1,(-1)n+1…该数列有界但是发散,所以数列有界是数列收敛的必要条件而不是充分条件。
定理(收敛数列与其子数列的关系)如果数列{xn}收敛于a,那么它的任一子数列也收敛于a.如果数列{xn}有两个子数列收敛于不同的极限,那么数列{xn}是发散的,如数列 1,-1,1,-1,(-1)n+1…中子数列{x2k-1}收敛于1,{xnk}收敛于-1,{xn}却是发散的;同时一个发散的数列的子数列也有可能是收敛的。
高数同济六版课件D31微分中值定理共29页

02.10.2019
高数同济六版
目录 上页 下页 返回 结束
例3. 证明不等式 xln 1 (x)x(x0). 1x
证: 设 f(t)ln 1 t(), 中值定理条件, 因此应有
即 因为 故
02.10.2019
高数同济六版
目录 上页 下页 返回 结束
三、柯西(Cauchy)中值定理
不妨设
则至少存在一点
使
则由费马引理得 f()0. y
注意:
yf(x)
1) 定理条件条件不全具备, 结论不一定 O a
bx
成立. 例如,
y
O
02.10.2019
1x
y
y
1 O
高数同济六版
1x O 1 x
目录 上页 下页 返回 结束
2) 定理条件只是充分的. 本定理可推广为
在 ( a , b ) 内可导, 且
备用题
1. 设 f ( x) 在 [0,1] 连续,(0 ,1) 可导,且 f(1)0,
求证存在 (0,1),使 证: 设辅助函数 (x)xnf(x)
显然 (x) 在 [ 0 ,1] 上满足罗尔定理条件,
因此至少存在 (0,1), 使得
() nn1f()nf() 0
limf(x) lim f (x)
xa
xb
在( a , b ) 内至少存在一点 使
证明提示: 设
证 F(x) 在 [a , b] 上满足罗尔定理 .
02.10.2019
高数同济六版
目录 上页 下页 返回 结束
例1. 证明方程
有且仅有一个小于1 的
正实根 .
证: 1) 存在性 .
设 f(x)x55x1,则 f (x) 在 [0 , 1 ] 连续 , 且
中值定理与导数的应用(高等数学)省名师优质课赛课获奖课件市赛课一等奖课件
定义 使导数为零的点(即方程f ( x) 0的实根)叫 做函数f ( x)的驻点.
定理(必要条件) 设 f ( x) 在点x0 处具有导数,且 在 x0处取得极值,那末必定 f '( x0 ) 0.
注意:可导函数 f ( x) 的极值点必定是它的驻 点, 但函数的驻点却不一定 是极值点.
2、罗必塔法则
(1). 0 型及 型未定式 0
定义 这种在一定条件下经过分子分母分别求导再 求极限来拟定未定式旳值旳措施称为罗必塔法则.
(2). 0 , , 00,1 , 0型未定式
关键:将其他类型未定式化为罗必塔法则可处理 旳类型 ( 0 ), ( ) .
0
定理 设(1)当x 0时,函数 f ( x) 及 F ( x) 都趋于零; (2) 在 a 点的某领域内(点 a 本身可以除外 ), f ( x) 及 F ( x) 都存在且 F ( x) 0; (3) lim f ( x) 存在(或为无穷大);
(2) 在开区间 ( a , b ) 内可导
(3)在开区间 ( a , b ) 内F(x) 0
至少存在一点
(a,b) , 使
f (b) f (a) F (b) F (a)
f ( ) . F( )
注意:若令F(x)=x,则柯西中值定理变为拉氏中值 定理,即拉
0
原式
lim
x
1
1
x 1 x2
2
lim
x
1
x
2
x
2
1.
例8
求
lim
x0
tan x x2 tan
x x
.
解
同济大学高等数学第六版上册第三章第三节Taylor泰勒公式

o
x0
x
LL LL
假设
0
Pn( k ) ( x0 ) = f ( k ) ( x0 ) k = 1,2,L, n
a = f ( x ),
1 ⋅ a = f ′( x ),
1 0
2!⋅a = f ′′( x )
2 0
L L , n!⋅a n = f ( n ) ( x 0 ) 1 (k ) 得 ak = f ( x0 ) ( k = 0,1,2,L , n ) k!
f ( x ) = f ( x 0 ) + f ′(ξ )( x − x 0 ) (ξ在x 0与x之间)
2.取 x 0 = 0, ξ 在0 与 x 之间,令ξ = θx
(0 < θ < 1) f ( n + 1) (θx ) n + 1 x 则余项 Rn ( x ) = ( n + 1)!
四、简单的应用
即 Rn ( x ) = o[( x − x0 )n ].
M ≤ ( x − x0 )n+1 (n + 1)!
皮亚诺形式的余项
∴ f ( x) = ∑
k =0
n
f
(k )
( x0 ) ( x − x0 )k + o[( x − x0 )n ] k!
注意:
1. 当 n = 0 时,泰勒公式变成拉氏中值公式
(n + 1) !
(1 + θ x)α −n−1 x n+1 (0 < θ < 1)
(5) f ( x) = ln(1 + x) ( x > −1) k −1 ( k − 1) ! (k ) (k = 1, 2 ,L) 已知 f ( x) = (−1) k (1 + x) 类似可得 x 2 x3 xn n −1 ln(1 + x) = x − − L + (−1) + + Rn (x) 2 3 n
55同济大学第六版高数第3章1PPT课件

C
Y f (x)
M
B
KAB f(b)f(a) F(b)FF(x)
D
X F(2)F(b)
弦 A:Y B f(a )f(b ) f(a )[X F (a )] F (b ) F (a )
一个小于1 的正实根 证 设 f(x ) x 5 5 x 1 ,则f(x)在 [0,1]连,续
且 f(0 ) 1 ,f( 1 ) 3 .
x0(0,1)使 , f(x0)0即为方程的小于1的正实根. 设x 1 另 (0 ,1 )x 有 1 , x 0 ,使 f(x1)0. 0x 0x 1 1 f(x)在x0,x1之间满足罗尔定 件, 理的条 至少存 (在 x 在 0,x1之 一 )使 间 ,个 f得 ()0.
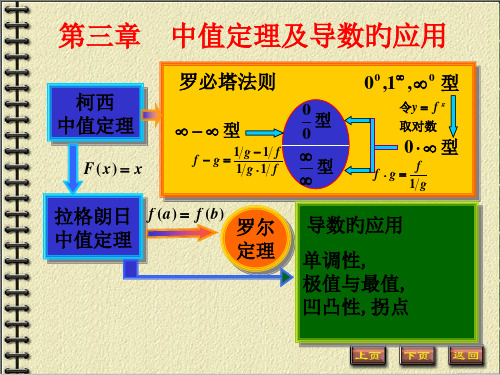
第三章 中值定理与导数的应用
第一节 中值定理
预备知识
y
① f( )lim f( x )f( )
x 0
x
②f()表示曲y线 f(x)
在x处 切 线 的 斜 率o
y=f(x)
x
1
一、罗尔(Rolle)定理
罗尔定理
若函数 f(x)满足
y
C
1 在闭 [a ,b 区 ]上间 连续
A
yf(x)
B
2在开 (a,b 区 )内间 可导
D
3 f(a )f(b )
oa
2 b x
则在 (a,b)内至少有一点(几何解释) 使f()0
2
证:f(x)在 [a,b]连,续 必有最 M大 和值 最m 小 . 值
(1)若 Mm. 则f(x)M. 由此 f(x得 )0.
(a,b), 都f有 ()0. (2)若 Mm . f(a)f(b), 最值不可能同时在取端得点 . 设 Mf(a), 则(在 a,b)内至少存 使 f(在 )M 一 . 点 f( x ) f( ) 0,
《高等数学(上册)》课件 第三章

高等数学
01 中值定理与洛 必达法那么
02 函数的单调性、 极值与最值
03 函数图形的描绘
例7
求
ln x
lim
x
xn
(n 0).
解 此题属于“ ”型未定式,应用洛必达法则有
1
xl im ln xnxxl im nxxn1
1 lim
xnxn
0
高等数学
01 中值定理与洛 必达法那么
02 函数的单调性、 极值与最值
高等数学
01 中值定理与洛 必达法那么
02 函数的单调性、 极值与最值
03 函数图形的描绘
在使用洛必达法则时,应注意如下几点:
0
0
lim f ( x ) g ( x )
lim f ( x ) g (x)
高等数学
01 中值定理与洛 必达法那么
02 函数的单调性、 极值与最值
03 函数图形的描绘
高等数学
推论2 如果对(a,b)内的任意x,均有f ’(x)= g ’(x) ,那么 在(a,b)内f(x)与g(x)之间只差一个常数,即f(x)= g(x) +C〔 C 为 常数〕.
高等数学
01 中值定理与洛 必达法那么
02 函数的单调性、 极值与最值
03 函数图形的描绘
高等数学
01 中值定理与洛 必达法那么
02 函数的单调性、 极值与最值
03 函数图形的描绘
例1 函数f(x)=1-x2在区间[-1,2]上是否满足拉格朗日 中值定理条件?假设满足,找出点.
解 函数f(x)=1-x2在区间[-1,2]上连续,在(-1,2)上可
导,因此,满足拉格朗日定理的条件,即至少存在一点
ξ ,使
同济高等数学第三章第一节课件

即 设
f ( x ) sin x x=x
F ( x ) = f ( x ) sin x
=0
验证 F ( x ) 在 [ 0 , ] 上满足罗尔定理条件.
首页
上页
返回
下页
结束
铃
2. 若 f ( x )可导, 试证在其两个零点间一定有
f ( x ) f ( x ) 的零点.
提示: 设 f ( x1 ) = f ( x2 ) = 0 , x1 < x2 ,
直线AB的斜率
f (b) f (a) k= ba f (b) f (a) f (x)= ba
首页 上页 返回 下页 结束 铃
拉格朗日中值定理 如果函数f(x)在闭区间[a b]上连续 在开区间(a b)内 可导 那么在(a b)内至少有一点x 使得 f(b)f(a)=f (x)(ba) 简要证明 令j(x)=f (x)f (a) f (b) f (a) (xa) ba 则函数j(x)在区间[a b]上满足罗尔定理的条件 于是至少存在一点x(a b) 使j (x)=0 即
1 由于 f (0)=0 f (x) = 因此上式即为 1 x ln(1 x) = x 1x 又由0<x<x 有 x < ln(1 x) < x 1 x
首页
上页
返回
下页
结束
铃
例4. (p132 6)证明等式
证: 设
由推论可知 令x=0,得
(常数)
又
故所证等式在定义域
上成立.
由此得
f (b) f (a) =0 j (x)=f (x) ba f(b)f(a)=f (x)(ba)
首页
上页
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x ln(1 x ) x . 1 x
x x 所以 x 1 x 1
1 1 练习 证明 ln( n 1) ln n . 1 n n
证: 设 f(x) = lnx 在[n,n+1]上, 由拉格朗日定理得:
ln( n 1) ln( n)
( 1) 证明至少存在一点 0, 使 f ( ) f ( ) 0
证 设 F(x) = x f (x)
因为f(x)在[0,1]上连续,在(0,1)内可导,
所以F(x)在[0,1]上连续,在(0,1)内可导,
又F(0)=0, F(1)=1· f(1)=0
( 1) 由罗尔定理:至少存在一点 0, 使 F ( ) 0
第三章 中值定理与导数的应用 第一节 中值定理
一、费马引理 设函数 f (x)在点的某邻域U(x0)内有定义, 且在x0点可导,若对任意x∈U(x0)有ff (x)≤ f(x00)) , (x)≥ f(x , 则 f ( x0 ) 0. 证明: 对任意x∈U(x0) 由f (x)≤ f(x0) 得f (x)- f(x0) ≤0
C
D
B
o a
1
2 b
x
f (b) f (a ) (x a) 证 设 F ( x) f ( x) ba
∵函数 f (x)在[a,b]上连续,在(a,b)内可导;
∴函数 F(x)在[a,b]上连续,在(a,b)内可导;
F (a ) f (a )
f (b) f (a ) F (b) f (b) (b a ) f (a ) ba 故至少存在一点ξ∈ (a,b) ,使得 F () 0.
f ( )
f (b) f (a ) 0 ba
注 1.设f(x)在[a,b]上连续,在(a,b)内可导
x0 , x0 x (a , b), 则有
f ( x0 x ) f ( x0 ) f ( x0 x ) x (0 1).
2. 若f(x)在[a,b]上可导, 则拉格朗日定理结论成立。
证 设F(x)=f(x)-tanx
F (0) f (0) 0, F ( ) f ( ) 1 0 4 4 ∴在 (0, ) 内至少有一个a, 使F(a)=0, 4 即 f(a)=tana
设在 (0, ) 内另有一个点b, 使f(b)=tanb 4 则F(b)= f(b)-tanb = 0 = F(a) ∵函数 f(x)在上 [0, ] 可导, 4 由罗尔定理:至少存在一点 (a , b ) 使 F ( ) 0
由f (x)在x0可导,知 f ( x0 ) f ( x0 ) f ( x0 ) f ( x0 ) 0
注:若x0∈(a,b), ( x0 ) 0.
二、罗尔(Rolle)定理 罗尔定理 若函数 f(x)满足
不妨设M不在区间端点取得,
则存在 (a , b), f ( ) M 由费马引理: f ( ) 0
例1 证明方程 x5 -5x+1=0有且仅有一个小于1 的正实根 证 设 f(x)= x5 -5x+1, 则f(x)在[0,1]上连续 且f(0)=1 ,f(1)=-3
由零点定理:至少存在一点x0∈(0,1)使 f ( x0 ) 0
故方程x5 -5x+1=0有小于1的正实根. 设方程x5 -5x+1=0另有一个小于1的正实根x1 得 f(x1) = 0
因 f(x)= x5 -5x+1在[x0, x1](或[x1, x0])上可导,
且 f(x0) = f(x1)
由罗尔定理知:在x0与x1之间至少存在一点ξ,
使 f () 0
1
( n n 1)
1 1 ln( n 1) ln n . 故: 1 n n
例5 若函数 f(x) 在[a,b]上连续, 在(a,b)内可导,
f(b) =f(a), 且f(x)不恒为常数,
证明至少存在一点ξ∈ (a,b) ,使得
f ( ) 0
证 因为f(b) =f(a),且f(x)不恒为常数,
由于 F ( x )在[1,c]上连续、可导,
故在(1,2)内至少存在一点ξ,使 F ( ) 0
注意:若罗尔定理的三个条件中有一个不满足, 其结论可能不成立。
y
y=f(x)
y
y=f(x)
A
B
A
B
o y
a
y=f(x)
b
B
x
o
a
b
x
A
f (b) f (a ) KAB ba f (b) f (a ) f () ba
c (a , b ), f (c ) f (a )
(1)若f(c) > f(a)= f(b) ,在[a,c]上由拉格朗日定理知,
f (c ) f (a ) 至少存在一点ξ∈ (a,c), 使 f ( ) 0 ca
(2)若f(c) < f(a)= f(b) ,在[c, b]上由拉格朗日定理知, 至少存在一点ξ∈ (c,b), 使
而在(0,1)内 f ( x ) 5 x 4 5 0, 矛盾, 故方程 x5 -5x+1=0有且仅有一个小于1 的正实根
练习 设函数 f(x)在上 [0, ] 可导,且 0<f(x)<1, 4 在 (0, ) 内 f ( x ) sec2 x 4 证明在 (0, ) 内有且仅有一个x,使f(x)=tanx 4
f (b) f (c ) f ( ) 0 bc
综上,至少存在一点ξ∈ (a,b) ,使得 f ( ) 0
X F ( x) L: Y f ( x)
Yy
CC
A A
y f ( x)
B B
端点:A( F (a ), f (a )), B( F (b ), f (b ))
四、柯西(Cauchy)中值定理
柯西定理 如果函数 f (x)、F(x)满足
(1)在闭区间[a, b]上连续, (2)在开区间(a, b)内可导,
且在(a, b)内每一点处 F ( x ) 均不为零,
Y
C
A
1
X F ( x) L: Y f ( x)
B
则在(a, b)内至少有一点ξ , o F (a ) F ( ) f ( b ) f ( a ) f ( ) 使等式 成立 F ( b ) F ( a ) F ( )
D
1
D
o (a ) o Fa ) F ( 1
K切 dY f ( ) dX F ( )
F ( 2 )F (b ) 2
b
x X
f (b) f (a ) KAB F (b) F (a )
f ( b ) f ( a ) f ( ) F ( b ) F ( a ) F ( )
证明至少存在一点 (0,1), 使 f ( ) 2[ f (1) f (0)]. 证 设 F ( x) x2 , 函数 f(x)、F(x)在[0,1]上满足柯西定理条件, 则至少存在一点ξ∈ (0,1) ,使 f (1) f (0) f ( ) f (1) f (0) f () , F (1) F (0) F ( ) 1 0 2
f () 2[ f (1) f (0)].
y
C
y f ( x)
几何解释: 连续曲线AB, 若除端点外,
B
D
A
o a
y
C
1
2
b
处处有不垂直于x 轴切线, 则该曲线上至少有一点的 x 切线平行于端点连线AB。
y f ( x)
Y
B
C
X F ( x) Y f ( x)
B
A
D
f (b) f (a ) f ( ). ba
f ( ) 0
罗尔定理、拉格朗日中值定理及柯西中值定理 之间的关系;
f (a ) f (b)
F ( x) x
Rolle 定理
Lagrange 中值定理
Cauchy 中值定理
例6
若函数 f(x) 在[0,1]上连续, 在(0,1)内可导,
(1)在闭区间[a,b]上连续
(2)在开区间(a,b)内可导 (3) f(a)= f(b) 则在(a,b)内至少存在一点ξ, 使 f () 0
y
C
y f ( x)
A
D
B
o a
2
b
x
(几何解释)
证 因函数 f(x)闭区间[a,b]上连续, 故 f(x)在[a,b]上必有最大值M和最小值m. (1)若M = m,则 f(x)= m (常数), 故 (a , b), f () 0 (2)若M≠m,因f(a)= f(b) 故M和m至少有一个不在区间端点取得,
f 当x< x0时, ( x ) f ( x0 ) 0 x x0 o f ( x ) f ( x0 ) ( x0 ) lim f 0 x x0 x x0
y
y=f(x)
x0
x
当x> x0时,f ( x ) f ( x0 ) 0 x x0 f ( x ) f ( x0 ) f ( x0 ) lim 0 x x0 x x0
F ( 2 )F (b )
X
当 F ( x ) x , F (b) F (a ) b a , F ( x ) 1,
f ( b ) f ( a ) f ( ) F ( b ) F ( a ) F ( )
当 f(b)=f(a)时,
f (b) f (a ) f ( ) ba
