二元一次方程组全章提升
中考数学总复习《二元一次方程组》专项提升练习(附答案)

中考数学总复习《二元一次方程组》专项提升练习(附答案)学校:___________班级:___________姓名:___________考号:___________知识点复习一、二元一次方程组定义1:含有两个未知数,并且含有未知数的项的次数都是1的方程叫做二元一次方程,它的一般形式是()00,0ax by c a b ++=≠≠。
定义2:把两个方程合在一起,就组成了方程组。
定义3:方程组中有两个未知数,含有每个未知数的项的次数都是1,并且一共有两个方程,这样的方程组叫做二元一次方程组。
定义4:使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解。
定义5:二元一次方程组的两个方程的公共解,叫做二元一次方程组的解。
二、解二元一次方程组的方法(1)代入消元法:把二元一次方程组中一个方程的一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解。
这种方法叫做代入消元法,简称代入法。
(2)加减消元法:当二元一次方程组的两个方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程。
这种方法叫做加减消元法,简称加减法。
三、方程(组)与实际问题解有关方程(组)的实际问题的一般步骤:第1步:审题。
认真读题,分析题中各个量之间的关系。
第2步:设未知数。
根据题意及各个量的关系设未知数。
第3步:列方程(组)。
根据题中各个量的关系列出方程(组)。
第4步:解方程(组)。
根据方程(组)的类型采用相应的解法。
第5步:答。
专题练习一、单选题1.已知关于x ,y 的二元一次方程组3221ax y x y +=⎧⎨-=⎩无解,则a 的值是( ) A .2 B .6 C .2- D .6-2.已知23a b -=,1a b +=则36a b -的值为( )A .6B .4C .3D .23.某班有x 人,分y 组活动,若每组7人,则余下3人;每组8人,则有一组差5人,根据题意下列方程组正确的是( )A .7385y x y x =+⎧⎨=+⎩B .7385y x x y =+⎧⎨=-⎩C .7385y x y x =-⎧⎨=+⎩D .7385x y x y =-⎧⎨=+⎩ 4.文峰超市以同样的价格卖出同样的牙刷和牙膏,以下是4天的记录:第1天,卖出13支牙刷和7盒牙膏,收入144元;第2天,卖出18支牙刷和11盒牙膏,收入219元;第3天,卖出23支牙刷和20盒牙膏,收入368元;第4天,卖出17支牙刷和11盒牙膏,收入216元.已知第1天和第2天的记录无误,第3天和第4天有一天的记录有误,则记录有误的一天收入( )A .多记1元B .多记2元C .少记1元D .少记2元5.两位同学在解方程组273ax by cx y +=⎧⎨+=⎩时,甲同学正确地解出11x y =-⎧⎨=-⎩,乙同学因把c 抄错了解得32x y =-⎧⎨=-⎩,则a 、b 、c 正确的值应为( )A .315a b c =-=-=-,,B .115a b c ==-=-,,C .2410a b c ==-=-,,D .315a b c ===-,,6.小华准备购买单价分别为4元和5元的两种瓶装饮料,且每种瓶装饮料的购买数量不为0.若小华将50元恰好用完,则购买方案共有( )A .2种B .3种C .4种D .5种7.在一个停车场,停了小轿车和摩托车一共32辆,这些车一共有108个轮子,则该停车场小轿车和摩托车的辆数分别为( )A .21,11B .22,10C .23,9D .24,8 8.已知关于x ,y 的方程2|18|(26)(2)0n m m x n y +--++=是二元一次方程,则m n +的值(若29m =,则3m =±)是( )A .5-B .3-C .1D .3二、填空题9.当方程组2520x ay x y +=⎧⎨-=⎩解是正整数时,整数a 值为 . 10.如果35x y =⎧⎨=-⎩是方程22mx y +=-的一组解,那么m 的值为 . 11.若关于x y ,的方程组1235x y c x y c +=⎧⎨+=⎩的解为56x y =⎧⎨=⎩,则方程组()()()()12113151x y c x y c ⎧-++=⎪⎨-++=⎪⎩的解为 .12.A,B两地相距80千米,一船从A出发顺水行驶4小时到达B,而从B出发逆水行驶5小时才能到达A,则船在静水中的航行速度是千米/时.13.若关于x的不等式组20,21xx m-<⎧⎨-≥-⎩恰有三个整数解,关于x的方程组26,3x yx y m+=⎧⎨-=⎩的解是正数,则m的取值范围是.三、解答题14.解方程组:(1)25 328 y xx y=-⎧⎨-=⎩(2)434 2312x yx y⎧+=⎪⎨⎪-=⎩15.已知方程组45321x yx y+=⎧⎨-=⎩和31ax byax by+=⎧⎨-=⎩有相同的解,求222a ab b-+的值.16.用加减法解方程组344328x y x y -=⎧⎨-=⎩①②其解题过程如下: 第一步:-①②,得4248y y --=-,解得23y =. 第二步:把23y =,代入①,得8343x -=,解得209x =. 第三步:所以这个方程组的解为20923x y ⎧=⎪⎪⎨⎪=⎪⎩上述解题过程是否正确?若不正确,则从第几步开始出现错误?请写出正确的解题过程.17.印江河是印江的母亲河,为了确保河道畅通,现需要对一段长为180米的河道进行清淤处理,清淤任务由A 、B 两个工程队先后接力完成,A 工程队每天完成12米,B 工程队每天完成8米,共用时20天. 根据题意,甲、乙两个同学分别列出了尚不完整的方程组如下:甲:128x y x y ⎧+=⎪⎨+=⎪⎩ 乙:128x y x y ⎧+=⎪⎨+=⎪⎩(1)根据甲同学所列的方程组,请你指出未知数x 、y 表示的意义.x 表示______,y 表示______;请你补全乙同学所列的方程组______(2)求A 、B 两工程队分别完成河道清淤多少米?(写出完整的解答过程)18.“一盔一带”安全守护行动在我县开展以来,市场上头盔出现了热销,某商场购进了一批头盔.已知购进6个A型头盔和4个B型头盔需要440元,购进4个A型头盔和6个B型头盔需要510元.(1)购进1个A型头盔和1个B型头盔分别需要多少元?(2)若该商场准备购进200个这两种型号的头盔,总费用不超过10200元,那么最多可购买B型头盔多少个?(3)在(2)的条件下,若该商场分别以售价为58元/个、98元/个的售价销售完A、B两类型号的头盔共200个,能否实现利润不少于6190元的目标?若能,直接写出相应的采购方案;若不能,请说明理由.参考答案:1.D2.A3.C4.C5.C6.A7.B8.B9.1或3-10.83/22311.65 xy⎧=⎨=⎩12.1813.21m-<≤-14.(1)21 xy=⎧⎨=-⎩(2)1083 xy=⎧⎪⎨=⎪⎩15.116.不正确,从第一步开始出现错误;正确的解题过程见解析,原方程组的解为:42 xy=⎧⎨=⎩17.(1)x表示A工程队工作的天数,y表示B工程队工作的天数,18020 128x yx y+=⎧⎪⎨+=⎪⎩(2)A工程队完成河道清淤60米,B工程队完成河道清淤120米18.(1)购进1个A型头盔30元,1个B型头盔65元;(2)最多可购买B型头盔120个;(3)三种购买方案。
《二元一次方程组》全章复习与巩固(提高)知识讲解
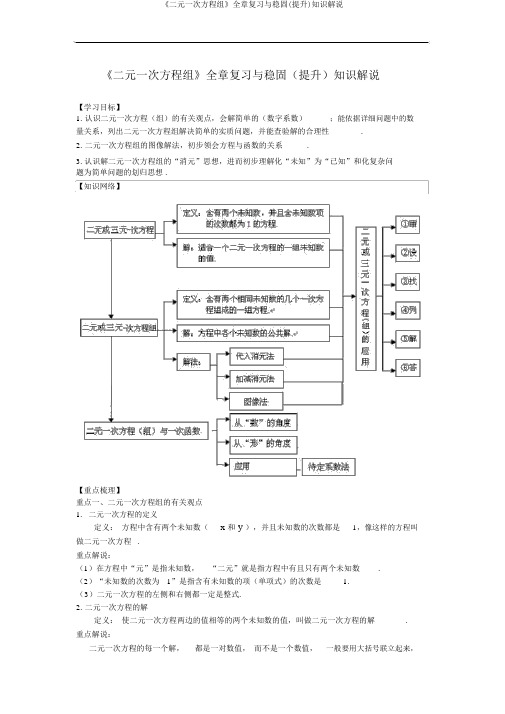
《二元一次方程组》全章复习与稳固(提升)知识解说【学习目标】1. 认识二元一次方程(组)的有关观点,会解简单的(数字系数);能依据详细问题中的数量关系,列出二元一次方程组解决简单的实质问题,并能查验解的合理性.2. 二元一次方程组的图像解法,初步领会方程与函数的关系.3.认识解二元一次方程组的“消元”思想,进而初步理解化“未知”为“已知”和化复杂问题为简单问题的划归思想 .【知识网络】【重点梳理】重点一、二元一次方程组的有关观点1.二元一次方程的定义定义:方程中含有两个未知数(x 和y),并且未知数的次数都是1,像这样的方程叫做二元一次方程.重点解说:(1)在方程中“元”是指未知数,“二元”就是指方程中有且只有两个未知数.(2)“未知数的次数为1”是指含有未知数的项(单项式)的次数是 1.(3)二元一次方程的左侧和右侧都一定是整式.2. 二元一次方程的解定义:使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.重点解说:二元一次方程的每一个解,都是一对数值,而不是一个数值,一般要用大括号联立起来,x=a即二元一次方程的解往常表示为的形式.y=b3.二元一次方程组的定义定义:把拥有同样未知数的两个二元一次方程合在一同,就构成了一个二元一次方程组.别的,构成方程组的各个方程也不用同时含有两个未知数. 比如,二元一次方程组3x4y5x2.重点解说:(1)它的一般形式为a1x b1 y c1(此中 a1, a2, b1, b2不一样时为零).a2 x b2 y c2(2)更一般地,假如两个一次方程合起来共有两个未知数,那么它们构成一个二元一次方程组.(3)符号“”表示同时知足,相当于“且”的意思.4.二元一次方程组的解定义:一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.重点解说:(1)方程组中每个未知数的值应同时知足两个方程,所以查验是不是方程组的解,应把数值代入两个方程,若两个方程同时建立,才是方程组的解,而方程组中某一个方程的某一组解不必定是方程组的解 .(2)方程组的解要用大括号联立;2x y5( 3)一般地,二元一次方程组的解只有一个,但也有特别状况,如方程组无2x y6x y1解,而方程组的解有无数个 .2x 2y2重点二、二元一次方程组的解法1.解二元一次方程组的思想消元二元一次方程组一元一次方程转变2.解二元一次方程组的基本方法:代入消元法、加减消元法和图像法(1)用代入消元法解二元一次方程组的一般过程:①从方程组中选定一个系数比较简单的方程进行变形,用含有 x(或y)的代数式表示y (或x ),即变为y ax b (或x ay b )的形式;②将y ax b (或x ay b )代入另一个方程(不可以代入原变形方程)中,消去y(或x ),获得一个对于x (或③解这个一元一次方程,求出y )的一元一次方程;x (或y)的值;④把x (或y )的值代入y ax b (或x ay b )中,求y (或x )的值;⑤用“”联立两个未知数的值,就是方程组的解.重点解说:(1) 用代入法解二元一次方程组时,应先察看各项系数的特色,尽可能选择变形后比较简单或代入后化简比较简单的方程变形;(2)变形后的方程不可以再代入原方程,只好代入原方程组中的另一个方程;(3)要擅长剖析方程的特色,找寻简易的解法 . 如将某个未知数连同它的系数作为一个整体用含另一个未知数的代数式来表示,代入另一个方程,或直接将某一方程代入另一个方程,这类方法叫做整体代入法 . 整体代入法是解二元一次方程组常用的方法之一,它的运用可使运算简易,提升运算速度及正确率 .(2)用加减消元法解二元一次方程组的一般过程:①依据“等式的两边都乘以(或除以)同一个不等于0 的数,等式仍旧建立”的性质,将原方程组化成有一个未知数的系数绝对值相等的形式;②依据“等式两边加上(或减去)同一个整式,所得的方程与原方程是同解方程”的性质,将变形后的两个方程相加(或相减),消去一个未知数,获得一个一元一次方程;③解这个一元一次方程,求出一个未知数的值;④把求得的未知数的值代入原方程组中比较简单的一个方程中,求出另一个未知数的值;⑤将两个未知数的值用“”联立在一同即可.重点解说:用加减消当方程组中有一个未知数的系数的绝对值相等或同一个未知数的系数成整数倍时,元法较简单 .(3)图像法解二元一次方程组的一般过程:①把二元一次方程化成一次函数的形式.②在直角坐标系中画出两个一次函数的图像,并标出交点.③交点坐标就是方程组的解.重点解说:二元一次方程组无解<=>一次函数的图像平行(无交点)二元一次方程组有一解<=>一次函数的图像订交(有一个交点)二元一次方程组有无数个解<=>一次函数的图像重合(有无数个交点)利用图像法求二元一次方程组的解是近似解,要获得正确解,一般还是用代入消元法和加减消元法解方程组 . 相反,求两条直线的交点坐标能够转变为求这两条直线对应的函数表达式联立的二元一次方程组的解.重点三、实质问题与二元一次方程组重点解说:(1)解实质应用问题一定写“答” ,并且在写答案前要依据应用题的实质意义,检查求得的结果能否合理,不切合题意的解应当舍去; (2)“设”、“答”两步,都要写清单位名称;(3)一般来说,设几个未知数就应当列出几个方程并构成方程组.重点四、二元一次方程(组)与一次函数 1. 二元一次方程与一次函数的关系( 1 ) 任 何 一 个 二 元 一 次 方 程 ax byc(a 、 b 0, c 为常数 ) 都 可 以 变 形 为a c 0c,为常数 即)为一个一次函数, 所以每个二元一次方程都对应一个一y - x(a 、bbb次函数 .( 2)我们知道每个二元一次方程都有无数组解,比如:方程x y5 我们列举出它的x 0, x 5, x 2, ( 0,5),( 5,0),几组整数解有y 0; y ,我们发现以这些整数解为坐标的点y 5; 3(2, 3)恰幸亏一次函数y =x 5 的图像上,反过来,在一次函数y 5 x 的图像上任取一点,它的坐标也合适方程 x y 5 .重点解说:1. 以二元一次方程的解为坐标的点都在相应的函数图像上;2. 一次函数图像上的点的坐标都合适相应的二元一次方程;3. 以二元一次方程的解为坐标的所有点构成的图像与相应一次函数的图像同样 .2. 二元一次方程组与一次函数每个二元一次方程组都对应两个一次函数,于是也对应两条直线. 从“数”的角度看,解方程组相当于考虑自变量为什么值时两个函数的值相等,以及这时的函数为什么值;从“形”的角度看,解方程组相当于确立两条直线交点的坐标 .3. 用二元一次方程组确立一次函数表达式待定系数法: 先设出函数表达式, 再依据所给的条件确立表达式中未知数的系数,进而获得函数表达式的方法,叫做待定系数法 .利用待定系数法解决问题的步骤: 1. 确立所求问题含有待定系数分析式.2. 依据所给条件 , 列出一组含有待定系数的方程 .3. 解方程组或许消去待定系数,进而使问题获得解决.重点五、三元一次方程组1.定义: 含有三个未知数,并且含有未知数的项的次数都是 1 的方程叫做三元一次方程; 含有三个同样的未知数,每个方程中含未知数的项的次数都是 1,并且一共有三个方程,像这样的方程组叫做三元一次方程组.4x y z 12,2a 7b3,3x 2 y z 5, 3a c1, 等都是三元一次方程组 .xy 5z1,b 3c4重点解说: 理解三元一次方程组的定义时,要注意以下几点:( 1)方程组中的每一个方程都是一次方程;( 2)假如三个一元一次方程合起来共有三个未知数,它们就能构成一个三元一次方程组. 2.三元一次方程组的解法解三元一次方程组的基本思想还是消元,一般的,应利用代入法或加减法消去一个未知数,进而化三元为二元, 而后解这个二元一次方程组,求出两个未知数,最后再求出另一个未知数.解三元一次方程组的一般步骤是:( 1)利用代入法或加减法, 把方程组中一个方程与另两个方程分别构成两组, 消去两组中的同一个未知数,获得对于此外两个未知数的二元一次方程组;( 2)解这个二元一次方程组,求出两个未知数的值;( 3)将求得的两个未知数的值代入原方程组中的一个系数比较简单的方程,获得一个一元一次方程;( 4)解这个一元一次方程,求出最后一个未知数的值; ( 5)将求得的三个未知数的值用“ { ”合写在一同.重点解说:( 1)有些特别的方程组可用特别的消元法,解题时要依据各方程特色追求比较简单的解法. ( 2)要查验求得的未知数的值是不是原方程组的解,将所求得的一组未知数的值分别代入原方程组里的每一个方程中, 看每个方程的左右两边能否相等, 若相等,则是原方程组的解,只需有一个方程的左、右两边不相等就不是原方程组的解. 3. 三元一次方程组的应用列三元一次方程组解应用题的一般步骤:( 1)弄清题意和题目中的数目关系,用字母 ( 如 x ,y , z) 表示题目中的两个 ( 或三个 ) 未知数;( 2)找出能够表达应用题所有含义的相等关系;( 3)依据这些相等关系列出需要的代数式,进而列出方程并构成方程组; ( 4)解这个方程组,求出未知数的值;( 5)写出答案 ( 包含单位名称 ) .重点解说:(1) 解实质应用题一定写“答”,并且在写答案前要依据应用题的实质意义,检查求得的结果能否合理,不切合题意的应当舍去.(2) “设”、“答”两步,都要写清单位名称,应注意单位能否一致. (3) 一般来说,设几个未知数,就应列出几个方程并构成方程组. 【典型例题】种类一、二元一次方程组的有关观点1.(2016春?潮州期末) 以下方程组中,不是二元一次方程组的是()x 1x y 1 x y 1 y xA.B.x y 0C.D.y 2 3xy 0x 2y 1【思路点拨】 依据二元一次方程组的定义判断即可.【答案】 C.【分析】 C 选项是二元二次方程组,不是二元一次方程组,故本选项切合题意,选 C.【总结升华】 熟记二元一次方程组的定义是解本题的重点.贯通融会:【变式 1】若对于 x 、 y 的方程m 1 xy m 2 是二元一次方程,则 m =.【答案】 1.x y 5 .【变式 2】已知方程组3 y 有无数多个解, 则 a 、b 的值等于ax b 1【答案】 a =﹣ 3, b =﹣ 14.种类二、二元一次方程组的解法2( x y)y 5①2. 解方程组33( x5 yy)3 ②22【思路点拨】 本题结构比较复杂,一般应先化简,再消元.认真察看题目,不难发现,方程 组中的每一个方程都含有 (x-y) ,所以能够把 (x-y) 看作一个整体,消去 (x-y) 可获得一个关于 y 的一元一次方程. 【答案与分析】解:由①× 9 得: 6(x-y)+9y = 45③②× 4 得: 6(x-y)-10y =-12 ④③ - ④得: 19y =57, 解得 y = 3.把 y =3 代入①,得x = 6.x 6 所以原方程组的解是.y3【总结升华】 本题奇妙运用整体法求解方程组, 明显比加减法或代入法要简单, 在平常求方程组的解时,要擅长发现方程组的特色,运用整体法求解会收到事半功倍的成效. 贯通融会:【变式】( 2015?黄冈模拟)若对于 x ,y 的二元一次方程组的解也是二元一次方程 2x+3y=6 的解,求 k 的值.【答案】 解:由方程组得:∵此方程组的解也是方程 2x+3y=6 的解∴ 2×7k+3×(﹣ 2k ) =6即 k= .3. 方程 x 2 y 3 x y 1 1的整数解的个数是.【思路点拨】 把 1 表示成两个非负整数的和,这两个数只好是1 与 0,于是一个方程裂变为多个方程组,经过解方程组来求解的个数. 【答案】 2 组【分析】x 2 y 3 0 x 2 y 3 1 解:由条件得或x y 1 1 x y 1即即x 2y 3 0 x y 1或 1x 2 y3 0x y 1 1或x 2y 31x y 1x 2 y 3 0 x 2 y 3 1 x 2y 3 1 x或x 或x ,y 1 1y 1 0y 1 012x 1xxx 0 解得,或 3 或3 或y 15 y5 y1y33【总结升华】 依据已知条件结构出方程组, 再选择合适方法求得方程组的解, 而后再所求得出答案. 贯通融会:种类三、实质问题与二元一次方程组4. ( 2015?旭日)为响应国家节能减排的呼吁,鼓舞居民节俭用电,各省先后出台了居民用电 “阶梯价钱 ”制度, 如表中是某省的电价标准(每个月).比如: 方女士家 5 月份用电 500度,电费 =180×0.6+220×二档电价 +100×三档电价 =352 元;李先生家 5 月份用电 460 度,交费 316 元,请问表中二档电价、三档电价各是多少? 阶梯 电量电价 一档 0﹣ 180 度 0.6 元 /度 二档 181﹣ 400 度 二档电价 三档401 度及以上三档电价【答案与分析】 解:设二档电价是 x 元 /度、三档电价是 y 元 /度,依据题意得,,解得,答:二档电价是 0.7 元 / 度、三档电价是 0.9 元 /度.【总结升华】 本题主要考察了二元一次方程组的应用,解题的重点是正确列出方程组. 贯通融会:【变式】甲、乙两班学生到市集上购置苹果,价钱以下:甲班分两次共购置苹果70 千克 ( 第二次多于第一次) ,共付出 189 元,而乙班则一次购置苹果 70 千克。
七年级数学下册 第八章 二元一次方程组章末小结与提升

( x,y )※( 1,-1 )=( 1,3 ),则 xy 的值是( C )
A.-1
B.0
= 3,
于 a,b 的方程组,即
解得
+ -4 = 1,
= 2.
【答案(dá àn)】 B
第三页,共十五页。
)
【针对训练】
1.方程( m2-9 )x2+x-( m+3 )y=0 是关于 x,y 的二元一次方程,则 m
的值为( B )
A.±3
B.3
C.-3
D.9
2.已知方程( a-2 )x|a|-1-( b+5 )y|b|-4=3 是关于 x,y 的二元一次方程,
= 10,
②当 x,y 的值互为相反数时,a=20;③不存在一个实数 a,使
= 20;
得 x=y;④若 25a-y=2-3,则 a=2.其中正确的是 ②③④ .( 填序
号 )
第六页,共十五页。
类型(lèixíng)3 解二元一次方程组
典例 3
解方程组:
3( + ) + 2( - ) = 10,
章末小结与提升。类型1 二元一次方程(yī cì fānɡ chénɡ)( 组 )的概念。A.3,1
B.3,2
C.2,1
D.2,-1。a=-2,b=5。【针对训练】。2.某
电脑公司有A、B、C三种型号的电脑,其中A型每台5000元、B型每台4000元、C型每台3000元,某中学现有资金100000元,计划全部用于从这家电脑公司购进30
2022年人教版七年级下册数学同步培优第八章二元一次方程组 章末小结与提升

章末小结与提升类型1 二元一次方程(组)的概念与解 1.方程组{2x +y =□,x +y =3的解为{x =2,y =△,则被遮盖的两个数△和□分别为( C )A .1,2B .1,3C .1,5D .2,42.若{x =1,y =-2是关于x ,y 的二元一次方程mx +ny =3的解,则2m -4n 的值等于( B )A .3B .6C .-1D .-2 3.若方程组{y -(a -1)x =5,y |a |+(b -5)xy =3是关于x ,y 的二元一次方程组,则代数式ab 的值是 -5 .4.若关于x ,y 的方程组{2x +3y =m ,3x +5y =m +2的解满足x +y =12,求m 的值.解:{2x +3y =m , ①3x +5y =m +2, ②由②-①,得x +2y =2, ③ ③与x +y =12联立,得{x +y =12,x +2y =2,解得{x =22,y =-10,所以m =2x +3y =44-30=14. 类型2 解二元一次方程组 5.解方程组:{x -4(y -14)=3,3+x5-2y +33=115.解:整理,得{x -4y =2, ①3x -10y =7. ②由②-①×3,得2y =1,解得y =12. 把y =12代入①,得x -2=2,解得x =4. 所以方程组的解为{x =4,y =12.6.已知关于x ,y 的方程组{mx +ny =7,2mx -3ny =4的解为{x =1,y =2,求m -5n 的值.解:将{x =1,y =2代入方程组{mx +ny =7,2mx -3ny =4,得{m +2n =7,2m -6n =4,解得{m =5,n =1,所以m -5n =5-5×1=0. 7.已知关于x ,y 的方程组{ax +by =3,5x -cy =1,甲同学正确解得{x =2,y =3,而乙同学粗心,把c 给看错了,解得{x =3,y =6.求abc 的值.解:将{x =2,y =3代入方程5x -cy =1,解得c =3.将{x =2,y =3和{x =3,y =6代入方程ax +by =3,得{2a +3b =3,3a +6b =3,解得{a =3,b =-1.所以abc =3×(-1)×3=-9.8.已知关于x ,y 的方程组{x +y =3m +1,2x -y =8-6n(m ,n 为实数).(1)当m =-3,n =2时,求方程组的解;(2)当m +4n =5时,试探究方程组的解x ,y 之间的关系.解:(1)当m =-3,n =2时,原方程组为{x +y =-8,2x -y =-4,解得{x =-4,y =-4.(2){x +y =3m +1, ①2x -y =8-6n , ②由①+②,得x =m -2n +3,代入①,得y=2m+2n-2,当m+4n=5时,m=5-4n,则x=5-4n-2n+3=8-6n,y=2(5-4n)+2n-2=8-6n,∴x=y.类型3二元一次方程组的应用9.观察下表:我们把某格中各字母的和所得多项式称为“特征多项式”.例如,第1格的“特征多项式”为4x+y,第2格的“特征多项式”为8x+4y.若第1格的“特征多项式”的值为-10,第2格的“特征多项式”的值为-16,则x=-3,y=2.10.小明要用16元钱买A,B两种型号的口罩,两种型号的口罩必须都买,16元钱全部用完.若A型口罩每个3元,B型口罩每个2元,则小明的购买方案有多少种?解:设可以购买x个A型口罩,y个B型口罩.根据题意,得3x+2y=16,∴y=8-32x.∵x,y均为正整数,∴{x=2,y=5或{x=4,y=2.答:小明有2种购买方案:购买2个A型口罩、5个B型口罩或购买4个A型口罩、2个B型口罩.11.某出租车公司有A,B两种不同型号的汽车,用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题:(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?(2)请你帮该物流公司设计租车方案.(3)若A型车每辆需租金200元/次,B型车每辆需租金240元/次.请你帮该物流公司设计最省钱的租车方案,并求出最少租车费.解:(1)设1辆A型车和1辆B型车都装满货物一次可分别运货x吨、y吨.由题意,得{2x+y=10,x+2y=11,解得{x=3,y=4.答:1辆A型车和1辆B型车都装满货物一次可分别运货3吨、4吨.(2)由题意,得3a+4b=31.∵a,b均为正整数,∴{a=1,b=7或{a=5,b=4或{a=9,b=1,∴该物流公司共有3种租车方案:方案1:租A型车1辆,B型车7辆;方案2:租A型车5辆,B型车4辆;方案3:租A型车9辆,B型车1辆.(3)结合(2)知方案1的租车费用为200×1+240×7=1880(元);方案2的租车费用为200×5+240×4=1960(元);方案3的租车费用为200×9+240×1=2040(元).∵1880<1960<2040,∴该物流公司最省钱的租车方案是租A型车1辆,B型车7辆,最少租车费为1880元.1.[长沙中考]《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?意思是:用一根绳子去量一根木头的长,绳子还剩余4.5尺;将绳子对折再量木头,则木头还剩余1尺,问木头长多少尺?可设木头长为x尺,绳子长为y尺,则所列方程组正确的是( A )A.{y=x+4.50.5y=x-1B.{y=x+4.5y=2x-1C.{y=x-4.50.5y=x+1D.{y=x-4.5y=2x-12.[泰安中考]《九章算术》中记载:今有甲、乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?其大意是:今有甲、乙二人,不知其钱包里有多少钱,若乙把其一半的钱给甲,则甲的钱数为50;而甲把其23的钱给乙,则乙的钱数也为50.问甲、乙各有多少钱?设甲的钱数为x,乙的钱数为y.根据题意,可列方程组为{x+12y=5023x+y=50.3.我国古代第一部数学专著《九章算术》中有这样一道题:今有上禾7束,减去其中之实1斗,加下禾2束,则得实10斗.下禾8束,加实1斗和上禾2束,则得实10斗.问上禾、下禾1束得实多少?译文为:今有上等禾7捆结出的粮食,减去1斗再加上2捆下等禾结出的粮食,共10斗;下等禾8捆结出的粮食,加上1斗和上等禾2捆结出的粮食,共10斗.问上等禾和下等禾1捆各能结出多少斗粮食?(斗为体积单位)解:设上等禾1捆能结出x斗粮食,下等禾1捆能结出y斗粮食.根据题意,得{7x-1+2y=10,8y+1+2x=10,解得{x=3526,y=4152.答:上等禾1捆能结出3526斗粮食,下等禾1捆能结出4152斗粮食.4.我国传统数学名著《九章算术》记载:今有牛五、羊二,直金十九两;牛二、羊五,直金十六两.问牛、羊各直金几何?译文:假设有5头牛、2只羊,值19两银子;2头牛、5只羊,值16两银子.问每头牛、每只羊分别值银子多少两?根据以上译文,提出以下两个问题:(1)求每头牛、每只羊各值多少两银子?(2)若某商人准备用19两银子买牛和羊(要求既有牛也有羊,且银两须全部用完),请问商人有几种购买方法?将这些购买方法列举出来.解:(1)设每头牛值x两银子,每只羊值y两银子.根据题意,得{5x+2y=19,2x+5y=16,解得{x=3,y=2.答:每头牛值3两银子,每只羊值2两银子.(2)设商人购买a头牛,b只羊.依题意,得3a+2b=19,所以b=19-3a2,因为a,b都是正整数,所以商人有3种购买方法:①购买1头牛,8只羊;②购买3头牛,5只羊;③购买5头牛,2只羊.。
七年级数学下册 第2章 二元一次方程本章总结提升课件

z=-3.
第十二页,共二十五页。
本章总结(zǒngjié)提升
x+y+z=0,① (2)x+4y+2z=3,②
x+9y-3z=28,③ ②-①,得 3y+z=3.④ ③-②,得 5y-5z=25,即 y-z=5.⑤ 再解由④⑤组成的二元一次方程组,得 yz==-2,3,将其代入①,得 x=1.
第二十四页,共二十五页。
内容(nèiróng)总结
第2章 二元一次方程组。本章总结(zǒngjié)提升。问题4 含参数的二元一次方程组问题。含有参数的方程组有哪几种常见的类型
No Image
12/10/2021
第二十五页,共二十五页。
第八页,共二十五页。
本章(běn zhānɡ)总结提升
例 3 解方程组:y3y=+2x2, x=8.
【解析】解方程组y3= y+2x2, x=①8,②因为方程组中相同未知数表示同一个 量,方程①中 y=2x,所以方程②中的 2x 可用 y 代替,这样,方程②就 转化成了关于 y 的一元一次方程.或将方程②中的 y 用 2x 代替,这样, 方程②就转化成了关于 x 的一元一次方程.
(10-8)y
16.2
第十八页,共二十五页。
本章总结(zǒngjié)提升
解:设不超过 8 立方米的水的单价为 x 元/米 3,超过 8 立方米的水的单价为 y 元/米 3. 根据题意列方程组,得88xx+ +( (1120- -88) )yy= =2126, .2, 解得xy= =12..39, . 答:每户居民每月用水收费标准是不超过 8 立方米的水的单价为 1.3 元/米 3,超过 8 立 方米的水的单价为 2.9 元/米 3.
本章(běn zhānɡ)总结提升
代数第一册(上)第五章《二元一次方程组》提高测试题

提高测试(一)填空题(每空2分,共28分):1.已知(a -2)x -by |a |-1=5是关于x 、y 的二元一次方程,则a =______,b =_____.【提示】要满足“二元”“一次”两个条件,必须a -2≠0,且b ≠0,及| a |-1=1.【答案】a =-2,b ≠0.2.若|2a +3b -7|与(2a +5b -1)2互为相反数,则a =______,b =______.【提示】由“互为相反数”,得|2a +3 b -7|+(2a +5b -1)2=0,再解方程组⎩⎨⎧=-+=-+01520732b a b a 【答案】a =8,b =-3.3.二元一次方程3x +2y =15的正整数解为_______________.【提示】将方程化为y =2315x -,由y >0、x >0易知x 比0大但比5小,且x 、y 均为整数.【答案】⎩⎨⎧==61y x ,⎩⎨⎧==.33y x 4.2x -3y =4x -y =5的解为_______________. 【提示】解方程组⎩⎨⎧=-=-54532y x y x .【答案】⎩⎨⎧-==.11y x 5.已知⎩⎨⎧==12y x -是方程组⎩⎨⎧=++=-274123ny x y mx 的解,则m 2-n 2的值为_________.【提示】把⎩⎨⎧==12y x -代入方程组,求m ,n 的值. 【答案】-438. 6.若满足方程组⎩⎨⎧=-+=-6)12(423y k kx y x 的x 、y 的值相等,则k =_______.【提示】作y =x 的代换,先求出x 、y 的值.【答案】k =65. 7.已知2a =3b =4c ,且a +b -c =121,则a =_______,b =_______,c =_______.【提示】即作方程组⎪⎪⎩⎪⎪⎨⎧=-+==121432c b a c b a ,故可设a =2 k ,b =3 k ,c = 4 k ,代入另一个方程求k 的值.【答案】a =61,b =41,c =31. 【点评】设“比例系数”是解有关数量比的问题的常用方法.8.解方程组⎪⎩⎪⎨⎧=+=+=+634323x z z y y x ,得x =______,y =______,z =______.【提示】根据方程组的特征,可将三个方程左、右两边分别相加,得2 x +3 y +z =6,再与3 y +z =4相减,可得x .【答案】x =1,y =31,z =3. (二)选择题(每小题2分,共16分):9.若方程组⎩⎨⎧=++=-10)1(232y k kx y x 的解互为相反数,则k 的值为…………………( ) (A )8 (B )9 (C )10 (D )11【提示】将y =-x 代入方程2 x -y =3,得x =1,y =-1,再代入含字母k 的方程求解.【答案】D .10.若⎩⎨⎧-==20y x ,⎪⎩⎪⎨⎧==311y x 都是关于x 、y 的方程|a |x +by =6的解,则a +b 的值为( ) (A )4 (B )-10 (C )4或-10 (D )-4或10【提示】将x 、y 对应值代入,得关于| a |,b 的方程组⎪⎩⎪⎨⎧=+=-.631||62b a b 【答案】C .【点评】解有关绝对值的方程,要分类讨论.11.关于x ,y 的二元一次方程ax +b =y 的两个解是⎩⎨⎧-==11y x ,⎩⎨⎧==12y x ,则这个二元一次方程是……………………………………………………………………………( )(A )y =2x +3 (B )y =2x -3(C )y =2x +1 (D )y =-2x +1【提示】将x 、y 的两对数值代入ax +b =y ,求得关于a 、b 的方程组,求得a 、b 再代入已知方程.【答案】B .【点评】通过列方程组求待定字母系数是常用的解题方法.12.由方程组⎩⎨⎧=+-=+-0432032z y x z y x 可得,x ∶y ∶z 是………………………………( )(A )1∶2∶1 (B )1∶(-2)∶(-1)(C )1∶(-2)∶1 (D )1∶2∶(-1)【提示】解方程组时,可用一个未知数的代数式表示另外两个未知数,再根据比例的性质求解.【答案】A .【点评】当方程组未知数的个数多于方程的个数时,把其中一个未知数看作已知常数来解方程组,是可行的方法.13.如果⎩⎨⎧=-=21y x 是方程组⎩⎨⎧=-=+10cy bx by ax 的解,那么,下列各式中成立的是…( ) (A )a +4c =2 (B )4a +c =2 (C )a +4c +2=0 (D )4a +c +2=0【提示】将⎩⎨⎧=-=21y x 代入方程组,消去b ,可得关于a 、c 的等式. 【答案】C . 14.关于x 、y 的二元一次方程组⎩⎨⎧=+=-2312y mx y x 没有解时,m 的值是…………( )(A )-6 (B )-6 (C )1 (D )0【提示】只要满足m ∶2=3∶(-1)的条件,求m 的值.【答案】B .【点评】对于方程组⎩⎨⎧=+=+222111c y b x a c y b x a ,仅当21a a =21b b ≠21c c 时方程组无解. 15.若方程组⎪⎩⎪⎨⎧=+=+52243y b ax y x 与⎪⎩⎪⎨⎧=-=-5243y x by x a 有相同的解,则a 、b 的值为( ) (A )2,3 (B )3,2 (C )2,-1 (D )-1,2【提示】由题意,有“相同的解”,可得方程组⎩⎨⎧=-=+52243y x y x ,解之并代入方程组⎪⎪⎩⎪⎪⎨⎧=-=-4352by x a y b ax ,求a 、b . 【答案】B .【点评】对方程组“解”的含义的正确理解是建立可解方程组的关键.16.若2a +5b +4z =0,3a +b -7z =0,则a +b -c 的值是……………………( )(A )0 (B )1 (C )2 (D )-1【提示】把c 看作已知数,解方程组⎩⎨⎧=-+=++0730452c b a c b a 用关于c 的代数式表示a 、b ,再代入a +b -c .【答案】A .【点评】本题还可采用整体代换(即把a +b -c 看作一个整体)的求解方法.(三)解方程组(每小题4分,共16分):17.⎪⎪⎩⎪⎪⎨⎧=+=-+.022325232y x y y x 【提示】将方程组化为一般形式,再求解. 【答案】⎪⎩⎪⎨⎧-==.232y x 18.⎪⎩⎪⎨⎧⨯=++=-8001005.8%60%10)503(5)150(2y x y x 【提示】将方程组化为整系数方程的一般形式,再用加减法消元.【答案】⎩⎨⎧==.30500y x 19.⎪⎩⎪⎨⎧=++-=+--.6)(2)(3152y x y x y x y x 【提示】用换元法,设x -y =A ,x +y =B ,解关于A 、B 的方程组⎪⎩⎪⎨⎧=+=-623152B A B A ,进而求得x ,y .【答案】⎩⎨⎧-==.11y x 20.⎪⎩⎪⎨⎧=---=+-=+-.441454y x z x z y z y x【提示】 将三个方程左,右两边分别相加,得4x -4y +4z =8,故 x -y +z =2 ④,把④分别与第一、二个方程联立,然后用加、减消元法即可求得x 、z 的值. 【答案】⎪⎪⎪⎩⎪⎪⎪⎨⎧=-==.15451z y x (四)解答题(每小题5分,共20分):21.已知⎩⎨⎧=+-=-+0254034z y x z y x ,xy z ≠0,求222223y x z xy x +++的值. 【提示】把z 看作已知数,用z 的代数式表示x 、y ,可求得x ∶y ∶z =1∶2∶3.设x =k , y =2 k ,z =3 k ,代入代数式. 【答案】516. 【点评】本题考查了方程组解法的灵活运用及比例的性质.若采用分别消去三个元可得方程21 y -14 z =0,21 x -7 z =0,14 x -7 y =0,仍不能由此求得x 、y 、z 的确定解,因为这三个方程不是互相独立的.22.甲、乙两人解方程组⎩⎨⎧=+-=-514by ax by x ,甲因看错a ,解得⎩⎨⎧==32y x ,乙将其中一个方程的b 写成了它的相反数,解得⎩⎨⎧-=-=21y x ,求a 、b 的值. 【提示】可从题意的反面入手,即没看错什么入手.如甲看错a ,即没看错b ,所求得的解应满足4 x -by =-1;而乙写错了一个方程中的b ,则要分析才能确定,经判断是将第二方程中的b 写错.【答案】a =1,b =3.23.已知满足方程2 x -3 y =m -4与3 x +4 y =m +5的x ,y 也满足方程2x +3y =3m -8,求m 的值.【提示】由题意可先解方程组⎩⎨⎧-=+-=-8332432m y x m y x 用m 的代数式表示x ,y 再代入3 x +4 y =m +5.【答案】m =5.24.当x =1,3,-2时,代数式ax 2+bx +c 的值分别为2,0,20,求:(1)a 、b 、c 的值;(2)当x =-2时,ax 2+bx +c 的值.【提示】由题得关于a 、b 、c 的三元一次方程组,求出a 、b 、c 再代入这个代数式.【答案】a =1,b =-5,c =6;20.【点评】本例若不设第一问,原则上也应在求出a 、b 、c 后先写出这个代数式,再利用它求值.用待定系数法求a 、b 、c ,是解这类问题常用的方法.(五)列方程组解应用题(第1题6分,其余各7分,共20分):25.有一个三位整数,将左边的数字移到右边,则比原来的数小45;又知百位上的数的9倍比由十位上的数与个位上的数组成的两位数小3.求原来的数.【提示】设百位上的数为x ,由十位上的数与个位上的数组成的两位数为y ,根据题意,得⎩⎨⎧=++=-+.y x x y y x 391045100 【答案】x =4,y =39,三位数是439.【点评】本例分别设十位上的数和个位上的数为不同的未知数,无论从列方程组还是解方程组都更加简捷易行.26.某人买了4 000元融资券,一种是一年期,年利率为9%,另一种是两年期,年利率是12%,分别在一年和两年到期时取出,共得利息780元.两种融资券各买了多少?【提示】若设一年期、二年期的融资券各买x 元,y 元,由题意,得⎪⎩⎪⎨⎧=⋅+=+78010012210090004y x y x 【答案】x =1 200,y =2 800.【点评】本题列方程组时,易将二年期的融资券的利息误认为是10012y 元,应弄清题设给出的是年利率,故几年到期的利息应该乘几.27.汽车从A 地开往B 地,如果在原计划时间的前一半时间每小时驶40千米,而后一半时间由每小时行驶50千米,可按时到达.但汽车以每小时40千米的速度行至离AB 中点还差40千米时发生故障,停车半小时后,又以每小时55千米的速度前进,结果仍按时到达B 地.求AB 两地的距离及原计划行驶的时间.【提示】设原计划用x 小时,AB 两地距离的一半为y 千米,根据题意,得 ⎪⎪⎩⎪⎪⎨⎧-=++-=⋅+⋅21554040402250240x y y y x x 【答案】x =8,2y =360.【点评】 与本例中设AB 两地距离的一半为y 千米一样,也可设原计划的一半时间为x 小时.恰当地设未知数,可以使列方程组和解方程组都更加简便.。
第五章二元一次方程组总结提升课件2024-2025学年 北师大版 八年级数学上册

2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
返回目录
(2) 原方程组的解.
− = ,
= ,
解:(2) 将
代入原方程组,得
− = ,
=
= ,
解得
=
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
返回目录
考点二
二元一次方程组的应用
20
返回目录
+ 3 = 4①,
2. 用加减消元法解二元一次方程组
时,下列方法中,无
2 − = 1②
法消元的是(
)
C
A. ①×2-②
B. ①×(-2)+②
C. ①-②×3
D. ②×(-3)-①
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
返回目录
3. 已知 a , b 都是有理数,观察表格中的运算,则 m 的值为
17
18
19
20
返回目录
7. 如图,在长方形 ABCD 中,放入5个形状、大小相同的小长方形(空
白部分),其中 AB =8cm, BC =12cm,则涂色部分的面积为
(
D
)
人教版七年级下《第八章二元一次方程组》综合提升卷(含答案)

第八章二元一次方程组 第Ⅰ卷 (选择题 共30分)一、选择题(每小题3分,共30分)1.下列各组数值中,是二元一次方程x +y =7的解的是( )A.⎩⎨⎧x =-2,y =5B.⎩⎨⎧x =3,y =4C.⎩⎨⎧x =1,y =7D.⎩⎨⎧x =-2,y =-5 2.若方程组⎩⎨⎧3x +9y =17,az +6y =-20是关于x ,y 的二元一次方程组,则a 的值是( )A .0B .1C .2D .33.将方程2x -3y -4=0变形为用含有y 的式子表示x ,正确的是( ) A .2x =3y +4 B .x =32y +2C .3y =2x -4D .y =2x -434.把一根长7 m 的钢管截成2 m 和1 m 两种规格的钢管(两种都有).如果没有剩余,那么截法有( )A .6种B .5种C .4种D .3种5.在解三元一次方程组⎩⎨⎧9x +6z =19,6x +4y +2z =16,x +8y +3z =5时,比较简便的方法是消去()A .未知数xB .未知数yC .未知数zD .常数6.解方程组⎩⎨⎧3m -4n =7,①9m -10n +25=0②的最好方法是( )A .由①,得m =7+4n3,再代入②B .由②,得m =10n -259,再代入①C .由①,得3m =4n +7,再代入②D .由②,得9m =10n -25,再代入①7.某班共有学生49人.一天,该班某男生因事请假,当天的男生人数恰为女生人数的一半.若设该班男生人数为x ,女生人数为y ,则下列方程组中,能计算出x ,y 的是( )A.⎩⎨⎧x -y =49,y =2(x +1)B.⎩⎨⎧x +y =49,y =2(x +1)C.⎩⎨⎧x -y =49,y =2(x -1)D.⎩⎨⎧x +y =49,y =2(x -1) 8.小红在超市买了一些纸杯,她把纸杯整齐地放在一起,如图8-T -1,根据图中的信息,3个纸杯的高度为9 cm ,8个纸杯的高度为14 cm.若她把70个纸杯放在一起时,纸杯的高度为( )图8-T -1A .70 cmB .76 cmC .80 cmD .84 cm9.王老师的数学课采用小组合作学习的方式,把班上40名学生分成若干个小组.如果要求每小组只能是5人或6人,那么分组方案有( )A .4种B .3种C .2种D .1种10.甲、乙、丙、丁四人到文具店购买同一种笔记本和计算器,购买的数量及总价分别如下表所示.若其中一人的总价算错了,则此人是( )甲 乙 丙 丁 笔记本(本) 18 15 24 27 计算器(个) 30 25 40 45 总价(元)396330528585A.甲 B .乙 C .丙 D .丁 请将选择题答案填入下表:题号 1 2 3 4 5 6 7 8 9 10 总分 答案第Ⅱ卷 (非选择题 共70分)二、填空题(每小题3分,共18分)11.若2x a +1-3y b -2=10是一个二元一次方程,则a -b =________.12.若方程组⎩⎨⎧2x +y =*,3x -y =3的解为⎩⎨⎧x =2,y =#,则“*”“#”的值分别为________.13.以方程组⎩⎨⎧y =-x +2,y =x -6的解为坐标的点(x ,y)在平面直角坐标系中的第________象限.14.已知等式y =kx +b ,当x =1时,y =2;当x =2时,y =-3.若x =-1,则y =________. 15.《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问:牛、羊各直金几何.”译文:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问:每头牛、每只羊各值金多少两.”设每头牛值金x 两,每只羊值金y 两,可列方程组为______________________.16.小华在八一建军节这天写信问候爷爷.折叠长方形信纸、装入标准信封时发现:若将信纸按图8-T -2①连续两次对折后,沿着信封口边线装入时,宽绰有3.8 cm ;若将信纸按图②三等分折叠后,同样方法装入时,宽绰1.4 cm .则信纸的纸长与信封的口宽分别是____________.图8-T -2三、解答题(共52分)17.(6分)解下列方程组:(1)⎩⎨⎧2x -y =5,2y +3x =4;(2)⎩⎨⎧x +3y =5,y -2z =5,x +z =5.18.(5分)解方程组:⎩⎨⎧22x +27y =4,7x +9y =3.解:原方程组可化为⎩⎨⎧x +3(7x +9y )=4,①7x +9y =3,②将②代入①,得x +3×3=4,即x =-5.把x =-5代入②,得y =389,∴原方程组的解为⎩⎨⎧x =-5,y =389.你能用这种方法解答下面的题目吗?解方程组:⎩⎨⎧3x +5y =2,11x +20y =6.19.(5分)如图8-T -3所示,3×3的方格中每个方格内均有一个单项式(图中只列出了部分单项式),方格中每一行、每一列以及每一条对角线上的三个单项式的和均相等.求a 的值.图8-T -320.(5分)已知关于x ,y 的二元一次方程组⎩⎨⎧x +y =3m +3,x -y =5-m.(1)若x ,y 互为相反数,求m 的值;(2)若x 是y 的2倍,求原方程组的解.21.(7分)阅读以下内容:已知实数x ,y 满足x +y =2,且⎩⎨⎧3x +2y =7k -2,2x +3y =6,求k 的值.三名同学分别提出了以下三种不同的解题思路:甲同学:先解关于x ,y 的方程组⎩⎨⎧3x +2y =7k -2,2x +3y =6,再求k 的值.乙同学:先将方程组中的两个方程相加,再求k 的值.丙同学:先解方程组⎩⎨⎧x +y =2,2x +3y =6,再求k 的值.你最欣赏以上哪名同学的解题思路?先根据你所选的思路解答此题,再对你选择的思路进行简要评价..... (评价参考建议:基于观察到题目的什么特征设计的相应思路,如何操作才能实现这些思路、运算的简洁性,以及你依此可以总结出什么解题策略等)22.(8分)如图8-T -4为地铁调价后的计价表.调价后小明、小伟从家到学校乘地铁分别需要4元和3元.由于刷卡坐地铁有优惠,因此,他们平均每次实付3.6元和2.9元.已知小明从家到学校乘地铁的里程比小伟从家到学校的里程多5 km ,且小明每千米享受的优惠金额是小伟的2倍,求小明和小伟从家到学校乘地铁的里程分别是多少千米.图8-T -423.(8分)某旅行社拟在暑假期间向学生推出“林州红旗渠一日游”活动,收费标准如下:人数m 0<m ≤100100<m ≤200m >200 收费标准(元/人)908575甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲学校报名参加的学生人数多于100,乙学校报名参加的学生人数少于100.经核算,若两校分别组团共需20800元;若两校联合组团只需18000元.(1)两所学校报名参加旅游的学生人数之和超过200了吗?为什么? (2)两所学校报名参加旅游的学生各有多少人?24.(8分)某商场计划从一厂家购进若干部新型手机以满足市场需求.已知该厂家生产三种不同型号的手机,出厂价分别是甲种型号手机1800元/部,乙种型号手机600元/部,丙种型号手机1200元/部.商场在经销中,甲种型号手机可赚200元/部,乙种型号手机可赚100元/部,丙种型号手机可赚120元/部.(1)若商场用6万元同时购进两种不同型号的手机共40部,并恰好将钱用完,请你通过计算分析进货方案;(2)在(1)的条件下,求盈利最多的进货方案.典题讲评与答案详析1.B [解析] 将⎩⎨⎧x =3,y =4代入二元一次方程x +y =7,方程左、右两边相等.2.A [解析] 只有当a =0时,方程az +6y =-20才变成6y =-20,方程组⎩⎨⎧3x +9y =17,6y =-20是二元一次方程组.3.B [解析] 方程2x -3y -4=0用含有y 的式子表示x 是x =3y +42=32y +2.4.D [解析] 设2 m 长的钢管有x 根,1 m 长的钢管有y 根.则有2x +y =7,所以有⎩⎨⎧x =1,y =5,⎩⎨⎧x =2,y =3,⎩⎨⎧x =3,y =13种截法. 5.B [解析] 方程9x +6z =19中不含有y ,所以利用其余两个方程消去y 是比较简便的方法.6.C [解析] 注意到②中的9m 是①中的3m 的3倍,因此由①,得3m =4n +7,再代入②是最好的方法.7.D8.B [解析] 设一个杯子的高度为x cm ,增加一个杯子增加的高度为y cm.依题意,得⎩⎨⎧x +2y =9,x +7y =14,解得⎩⎨⎧x =7,y =1,所以把70个纸杯放在一起时,纸杯的高度为7+69=76(cm).9.C10.D [解析] 设每本笔记本的价格为x 元,每个计算器的价格为y 元. 甲:18x +30y =6(3x +5y )=396, 3x +5y =396÷6=66;乙:15x +25y =5(3x +5y )=330, 3x +5y =330÷5=66;丙:24x +40y =8(3x +5y )=528, 3x +5y =528÷8=66;丁:27x +45y =9(3x +5y )=585, 3x +5y =585÷9=65.因为甲、乙、丙中3x +5y 都为66,丁为65,所以选D.11.-3 [解析] 由题意,得a +1=1,b -2=1,所以a =0,b =3,所以a -b =-3. 12.7,3 [解析] 将x =2代入方程3x -y =3,得y =3.将x =2,y =3代入2x +y =*,得*=7.13.四 [解析] 解方程组⎩⎨⎧y =-x +2,y =x -6,得⎩⎨⎧x =4,y =-2,所以点(4,-2)在第四象限.14.12 [解析] 由题意,得⎩⎨⎧2=k +b ,-3=2k +b ,解得⎩⎨⎧k =-5,b =7,所以y =-5x +7,当x =-1时,y =12.15.⎩⎨⎧5x +2y =10,2x +5y =816.28.8 cm ,11 cm [解析] 设信纸的纸长为x cm ,信封的口宽为y cm.根据题意,得⎩⎪⎨⎪⎧x4=y -3.8,x 3=y -1.4,解得⎩⎨⎧x =28.8,y =11.即信纸的纸长为28.8 cm ,信封的口宽为11 cm.17.解:(1)⎩⎨⎧2x -y =5,①2y +3x =4.②由①,得y =2x -5.③将③代入②,得2(2x -5)+3x =4, 解得x =2.将x =2代入③,得y =-1,所以方程组的解为⎩⎨⎧x =2,y =-1.(2)⎩⎨⎧x +3y =5,①y -2z =5,②x +z =5,③由①,得x =5-3y .④把④代入③,得5-3y +z =5.⑤联立②⑤,得⎩⎨⎧y =-1,z =-3.把y =-1代入①,得x =8,所以方程组的解为⎩⎨⎧x =8,y =-1,z =-3.18.解:原方程组可化为⎩⎨⎧3x +5y =2,①4(3x +5y )-x =6,②将①代入②,得4×2-x =6,即x =2.把x =2代入①,得y =-45,所以原方程组的解为⎩⎨⎧x =2,y =-45.19.解:由题意,得⎩⎨⎧y -3x +3y =y -5x +5,y -5x +5=5+4+3y ,解得⎩⎨⎧x =-2,y =3.所以5-3x +a =5+4+3y ,所以a =7.20.解:(1)若x ,y 互为相反数,则x +y =0, 所以有3m +3=0,解得m =-1. (2)若x 是y 的2倍,则x =2y ,原方程组可化为⎩⎨⎧3y =3m +3,y =5-m ,解得⎩⎨⎧y =3,m =2,所以方程组的解为⎩⎨⎧x =6,y =3.21.解:最欣赏乙同学的解题思路.⎩⎨⎧3x +2y =7k -2,①2x +3y =6,② ①+②,得5x +5y =7k +4.③将x +y =2整体代入③,得7k +4=10. 解得k =67.评价:甲同学是直接根据方程组的解的概念先解方程组,得到用含k 的式子表示x ,y 的表达式,再代入x +y =2得到关于k 的方程,没有经过更多的观察和思考,解法比较烦琐,计算量大;乙同学观察到了方程组中未知数x ,y 的系数与x +y =2中未知数的系数的特殊关系,利用整体代入简化计算,而且不用求出x ,y 的值就能解决问题,思路比较灵活,计算量小;丙同学将三个方程作为一个整体,看成关于x ,y ,k 的三元一次方程组,并且选择先解其中只含有两个未知数x ,y 的二元一次方程组,相对计算量较小,但不如乙同学的简洁、灵活.22.解:设小明和小伟从家到学校乘地铁的里程分别是x 千米、y 千米.根据题意得⎩⎨⎧x -y =5,2(3-2.9)x =(4-3.6)y , 解得⎩⎨⎧x =10,y =5.答:小明和小伟从家到学校乘地铁的里程分别是10千米、5千米.23.解:(1)两所学校报名参加旅游的学生人数之和超过200了.理由:设两所学校人数之和为a .若a >200,则a =18000÷75=240.若100<a ≤200,则a =18000÷85=2111317,不合题意.所以这两所学校报名参加旅游的学生人数之和等于240,超过200了.(2)设甲学校报名参加旅游的学生有x 人,乙学校报名参加旅游的学生有y 人,则①当100<x ≤200时,得⎩⎨⎧x +y =240,85x +90y =20800.解得⎩⎨⎧x =160,y =80.②当x >200时,得⎩⎨⎧x +y =240,75x +90y =20800.解得⎩⎪⎨⎪⎧x =5313,y =18623,此解不合题意,舍去.所以甲学校报名参加旅游的学生有160人,乙学校报名参加旅游的学生有80人. 24.解:(1)设购进甲种型号手机x 部,乙种型号手机y 部,丙种型号手机z 部. 根据题意,得①⎩⎨⎧x +y =40,1800x +600y =60000,解得⎩⎨⎧x =30,y =10.②⎩⎨⎧x +z =40,1800x +1200z =60000,解得⎩⎨⎧x =20,z =20.③⎩⎨⎧y +z =40,600y +1200z =60000,11 解得⎩⎨⎧y =-20,z =60.(不合题意,舍去) 故有两种进货方案:方案一,甲种型号手机购进30部,乙种型号手机购进10部;方案二,甲种型号手机购进20部,丙种型号手机购进20部.(2)方案一盈利:200×30+100×10=7000(元);方案二盈利:200×20+120×20=6400(元).因为7000元>6400元,所以购进甲种型号手机30部,乙种型号手机10部盈利最多.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二元一次方程组(提高题) 济宁学院附中李涛
类型一:二元一次方程的概念及求解
例(1).已知(a -2)x -by |a |-1=5是关于x 、y 的二元一次方程,则a =______,b =_____.
(2).二元一次方程3x +2y =15的正整数解为_______________.
类型二:二元一次方程组的求解
例(3).若|2a +3b -7|与(2a +5b -1)2
互为相反数,则a =______,b =______.
(4).2x -3y =4x -y =5的解为_______________. 类型三:已知方程组的解,而求待定系数。
例(5).已知⎩⎨⎧==1
2y x -是方程组⎩⎨⎧=++=-274123ny x y mx 的解,则m 2-n 2的值为_________.
(6).若满足方程组⎩⎨⎧=-+=-6
)12(423y k kx y x 的x 、y 的值相等,则k =_______. 练习:若方程组⎩
⎨⎧=++=-10)1(232y k kx y x 的解互为相反数,则k 的值为 。
若方程组⎪⎩⎪⎨⎧=+=+52243y b ax y x 与⎪⎩⎪⎨⎧=-=-5
243y x by x a 有相同的解,则a = ,b= 。
类型四:涉及三个未知数的方程,求出相关量。
设“比例系数”是解有关数量比的问题的常用方法.
例(7).已知2a =3b =4c ,且a +b -c =12
1,则a =_______,b =_______,c =_______. (8).解方程组⎪⎩
⎪⎨⎧=+=+=+63432
3x z z y y x ,得x =______,y =______,z =______.
练习:若2a +5b +4c =0,3a +b -7c =0,则a +b -c = 。
由方程组⎩⎨⎧=+-=+-0
432032z y x z y x 可得,x ∶y ∶z 是( )
A 、1∶2∶1
B 、1∶(-2)∶(-1)
C 、1∶(-2)∶1
D 、1∶2∶(-1)
说明:解方程组时,可用一个未知数的代数式表示另外两个未知数,再根据比例的性质求解.
当方程组未知数的个数多于方程的个数时,把其中一个未知数看作已知常数来解方程
组。
类型五:列方程组求待定字母系数是常用的解题方法.
例(9).若⎩⎨⎧-==20y x ,⎪⎩
⎪⎨⎧==311y x 都是关于x 、y 的方程|a |x +by =6的解,则a +b 的值为 (10).关于x ,y 的二元一次方程ax +b =y 的两个解是⎩⎨
⎧-==11y x ,⎩⎨⎧==12y x ,则这个二元一次方程是
练习:如果⎩⎨⎧=-=21y x 是方程组⎩⎨⎧=-=+1
0cy bx by ax 的解,那么,下列各式中成立的是 ( )
A 、a +4c =2
B 、4a +c =2
C 、a +4c +2=0
D 、4a +c +2=0
类型六:方程组有解的情况。
(方程组有唯一解、无解或无数解的情况)
方程组⎩⎨⎧=+=+2
22111c y b x a c y b x a 满足 条件时,有唯一解;
满足 条件时,有无数解;
满足 条件时,有无解。
例(11).关于x 、y 的二元一次方程组⎩⎨⎧=+=-2
312y mx y x 没有解时,m
(12)二元一次方程组23
x y m x ny -=⎧⎨+=-⎩ 有无数解,则m= ,n= 。
类型七:解方程组
例(13).⎪⎪⎩⎪⎪⎨⎧=+=-+.022
325232y x y y x (14).⎪⎩⎪⎨⎧⨯=++=-8001005.8%60%10)503(5)150(2y x y x
(15).⎪⎩⎪⎨⎧=++-=+--.6)(2)(3152y x y x y x y x (16).⎪⎩
⎪⎨⎧=---=+-=+-.441454y x z x z y z y x
类型八:解答题
例(17).已知⎩⎨⎧=+-=-+0
254034z y x z y x ,xyz ≠0,求222
223y x z xy x +++的值. (18).甲、乙两人解方程组⎩⎨⎧=+-=-514by ax by x ,甲因看错a ,解得⎩
⎨⎧==32y x ,乙将其中一个方程的b 写成了它的相反数,解得⎩⎨
⎧-=-=21y x ,求a 、b 的值.
练习:甲、乙两人共同解方程组⎩⎨
⎧-=-=+ ②by x ①y ax 24155,由于甲看错了方程①中的a ,得到
方程组的解为 ⎩⎨⎧-=-=13y x ;乙看错了方程②中的b ,得到方程组的解为⎩
⎨⎧==45y x 。
试计算20052004
101⎪⎭⎫ ⎝⎛-+b a 的值.
(19).已知满足方程2 x -3 y =m -4与3 x +4 y =m +5的x ,y 也满足方程2x +3y =3m -8,
求m 的值.
(20).当x=1,3,-2时,代数式ax2+bx+c的值分别为2,0,20,求:(1)a、b、c的值;(2)当x=-2时,ax2+bx+c的值.
类型九:列方程组解应用题
(21).有一个三位整数,将左边的数字移到右边,则比原来的数小45;又知百位上的数的9倍比由十位上的数与个位上的数组成的两位数小3.求原来的数.
(22).某人买了4 000元融资券,一种是一年期,年利率为9%,另一种是两年期,年利率是12%,分别在一年和两年到期时取出,共得利息780元.两种融资券各买了多少?(23).汽车从A地开往B地,如果在原计划时间的前一半时间每小时驶40千米,而后一半时间由每小时行驶50千米,可按时到达.但汽车以每小时40千米的速度行至离AB中点还差40千米时发生故障,停车半小时后,又以每小时55千米的速度前进,结果仍按时到达B地.求AB两地的距离及原计划行驶的时间.。
