常用数学符号英文对照
国际上的数学符号
国际上的数学符号数学符号是一种用于表示数学概念和公式的特殊符号和记号。
它们在数学中起着重要的作用，因为它们可以简化和准确地表示复杂的数学公式和概念。
在国际上，数学符号通常是标准化的，以确保它们被所有人理解和使用。
以下是一些常见的国际数学符号：1. Σ (sigma)：表示求和符号，用于表示一系列数的总和。
2. ∫ (integral)：表示积分符号，用于表示函数的面积或曲线的长度。
3. ∞ (infinity)：表示无穷大，用于表示某些数学量可以无限增大或无限减小。
4. ≠ (not equal to)：表示不等于符号，用于表示两个数或表达式不相等。
5. ≤ (less than or equal to)：表示小于或等于符号，用于表示一个数小于或等于另一个数。
6. ≥ (greater than or equal to)：表示大于或等于符号，用于表示一个数大于或等于另一个数。
7. × (multiplication)：表示乘法符号，用于表示两个数或表达式相乘。
8. ÷ (division)：表示除法符号，用于表示一个数被另一个数除。
9. √ (square root)：表示平方根符号，用于表示一个数的平方根。
10. π (pi)：表示圆周率，用于表示圆的周长与直径的比值。
除了这些常见的数学符号外，还有许多其他的符号和记号，用于表示各种数学概念和公式。
例如，向量符号、矩阵符号、微分符号等等。
总的来说，数学符号在数学中扮演着非常重要的角色，以便简化和准确地表示数学概念和公式。
它们是国际化的，确保数学符号被全世界的数学家们理解和使用。
数学术语英文对照表
数学术语英文对照表在学习数学时，不可避免地需要掌握一些数学术语。
下面是一些常见的数学术语的中英文对照表：1. 数学 Mathematics2. 数学符号 Mathematical symbol3. 数字 Digit4. 字符 Character5. 算术 Arithmetic6. 代数 Algebra7. 几何 Geometry8. 统计学 Statistics9. 概率 Probability10. 三角学 Trigonometry11. 微积分 Calculus12. 矩阵 Matrix13. 向量 Vector14. 线性代数 Linear algebra15. 数学模型 Mathematical model16. 方程 Equation17. 垂直 Perpendicular18. 平行 Parallel19. 正比例 Direct proportion20. 反比例 Inverse proportion21. 旋转 Rotation22. 缩放 Scaling23. 变形 Deformation24. 函数 Function25. 极限 Limit26. 微分 Differential27. 积分 Integral28. 中心 Central29. 对称 Symmetry30. 相似 Similarity31. 等式 Equality32. 不等式 Inequality33. 方形 Rectangle34. 正方形 Square35. 圆 Circle36. 椭圆 Ellipse37. 球球体 Sphere38. 三角形 Triangle39. 直角三角形 Right triangle40. 等腰三角形 Isosceles triangle41. 等边三角形 Equilateral triangle42. 直线 Line43. 射线 Ray44. 线段 Line segment45. 弧 Arc46. 正弦 Sine47. 余弦 Cosine48. 正切 Tangent49. 余切 Cotangent50. 弦 Chord总之，数学术语是数学学习的基础，掌握数学术语对于提高数学能力以及学好数学至关重要。
最新常用数学术语英文对照表
代数部分1.有关数学运算add，plus加subtract减difference差multiply,times乘product积divide除divisible可被整除的dividedevenly被整除dividend被除数，红利divisor因子，除数quotient商remainder余数factorial阶乘power乘方radicalsign,rootsign根号 roundto四舍五入tothenearest四舍五入2.有关集合union并集 subset真子集 set解集3.有关代数式、方程和不等式algebraic term代数项like terms,similar terms同类项numerical coefficient数字系数literal coefficient字母系数inequality不等式triangle inequality三角不等式range值域original equation原方程equivalent equation同解方程，等价方程linear equation线性方程(e.g.54.有关分数和小数proper fraction真分数 fraction假分数 number带分数 fraction，common fraction普通分数 fraction简分数 fraction繁分数分子分母 denominator(最小)公分母四分之一imal fraction纯小数 decimal无穷小数 decimal循环小数十分位5.基本数学概念arithmetic mean算术平均值 average加权平均值 mean几何平均数指数，幂乘幂的底数,底边立方数，立方体 root平方根立方根 logarithm常用对数数字nt常数变量 inversefunction反函数 function余函数一次的，线性的 factorization因式分解 value绝对值，e.g.｜-32｜=32 off四舍五入6.有关数论natural number自然数 number正数 number负数 integer,odd number 奇数en integer,even number偶数 number整数 whole number正整数 whole number负整数 number连续整数 lnumber,rational number实数,有理数无理数倒数 number合数 e.g.4,6,8,9,10,12,14,15…… number质数e.g.2,3,5,7,11,13,15……注意：所有的质数(2除外)都是奇数，但奇数不一定是质数reciprocal 倒数 divisor公约数倍数 multiple(最小)公倍数质)因子 factor公因子十进制非负的十位个位众数中数ratio公比7.数列arithmetic progression(sequence)等差数列 progression(sequence)等比数列其它近似逆)顺时针方向基数序数directproportion正比不同的估计，近似括号 proportion 比例排列组合表格gonometric function三角函数单位,位几何部分1.所有的角alternate angle内错角 angle同位角 angle对顶角 angle 圆心角 angle内角 angle外角 aryangles补角aryangle余角 angle邻角 angle锐角 angle钝角right angle直角round angle周角 angle平角 angle夹角2.所有的三角形equilateral triangle等边三角形 triangle不等边三角形 triangle等腰三角形 triangle直角三角形斜三角形 triangle内接三角形3.有关收敛的平面图形，除三角形外semicircle半圆concentric circles同心圆四边形五边形六边形七边形八边形九边形十边形多边形平行四边形等边形平面正方形，平方长方形 polygon正多边形菱形梯形4.其它平面图形arc弧 line直线 segment线段 lines平行线 of a circle弧形5.有关立体图形cube立方体，立方数 solid长方体 solid/regular polyhedron正多面体 cylinder圆柱体圆锥球体d立体的6.有关图形上的附属物altitude高深度边长周长弧度 area 表面积体积直角三角形的股 ssection横截面 of acircle圆心chord弦半径 bisector角平分线对角线直径棱face of a solid立体的面ypotenuse斜边 side夹边三角形的直角边medianofatriangle三角形的中线底边，底数(e.g.2的5次方，2就是底数)直角三角形中的对边中点端点复数形式vertices)顶点切线的截线截距7.有关坐标coordinate system坐标系 coordinate直角坐标系原点issa横坐标纵坐标数轴象限斜率 plane复平面8.其它plane geometry平面几何三角学平分外切内切相交垂直 theorem勾股定理全等的multilateral多边的其它1.单位类cent美分一美分硬币美分硬币一角硬币打(12个)廿(20个)摄氏华氏夸脱加仑(1gallon=4quart)d 码 meter米微米英寸英尺分(角度的度量单位，60分=1度) squaremeasure平方单位制立方米品脱(干量或液量的单位)2.有关文字叙述题，主要是有关商业intercalary year(leapyear)闰年(366天) year平年(365天)折旧payment直接付款打折利润利润利息interest单利 interest复利红利 to减少到by减少了 to增加到 by增加了表示 price标价arkup涨价 capita每人比率 price零售价打。
常用数学符号英文对照
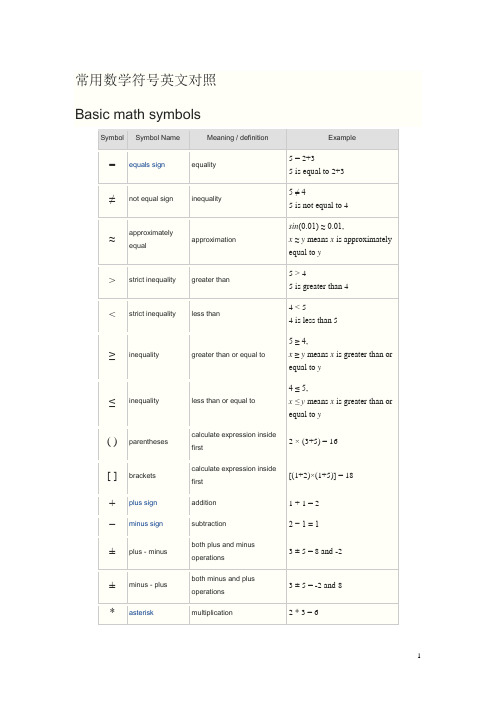
常用数学符号英文对照Basic math symbolsSymbol Symbol Name Meaning / definition Example= equals sign equality 5 = 2+35 is equal to 2+3≠not equal sign inequality 5 ≠ 45 is not equal to 4≈approximatelyequal approximationsin(0.01) ≈ 0.01,x≈y means x is approximatelyequal to y> strict inequality greater than 5 > 45 is greater than 4< strict inequality less than 4 < 54 is less than 5≥inequality greater than or equal to 5 ≥ 4,x≥y means x is greater than or equal to y≤inequality less than or equal to 4 ≤ 5,x ≤ y means x is greater than or equal to y( ) parentheses calculate expression insidefirst2 × (3+5) = 16[ ] brackets calculate expression insidefirst[(1+2)×(1+5)] = 18 + plus sign addition 1 + 1 = 2−minus sign subtraction 2 − 1 = 1±plus - minus both plus and minusoperations3 ± 5 = 8 and -2±minus - plus both minus and plusoperations3 ± 5 = -2 and 8 * asterisk multiplication 2 * 3 = 6×times sign multiplication 2 × 3 = 6 ·multiplication dot multiplication 2 · 3 = 6÷division sign /division 6 ÷ 2 = 3obelus/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimal2.56 = 2+56/100separatora b power exponent 23= 8a^b caret exponent 2 ^ 3= 8√a square root √a ·√a = a√9 = ±33√a cube root 3√a ·3√a ·3√a = a3√8 = 24√a fourth root 4√a ·4√a ·4√a ·4√a = a4√16 = ±2n√a n-th root (radical) for n=3, n√8 = 2% percent1% = 1/100 10% × 30 = 3‰per-mille1‰ = 1/1000 = 0.1%10‰ × 30 = 0.3ppm per-million1ppm = 1/1000000 10ppm × 30 = 0.0003ppb per-billion 1ppb = 1/1000000000 10ppb × 30 = 3×10-7ppt per-trillion 1ppt = 10-1210ppt × 30 = 3×10-10ABC = 30°AOB = 30°°degree 1 turn = 360°α = 60°deg degree 1 turn = 360deg α = 60deg′prime arcminute, 1° = 60′α = 60°59′″double prime arcsecond, 1′ = 60″α = 60°59′59″line infinite lineAB line segment line from point A to point Bray line that start from point Aarc arc from point A to point B= 60°⊥perpendicular perpendicular lines (90° angle) AC ⊥ BC| | parallel parallel lines AB | | CD≅congruent to equivalence of geometric shapes and size ∆ABC≅∆XYZ ~ similarity same shapes, not same size ∆ABC~ ∆XYZ Δtriangle triangle shape ΔABC≅ΔBCD |x-y| distance distance between points x and y | x-y | = 5πpi constant π = 3.141592654...is the ratio between the circumference and diameter of acirclec = π·d = 2·π·rrad radians radians angle unit 360° = 2π rad c radians radians angle unit 360° = 2πcgrad gradians / gons grads angle unit 360° = 400 gradg gradians / gons grads angle unit 360° = 400 gx x variableto findwhen 2x = 4, then x = 2≡equivalence identical to≜equal by definition equal bydefinition:= equal by definition equal bydefinition~ approximately equal weakapproximation11 ~ 10≈approximately equal approximation sin(0.01) ≈ 0.01∝proportional to proportional to y∝x when y = kx, k constant ∞lemniscate infinity symbol≪much less than much less than 1 ≪1000000≫much greater than much greaterthan1000000 ≫1( ) parentheses calculateexpressioninside first2 * (3+5) = 16[ ] brackets calculateexpressioninside first[(1+2)*(1+5)] = 18{ } braces set⌊x⌋floor brackets rounds numberto lower integer⌊4.3⌋ = 4⌈x⌉ceiling brackets rounds numberto upper integer⌈4.3⌉ = 5x! exclamation mark factorial4! = 1*2*3*4 = 24 | x | single vertical bar absolute value | -5 | = 5f (x) function of x maps values ofx to f(x)f (x) = 3x+5(f∘g) function composition (f∘g) (x)= f (g(x))f (x)=3x,g(x)=x-1 ⇒(f∘g)(x)=3(x-1)(a,b) open interval (a,b) = x∈(2,6)[a ,b ] closed interval[a ,b ] = {x | a ≤ x ≤ b }x ∈ [2,6]∆ delta change / difference∆t = t 1 - t 0∆ discriminantΔ = b 2 - 4ac∑sigmasummation -sum of all values in range of series ∑ x i = x 1+x 2+...+x n∑∑sigmadouble summation∏capital piproduct -product of all values in range of series∏ x i =x 1∙x 2∙...∙x ne e constant / Euler's numbere =2.718281828... e = lim (1+1/x )x , x →∞γ Euler-Mascheroni constant γ =0.527721566...φgolden ratio golden ratio constantπpi constant π =3.141592654...is the ratiobetween the circumference and diameter of a circlec = π·d = 2·π·rA ⊗Btensor product tensor product of A and BA ⊗ Binner product[ ] brackets matrix of numbers ( ) parentheses matrix of numbers| A | determinant determinant of matrix A det(A ) determinant determinant of matrix A|| x || double vertical bars normA T transpose matrix transpose(A T )ij = (A )ji A † Hermitian matrix matrix conjugate transpose (A †)ij = (A )ji A * Hermitian matrix matrix conjugate transpose(A *)ij = (A )jiA -1inverse matrixA A -1 = Irank(A ) matrix rank rank of matrix A rank(A ) = 3 dim(U )dimensiondimension of matrix Arank(U ) = 3Probability and statistics symbolsSymbolSymbol Name Meaning / definitionExampleP (A )probability function probability of event A P (A ) = 0.5P (A ∩ B ) probability ofeventsintersection probability that of events A and BP (A ∩B ) = 0.5P (A ∪B ) probability ofevents unionprobability that of events A or B P (A ∪B ) = 0.5P (A | B )conditionalprobability function probability of event A given event B occuredP (A | B ) = 0.3f (x ) probabilitydensity function (pdf) P (a ≤ x ≤ b ) = ∫ f (x ) dxF (x )cumulativeF (x ) = P (X ≤ x )distribution function (cdf)μ population mean mean of population valuesμ = 10E (X )expectation valueexpected value of random variable X E (X ) = 10E (X | Y )conditional expectationexpected value of random variable X given YE (X | Y=2) = 5var (X ) variance variance of random variable X var (X ) = 4σ2variancevariance of population values σ2 = 4std (X ) standard deviationstandard deviation of random variable X std (X ) = 2σXstandard deviationstandard deviation value of random variable X σX = 2medianmiddle value of random variable xcov (X ,Y )covariance covariance ofrandom variables X and Y cov (X,Y ) = 4corr (X ,Y ) correlationcorrelation ofrandom variables X and Y corr (X,Y ) = 0.6ρX ,Ycorrelation correlation ofrandom variables X and YρX ,Y = 0.6∑summation summation - sum ofall values in range of series∑∑double summationdouble summationMo mode value that occurs most frequently in populationMR mid-range MR = (x max+x min)/2 Md sample median half the population isbelow this valueQ1lower / firstquartile 25% of population are below this valueQ2median /second quartile 50% of population are below this value = median of samplesQ3upper / thirdquartile 75% of population are below this valuex sample mean average / arithmeticmeanx = (2+5+9) / 3 = 5.333s2samplevariance population samples variance estimators2 = 4s samplestandarddeviationpopulation samplesstandard deviationestimators = 2z x standard score z x = (x-x) / s xX ~ distribution of X distribution ofrandom variable XX ~ N(0,3)N(μ,σ2) normaldistributiongaussian distribution X ~ N(0,3)U(a,b) uniformdistributionequal probability inrange a,bX ~ U(0,3)exp(λ)exponentialdistributionf (x) = λe-λx , x≥0gamma(c, λ)gammadistributionf (x) = λ c x c-1e-λx /Γ(c), x≥0χ 2(k) chi-squaredistributionf (x) = x k/2-1e-x/2 /( 2k/2 Γ(k/2) )F (k1, k2) F distributionBin (n ,p )binomial distribution f (k ) = n C k p k (1-p )n-kPoisson (λ)Poisson distribution f (k ) = λk e -λ / k !Geom (p )geometric distribution f (k ) = p (1-p ) kHG (N ,K ,n ) hyper-geometric distributionBern (p ) Bernoulli distributionsubset the set {9,14,28} A ⊄ B not subset left set not a subset of right set{9,66} ⊄{9,14,28} A ⊇B supersetset A has more elements or equalto the set B{9,14,28} ⊇{9,14,28} A ⊃Bproper superset / strictsupersetset A has more elements than setB{9,14,28} ⊃{9,14}A ⊅B not superset set A is not a superset of set B{9,14,28} ⊅{9,66} 2A power set all subsets of Apower set all subsets of AA =B equalityboth sets have the samemembersA={3,9,14},B={3,9,14},A=BA c complementall the objects that do not belongto set AA \B relative complementobjects that belong to A and notto BA = {3,9,14},B = {1,2,3},A-B = {9,14} A - B relative complementobjects that belong to A and notto BA = {3,9,14},B = {1,2,3},A-B = {9,14} A ∆ B symmetric differenceobjects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ∆B ={1,2,9,14} A ⊖ B symmetric differenceobjects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ⊖B ={1,2,9,14}a∈A element of set membership A={3,9,14}, 3 ∈Ax∉A not element of no set membership A={3,9,14}, 1 ∉A(a ,b ) ordered pair collection of 2 elementsA×B cartesian product set of all ordered pairs from Aand B|A| cardinality the number of elements of set AA={3,9,14}, |A|=3 #A cardinality the number of elements of set AA={3,9,14}, #A=3aleph-nullinfinite cardinality of naturalnumbers setaleph-one cardinality of countable ordinalnumbers setØ empty set Ø = { }C = {Ø}universal set set of all possible valuesnatural numbers / whole numbers set (with zero) 0 = {0,1,2,3,4,...}0 ∈ 01natural numbers / wholenumbers set (withoutzero)1 = {1,2,3,4,5,...}6 ∈ 1integer numbers set= {...-3,-2,-1,0,1,2,3,...} -6 ∈rational numbers set= {x | x =a /b , a ,b ∈}2/6 ∈real numbers set= {x | -∞ < x <∞} 6.343434∈complex numbers set= {z | z=a +bi ,-∞<a <∞, -∞<b <∞}6+2i ∈∨reversed caret or x∨y | vertical line or x | y x' single quote not - negation x'x bar not - negation x¬not not - negation ¬x ! exclamation mark not - negation ! x ⊕circled plus / oplus exclusive or - xor x⊕y ~ tilde negation ~ x ⇒implies⇔equivalent if and only if (iff)↔equivalent if and only if (iff)∀for all∃there exists∄there does not exists∴therefore∵because / sincee e constant / Euler'snumber e = 2.718281828...e = lim(1+1/x)x ,x→∞y ' derivative derivative - Lagrange's notation (3x3)' = 9x2y '' second derivative derivative of derivative (3x3)'' = 18xy(n)nth derivative n times derivation (3x3)(3) = 18derivative derivative - Leibniz's notation d(3x3)/dx = 9x2second derivative derivative of derivative d2(3x3)/dx2 = 18xnth derivative n times derivationtime derivative derivative by time - Newton's notationtime secondderivativederivative of derivativeD x y derivative derivative - Euler's notationD x2y second derivative derivative of derivativepartial derivative ∂(x2+y2)/∂x = 2x ∫integral opposite to derivation ∫f(x)dx∫∫double integral integration of function of 2variables∫∫f(x,y)dxdy∫∫∫triple integral integration of function of 3variables∫∫∫f(x,y,z)dxdydz∮closed contour / lineintegral∯closed surfaceintegral∰closed volumeintegral[a,b] closed interval [a,b] = {x | a ≤ x ≤ b}(a,b) open interval (a,b) = {x | a < x < b}i imaginary unit i≡ √-1 z = 3 + 2i z* complex conjugate z = a+bi→z*=a-bi z* = 3 - 2i z complex conjugate z = a+bi→z = a-bi z = 3 - 2i ∇nabla / del gradient / divergence operator ∇f (x,y,z)vectorunit vectorx * y convolution y(t) = x(t) * h(t)Laplace transform F(s) = {f (t)}Fourier transform X(ω) = {f (t)}δdelta function∞lemniscate infinity symbol。
数学符号的中英文读法
section; division
分节号
→
arrow
箭号；参见号
＋
plus
加号；正号
－
minus
减号；负号
±
plus or minus
正负号
×
is multiplied by
乘号
÷
is divided by
除号
＝
is equal to
等于号
≠
is not equal to
不等于号
≡
is equivalent to
Ν
（纽）
Ξ
（可系）
Ο
（奥密克戎）
Π
（派）
Ρ
（若）
Σ
（西格马）
Τ
（套）
Υ
（英文或拉丁字母）
Φ
（斐）
Χ
（喜）
Ψ
（普西）
Ω
（欧米伽）
Mu
Ν ν： 拗
Nu
Ξ ξ： 克西
KeXi
Ο ο： 欧麦克轮 Omicron
∏ π： 派
Pi
Ρ ρ： 柔
Rho
∑ σ： 西格玛
Sigma
Τ τ： 套
Tau
Υ υ： 宇普西龙 Upsilon
Φ φ： fai
Phi
Χ χ： 器
Chi
Ψ ψ： 普赛
Psi
Ω ω： 欧米伽
Omega
希腊字母怎么打:打开 Office 文档之后，在你需要输入希腊字母的时候，先将输入法切换为
ω（欧米伽）。
更全面：
1 Α α alpha a:lf
阿尔法 角度系数
2 Β β beta bet
贝塔 磁通系数 角度系数
数学符号英文对照表
1．Professional Basics Knowledge1/21/32/31/41/1001/1000 113/3244320.25＋－±×÷＝≈( ) [ ] { }≢≣∞∵∴→x＋y (a + b ) a = ba ≠b a ±b a ≈b a ＞b a ＞＞b a ≣b a ＜b a ＜＜b a ≢b a ⊥b x →∞a ≡b ∟a a half, one halfa third, one thirdtwo thirdsa quarter, one quarter , a fourth, one fourtha (one) hundredtha (one) thousandthone hundred and thirteen over three hundred and twenty four four and two thirdszero (0, naught) point two fiveplus, positiveminus, negativeplus or minusmultiplied by, timesdivided bybe equal to, equalsbe approximately equal to, approximately equalsround brackets; parenthesessquare (angular) bracketsbracesless than or equal tomore than or equal toinfinitybecausethereforemaps intox plus ybracket a plus b bracket closeda equals b, a is equal to b, a is ba is not equal to b, a is not ba plus or minus ba is approximately equal to ba is greater than ba is much [far] greater than ba is greater than or equal to ba is less than ba is much less than ba is less than or equal to ba is perpendicular to bx approaches infinitya is identically equal to b, a is of identity to bangle aa ～ba ∠ba ∝ bx 2x 3x3x %2%‰5‰㏒n x㏒10x㏒e x,㏑xe x ,exp(x)x nx1/n or n xsincostg, tanctg, cotsc, seccsc, cosecsin -1 arcsincos -1 ,arcossinhcosh∑∑=ni ix 1∏∏=ni ix 1∣x ∣xb ’b ’’ the difference between a and b a is parallel to b a varies directly as b x square; x squared; the square of x~, the second power of x, x to second power x cube; x cubed; the cube of x; the third power of x, x to the third power the square root of x the cube root of x percent two percent per mill five per mill log x to the base n log x to the base 10; common logarithm log x to the base e , natural logarithm, Napierian logarithm exponential function of x; e to the power x the nth power of x; x to the power n the nth root of x, x to the power one over n sine cosine tangent cotangent secont cosecant arc sine arc cosine the hyperbolic sine the hyperbolic cosine the summation of the summation of x sub i ,where i goes from 1 to n the product of the product of x sub i , where i goes from 1to n the absolute value of x the mean value of x, x bar b primeb double prime; b second primeb ’’’ f(x) △ x, δx dx dx dy 22dx y d n n dx y d u y ∂∂ ⎰ ⎰⎰ ⎰…⎰ ⎰b aF a 22007’13’’00C1000C320Fb triple primefunction f of xfinite difference or incrementthe increment of xdee x; dee of x; differential xthe differential coefficient of y with respect to x, the first derivative of y with respect of xthe second derivative of y with respect of xthe nth derivative of y with respect of xThe partial derivative of y with respect of u, where y is a function of u and another variable (or variables)integral ofdouble integral ofn-fold integral ofintegral between limits a and b (…from a to b)vector F a sub two twenty degreesseven minutes; seven feetthirteen seconds; thirteen inches zero degree Centigrade [Celsius]one [a] hundred degrees Centigrade thirty-two degrees Fahrenheit。
常用数学符号的英文表达
常用数学符号的英文表达第一章函数与极限Chapter1 Function and Limit集合set元素element子集subset空集empty set并集union交集intersection差集difference of set基本集basic set补集complement set直积direct product笛卡儿积Cartesian product开区间open interval闭区间closed interval半开区间half open interval有限区间finite interval区间的长度length of an interval无限区间infinite interval领域neighborhood领域的中心centre of a neighborhood领域的半径radius of a neighborhood左领域left neighborhood右领域right neighborhood映射mappingX到Y的映射mapping of X ontoY满射surjection单射injection一一映射one-to-one mapping双射bijection算子operator变化transformation函数function逆映射inverse mapping复合映射composite mapping自变量independent variable因变量dependent variable定义域domain函数值value of function函数关系function relation值域range自然定义域natural domain单值函数single valued function多值函数multiple valued function单值分支one-valued branch函数图形graph of a function绝对值函数absolute value符号函数sigh function整数部分integral part阶梯曲线step curve当且仅当if and only if(iff)分段函数piecewise function上界upper bound下界lower bound有界boundedness无界unbounded函数的单调性monotonicity of a function单调增加的increasing单调减少的decreasing单调函数monotone function函数的奇偶性parity(odevity) of a function 对称symmetry偶函数even function奇函数odd function函数的周期性periodicity of a function周期period反函数inverse function直接函数direct function复合函数composite function中间变量intermediate variable函数的运算operation of function基本初等函数basic elementary function初等函数elementary function幂函数power function指数函数exponential function对数函数logarithmic function三角函数trigonometric function反三角函数inverse trigonometric function 常数函数constant function双曲函数hyperbolic function双曲正弦hyperbolic sine双曲余弦hyperbolic cosine双曲正切hyperbolic tangent反双曲正弦inverse hyperbolic sine反双曲余弦inverse hyperbolic cosine反双曲正切inverse hyperbolic tangent极限limit数列 sequence of number收敛 convergence收敛于 a converge to a发散 divergent极限的唯一性 uniqueness of limits收敛数列的有界性 boundedness of a convergent sequence子列 subsequence函数的极限 limits of functions函数()f x 当x 趋于x 0时的极限 limit of functions ()f x as x approaches x 0 左极限 left limit右极限 right limit单侧极限 one-sided limits水平渐近线 horizontal asymptote无穷小 infinitesimal无穷大 infinity铅直渐近线 vertical asymptote夹逼准则 squeeze rule单调数列 monotonic sequence高阶无穷小 infinitesimal of higher order低阶无穷小 infinitesimal of lower order同阶无穷小 infinitesimal of the same order等阶无穷小 equivalent infinitesimal函数的连续性 continuity of a function增量 increment函数()f x 在x 0连续 the function ()f x is continuous at x 0左连续 left continuous右连续 right continuous区间上的连续函数 continuous function函数()f x 在该区间上连续 function ()f x is continuous on an interval不连续点discontinuity point第一类间断点discontinuity point of the first kind第二类间断点discontinuity point of the second kind初等函数的连续性continuity of the elementary functions 定义区间defined interval最大值global maximum value (absolute maximum)最小值global minimum value (absolute minimum)零点定理the zero point theorem介值定理intermediate value theorem。
常用数学符号英文对照
常用数学符号英文对照Basic math symbolsSymbol Symbol Name Meaning / definition Example= equals sign equality 5 = 2+35 is equal to 2+3≠not equal sign inequality 5 ≠ 45 is not equal to 4≈approximatelyequal approximationsin(0.01) ≈ 0.01,x≈y means x isapproximately equal to y> strict inequality greater than 5 > 45 is greater than 4< strict inequality less than 4 < 54 is less than 5≥inequality greater than or equal to 5 ≥ 4,x≥y means x is greater than or equal to y≤inequality less than or equal to 4 ≤ 5,x ≤ y means x is greater than or equal to y( ) parentheses calculate expressioninside first2 × (3+5) = 16[ ] brackets calculate expressioninside first[(1+2)×(1+5)] = 18 + plus sign addition 1 + 1 = 2−minus sign subtraction 2 − 1 = 1±plus - minus both plus and minusoperations3 ± 5 = 8 and -2±minus - plus both minus and plusoperations3 ± 5 = -2 and 8* asterisk multiplication 2 * 3 = 6×times sign multiplication 2 × 3 = 6 ·multiplicationmultiplication 2 · 3 = 6dot÷division sign /division 6 ÷ 2 = 3 obelus/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimal2.56 = 2+56/100separatora b power exponent 23= 8a^b caret exponent 2 ^ 3= 8√a square root √a ·√a= a√9= ±33√a cube root 3√a ·3√a ·3√a= a3√8= 24√a fourth root 4√a ·4√a ·4√a ·4√a= a4√16= ±2n√a n-th rootfor n=3,n√8= 2 (radical)% percent 1% = 1/100 10% × 30 = 3‰per-mille 1‰ = 1/1000 = 0.1% 10‰× 30 = 0.3 ppm per-million 1ppm = 1/1000000 10ppm × 30 = 0.0003 ppb per-billion 1ppb = 1/1000000000 10ppb × 30 = 3×10-7 ppt per-trillion 1ppt = 10-1210ppt × 30 = 3×10-10 Geometry symbolsSymbol Symbol Name Meaning / definition Example∠angle formed by two rays ∠ABC = 30°measured angle ABC = 30°sphericalangle AOB = 30° ∟ right angle = 90°α = 90° °degree 1 turn = 360° α = 60° degdegree 1 turn = 360degα = 60deg ′ prime arcminute, 1° = 60′ α = 60°59′ ″ double primearcsecond, 1′ = 60″α = 60°59′59″line infinite lineABline segment line from point A to point Bray line that start from point Aarc arc from point A to point B= 60° ⊥ perpendicular perpendicular lines (90° angle)AC ⊥ BC| | parallel parallel lines AB | | CD≅ congruent to equivalence of geometric shapes and size ∆ABC ≅ ∆XYZ~ similarity same shapes, not same size ∆ABC~ ∆XYZ Δtriangle triangle shapeΔABC ≅ ΔBCD |x -y | distancedistance between points x and y| x -y | = 5πpi constantπ = 3.141592654...is the ratio between the circumference and diameter of a circlec = π·d = 2·π·rAlgebra symbolsSymbol Symbol NameMeaning /definitionExamplex x variable unknown value tofindwhen 2x= 4, then x= 2≡equivalence identical to≜equal by definition equal bydefinition:= equal by definition equal bydefinition~ approximately equal weakapproximation11 ~ 10≈approximately equal approximation sin(0.01) ≈ 0.01∝proportional to proportional to y∝x when y=kx, k constant ∞lemniscate infinity symbol≪much less than much less than 1 ≪ 1000000≫much greater than much greater than 1000000 ≫ 1( ) parentheses calculateexpressioninside first2 * (3+5) = 16[ ] brackets calculateexpressioninside first[(1+2)*(1+5)] = 18{ } braces set⌊x⌋floor brackets rounds number tolower integer⌊4.3⌋ = 4⌈x⌉ceiling brackets rounds number toupper integer⌈4.3⌉ = 5x! exclamation mark factorial 4! = 1*2*3*4 = 24 |x| single vertical bar absolute value | -5 | = 5f(x) function of x maps values of xto f(x)f(x) = 3x+5(f∘g) function composition (f∘g) (x)=f(g(x))f(x)=3x,g(x)=x-1 ⇒(f∘g)(x)=3(x-1)(a,b) open interval (a,b) ={x|a<x<b}x∈ (2,6)[a,b] closed interval [a,b] ={x|a≤x≤b}x∈ [2,6]∆delta change /difference∆t=t1-t0∆discriminant Δ =b2- 4ac∑sigma summation - sumof all values inrange of series∑x i= x1+x2+...+x n∑∑sigma double summation∏capital pi product - productof all values inrange of series∏x i=x1∙x2∙...∙x ne e constant/ Euler's number e=2.718281828...e= lim (1+1/x)x,x→∞γEuler-Mascheroni constant γ =0.527721566...φgolden ratio golden ratioconstantπpi constant π=3.141592654...is the ratioc=π·d= 2·π·rLinear Algebra SymbolsSymbol Symbol Name Meaning / definition Example·dot scalar product a·b×cross vector product a×bA⊗B tensor product tensor product of A and B A⊗Binner product[ ] brackets matrix of numbers( ) parentheses matrix of numbers|A| determinant determinant of matrix Adet(A) determinant determinant of matrix A||x|| double vertical bars normA T transpose matrix transpose (A T)ij= (A)jiA†Hermitian matrix matrix conjugate transpose (A†)ij= (A)ji A*Hermitian matrix matrix conjugate transpose (A*)ij= (A)ji A-1inverse matrix A A-1=Irank(A) matrix rank rank of matrix A rank(A) = 3Probability and statistics symbols Symbol Symbol Name Meaning / definition ExampleP(A) probabilityfunction probability of eventAP(A) = 0.5P(A∩B) probability ofeventsintersectionprobability that ofevents A and BP(A∩B) = 0.5P(A∪B) probability ofevents union probability that ofevents A or BP(A∪B) = 0.5P(A|B) conditionalprobabilityfunctionprobability of eventA given event BoccuredP(A | B) = 0.3f(x) probabilitydensityfunction (pdf)P(a≤x≤b) =∫f(x)dxF(x) cumulativedistributionfunction (cdf)F(x) =P(X≤x)μpopulation mean mean of populationvaluesμ= 10E(X) expectationvalue expected value ofrandom variable XE(X) = 10E(X | Y) conditionalexpectation expected value ofrandom variable Xgiven YE(X | Y=2) = 5var(X) variance variance of randomvariable Xvar(X) = 4σ2variance variance ofpopulation valuesσ2= 4std(X) standarddeviation standard deviation ofrandom variable Xstd(X) = 2σXstandard deviationstandard deviation value of random variable X σX = 2medianmiddle value of random variable xcov (X ,Y )covariancecovariance of random variables X and Y cov (X,Y ) = 4corr (X ,Y ) correlationcorrelation of random variables X and Y corr (X,Y ) = 0.6ρX ,Y correlationcorrelation of random variables X and Y ρX ,Y = 0.6∑summation summation - sum of allvalues in range of series∑∑double summationdouble summationMo mode value that occursmost frequently in populationMR mid-rangeMR = (x max +x min )/2Mdsample median half the population is below this valueQ 1lower / first quartile25% of population are below this valueQ 2median / second quartile50% of population are below this value = median of samplesQ 3upper / third quartile75% of population are below this valuex sample meanaverage / arithmetic meanx = (2+5+9) / 3 = 5.333s 2sample variancepopulation samples variance estimators 2 = 4s sample standard deviationpopulation samples standard deviation estimators = 2z x standard scorez x = (x -x ) / s xX ~distributionof X distribution of random variable X X ~ N (0,3)N (μ,σ2)normal distribution gaussian distribution X ~ N (0,3)U (a ,b ) uniform distribution equal probability in range a,bX ~ U (0,3)exp (λ)exponential distribution f (x ) = λe -λx , x ≥0 gamma (c , λ)gamma distribution f (x ) = λ c x c-1e -λx /Γ(c ), x ≥0χ 2(k )chi-square distributionf (x ) = x k /2-1e -x /2 /( 2k/2Γ(k /2) )F (k 1, k 2)F distributionBin (n ,p ) binomial distribution f (k ) = n C k p k (1-p )n-kPoisson (λ)Poisson distribution f (k ) = λk e -λ / k !Geom (p )geometric distribution f (k ) = p (1-p ) kHG (N ,K ,n )hyper-geometric distributionBern (p )Bernoulli distributionSet theory symbolsSymbolSymbol NameMeaning / definitionExample{ }set a collection of elementsA = {3,7,9,14},B = {9,14,28} A ∩ B intersectionobjects that belong to set A and set BA ∩B = {9,14}A ∪B unionobjects that belong to set A or set BA ∪B = {3,7,9,14,28}A ⊆B subsetsubset has fewer elements or equal to the set{9,14,28} ⊆ {9,14,28}A ⊂ Bproper subset / strict subsetsubset has fewer elements than the set{9,14} ⊂ {9,14,28} A ⊄ B not subset left set not a subset of right set{9,66} ⊄ {9,14,28}A ⊇B supersetset A has more elements or equal to the set B{9,14,28} ⊇ {9,14,28} A ⊃ B proper superset / strict supersetset A has more elements than set B{9,14,28} ⊃ {9,14} A ⊅ B not superset set A is not a superset of set B{9,14,28} ⊅ {9,66}2Apower set all subsets of Apower set all subsets of AA =B equality both sets have the same membersA={3,9,14}, B={3,9,14},A=BA c complementall the objects that do not belong toset AA \B relative complementobjects that belong to A and not toBA = {3,9,14},B = {1,2,3},A-B = {9,14} A - B relative complementobjects that belong to A and not toBA = {3,9,14},B = {1,2,3},A-B = {9,14} A ∆ Bsymmetricdifferenceobjects that belong to A or B but notto their intersectionA = {3,9,14},B = {1,2,3},A ∆B ={1,2,9,14}A ⊖ Bsymmetricdifferenceobjects that belong to A or B but notto their intersectionA = {3,9,14},B = {1,2,3},A ⊖B ={1,2,9,14}a∈A element of set membership A={3,9,14}, 3 ∈Ax∉A not element of no set membership A={3,9,14}, 1 ∉A(a,b) ordered pair collection of 2 elementsA×B cartesian product set of all ordered pairs from A andB|A| cardinality the number of elements of set A A={3,9,14},|A|=3#A cardinality the number of elements of set A A={3,9,14},#A=3aleph-nullinfinite cardinality of naturalnumbers setaleph-onecardinality of countable ordinalnumbers setØempty set Ø = { } C = {Ø}universal set set of all possible valuesnatural numbers /whole numbers set (with zero) 0= {0,1,2,3,4,...} 0 ∈1natural numbers /whole numbers set (without zero)1= {1,2,3,4,5,...} 6 ∈1integer numbers set = {...-3,-2,-1,0,1,2,3,...} -6 ∈rational numbers set= {x | x =a /b , a ,b ∈}2/6 ∈real numbers set= {x | -∞ < x <∞} 6.343434∈complex numbers set= {z | z=a +bi , -∞<a <∞, -∞<b <∞}6+2i ∈Logic symbolsSymbolSymbol NameMeaning / definitionExample· andandx · y ^ caret / circumflex andx ^ y& ampersand andx & y+ plus orx + y∨ reversed caret orx ∨ y|vertical line orx | yx ' single quote not - negationx 'xbar not - negationx¬not not - negation¬ x! exclamation mark not - negation !x ⊕circled plus / oplus exclusive or - xor x⊕y ~ tilde negation ~x ⇒implies⇔equivalent if and only if (iff)↔equivalent if and only if (iff)∀for all∃there exists∄there does not exists∴therefore∵because / sinceCalculus & analysis symbolsSymbol Symbol Name Meaning / definition Examplelimit limit value of a functionεepsilon represents a very smallnumber, near zeroε→0e e constant/Euler's number e= 2.718281828...e= lim(1+1/x)x,x→∞y' derivative derivative - Lagrange'snotation(3x3)' = 9x2y'' second derivative derivative of derivative (3x3)'' = 18x y(n)nth derivative n times derivation (3x3)(3)= 18derivative derivative - Leibniz'snotationd(3x3)/dx= 9x2second derivative derivative of derivative d2(3x3)/dx2= 18xnth derivative n times derivationtime derivative derivative by time - Newton's notationtime secondderivativederivative of derivativeD x y derivative derivative - Euler'snotationD x2y second derivative derivative of derivativepartial derivative ∂(x2+y2)/∂x= 2x∫integral opposite to derivation ∫f(x)dx∫∫double integral integration of function of 2variables∫∫f(x,y)dxdy∫∫∫triple integral integration of function of 3variables∫∫∫f(x,y,z)dxdydz∮closed contour /line integral∯closed surfaceintegral∰closed volumeintegral[a,b] closed interval [a,b] = {x|a≤x≤b}(a,b) open interval (a,b) = {x|a<x<b}i imaginary unit i≡√-1 z= 3 + 2i z* complex conjugate z=a+bi→z*=a-bi z*= 3 - 2i z complex conjugate z=a+bi→z=a-bi z= 3 - 2i ∇nabla / del gradient / divergence∇f(x,y,z)operatorvectorunit vectorx*y convolution y(t) =x(t) *h(t)Laplace transform F(s) = {f(t)}Fourier transform X(ω) ={f(t)}δdelta function∞lemniscate infinity symbol欢迎您的下载，资料仅供参考！致力为企业和个人提供合同协议，策划案计划书，学习资料等等打造全网一站式需求。
你知道这些数学符号和名称如何用英文表达吗？
你知道这些数学符号和名称如何用英文表达吗？加法：addition表达“加”的含义的词：add, and, more, sum, increase, plus, total, together减法：subtraction表达“减”的含义的词：fewer, minus, take away, difference between, take from, reduce, decrease乘法：multiplication表达“乘”的含义的词：multiply, times, groups of, multiplied by, lots of, product除法：division表达“除”的含义的词：divide, share, divisible by, share equally, divide into group, divided by等于：equals表达“等于”的含义的词：makes, totals, is equivalent to, is the same as大于 is greater than小于 is less than运算符 operator数字 digit数 number自然数 natural number整数 integer质数 prime number小数 decimal小数点 decimal point分数 fraction分子 numerator分母 denominator比 ratio正 positive负 negative零 null, zero, nought, nil十进制 decimal system二进制 binary system十六进制 hexadecimal system四舍五入 round下舍入 round down上舍入 round up代数 algebra公式 formula, formulae(pl.)单项式 monomial多项式 polynomial, multinomial系数 coefficient未知数 unknown, x-factor, y-factor, z-factor 等式，方程式 equation一次方程 simple equation二次方程 quadratic equation三次方程 cubic equation四次方程 quartic equation不等式 inequation阶乘 factorial对数 logarithm指数，幂 exponent乘方 power二次方，平方 square三次方，立方 cube四次方 the power of four, the fourth power n次方 the power of n, the nth power开方 evolution, extraction二次方根，平方根 square root三次方根，立方根 cube root四次方根 the root of four, the fourth root n次方根 the root of n, the nth root集合 aggregate元素 element空集 void子集 subset交集 intersection并集 union补集 complement映射 mapping函数 function定义域 domain, field of definition 值域 range常量 constant变量 variable单调性 monotonicity奇偶性 parity周期性 periodicity图象 image数列，级数 series微积分 calculus微分 differential导数 derivative极限 limit无穷大 infinite(a.) infinity(n.)无穷小 infinitesimal积分 integral定积分 definite integral不定积分 indefinite integral有理数 rational number无理数 irrational number实数 real number虚数 imaginary number复数 complex number矩阵 matrix行列式 determinant几何 geometry点 point线 line面 plane体 solid线段 segment射线 radial平行 parallel相交 intersect角 angle角度 degree弧度 radian锐角 acute angle直角 right angle钝角 obtuse angle平角 straight angle周角 perigon底 base边 side高 height三角形 triangle锐角三角形 acute triangle直角三角形 right triangle直角边 leg斜边 hypotenuse勾股定理 Pythagorean theorem 钝角三角形 obtuse triangle不等边三角形 scalene triangle 等腰三角形 isosceles triangle 等边三角形 equilateral triangle四边形 quadrilateral平行四边形 parallelogram矩形 rectangle长 length宽 width菱形 rhomb, rhombus, rhombi(pl.), diamond 正方形 square梯形 trapezoid（美），trapezium（英）直角梯形 right trapezoid等腰梯形 isosceles trapezoid五边形 pentagon六边形 hexagon七边形 heptagon八边形 octagon九边形 enneagon十边形 decagon十一边形 hendecagon十二边形 dodecagon多边形 polygon正多边形 equilateral polygon圆 circle圆心 centre（英）, center（美）半径 radius直径 diameter圆周率 pi弧 arc半圆 semicircle扇形 sector环 ring椭圆 ellipse圆周 circumference周长 perimeter面积 area轨迹 locus, loca(pl.)相似 similar全等 congruent立方体 cube四面体 tetrahedron五面体 pentahedron六面体 hexahedron平行六面体 parallelepiped 七面体 heptahedron八面体 octahedron九面体 enneahedron十面体 decahedron十一面体 hendecahedron 十二面体 dodecahedron 二十面体 icosahedron多面体 polyhedron棱锥 pyramid棱柱 prism棱台 frustum of a prism 旋转 rotation轴 axis圆锥 cone圆柱 cylinder圆台 frustum of a cone 球 sphere半球 hemisphere底面 undersurface表面积 surface area体积 volume空间 space坐标系 coordinates坐标轴 x-axis, y-axis, z-axis 横坐标 x-coordinate纵坐标 y-coordinate原点 origin双曲线 hyperbola抛物线 parabola三角 trigonometry正弦 sine余弦 cosine正切 tangent余切 cotangent正割 secant余割 cosecant反正弦 arc sine反余弦 arc cosine反正切 arc tangent反余切 arc cotangent反正割 arc secant反余割 arc cosecant相位 phase周期 period振幅 amplitude内切圆 inscribed circle外切圆 circumcircle统计 statistics平均数 average加权平均数 weighted average方差 variance标准差 root-mean-square deviation, standard deviation 比例 propotion百分比 percent百分点 percentage排列 permutation组合 combination概率，或然率 probability分布 distribution正态分布 normal distribution非正态分布 abnormal distribution图表 graph条形统计图 bar graph柱形统计图 histogram折线统计图 broken line graph曲线统计图 curve diagram扇形统计图 pie diagram公理 axiom定理 theorem计算 calculation运算 operation证明 prove假设 hypothesis, hypotheses(pl.) 命题 proposition。
数学符号英文表示
以下是一些通用的标点符号英文翻译，常用的都在这儿了。
= equal, comma; semicolon: colon? question mark! exclamation mark/ slash/ backslash| bar@ at# number sign$ dollar% percent^ caret& ampersand* asterisk 通配符_ under score( left parentheses) right parentheses[ left bracket] right bracket{ left brace} right brace' quote' back quote" double quote~ tilde. period< less> greater' apostrophe 省略号；所有格符号-- dash 破折号' ' single quotation marks 单引号" " double quotation marks 双引号( ) parentheses 圆括号[ ] square brackets 方括号<> Angle bracket{} Brace... ellipsis 省略号- hyphen 连字符加减乘除、以及space和enter 符号这里略去，想必大家都会；最后一个hyphen 连字符有点难度，估计很多人不知道怎么念，用minus代替了。
下面列一些数学符号的英文《》French quotes 法文引号；书名号¨tandem colon 双点号" ditto 同上‖parallel 双线号／virgule 斜线号＆ampersand = and～swung dash 代字号§section; division 分节号→arrow 箭号；参见号＋positive sign 正号－minus 负号or negativeªplus or minus 正负号×is multiplied by 乘号÷is divided by 除号＝is equal to 等于号≠is not equal to 不等于号≡is equivalent to 全等于号≌is equal to or approximately equal to 等于或约等于号≈is approximately equal to 约等于号＜is less than 小于号＞is more than 大于号≤is not less than 不小于号≥is not more than 不大于号≢is less than or equal to 小于或等于号≣is more than or equal to 大于或等于号％per cent 百分之…‰per mill 千分之…∞infinity 无限大号∝varies as 与…成比例√(square) root 平方根∵since; because 因为∴hence 所以∷equals, as (proportion) 等于，成比例∟angle 角≨semicircle 半圆≦circle 圆○circumference 圆周πpi 圆周率△triangle 三角形≧perpendicular to 垂直于∪union of 并，合集∩intersection of 交，通集∫the integral of …的积分∑(sigma) summation of 总和©degree 度′minute 分″second 秒＃number …号℃Celsius system 摄氏度＠at 单价x'是x prime(比如转置矩阵) x"是x double-prime。
常用数学符号英文对照
常用数学符号英文对照Basic math symbolsSymbol Symbol Name Meaning / definition Example= equals sign equality 5 = 2+35 is equal to 2+3≠not equal sign inequality 5 ≠ 45 is not equal to 4≈approximatelyequal approximationsin(0.01) ≈ 0.01,x≈y means x is approximatelyequal to y> strict inequality greater than 5 > 45 is greater than 4< strict inequality less than 4 < 54 is less than 5≥inequality greater than or equal to 5 ≥ 4,x≥y means x is greater than or equal to y≤inequality less than or equal to 4 ≤ 5,x ≤ y means x is greater than or equal to y( ) parentheses calculate expression insidefirst2 × (3+5) = 16[ ] brackets calculate expression insidefirst[(1+2)×(1+5)] = 18 + plus sign addition 1 + 1 = 2−minus sign subtraction 2 − 1 = 1±plus - minus both plus and minusoperations3 ± 5 = 8 and -2±minus - plus both minus and plusoperations3 ± 5 = -2 and 8 * asterisk multiplication 2 * 3 = 6×times sign multiplication 2 × 3 = 6 ·multiplication dot multiplication 2 · 3 = 6÷division sign /division 6 ÷ 2 = 3obelus/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimal2.56 = 2+56/100separatora b power exponent 23= 8a^b caret exponent 2 ^ 3= 8√a square root √a ·√a = a√9 = ±33√a cube root 3√a ·3√a ·3√a = a3√8 = 24√a fourth root 4√a ·4√a ·4√a ·4√a = a4√16 = ±2n√a n-th root (radical) for n=3, n√8 = 2% percent1% = 1/100 10% × 30 = 3‰per-mille1‰ = 1/1000 = 0.1%10‰ × 30 = 0.3ppm per-million1ppm = 1/1000000 10ppm × 30 = 0.0003ppb per-billion 1ppb = 1/1000000000 10ppb × 30 = 3×10-7ppt per-trillion 1ppt = 10-1210ppt × 30 = 3×10-10ABC = 30°AOB = 30°°degree 1 turn = 360°α = 60°deg degree 1 turn = 360deg α = 60deg′prime arcminute, 1° = 60′α = 60°59′″double prime arcsecond, 1′ = 60″α = 60°59′59″line infinite lineAB line segment line from point A to point Bray line that start from point Aarc arc from point A to point B= 60°⊥perpendicular perpendicular lines (90° angle) AC ⊥ BC| | parallel parallel lines AB | | CD≅congruent to equivalence of geometric shapes and size ∆ABC≅∆XYZ ~ similarity same shapes, not same size ∆ABC~ ∆XYZ Δtriangle triangle shape ΔABC≅ΔBCD |x-y| distance distance between points x and y | x-y | = 5πpi constant π = 3.141592654...is the ratio between the circumference and diameter of acirclec = π·d = 2·π·rrad radians radians angle unit 360° = 2π rad c radians radians angle unit 360° = 2πcgrad gradians / gons grads angle unit 360° = 400 gradg gradians / gons grads angle unit 360° = 400 gx x variableto findwhen 2x = 4, then x = 2≡equivalence identical to≜equal by definition equal bydefinition:= equal by definition equal bydefinition~ approximately equal weakapproximation11 ~ 10≈approximately equal approximation sin(0.01) ≈ 0.01∝proportional to proportional to y∝x when y = kx, k constant ∞lemniscate infinity symbol≪much less than much less than 1 ≪1000000≫much greater than much greaterthan1000000 ≫1( ) parentheses calculateexpressioninside first2 * (3+5) = 16[ ] brackets calculateexpressioninside first[(1+2)*(1+5)] = 18{ } braces set⌊x⌋floor brackets rounds numberto lower integer⌊4.3⌋ = 4⌈x⌉ceiling brackets rounds numberto upper integer⌈4.3⌉ = 5x! exclamation mark factorial4! = 1*2*3*4 = 24 | x | single vertical bar absolute value | -5 | = 5f (x) function of x maps values ofx to f(x)f (x) = 3x+5(f∘g) function composition (f∘g) (x)= f (g(x))f (x)=3x,g(x)=x-1 ⇒(f∘g)(x)=3(x-1)(a,b) open interval (a,b) = x∈(2,6)[a ,b ] closed interval[a ,b ] = {x | a ≤ x ≤ b }x ∈ [2,6]∆ delta change / difference∆t = t 1 - t 0∆ discriminantΔ = b 2 - 4ac∑sigmasummation -sum of all values in range of series ∑ x i = x 1+x 2+...+x n∑∑sigmadouble summation∏capital piproduct -product of all values in range of series∏ x i =x 1∙x 2∙...∙x ne e constant / Euler's numbere =2.718281828... e = lim (1+1/x )x , x →∞γ Euler-Mascheroni constant γ =0.527721566...φgolden ratio golden ratio constantπpi constant π =3.141592654...is the ratiobetween the circumference and diameter of a circlec = π·d = 2·π·rA ⊗Btensor product tensor product of A and BA ⊗ Binner product[ ] brackets matrix of numbers ( ) parentheses matrix of numbers| A | determinant determinant of matrix A det(A ) determinant determinant of matrix A|| x || double vertical bars normA T transpose matrix transpose(A T )ij = (A )ji A † Hermitian matrix matrix conjugate transpose (A †)ij = (A )ji A * Hermitian matrix matrix conjugate transpose(A *)ij = (A )jiA -1inverse matrixA A -1 = Irank(A ) matrix rank rank of matrix A rank(A ) = 3 dim(U ) dimensiondimension of matrix Arank(U ) = 3Probability and statistics symbolsSymbolSymbol Name Meaning / definitionExampleP (A )probability function probability of event A P (A ) = 0.5P (A ∩ B ) probability ofeventsintersection probability that of events A and BP (A ∩B ) = 0.5P (A ∪B ) probability ofevents unionprobability that of events A or B P (A ∪B ) = 0.5P (A | B )conditionalprobability function probability of event A given event B occuredP (A | B ) = 0.3f (x ) probabilitydensity function (pdf) P (a ≤ x ≤ b ) = ∫ f (x ) dxF (x )cumulativeF (x ) = P (X ≤ x )distribution function (cdf)μ population mean mean of population valuesμ = 10E (X )expectation valueexpected value of random variable X E (X ) = 10E (X | Y )conditional expectationexpected value of random variable X given YE (X | Y=2) = 5var (X ) variance variance of random variable X var (X ) = 4σ2variancevariance of population values σ2 = 4std (X ) standard deviationstandard deviation of random variable X std (X ) = 2σXstandard deviationstandard deviation value of random variable X σX = 2medianmiddle value of random variable xcov (X ,Y )covariance covariance ofrandom variables X and Y cov (X,Y ) = 4corr (X ,Y ) correlationcorrelation ofrandom variables X and Y corr (X,Y ) = 0.6ρX ,Ycorrelation correlation ofrandom variables X and YρX ,Y = 0.6∑summation summation - sum ofall values in range of series∑∑double summationdouble summationMo mode value that occurs most frequently in populationMR mid-range MR = (x max+x min)/2 Md sample median half the population isbelow this valueQ1lower / firstquartile 25% of population are below this valueQ2median /second quartile 50% of population are below this value = median of samplesQ3upper / thirdquartile 75% of population are below this valuex sample mean average / arithmeticmeanx = (2+5+9) / 3 = 5.333s2samplevariance population samples variance estimators2 = 4s samplestandarddeviationpopulation samplesstandard deviationestimators = 2z x standard score z x = (x-x) / s xX ~ distribution of X distribution ofrandom variable XX ~ N(0,3)N(μ,σ2) normaldistributiongaussian distribution X ~ N(0,3)U(a,b) uniformdistributionequal probability inrange a,bX ~ U(0,3)exp(λ)exponentialdistributionf (x)= λe-λx , x≥0gamma(c, λ)gammadistributionf (x) = λ c x c-1e-λx /Γ(c), x≥0χ 2(k) chi-squaredistributionf (x) = x k/2-1e-x/2 /( 2k/2 Γ(k/2) )F (k1, k2) F distributionBin (n ,p )binomial distribution f (k ) = n C k p k (1-p )n-kPoisson (λ)Poisson distribution f (k ) = λk e -λ / k !Geom (p )geometric distribution f (k ) = p (1-p ) kHG (N ,K ,n ) hyper-geometric distributionBern (p ) Bernoulli distributionSet theory symbolsSymbolSymbol NameMeaning / definitionExample{ }set a collection of elementsA = {3,7,9,14},B = {9,14,28} A ∩ B intersectionobjects that belong to set A and set BA ∩B = {9,14} A ∪ B unionobjects that belong to set A or set BA ∪B = {3,7,9,14,28} A ⊆ B subsetsubset has fewer elements or equal to the set{9,14,28} ⊆ {9,14,28} A ⊂ B proper subset / strictsubset has fewer elements than{9,14} ⊂subset the set {9,14,28}A ⊄B not subset left set not a subset of right set{9,66} ⊄{9,14,28}A ⊇B supersetset A has more elements or equalto the set B{9,14,28} ⊇{9,14,28}A ⊃Bproper superset / strictsupersetset A has more elements than setB{9,14,28} ⊃{9,14}A ⊅B not superset set A is not a superset of set B{9,14,28} ⊅{9,66} 2A power set all subsets of Apower set all subsets of AA =B equality both sets have the same membersA={3,9,14},B={3,9,14},A=BA c complementall the objects that do not belong toset AA \B relative complementobjects that belong to A and not toBA = {3,9,14},B = {1,2,3},A-B = {9,14} A - B relative complementobjects that belong to A and not toBA = {3,9,14},B = {1,2,3},A-B = {9,14} A ∆ B symmetric differenceobjects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ∆B ={1,2,9,14}A ⊖B symmetric differenceobjects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ⊖B ={1,2,9,14}a∈A element of set membership A={3,9,14}, 3 ∈Ax∉A not element of no set membership A={3,9,14}, 1 ∉A(a ,b ) ordered pair collection of 2 elementsA×B cartesian product set of all ordered pairs from A and B|A| cardinality the number of elements of set AA={3,9,14}, |A|=3 #A cardinality the number of elements of set AA={3,9,14}, #A=3aleph-nullinfinite cardinality of natural numbers setaleph-one cardinality of countable ordinal numbers setØ empty set Ø = { }C = {Ø}universal setset of all possible valuesnatural numbers / whole numbers set (with zero) 0 = {0,1,2,3,4,...}0 ∈ 01natural numbers / wholenumbers set (without zero)1 = {1,2,3,4,5,...}6 ∈ 1integer numbers set= {...-3,-2,-1,0,1,2,3,...} -6 ∈rational numbers set= {x | x =a /b , a ,b ∈}2/6 ∈real numbers set= {x | -∞ < x <∞} 6.343434∈complex numbers set= {z | z=a +bi ,-∞<a <∞, -∞<b <∞}6+2i ∈∨reversed caret or x∨y | vertical line or x | y x' single quote not - negation x'x bar not - negation x¬not not - negation ¬x ! exclamation mark not - negation ! x ⊕circled plus / oplus exclusive or - xor x⊕y ~ tilde negation ~ x ⇒implies⇔equivalent if and only if (iff)↔equivalent if and only if (iff)∀for all∃there exists∄there does not exists∴therefore∵because / sincee e constant / Euler'snumber e = 2.718281828...e = lim(1+1/x)x ,x→∞y ' derivative derivative - Lagrange's notation (3x3)' = 9x2y '' second derivative derivative of derivative (3x3)'' = 18xy(n)nth derivative n times derivation (3x3)(3) = 18derivative derivative - Leibniz's notation d(3x3)/dx = 9x2second derivative derivative of derivative d2(3x3)/dx2 = 18xnth derivative n times derivationtime derivative derivative by time - Newton's notationtime secondderivativederivative of derivativeD x y derivative derivative - Euler's notationD x2y second derivative derivative of derivativepartial derivative ∂(x2+y2)/∂x = 2x ∫integral opposite to derivation ∫f(x)dx∫∫double integral integration of function of 2variables∫∫f(x,y)dxdy∫∫∫triple integral integration of function of 3variables∫∫∫f(x,y,z)dxdydz∮closed contour / lineintegral∯closed surfaceintegral∰closed volumeintegral[a,b] closed interval [a,b] = {x | a ≤ x ≤ b}(a,b) open interval (a,b) = {x | a < x < b}i imaginary unit i≡ √-1 z = 3 + 2i z* complex conjugate z = a+bi→z*=a-bi z* = 3 - 2i z complex conjugate z = a+bi→z = a-bi z = 3 - 2i ∇nabla / del gradient / divergence operator ∇f (x,y,z)vectorunit vectorx * y convolution y(t) = x(t) * h(t)Laplace transform F(s) = {f (t)}Fourier transform X(ω) = {f (t)}δdelta function∞lemniscate infinity symbol。
数学符号对应的英文的读法
一、一般符号对应的英文单词．period 句号，comma 逗号：colon 冒号；semicolon 分号！exclamation 惊叹号？question mark 问号─ hyphen 连字符‟ apostrophe 省略号；所有格符号— dash 破折号…‟single quotation marks 单引号“”double quotation marks 双引号( ) parentheses 圆括号[ ] square brackets 方括号《》French quotes 法文引号；书名号... ellipsis 省略号¨ tandem colon 双点号" ditto 同上‖parallel 平行／virgule 斜线号＆ampersand = and～swung dash 代字号§ section; division 分节号→ arrow 箭号；参见号＋plus 加号；正号－minus 减号；负号± plus or minus 正负号× is multiplied by or cross 叉乘÷ is divided by 除号＝is equal to 等于号≠ is not equal to 不等于号≡ is equivalent to 全等于号≌is equal to or approximately equal to 等于或约等于号≈ is approximately equal to 约等于号＜is less than 小于号＞is more than （is greater than在数学中更常用）大于号≮is not less than 不小于号≯is not more than 不大于号≤ is less than or equal to 小于或等于号≥ is more than or equal to 大于或等于号％per cent 百分之…‰ per mill 千分之…∞ infinity 无限大号∝varies as 与…成比例√ (square) root 平方根∵since; because 因为∴hence 所以∷equals, as (proportion) 等于，成比例∠angle 角≲semicircle 半圆≰circle 圆○ circumference 圆周π pi 圆周率△triangle 三角形≱perpendicular to 垂直于；另外normal to，right to也都有垂直的意思。
数学符号以及希腊字母的英文表达
数学符号以及希腊字母的英文表达+ plus加号；正号- minus减号；负号±plus or minus正负号×is multiplied by乘号÷is divided by除号＝is equal to等于号≠is not equal to不等于号≡is equivalent to全等于号∈ is a member of the set⊂ is a subset of∽ similar to≌is equal to or approximately equal to等于或约等于号≈is approximately equal to约等于号＜is less than小于号＞is more than大于号≮is not less than不小于号≯is not more than不大于号≤is less than or equal to小于或等于号≥is more than or equal to大于或等于号% per cent百分之…‰per mill千分之…∞infinity无限大号∝varies as与…成比例√(square) root平方根e the base of natural logarithms,approx.2.71828 x! factorial x, x(x-1)(x-2)---1log n x log x to the base nlnx log x to the base e(natural logarithm)lgx log x to the base 10(common logarithm)|x| the absolute value of x∵since; because因为∴hence所以∷equals, as (proportion)等于，成比例∠angle角⌒semicircle半圆⊙circle圆○circumference圆周πpi 圆周率△triangle三角形∥ parallel to⊥perpendicular to垂直于∪union of并，合集∩intersection of 交，通集∫the integral of …的积分∑(sigma) summation of总和°degree度′minute分〃second秒℃Celsius system摄氏度°F Fahrenheit 华氏{open brace, open curly左花括号}close brace, close curly右花括号(open parenthesis, open paren左圆括号)close parenthesis, close paren右圆括号() brakets/ parentheses括号[open bracket 左方括号]close bracket 右方括号[] square brackets方括号.period, dot句号，点vertical bar, vertical virgule竖线&ersand, and, reference, ref和，引用*asterisk, multiply, star, pointer星号，乘号，星，指针/slash, divide, oblique 斜线，斜杠，除号//slash-slash, comment 双斜线，注释符#AmE pound or BrE hash井号\backslash, sometimes escape反斜线转义符，有时表示转义符或续行符~tilde波浪符.full stop句号,comma逗号:colon冒号;semicolon分号?question mark问号!exclamation mark (英式英语) exclamation point (美式英语)'apostrophe撇号-hyphen连字号-- dash 破折号...dots/ ellipsis省略号"single quotation marks 单引号""double quotation marks 双引号‖ parallel 双线号&ersand = and～swung dash 代字号§section; division 分节号→arrow 箭号；参见号α Α alpha 【'æfə】β Β beta 【'beitə】γ Γ gamma 【'gæmə】δ Δ delta 【'deltə】ε Ε epsilon 【'epsilən】ζ Ζ zeta 【'zi:tə】η Η eta 【'i:tə】θ Θ theta 【'θi:tə】ι Ι iota 【aɪ'əʊtə】κ Κ kappa 【'kæpə】λ ∧ lambda 【'læmdə】μΜ mu 【mju:】νΝ nu 【nju:】ξΞ xi 【ksi:】ο Ο omicron 【əu'maikrən】π∏ pi 【pai】ρ Ρ rho 【rəu】σ ∑ sigma 【'sigmə】τ Τ tau【taʊ】υ Υ upsilon 【'epsilən】φΦ phi 【fai】χΧ chi 【ki:】ψΨ psi 【psai】ω Ω omega 【'əumigə】。
sci文章 数学符号
sci文章数学符号
在SCI发表的论文中，常常使用一些特定的符号来表示数学、物理、化学等领域的概念。
以下是一些科研论文中SCI常用的符号，以及它们的中文解释：
1.数学符号：
–∑（Sigma）：表示求和。
–∫（Integral）：表示积分。
–α、β、γ：表示变量。
–Δ（Delta）：表示差异或变化。
–θ（Theta）：表示角度。
2.物理学符号：
–c：表示光速。
–λ（Lambda）：表示波长。
–E：表示能量。
–h：表示普朗克常数。
–μ：表示磁导率。
3.化学符号：
–H₂O：表示水分子。
–CO₂：表示二氧化碳。
–NaCl：表示氯化钠（食盐）。
–C₆H₁₂O₆：表示葡萄糖。
4.统计学符号：
–μ（Mu）：表示总体均值。
–σ（Sigma）：表示总体标准差。
–X̄（X-bar）：表示样本均值。
–s：表示样本标准差。
5.生物学符号：
–DNA：表示脱氧核糖核酸。
–RNA：表示核糖核酸。
–ATP：表示三磷酸腺苷。
–β：表示生物学中的倍增因子。
6.工程学符号：
–ω（Omega）：表示角速度。
–V：表示电压。
–I：表示电流。
–R：表示电阻。
数学常用英文词汇表
数学常用英文词汇表本文介绍了数学常用的英文词汇，包括数学符号、运算、函数、几何、代数、微积分、概率统计等方面的内容。
文章使用表格的形式，将中文和英文对照列出，方便读者学习和记忆。
文章还提供了一些例句和注释，帮助读者理解和运用这些词汇。
一、数学符号中文英文例句等于equal to, equals, is equal to2+3=5 Two plus three equals five.不等于not equal to, is not equal to2+3≠4 Two plus three is not equal to four.大于greater than, is greater than5>4 Five is greater than four.小于less than, is less than4<5 Four is less than five.大于等于greater than or equal to, is greater than or equalto5≥4 Five is greater than or equal to four.小于等于less than or equal to, is less than or equal to4≤5 Four is less than or equal to five.加号plus sign, plus2+3=5 Two plus three equals five.减号minus sign, minus5-3=2 Five minus three equals two.乘号multiplication sign, times2×3=6 Two times three equals six.除号division sign, divided by6÷3=2 Six divided by three equals two.等号equal sign, equals sign2+3=5 Two plus three equals five.不等号inequality sign, inequality symbol2+3≠4 Two plus three is not equal to four.括号parentheses, brackets(2+3)×4=20 (Two plus three) times four equalstwenty.方括号square brackets, brackets[a,b]表示闭区间[a,b] means a closed interval.花括号curly brackets, braces{x绝对值符号absolute value sign, modulus sign|x|=y表示x的绝对值等于y注释：在英语中，有时会用is来表示等于，如2+3 is 5，但更常用的是equals。
主要数学符号(English)
主要数学符号的英文读法+ plus 加号；正号- minus 减号；负号± plus or minus 正负号× multiplied by 乘号÷ divided by 除号＝be equal to 等于号≠be not equal to 不等于号≡be equivalent to 全等于号≌ be equal to or approximately equal to 等于或约等于号≈be approximately equal to 约等于号＜be less than 小于号＞be more than 大于号≮be not less than 不小于号≯be not more than 不大于号≤be less than or equal to 小于或等于号≥be more than or equal to 大于或等于号% per cent 百分之…‰ per mille 千分之…∞infinity 无限大号∝varies as 与…成比例√(square) root 平方根∵since; because 因为∴hence 所以∷equals, as (proportion) 等于，成比例∠angle 角⌒semicircle 半圆⊙circle 圆○circumference 圆周πpi 圆周率△triangle 三角形⊥perpendicular to 垂直于∪union of 并，合集∩intersection of 交，通集∫the integral of …的积分∑(sigma) summation of 总和° degree 度′minute 分〃second 秒℃Celsius system 摄氏度() round brackets(parentheses)[] square brackets{} braces( open parenthesis, open paren 左圆括号) close parenthesis, close paren 右圆括号[ open bracket 左方括号] close bracket 右方括号{ open brace, open curly 左花括号} close brace, close curly 右花括号《》 French quotes 法文引号;书名号. period, dot 句号，点| vertical bar, vertical virgule 竖线ǁparallel 双线号& ampersand, and, reference, ref 和，引用/ slash, divide, oblique, virgule 斜线，斜杠，除号// slash-slash, comment 双斜线，注释符# pound 井号\ backslash, sometimes escape 反斜线转义符，有时表示转义符或续行符~ tilde 波浪符. full stop 句号, comma 逗号: colon 冒号; semicolon 分号? question mark 问号! exclamation mark (英式英语) exclamation point (美式英语)' apostrophe 撇号- hyphen 连字号-- dash 破折号... dots/ ellipsis 省略号" single quotation marks 单引号"" double quotation marks 双引号§ section; division 分节号→arrow 箭号；参见号_ underscore 下划线¨ tandem colon 双点号" ditto同上符号～swung dash 代字号LognX logx to the base nf(x) the function of xdx diffrencial of xx+y x plus y(a+b) bracket a plus b bracket closeda=b a equals ba≠b a isn't equal to ba>b a is greater than ba>>b a is much greater than ba≥b a is greater than or equal to bx→∞x approches infinityx2 x squarex3 x cubexn the nth power of x√￣x the square root of x3√￣x the cube root of xn√￣x the nth root of x6 % 6 percent3‰ 3 per mille3‰ three peimilln∑i=1xi the summation of x where x goes from 1to nn∏i=1xi the product of x sub i where igoes from 1to n∫ab integral betweens a and b>> is approximately equal to( ) round brackets; parentheses[ ] square brackets{ } braces2 :3 the ratio of two to threeD x or d x the increment of xdx differential xdy/dx the first derivative of y with respect to x1/2 a half; one half2/3 two thirds5/123 five over a hundred and twenty-three0.01 O point O one; zero point zero one; nought point nought one r=xd r equals x multiplied by d5* 2=10 five times two equals tenx3/8=y2 x raised to the third power divided by eight equals y squared (a+b-c* d)/e=f a plus b minus c multiplied by d all divided by e equals fy = (Wt-W)/x y equals W sub t minus W over xΑ α alpha alfa 阿耳法 Β β beta beta 贝塔 Γ γ gamma gamma 伽马 Δ δ delta delta 德耳塔 Ε ε epsilon epsilon 艾普西隆 Ζ ζ zeta zeta 截塔 Η η eta eta 艾塔 Θ θ theta θita 西塔 Ι ι iota iota 约塔 Κ κ kappa kappa 卡帕 ∧ λ lambda lambda 兰姆达 Μ μ mu miu 缪 Ν ν nu niu 纽 Ξ ξ xi ksi 可塞 Ο ο omicron omikron 奥密可戎 ∏ π pi pai 派 Ρ ρ rho rou 柔 ∑ σ sigma sigma 西格马 Τ τ tau tau 套 Υ υ upsilon jupsilon 衣普西隆 Φ φ phi fai 斐 Χ χ chi khai 喜 Ψ ψ psi psai 普西 Ω ω omega omiga 欧米伽。
各种数学符号英文翻译
+ plus加号；正号- minus减号；负号±plus or minus正负号×is multiplied by乘号÷is divided by除号＝is equal to等于号≠is not equal to不等于号≡is equivalent to全等于号≌is equal to or approximately equal to等于或约等于号≈is approximately equal to约等于号＜is less than小于号＞is greater than大于号≮is not less than不小于号≯is not more than不大于号≤is less than or equal to小于或等于号≥is more than or equal to大于或等于号% per cent百分之…‰per mill千分之…∞infinity无限大号∝varies as与…成比例√square root平方根∵since; because因为∴hence所以∷equals, as proportion等于,成比例∠angle角⌒semicircle半圆⊙circle圆○circumference圆周△triangle三角形⊥perpendicular to垂直于∪union of并,合集∩intersection of 交,通集∫the integral of …的积分∑sigma summation of总和°degree度′minute分″second秒℃Celsius system摄氏度{open brace, open curly左花括号}close brace, close curly右花括号open parenthesis, open paren左圆括号close parenthesis, close paren右圆括号brakets/ parentheses括号open bracket 左方括号close bracket 右方括号square brackets方括号.period, dot句号,点|vertical bar, vertical virgule竖线&ersand, and, reference, ref和,引用asterisk, multiply, star, pointer星号,乘号,星,指针/slash, divide, oblique 斜线,斜杠,除号ull stop句号,comma逗号;semicolon分号question mark问号exclamation mark 英式英语exclamation point 美式英语'apostrophe撇号-hyphen连字号-- dash 破折号...dots/ ellipsis省略号"single quotation marks 单引号""double quotation marks 双引号‖parallel 双线号&ersand = and～swung dash 代字号§section; division 分节号→arrow 箭号；参见号。
常用数学符号英文对照
常用数学符号英文对照Basic math symbolsSymbol Symbol Name Meaning / definition Example= equals sign equality 5 = 2+35 is equal to 2+3≠not equal sign inequality 5 ≠ 45 is not equal to 4≈approximatelyequal approximationsin(0.01) ≈ 0.01,x≈y means x isapproximately equal to y> strictinequality greater than5 > 45 is greater than 4< strictinequality less than4 < 54 is less than 5≥inequality greater than or equal to 5 ≥ 4,x≥y means x is greater than or equal to y≤inequality less than or equal to 4 ≤ 5,x ≤ y means x is greater than or equal to y( ) parentheses calculate expression insidefirst2 × (3+5) = 16[ ] brackets calculate expression insidefirst[(1+2)×(1+5)] = 18 + plus sign addition 1 + 1 = 2−minus sign subtraction 2 − 1 = 1±plus - minus both plus and minusoperations3 ± 5 = 8 and -2±minus - plus both minus and plusoperations3 ± 5 = -2 and 8* asterisk multiplication 2 * 3 = 6×times sign multiplication 2 × 3 = 6·multiplicationdotmultiplication 2 · 3 = 6÷division sign /obelusdivision 6 ÷ 2 = 3/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimalseparator2.56 = 2+56/100a b power exponent 23= 8a^b caret exponent 2 ^ 3= 8√a square root √a ·√a = a√9 = ±33√a cube root 3√a ·3√a ·3√a = a3√8 = 24√a fourth root 4√a ·4√a ·4√a ·4√a = a4√16 = ±2n√a n-th root(radical)for n=3, n√8 = 2 % percent1% = 1/100 10% × 30 = 3‰per-mille1‰ = 1/1000 = 0.1% 10‰× 30 = 0.3 ppm per-million1ppm = 1/1000000 10ppm × 30 = 0.0003 ppb per-billion 1ppb = 1/1000000000 10ppb × 30 = 3×10-7 ppt per-trillion 1ppt = 10-1210ppt × 30 = 3×10-10Geometry symbolsSymbolSymbol NameMeaning / definitionExample∠angle formed by two rays ∠ABC = 30°measured angle ABC = 30°sphericalangleAOB = 30°∟ right angle = 90° α = 90°°degree 1 turn = 360° α = 60° deg degree1 turn = 360degα = 60deg ′ primearcminute, 1° = 60′α = 60°59′ ″double prime arcsecond, 1′ = 60″α = 60°59′59″line infinite lineABline segment line from point A to point Bray line that start from point Aarc arc from point A to point B= 60° ⊥perpendicular perpendicular lines (90° angle)AC ⊥ BC| | parallel parallel lines AB | | CD ≅ congruent toequivalence of geometric shapes and size∆ABC ≅ ∆XYZ~similarity same shapes, not same size∆ABC~ ∆XYZΔtriangle triangle shape ΔABC≅ΔBCD|x-y|distance distance between points x and y | x-y| = 5πpi constant π= 3.141592654...is the ratio between the circumference anddiameter of a circlec= π·d= 2·π·rrad radians radians angle unit 360° = 2πradc radians radians angle unit360° = 2πcgrad gradians / gons grads angle unit 360° = 400 gradg gradians / gons grads angle unit360° =400 g Algebra symbolsSymbol Symbol Name Meaning /definitionExamplex x variable unknown valueto findwhen 2x= 4, then x= 2 ≡equivalence identical to≜equal by definition equal bydefinition:= equal by definition equal bydefinition~ approximately equal weakapproximation11 ~ 10≈approximately equal approximation sin(0.01) ≈ 0.01∝proportional to proportionalto y∝x when y= kx, k constant∞lemniscate infinitysymbol≪much less than much less than 1 ≪ 1000000≫much greater than much greaterthan1000000 ≫ 1( ) parentheses calculateexpressioninside first2 * (3+5) = 16[ ] brackets calculateexpressioninside first[(1+2)*(1+5)] = 18{ } braces set ⌊x⌋floor bracketsrounds numberto lowerinteger⌊ 4.3⌋ = 4⌈x⌉ceiling bracketsrounds numberto upperinteger⌈ 4.3⌉ = 5x! exclamation mark factorial4! = 1*2*3*4 = 24 | x|single vertical bar absolute value | -5 | = 5f (x) function of xmaps values ofx to f(x)f (x) = 3x+5(f∘g ) function composition(f∘g)(x)= f (g(x))f (x)=3x,g(x)=x-1 ⇒(f∘g)(x)=3(x-1)(a,b) open interval(a,b) ={x| a<x< b}x∈ (2,6)[a ,b] closed interval[a ,b ] ={x | a ≤ x ≤ b }x ∈[2,6] ∆ deltachange / difference∆t = t 1- t 0∆discriminantΔ = b 2- 4ac∑sigmasummation - sumof all values in range of series∑ x i = x 1+x 2+...+x n∑∑ sigmadouble summation∏capital piproduct -product of all values in range of series∏ x i =x 1∙x 2∙...∙x nee constant / Euler's numbere =2.718281828... e = lim (1+1/x )x, x →∞ γ Euler-Mascheroni const antγ =0.527721566...φgolden ratiogolden ratio constantπpi constantπ =3.141592654...is the ratio between the circumference and diameter of a circlec = π·d = 2·π·r·dot scalar product a ·b ×cross vector product a ×b A⊗B tensor product tensor product of A and B A⊗Binner product[ ] brackets matrix of numbers( ) parentheses matrix of numbers| Adeterminant determinant of matrix A|det(A) determinant determinant of matrix A|| xdouble vertical bars norm||(A T)ij=A T transpose matrix transpose(A)ji(A†)ij= A†Hermitian matrix matrix conjugate transpose(A)ji(A*)ij= A*Hermitian matrix matrix conjugate transpose(A)jiA-1inverse matrix A A-1= Irank(A) matrix rank rank of matrix A rank(A) = 3Probability and statistics symbolsSymbol Symbol Name Meaning /definitionExampleP(A) probabilityfunction probability ofevent AP(A) = 0.5P(A∩B) probability ofeventsintersectionprobability that ofevents A and BP(A∩B) = 0.5P(A∪B) probability ofevents unionprobability that ofevents A or BP(A∪B) = 0.5P(A|B) conditionalprobabilityfunctionprobability ofevent A given eventB occuredP(A | B) = 0.3f (x) probabilitydensityfunction (pdf)P(a ≤x ≤b) = ∫f (x)dxF(x) cumulativedistributionfunction (cdf)F(x) = P(X≤x)μpopulationmean mean of populationvaluesμ= 10E(X) expectationvalue expected value ofrandom variable XE(X) = 10E(X | Y) conditionalexpectation expected value ofrandom variable Xgiven YE(X | Y=2) = 5var(X) variance variance of randomvariable Xvar(X) = 4σ2variance variance ofpopulation valuesσ2 = 4std (X )standard deviationstandard deviation of random variable X std (X ) = 2σXstandard deviationstandard deviation value of random variable X σX = 2medianmiddle value of random variable xcov (X ,Y)covariancecovariance of random variables X and Ycov (X,Y ) = 4corr (X ,Y ) correlationcorrelation of random variables X and Ycorr (X,Y ) = 0.6ρX ,Ycorrelationcorrelation ofrandom variables X and YρX ,Y= 0.6∑summation summation - sum ofall values in range of series∑∑double summationdouble summationMo mode value that occursmost frequently in populationMR mid-rangeMR = (x max +x min )/2Mdsample median half the population is below this valueQ 1lower / first quartile25% of population are below this valueQ 2median / second quartile50% of populationare below this value = median of samplesQ3upper / thirdquartile 75% of population are below this valuex sample mean average /arithmetic meanx= (2+5+9) / 3 = 5.333s2samplevariance population samplesvariance estimators2= 4s samplestandarddeviationpopulation samplesstandard deviationestimators= 2z x standard score z x= (x-x) /s xX ~ distributionof X distribution ofrandom variable XX ~N(0,3)N(μ,σ2) normaldistributiongaussiandistributionX ~N(0,3)U(a,b) uniformdistributionequal probabilityin range a,bX ~U(0,3)exp(λ) exponentialdistributionf (x)= λe-λx, x≥0gamma(c,λ) gammadistributionf (x)= λ cx c-1e-λx/ Γ(c), x≥0χ2(k) chi-squaredistributionf (x)=x k/2-1e-x/2/( 2k/2 Γ(k/2) )F (k1, k2) F distributionBin(n,p) binomialdistributionf (k)= n C kp k(1-p)n-kPoisson(λ) Poissondistributionf (k)= λk e-λ/ k!Geom(p) geometricdistributionf (k)= p(1-p)kHG(N,K,n) hyper-geometri c distributionSet theory symbolsSymbol Symbol Name Meaning / definition Example{ } set a collection of elements A ={3,7,9,14},B = {9,14,28}A ∩B intersection objects that belong to set A andset BA ∩B ={9,14}A ∪B union objects that belong to set A orset BA ∪B ={3,7,9,14,28}A ⊆B subset subset has fewer elements orequal to the set{9,14,28} ⊆{9,14,28}A ⊂B proper subset / strictsubsetsubset has fewer elements thanthe set{9,14} ⊂{9,14,28}A ⊄B not subset left set not a subset of right set {9,66} ⊄{9,14,28}A ⊇B superset set A has more elements or equalto the set B{9,14,28} ⊇{9,14,28}A ⊃ Bproper superset / strict supersetset A has more elements than set B{9,14,28} ⊃ {9,14} A ⊅ B not superset set A is not a superset of set B{9,14,28} ⊅ {9,66}2Apower set all subsets of Apower set all subsets of AA =B equalityboth sets have the same members A={3,9,14},B={3,9,14},A=BA ccomplementall the objects that do not belong to set AA \B relative complementobjects that belong to A and not to BA = {3,9,14},B = {1,2,3}, A-B = {9,14} A - B relative complementobjects that belong to A and not to BA = {3,9,14},B = {1,2,3}, A-B = {9,14} A ∆ B symmetric differenceobjects that belong to A or B but not to their intersectionA = {3,9,14},B = {1,2,3}, A ∆ B = {1,2,9,14} A ⊖ B symmetric differenceobjects that belong to A or B but not to their intersectionA = {3,9,14},B = {1,2,3}, A ⊖ B = {1,2,9,14}a ∈A element of set membershipA={3,9,14}, 3 ∈ Ax ∉ A not element ofno set membershipA={3,9,14}, 1 ∉ A(a ,b ) ordered pair collection of 2 elementsA ×Bcartesian productset of all ordered pairs from A and B|A| cardinality the number of elements of set AA={3,9,14}, |A|=3 #A cardinality the number of elements of set AA={3,9,14}, #A=3aleph-nullinfinite cardinality of natural numbers setaleph-one cardinality of countable ordinal numbers setØ empty set Ø = { }C = {Ø}universal setset of all possible valuesnatural numbers / wholenumbers set (with zero)= {0,1,2,3,4,...} 0 ∈1natural numbers / wholenumbers set (without zero)1= {1,2,3,4,5,...} 6 ∈1integer numbers set={...-3,-2,-1,0,1,2,3,...}-6 ∈rational numbers set= {x | x =a /b , a ,b ∈}2/6 ∈real numbers set= {x | -∞ < x <∞} 6.343434∈complex numbers set= {z | z=a +bi , -∞<a <∞, -∞<b <∞}6+2i ∈& ampersand and x& y + plus or x+ y ∨reversed caret or x∨y | vertical line or x| y x' single quote not - negation x'x bar not - negation x¬not not - negation ¬x ! exclamation mark not - negation ! x⊕circled plus / oplus exclusive or - xor x⊕y ~ tilde negation ~ x⇒implies⇔equivalent if and only if (iff)↔equivalent if and only if (iff)∀for all∃there exists∄there does not exists∴thereforeCalculus & analysis symbolsSymbol Symbol Name Meaning / definition Examplelimit limit value of a functionεepsilon represents a very smallnumber, near zeroε→0e e constant/Euler's number e= 2.718281828...e= lim(1+1/x)x,x→∞y' derivative derivative - Lagrange'snotation(3x3)' = 9x2 y'' second derivative derivative of derivative (3x3)'' = 18x y(n)nth derivative n times derivation (3x3)(3)= 18derivative derivative - Leibniz'snotationd(3x3)/dx= 9x2second derivative derivative of derivative d2(3x3)/dx2= 18xnth derivative n times derivationtime derivative derivative by time - Newton's notationtime secondderivativederivative of derivativeD x y derivative derivative - Euler's notation D x2y second derivative derivative of derivativepartial derivative∂(x2+y2)/∂x=2x∫integral opposite to derivation ∫f(x)dx∫∫double integral integration of function of 2variables∫∫f(x,y)dxdy∫∫∫triple integral integration of function of 3variables∫∫∫f(x,y,z)dxdydz∮closed contour /line integral∯closed surfaceintegral∰closed volumeintegral[a,b] closed interval [a,b] ={x | a ≤x ≤b}(a,b) open interval (a,b) ={x | a <x <b}i imaginary unit i≡√-1 z= 3 + 2iz* complex conjugate z =a+bi→z*=a-bi z*= 3 - 2iz complex conjugate z =a+bi→z =a-biz= 3 - 2i ∇nabla / del gradient / divergence operator ∇f(x,y,z) vectorunit vectorx *y convolution y(t) = x(t) * h(t)) = {{。
常用数学符号英文对照
常用数学符号英文对照Basic math symbolsSymbol Symbol Name Meaning / definition Example= equals sign equality 5 = 2+35 is equal to 2+3≠not equal sign inequality 5 ≠ 45 is not equal to 4≈approximatelyequal approximationsin(0.01) ≈ 0.01,x≈y means x isapproximately equal to y> strictinequality greater than5 > 45 is greater than 4< strictinequality less than4 < 54 is less than 5≥inequality greater than or equal to 5 ≥ 4,x≥y means x is greater than or equal to y≤inequality less than or equal to 4 ≤ 5,x ≤ y means x is greater than or equal to y( ) parentheses calculate expressioninside first2 × (3+5) = 16[ ] brackets calculate expressioninside first[(1+2)×(1+5)] = 18 + plus sign addition 1 + 1 = 2−minus sign subtraction 2 − 1 = 1±plus - minus both plus and minusoperations3 ± 5 = 8 and -2±minus - plus both minus and plusoperations3 ± 5 = -2 and 8* asterisk multiplication 2 * 3 = 6×times sign multiplication 2 × 3 = 6·multiplicationdotmultiplication 2 · 3 = 6÷division sign /obelusdivision 6 ÷ 2 = 3/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimalseparator2.56 = 2+56/100a b power exponent 23= 8a^b caret exponent 2 ^ 3= 8√a square root √a ·√a = a√9 = ±33√a cube root 3√a ·3√a ·3√a = a3√8 = 24√a fourth root 4√a ·4√a ·4√a ·4√a =a4√16 = ±2n√a n-th root(radical)for n=3, n√8 = 2 % percent1% = 1/100 10% × 30 = 3‰per-mille1‰ = 1/1000 = 0.1% 10‰× 30 = 0.3 ppm per-million1ppm = 1/1000000 10ppm × 30 = 0.0003 ppb per-billion 1ppb = 1/1000000000 10ppb × 30 = 3×10-7Geometry symbolsSymbolSymbol NameMeaning / definitionExample∠angle formed by two rays ∠ABC = 30°measured angle ABC = 30°sphericalangleAOB = 30°∟ right angle = 90° α = 90°°degree 1 turn = 360° α = 60° degdegree1 turn = 360degα = 60deg ′ primearcminute, 1° = 60′α = 60°59′″double prime arcsecond, 1′ = 60″ α = 60°59′59″line infinite lineABline segment line from point A to point Bray line that start from point Aarc arc from point A to point B= 60°⊥ perpendicular perpendicular lines (90° angle) AC ⊥ BC| | parallel parallel lines AB | | CD≅ congruent toequivalence of geometric shapes and size∆ABC ≅ ∆XYZ~similarity same shapes, not same size ∆ABC~ ∆XYZΔtriangle triangle shape ΔABC≅ΔBCD |x-y| distance distance between points x and y | x-y| = 5πpi constant π= 3.141592654...is the ratio between the circumferenceand diameter of a circlec= π·d=2·π·rrad radians radians angle unit 360° = 2π rad c radians radians angle unit 360° = 2πcgrad gradians /gonsgrads angle unit 360° = 400 gradggradians /gonsgrads angle unit 360° = 400 gAlgebra symbolsSymbol Symbol Name Meaning / definition Examplex x variable unknown value to find when 2x= 4, then x= 2 ≡equivalence identical to≜equal by definition equal by definition:= equal by definition equal by definition~ approximately equal weak approximation 11 ~ 10≈approximately equal approximation sin(0.01) ≈ 0.01∝proportional to proportional to y∝x when y= kx,k constant ∞lemniscate infinity symbol≪much less than much less than 1 ≪ 1000000≫much greater than much greater than 1000000 ≫ 1( ) parentheses calculate expressioninside first2 * (3+5) = 16[ ] brackets calculate expressioninside first[(1+2)*(1+5)] = 18 { } braces set⌊x⌋floor brackets rounds number to lowerinteger⌊ 4.3⌋ = 4⌈x⌉ceiling brackets rounds number to upperinteger⌈ 4.3⌉ = 5x! exclamation mark factorial4! = 1*2*3*4 = 24 | x|single vertical bar absolute value | -5 | = 5f (x) function of x maps values of x to f(x) f (x) = 3x+5(f∘g) function composition(f∘g) (x)= f (g(x))f (x)=3x,g(x)=x-1 ⇒(f∘g)(x)=3(x-1)(a,b) open interval (a,b) ={x| a< x< b}x∈ (2,6)[a,b] closed interval [a,b] ={x| a≤x≤b}x∈ [2,6]∆delta change / difference ∆t= t1 -t0∆discriminant Δ = b2- 4ac∑sigma summation - sum of allvalues in range of series∑x i= x1+x2+...+x n∑∑sigma double summation∏capital piproduct - product of all values in range of series∏ x i =x 1∙x 2∙...∙x nee constant / Euler's numbere = 2.718281828... e = lim (1+1/x )x , x →∞γ Euler-Mascheroni const antγ = 0.527721566...φgolden ratio golden ratio constantπpi constantπ = 3.141592654...is the ratio between the circumference and diameter of a circlec = π·d = 2·π·rLinear Algebra SymbolsSymbolSymbol NameMeaning / definitionExample· dot scalar producta ·b ×cross vector producta ×b A ⊗Btensor product tensor product of A and BA ⊗ Binner product[ ] brackets matrix of numbers( ) parentheses matrix of numbers| A | determinant determinant of matrix Adet(A )determinant determinant of matrix A|| x || double vertical bars normA Ttranspose matrix transpose(A T)ij = (A )jiProbability and statistics symbols Symbol Symbol Name Meaning / definition Example P(A) probabilityfunctionprobability of event A P(A) = 0.5P(A∩B) probability ofeventsintersectionprobability that of events Aand BP(A∩B) = 0.5P(A∪B) probability ofevents union probability that of events Aor BP(A∪B) = 0.5P(A| B) conditionalprobabilityfunctionprobability of event A givenevent B occuredP(A | B) = 0.3f (x) probabilitydensityfunction (pdf)P(a ≤x ≤b)= ∫ f (x)dxF(x) cumulativedistributionfunction (cdf)F(x) = P(X≤x)μpopulation mean mean of population values μ= 10E(X) expectationvalue expected value of randomvariable XE(X) = 10E(X | Y) conditionalexpectation expected value of randomvariable X given YE(X | Y=2) = 5var (X )variancevariance of random variable Xvar (X ) = 4σ2variance variance of population valuesσ2 = 4std (X )standard deviation standard deviation of random variable Xstd (X ) = 2σX standard deviationstandard deviation value of random variable X σX = 2medianmiddle value of random variable xcov (X ,Y ) covariancecovariance of random variables X and Y cov (X,Y ) = 4corr (X ,Y ) correlationcorrelation of random variables X and Y corr (X,Y ) = 0.6ρX ,Ycorrelationcorrelation of random variables X and YρX ,Y= 0.6∑summationsummation - sum of all values in range of series∑∑double summationdouble summationMo mode value that occurs most frequently in populationMR mid-rangeMR = (x max +x min )/2Mdsample median half the population is below this valueQ 1lower / first quartile25% of population are below this valueQ 2median / second quartile50% of population are below this value = median of samplesQ3upper / thirdquartile 75% of population are below this valuex sample mean average / arithmetic mean x= (2+5+9) / 3 = 5.333s2sample variance population samples varianceestimators2= 4s sample standarddeviation population samples standard deviation estimators= 2z x standard score z x= (x-x) /s xX ~ distribution of X distribution of randomvariable XX ~N(0,3)N(μ,σ2) normaldistributiongaussian distribution X ~N(0,3)U(a,b) uniformdistributionequal probability in rangea,bX ~U(0,3)exp(λ) exponentialdistributionf (x)= λe-λx, x≥0gamma(c, λ) gammadistributionf (x)= λ c x c-1e-λx/ Γ(c), x≥0χ2(k) chi-squaredistributionf (x)= x k/2-1e-x/2/( 2k/2 Γ(k/2) )F (k1, k2) F distributionBin(n,p) binomialdistributionf (k)= n C k p k(1-p)n-kPoisson(λ) Poissondistributionf (k)= λk e-λ/ k!Geom(p) geometricdistributionf (k)= p(1-p)kHG(N,K,n) hyper-geometric distributionBern(p) Bernoulli distributionSet theory symbolsSymbol Symbol Name Meaning / definition Example{ } set a collection of elements A = {3,7,9,14},B = {9,14,28}A ∩B intersection objects that belong to set A and setBA ∩B = {9,14}A ∪B union objects that belong to set A or setBA ∪B ={3,7,9,14,28}A ⊆B subset subset has fewer elements or equal tothe set{9,14,28} ⊆{9,14,28}A ⊂B proper subset /strict subsetsubset has fewer elements than theset{9,14} ⊂{9,14,28}A ⊄B not subset left set not a subset of right set {9,66} ⊄{9,14,28}A ⊇B superset set A has more elements or equal tothe set B{9,14,28} ⊇{9,14,28}A ⊃B proper superset /strict supersetset A has more elements than set B{9,14,28} ⊃{9,14}A ⊅B not superset set A is not a superset of set B {9,14,28} ⊅{9,66}2Apower set all subsets of Apower set all subsets of AA =B equalityboth sets have the same membersA={3,9,14},B={3,9,14}, A=BA ccomplementall the objects that do not belong to set AA \B relative complementobjects that belong to A and not to BA = {3,9,14},B = {1,2,3}, A-B = {9,14} A - B relative complementobjects that belong to A and not to BA = {3,9,14},B = {1,2,3}, A-B = {9,14} A ∆ Bsymmetric differenceobjects that belong to A or B but not to their intersectionA = {3,9,14},B = {1,2,3}, A ∆ B = {1,2,9,14} A ⊖ Bsymmetric differenceobjects that belong to A or B but not to their intersectionA = {3,9,14},B = {1,2,3}, A ⊖ B = {1,2,9,14}a ∈Aelement of set membershipA={3,9,14}, 3 ∈ Ax ∉ A not element ofno set membershipA={3,9,14}, 1 ∉ A(a ,b ) ordered pair collection of 2 elementsA ×B cartesian product set of all ordered pairs from A and B|A| cardinalitythe number of elements of set AA={3,9,14}, |A|=3 #Acardinality the number of elements of set AA={3,9,14}, #A=3aleph-nullinfinite cardinality of natural numbers setaleph-one cardinality of countable ordinal numbers setØ empty set Ø = { }C = {Ø}universal set set of all possible valuesnatural numbers /whole numbers set (with zero) 0= {0,1,2,3,4,...} 0 ∈1natural numbers /whole numbers set (without zero)1= {1,2,3,4,5,...} 6 ∈1integer numbers set={...-3,-2,-1,0,1,2,3,...}-6 ∈rational numbers set= {x | x =a /b , a ,b ∈}2/6 ∈real numbers set= {x | -∞ < x <∞} 6.343434∈complex numbers set= {z | z=a +bi , -∞<a <∞, -∞<b <∞}6+2i ∈∨reversed caret or x∨y | vertical line or x| y x' single quote not - negation x'x bar not - negation x¬not not - negation ¬x ! exclamation mark not - negation ! x⊕circled plus / oplus exclusive or - xor x⊕y ~ tilde negation ~ x⇒implies⇔equivalent if and only if (iff)↔equivalent if and only if (iff)∀for all∃there exists∄there does not exists∴therefore∵because / sinceCalculus & analysis symbolsSymbol Symbol Name Meaning / definition Examplelimit limit value of a functionεepsilonrepresents a very small number, near zeroε → 0eeconstant / Euler's numbere = 2.718281828...e = lim(1+1/x )x,x →∞y ' derivativederivative - Lagrange's notation (3x 3)' = 9x 2y '' second derivative derivative of derivative(3x 3)'' = 18xy (n )nth derivativen times derivation(3x 3)(3)= 18derivativederivative - Leibniz's notation d (3x 3)/dx = 9x 2secondderivativederivative of derivatived 2(3x 3)/dx 2 = 18xnthderivativen times derivationtime derivative derivative by time - Newton's notationtime second derivativederivative of derivativeD x y derivative derivative - Euler's notationD x 2ysecond derivativederivative of derivativepartialderivative∂(x 2+y 2)/∂x = 2x∫ integral opposite to derivation∫ f(x)dx∫∫ double integral integration of function of 2 variables∫∫ f(x,y)dxdy ∫∫∫triple integral integration of function of 3 variables∫∫∫ f(x,y,z)dxdydz∮closedcontour / line integral∯closedsurface integral∰closedvolume integral[a ,b ] closed interval [a ,b ] ={x | a ≤ x ≤ b }(a ,b )open interval (a ,b ) ={x | a < x < b }i imaginary unit i ≡ √-1 z = 3 + 2iz * complex conjugate z = a +bi → z *=a -bi z* = 3 - 2izcomplex conjugatez = a +bi → z = a -bi z = 3 - 2i∇ nabla / del gradient / divergence operator ∇f (x ,y ,z )vectorunit vectorx * y convolutiony (t ) = x (t ) * h (t )) = {{。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
常用数学符号英文对照Basic math symbolsSymbol Symbol Name Meaning / definition Example= equals sign equality 5 = 2+35 is equal to 2+3≠not equal sign inequality 5 ≠ 45 is not equal to 4≈approximatelyequal approximationsin(0.01) ≈ 0.01,x≈y means x isapproximately equal to y> strictinequality greater than5 > 45 is greater than 4< strictinequality less than4 < 54 is less than 5≥inequality greater than or equal to 5 ≥ 4,x≥y means x is greater than or equal to y≤inequality less than or equal to 4 ≤ 5,x ≤ y means x is greater than or equal to y( ) parentheses calculate expressioninside first2 × (3+5) = 16[ ] brackets calculate expressioninside first[(1+2)×(1+5)] = 18 + plus sign addition 1 + 1 = 2−minus sign subtraction 2 − 1 = 1±plus - minus both plus and minusoperations3 ± 5 = 8 and -2±minus - plus both minus and plusoperations3 ± 5 = -2 and 8* asterisk multiplication 2 * 3 = 6×times sign multiplication 2 × 3 = 6·multiplicationdotmultiplication 2 · 3 = 6÷division sign /obelusdivision 6 ÷ 2 = 3/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimalseparator2.56 = 2+56/100a b power exponent 23= 8a^b caret exponent 2 ^ 3= 8√a square root √a ·√a = a√9 = ±33√a cube root 3√a ·3√a ·3√a = a3√8 = 24√a fourth root 4√a ·4√a ·4√a ·4√a =a4√16 = ±2n√a n-th root(radical)for n=3, n√8 = 2 % percent1% = 1/100 10% × 30 = 3‰per-mille1‰ = 1/1000 = 0.1% 10‰× 30 = 0.3 ppm per-million1ppm = 1/1000000 10ppm × 30 = 0.0003 ppb per-billion 1ppb = 1/1000000000 10ppb × 30 = 3×10-7Geometry symbolsSymbolSymbol NameMeaning / definitionExample∠angle formed by two rays ∠ABC = 30°measured angle ABC = 30°sphericalangleAOB = 30°∟ right angle = 90° α = 90°°degree 1 turn = 360° α = 60° degdegree1 turn = 360degα = 60deg ′ primearcminute, 1° = 60′α = 60°59′″double prime arcsecond, 1′ = 60″ α = 60°59′59″line infinite lineABline segment line from point A to point Bray line that start from point Aarc arc from point A to point B= 60°⊥ perpendicular perpendicular lines (90° angle) AC ⊥ BC| | parallel parallel lines AB | | CD≅ congruent toequivalence of geometric shapes and size∆ABC ≅ ∆XYZ~similarity same shapes, not same size ∆ABC~ ∆XYZΔtriangle triangle shape ΔABC≅ΔBCD |x-y| distance distance between points x and y | x-y| = 5πpi constant π= 3.141592654...is the ratio between the circumferenceand diameter of a circlec= π·d=2·π·rrad radians radians angle unit 360° = 2π rad c radians radians angle unit 360° = 2πcgrad gradians /gonsgrads angle unit 360° = 400 gradggradians /gonsgrads angle unit 360° = 400 gAlgebra symbolsSymbol Symbol Name Meaning / definition Examplex x variable unknown value to find when 2x= 4, then x= 2 ≡equivalence identical to≜equal by definition equal by definition:= equal by definition equal by definition~ approximately equal weak approximation 11 ~ 10≈approximately equal approximation sin(0.01) ≈ 0.01∝proportional to proportional to y∝x when y= kx,k constant ∞lemniscate infinity symbol≪much less than much less than 1 ≪ 1000000≫much greater than much greater than 1000000 ≫ 1( ) parentheses calculate expressioninside first2 * (3+5) = 16[ ] brackets calculate expressioninside first[(1+2)*(1+5)] = 18 { } braces set⌊x⌋floor brackets rounds number to lowerinteger⌊ 4.3⌋ = 4⌈x⌉ceiling brackets rounds number to upperinteger⌈ 4.3⌉ = 5x! exclamation mark factorial4! = 1*2*3*4 = 24 | x|single vertical bar absolute value | -5 | = 5f (x) function of x maps values of x to f(x) f (x) = 3x+5(f∘g) function composition(f∘g) (x)= f (g(x))f (x)=3x,g(x)=x-1 ⇒(f∘g)(x)=3(x-1)(a,b) open interval (a,b) ={x| a< x< b}x∈ (2,6)[a,b] closed interval [a,b] ={x| a≤x≤b}x∈ [2,6]∆delta change / difference ∆t= t1 -t0∆discriminant Δ = b2- 4ac∑sigma summation - sum of allvalues in range of series∑x i= x1+x2+...+x n∑∑sigma double summation∏capital piproduct - product of all values in range of series∏ x i =x 1∙x 2∙...∙x nee constant / Euler's numbere = 2.718281828... e = lim (1+1/x )x , x →∞γ Euler-Mascheroni const antγ = 0.527721566...φgolden ratio golden ratio constantπpi constantπ = 3.141592654...is the ratio between the circumference and diameter of a circlec = π·d = 2·π·rLinear Algebra SymbolsSymbolSymbol NameMeaning / definitionExample· dot scalar producta ·b ×cross vector producta ×b A ⊗Btensor product tensor product of A and BA ⊗ Binner product[ ] brackets matrix of numbers( ) parentheses matrix of numbers| A | determinant determinant of matrix Adet(A )determinant determinant of matrix A|| x || double vertical bars normA Ttranspose matrix transpose(A T)ij = (A )jiProbability and statistics symbols Symbol Symbol Name Meaning / definition Example P(A) probabilityfunctionprobability of event A P(A) = 0.5P(A∩B) probability ofeventsintersectionprobability that of events Aand BP(A∩B) = 0.5P(A∪B) probability ofevents union probability that of events Aor BP(A∪B) = 0.5P(A| B) conditionalprobabilityfunctionprobability of event A givenevent B occuredP(A | B) = 0.3f (x) probabilitydensityfunction (pdf)P(a ≤x ≤b)= ∫ f (x)dxF(x) cumulativedistributionfunction (cdf)F(x) = P(X≤x)μpopulation mean mean of population values μ= 10E(X) expectationvalue expected value of randomvariable XE(X) = 10E(X | Y) conditionalexpectation expected value of randomvariable X given YE(X | Y=2) = 5var (X )variancevariance of random variable Xvar (X ) = 4σ2variance variance of population valuesσ2 = 4std (X )standard deviation standard deviation of random variable Xstd (X ) = 2σX standard deviationstandard deviation value of random variable X σX = 2medianmiddle value of random variable xcov (X ,Y ) covariancecovariance of random variables X and Y cov (X,Y ) = 4corr (X ,Y ) correlationcorrelation of random variables X and Y corr (X,Y ) = 0.6ρX ,Ycorrelationcorrelation of random variables X and YρX ,Y= 0.6∑summationsummation - sum of all values in range of series∑∑double summationdouble summationMo mode value that occurs most frequently in populationMR mid-rangeMR = (x max +x min )/2Mdsample median half the population is below this valueQ 1lower / first quartile25% of population are below this valueQ 2median / second quartile50% of population are below this value = median of samplesQ3upper / thirdquartile 75% of population are below this valuex sample mean average / arithmetic mean x= (2+5+9) / 3 = 5.333s2sample variance population samples varianceestimators2= 4s sample standarddeviation population samples standard deviation estimators= 2z x standard score z x= (x-x) /s xX ~ distribution of X distribution of randomvariable XX ~N(0,3)N(μ,σ2) normaldistributiongaussian distribution X ~N(0,3)U(a,b) uniformdistributionequal probability in rangea,bX ~U(0,3)exp(λ) exponentialdistributionf (x)= λe-λx, x≥0gamma(c, λ) gammadistributionf (x)= λ c x c-1e-λx/ Γ(c), x≥0χ2(k) chi-squaredistributionf (x)= x k/2-1e-x/2/( 2k/2 Γ(k/2) )F (k1, k2) F distributionBin(n,p) binomialdistributionf (k)= n C k p k(1-p)n-kPoisson(λ) Poissondistributionf (k)= λk e-λ/ k!Geom(p) geometricdistributionf (k)= p(1-p)kHG(N,K,n) hyper-geometric distributionBern(p) Bernoulli distributionSet theory symbolsSymbol Symbol Name Meaning / definition Example{ } set a collection of elements A = {3,7,9,14},B = {9,14,28}A ∩B intersection objects that belong to set A and setBA ∩B = {9,14}A ∪B union objects that belong to set A or setBA ∪B ={3,7,9,14,28}A ⊆B subset subset has fewer elements or equal tothe set{9,14,28} ⊆{9,14,28}A ⊂B proper subset /strict subsetsubset has fewer elements than theset{9,14} ⊂{9,14,28}A ⊄B not subset left set not a subset of right set {9,66} ⊄{9,14,28}A ⊇B superset set A has more elements or equal tothe set B{9,14,28} ⊇{9,14,28}A ⊃B proper superset /strict supersetset A has more elements than set B{9,14,28} ⊃{9,14}A ⊅B not superset set A is not a superset of set B {9,14,28} ⊅{9,66}2Apower set all subsets of Apower set all subsets of AA =B equalityboth sets have the same membersA={3,9,14},B={3,9,14}, A=BA ccomplementall the objects that do not belong to set AA \B relative complementobjects that belong to A and not to BA = {3,9,14},B = {1,2,3}, A-B = {9,14} A - B relative complementobjects that belong to A and not to BA = {3,9,14},B = {1,2,3}, A-B = {9,14} A ∆ Bsymmetric differenceobjects that belong to A or B but not to their intersectionA = {3,9,14},B = {1,2,3}, A ∆ B = {1,2,9,14} A ⊖ Bsymmetric differenceobjects that belong to A or B but not to their intersectionA = {3,9,14},B = {1,2,3}, A ⊖ B = {1,2,9,14}a ∈Aelement of set membershipA={3,9,14}, 3 ∈ Ax ∉ A not element ofno set membershipA={3,9,14}, 1 ∉ A(a ,b ) ordered pair collection of 2 elementsA ×B cartesian product set of all ordered pairs from A and B|A| cardinalitythe number of elements of set AA={3,9,14}, |A|=3 #Acardinality the number of elements of set AA={3,9,14}, #A=3aleph-nullinfinite cardinality of natural numbers setaleph-one cardinality of countable ordinal numbers setØ empty set Ø = { }C = {Ø}universal set set of all possible valuesnatural numbers /whole numbers set (with zero) 0= {0,1,2,3,4,...} 0 ∈1natural numbers /whole numbers set (without zero)1= {1,2,3,4,5,...} 6 ∈1integer numbers set={...-3,-2,-1,0,1,2,3,...}-6 ∈rational numbers set= {x | x =a /b , a ,b ∈}2/6 ∈real numbers set= {x | -∞ < x <∞} 6.343434∈complex numbers set= {z | z=a +bi , -∞<a <∞, -∞<b <∞}6+2i ∈∨reversed caret or x∨y | vertical line or x| y x' single quote not - negation x'x bar not - negation x¬not not - negation ¬x ! exclamation mark not - negation ! x⊕circled plus / oplus exclusive or - xor x⊕y ~ tilde negation ~ x⇒implies⇔equivalent if and only if (iff)↔equivalent if and only if (iff)∀for all∃there exists∄there does not exists∴therefore∵because / sinceCalculus & analysis symbolsSymbol Symbol Name Meaning / definition Examplelimit limit value of a functionεepsilonrepresents a very small number, near zeroε → 0eeconstant / Euler's numbere = 2.718281828...e = lim(1+1/x )x,x →∞y ' derivativederivative - Lagrange's notation (3x 3)' = 9x 2y '' second derivative derivative of derivative(3x 3)'' = 18xy (n )nth derivativen times derivation(3x 3)(3)= 18derivativederivative - Leibniz's notation d (3x 3)/dx = 9x 2secondderivativederivative of derivatived 2(3x 3)/dx 2 = 18xnthderivativen times derivationtime derivative derivative by time - Newton's notationtime second derivativederivative of derivativeD x y derivative derivative - Euler's notationD x 2ysecond derivativederivative of derivativepartialderivative∂(x 2+y 2)/∂x = 2x∫ integral opposite to derivation∫ f(x)dx∫∫ double integral integration of function of 2 variables∫∫ f(x,y)dxdy ∫∫∫triple integral integration of function of 3 variables∫∫∫ f(x,y,z)dxdydz∮closedcontour / line integral∯closedsurface integral∰closedvolume integral[a ,b ] closed interval [a ,b ] ={x | a ≤ x ≤ b }(a ,b )open interval (a ,b ) ={x | a < x < b }i imaginary unit i ≡ √-1 z = 3 + 2iz * complex conjugate z = a +bi → z *=a -bi z* = 3 - 2izcomplex conjugatez = a +bi → z = a -bi z = 3 - 2i∇ nabla / del gradient / divergence operator ∇f (x ,y ,z )vectorunit vectorx * y convolutiony (t ) = x (t ) * h (t )) = {{。