常用数学符号英文对照

合集下载

数学术语英文对照表

数学术语英文对照表在学习数学时，不可避免地需要掌握一些数学术语。

下面是一些常见的数学术语的中英文对照表：1. 数学 Mathematics2. 数学符号 Mathematical symbol3. 数字 Digit4. 字符 Character5. 算术 Arithmetic6. 代数 Algebra7. 几何 Geometry8. 统计学 Statistics9. 概率 Probability10. 三角学 Trigonometry11. 微积分 Calculus12. 矩阵 Matrix13. 向量 Vector14. 线性代数 Linear algebra15. 数学模型 Mathematical model16. 方程 Equation17. 垂直 Perpendicular18. 平行 Parallel19. 正比例 Direct proportion20. 反比例 Inverse proportion21. 旋转 Rotation22. 缩放 Scaling23. 变形 Deformation24. 函数 Function25. 极限 Limit26. 微分 Differential27. 积分 Integral28. 中心 Central29. 对称 Symmetry30. 相似 Similarity31. 等式 Equality32. 不等式 Inequality33. 方形 Rectangle34. 正方形 Square35. 圆 Circle36. 椭圆 Ellipse37. 球球体 Sphere38. 三角形 Triangle39. 直角三角形 Right triangle40. 等腰三角形 Isosceles triangle41. 等边三角形 Equilateral triangle42. 直线 Line43. 射线 Ray44. 线段 Line segment45. 弧 Arc46. 正弦 Sine47. 余弦 Cosine48. 正切 Tangent49. 余切 Cotangent50. 弦 Chord总之，数学术语是数学学习的基础，掌握数学术语对于提高数学能力以及学好数学至关重要。

常用数学符号英文对照

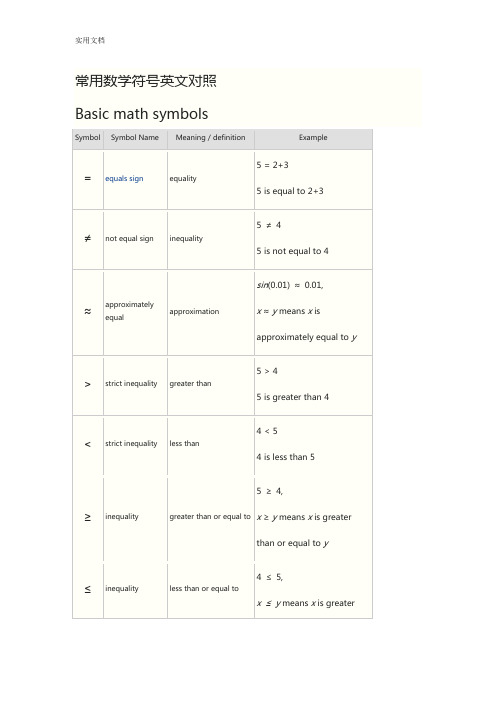
than or equal to y ( ) parentheses calculate expression2 ×(3+5) = 16inside first[ ] brackets calculate expression[(1+2)×(1+5)] = 18inside first+ plus sign addition 1 + 1 = 2−minus sign subtraction 2 −1 = 1±plus - minus both plus and minus3 ±5 = 8 and -2operations±minus - plus both minus and plus3 ±5 = -2 and 8operations* asterisk multiplication 2 * 3 = 6×times sign multiplication 2 ×3 = 6 ·multiplicationmultiplication 2 ·3 = 6dot÷division sign /division 6 ÷2 = 3 obelus/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimal2.56 = 2+56/100separatora b power exponent 23= 8a^b caret exponent 2 ^ 3= 83√a cube root 3√a ·3√a ·3√a = a3√8 = 24√a fourth root 4√a ·4√a ·4√a ·4√a = a4√16 = ±2n√a n-th root(radical)for n=3, n√8 = 2% percent1% = 1/100 10% ×30 = 3‰per-mille1‰= 1/1000 =0.1%10‰×30 = 0.3ppm per-million1ppm = 1/1000000 10ppm ×30 = 0.0003 ppb per-billion1ppb =1/100000000010ppb ×30 = 3×10-7ppt per-trillion 1ppt = 10-1210ppt ×30 = 3×10-10 Geometry symbolsSymbol Symbol Name Meaning / definition Example ∠angle formed by two rays ∠ABC = 30°measuredangleABC = 30°spherical angle AOB = 30°∟right angle = 90°α= 90°deg degree 1 turn = 360deg α= 60deg ′prime arcminute, 1°= 60′α= 60°59′α= 60°59′″double prime arcsecond, 1′= 60″59″line infinite lineAB line segment line from point A to point Bray line that start from point Aarc arc from point A to point B = 60°⊥perpendicular perpendicular lines (90°angle) AC ⊥ BC| | parallel parallel lines AB | | CD≅congruent to equivalence of geometric shapes and size ∆ABC≅∆XYZ ~ similarity same shapes, not same size ∆ABC~ ∆XYZΔABC≅ΔΔtriangle triangle shapeBCD|x-y| distance distance between points x and y | x-y | = 5πpi constant π = 3.141592654...c = π·d =is the ratio between the circumference andin range ofseries∑∑sigma doublesummation∏capital pi product -product of allvalues in rangeof series∏ x i=x1·x2·...·x ne e constant / Euler's numbere =2.718281828...e = lim (1+1/x)x , x→∞γEuler-Mascheroni constantγ=0.527721566...φgolden ratio golden ratioconstantπpi constant π =3.141592654...is the ratiobetween thecircumferenceand diameter of acirclec = π·d = 2·π·rLinear Algebra SymbolsSymbol Symbol Name Meaning / definition Example ·dot scalar product a · b×cross vector product a × bA⊗B tensor product tensor product of A and B A⊗Binner product[ ] brackets matrix of numbers( ) parentheses matrix of numbers| A | determinant determinant of matrix Adet(A) determinant determinant of matrix A|| x || double vertical bars normA T transpose matrix transpose (A T)ij = (A)ji A†Hermitian matrix matrix conjugate transpose (A†)ij = (A)ji A*Hermitian matrix matrix conjugate transpose (A*)ij = (A)ji A-1inverse matrix A A-1 = Irank(A) matrix rank rank of matrix A rank(A) = 3 dim(U) dimension dimension of matrix A rank(U) = 3Probability and statistics symbols Symbol Symbol Name Meaning / definition Example P(A) probabilityfunctionprobability of event A P(A) = 0.5P(A∩B) probability ofeventsintersectionprobability that ofevents A and BP(A∩B) = 0.5P(A∪B) probability ofevents union probability that ofevents A or BP(A∪B) = 0.5P(A | B) conditionalprobabilityfunctionprobability of event Agiven event B occuredP(A | B) = 0.3f (x) probabilitydensity function(pdf)P(a ≤ x ≤ b) = ∫f (x) dxF(x) cumulativedistributionfunction (cdf)F(x) = P(X≤ x)μpopulationmean mean of populationvaluesμ = 10E(X) expectationvalue expected value ofrandom variable XE(X) = 10E(X | Y) conditionalexpectation expected value ofrandom variable Xgiven YE(X | Y=2) = 5var(X) variance variance of randomvariable Xvar(X) = 4σ2variance variance of populationvaluesσ2 = 4std(X) standarddeviation standard deviation ofrandom variable Xstd(X) = 2σX standarddeviation standard deviationvalue of randomvariable XσX=2median middle value of random variable xcov(X,Y) covariance covariance of randomvariables X and Ycov(X,Y) = 4corr(X,Y) correlation correlation of randomvariables X and Ycorr(X,Y) = 0.6ρX,Y correlation correlation of randomvariables X and YρX,Y = 0.6∑summation summation - sum of all values in range of series∑∑doublesummationdouble summationMo mode value that occurs most frequently in populationMR mid-range MR = (x max+x min)/2 Md sample median half the population isbelow this valueQ1lower / firstquartile 25% of population are below this valueQ2median / secondquartile 50% of population are below this value = median of samplesQ3upper / thirdquartile 75% of population are below this valuex sample mean average / arithmeticmeanx = (2+5+9) / 3 = 5.333s2sample variance population samplesvariance estimators2 = 4s sample standarddeviation population samples standard deviation estimators = 2z x standard score z x = (x-x) / s xX ~ distribution of X distribution of randomvariable XX ~ N(0,3)N(μ,σ2) normaldistributiongaussian distribution X ~ N(0,3)U(a,b) uniformdistribution equal probability inrange a,bX ~ U(0,3)exp(λ) exponentialdistributionf (x) = λe-λx , x≥0gamma(c,λ) gammadistributionf (x) = λc x c-1e-λx /Γ(c), x≥0χ 2(k) chi-squaredistributionf (x) = x k/2-1e-x/2 /( 2k/2 Γ(k/2) )F (k1, k2) F distributionBin(n,p) binomialdistributionf (k) = n C k p k(1-p)n-kPoisson(λ) Poissondistributionf (k) = λk e-λ / k!Geom(p) geometricdistributionf (k) = p(1-p) kHG(N,K,n) hyper-geometricdistributionBern(p) BernoullidistributionCombinatorics SymbolsSymbol Symbol Name Meaning / definition Examplen! factorial n! = 1·2·3·...·n5! = 1·2·3·4·5 = 120 n P k permutation 5P3 = 5! / (5-3)! = 60n C kcombination 5C3 = 5!/[3!(5-3)!]=10Set theory symbolsSymbol Symbol Name Meaning / definition Example { } set a collection of elementsA = {3,7,9,14},B = {9,14,28}A ∩B intersection objects that belong to set A andset BA ∩B = {9,14}A ∪B union objects that belong to set A orset BA ∪B ={3,7,9,14,28}A ⊆B subset subset has fewer elements orequal to the set{9,14,28} ⊆{9,14,28}A ⊂B proper subset / strictsubsetsubset has fewer elements thanthe set{9,14} ⊂{9,14,28}A ⊄B not subset left set not a subset of right set{9,66} ⊄{9,14,28}A ⊇B superset set A has more elements orequal to the set B{9,14,28} ⊇{9,14,28}A ⊃B proper superset / strictsupersetset A has more elements thanset B{9,14,28} ⊃{9,14}A ⊅B not superset set A is not a superset of set B{9,14,28} ⊅{9,66}2A power set all subsets of Apower set all subsets of AA =B equality both sets have the samemembersA={3,9,14},B={3,9,14},A=BA c complement all the objects that do not belong to set AA \B relative complement objects that belong to A and notto BA = {3,9,14},B = {1,2,3},A-B = {9,14}A -B relative complement objects that belong to A and notto BA = {3,9,14},B = {1,2,3},A-B = {9,14}A ∆B symmetric difference objects that belong to A or Bbut not to their intersectionA = {3,9,14},B = {1,2,3},A ∆B ={1,2,9,14}A ⊖B symmetric difference objects that belong to A or Bbut not to their intersectionA = {3,9,14},B = {1,2,3},A ⊖B ={1,2,9,14}a∈A element of set membership A={3,9,14}, 3 ∈Ax∉A not element of no set membershipA={3,9,14}, 1∉ A (a,b) ordered pair collection of 2 elementsA×B cartesian product set of all ordered pairs from Aand B|A| cardinality the number of elements of set AA={3,9,14},|A|=3#A cardinality the number of elements of set AA={3,9,14},#A=3aleph-null infinite cardinality of natural numbers setaleph-one cardinality of countable ordinal numbers setØempty set Ø = { } C = {Ø} universal set set of all possible values0natural numbers / wholenumbers set (withzero)= {0,1,2,3,4,...} 0 ∈01natural numbers / wholenumbers set (without 1= {1,2,3,4,5,...} 6 ∈1zero)integer numbers set = {...-3,-2,-1,0,1,2,3,...} -6 ∈rational numbers set = {x | x=a/b, a,b∈} 2/6 ∈real numbers set = {x | -∞< x <∞} 6.343434∈= {z | z=a+bi, -∞<a<6+2i∈complex numbers set∞, -∞<b<∞}Logic symbolsSymbol Symbol Name Meaning / definition Example ·and and x·y^ caret / circumflex and x ^ y& ampersand and x & y + plus or x + y∨reversed caret or x∨y| vertical line or x | yx' single quote not - negation x'x bar not - negation x¬not not - negation ¬x! exclamation mark not - negation ! x~ tilde negation ~ x ⇒implies⇔equivalent if and only if (iff)↔equivalent if and only if (iff)∀for all∃there exists∄there does not exists∴therefore∵because / sinceCalculus & analysis symbolsSymbol Symbol Name Meaning / definition Example limit limit value of a functionεepsilon represents a very smallnumber, near zeroε→0e e constant /Euler's number e = 2.718281828...e = lim (1+1/x)x ,x→∞y ' derivative derivative - Lagrange'snotation(3x3)' = 9x2y(n)nth derivative n times derivation (3x3)(3) = 18 derivative derivative - Leibniz's notation d(3x3)/dx = 9x2second derivative derivative of derivative d2(3x3)/dx2 = 18xnth derivative n times derivationtime derivative derivative by time - Newton's notationtime secondderivativederivative of derivativeD x y derivative derivative - Euler's notationD x2y second derivative derivative of derivativepartial derivative ∂(x2+y2)/∂x = 2x ∫integral opposite to derivation ∫f(x)dx∫∫double integral integration of function of 2variables∫∫f(x,y)dxdy∫∫∫triple integral integration of function of 3variables ∫∫∫f(x,y,z)dxdydz∮closed contour /line integral∯closed surface integral∰closed volume integral[a,b] closed interval [a,b] = {x | a ≤ x ≤ b}(a,b) open interval (a,b) = {x | a < x < b}i imaginary unit i≡√-1 z = 3 + 2i z* complexconjugatez = a+bi→z*=a-bi z* = 3 - 2iz complexconjugatez = a+bi→z = a-bi z = 3 - 2i∇nabla / del gradient / divergenceoperator∇f (x,y,z) vectorunit vectorx * y convolution y(t) = x(t) * h(t)Laplace transform F(s) = {f (t)}Fourier transform X(ω) = {f (t)}δdelta function∞lemniscate infinity symbol。

中小学数学代数几何常用概念中英文数学对照

中英文数学对照代数Algebra正数positive负数negative零zero数字digit/number整数integer分数fractions假分数proper fraction带分数mixture fractions/improper fraction 分子numerator分母denominator小数decimal百分数percentage/percent数字1one2two3three4four5five6six7seven8eight9nine10ten11eleven12twelve13thirteen14fourteen15fifteen16sixteen17seventeen18eighteen19nineteen20twenty100hundred1000thousand10000million1000000000billion奇数odd偶数even质数prime合数composite最大公约数maximum common factor 最小公倍数least common multiples加法addition减法subtraction乘法multiple除法division被除数dividend除数divisor商quotient和sum乘积product因数factor结合律association交换律communication分配律distribution因式分解factoring因子factors简化simplify等式/方程equation不等式inequation倒数receiption符号symbol约等于/近似approximately估算estimation实数real numbers有理数rational numbers无理数irrational numbers一元二次方程linear equations二元一次方程quadratic equations绝对值方程absolute equations方程的根root方程组system of equations变量variable常量constant多项式polynomial单项式monomial反比例函数inverse proportional function 正比例函数proportional function指数函数exponential function对数函数logarithmic function三角函数trigonometric function消元法elimination代入法substitute集合set并集union set交集intersection set空集empty set坐标轴axis横轴x-axis纵轴y-axis截距x,y-intercepts象限quadrant抛物线parabola顶点vertex准线directrix对称轴symmetric axis主轴Major axis副轴Minor axis水平对称轴horizontal symmetric axis垂直对称轴vertical symmetric axis数列sequence/series等差数列arithmetic sequence等比数列geometric sequence几何geometric点point线line面plane曲线curve多边形polygon平行四边形parallelogram菱形rhombus长方形rectangular正方形square梯形trapezoid三角形triangle斜三角形skew triangle正三角形right triangle等腰三角形isosceles triangle锐角三角形acute triangle直角三角形right triangle钝角三角形obtuse triangle凹多边形concave polygon凸多边形convex polygon对边opposite site邻边adjacent side斜边hypotenuse side对角线diagonal髙height底面base中线midline垂直平分线perpendicular bisector 垂直perpendicular平分bisector重心gravity垂心orthocenter角angle锐角acute angle直角right angle钝角obtuse angle圆circle半径radius直径diameter弦chord弧arc优弧major arc劣弧minor arc切线tangent line割线secant line长方形rectangle正方形square边side椭圆ellipse抛物线parabola双曲线hyperbola相交intersection相切tangent正交orthogonal立体图形solid立方体cube三棱柱triangular prism棱柱prism棱锥pyramid圆锥cone圆柱cylinder球sphere规则多边体不规则多边体勾股定理Pythagorean theorem 边长side length面积area周长perimeter/circumference 体积volume表面积surface area侧面积lateral area底面积base area斜边slant立方体的高altitude位似变化transformation位移translation水平平移horizontal shift垂直平移vertical shift对称reflection放大/缩小dilation strectch/compress 旋转rotation公式formula定理theorem矩阵matrix行列式determinant行row列column排列permutation组合combination概率probability极限limit导数derivative微分differential积分integral平均数average/mean方差variance标准差standard variance中位数median众数mode。

常用数学符号英文对照

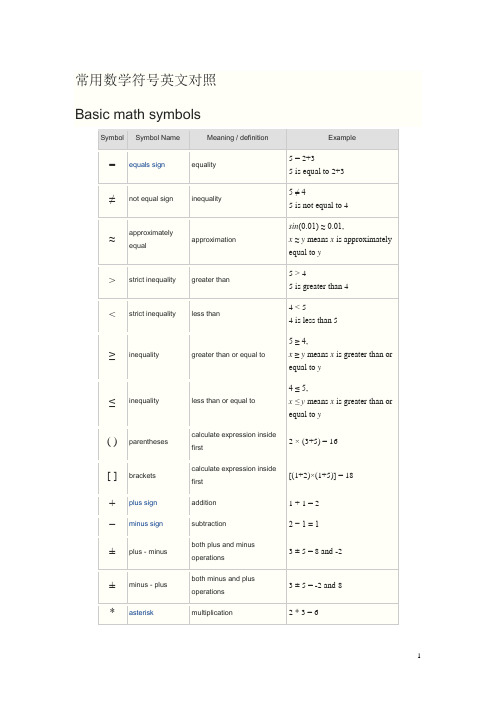
常用数学符号英文对照Basic math symbolsSymbol Symbol Name Meaning / definition Example= equals sign equality 5 = 2+35 is equal to 2+3≠not equal sign inequality 5 ≠ 45 is not equal to 4≈approximatelyequal approximationsin(0.01) ≈ 0.01,x≈y means x is approximatelyequal to y> strict inequality greater than 5 > 45 is greater than 4< strict inequality less than 4 < 54 is less than 5≥inequality greater than or equal to 5 ≥ 4,x≥y means x is greater than or equal to y≤inequality less than or equal to 4 ≤ 5,x ≤ y means x is greater than or equal to y( ) parentheses calculate expression insidefirst2 × (3+5) = 16[ ] brackets calculate expression insidefirst[(1+2)×(1+5)] = 18 + plus sign addition 1 + 1 = 2−minus sign subtraction 2 − 1 = 1±plus - minus both plus and minusoperations3 ± 5 = 8 and -2±minus - plus both minus and plusoperations3 ± 5 = -2 and 8 * asterisk multiplication 2 * 3 = 6×times sign multiplication 2 × 3 = 6 ·multiplication dot multiplication 2 · 3 = 6÷division sign /division 6 ÷ 2 = 3obelus/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimal2.56 = 2+56/100separatora b power exponent 23= 8a^b caret exponent 2 ^ 3= 8√a square root √a ·√a = a√9 = ±33√a cube root 3√a ·3√a ·3√a = a3√8 = 24√a fourth root 4√a ·4√a ·4√a ·4√a = a4√16 = ±2n√a n-th root (radical) for n=3, n√8 = 2% percent1% = 1/100 10% × 30 = 3‰per-mille1‰ = 1/1000 = 0.1%10‰ × 30 = 0.3ppm per-million1ppm = 1/1000000 10ppm × 30 = 0.0003ppb per-billion 1ppb = 1/1000000000 10ppb × 30 = 3×10-7ppt per-trillion 1ppt = 10-1210ppt × 30 = 3×10-10ABC = 30°AOB = 30°°degree 1 turn = 360°α = 60°deg degree 1 turn = 360deg α = 60deg′prime arcminute, 1° = 60′α = 60°59′″double prime arcsecond, 1′ = 60″α = 60°59′59″line infinite lineAB line segment line from point A to point Bray line that start from point Aarc arc from point A to point B= 60°⊥perpendicular perpendicular lines (90° angle) AC ⊥ BC| | parallel parallel lines AB | | CD≅congruent to equivalence of geometric shapes and size ∆ABC≅∆XYZ ~ similarity same shapes, not same size ∆ABC~ ∆XYZ Δtriangle triangle shape ΔABC≅ΔBCD |x-y| distance distance between points x and y | x-y | = 5πpi constant π = 3.141592654...is the ratio between the circumference and diameter of acirclec = π·d = 2·π·rrad radians radians angle unit 360° = 2π rad c radians radians angle unit 360° = 2πcgrad gradians / gons grads angle unit 360° = 400 gradg gradians / gons grads angle unit 360° = 400 gx x variableto findwhen 2x = 4, then x = 2≡equivalence identical to≜equal by definition equal bydefinition:= equal by definition equal bydefinition~ approximately equal weakapproximation11 ~ 10≈approximately equal approximation sin(0.01) ≈ 0.01∝proportional to proportional to y∝x when y = kx, k constant ∞lemniscate infinity symbol≪much less than much less than 1 ≪1000000≫much greater than much greaterthan1000000 ≫1( ) parentheses calculateexpressioninside first2 * (3+5) = 16[ ] brackets calculateexpressioninside first[(1+2)*(1+5)] = 18{ } braces set⌊x⌋floor brackets rounds numberto lower integer⌊4.3⌋ = 4⌈x⌉ceiling brackets rounds numberto upper integer⌈4.3⌉ = 5x! exclamation mark factorial4! = 1*2*3*4 = 24 | x | single vertical bar absolute value | -5 | = 5f (x) function of x maps values ofx to f(x)f (x) = 3x+5(f∘g) function composition (f∘g) (x)= f (g(x))f (x)=3x,g(x)=x-1 ⇒(f∘g)(x)=3(x-1)(a,b) open interval (a,b) = x∈(2,6)[a ,b ] closed interval[a ,b ] = {x | a ≤ x ≤ b }x ∈ [2,6]∆ delta change / difference∆t = t 1 - t 0∆ discriminantΔ = b 2 - 4ac∑sigmasummation -sum of all values in range of series ∑ x i = x 1+x 2+...+x n∑∑sigmadouble summation∏capital piproduct -product of all values in range of series∏ x i =x 1∙x 2∙...∙x ne e constant / Euler's numbere =2.718281828... e = lim (1+1/x )x , x →∞γ Euler-Mascheroni constant γ =0.527721566...φgolden ratio golden ratio constantπpi constant π =3.141592654...is the ratiobetween the circumference and diameter of a circlec = π·d = 2·π·rA ⊗Btensor product tensor product of A and BA ⊗ Binner product[ ] brackets matrix of numbers ( ) parentheses matrix of numbers| A | determinant determinant of matrix A det(A ) determinant determinant of matrix A|| x || double vertical bars normA T transpose matrix transpose(A T )ij = (A )ji A † Hermitian matrix matrix conjugate transpose (A †)ij = (A )ji A * Hermitian matrix matrix conjugate transpose(A *)ij = (A )jiA -1inverse matrixA A -1 = Irank(A ) matrix rank rank of matrix A rank(A ) = 3 dim(U )dimensiondimension of matrix Arank(U ) = 3Probability and statistics symbolsSymbolSymbol Name Meaning / definitionExampleP (A )probability function probability of event A P (A ) = 0.5P (A ∩ B ) probability ofeventsintersection probability that of events A and BP (A ∩B ) = 0.5P (A ∪B ) probability ofevents unionprobability that of events A or B P (A ∪B ) = 0.5P (A | B )conditionalprobability function probability of event A given event B occuredP (A | B ) = 0.3f (x ) probabilitydensity function (pdf) P (a ≤ x ≤ b ) = ∫ f (x ) dxF (x )cumulativeF (x ) = P (X ≤ x )distribution function (cdf)μ population mean mean of population valuesμ = 10E (X )expectation valueexpected value of random variable X E (X ) = 10E (X | Y )conditional expectationexpected value of random variable X given YE (X | Y=2) = 5var (X ) variance variance of random variable X var (X ) = 4σ2variancevariance of population values σ2 = 4std (X ) standard deviationstandard deviation of random variable X std (X ) = 2σXstandard deviationstandard deviation value of random variable X σX = 2medianmiddle value of random variable xcov (X ,Y )covariance covariance ofrandom variables X and Y cov (X,Y ) = 4corr (X ,Y ) correlationcorrelation ofrandom variables X and Y corr (X,Y ) = 0.6ρX ,Ycorrelation correlation ofrandom variables X and YρX ,Y = 0.6∑summation summation - sum ofall values in range of series∑∑double summationdouble summationMo mode value that occurs most frequently in populationMR mid-range MR = (x max+x min)/2 Md sample median half the population isbelow this valueQ1lower / firstquartile 25% of population are below this valueQ2median /second quartile 50% of population are below this value = median of samplesQ3upper / thirdquartile 75% of population are below this valuex sample mean average / arithmeticmeanx = (2+5+9) / 3 = 5.333s2samplevariance population samples variance estimators2 = 4s samplestandarddeviationpopulation samplesstandard deviationestimators = 2z x standard score z x = (x-x) / s xX ~ distribution of X distribution ofrandom variable XX ~ N(0,3)N(μ,σ2) normaldistributiongaussian distribution X ~ N(0,3)U(a,b) uniformdistributionequal probability inrange a,bX ~ U(0,3)exp(λ)exponentialdistributionf (x) = λe-λx , x≥0gamma(c, λ)gammadistributionf (x) = λ c x c-1e-λx /Γ(c), x≥0χ 2(k) chi-squaredistributionf (x) = x k/2-1e-x/2 /( 2k/2 Γ(k/2) )F (k1, k2) F distributionBin (n ,p )binomial distribution f (k ) = n C k p k (1-p )n-kPoisson (λ)Poisson distribution f (k ) = λk e -λ / k !Geom (p )geometric distribution f (k ) = p (1-p ) kHG (N ,K ,n ) hyper-geometric distributionBern (p ) Bernoulli distributionsubset the set {9,14,28} A ⊄ B not subset left set not a subset of right set{9,66} ⊄{9,14,28} A ⊇B supersetset A has more elements or equalto the set B{9,14,28} ⊇{9,14,28} A ⊃Bproper superset / strictsupersetset A has more elements than setB{9,14,28} ⊃{9,14}A ⊅B not superset set A is not a superset of set B{9,14,28} ⊅{9,66} 2A power set all subsets of Apower set all subsets of AA =B equalityboth sets have the samemembersA={3,9,14},B={3,9,14},A=BA c complementall the objects that do not belongto set AA \B relative complementobjects that belong to A and notto BA = {3,9,14},B = {1,2,3},A-B = {9,14} A - B relative complementobjects that belong to A and notto BA = {3,9,14},B = {1,2,3},A-B = {9,14} A ∆ B symmetric differenceobjects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ∆B ={1,2,9,14} A ⊖ B symmetric differenceobjects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ⊖B ={1,2,9,14}a∈A element of set membership A={3,9,14}, 3 ∈Ax∉A not element of no set membership A={3,9,14}, 1 ∉A(a ,b ) ordered pair collection of 2 elementsA×B cartesian product set of all ordered pairs from Aand B|A| cardinality the number of elements of set AA={3,9,14}, |A|=3 #A cardinality the number of elements of set AA={3,9,14}, #A=3aleph-nullinfinite cardinality of naturalnumbers setaleph-one cardinality of countable ordinalnumbers setØ empty set Ø = { }C = {Ø}universal set set of all possible valuesnatural numbers / whole numbers set (with zero) 0 = {0,1,2,3,4,...}0 ∈ 01natural numbers / wholenumbers set (withoutzero)1 = {1,2,3,4,5,...}6 ∈ 1integer numbers set= {...-3,-2,-1,0,1,2,3,...} -6 ∈rational numbers set= {x | x =a /b , a ,b ∈}2/6 ∈real numbers set= {x | -∞ < x <∞} 6.343434∈complex numbers set= {z | z=a +bi ,-∞<a <∞, -∞<b <∞}6+2i ∈∨reversed caret or x∨y | vertical line or x | y x' single quote not - negation x'x bar not - negation x¬not not - negation ¬x ! exclamation mark not - negation ! x ⊕circled plus / oplus exclusive or - xor x⊕y ~ tilde negation ~ x ⇒implies⇔equivalent if and only if (iff)↔equivalent if and only if (iff)∀for all∃there exists∄there does not exists∴therefore∵because / sincee e constant / Euler'snumber e = 2.718281828...e = lim(1+1/x)x ,x→∞y ' derivative derivative - Lagrange's notation (3x3)' = 9x2y '' second derivative derivative of derivative (3x3)'' = 18xy(n)nth derivative n times derivation (3x3)(3) = 18derivative derivative - Leibniz's notation d(3x3)/dx = 9x2second derivative derivative of derivative d2(3x3)/dx2 = 18xnth derivative n times derivationtime derivative derivative by time - Newton's notationtime secondderivativederivative of derivativeD x y derivative derivative - Euler's notationD x2y second derivative derivative of derivativepartial derivative ∂(x2+y2)/∂x = 2x ∫integral opposite to derivation ∫f(x)dx∫∫double integral integration of function of 2variables∫∫f(x,y)dxdy∫∫∫triple integral integration of function of 3variables∫∫∫f(x,y,z)dxdydz∮closed contour / lineintegral∯closed surfaceintegral∰closed volumeintegral[a,b] closed interval [a,b] = {x | a ≤ x ≤ b}(a,b) open interval (a,b) = {x | a < x < b}i imaginary unit i≡ √-1 z = 3 + 2i z* complex conjugate z = a+bi→z*=a-bi z* = 3 - 2i z complex conjugate z = a+bi→z = a-bi z = 3 - 2i ∇nabla / del gradient / divergence operator ∇f (x,y,z)vectorunit vectorx * y convolution y(t) = x(t) * h(t)Laplace transform F(s) = {f (t)}Fourier transform X(ω) = {f (t)}δdelta function∞lemniscate infinity symbol。

数学符号的中英文读法

section; division
分节号
→
arrow
箭号；参见号
＋
plus
加号；正号
－
minus
减号；负号
±
plus or minus
正负号
×
is multiplied by
乘号
÷
is divided by
除号
＝
is equal to
等于号
≠
is not equal to
不等于号
≡
is equivalent to
Ν
（纽）
Ξ
（可系）
Ο
（奥密克戎）
Π
（派）
Ρ
（若）
Σ
（西格马）
Τ
（套）
Υ
（英文或拉丁字母）
Φ
（斐）
Χ
（喜）
Ψ
（普西）
Ω
（欧米伽）
Mu
Ν ν：拗
Nu
Ξ ξ：克西
KeXi
Ο ο：欧麦克轮 Omicron
∏ π：派
Pi
Ρ ρ：柔
Rho
∑ σ：西格玛
Sigma
Τ τ：套
Tau
Υ υ：宇普西龙 Upsilon
Φ φ： fai
Phi
Χ χ：器
Chi
Ψ ψ：普赛
Psi
Ω ω：欧米伽
Omega
希腊字母怎么打:打开 Office 文档之后，在你需要输入希腊字母的时候，先将输入法切换为
ω（欧米伽）。
更全面：
1 Α α alpha a:lf
阿尔法角度系数
2 Β β beta bet
贝塔磁通系数角度系数

数学符号英文对照表

1．Professional Basics Knowledge1/21/32/31/41/1001/1000 113/3244320.25＋－±×÷＝≈( ) [ ] { }≢≣∞∵∴→x＋y (a + b ) a = ba ≠b a ±b a ≈b a ＞b a ＞＞b a ≣b a ＜b a ＜＜b a ≢b a ⊥b x →∞a ≡b ∟a a half, one halfa third, one thirdtwo thirdsa quarter, one quarter , a fourth, one fourtha (one) hundredtha (one) thousandthone hundred and thirteen over three hundred and twenty four four and two thirdszero (0, naught) point two fiveplus, positiveminus, negativeplus or minusmultiplied by, timesdivided bybe equal to, equalsbe approximately equal to, approximately equalsround brackets; parenthesessquare (angular) bracketsbracesless than or equal tomore than or equal toinfinitybecausethereforemaps intox plus ybracket a plus b bracket closeda equals b, a is equal to b, a is ba is not equal to b, a is not ba plus or minus ba is approximately equal to ba is greater than ba is much [far] greater than ba is greater than or equal to ba is less than ba is much less than ba is less than or equal to ba is perpendicular to bx approaches infinitya is identically equal to b, a is of identity to bangle aa ～ba ∠ba ∝ bx 2x 3x3x %2%‰5‰㏒n x㏒10x㏒e x,㏑xe x ,exp(x)x nx1/n or n xsincostg, tanctg, cotsc, seccsc, cosecsin -1 arcsincos -1 ,arcossinhcosh∑∑=ni ix 1∏∏=ni ix 1∣x ∣xb ’b ’’ the difference between a and b a is parallel to b a varies directly as b x square; x squared; the square of x~, the second power of x, x to second power x cube; x cubed; the cube of x; the third power of x, x to the third power the square root of x the cube root of x percent two percent per mill five per mill log x to the base n log x to the base 10; common logarithm log x to the base e , natural logarithm, Napierian logarithm exponential function of x; e to the power x the nth power of x; x to the power n the nth root of x, x to the power one over n sine cosine tangent cotangent secont cosecant arc sine arc cosine the hyperbolic sine the hyperbolic cosine the summation of the summation of x sub i ,where i goes from 1 to n the product of the product of x sub i , where i goes from 1to n the absolute value of x the mean value of x, x bar b primeb double prime; b second primeb ’’’ f(x) △ x, δx dx dx dy 22dx y d n n dx y d u y ∂∂ ⎰ ⎰⎰ ⎰…⎰ ⎰b aF a 22007’13’’00C1000C320Fb triple primefunction f of xfinite difference or incrementthe increment of xdee x; dee of x; differential xthe differential coefficient of y with respect to x, the first derivative of y with respect of xthe second derivative of y with respect of xthe nth derivative of y with respect of xThe partial derivative of y with respect of u, where y is a function of u and another variable (or variables)integral ofdouble integral ofn-fold integral ofintegral between limits a and b (…from a to b)vector F a sub two twenty degreesseven minutes; seven feetthirteen seconds; thirteen inches zero degree Centigrade [Celsius]one [a] hundred degrees Centigrade thirty-two degrees Fahrenheit。

常用数学符号的英文表达

常用数学符号的英文表达第一章函数与极限Chapter1 Function and Limit集合set元素element子集subset空集empty set并集union交集intersection差集difference of set基本集basic set补集complement set直积direct product笛卡儿积Cartesian product开区间open interval闭区间closed interval半开区间half open interval有限区间finite interval区间的长度length of an interval无限区间infinite interval领域neighborhood领域的中心centre of a neighborhood领域的半径radius of a neighborhood左领域left neighborhood右领域right neighborhood映射mappingX到Y的映射mapping of X ontoY满射surjection单射injection一一映射one-to-one mapping双射bijection算子operator变化transformation函数function逆映射inverse mapping复合映射composite mapping自变量independent variable因变量dependent variable定义域domain函数值value of function函数关系function relation值域range自然定义域natural domain单值函数single valued function多值函数multiple valued function单值分支one-valued branch函数图形graph of a function绝对值函数absolute value符号函数sigh function整数部分integral part阶梯曲线step curve当且仅当if and only if(iff)分段函数piecewise function上界upper bound下界lower bound有界boundedness无界unbounded函数的单调性monotonicity of a function单调增加的increasing单调减少的decreasing单调函数monotone function函数的奇偶性parity(odevity) of a function 对称symmetry偶函数even function奇函数odd function函数的周期性periodicity of a function周期period反函数inverse function直接函数direct function复合函数composite function中间变量intermediate variable函数的运算operation of function基本初等函数basic elementary function初等函数elementary function幂函数power function指数函数exponential function对数函数logarithmic function三角函数trigonometric function反三角函数inverse trigonometric function 常数函数constant function双曲函数hyperbolic function双曲正弦hyperbolic sine双曲余弦hyperbolic cosine双曲正切hyperbolic tangent反双曲正弦inverse hyperbolic sine反双曲余弦inverse hyperbolic cosine反双曲正切inverse hyperbolic tangent极限limit数列 sequence of number收敛 convergence收敛于 a converge to a发散 divergent极限的唯一性 uniqueness of limits收敛数列的有界性 boundedness of a convergent sequence子列 subsequence函数的极限 limits of functions函数()f x 当x 趋于x 0时的极限 limit of functions ()f x as x approaches x 0 左极限 left limit右极限 right limit单侧极限 one-sided limits水平渐近线 horizontal asymptote无穷小 infinitesimal无穷大 infinity铅直渐近线 vertical asymptote夹逼准则 squeeze rule单调数列 monotonic sequence高阶无穷小 infinitesimal of higher order低阶无穷小 infinitesimal of lower order同阶无穷小 infinitesimal of the same order等阶无穷小 equivalent infinitesimal函数的连续性 continuity of a function增量 increment函数()f x 在x 0连续 the function ()f x is continuous at x 0左连续 left continuous右连续 right continuous区间上的连续函数 continuous function函数()f x 在该区间上连续 function ()f x is continuous on an interval不连续点discontinuity point第一类间断点discontinuity point of the first kind第二类间断点discontinuity point of the second kind初等函数的连续性continuity of the elementary functions 定义区间defined interval最大值global maximum value (absolute maximum)最小值global minimum value (absolute minimum)零点定理the zero point theorem介值定理intermediate value theorem。

常用数学符号英文对照

常用数学符号英文对照Basic math symbolsSymbol Symbol Name Meaning / definition Example= equals sign equality 5 = 2+35 is equal to 2+3≠not equal sign inequality 5 ≠ 45 is not equal to 4≈approximatelyequal approximationsin(0.01) ≈ 0.01,x≈y means x is approximatelyequal to y> strict inequality greater than 5 > 45 is greater than 4< strict inequality less than 4 < 54 is less than 5≥inequality greater than or equal to 5 ≥ 4,x≥y means x is greater than or equal to y≤inequality less than or equal to 4 ≤ 5,x ≤ y means x is greater than or equal to y( ) parentheses calculate expression insidefirst2 × (3+5) = 16[ ] brackets calculate expression insidefirst[(1+2)×(1+5)] = 18 + plus sign addition 1 + 1 = 2−minus sign subtraction 2 − 1 = 1±plus - minus both plus and minusoperations3 ± 5 = 8 and -2±minus - plus both minus and plusoperations3 ± 5 = -2 and 8 * asterisk multiplication 2 * 3 = 6×times sign multiplication 2 × 3 = 6 ·multiplication dot multiplication 2 · 3 = 6÷division sign /division 6 ÷ 2 = 3obelus/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimal2.56 = 2+56/100separatora b power exponent 23= 8a^b caret exponent 2 ^ 3= 8√a square root √a ·√a = a√9 = ±33√a cube root 3√a ·3√a ·3√a = a3√8 = 24√a fourth root 4√a ·4√a ·4√a ·4√a = a4√16 = ±2n√a n-th root (radical) for n=3, n√8 = 2% percent1% = 1/100 10% × 30 = 3‰per-mille1‰ = 1/1000 = 0.1%10‰ × 30 = 0.3ppm per-million1ppm = 1/1000000 10ppm × 30 = 0.0003ppb per-billion 1ppb = 1/1000000000 10ppb × 30 = 3×10-7ppt per-trillion 1ppt = 10-1210ppt × 30 = 3×10-10ABC = 30°AOB = 30°°degree 1 turn = 360°α = 60°deg degree 1 turn = 360deg α = 60deg′prime arcminute, 1° = 60′α = 60°59′″double prime arcsecond, 1′ = 60″α = 60°59′59″line infinite lineAB line segment line from point A to point Bray line that start from point Aarc arc from point A to point B= 60°⊥perpendicular perpendicular lines (90° angle) AC ⊥ BC| | parallel parallel lines AB | | CD≅congruent to equivalence of geometric shapes and size ∆ABC≅∆XYZ ~ similarity same shapes, not same size ∆ABC~ ∆XYZ Δtriangle triangle shape ΔABC≅ΔBCD |x-y| distance distance between points x and y | x-y | = 5πpi constant π = 3.141592654...is the ratio between the circumference and diameter of acirclec = π·d = 2·π·rrad radians radians angle unit 360° = 2π rad c radians radians angle unit 360° = 2πcgrad gradians / gons grads angle unit 360° = 400 gradg gradians / gons grads angle unit 360° = 400 gx x variableto findwhen 2x = 4, then x = 2≡equivalence identical to≜equal by definition equal bydefinition:= equal by definition equal bydefinition~ approximately equal weakapproximation11 ~ 10≈approximately equal approximation sin(0.01) ≈ 0.01∝proportional to proportional to y∝x when y = kx, k constant ∞lemniscate infinity symbol≪much less than much less than 1 ≪1000000≫much greater than much greaterthan1000000 ≫1( ) parentheses calculateexpressioninside first2 * (3+5) = 16[ ] brackets calculateexpressioninside first[(1+2)*(1+5)] = 18{ } braces set⌊x⌋floor brackets rounds numberto lower integer⌊4.3⌋ = 4⌈x⌉ceiling brackets rounds numberto upper integer⌈4.3⌉ = 5x! exclamation mark factorial4! = 1*2*3*4 = 24 | x | single vertical bar absolute value | -5 | = 5f (x) function of x maps values ofx to f(x)f (x) = 3x+5(f∘g) function composition (f∘g) (x)= f (g(x))f (x)=3x,g(x)=x-1 ⇒(f∘g)(x)=3(x-1)(a,b) open interval (a,b) = x∈(2,6)[a ,b ] closed interval[a ,b ] = {x | a ≤ x ≤ b }x ∈ [2,6]∆ delta change / difference∆t = t 1 - t 0∆ discriminantΔ = b 2 - 4ac∑sigmasummation -sum of all values in range of series ∑ x i = x 1+x 2+...+x n∑∑sigmadouble summation∏capital piproduct -product of all values in range of series∏ x i =x 1∙x 2∙...∙x ne e constant / Euler's numbere =2.718281828... e = lim (1+1/x )x , x →∞γ Euler-Mascheroni constant γ =0.527721566...φgolden ratio golden ratio constantπpi constant π =3.141592654...is the ratiobetween the circumference and diameter of a circlec = π·d = 2·π·rA ⊗Btensor product tensor product of A and BA ⊗ Binner product[ ] brackets matrix of numbers ( ) parentheses matrix of numbers| A | determinant determinant of matrix A det(A ) determinant determinant of matrix A|| x || double vertical bars normA T transpose matrix transpose(A T )ij = (A )ji A † Hermitian matrix matrix conjugate transpose (A †)ij = (A )ji A * Hermitian matrix matrix conjugate transpose(A *)ij = (A )jiA -1inverse matrixA A -1 = Irank(A ) matrix rank rank of matrix A rank(A ) = 3 dim(U ) dimensiondimension of matrix Arank(U ) = 3Probability and statistics symbolsSymbolSymbol Name Meaning / definitionExampleP (A )probability function probability of event A P (A ) = 0.5P (A ∩ B ) probability ofeventsintersection probability that of events A and BP (A ∩B ) = 0.5P (A ∪B ) probability ofevents unionprobability that of events A or B P (A ∪B ) = 0.5P (A | B )conditionalprobability function probability of event A given event B occuredP (A | B ) = 0.3f (x ) probabilitydensity function (pdf) P (a ≤ x ≤ b ) = ∫ f (x ) dxF (x )cumulativeF (x ) = P (X ≤ x )distribution function (cdf)μ population mean mean of population valuesμ = 10E (X )expectation valueexpected value of random variable X E (X ) = 10E (X | Y )conditional expectationexpected value of random variable X given YE (X | Y=2) = 5var (X ) variance variance of random variable X var (X ) = 4σ2variancevariance of population values σ2 = 4std (X ) standard deviationstandard deviation of random variable X std (X ) = 2σXstandard deviationstandard deviation value of random variable X σX = 2medianmiddle value of random variable xcov (X ,Y )covariance covariance ofrandom variables X and Y cov (X,Y ) = 4corr (X ,Y ) correlationcorrelation ofrandom variables X and Y corr (X,Y ) = 0.6ρX ,Ycorrelation correlation ofrandom variables X and YρX ,Y = 0.6∑summation summation - sum ofall values in range of series∑∑double summationdouble summationMo mode value that occurs most frequently in populationMR mid-range MR = (x max+x min)/2 Md sample median half the population isbelow this valueQ1lower / firstquartile 25% of population are below this valueQ2median /second quartile 50% of population are below this value = median of samplesQ3upper / thirdquartile 75% of population are below this valuex sample mean average / arithmeticmeanx = (2+5+9) / 3 = 5.333s2samplevariance population samples variance estimators2 = 4s samplestandarddeviationpopulation samplesstandard deviationestimators = 2z x standard score z x = (x-x) / s xX ~ distribution of X distribution ofrandom variable XX ~ N(0,3)N(μ,σ2) normaldistributiongaussian distribution X ~ N(0,3)U(a,b) uniformdistributionequal probability inrange a,bX ~ U(0,3)exp(λ)exponentialdistributionf (x)= λe-λx , x≥0gamma(c, λ)gammadistributionf (x) = λ c x c-1e-λx /Γ(c), x≥0χ 2(k) chi-squaredistributionf (x) = x k/2-1e-x/2 /( 2k/2 Γ(k/2) )F (k1, k2) F distributionBin (n ,p )binomial distribution f (k ) = n C k p k (1-p )n-kPoisson (λ)Poisson distribution f (k ) = λk e -λ / k !Geom (p )geometric distribution f (k ) = p (1-p ) kHG (N ,K ,n ) hyper-geometric distributionBern (p ) Bernoulli distributionSet theory symbolsSymbolSymbol NameMeaning / definitionExample{ }set a collection of elementsA = {3,7,9,14},B = {9,14,28} A ∩ B intersectionobjects that belong to set A and set BA ∩B = {9,14} A ∪ B unionobjects that belong to set A or set BA ∪B = {3,7,9,14,28} A ⊆ B subsetsubset has fewer elements or equal to the set{9,14,28} ⊆ {9,14,28} A ⊂ B proper subset / strictsubset has fewer elements than{9,14} ⊂subset the set {9,14,28}A ⊄B not subset left set not a subset of right set{9,66} ⊄{9,14,28}A ⊇B supersetset A has more elements or equalto the set B{9,14,28} ⊇{9,14,28}A ⊃Bproper superset / strictsupersetset A has more elements than setB{9,14,28} ⊃{9,14}A ⊅B not superset set A is not a superset of set B{9,14,28} ⊅{9,66} 2A power set all subsets of Apower set all subsets of AA =B equality both sets have the same membersA={3,9,14},B={3,9,14},A=BA c complementall the objects that do not belong toset AA \B relative complementobjects that belong to A and not toBA = {3,9,14},B = {1,2,3},A-B = {9,14} A - B relative complementobjects that belong to A and not toBA = {3,9,14},B = {1,2,3},A-B = {9,14} A ∆ B symmetric differenceobjects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ∆B ={1,2,9,14}A ⊖B symmetric differenceobjects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ⊖B ={1,2,9,14}a∈A element of set membership A={3,9,14}, 3 ∈Ax∉A not element of no set membership A={3,9,14}, 1 ∉A(a ,b ) ordered pair collection of 2 elementsA×B cartesian product set of all ordered pairs from A and B|A| cardinality the number of elements of set AA={3,9,14}, |A|=3 #A cardinality the number of elements of set AA={3,9,14}, #A=3aleph-nullinfinite cardinality of natural numbers setaleph-one cardinality of countable ordinal numbers setØ empty set Ø = { }C = {Ø}universal setset of all possible valuesnatural numbers / whole numbers set (with zero) 0 = {0,1,2,3,4,...}0 ∈ 01natural numbers / wholenumbers set (without zero)1 = {1,2,3,4,5,...}6 ∈ 1integer numbers set= {...-3,-2,-1,0,1,2,3,...} -6 ∈rational numbers set= {x | x =a /b , a ,b ∈}2/6 ∈real numbers set= {x | -∞ < x <∞} 6.343434∈complex numbers set= {z | z=a +bi ,-∞<a <∞, -∞<b <∞}6+2i ∈∨reversed caret or x∨y | vertical line or x | y x' single quote not - negation x'x bar not - negation x¬not not - negation ¬x ! exclamation mark not - negation ! x ⊕circled plus / oplus exclusive or - xor x⊕y ~ tilde negation ~ x ⇒implies⇔equivalent if and only if (iff)↔equivalent if and only if (iff)∀for all∃there exists∄there does not exists∴therefore∵because / sincee e constant / Euler'snumber e = 2.718281828...e = lim(1+1/x)x ,x→∞y ' derivative derivative - Lagrange's notation (3x3)' = 9x2y '' second derivative derivative of derivative (3x3)'' = 18xy(n)nth derivative n times derivation (3x3)(3) = 18derivative derivative - Leibniz's notation d(3x3)/dx = 9x2second derivative derivative of derivative d2(3x3)/dx2 = 18xnth derivative n times derivationtime derivative derivative by time - Newton's notationtime secondderivativederivative of derivativeD x y derivative derivative - Euler's notationD x2y second derivative derivative of derivativepartial derivative ∂(x2+y2)/∂x = 2x ∫integral opposite to derivation ∫f(x)dx∫∫double integral integration of function of 2variables∫∫f(x,y)dxdy∫∫∫triple integral integration of function of 3variables∫∫∫f(x,y,z)dxdydz∮closed contour / lineintegral∯closed surfaceintegral∰closed volumeintegral[a,b] closed interval [a,b] = {x | a ≤ x ≤ b}(a,b) open interval (a,b) = {x | a < x < b}i imaginary unit i≡ √-1 z = 3 + 2i z* complex conjugate z = a+bi→z*=a-bi z* = 3 - 2i z complex conjugate z = a+bi→z = a-bi z = 3 - 2i ∇nabla / del gradient / divergence operator ∇f (x,y,z)vectorunit vectorx * y convolution y(t) = x(t) * h(t)Laplace transform F(s) = {f (t)}Fourier transform X(ω) = {f (t)}δdelta function∞lemniscate infinity symbol。

数学符号英语表达

数学符号英语表达
数学符号是用来表示数学概念和运算的特殊符号。

在数学中，不同的符号有不同的含义和用法。

下面是一些常见的数学符号及其英语表达：
+ 加 (plus)
- 减 (minus)
×乘 (times)
÷除 (divided by)
= 等于 (equals)
≠不等于 (not equal to)
< 小于 (less than)
> 大于 (greater than)
≤小于等于 (less than or equal to)
≥大于等于 (greater than or equal to)
√开方 (square root)
^ 幂 (exponent)
% 百分号 (percent)
π圆周率 (pi)
e 自然对数的底数 (Euler's number)
除了这些常见的数学符号外，还有很多其他符号，如集合符号、积分符号、极限符号等等。

掌握这些符号的英语表达，可以帮助我们更好地理解和应用数学知识。

数值分析中常用数学词汇英中文对照翻译.

数值分析中常用数学词汇英中文对照abbreviation 简写符号;简写absolute error 绝对误差absolute value 绝对值accelerate 加速accumulation 累积accuracy 准确度act on 施于action 作用; 作用力add 加addition 加法addition formula 加法公式addition law 加法定律additive property 可加性adjoint matrix 伴随矩阵algebra 代数algebraic 代数的algebraic equation 代数方程algebraic expression 代数式algebraic fraction 代数分式;代数分数式algebraic inequality 代数不等式algebraic number 代数数algebraic operation 代数运算algorithm 算法系统; 规则系统alternating series 交错级数alternative hypothesis 择一假设; 备择假设; 另一假设analysis 分析;解析angle 角anti-clockwise direction 逆时针方向;返时针方向anti-derivative 反导数; 反微商anti-logarithm 逆对数;反对数anti-symmetric 反对称approach 接近;趋近approximate value 近似值approximation 近似;略计;逼近Arabic system 阿刺伯数字系统arbitrary 任意arbitrary constant 任意常数arc 弧arc-cosine function 反余弦函数arc-sin function 反正弦函数arc-tangent function 反正切函数area 面积argument (1论证; (2辐角argument of a function 函数的自变量arithmetic 算术array 数组; 数组ascending order 递升序ascending powers of X X 的升幂assumption 假定;假设asymmetrical 非对称asymptote 渐近augmented matrix 增广矩阵average 平均;平均数;平均值axiom 公理back substitution 回代base (1底;(2基;基数basis 基belong to 属于bias 偏差;偏倚billion 十亿binary number 二进数binary operation 二元运算binary system 二进制binomial 二项式bisection method 分半法;分半方法boundary condition 边界条件boundary line 界(线;边界bounded 有界的bounded above 有上界的;上有界的bounded below 有下界的;下有界的bounded function 有界函数bounded sequence 有界序列brace 大括号bracket 括号breadth 阔度calculation 计算calculator 计算器;计算器calculus (1 微积分学; (2 演算cancel 消法;相消Cartesian coordinates 笛卡儿坐标category 类型;范畴centre 中心;心chain rule 链式法则chance 机会change of base 基的变换change of variable 换元;变量的换characteristic equation 特征(征方程characteristic function 特征(征函数characteristic root 特征(征根chart 图;图表check digit 检验数位checking 验算circle 圆classification 分类clockwise direction 顺时针方向clockwise moment 顺时针力矩closed convex region 闭凸区域closed interval 闭区间coefficient 系数cofactor 余因子; 余因式coincide 迭合;重合collection of terms 并项collinear 共线collinear planes 共线面column (1列;纵行;(2 柱column matrix 列矩阵column vector 列向量combination 组合common denominator 同分母;公分母common difference 公差common divisor 公约数;公约common factor 公因子;公因子common multiple 公位数;公倍comparable 可比较的complement 余;补余completing the square 配方complex number 复数complex number plane 复数平面complex root 复数根component 分量composite function 复合函数; 合成函数computation 计算computer 计算机;电子计算器concept 概念conclusion 结论condition 条件conditional 条件句;条件式conjugate 共轭constant 常数constant of integration 积分常数constraint 约束;约束条件continuity 连续性continuous function 连续函数contradiction 矛盾converge 收敛convergence 收敛性convergent 收敛的convergent iteration 收敛的迭代convergent sequence 收敛序列convergent series 收敛级数convex 凸convexity 凸性coordinate 坐标corollary 系定理; 系; 推论correspondence 对应counter clockwise direction 逆时针方向;返时针方向counter example 反例counting 数数;计数criterion 准则critical point 临界点critical region 临界域cirtical value 临界值cube 正方体;立方;立方体cubic 三次方;立方;三次(的 cubic equation 三次方程cubic roots of unity 单位的立方根cumulative 累积的curve 曲线decimal 小数decimal place 小数位decimal point 小数点decimal system 十进制definite integral 定积分definition 定义degree (1 度; (2 次degree of a polynomial 多项式的次数degree of accuracy 准确度degree of ODE 常微分方程次数delete 删除; 删去denary number 十进数denominator 分母dependence (1相关; (2应变derivable 可导derivative 导数determinant 行列式diagonal 对角线diagonal matrix 对角矩阵difference 差difference equation 差分方程differentiable 可微differential 微分differential coefficient 微商; 微分系数differential equation 微分方程differential mean value theorem 微分中值定理differentiate 求...的导数differentiation 微分法digit 数字dimension 量; 量网; 维(数direction 方向; 方位discontinuity 不连续性discontinuous 间断(的;连续(的; 不连续(的discontinuous point 不连续点discrete 分立; 离散distance 距离diverge 发散divergence 发散(性divergent 发散的divergent iteration 发散性迭代divergent sequence 发散序列divide 除dividend (1被除数;divisible 可整除division 除法division algorithm 除法算式divisor 除数;除式;因子dot 点dot product 点积echelon form 梯阵式echelon matrix 梯矩阵eigenvalue 本征值eigenvector 本征向量element 元素elementary row operation 基本行运算elimination 消法elimination method 消去法;消元法empty set 空集equivalent 等价(的error 误差error estimate 误差估计error term 误差项estimate 估计;估计量evaluate 计值exact 真确exact solution 准确解;精确解;真确解exact value 法确解;精确解;真确解example 例expand 展开experiment 实验;试验experimental 试验的exponent 指数exponential function 指数函数express…in terms of… 以………表达extreme point 极值点extreme value 极值extremum 极值factor 因子;因式;商factor method 因式分解法factorial 阶乘factorization 因子分解;因式分解fallacy 谬误FALSE 假(的falsehood 假值finite 有限finite sequence 有限序列first derivative 一阶导数first order differential equation 一阶微分方程fixed point 不动点fixed point iteration method 不动点迭代法for all X 对所有X for each /every X 对每一Xform 形式;型format 格式;规格formula(formulae 公式fraction 分数;分式function 函数fundamental theorem of calculus 微积分基本定理Gaussian elimination 高斯消去法general form 一般式;通式general solution 通解;一般解general term 通项given 给定;已知global 全局; 整体global maximum 全局极大值; 整体极大值global minimum 全局极小值; 整体极小值gradient (1斜率;倾斜率;(2梯度graph 图像;图形;图表graphical method 图解法graphical representation 图示;以图样表达graphical solution 图解growth 增长higher order derivative 高阶导数horizontal 水平的;水平hypothesis 假设identity 等(式identity matrix 恒等矩阵if and only if/iff 当且仅当;若且仅若if…, then 若….则;如果…..则illustration 例证;说明image 像点;像imaginary number 虚数implicit function 隐函数imply 蕴涵;蕴含improper integral 广义积分; 非正常积分increase 递增;增加indefinite integral 不定积分independence 独立;自变inequality 不等式;不等inequality sign 不等号infinite 无限;无穷infinite sequence 无限序列;无穷序列infinite series 无限级数;无穷级数infinitesimal 无限小;无穷小infinity 无限(大;无穷(大initial approximation 初始近似值initial condition 原始条件;初值条件initial value 初值;始值initial-value problem 初值问题inner product 内积input 输入integer 整数integral 积分integrate 积;积分;......的积分integration 积分法integration by parts 分部积分法integration by substitution 代换积分法;换元积分法interchange 互换intermediate value theorem 介值定理interpolating polynomial 插值多项式interpolation 插值interval 区间intuition 直观invalid 失效;无效invariance 不变性invariant (1不变的;(2不变量;不变式inverse 反的;逆的inverse function 反函数;逆函数inverse matrix 逆矩阵inverse problem 逆算问题invertible 可逆的invertible matrix 可逆矩阵iterate (1迭代值; (2迭代iteration 迭代iterative method 迭代法known 己知Lagrange interpolating polynomial 拉格朗日插值多项代leading coefficient 首项系数leading diagonal 主对角线lemma 引理limit 极限limit of sequence 序列的极限line of best-fit 最佳拟合line segment 线段linear 线性;一次linear convergence 线性收敛性linear differeantial equation 线性微分方程linear equation 线性方程;一次方程linear equation in two unknowns 二元一次方程;二元线性方程linearly dependent 线性相关的linearly independent 线性无关的local maximum 局部极大(值local minimum 局部极小(值logic 逻辑long division method 长除法loop 回路lower bound 下界lower triangular matrix 下三角形矩阵Maclaurin expansion 麦克劳林展开式magnitude 量;数量;长度;大小mantissa 尾数matrix 阵; 矩阵matrix addition 矩阵加法matrix equation 矩阵方程matrix multiplication 矩阵乘法matrix operation 矩阵运算maximize 极大maximum absolute error 最大绝对误差mean value theorem 中值定理method of completing square 配方法method of interpolation 插值法; 内插法method of least squares 最小二乘法; 最小平方法method of substitution 代换法;换元法method of successive substitution 逐次代换法; 逐次调替法minimize 极小minus 减modulus of a complex number 复数的模monomial 单项式multiple 倍数multiple root 多重根multiplication 乘法multiplicity 重数multiplier 乘数;乘式multiply 乘mutually independent 独立; 互相独立mutually perpendicular lines 互相垂直n factorial n阶乘n th derivative n阶导数n th root n次根;n次方根n the root of unity 单位的n次根natural logarithm 自然对数necessary and sufficient condition 充要条件necessary condition 必要条件negative 负neighborhood 邻域Newton-Cote's rule 牛顿- 高斯法则Newton-Raphson's method 牛顿- 纳逊方法Newton's formula 牛顿公式Newton's method 牛顿方法non-linear 非线性non-linear equation 非线性方程non-negative 非负的non-singular (1满秩的; (2非奇异的non-singular matrix 满秩矩阵non-trivial 非平凡的non-zero 非零norm 模方; 范数normal (1垂直的;正交的;法线的(2正态的(3正常的;正规的normalize 正规化normalized form 标准型notation 记法;记号null 零; 空null set 空集null vector 零向量number 数numerator 分子numerical method 计算方法;数值法objective function 目标函数octant 卦限odd function 奇函数one-to-one 一个对一个one-one correspondence 一一对应operation 运算order of a matrix 矩阵的阶ordinary differential equation 常微分方程origin 原点orthogonal 正交orthogonality 正交性 outcome 结果 output 输出 parameter 参数；参变量parametric equation 参数方程 partition 分割; 划分 periodic function 周期函数permutation 排列 perpendicular 垂线；垂直(于 phase 相; 位相 pivot 支点 plot 绘图plus 加 point 点 polynomial 多项式 polynomial equation 多项式方程 positive 正 post-multiply 后乘; 自右乘 premultiply 前乘; 自左乘 prime 素 product 乘积；积 proper integral 正常积分 property 性质 quadratic convergence 二阶收敛性 quadratic formula 二次公式 quadratic function 二次函数 quadratic inequality 二次不等式 quadrature 求积法 quadrilateral 四边形 quotient 商；商式 quotient rule 商法则 R.H.S 右 rank 秩 rate of convergence 收敛率 ratio 比 ; 比率 rational function 有理函数 real number 实数 real part 实部 real root 实根 reciprocal 倒数 rectangle 长方形；矩形 recurrence formula 递推公式 recurrent 循环的 recurring decimal 循环小数 reduce 简化 region 区域 region of convergency 收敛区域 regular 正；规则 relative error 相对误差 remainder term 余项root 根 rotation 旋转 rounded number 舍数 rounding(off 舍入；四舍五入 row 行；棋行 row vector 行向量; 行矢量 rule 规则；法(则 satisfy 满足；适合 scalar 纯量; 无向量, 标量 scalar matrix 纯量矩阵 scale 比例尺；标度；图尺 scientific notation 科学记数法 secant (1正割; (2割线 secant method 正割法 second derivative 二阶导数 second order ordinary differential equation 二阶常微分方程 sentence 句；语句 sequence 序列series 级数 set 集 shaded portion 有阴影部分 shape 形状 shear 位移 side 边；侧 sign 符号；记号 signed number 有符号数 significant figure 有效数字 signum 正负号函数similar 相似 simplify 简化 Simpson's integral 森逊积分 Simpson's rule 森逊法则singular 奇的 singular matrix 奇异矩阵; 不可逆矩阵 span 生成 square (1平方；(2正方形 square bracket 方括号square matrix 方(矩阵 stability 稳度 stationary 平稳 stationary point 平稳点; 逗留点; 驻点 straight line 直线 subset 子集 substitute 代入 substitution 代入; 代入法subtract 减 subtraction 减法 successive approximation 逐次逼近法 successive derivative 逐次导数 successive differentiation 逐次微分法 sufficiency 充份性 sufficient and necessary condition 充要条件 sufficient condition 充份条件 sufficiently close 充份接近suffix 下标 sum 和 summation 求和法; 总和 symbol 符号; 记号 symmetry 对称; 对称性Taylor’s expansion 泰勒展开式 term 项 transpose 移项；转置 transpose of matrix 倒置矩阵；转置矩阵 trapezium 梯形 trapezoidal integral 梯形积分 trapezoidal rule 梯形法则 trial 试；试验 triangle 三角形 triangular matrix 三角矩阵 trigonometric equation 三角方程 trigonometric function 三角函数 triple 三倍 trivial solution 平凡解truncation error 截断误差 undefined 未下定义(的 undetermined coefficient 待定系数unequal 不等 unique solution 唯一解 uniqueness 唯一性 unit 单位 unit area 单位面积unit circle 单位圆 unknown 未知数；未知量 upper bound 上界 upper limit 上限 upper triangular matrix 上三角形矩阵 validity 真确性; 有效性 variable 变项；变量；元；变元；变数 vector 向量; 矢量 vector function 向量函数; 矢量函数 vector product 矢量积; 矢量积 vector space 向量空间 verify 证明；验证 weight (1重量；(2权 weighted average, weighted mean 加权平均数 without loss of generality 不失一般性 x-axis x 轴x-coordinate x 坐标 x-intercept x 轴截距 y-axis y 轴 y-coordinate y 坐标 y-intercept y轴截距 zero 零 zero factor 零因子 zero matrix 零矩阵 zero vector 零向量 zeros of a function 函数零值。

数学相关英语单词及各种符号英语

有关基本运算：add,plus加subtract减difference差multiply,times乘product积divide除divisible可被整除的dividedevenly被整除dividend被除数divisor因子,除数quotient商remainder余数factorial阶乘power乘方radicalsign,rootsign根号roundto四舍五入tothenearest四舍五入2.有关集合union并集proper subset真子集solution set解集3.有关代数式、方程和不等式algebraic term代数项like terms,similar terms同类项numerical coefficient数字系数literal coefficient字母系数inequality不等式triangle inequality三角不等式range值域original equation原方程equivalent equation同解方程等价方程linear equation线性方程4.有关分数和小数proper fraction真分数improper fraction假分数mixed number带分数vulgar fraction,common fraction普通分数simple fraction简分数complex fraction繁分数numerator分子denominator分母leastcommon denominator最小公分母quarter四分之一decimal fraction纯小数infinite decimal无穷小数recurring decimal循环小数tenthsunit十分位arithmetic mean算术平均值weighted average加权平均值geometric mean几何平均数exponent指数,幂base乘幂的底数,底边cube立方数,立方体square root平方根cube root立方根common logarithm常用对数digit数字constant常数variable变量inversefunction反函数complementary function余函数linear一次的,线性的factorization因式分解absolute value绝对值,.｜-32｜=32round off四舍五入6.有关数论natural number自然数positive number正数negative number负数odd integer,odd number奇数even integer,even number偶数integer,whole number整数positive whole number正整数negative whole number负整数consecutive number连续整数rea lnumber,rational number实数,有理数irrationalnumber无理数inverse倒数composite number合数……prime number质数……reciprocal倒数common divisor公约数multiple倍数leastcommon multiple最小公倍数primefactor质因子common factor公因子ordinaryscale,decimalscale十进制nonnegative非负的tens十位units个位mode众数median中数common ratio公比7.数列arithmetic progressionsequence等差数列geometric progressionsequence等比数列approximate近似anticlockwise逆顺时针方向cardinal基数ordinal序数directproportion正比distinct不同的estimation估计,近似parentheses括号proportion比例permutation排列combination组合table表格trigonometric function三角函数unit单位,位几何部分1.所有的角alternate angle内错角corresponding angle同位角vertical angle对顶角central angle圆心角interior angle内角exterior angle外角supplement aryangles补角complement aryangle余角adjacent angle邻角acute angle锐角obtuse angle钝角right angle直角round angle周角straight angle平角included angle夹角2.所有的三角形equilateral triangle等边三角形scalene triangle不等边三角形isosceles triangle等腰三角形right triangle直角三角形oblique斜三角形inscribed triangle内接三角形3.有关收敛的平面图形,除三角形外semicircle半圆concentric circles同心圆quadrilateral四边形pentagon五边形hexagon六边形heptagon七边形octagon八边形nonagon九边形decagon十边形parallelogram平行四边形equilateral等边形plane平面square正方形,平方rectangle长方形regular polygon正多边形rhombus菱形trapezoid梯形4.其它平面图形arc弧line,straight line直线line segment线段parallel lines平行线segment of a circle弧形5.有关立体图形cube立方体,立方数rectangular solid长方体regular solid/regular polyhedron正多面体circular cylinder圆柱体cone圆锥sphere球体solid立体的6.有关图形上的附属物altitude高depth深度side边长circumference,perimeter周长radian弧度surface area 表面积volume体积arm直角三角形的股cros ssection横截面center of acircle圆心chord弦radius半径angle bisector角平分线diagonal对角线diameter直径edge棱face of a solid立体的面hypotenuse斜边included side夹边leg三角形的直角边medianofatriangle三角形的中线base底边,底数的5次方,2就是底数opposite直角三角形中的对边midpoint中点endpoint端点vertex复数形式vertices顶点transversal截线intercept截距7.有关坐标coordinate system坐标系rectangular coordinate直角坐标系origin原点abscissa横坐标ordinate纵坐标numberline数轴quadrant象限slope斜率complex plane复平面8.其它plane geometry平面几何trigonometry三角学bisect平分circumscribe外切inscribe内切intersect相交perpendicular垂直pythagorean theorem勾股定理congruent全等的multilateral多边的+plus加号；正号-minus减号；负号±plus or minus正负号×is multiplied by乘号÷is divided by除号＝is equal to等于号≠is not equal to不等于号≡is equivalent to全等于号≌is equal to or approximately equal to等于或约等于号≈is approximately equal to约等于号＜is less than小于号＞is greater than大于号≮is not less than不小于号≯is not more than不大于号≤is less than or equal to小于或等于号≥is more than or equal to大于或等于号%per cent百分之…‰per mill千分之…∞infinity无限大号∝varies as与…成比例√square root平方根∵since; because因为∴hence所以∷equals, as proportion等于,成比例∠angle角⊙circle圆○circumference圆周πpi 圆周率△triangle三角形⊥perpendicular to垂直于∪union of并,合集∩intersection of 交,通集∫the integral of …的积分∑sigma summation of总和°degree度′minute分″second秒℃Celsius system摄氏度{open brace, open curly左花括号}close brace, close curly右花括号open parenthesis, open paren左圆括号close parenthesis, close paren右圆括号brakets/ parentheses括号open bracket 左方括号close bracket 右方括号square brackets方括号.period, dot句号,点|vertical bar, vertical virgule竖线&ampersand, and, reference, ref和,引用asterisk, multiply, star, pointer星号,乘号,星,指针/slash, divide, oblique 斜线,斜杠,除号full stop句号,comma逗号:colon冒号;semicolon分号question mark问号exclamation mark 英式英语exclamation point 美式英语'apostrophe撇号-hyphen连字号-- dash 破折号...dots/ ellipsis省略号"single quotation marks 单引号""double quotation marks 双引号‖parallel 双线号&ampersand = and～swung dash 代字号§section; division 分节号→arrow 箭号；参见号。

高等数学(微积分学)专业术语名词、概念、定理等英汉对照.

目录第一部分英汉微积分词汇Part 1 English-Chinese Calculus Vocabulary第一章函数与极限Chapter 1 function and Limit (1)第二章导数与微分Chapter 2 Derivative and Differential (2)第三章微分中值定理Chapter 3 Mean Value theorem of differentials and theApplicati on of Derivatives (3)第四章不定积分Chapter 4 Indefinite Intergrals (3)第五章定积分Chapter 5 Definite Integral (3)第六章定积分的应用Chapter 6 Application of the Definite Integrals (4)第七章空间解析几何与向量代数Chapter 7 Space Ana lytic Geomertry and Vector Algebra (4)第八章多元函数微分法及其应用Chapter 8 Differentiation of functions Several variablesand Its Application (5)第九章重积分Multiple Integrals (6)第十章曲线积分与曲面积分Chapter 10 Line(Curve ) Integrals and Sur face Integrals……………………6 第十一章无穷级数Chapter 11 Infinite Series……………………………………………………6 第十二章微分方程Chapter 12 Differential Equation (7)第二部分定理定义公式的英文表达 Part 2 English Expression for Theorem, Definition and Formula第一章函数与极限Chapter 1 Function and L imit (19)1.1 映射与函数(Mapping and Function ) (19)1.2 数列的极限(Limit of the Sequence of Number) (20)1.3 函数的极限(Limit of Function) (21)1.4 无穷小与无穷大(Infinitesimal and Inifinity) (23)1.5 极限运算法则(Operation Rule of L imit) (24)1.6 极限存在准则两个重要的极限(Rule for theExistence of Limits Two Important Limits) (25)1.7 无穷小的比较(The Comparison of infinitesimal) (26)1.8 函数的连续性与间断点(Continuity of FunctionAnd Discontinuity Points) (28)1.9 连续函数的运酸与初等函数的连续性(OperationOf Continuous Functions and Continuity ofElementary Functions) (28)1.10 闭区间上联系汗水的性质(Properties ofContinuous Functions on a Closed Interval) (30)第二章导数与数分Chapter2 Derivative and Differential (31)2.1 导数的概念(The Concept of Derivative) (31)2.2 函数的求导法则(Rules for Finding Derivatives) (33)2.3 高阶导数(Higher-order Derivatives) (34)2.4 隐函数及由参数方程所确定的函数的导数相关变化率(Derivatives of Implicit Functions and Functions Determined by Parametric Equation and Correlative Change Rate) (34)2.5 函数的微分(Differential of a Function) (35)第三章微分中值定理与导数的应用Chapter 3 Mean Value Theorem of Differentials and theApplication of Derivatives (36)3.1 微分中值定理(The Mean Value Theorem) (36)3.2 洛必达法则(L’Hopital’s Rule) (38)3.3 泰勒公式(Taylor’s Formula) (41)3.4 函数的单调性和曲线的凹凸性(Monotonicityof Functions and Concavity of Curves) (43)3.5 函数的极值与最大最小值(Extrema, Maximaand Minima of Functions) (46)3.6 函数图形的描绘(Graphing Functions) (49)3.7 曲率(Curvature) (50)3.8 方程的近似解(Solving Equation Numerically) (53)第四章不定积分Chapter 4 Indefinite Integrals (54)4.1 不定积分的概念与性质(The Concept andProperties of Indefinite Integrals) (54)4.2 换元积分法(Substitution Rule for Indefinite Integrals) (56)4.3 分部积分法(Integration by Parts) (57)4.4 有理函数的积分(Integration of Rational Functions) (58)第五章定积分Chapter 5 Definite Integrals (61)5.1 定积分的概念和性质(Concept of Definite Integraland its Properties) (61)5.2 微积分基本定理(Fundamental Theorem of Calculus) (67)5.3 定积分的换元法和分部积分法(Integration by Substitution andDefinite Integrals by Parts) (69)5.4 反常积分(Improper Integrals) (70)第六章定积分的应用Chapter 6 Applications of the Definite Integrals (75)6.1 定积分的元素法(The Element Method of Definite Integra (75)6.2 定积分在几何学上的应用(Applications of the DefiniteIntegrals to Geometry) (76)6.3 定积分在物理学上的应用(Applications of the DefiniteIntegrals to Physics) (79)第七章空间解析几何与向量代数Chapter 7 Space Analytic Geometry and Vector Algebar (80)7.1 向量及其线性运算(Vector and Its Linear Operation) (80)7.2 数量积向量积(Dot Produc t and Cross Product) (86)7.3 曲面及其方程(Surface and Its Equation) (89)7.4 空间曲线及其方程(The Curve in Three-space and Its Equation (91)7.5 平面及其方程（Plane in Space and Its Equation) (93)7.6 空间直线及其方程（Lines in and Their Equations) (95)第八章多元函数微分法及其应用Chapter 8 Differentiation of Functions of SeveralVariables and Its Application (99)8.1 多元函数的基本概念（The Basic Concepts of Functionsof Several Variables) (99)8.2 偏导数(Partial Derivative) (102)8.3 全微分(Total Differential) (103)8.4 链式法则（The Chain Rule) (104)8.5 隐函数的求导公式(Derivative Formula for Implicit Functions). (104)8.6 多元函数微分学的几何应用(Geometric Applications of Differentiationof Ffunctions of Severalvariables) (106)8.7方向导数与梯度(Directional Derivatives and Gradients) (107)8.8多元函数的极值(Extreme Value of Functions of Several Variables) (108)第九章重积分Chapter 9 Multiple Integrals (111)9.1二重积分的概念与性质(The Concept of Double Integralsand Its Properities) (111)9.2二重积分的计算法(Evaluation of double Integrals) (114)9.3三重积分(Triple Integrals) (115)9.4重积分的应用(Applications of Multiple Itegrals) (120)第十章曲线积分与曲面积分Chapte 10 Line Integrals and Surface Integrals………………………………121 10.1 对弧长的曲线积分(line Intergrals with Respect to Arc Length) ………121 10.2 对坐标的曲线积分(Line Integrals with respect toCoordinate Variables) ……………………………………………………123 10.3 格林公式及其应用(Green's Formula and Its Applications) ………………124 10.4 对面积的曲面积分(Surface Integrals with Respect to Aarea) ……………126 10.5 对坐标的曲面积分(Surface Integrals with Respect toCoordinate Variables) ………………………………………………………128 10.6 高斯公式通量与散度(Gauss's Formula Flux and Divirgence) …… 130 10.7 斯托克斯公式环流量与旋度(Stokes's Formula Circulationand Rotation) (131)第十一章无穷级数Chapter 11 Infinite Series (133)11.1 常数项级数的概念与性质(The concept and Properties ofThe Constant series) ………………………………………………………133 11.2 常数项级数的审敛法(Test for Convergence of the Constant Series) ……137 11.3 幂级数(powe r Series). ……………………………………………………143 11.4 函数展开成幂级数(Represent the Function as Power Series) ……………148 11.5 函数的幂级数展开式的应用(the Appliacation of the Power Seriesrepresentation of a Function) (148)11.6 函数项级数的一致收敛性及一致收敛级数的基本性质(The Unanimous Convergence of the Ser ies of Functions and Its properties) (149)11.7 傅立叶级数（Fourier Series）.............................................152 11.8 一般周期函数的傅立叶级数(Fourier Series of Periodic Functions) (153)第十二章微分方程Chapter 12 Differential Equation……………………………………………155 12.1 微分方程的基本概念（The Concept of DifferentialEqu ation) ……155 12.2 可分离变量的微分方程(Separable Differential Equation) ………156 12.3 齐次方程(Homogeneous Equation) ………………………………156 12.4 一次线性微分方程(Linear Differential Equation of theFirst Order) (157)12.5 全微分方程(Total Differential Equation) …………………………158 12.6 可降阶的高阶微分方程(Higher-order DifferentialEquation Turned to Lower-order DifferentialEquation) (159)12.7 高阶线性微分方程(Linear Differential Equation of Higher Order) …159 12.8 常系数齐次线性微分方程(Homogeneous LinearDifferential Equation with Constant Coefficient) (163)12.9 常系数非齐次线性微分方程(Non HomogeneousDifferential Equation with Constant Coefficient) (164)12.10 欧拉方程(Euler Equation) …………………………………………164 12.11 微分方程的幂级数解法(Power Series Solutionto Differential Equation) (164)第三部分常用数学符号的英文表达Part 3 English Expression of the Mathematical Symbol in Common Use第一部分英汉微积分词汇Part1 English-Chinese Calculus Vocabulary映射 mappingX到Y的映射 mapping of X ontoY 满射 surjection 单射 injection一一映射 one-to-one mapping 双射 bijection 算子 operator变化 transformation 函数 function逆映射 inverse mapping复合映射 composite mapping 自变量 independent variable 因变量 dependent variable 定义域 domain函数值 value of function 函数关系 function relation 值域 range自然定义域 natural domain 单值函数 single valued function 多值函数 multiple valued function 单值分支 one-valued branch 函数图形 graph of a function 绝对值函数 absolute value 符号函数 sigh function 整数部分 integral part 阶梯曲线 step curve 第一章函数与极限Chapter1 Function and Limit 集合 set元素 element 子集 subset 空集 empty set 并集 union交集 intersection 差集 difference of set 基本集 basic set补集 complement set 直积 direct product笛卡儿积 Cartesian product 开区间 open interval 闭区间 closed interval 半开区间half open interval 有限区间 finite interval区间的长度 length of an interval 无限区间 infinite interval 领域 neighborhood领域的中心 centre of a neighborhood 领域的半径 radius of a neighborhood 左领域left neighborhood 右领域 right neighborhood当且仅当 if and only if(iff) 分段函数 piecewise function 上界 upper bound 下界lower bound 有界 boundedness 无界 unbounded函数的单调性 monotonicity of a function 单调增加的 increasing 单调减少的decreasing单调函数 monotone function函数的奇偶性 parity(odevity) of a function对称 symmetry 偶函数 even function 奇函数 odd function函数的周期性 periodicity of a function 周期 period反函数 inverse function 直接函数 direct function 复合函数 composite function 中间变量 intermediate variable 函数的运算 operation of function基本初等函数 basic elementary function 初等函数 elementary function 幂函数 power function指数函数 exponential function 对数函数 logarithmic function 三角函数 trigonometric function反三角函数 inverse trigonometric function 常数函数 constant function 双曲函数hyperbolic function 双曲正弦 hyperbolic sine 双曲余弦 hyperbolic cosine 双曲正切hyperbolic tangent反双曲正弦 inverse hyperbolic sine 反双曲余弦 inverse hyperbolic cosine 反双曲正切 inverse hyperbolic tangent 极限 limit数列 sequence of number 收敛 convergence 收敛于 a converge to a 发散 divergent极限的唯一性 uniqueness of limits收敛数列的有界性 boundedness of aconvergent sequence子列 subsequence函数的极限 limits of functions函数f(x)当x趋于x0时的极限 limit of functions f(x) as x approaches x0 左极限 left limit 右极限 right limit单侧极限 one-sided limits水平渐近线 horizontal asymptote 无穷小 infinitesimal 无穷大 infinity铅直渐近线 vertical asymptote 夹逼准则 squeeze rule单调数列 monotonic sequence高阶无穷小 infinitesimal of higher order 低阶无穷小 infinitesimal of lower order 同阶无穷小 infinitesimal of the same order 等阶无穷小 equivalent infinitesimal 函数的连续性 continuity of a function 增量 increment函数f(x)在x0连续 the function f(x) is continuous at x0左连续 left continuous 右连续 right continuous区间上的连续函数 continuous function 函数f(x)在该区间上连续 function f(x) is continuous on an interval 不连续点 discontinuity point第一类间断点 discontinuity point of the first kind第二类间断点 discontinuity point of the second kind初等函数的连续性 continuity of the elementary functions定义区间 defined interval最大值 global maximum value (absolute maximum)最小值 global minimum value (absolute minimum)零点定理 the zero point theorem介值定理 intermediate value theorem 第二章导数与微分Chapter2 Derivative and Differential 速度 velocity匀速运动 uniform motion 平均速度 average velocity瞬时速度 instantaneous velocity 圆的切线 tangent line of a circle 切线 tangent line切线的斜率 slope of the tangent line 位置函数 position function 导数 derivative 可导derivable函数的变化率问题 problem of the change rate of a function导函数 derived function 左导数 left-hand derivative 右导数 right-hand derivative 单侧导数 one-sided derivativesf(x)在闭区间【a,b】上可导 f(x)isderivable on the closed interval [a,b] 切线方程 tangent equation 角速度 angular velocity 成本函数 cost function 边际成本 marginal cost 链式法则 chain rule隐函数 implicit function 显函数 explicit function 二阶函数 second derivative 三阶导数 third derivative 高阶导数 nth derivative莱布尼茨公式 Leibniz formula 对数求导法 log- derivative 参数方程 parametric equation 相关变化率 correlative change rata 微分 differential 可微的 differentiable 函数的微分 differential of function自变量的微分 differential of independent variable微商 differential quotient间接测量误差 indirect measurement error 绝对误差 absolute error相对误差 relative error第三章微分中值定理与导数的应用Chapter3 MeanValue Theorem of Differentials and the Application of Derivatives 罗马定理Rolle’s theorem 费马引理Fermat’s lemma拉格朗日中值定理Lagrange’s mean value theorem驻点 stationary point 稳定点 stable point 临界点 critical point辅助函数 auxiliary function拉格朗日中值公式Lagrange’s mean value formula柯西中值定理Cauchy’s mean value theorem洛必达法则L’Hospital’s Rule0/0型不定式 indeterminate form of type 0/0不定式 indeterminate form泰勒中值定理Taylor’s mean value theorem泰勒公式 Taylor formula 余项 remainder term拉格朗日余项 Lagrange remainder term 麦克劳林公式Maclaurin’s formula 佩亚诺公式 Peano remainder term 凹凸性 concavity凹向上的 concave upward, cancave up 凹向下的，向上凸的concave downward’ concave down拐点 inflection point函数的极值 extremum of function 极大值 local(relative) maximum 最大值global(absolute) mximum 极小值 local(relative) minimum 最小值 global(absolute) minimum 目标函数 objective function 曲率 curvature弧微分 arc differential平均曲率 average curvature 曲率园 circle of curvature 曲率中心 center of curvature 曲率半径 radius of curvature渐屈线 evolute 渐伸线 involute根的隔离 isolation of root 隔离区间 isolation interval 切线法 tangent line method第四章不定积分Chapter4 Indefinite Integrals原函数 primitive function(antiderivative) 积分号 sign of integration 被积函数integrand积分变量 integral variable 积分曲线 integral curve 积分表 table of integrals换元积分法 integration by substitution 分部积分法 integration by parts分部积分公式 formula of integration by parts有理函数 rational function 真分式 proper fraction 假分式 improper fraction第五章定积分Chapter5 Definite Integrals 曲边梯形 trapezoid with 曲边 curve edge窄矩形 narrow rectangle曲边梯形的面积 area of trapezoid with curved edge积分下限 lower limit of integral 积分上限 upper limit of integral 积分区间 integral interval 分割 partition积分和 integral sum 可积 integrable矩形法 rectangle method积分中值定理 mean value theorem of integrals函数在区间上的平均值 average value of a function on an integvals牛顿－莱布尼茨公式 Newton-Leibniz formula微积分基本公式 fundamental formula of calculus换元公式 formula for integration by substitution递推公式 recurrence formula 反常积分 improper integral反常积分发散 the improper integral is divergent反常积分收敛 the improper integral is convergent无穷限的反常积分 improper integral on an infinite interval无界函数的反常积分 improper integral of unbounded functions绝对收敛 absolutely convergent第六章定积分的应用Chapter6 Applications of the Definite Integrals元素法 the element method 面积元素 element of area平面图形的面积 area of a luane figure 直角坐标又称“笛卡儿坐标 (Cartesian coordinates)”极坐标 polar coordinates 抛物线 parabola 椭圆 ellipse旋转体的面积 volume of a solid of rotation旋转椭球体 ellipsoid of revolution, ellipsoid of rotation曲线的弧长 arc length of acurve 可求长的 rectifiable 光滑 smooth 功 work水压力 water pressure 引力 gravitation 变力 variable force第七章空间解析几何与向量代数Chapter7 Space Analytic Geometry and Vector Algebra向量 vector自由向量 free vector 单位向量 unit vector 零向量 zero vector 相等 equal 平行parallel向量的线性运算 linear poeration of vector 三角法则 triangle rule平行四边形法则 parallelogram rule 交换律 commutative law 结合律 associative law 负向量 negative vector 差 difference分配律 distributive law空间直角坐标系 space rectangular coordinates坐标面 coordinate plane 卦限 octant向量的模 modulus of vector向量a与b的夹角 angle between vector a and b方向余弦 direction cosine 方向角 direction angle向量在轴上的投影 projection of a vector onto an axis数量积，外积，叉积 scalar product,dot product,inner product曲面方程 equation for a surface 球面 sphere旋转曲面 surface of revolution 母线 generating line 轴 axis圆锥面 cone 顶点 vertex旋转单叶双曲面 revolution hyperboloids of one sheet旋转双叶双曲面 revolution hyperboloids of two sheets柱面 cylindrical surface ,cylinder 圆柱面 cylindrical surface 准线 directrix抛物柱面 parabolic cylinder 二次曲面 quadric surface 椭圆锥面 dlliptic cone 椭球面ellipsoid单叶双曲面 hyperboloid of one sheet 双叶双曲面 hyperboloid of two sheets 旋转椭球面 ellipsoid of revolution 椭圆抛物面 elliptic paraboloid旋转抛物面 paraboloid of revolution 双曲抛物面 hyperbolic paraboloid 马鞍面 saddle surface椭圆柱面 elliptic cylinder 双曲柱面 hyperbolic cylinder 抛物柱面 parabolic cylinder 空间曲线 space curve空间曲线的一般方程 general form equations of a space curve空间曲线的参数方程 parametric equations of a space curve 螺转线 spiral 螺矩 pitch 投影柱面 projecting cylinder 投影 projection平面的点法式方程 pointnorm form eqyation of a plane法向量 normal vector平面的一般方程 general form equation of a plane两平面的夹角 angle between two planes 点到平面的距离 distance from a point to a plane空间直线的一般方程 general equation of a line in space方向向量 direction vector直线的点向式方程 pointdirection form equations of a line方向数 direction number直线的参数方程 parametric equations of a line两直线的夹角 angle between two lines 垂直 perpendicular直线与平面的夹角 angle between a line and a planes平面束 pencil of planes平面束的方程 equation of a pencil of planes行列式 determinant系数行列式 coefficient determinant第八章多元函数微分法及其应用Chapter8 Differentiation of Functions of Several Variables and Its Application 一元函数 function of one variable 多元函数 function of several variables 内点 interior point 外点 exterior point 边界点 frontier point,boundary point 聚点 point of accumulation 开集 openset 闭集 closed set 连通集 connected set 开区域 open region 闭区域 closed region有界集 bounded set 无界集 unbounded setn维空间 n-dimentional space 二重极限 double limit 多元函数的连续性 continuity of function of seveal 连续函数 continuous function 不连续点 discontinuity point 一致连续 uniformly continuous 偏导数 partial derivative 对自变量x的偏导数 partial derivative with respect to independent variable x 高阶偏导数 partial derivative of higher order 二阶偏导数 second order partial derivative 混合偏导数 hybrid partial derivative 全微分 total differential 偏增量 oartial increment 偏微分 partial differential 全增量 total increment 可微分 differentiable 必要条件 necessary condition充分条件 sufficient condition 叠加原理 superpostition principle 全导数 total derivative中间变量 intermediate variable 隐函数存在定理 theorem of the existence of implicit function 曲线的切向量 tangent vector of a curve 法平面 normal plane 向量方程vector equation 向量值函数 vector-valued function 切平面 tangent plane 法线 normal line 方向导数 directional derivative梯度 gradient数量场 scalar field 梯度场 gradient field 向量场 vector field 势场 potential field 引力场 gravitational field 引力势 gravitational potential 曲面在一点的切平面 tangent plane to asurface at a point 曲线在一点的法线 normal line to asurface at a point 无条件极值 unconditional extreme values 条件极值 conditional extreme values 拉格朗日乘数法 Lagrange multiplier method 拉格朗日乘子 Lagrange multiplier 经验公式 empirical formula 最小二乘法 method of least squares 均方误差mean square error 第九章重积分 Chapter9 Multiple Integrals 二重积分 double integral 可加性 additivity累次积分 iterated integral 体积元素 volume element 三重积分 triple integral 直角坐标系中的体积元素 volumeelement in rectangular coordinate system 柱面坐标 cylindrical coordinates 柱面坐标系中的体积元素 volumeelement in cylindrical coordinate system 球面坐标 spherical coordinates 球面坐标系中的体积元素 volumeelement in spherical coordinate system 反常二重积分 improper double integral 曲面的面积 area of a surface 质心 centre of mass 静矩 static moment 密度 density 形心centroid 转动惯量 moment of inertia 参变量 parametric variable 第十章曲线积分与曲面积分Chapter10 Line(Curve)Integrals and Surface Integrals对弧长的曲线积分 line integrals with respect to arc hength第一类曲线积分 line integrals of the first type对坐标的曲线积分 line integrals with respect to x,y,and z第二类曲线积分 line integrals of the second type有向曲线弧 directed arc单连通区域 simple connected region 复连通区域 complex connected region 格林公式Green formula第一类曲面积分 surface integrals of the first type对面的曲面积分 surface integrals with respect to area有向曲面 directed surface对坐标的曲面积分 surface integrals with respect to coordinate elements第二类曲面积分 surface integrals of the second type有向曲面元 element of directed surface 高斯公式 gauss formula拉普拉斯算子 Laplace operator 格林第一公式Green’s first formula 通量 flux散度 divergence斯托克斯公式 Stokes formula 环流量 circulation 旋度 rotation,curl第十一章无穷级数Chapter11 Infinite Series 一般项 general term 部分和 partial sum 余项 remainder term 等比级数 geometric series 几何级数 geometric series 公比 common ratio调和级数 harmonic series柯西收敛准则 Cauchy convergence criteria, Cauchy criteria for convergence 正项级数series of positive terms 达朗贝尔判别法D’Alembert test 柯西判别法 Cauchy test交错级数 alternating series 绝对收敛 absolutely convergent 条件收敛 conditionally convergent 柯西乘积 Cauchy product 函数项级数 series of functions 发散点 point of divergence 收敛点 point of convergence 收敛域 convergence domain 和函数 sum function 幂级数 power series幂级数的系数 coeffcients of power series 阿贝尔定理 Abel Theorem收敛半径 radius of convergence 收敛区间 interval of convergence 泰勒级数 Taylor series麦克劳林级数 Maclaurin series 二项展开式 binomial expansion 近似计算approximate calculation舍入误差 round-off error,rounding error 欧拉公式Euler’s formula魏尔斯特拉丝判别法 Weierstrass test 三角级数 trigonometric series 振幅 amplitude 角频率 angular frequency 初相 initial phase 矩形波 square wave谐波分析 harmonic analysis 直流分量 direct component 基波 fundamental wave 二次谐波 second harmonic三角函数系 trigonometric function system 傅立叶系数 Fourier coefficient 傅立叶级数 Forrier series 周期延拓 periodic prolongation 正弦级数 sine series 余弦级数cosine series 奇延拓 odd prolongation 偶延拓 even prolongation傅立叶级数的复数形式 complex form of Fourier series第十二章微分方程Chapter12 Differential Equation解微分方程 solve a dirrerential equation 常微分方程 ordinary differential equation偏微分方程 partial differential equation,PDE微分方程的阶 order of a differential equation微分方程的解 solution of a differential equation微分方程的通解 general solution of a differential equation初始条件 initial condition微分方程的特解 particular solution of a differential equation初值问题 initial value problem微分方程的积分曲线 integral curve of a differential equation可分离变量的微分方程 variable separable differential equation隐式解 implicit solution隐式通解 inplicit general solution 衰变系数 decay coefficient 衰变 decay齐次方程 homogeneous equation一阶线性方程 linear differential equation of first order非齐次 non-homogeneous齐次线性方程 homogeneous linear equation非齐次线性方程 non-homogeneous linear equation常数变易法 method of variation of constant暂态电流 transient stata current 稳态电流 steady state current 伯努利方程 Bernoulli equation全微分方程 total differential equation 积分因子 integrating factor高阶微分方程 differential equation of higher order悬链线 catenary高阶线性微分方程 linera differentialequation of higher order自由振动的微分方程 differential equation of free vibration强迫振动的微分方程 differential equation of forced oscillation串联电路的振荡方程 oscillation equation of series circuit二阶线性微分方程 second order linera differential equation线性相关 linearly dependence 线性无关 linearly independce二阶常系数齐次线性微分方程 second order homogeneour linear differential equation with constant coefficient二阶变系数齐次线性微分方程 second order homogeneous linear differential equation with variable coefficient 特征方程 characteristic equation无阻尼自由振动的微分方程 differential equation of free vibration with zero damping 固有频率 natural frequency简谐振动 simple harmonic oscillation,simple harmonic vibration微分算子 differential operator待定系数法 method of undetermined coefficient共振现象 resonance phenomenon 欧拉方程 Euler equation幂级数解法 power series solution 数值解法 numerial solution 勒让德方程 Legendre equation微分方程组 system of differential equations常系数线性微分方程组 system of linera differential equations with constant coefficient第二部分定理定义公式的英文表达Part2 English Expression for Theorem, Definition and Formula第一章函数与极限Chapter 1 Function and Limit1.1 映射与函数 (Mapping and Function)一、集合 (Set)二、映射 (Mapping)映射概念 (The Concept of Mapping) 设X, Y是两个非空集合 , 如果存在一个法则f，使得对X中每个元素x，按法则f，在Y中有唯一确定的元素y与之对应 ,则称f为从X到 Y的映射 , 记作f:X→Y。

sci文章数学符号

sci文章数学符号
在SCI发表的论文中，常常使用一些特定的符号来表示数学、物理、化学等领域的概念。

以下是一些科研论文中SCI常用的符号，以及它们的中文解释：
1.数学符号：
–∑（Sigma）：表示求和。

–∫（Integral）：表示积分。

–α、β、γ：表示变量。

–Δ（Delta）：表示差异或变化。

–θ（Theta）：表示角度。

2.物理学符号：
–c：表示光速。

–λ（Lambda）：表示波长。

–E：表示能量。

–h：表示普朗克常数。

–μ：表示磁导率。

3.化学符号：
–H₂O：表示水分子。

–CO₂：表示二氧化碳。

–NaCl：表示氯化钠（食盐）。

–C₆H₁₂O₆：表示葡萄糖。

4.统计学符号：
–μ（Mu）：表示总体均值。

–σ（Sigma）：表示总体标准差。

–X̄（X-bar）：表示样本均值。

–s：表示样本标准差。

5.生物学符号：
–DNA：表示脱氧核糖核酸。

–RNA：表示核糖核酸。

–ATP：表示三磷酸腺苷。

–β：表示生物学中的倍增因子。

6.工程学符号：
–ω（Omega）：表示角速度。

–V：表示电压。

–I：表示电流。

–R：表示电阻。

数学常用英文词汇表

数学常用英文词汇表本文介绍了数学常用的英文词汇，包括数学符号、运算、函数、几何、代数、微积分、概率统计等方面的内容。

文章使用表格的形式，将中文和英文对照列出，方便读者学习和记忆。

文章还提供了一些例句和注释，帮助读者理解和运用这些词汇。

一、数学符号中文英文例句等于equal to, equals, is equal to2+3=5 Two plus three equals five.不等于not equal to, is not equal to2+3≠4 Two plus three is not equal to four.大于greater than, is greater than5>4 Five is greater than four.小于less than, is less than4<5 Four is less than five.大于等于greater than or equal to, is greater than or equalto5≥4 Five is greater than or equal to four.小于等于less than or equal to, is less than or equal to4≤5 Four is less than or equal to five.加号plus sign, plus2+3=5 Two plus three equals five.减号minus sign, minus5-3=2 Five minus three equals two.乘号multiplication sign, times2×3=6 Two times three equals six.除号division sign, divided by6÷3=2 Six divided by three equals two.等号equal sign, equals sign2+3=5 Two plus three equals five.不等号inequality sign, inequality symbol2+3≠4 Two plus three is not equal to four.括号parentheses, brackets(2+3)×4=20 (Two plus three) times four equalstwenty.方括号square brackets, brackets[a,b]表示闭区间[a,b] means a closed interval.花括号curly brackets, braces{x绝对值符号absolute value sign, modulus sign|x|=y表示x的绝对值等于y注释：在英语中，有时会用is来表示等于，如2+3 is 5，但更常用的是equals。

主要数学符号(English)

主要数学符号的英文读法+ plus 加号；正号- minus 减号；负号± plus or minus 正负号× multiplied by 乘号÷ divided by 除号＝be equal to 等于号≠be not equal to 不等于号≡be equivalent to 全等于号≌ be equal to or approximately equal to 等于或约等于号≈be approximately equal to 约等于号＜be less than 小于号＞be more than 大于号≮be not less than 不小于号≯be not more than 不大于号≤be less than or equal to 小于或等于号≥be more than or equal to 大于或等于号% per cent 百分之…‰ per mille 千分之…∞infinity 无限大号∝varies as 与…成比例√(square) root 平方根∵since; because 因为∴hence 所以∷equals, as (proportion) 等于，成比例∠angle 角⌒semicircle 半圆⊙circle 圆○circumference 圆周πpi 圆周率△triangle 三角形⊥perpendicular to 垂直于∪union of 并，合集∩intersection of 交，通集∫the integral of …的积分∑(sigma) summation of 总和° degree 度′minute 分〃second 秒℃Celsius system 摄氏度() round brackets(parentheses)[] square brackets{} braces( open parenthesis, open paren 左圆括号) close parenthesis, close paren 右圆括号[ open bracket 左方括号] close bracket 右方括号{ open brace, open curly 左花括号} close brace, close curly 右花括号《》 French quotes 法文引号;书名号. period, dot 句号，点| vertical bar, vertical virgule 竖线ǁparallel 双线号& ampersand, and, reference, ref 和，引用/ slash, divide, oblique, virgule 斜线，斜杠，除号// slash-slash, comment 双斜线，注释符# pound 井号\ backslash, sometimes escape 反斜线转义符，有时表示转义符或续行符~ tilde 波浪符. full stop 句号, comma 逗号: colon 冒号; semicolon 分号? question mark 问号! exclamation mark (英式英语) exclamation point (美式英语)' apostrophe 撇号- hyphen 连字号-- dash 破折号... dots/ ellipsis 省略号" single quotation marks 单引号"" double quotation marks 双引号§ section; division 分节号→arrow 箭号；参见号_ underscore 下划线¨ tandem colon 双点号" ditto同上符号～swung dash 代字号LognX logx to the base nf(x) the function of xdx diffrencial of xx+y x plus y(a+b) bracket a plus b bracket closeda=b a equals ba≠b a isn't equal to ba>b a is greater than ba>>b a is much greater than ba≥b a is greater than or equal to bx→∞x approches infinityx2 x squarex3 x cubexn the nth power of x√￣x the square root of x3√￣x the cube root of xn√￣x the nth root of x6 % 6 percent3‰ 3 per mille3‰ three peimilln∑i=1xi the summation of x where x goes from 1to nn∏i=1xi the product of x sub i where igoes from 1to n∫ab integral betweens a and b>> is approximately equal to( ) round brackets; parentheses[ ] square brackets{ } braces2 :3 the ratio of two to threeD x or d x the increment of xdx differential xdy/dx the first derivative of y with respect to x1/2 a half; one half2/3 two thirds5/123 five over a hundred and twenty-three0.01 O point O one; zero point zero one; nought point nought one r=xd r equals x multiplied by d5* 2=10 five times two equals tenx3/8=y2 x raised to the third power divided by eight equals y squared (a+b-c* d)/e=f a plus b minus c multiplied by d all divided by e equals fy = (Wt-W)/x y equals W sub t minus W over xΑ α alpha alfa 阿耳法 Β β beta beta 贝塔 Γ γ gamma gamma 伽马 Δ δ delta delta 德耳塔 Ε ε epsilon epsilon 艾普西隆 Ζ ζ zeta zeta 截塔 Η η eta eta 艾塔 Θ θ theta θita 西塔 Ι ι iota iota 约塔 Κ κ kappa kappa 卡帕 ∧ λ lambda lambda 兰姆达 Μ μ mu miu 缪 Ν ν nu niu 纽 Ξ ξ xi ksi 可塞 Ο ο omicron omikron 奥密可戎 ∏ π pi pai 派 Ρ ρ rho rou 柔 ∑ σ sigma sigma 西格马 Τ τ tau tau 套 Υ υ upsilon jupsilon 衣普西隆 Φ φ phi fai 斐 Χ χ chi khai 喜 Ψ ψ psi psai 普西 Ω ω omega omiga 欧米伽。

常用数学符号英文对照

常用数学符号英文对照Basic math symbolsSymbol Symbol Name Meaning / definition Example= equals sign equality 5 = 2+35 is equal to 2+3≠not equal sign inequality 5 ≠ 45 is not equal to 4≈approximatelyequal approximationsin(0.01) ≈ 0.01,x≈y means x isapproximately equal to y> strictinequality greater than5 > 45 is greater than 4< strictinequality less than4 < 54 is less than 5≥inequality greater than or equal to 5 ≥ 4,x≥y means x is greater than or equal to y≤inequality less than or equal to 4 ≤ 5,x ≤ y means x is greater than or equal to y( ) parentheses calculate expression insidefirst2 × (3+5) = 16[ ] brackets calculate expression insidefirst[(1+2)×(1+5)] = 18 + plus sign addition 1 + 1 = 2−minus sign subtraction 2 − 1 = 1±plus - minus both plus and minusoperations3 ± 5 = 8 and -2±minus - plus both minus and plusoperations3 ± 5 = -2 and 8* asterisk multiplication 2 * 3 = 6×times sign multiplication 2 × 3 = 6·multiplicationdotmultiplication 2 · 3 = 6÷division sign /obelusdivision 6 ÷ 2 = 3/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimalseparator2.56 = 2+56/100a b power exponent 23= 8a^b caret exponent 2 ^ 3= 8√a square root √a ·√a = a√9 = ±33√a cube root 3√a ·3√a ·3√a = a3√8 = 24√a fourth root 4√a ·4√a ·4√a ·4√a = a4√16 = ±2n√a n-th root(radical)for n=3, n√8 = 2 % percent1% = 1/100 10% × 30 = 3‰per-mille1‰ = 1/1000 = 0.1% 10‰× 30 = 0.3 ppm per-million1ppm = 1/1000000 10ppm × 30 = 0.0003 ppb per-billion 1ppb = 1/1000000000 10ppb × 30 = 3×10-7 ppt per-trillion 1ppt = 10-1210ppt × 30 = 3×10-10Geometry symbolsSymbolSymbol NameMeaning / definitionExample∠angle formed by two rays ∠ABC = 30°measured angle ABC = 30°sphericalangleAOB = 30°∟ right angle = 90° α = 90°°degree 1 turn = 360° α = 60° deg degree1 turn = 360degα = 60deg ′ primearcminute, 1° = 60′α = 60°59′ ″double prime arcsecond, 1′ = 60″α = 60°59′59″line infinite lineABline segment line from point A to point Bray line that start from point Aarc arc from point A to point B= 60° ⊥perpendicular perpendicular lines (90° angle)AC ⊥ BC| | parallel parallel lines AB | | CD ≅ congruent toequivalence of geometric shapes and size∆ABC ≅ ∆XYZ~similarity same shapes, not same size∆ABC~ ∆XYZΔtriangle triangle shape ΔABC≅ΔBCD|x-y|distance distance between points x and y | x-y| = 5πpi constant π= 3.141592654...is the ratio between the circumference anddiameter of a circlec= π·d= 2·π·rrad radians radians angle unit 360° = 2πradc radians radians angle unit360° = 2πcgrad gradians / gons grads angle unit 360° = 400 gradg gradians / gons grads angle unit360° =400 g Algebra symbolsSymbol Symbol Name Meaning /definitionExamplex x variable unknown valueto findwhen 2x= 4, then x= 2 ≡equivalence identical to≜equal by definition equal bydefinition:= equal by definition equal bydefinition~ approximately equal weakapproximation11 ~ 10≈approximately equal approximation sin(0.01) ≈ 0.01∝proportional to proportionalto y∝x when y= kx, k constant∞lemniscate infinitysymbol≪much less than much less than 1 ≪ 1000000≫much greater than much greaterthan1000000 ≫ 1( ) parentheses calculateexpressioninside first2 * (3+5) = 16[ ] brackets calculateexpressioninside first[(1+2)*(1+5)] = 18{ } braces set ⌊x⌋floor bracketsrounds numberto lowerinteger⌊ 4.3⌋ = 4⌈x⌉ceiling bracketsrounds numberto upperinteger⌈ 4.3⌉ = 5x! exclamation mark factorial4! = 1*2*3*4 = 24 | x|single vertical bar absolute value | -5 | = 5f (x) function of xmaps values ofx to f(x)f (x) = 3x+5(f∘g ) function composition(f∘g)(x)= f (g(x))f (x)=3x,g(x)=x-1 ⇒(f∘g)(x)=3(x-1)(a,b) open interval(a,b) ={x| a<x< b}x∈ (2,6)[a ,b] closed interval[a ,b ] ={x | a ≤ x ≤ b }x ∈[2,6] ∆ deltachange / difference∆t = t 1- t 0∆discriminantΔ = b 2- 4ac∑sigmasummation - sumof all values in range of series∑ x i = x 1+x 2+...+x n∑∑ sigmadouble summation∏capital piproduct -product of all values in range of series∏ x i =x 1∙x 2∙...∙x nee constant / Euler's numbere =2.718281828... e = lim (1+1/x )x, x →∞ γ Euler-Mascheroni const antγ =0.527721566...φgolden ratiogolden ratio constantπpi constantπ =3.141592654...is the ratio between the circumference and diameter of a circlec = π·d = 2·π·r·dot scalar product a ·b ×cross vector product a ×b A⊗B tensor product tensor product of A and B A⊗Binner product[ ] brackets matrix of numbers( ) parentheses matrix of numbers| Adeterminant determinant of matrix A|det(A) determinant determinant of matrix A|| xdouble vertical bars norm||(A T)ij=A T transpose matrix transpose(A)ji(A†)ij= A†Hermitian matrix matrix conjugate transpose(A)ji(A*)ij= A*Hermitian matrix matrix conjugate transpose(A)jiA-1inverse matrix A A-1= Irank(A) matrix rank rank of matrix A rank(A) = 3Probability and statistics symbolsSymbol Symbol Name Meaning /definitionExampleP(A) probabilityfunction probability ofevent AP(A) = 0.5P(A∩B) probability ofeventsintersectionprobability that ofevents A and BP(A∩B) = 0.5P(A∪B) probability ofevents unionprobability that ofevents A or BP(A∪B) = 0.5P(A|B) conditionalprobabilityfunctionprobability ofevent A given eventB occuredP(A | B) = 0.3f (x) probabilitydensityfunction (pdf)P(a ≤x ≤b) = ∫f (x)dxF(x) cumulativedistributionfunction (cdf)F(x) = P(X≤x)μpopulationmean mean of populationvaluesμ= 10E(X) expectationvalue expected value ofrandom variable XE(X) = 10E(X | Y) conditionalexpectation expected value ofrandom variable Xgiven YE(X | Y=2) = 5var(X) variance variance of randomvariable Xvar(X) = 4σ2variance variance ofpopulation valuesσ2 = 4std (X )standard deviationstandard deviation of random variable X std (X ) = 2σXstandard deviationstandard deviation value of random variable X σX = 2medianmiddle value of random variable xcov (X ,Y)covariancecovariance of random variables X and Ycov (X,Y ) = 4corr (X ,Y ) correlationcorrelation of random variables X and Ycorr (X,Y ) = 0.6ρX ,Ycorrelationcorrelation ofrandom variables X and YρX ,Y= 0.6∑summation summation - sum ofall values in range of series∑∑double summationdouble summationMo mode value that occursmost frequently in populationMR mid-rangeMR = (x max +x min )/2Mdsample median half the population is below this valueQ 1lower / first quartile25% of population are below this valueQ 2median / second quartile50% of populationare below this value = median of samplesQ3upper / thirdquartile 75% of population are below this valuex sample mean average /arithmetic meanx= (2+5+9) / 3 = 5.333s2samplevariance population samplesvariance estimators2= 4s samplestandarddeviationpopulation samplesstandard deviationestimators= 2z x standard score z x= (x-x) /s xX ~ distributionof X distribution ofrandom variable XX ~N(0,3)N(μ,σ2) normaldistributiongaussiandistributionX ~N(0,3)U(a,b) uniformdistributionequal probabilityin range a,bX ~U(0,3)exp(λ) exponentialdistributionf (x)= λe-λx, x≥0gamma(c,λ) gammadistributionf (x)= λ cx c-1e-λx/ Γ(c), x≥0χ2(k) chi-squaredistributionf (x)=x k/2-1e-x/2/( 2k/2 Γ(k/2) )F (k1, k2) F distributionBin(n,p) binomialdistributionf (k)= n C kp k(1-p)n-kPoisson(λ) Poissondistributionf (k)= λk e-λ/ k!Geom(p) geometricdistributionf (k)= p(1-p)kHG(N,K,n) hyper-geometri c distributionSet theory symbolsSymbol Symbol Name Meaning / definition Example{ } set a collection of elements A ={3,7,9,14},B = {9,14,28}A ∩B intersection objects that belong to set A andset BA ∩B ={9,14}A ∪B union objects that belong to set A orset BA ∪B ={3,7,9,14,28}A ⊆B subset subset has fewer elements orequal to the set{9,14,28} ⊆{9,14,28}A ⊂B proper subset / strictsubsetsubset has fewer elements thanthe set{9,14} ⊂{9,14,28}A ⊄B not subset left set not a subset of right set {9,66} ⊄{9,14,28}A ⊇B superset set A has more elements or equalto the set B{9,14,28} ⊇{9,14,28}A ⊃ Bproper superset / strict supersetset A has more elements than set B{9,14,28} ⊃ {9,14} A ⊅ B not superset set A is not a superset of set B{9,14,28} ⊅ {9,66}2Apower set all subsets of Apower set all subsets of AA =B equalityboth sets have the same members A={3,9,14},B={3,9,14},A=BA ccomplementall the objects that do not belong to set AA \B relative complementobjects that belong to A and not to BA = {3,9,14},B = {1,2,3}, A-B = {9,14} A - B relative complementobjects that belong to A and not to BA = {3,9,14},B = {1,2,3}, A-B = {9,14} A ∆ B symmetric differenceobjects that belong to A or B but not to their intersectionA = {3,9,14},B = {1,2,3}, A ∆ B = {1,2,9,14} A ⊖ B symmetric differenceobjects that belong to A or B but not to their intersectionA = {3,9,14},B = {1,2,3}, A ⊖ B = {1,2,9,14}a ∈A element of set membershipA={3,9,14}, 3 ∈ Ax ∉ A not element ofno set membershipA={3,9,14}, 1 ∉ A(a ,b ) ordered pair collection of 2 elementsA ×Bcartesian productset of all ordered pairs from A and B|A| cardinality the number of elements of set AA={3,9,14}, |A|=3 #A cardinality the number of elements of set AA={3,9,14}, #A=3aleph-nullinfinite cardinality of natural numbers setaleph-one cardinality of countable ordinal numbers setØ empty set Ø = { }C = {Ø}universal setset of all possible valuesnatural numbers / wholenumbers set (with zero)= {0,1,2,3,4,...} 0 ∈1natural numbers / wholenumbers set (without zero)1= {1,2,3,4,5,...} 6 ∈1integer numbers set={...-3,-2,-1,0,1,2,3,...}-6 ∈rational numbers set= {x | x =a /b , a ,b ∈}2/6 ∈real numbers set= {x | -∞ < x <∞} 6.343434∈complex numbers set= {z | z=a +bi , -∞<a <∞, -∞<b <∞}6+2i ∈& ampersand and x& y + plus or x+ y ∨reversed caret or x∨y | vertical line or x| y x' single quote not - negation x'x bar not - negation x¬not not - negation ¬x ! exclamation mark not - negation ! x⊕circled plus / oplus exclusive or - xor x⊕y ~ tilde negation ~ x⇒implies⇔equivalent if and only if (iff)↔equivalent if and only if (iff)∀for all∃there exists∄there does not exists∴thereforeCalculus & analysis symbolsSymbol Symbol Name Meaning / definition Examplelimit limit value of a functionεepsilon represents a very smallnumber, near zeroε→0e e constant/Euler's number e= 2.718281828...e= lim(1+1/x)x,x→∞y' derivative derivative - Lagrange'snotation(3x3)' = 9x2 y'' second derivative derivative of derivative (3x3)'' = 18x y(n)nth derivative n times derivation (3x3)(3)= 18derivative derivative - Leibniz'snotationd(3x3)/dx= 9x2second derivative derivative of derivative d2(3x3)/dx2= 18xnth derivative n times derivationtime derivative derivative by time - Newton's notationtime secondderivativederivative of derivativeD x y derivative derivative - Euler's notation D x2y second derivative derivative of derivativepartial derivative∂(x2+y2)/∂x=2x∫integral opposite to derivation ∫f(x)dx∫∫double integral integration of function of 2variables∫∫f(x,y)dxdy∫∫∫triple integral integration of function of 3variables∫∫∫f(x,y,z)dxdydz∮closed contour /line integral∯closed surfaceintegral∰closed volumeintegral[a,b] closed interval [a,b] ={x | a ≤x ≤b}(a,b) open interval (a,b) ={x | a <x <b}i imaginary unit i≡√-1 z= 3 + 2iz* complex conjugate z =a+bi→z*=a-bi z*= 3 - 2iz complex conjugate z =a+bi→z =a-biz= 3 - 2i ∇nabla / del gradient / divergence operator ∇f(x,y,z) vectorunit vectorx *y convolution y(t) = x(t) * h(t)) = {{。

数学常用词汇英汉互译对照文库

数学词汇中英文对照abbreviation 简写符号；简写abscissa 横坐标absolute complement 绝对补集absolute error 绝对误差absolute inequality 绝不等式absolute maximum 绝对极大值absolute minimum 绝对极小值absolute monotonic 绝对单调absolute value 绝对值accelerate 加速acceleration 加速度acceleration due to gravity 重力加速度; 地心加速度accumulation 累积accumulative 累积的accuracy 准确度act on 施于action 作用; 作用力acute angle 锐角acute-angled triangle 锐角三角形add 加addition 加法addition formula 加法公式addition law 加法定律addition law(of probability) （概率）加法定律additive inverse 加法逆元; 加法反元additive property 可加性adjacent angle 邻角adjacent side 邻边adjoint matrix 伴随矩阵algebra 代数algebraic 代数的algebraic equation 代数方程algebraic expression 代数式algebraic fraction 代数分式；代数分数式algebraic inequality 代数不等式algebraic number 代数数algebraic operation 代数运算algebraically closed 代数封闭algorithm 算法系统; 规则系统alternate angle （交）错角alternate segment 内错弓形alternating series 交错级数alternative hypothesis 择一假设; 备择假设; 另一假设altitude 高；高度；顶垂线；高线ambiguous case 两义情况；二义情况amount 本利和；总数analysis 分析；解析analytic geometry 解析几何angle 角angle at the centre 圆心角angle at the circumference 圆周角angle between a line and a planeangle between two planes 两平面的交角angle bisection 角平分angle bisectorangle in the alternate segment 交错弓形的圆周角angle in the same segment 同弓形内的圆周角angle of depression 俯角angle of elevation 仰角angle of friction 静摩擦角; 极限角angle of greatest slope 最大斜率的角angle of inclination 倾斜角angle of intersection 相交角；交角angle of projection 投射角angle of rotation 旋转角angle of the sector 扇形角angle sum of a triangle 三角形内角和angles at a point 同顶角angular displacement 角移位angular momentum 角动量angular motion 角运动angular velocity 角速度annum(X% per annum) 年（年利率X%）anti-clockwise direction 逆时针方向；返时针方向anti-clockwise moment 逆时针力矩anti-derivative 反导数; 反微商anti-logarithm 逆对数；反对数anti-symmetric 反对称apex 顶点approach 接近；趋近approximate value 近似值approximation 近似；略计；逼近Arabic system 阿刺伯数字系统arbitrary 任意arbitrary constant 任意常数arc 弧arc length 弧长arc-cosine function 反余弦函数arc-sin function 反正弦函数arc-tangent function 反正切函数area 面积Argand diagram 阿根图, 阿氏图argument (1)论证; (2)辐角argument of a complex number 复数的辐角argument of a function 函数的自变量arithmetic 算术arithmetic mean 算术平均；等差中顶；算术中顶arithmetic progression 算术级数；等差级数arithmetic sequence 等差序列arithmetic series 等差级数arm 边array 数组; 数组arrow 前号ascending order 递升序ascending powers of X X 的升幂assertion 断语; 断定associative law 结合律assumed mean 假定平均数assumption 假定；假设asymmetrical 非对称asymptoteasymptotic error constant 渐近误差常数at rest 静止augmented matrix 增广矩阵auxiliary angle 辅助角auxiliary circle 辅助圆auxiliary equation 辅助方程average 平均；平均数；平均值average speed 平均速率axiom 公理axiom of existence 存在公理axiom of extension 延伸公理axiom of inclusion 包含公理axiom of pairing 配对公理axiom of power 幂集公理axiom of specification 分类公理axiomatic theory of probability 概率公理论axis 轴axis of parabola 抛物线的轴axis of revolution 旋转轴axis of rotation 旋转轴axis of symmetry 对称轴back substitution 回代bar chart 棒形图；条线图；条形图；线条图base （1）底；（2）基；基数base angle 底角base area 底面base linebase number 底数；基数base of logarithm 对数的底basis 基Bayes theorem 贝叶斯定理bearing 方位（角）；角方向（角）bell-shaped curve 钟形图belong to 属于Bernoulli distribution 伯努利分布Bernoulli trials 伯努利试验bias 偏差；偏倚biconditional 双修件式; 双修件句bijection 对射; 双射; 单满射bijective function 对射函数; 只射函数billion 十亿bimodal distribution 双峰分布binary number 二进数binary operation 二元运算binary scale 二进法binary system 二进制binomial 二项式binomial distribution 二项分布binomial expression 二项式binomial series 二项级数binomial theorem 二项式定理bisect 平分；等分bisection method 分半法；分半方法bisectorBoolean algebra 布尔代数boundary condition 边界条件boundary line 界（线）；边界bounded 有界的bounded above 有上界的；上有界的bounded below 有下界的；下有界的bounded function 有界函数bounded sequence 有界序列brace 大括号bracket 括号breadth 阔度broken line graph 折线图calculation 计算calculator 计算器；计算器calculus (1) 微积分学; (2) 演算cancel 消法；相消canellation law 消去律canonical 典型; 标准capacity 容量cardioidCartesian coordinates 笛卡儿坐标Cartesian equation 笛卡儿方程Cartesian plane 笛卡儿平面Cartesian product 笛卡儿积category 类型；范畴catenaryCauchy sequence 柯西序列Cauchy s principal value 柯西主值Cauchy-Schwarz inequality 柯西 - 许瓦尔兹不等式central limit theorem 中心极限定理central linecentral tendency 集中趋centre 中心；心centre of a circle 圆心centre of gravity 重心centre of mass 质量中心centrifugal force 离心力centripedal acceleration 向心加速度centripedal force force 向心力centroid 形心；距心certain event 必然事件chain rule 链式法则chance 机会change of axes 坐标轴的变换change of base 基的变换change of coordinates 坐标轴的变换change of subject 主项变换change of variable 换元；变量的换characteristic equation 特征(征)方程characteristic function 特征(征)函数characteristic of logarithm 对数的首数; 对数的定位部characteristic root 特征(征)根chart 图；图表check digit 检验数位checking 验算chord 弦chord of contact 切点弦circle 圆circular 圆形；圆的circular function 圆函数；三角函数circular measure 弧度法circular motion 圆周运动circular permutation 环形排列; 圆形排列; 循环排列circumcentre 外心；外接圆心circumcircle 外接圆circumference 圆周circumradius 外接圆半径circumscribed circle 外接圆cissoidclass 区；组；类class boundary 组界class interval 组区间；组距class limit 组限；区限class mark 组中点；区中点classical theory of probability 古典概率论classification 分类clnometer 测斜仪clockwise direction 顺时针方向clockwise moment 顺时针力矩closed convex region 闭凸区域closed interval 闭区间coaxial 共轴coaxial circles 共轴圆coaxial system 共轴系coded data 编码数据coding method 编码法co-domain 上域coefficient 系数coefficient of friction 摩擦系数coefficient of restitution 碰撞系数; 恢复系数coefficient of variation 变差系数cofactor 余因子; 余因式cofactor matrix 列矩阵coincide 迭合；重合collection of terms 并项collinearcollinear planes 共线面collision 碰撞column (1)列；纵行；(2) 柱column matrix 列矩阵column vector 列向量combination 组合common chord 公弦common denominator 同分母；公分母common difference 公差common divisor 公约数；公约common factor 公因子；公因子common logarithm 常用对数common multiple 公位数；公倍common ratio 公比common tangentcommutative law 交换律comparable 可比较的compass 罗盘compass bearing 罗盘方位角compasses 圆规compasses construction 圆规作图compatible 可相容的complement 余；补余complement law 补余律complementary angle 余角complementary equation 补充方程complementary event 互补事件complementary function 余函数complementary probability 互补概率complete oscillation 全振动completing the square 配方complex conjugate 复共轭complex number 复数complex unmber plane 复数平面complex root 复数根component 分量component of force 分力composite function 复合函数; 合成函数composite number 复合数；合成数composition of mappings 映射构合composition of relations 复合关系compound angle 复角compound angle formula 复角公式compound bar chart 综合棒形图compound discount 复折扣compound interest 复利；复利息compound probability 合成概率compound statement 复合命题; 复合叙述computation 计算computer 计算机；电子计算器concave 凹concave downward 凹向下的concave polygon 凹多边形concave upward 凹向上的concentric circles 同心圆concept 概念conclusion 结论concurrent 共点concyclic 共圆concyclic points 共圆点condition 条件conditional 条件句；条件式conditional identity 条件恒等式conditional inequality 条件不等式conditional probability 条件概率cone 锥；圆锥（体）confidence coefficient 置信系数confidence interval 置信区间confidence level 置信水平confidence limit 置信极限confocal sectioncongruence (1)全等；(2)同余congruence class 同余类congruent 全等congruent figures 全等图形congruent triangles 全等三角形conic ;conic section ;conical pendulum 圆锥摆conjecture 猜想conjugate 共轭conjugate axis 共轭conjugate diameters 共轭轴conjugate hyperbola 共轭(直)径conjugate imaginary / complex number conjugate radical 共轭虚/复数conjugate surd 共轭根式; 共轭不尽根conjunction 合取connective 连词connector box 捙接框consecutive integers 连续整数consecutive numbers 连续数；相邻数consequence 结论；推论consequent 条件；后项conservation of energy 能量守恒conservation of momentum 动量守恒conserved 守恒consistency condition 相容条件consistent 一贯的；相容的consistent estimator 相容估计量constant 常数constant acceleration 恒加速度constant force 恒力constant of integration 积分常数constant speed 恒速率constant term 常项constant velocity 怛速度constraint 约束；约束条件construct 作construction 作图construction of equation 方程的设立continued proportion 连比例continued ratio 连比continuity 连续性continuity correction 连续校正continuous 连续的continuous data 连续数据continuous function 连续函数continuous proportion 连续比例continuous random variable 连续随机变量contradiction 矛盾converge 收敛convergence 收敛性convergent 收敛的convergent iteration 收敛的迭代convergent sequence 收敛序列convergent series 收敛级数converse 逆(定理)converse of a relation 逆关系converse theorem 逆定理conversion 转换convex 凸convex polygon 凸多边形convexity 凸性coordinate 坐标coordinate geometry 解析几何；坐标几何coordinate system 坐标系系定理；系；推论coplanar 共面coplanar forces 共面力coplanar linesco-prime 互质; 互素corollary 系定理; 系; 推论correct to 准确至；取值至correlation 相关correlation coefficient 相关系数correspondence 对应corresponding angles (1)同位角；(2)对应角corresponding element 对应边corresponding sides 对应边cosecant 余割cosine 余弦cosine formula 余弦公式cost price 成本cotangent 余切countable 可数countable set 可数集countably infinite 可数无限counter clockwise direction 逆时针方向；返时针方向counter example 反例counting 数数；计数couple 力偶Carmer s rule 克莱玛法则criterion 准则critical point 临界点critical region 临界域cirtical value 临界值cross-multiplication 交叉相乘cross-section 横切面；横截面；截痕cube 正方体；立方；立方体cube root 立方根cubic 三次方；立方；三次(的)cubic equation 三次方程cubic roots of unity 单位的立方根cuboid 长方体；矩体cumulative 累积的cumulative distribution function 累积分布函数cumulative frequecy 累积频数；累积频率cumulative frequency curvecumulative frequcncy distribution 累积频数分布cumulative frequency polygon 累积频数多边形；累积频率直方图curvature of a curve 曲线的曲率curvecurve sketching 曲线描绘(法)curve tracing 曲线描迹(法)curved linecurved surface 曲面curved surface area 曲面面积cyclic expression 输换式cyclic permutation 圆形排列cyclic quadrilateral 圆内接四边形cycloid 旋输线; 摆线cylinder 柱；圆柱体cylindrical 圆柱形的damped oscillation 阻尼振动data 数据De Moivre s theorem 棣美弗定理De Morgan s law 德摩根律decagon 十边形decay 衰变decay factor 衰变因子decelerate 减速decelaration 减速度decile 十分位数decimal 小数decimal place 小数位decimal point 小数点decimal system 十进制decision box 判定框declarative sentence 说明语句declarative statement 说明命题decoding 译码decrease 递减decreasing function 递减函数；下降函数decreasing sequence 递减序列；下降序列decreasing series 递减级数；下降级数decrement 减量deduce 演绎deduction 推论deductive reasoning 演绎推理definite 确定的；定的definite integral 定积分definition 定义degenerated conic section 降级锥曲线degree (1) 度; (2) 次degree of a polynomial 多项式的次数degree of accuracy 准确度degree of confidence 置信度degree of freedom 自由度degree of ODE 常微分方程次数degree of precision 精确度delete 删除; 删去denary number 十进数denominator 分母dependence (1)相关; (2)应变dependent event(s) 相关事件; 相依事件; 从属事件dependent variable 应变量; 应变数depreciation 折旧derivable 可导derivative 导数derived curve 导函数曲线derived function 导函数derived statistics 推算统计资料; 派生统计资料descending order 递降序descending powers of x x的降序descriptive statistics 描述统计学detached coefficients 分离系数(法)determinant 行列式deviation 偏差; 变差deviation from the mean 离均差diagonal 对角线diagonal matrix 对角矩阵diagram 图; 图表diameter 直径diameter of a conic 二次曲线的直径difference 差difference equation 差分方程difference of sets 差集differentiable 可微differential 微分differential coefficient 微商; 微分系数differential equation 微分方程differential mean value theorem 微分中值定理differentiate 求...的导数differentiate from first principle 从基本原理求导数differentiation 微分法digit 数字dimension 量; 量网; 维(数)direct impact 直接碰撞direct image 直接像direct proportion 正比例direct tax, direct taxation 直接税direct variation 正变(分)directed angle 有向角directed line 有向直线directed line segment 有向线段directed number 有向数direction 方向; 方位direction angle 方向角direction cosine 方向余弦direction number 方向数direction ratio 方向比directrix 准线Dirichlet function 狄利克来函数discontinuity 不连续性discontinuous 间断(的);连续(的); 不连续(的) discontinuous point 不连续点discount 折扣discrete 分立; 离散discrete data 离散数据; 间断数据discrete random variable 间断随机变数discrete uniform distribution 离散均匀分布discriminant 判别式disjoint 不相交的disjoint sets 不相交的集disjunction 析取dispersion 离差displacement 位移disprove 反证distance 距离distance formula 距离公式distinct roots 相异根distincr solution 相异解distribution 公布distributive law 分配律diverge 发散divergence 发散(性)divergent 发散的divergent iteration 发散性迭代divergent sequence 发散序列divergent series 发散级数divide 除dividend (1)被除数；(2)股息divisible 可整除division 除法division algorithm 除法算式divisor 除数；除式；因子divisor of zero 零因子dodecagon 十二边形domain 定义域dot 点dot product 点积double angle 二倍角double angle formula 二倍角公式double root 二重根dual 对偶duality (1)对偶性; (2) 双重性due east/ south/ west /north 向东/ 南/ 西/ 北dynamics 动力学eccentric angle 离心角eccentric circles 离心圆eccentricity 离心率echelon form 梯阵式echelon matrix 梯矩阵edge 棱；边efficient estimator 有效估计量effort 施力eigenvalue 本征值eigenvector 本征向量elastic body 弹性体elastic collision 弹性碰撞elastic constant 弹性常数elastic force 弹力elasticity 弹性element 元素elementary event 基本事件elementary function 初等函数elementary row operation 基本行运算elimination 消法elimination method 消去法；消元法ellipse 椭圆ellipsiod 椭球体elliptic function 椭圆函数elongation 伸张；展empirical data 实验数据empirical formula 实验公式empirical probability 实验概率；经验概率empty set 空集encoding 编码enclosure 界限end point 端点energy 能; 能量entire surd 整方根epicycloid 外摆线equal 相等equal ratios theorem 等比定理equal roots 等根equal sets 等集equality 等(式)equality sign 等号equation 方程equation in one unknown 一元方程equation in two unknowns(variables) 二元方程equation of a straight line 直线方程equation of locus 轨迹方程equiangular 等角(的)equidistant 等距(的)equilateral 等边(的)equilateral polygon 等边多边形equilateral triangle 等边三角形equilibrium 平衡equiprobable 等概率的equiprobable space 等概率空间equivalence 等价equivalence class 等价类equivalence relation 等价关系equivalent 等价(的)error 误差error allowance 误差宽容度error estimate 误差估计error term 误差项error tolerance 误差宽容度escribed circle 旁切圆estimate 估计；估计量estimator 估计量Euclidean algorithm 欧几里德算法Euclidean geometry 欧几里德几何Euler s formula 尤拉公式；欧拉公式evaluate 计值even function 偶函数even number 偶数evenly distributed 均匀分布的event 事件exact 真确exact differential form 恰当微分形式exact solution 准确解；精确解；真确解exact value 法确解；精确解；真确解example 例excentre 外心exception 例外excess 起exclusive 不包含exclusive disjunction 不包含性析取exclusive events 互斥事件exercise 练习exhaustive event(s) 彻底事件existential quantifier 存在量词expand 展开expand form 展开式expansion 展式expectation 期望expectation value, expected value 期望值；预期值experiment 实验；试验experimental 试验的experimental probability 实验概率explicit function 显函数exponent 指数exponential function 指数函数exponential order 指数阶; 指数级express…in terms of…以………表达expression 式；数式extension 外延；延长；扩张；扩充extension of a function 函数的扩张exterior angle 外角external angle bisectorexternal point of division 外分点extreme point 极值点extreme value 极值extremum 极值face 面factor 因子；因式；商factor method 因式分解法factor theorem 因子定理；因式定理factorial 阶乘factorization 因子分解；因式分解factorization of polynomial 多项式因式分解fallacy 谬误FALSE 假(的)falsehood 假值family 族family of circles 圆族family of concentric circles 同心圆族family of straight lines 直线族feasible solution 可行解；容许解Fermat s last theorem 费尔马最后定理Fibonacci number 斐波那契数；黄金分割数Fibonacci sequence 斐波那契序列fictitious mean 假定平均数figure (1)图(形)；(2)数字final velocity 末速度finite 有限finite dimensional vector space 有限维向量空间finite population 有限总体finite probability space 有限概率空间finite sequence 有限序列finite series 有限级数finite set 有限集first approximation 首近似值first derivative 一阶导数first order differential equation 一阶微分方程first projection 第一投影; 第一射影first quartile 第一四分位数first term 首项fixed deposit 定期存款fixed point 定点fixed point iteration method 定点迭代法fixed pulley 定滑轮flow chart 流程图focal axis 焦轴focal chord 焦弦focal length 焦距focus(foci) 焦点folium of Descartes 笛卡儿叶形线foot of perpendicular 垂足for all X 对所有Xfor each /every X 对每一Xforce 力forced oscillation 受迫振动form 形式；型formal proof 形式化的证明format 格式；规格formula(formulae) 公式four leaved rose curve 四瓣玫瑰线four rules 四则four-figure table 四位数表fourth root 四次方根fraction 分数；分式fraction in lowest term 最简分数fractional equation 分式方程fractional index 分数指数fractional inequality 分式不等式free fall 自由下坠free vector 自由向量; 自由矢量frequency 频数；频率frequency distribution 频数分布；频率分布frequency distribution table 频数分布表frequency polygon 频数多边形；频率多边形friction 摩擦; 摩擦力frictionless motion 无摩擦运动frustum 平截头体fulcrum 支点function 函数function of function 复合函数；迭函数functional notation 函数记号fundamental theorem of algebra 代数基本定理fundamental theorem of calculus 微积分基本定理gain 增益；赚；盈利gain perent 赚率；增益率；盈利百分率game （1）对策；（2）博奕Gaussian distribution 高斯分布Gaussian elimination 高斯消去法general form 一般式；通式general solution 通解；一般解general term 通项generating function 母函数; 生成函数generator (1)母线; (2)生成元geoborad 几何板geometric distribution 几何分布geometric mean 几何平均数；等比中项geometric progression 几何级数；等比级数geometric sequence 等比序列geometric series 等比级数geometry 几何；几何学given 给定；已知global 全局; 整体global maximum 全局极大值; 整体极大值global minimum 全局极小值; 整体极小值golden section 黄金分割grade 等级gradient (1)斜率；倾斜率；(2)梯度grand total 总计graph 图像；图形；图表graph paper 图表纸graphical method 图解法graphical representation 图示；以图样表达graphical solution 图解gravitational acceleration 重力加速度gravity 重力greatest term 最大项greatest value 最大值grid lines 网网格线groupgrouped data 分组数据；分类数据grouping terms 并项；集项growth 增长growth factor 增长因子half angle 半角half angle formula 半角公式half closed interval 半闭区间half open interval 半开区间harmonic mean (1) 调和平均数; (2) 调和中项harmonic progression 调和级数head 正面（钱币）height 高（度）helix 螺旋线hemisphere 半球体；半球heptagon 七边形Heron s formula 希罗公式heterogeneous (1)参差的; (2)不纯一的hexagon 六边形higher order derivative 高阶导数highest common factor(H.C.F) 最大公因子；最高公因式；最高公因子Hindu-Arabic numeral 阿刺伯数字histogram 组织图；直方图；矩形图Holder s Inequality 赫耳德不等式homogeneous 齐次的homogeneous equation 齐次方程Hooke s law 虎克定律horizontal 水平的；水平horizontal asymptote 水平渐近线horizontal component 水平分量horizontal linehorizontal range 水平射程hyperbolahyperbolic function 双曲函数hypergeometric distribution 超几何分布hypocycloid 内摆线hypotenuse 斜边hypothesis 假设hypothesis testing 假设检验hypothetical syllogism 假设三段论hypotrochoid 次内摆线idempotent 全幂等的identical 全等；恒等identity 等（式）identity element 单位元identity law 同一律identity mapping 恒等映射identity matrix 恒等矩阵identity relation 恒等关系式if and only if/iff 当且仅当；若且仅若if…, then 若….则；如果…..则illustration 例证；说明image 像点；像image axis 虚轴imaginary circle 虚圆imaginary number 虚数imaginary part 虚部imaginary root 虚根imaginary unit 虚数单位impact 碰撞implication 蕴涵式；蕴含式implicit definition 隐定义implicit function 隐函数imply 蕴涵；蕴含impossible event 不可能事件improper fraction 假分数improper integral 广义积分; 非正常积分impulse 冲量impulsive force 冲力incentre 内力incircle 内切圆inclination 倾角；斜角inclined plane 斜面included angle 夹角included side 夹边inclusion mapping 包含映射inclusive 包含的；可兼的inclusive disjunction 包含性析取；可兼析取inconsistent 不相的(的)；不一致(的) increase 递增；增加increasing function 递增函数increasing sequence 递增序列increasing series 递增级数increment 增量indefinite integral 不定积分idenfinite integration 不定积分法independence 独立；自变independent equations 独立方程independent event 独立事件independent variable 自变量；独立变量indeterminate (1)不定的；(2)不定元；未定元indeterminate coefficient 不定系数；未定系数indeterminate form 待定型；不定型index,indices 指数；指index notation 指数记数法induced operation 诱导运算induction hypothesis 归纳法假设inelastic collision 非弹性碰撞inequality 不等式；不等inequality sign 不等号inertia 惯性；惯量infer 推断inference 推论infinite 无限；无穷infinite dimensional 无限维infinite population 无限总体infinite sequence 无限序列；无穷序列infinite series 无限级数；无穷级数infinitely many 无穷多infinitesimal 无限小；无穷小infinity 无限(大)；无穷(大)inflection (inflexion) point 拐点；转折点inherent error 固有误差initial approximation 初始近似值initial condition 原始条件；初值条件initial point 始点；起点initial side 始边initial value 初值；始值initial velocity 初速度initial-value problem 初值问题injection 内射injective function 内射函数inner product 内积input 输入input box 输入inscribed circle 内切圆insertion 插入insertion of brackets 加括号instantaneous 瞬时的instantaneous acceleration 瞬时加速度instantaneous speed 瞬时速率instantaneous velocity 瞬时速度integer 整数integrable 可积integrable function 可积函数integral 积分integral index 整数指数integral mean value theorem 积数指数integral part 整数部份integral solution 整数解integral value 整数值integrand 被积函数integrate 积；积分；......的积分integrating factor 积分因子integration 积分法integration by parts 分部积分法integration by substitution 代换积分法；换元积分法integration constant 积分常数interaction 相互作用intercept 截距；截段intercept form 截距式intercept theorem 截线定理interchange 互换interest 利息interest rate 利率interest tax 利息税interior angle 内角interior angles on the same side of the transversal 同旁内角interior opposite angle 内对角intermediate value theorem 介值定理internal bisectorinternal division 内分割internal energy 内能internal force 内力internal point of division 内分点interpolating polynomial 插值多项式interpolation 插值inter-quartile range 四分位数间距intersect 相交intersection (1)交集；(2)相交；(3)交点interval 区间interval estimation 区间估计；区域估计intuition 直观invalid 失效；无效invariance 不变性invariant (1)不变的；(2)不变量；不变式inverse 反的；逆的inverse circular function 反三角函数inverse cosine function 反余弦函数inverse function 反函数；逆函数inverse cosine function 反三角函数inverse function 反函数；逆映射inverse mapping 反向映射；逆映射inverse matrix 逆矩阵inverse problem 逆算问题inverse proportion 反比例；逆比例inverse relation 逆关系inverse sine function 反正弦函数inverse tangent function 反正切函数inverse variation 反变(分)；逆变(分)invertible 可逆的invertible matrix 可逆矩阵irrational equation 无理方程irrational number 无理数irreducibility 不可约性irregular 不规则isomorphism 同构isosceles triangle 等腰三角形iterate (1)迭代值; (2)迭代iteration 迭代iteration form 迭代形iterative function 迭代函数iterative method 迭代法jet propulsion 喷气推进joint variation 联变(分)；连变(分)kinetic energy 动能kinetic friction 动摩擦known 己知L.H.S. 末项L Hospital s rule 洛必达法则Lagrange interpolating polynomial 拉格朗日插值多项代Lagrange theorem 拉格朗日定理Lami s law 拉密定律Laplace expansion 拉普拉斯展式last term 末项latent root 本征根; 首通径lattice point 格点latus rectum 正焦弦; 首通径law 律；定律law of conservation of momentum 动量守恒定律law of indices 指数律；指数定律law of inference 推论律law of trichotomy 三分律leading coefficient 首项系数leading diagonal 主对角线least common multiple, lowest common multiple (L.C.M) 最小公倍数；最低公倍式least value 最小值left hand limit 左方极限lemma 引理lemniscate 双纽线length 长(度)letter 文字；字母like surd 同类根式like terms 同类项limacon 蜗牛线limit 极限limit of sequence 序列的极限limiting case 极限情况limiting friction 最大静摩擦limiting position 极限位置line 线；行line of action 作用力线line of best-fitline of greatest slopeline of intersectionline segment 线段linear 线性；一次linear convergence 线性收敛性linear differeantial equation 线性微分方程linear equation 线性方程；一次方程linear equation in two unknowns 二元一次方程；二元线性方程linear inequality 一次不等式；线性不等式linear momentum 线动量linear programming 线性规划linearly dependent 线性相关的linearly independent 线性无关的literal coefficient 文字系数literal equation 文字方程load 负荷loaded coin 不公正钱币loaded die 不公正骰子local maximum 局部极大(值)local minimum 局部极小(值)locus, loci 轨迹logarithm 对数logarithmic equation 对数方程logarithmic function 对数函数logic 逻辑logical deduction 逻辑推论；逻辑推理logical step 逻辑步骤long division method 长除法loop 回路loss 赔本；亏蚀loss per cent 赔率；亏蚀百分率lower bound 下界lower limit 下限lower quartile 下四分位数lower sum 下和lower triangular matrix 下三角形矩阵lowest common multiple(L.C.M) 最小公倍数machine 机械Maclaurin expansion 麦克劳林展开式Maclaurin series 麦克劳林级数magnitude 量；数量；长度；大小major arc 优弧；大弧major axis 长轴major sector 优扇形；大扇形major segment 优弓形；大弓形mantissa 尾数mantissa of logarithm 对数的尾数；对数的定值部many to one 多个对一个many-sided figure 多边形many-valued 多值的map into 映入map onto 映上mapping 映射marked price 标价Markov chain 马可夫链mass 质量mathematical analysis 数学分析mathematical induction 数学归纳法mathematical sentence 数句mathematics 数学matrix 阵; 矩阵matrix addition 矩阵加法matrix equation 矩阵方程matrix multiplication 矩阵乘法matrix operation 矩阵运算maximize 极大maximum absolute error 最大绝对误差maximum point 极大点maximum value 极大值mean 平均(值)；平均数；中数mean deviation 中均差；平均偏差mean value theorem 中值定理measure of dispersion 离差的量度measurement 量度mechanical energy 机械能median (1)中位数；(2)meet 相交；相遇mensuration 计量；求积法method 方法method of completing square 配方法method of interpolation 插值法; 内插法method of least squares 最小二乘法; 最小平方法method of substitution 代换法；换元法method of successive substitution 逐次代换法; 逐次调替法method of superposition 迭合法metric unit 十进制单位mid-point 中点mid-point formula 中点公式mid-point theorem 中点定理million 百万minimize 极小minimum point 极小点minimum value 极小值Minkowski Inequality 闵可夫斯基不等式minor (1)子行列式；(2)劣；较小的minor arc 劣弧；小弧minor axis 短轴minor of a determinant 子行列式minor sector 劣扇形；小扇形minor segment 劣弓形；小弓形minus 减minute 分mixed number(fraction) 带分数modal class 众数组mode 众数model 模型modulo (1)模; 模数; (2)同余modulo arithmetic 同余算术modulus 模; 模数modulus of a complex number 复数的模modulus of elasticity 弹性模(数)moment arm (1)矩臂; (2)力臂moment of a force 力矩moment of inertia 贯性矩momentum 动量monomial 单项式monotone 单调monotonic convergence 单调收敛性monotonic decreasing 单调递减monotonic decreasing function 单调递减函数monotonic function 单调函数monotonic increasing 单调递增monotonic increasing function 单调递增函数motion 运动movable pulley 动滑轮multinomial 多项式multiple 倍数multiple angle 倍角multiple-angle formula 倍角公式multiple root 多重根multiplicand 被乘数multiplication 乘法multiplication law (of probability) (概率)乘法定律multiplicative inverse 乘法逆元multiplicative property 可乘性multiplicity 重数multiplier 乘数；乘式multiply 乘multi-value 多值的mulually disjoint 互不相交mutually exclusive events 互斥事件mutually independent 独立; 互相独立mutually perpendicular linesn factorial n阶乘n th derivative n阶导数n th root n次根；n次方根n the root of unity 单位的n次根Napierian logarithm 纳皮尔对数; 自然对数natural logarithm 自然对数natural number 自然数natural surjection 自然满射necessary and sufficient condition 充要条件necessary condition 必要条件negation 否定式negative 负negative angle 负角negative binomial distribution 负二项式分布negative index 负指数negative integer 负整数negative number 负数negative vector 负向量; 负矢量neighborhood 邻域net 净(值)net force 净力Newton-Cote s rule 牛顿 - 高斯法则Newton-Raphson s method 牛顿 - 纳逊方法Newton s formula 牛顿公式Newton s law of motion 牛顿运动定律Newton s method 牛顿方法n-gon n边形nonagon 九边形non-collinearnon-commutative 非交换的non-linear 非线性non-linear equation 非线性方程non-negative 非负的。

主要数学符号的英文读法

主要数学符号的英文读法＜is less than＞is more than≮is not less than≯is not more than≤is less than or equal to 小于或等于号- hyphen 连字符≥is more than or equal to 大于或等于号' apostrophe 省略号,英文中省略字符用的撇号;所有格符号％percent－dash 破折号‰per mille∞infinity 无限大号∝varies as 与…成比例( ) parentheses 圆括号√(square) root 平方根[ ] square brackets 方括号∵since; because 因为《》French quotes 法文引号;书名号∴hence 所以…ellipsis 省略号∷equals, as (proportion) 等于，成比例¨tandem colon 双点号∠angle 角∶ditto 双点号≲semicircle 半圆‖parallel 双线号≰circle 圆／virgule 斜线号○circumference 圆周～swung dash 代字号△triangle 三角形§section; division 分节号≱perpendicular to 垂直于→arrow 箭号；参见号∪union of 并，合集∩intersection of 交，通集∫the integral of …的积分±plus or minus 正负号∑summation of 总和×is multiplied by 乘号°degree 度÷is divided by 除号′minute 分″second 秒≠is not equal to 不等于号≡is equivalent to 全等于号℃Celsius degree 摄氏度≌is equal to or approximately equal to 等于或约等于号+ plus 加号；正号- minus 减号；负号±plus or minus 正负号×is multiplied by 乘号÷is divided by 除号＝is equal to 等于号≠is not equal to 不等于号≡is equivalent to 全等于号≌is equal to or approximately equal to 等于或约等于号≈is approximately equal to 约等于号＜is less than 小于号＞is more than 大于号≮is not less than 不小于号≯is not more than 不大于号≤is less than or equal to 小于或等于号≥is more than or equal to 大于或等于号% per cent 百分之…‰per mill 千分之…∞infinity 无限大号∝varies as 与…成比例√(square) root 平方根∵since; because 因为∴hence 所以∷equals, as (proportion) 等于，成比例∠angle 角≲semicircle 半圆≰circle 圆○circumference 圆周πpi 圆周率△triangle 三角形≱perpendicular to 垂直于∪union of 并，合集∩intersection of 交，通集∫the integral of …的积分∑(sigma) summation of 总和°degree 度′minute 分〃second 秒℃Celsius system 摄氏度{ open brace, open curly 左花括号} close brace, close curly 右花括号( open parenthesis, open paren 左圆括号) close parenthesis, close paren 右圆括号() brakets/ parentheses 括号[ open bracket 左方括号] close bracket 右方括号[] square brackets 方括号. period, dot 句号，点| vertical bar, vertical virgule 竖线& ampersand, and, reference, ref 和，引用/ slash, divide, oblique 斜线，斜杠，除号// slash-slash, comment 双斜线，注释符# pound 井号\ backslash, sometimes escape 反斜线转义符，有时表示转义符或续行符~ tilde 波浪符. full stop 句号, comma 逗号: colon 冒号; semicolon 分号? question mark 问号! exclamation mark (英式英语) exclamation point (美式英语)' apostrophe 撇号- hyphen 连字号-- dash 破折号... dots/ ellipsis 省略号" single quotation marks 单引号"" double quotation marks 双引号‖parallel 双线号& ampersand = and～swung dash 代字号§section; division 分节号→arrow 箭号；参见号_ underscore 下划线+ plus(positive正的)- minus（negative负的）±plus or minus* multiplied by÷divided by= be equal to≈ be approximately equal to() round brackets(parenthess)[] square brackets{} braces∵because∴therefore≤ less than or equal to≥ greater than or equal to∞ infinityLognX logx to the base nf(x) the function of xdx diffrencial of xx+y x plus y(a+b) bracket a plus b bracket closeda=b a equals ba≠b a isn't equal to ba>b a is greater than ba>>b a is much greater than ba≥b a is greater than or equal to bx→∞ x approches infinityx2 x squarex3 x cubexn the nth power of x√￣x the square root of x3√￣x the cube root of xn√￣x the nth root of x6 % 6 percent3‰ 3 per mille3‰ three peimilln∑i=1xi the summation of x where x goes from 1to nn∏i=1xi the product of x sub i where igoes from 1to n∫ab integral betweens a and b>> is approximately equal to( ) round brackets; parentheses[ ] square brackets{ } braces2 :3 the ratio of two to threeD x or d x the increment of xdx differential xdy/dx the first derivative of y with respect to x1/2 a half; one half2/3 two thirds5/123 five over a hundred and twenty-three0.01 O point O one; zero point zero one; nought point nought one r=xd r equals x multiplied by d5* 2=10 five times two equals tenx3/8=y2 x raised to the third power divided by eight equals y squared (a+b-c* d)/e=f a plus b minus c multiplied by d all divided by e equals fy = (Wt-W)/x y equals W sub t minus W over xΑ α alpha alfa 阿耳法Β β beta beta 贝塔Γ γ gamma gamma 伽马Γ δ deta delta 德耳塔Δ ε epsilon epsilon 艾普西隆Ε δ zeta zeta 截塔Ζ ε eta eta 艾塔Θ ζ theta ζita 西塔Η η iota iota 约塔Κ θ kappa kappa 卡帕∧ ι lambda lambda 兰姆达Μ κ mu miu 缪Ν λ nu ni u 纽Ξ μ xi ksi 可塞Ο ν omicron omikron 奥密可戎∏ π pi pai 派Ρ ξ rho rou 柔∑ ζ sigma sigma 西格马Τ η tau tau 套Υ υ upsilon jupsilon 衣普西隆Φ θ phi fai 斐Φ χ chi khai 喜Χ ψ psi psai 普西Ψ ω omega omiga 欧米伽。

数学符号中英文对照表

几何符号∻‖ⅶ∼∺∵∳△2 代数符号ⅴ∧∨～∫∴∶∷∲ⅵ∯3运算符号×÷ⅳ±4集合符号∪∩ⅰ5特殊符号ⅲπ（圆周率）6推理符号|a| ∻∱△ⅶ∩∪∴∵±∷∶ⅰⅬⅭⅮⅯ↖↗↘↙‖∧∨&; §∽∾∿≀≁≂≃≄≅≆ΓΔΘ∧ΞΟⅱⅲΦΧΨΩα β γ δ ε δ ε ζ η θ ι κ λμ ν π ξ ζ η υ θ χ ψ ωⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹⅰⅱⅲ↚ⅳⅴⅵ↛ⅶ↜‖∧∨∩∪∫∬∭∮∯∰∱∲∳∲∴∵∶∷∶∷∸∹⊕∺∻⊿∼℃上述符号所表示的意义和读法（中英文参照）＋plus 加号；正号－minus 减号；负号±plus or minus 正负号×is multiplied by 乘号÷is divided by 除号＝is equal to 等于号∴is not equal to 不等于号∵is equivalent to 全等于号∳is approximately equal to 约等于∲is approximately equal to 约等于号＜is less than 小于号＞is more than 大于号∶is less than or equal to 小于或等于∷is more than or equal to 大于或等于％per cent 百分之…ⅵinfinity 无限大号ⅳ(square) root 平方根X squared X的平方X cubed X的立方∮since; because 因为∭hence 所以ⅶangle 角∼semicircle 半圆∺circle 圆○circumference 圆周△triangle 三角形∻perpendicular to 垂直于∪intersection of 并，合集∩union of 交，通集∫the integral of …的积分ⅲ(sigma) summation of 总和°degree 度′minute 分〃second 秒＃number …号＠at 单价。

常用数学符号英文对照

数学术语英文对照表

常用数学符号英文对照

中小学数学代数几何常用概念中英文数学对照

常用数学符号英文对照

数学符号的中英文读法

数学符号英文对照表

常用数学符号的英文表达

常用数学符号英文对照

数学符号英语表达

数值分析中常用数学词汇英中文对照翻译.

数学相关英语单词及各种符号英语

高等数学(微积分学)专业术语名词、概念、定理等英汉对照.

sci文章 数学符号

数学常用英文词汇表

主要数学符号(English)

常用数学符号英文对照

数学常用词汇英汉互译对照文库

主要数学符号的英文读法

数学符号中英文对照表

sci文章数学符号