origin拟合准一级准二级动力学方程详解39566讲课稿
origin拟合准一级准二级动力学方程详解

建立用户自定义函数得步骤:1、选择Tools: Fitting Function Organizer(快捷键F9) ,打开Fittingfunctionorganizer、单击New Category按钮,创建一个函数类,可以根据自己需要重命名,比如yxz、然后单击New Function,在这个类下面创建一个新得函数,然后命名,比如thepseudosecondorderkinetic 1:2、对该函数进行简短得描述,Brief Description栏输入:To used for the pseudo secondorder kineticfitting,定义函数所需参数,ParameterNames:a,k;输入函数方程。
Function 栏输入需编写得方程:y=((a^2)*k*x)/(1+a*k*x)这个方程得逻辑关系一定要对!3、然后进行点击Function右侧得按钮4、编译正确就是前提就是:方程正确,方程中得相关参数在方程之前进行了创建,参数声明与方程建立完成之后,单击进入编译界面,单击pile5、当出现上图红框中文字就是,证明公式定义成功,否则失败!须重新定义。
6、在file中单击save,然后单击return to dialog,再单击OK.7、至此,用户自定义函数得建立已经完成.二、自定义拟合函数得使用:1先建立原文件图用点格式绘图2、完成后点击工具栏里得Analysis-———Fitting---—3、选择刚建立得yxz下得thepseudosecondorderkinetic 1 公式.4、点击Parameters5、在参数栏中分别设置a与k得初始值(可以根据经验任意设置),设置数值就是只需在value 这一栏双击鼠标,就可以输入数据!6、随后点击单击一次拟合之后,得到以下结果:7、拟合并不很理想,然后直接拟合到收敛,可以瞧到拟合结果满意,单击OK:拟合到收敛8拟合完成结果如图Array 9、拟合曲线数据点,点击上图中Fit NLCURvel输出10、可以根据上述拟合数据作图。
origin拟合准一级准二级动力学方程详解

建立用户自定义函数的步骤:1.选择Tools: Fitting Function Organizer (快捷键F9) ,打开Fitting function organizer. 单击New Category 按钮,创建一个函数类,可以根据自己需要重命名,比如yxz.然后单击New Function,在这个类下面创建一个新的函数,然后命名,比如thepseudosecondorderkinetic 1:2. 对该函数进行简短的描述,Brief Description栏输入:To used for the pseudo second order kinetic fitting,定义函数所需参数,ParameterNames:a,k;输入函数方程。
Function 栏输入需编写的方程:y=((a^2)*k*x)/(1+a*k*x) 这个方程的逻辑关系一定要对!3.然后进行点击Function 右侧的按钮4.编译正确是前提是:方程正确,方程中的相关参数在方程之前进行了创建,参数声明和方程建立完成之后,单击进入编译界面,单击Compile5.当出现上图红框中文字是,证明公式定义成功,否则失败!须重新定义。
6.在file中单击save,然后单击return to dialog,再单击OK。
7.至此,用户自定义函数的建立已经完成。
二、自定义拟合函数的使用:1先建立原文件图用点格式绘图2.完成后点击工具栏里的Analysis----Fitting----3. 选择刚建立的yxz 下的thepseudosecondorderkinetic 1 公式。
4. 点击Parameters5.在参数栏中分别设置a和k 的初始值(可以根据经验任意设置),设置数值是只需在value 这一栏双击鼠标,就可以输入数据!6.随后点击单击一次拟合之后,得到以下结果:7.拟合并不很理想,然后直接拟合到收敛,可以看到拟合结果满意,单击OK:拟合到收敛8 拟合完成结果如图9.拟合曲线数据点,点击上图中Fit NLCURvel 输出10.可以根据上述拟合数据作图。
origin拟合准一级准二级动力学方程详解
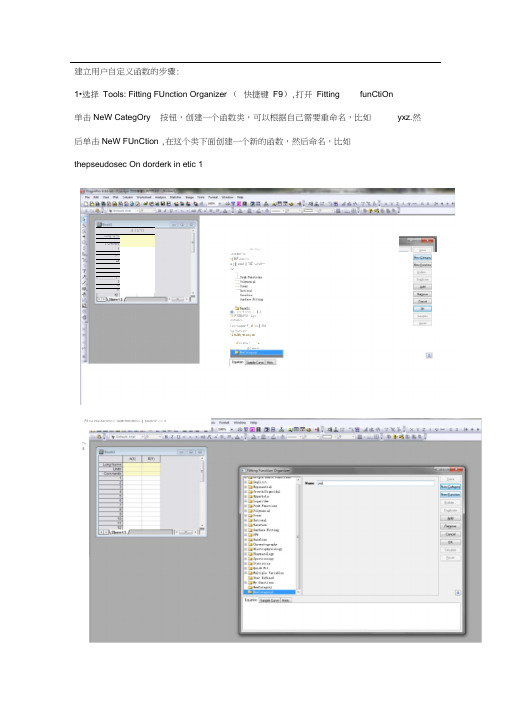
4 I IrYILeng ⅛∏⅛L Crn-Hfrti1Γ■4L __________ L2I]I1I建立用户自定义函数的步骤:1•选择Tools: Fitting FUnction Organizer (快捷键F9),打开Fitting funCtiOn单击NeW CategOry 按钮,创建一个函数类,可以根据自己需要重命名,比如yxz.然后单击NeW FUnCtion ,在这个类下面创建一个新的函数,然后命名,比如thepseudosec On dorderk in etic 1IlU- . F⅛∙.l,J⅛f4h÷∙⅛-I j IhF B MC∕.L*3■ j∣αwZ∣*4Z -a J⅛5^-⅛-■> £蚀^1佯时・∣3*3 !P"DMhF!U・L.y rJ⅛f⅛≡L⅛I J⅛"⅛wβW* F _dl ζ.i⅜∣:IIril⅞g -j⅛i-⅛ Fl b--J feJkh r^B ln≡ j ≡E:丄二二J h⅜ Ml-M ”■∣ςι UKL P.Γ⅞:SFtt l⅛l Vitw Adr 01U 時l A4M1HHt! M4⅜⅞∣SiInHi⅞F 丹申ħ2.对该函数进行简短的描述, Brief DeSCriPtiOn 栏输入:TO USed for the PSeUdO SeCOnd order kinetic fitting ,定义函数所需参数,ParameterNames: a,k;输入函数方程。
FUnction 栏输入需编写的方程:y=((a^2)*k*x)∕(1+a*k*x)这个方程的逻辑关系一定要对!3.然后进行点击FUnGtiQn右侧的按钮4•编译正确是前提是:方程正确,方程中的相关参数在方程之前进行了创建,参数声明和方程建立完成之后,单击=进入编译界面,单击Compile I5•当出现上图红框中文字是,证明公式定义成功,否则失败!须重新定义。
origin拟合准一级准二级动力学方程详解

建立用户自定义函数的步骤:
1.选择 : (快捷键F9) ,打开 . 单击按钮,创建一个函数类,可以根据自己需要重命名,比如 .然后单击,在这个类下面创建一个新的函数,然后命名,比如 1:
2. 对该函数进行简短的描述,栏输入:,定义函数所需参数,:;输入函数方程。
栏输入需编写的方程:
((a^2)*k*x)/(1*k*x) 这个方程的逻辑关系一定要对!
3.然后进行点击右侧的按钮
4. 编译正确是前提是:方程正确,方程中的相关参数在方程之前进行了创建,参数声明和方程建立完成之后,单击
进入编译界面,单击
5.当出现上图红框中文字是,证明公式定义成功,否则失败!须重新定义。
6. 在中单击,然后单击,再单击。
7.至此,用户自定义函数的建立已经完成。
二、自定义拟合函数的使用:
1先建立原文件图用点格式绘图
2. 完成后点击工具栏里的
3. 选择刚建立的下的 1 公式。
4. 点击
5.在参数栏中分别设置 a和k 的初始值(可以根据经验任意设置),设置数值是只需在这一栏双击鼠标,就可以输入数据!
6.随后点击单击一次拟合之后,得到以下结果:
7.拟合并不很理想,然后直接拟合到收敛,可以看到拟合结果满意,单击:
拟合到8 拟合完成结果如图
9.拟合曲线数据点,点击上图中输出
10.可以根据上述拟合数据作图。
11 / 11。
origin拟合准一级准二级动力学方程详解

建立用户自定义函数的步骤:1、选择Tools: Fitting Function Organizer (快捷键F9) ,打开Fitting function organizer、单击New Category 按钮,创建一个函数类,可以根据自己需要重命名,比如yxz、然后单击New Function,在这个类下面创建一个新的函数,然后命名,比如thepseudosecondorderkinetic 1:2、对该函数进行简短的描述,Brief Description栏输入:To used for the pseudo second order kinetic fitting,定义函数所需参数,ParameterNames:a,k;输入函数方程。
Function 栏输入需编写的方程:y=((a^2)*k*x)/(1+a*k*x) 这个方程的逻辑关系一定要对!3、然后进行点击Function 右侧的按钮4、编译正确就是前提就是:方程正确,方程中的相关参数在方程之前进行了创建,参数声明与方程建立完成之后,单击进入编译界面,单击Compile5、当出现上图红框中文字就是,证明公式定义成功,否则失败!须重新定义。
6、在file中单击save,然后单击return to dialog,再单击OK。
7、至此,用户自定义函数的建立已经完成。
二、自定义拟合函数的使用:1先建立原文件图用点格式绘图2、完成后点击工具栏里的Analysis----Fitting----3、选择刚建立的yxz 下的thepseudosecondorderkinetic 1 公式。
4、点击Parameters5、在参数栏中分别设置a与k 的初始值(可以根据经验任意设置),设置数值就是只需在value 这一栏双击鼠标,就可以输入数据!6、随后点击单击一次拟合之后,得到以下结果:7、拟合并不很理想,然后直接拟合到收敛,可以瞧到拟合结果满意,单击OK:拟合到收敛8 拟合完成结果如图9、拟合曲线数据点,点击上图中Fit NLCURvel 输出10、可以根据上述拟合数据作图。
准二级动力学方程origin拟合

准二级动力学方程origin拟合动力学方程是描绘物体在运动中的状态和变化的数学描述,是现代物理学的基础之一。
其中,准二级动力学方程是一种应用广泛的动力学方程类型,可以很好地描述物体的运动状态。
本文将主要介绍准二级动力学方程的定义、特点以及如何进行Origin拟合。
准二级动力学方程定义准二级动力学方程是指物体在运动中受到二级阻尼力影响时的运动方程。
这种运动方程的特点是,临界阻尼值(即阻尼系数和共振频率相等时的阻尼系数)一定存在,当阻尼系数小于临界阻尼值时,运动状态为过阻尼(overdamped);当阻尼系数等于临界阻尼值时,运动状态为临界阻尼(critical damping);当阻尼系数大于临界阻尼值时,运动状态为欠阻尼(underdamped)。
准二级动力学方程特点有几个显著的特点值得我们注意:一、准二级动力学方程与振幅振动非常相关。
Am即振幅,当摩擦不会导致振幅衰减,就会发生振幅振动。
二、在临界阻尼条件下,准二级动力学方程达到极值点后的变化速度恰好为0。
三、在欠阻尼情况下,振幅随时间变化的规律呈幅度衰减,频率保持不变。
振幅随时间呈指数函数下降,随时间的平方函数振荡。
四、另一个显著的特点,它可以应用于各种物理现象的研究,例如自然界中的自由振动、电路中的振荡现象、化学反应的动力学问题等等。
如何进行Origin拟合进行准二级动力学方程的Origin拟合需要注意以下几点:一、确定数据根据实验测量得到的数据,包括时间与振荡振幅的关系。
二、创建分析模型打开Origin软件,创建一个新工作簿,输入数据。
然后选择Plot > New Plot,将数据绘制在图表中。
接下来,选择Analysis > Nonlinear Curve Fit > Peak: Ad-hoc with Fixed Half Width 这个选项。
三、设置曲线拟合在设置曲线拟合之前,需要先定义模型函数,即准二级动力学方程。
准二级动力学方程origin拟合

准二级动力学方程origin拟合准二级动力学方程拟合是数据分析和统计学中非常重要的一种方法,它通常用来描述一些复杂的物理、化学和生物过程。
在很多实际应用中,该方法常常被用来预测某些数据集的行为模式和趋势性。
下文将围绕准二级动力学方程拟合,分步骤阐述其原理和拟合过程。
一、准二级动力学方程的定义准二级方程通常被定义为一个解析式,其中包含参数a、b、c和d,形式如下:y(t) = a/(b+t)^c + d其中y(t)代表某个物理量在时刻t的值,a、b、c和d都是未知参数,需要通过数据拟合获得。
二、拟合过程在实际应用中,我们通常会将若干个数据点代入准二级方程中,使用最小二乘法或其他拟合技巧来计算出参数a、b、c和d的值。
这个过程可以简单分为以下几个步骤:1. 数据预处理:对于任何数据分析任务,数据预处理都是至关重要的一步。
在进行准二级方程拟合时,我们需要先将数据进行预处理,如去除噪声,平滑数据等。
2. 数据建模:在进行准二级方程拟合之前,我们需要先将数据转化为可供分析的形式。
通常,我们需要将所有的自变量和因变量转化为对数形式,这样才能做到线性拟合。
3. 拟合过程:在得到数据模型后,我们需要使用拟合算法来确定模型的参数值。
对于准二级方程,我们通常采用非线性最小二乘算法来进行拟合。
这个过程中,我们需要指定初始值并确保算法能够顺利找到拟合值域。
4. 参数评价:在进行准二级方程拟合时,我们需要使用各种评价指标来衡量该模型的准确性和可信度。
这些指标通常包括拟合误差、均方根误差、决定系数等等。
5. 结果解读:最后,我们需要对拟合结果进行解读,确定该模型是否具有实用性和可靠性。
如果需要,我们还可以利用该模型进行预测和优化。
三、应用领域准二级动力学方程拟合在众多领域中都有广泛应用。
其中包括:1. 化学动力学:准二级方程可以被用来描述各种化学反应的速率与浓度之间的关系,帮助化学家优化反应过程和预测反应行为。
2. 生物学:准二级方程也被广泛用于分析细菌生长、细胞增殖等生命科学问题,帮助生物学家了解生物过程的动力学本质。
origin拟合准二级动力学方程

Origin拟合准二级动力学方程概述准二级动力学方程是一种常见的动力学模型,用于描述化学反应、生物动力学、环境系统等领域中的动态过程。
在实际研究中,根据实验数据来拟合准二级动力学方程是非常重要的,可以帮助我们深入理解和预测系统的行为。
理论基础准二级动力学方程可以表示为:r = k * (A - B * t) / (1 + C * t)其中,r是反应速率,k是速率常数,A和B是反应物的浓度,t是反应时间,C是另一个常数。
Origin软件Origin是一款功能强大的数据分析和可视化软件,可以广泛应用于物理、化学、生物等领域的科研工作。
Origin提供了许多工具和功能,可以方便地进行数据拟合和分析。
准备数据在使用Origin进行准二级动力学方程的拟合之前,我们首先需要获得一组实验数据。
这些数据应包括反应时间和对应的反应速率。
数据导入1.打开Origin软件并创建一个新项目。
2.在工作表中输入实验数据,第一列为时间,第二列为速率。
拟合准二级动力学方程1.在工作表中选择要拟合的数据。
2.点击菜单栏中的Analysis,选择Fitting,再选择Nonlinear Curve Fit。
3.在弹出的对话框中,选择User-defined Function作为拟合函数类型。
4.在拟合函数中输入准二级动力学方程的表达式。
5.定义拟合参数和初始值。
6.点击Fit按钮进行拟合。
7.查看拟合结果和拟合图像,评估拟合质量。
拟合结果分析拟合结果中的参数值和拟合曲线可以帮助我们理解实验数据和了解反应过程。
下面是一些拟合结果的分析方法:1.检查拟合参数的物理意义和单位。
2.计算拟合曲线和实验数据之间的残差。
3.计算拟合函数的相关系数,评估拟合曲线和实验数据的拟合程度。
4.进行统计分析,例如计算拟合参数的置信区间和假设检验。
5.根据拟合曲线对反应过程进行预测和优化。
结论使用Origin软件拟合准二级动力学方程可以帮助我们深入理解系统的动力学行为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
o r i g i n拟合准一级准二级动力学方程详解
39566
建立用户自定义函数的步骤:
1.选择 Tools: Fitting Function Organizer (快捷键F9) ,打开 Fitting function organizer. 单击 New Category 按钮,创建一个函数类,可以根据自己需要重命名,比如 yxz.然后单击 New Function,在这个类下面创建一个新的函数,然后命名,比如 thepseudosecondorderkinetic 1:
2. 对该函数进行简短的描述,Brief Description栏输入:To used for the pseudo second order kinetic fitting,定义函数所需参数,ParameterNames:a,k;输入函数方程。
Function 栏输入需编写的方程:y=((a^2)*k*x)/(1+a*k*x) 这个方程的逻辑关系一定要对!
3.然后进行点击Function 右侧的按钮
4.编译正确是前提是:方程正确,方程中的相关参数在方程之前进行了创建,
参数声明和方程建立完成之后,单击进入编译界面,单击Compile
5.当出现上图红框中文字是,证明公式定义成功,否则失败!须重新定义。
6.在file中单击 save,然后单击return to dialog,再单击OK。
7.至此,用户自定义函数的建立已经完成。
二、自定义拟合函数的使用:
1先建立原文件图用点格式绘图
2.完成后点击工具栏里的Analysis----Fitting----
3. 选择刚建立的yxz 下的thepseudosecondorderkinetic 1 公式。
4. 点击 Parameters
5.在参数栏中分别设置 a和k 的初始值(可以根据经验任意设置),设置数值是只需在 value 这一栏双击鼠标,就可以输入数据!
6.随后点击单击一次拟合之后,得到以下结果:
7.拟合并不很理想,然后直接拟合到收敛,可以看到拟合结果满意,单击OK:
拟合到收8 拟合完成结果如图
9.拟合曲线数据点,点击上图中 Fit NLCURvel 输出
10.可以根据上述拟合数据作图。
