动力学方程拟合模型.
动力学方程拟合模型

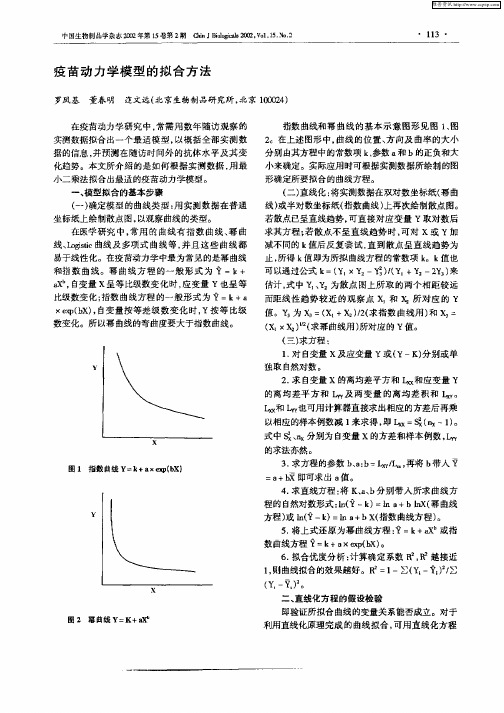
动力学方程拟合模型动力学方程拟合模型主要分为幂函数型模型和双曲线型模型。
在幂函数型动力学方程中,温度和浓度被认为是独立地影响反应速率的,可以表示为:在双曲线型动力方程中强调模型方程中的吸附常数不能靠单独测定吸附性质来确定,而必须和反应速率常数一起由反应动力学实验确定。
这说明模型方程中的吸附平衡常数并不是真正的吸附平衡常数,模型假设的反应机理和实际反应机理也会有相当的距离。
双曲线型动力学方程的一般表达形式为上述两类动力学模型都具有很强的拟合实验数据的能力,都既可用于均相反应体系,也可用于非均相反应体系。
对气固相催化反应过程,幂函数型动力学方程可由捷姆金的非均匀表面吸附理论导出,但更常见的是将它作为一种纯经验的关联方式去拟合反应动力学的实验数据。
虽然,在这种情况中幂函数型动力学方程不能提供关于反应机理的任何信息,但因为这种方程形式简单、参数数目少,通常也能足够精确地拟合实验数据,所以在非均相反应过程开发和工业反应器设计中还是得到了广泛的应用。
1.幂函数拟合刘晓青[1]等人研究了HNO3介质中TiAP萃取Th(Ⅳ)的动力学模式和萃取动力学反应速率方程。
对于本萃取体系,由反应速率方程的一般形式可知:可用孤立变量法求得各反应物的分反应级数a、b与c,从而确立萃取动力学方程。
第一步:分级数的求算1.求a固定反应物中TiAP和HNO3的浓度,当TiAP的浓度远远大于体系中Th的初始浓度时,可以认为体系中TiAP浓度在整个萃取过程中没有变化而为一定値,则速率方程可以简化为两边取对数后得:ln{-d[Th-]/dt}=aln[Th]+ln1,用ln{-d[Th-]/dt}对ln[Th]作图得到一条直线(r=0.9973),其斜率即为a。
结果如图1所示,从图中可知斜率为1.05,即此动力学速率方程中Th(Ⅳ)的分反应级数a=1.05。
2.求b和c同求Th(Ⅳ)分反应级数类似,固定反应物中Th(Ⅳ)和HNO3的浓度,则速率方程可以简化为固定反应物中Th(Ⅳ)和TiAP的浓度,则速率方程可以简化为画图可得:TiAP的分反应级数为1.77,HNO3的分反应级数为0.38。
疫苗动力学模型的拟合方法
Y
独 取 自然对 数 。
2 求 自变量 x的离均差平方和 L . 和应变量 Y 的离均差平 方和 I 及两变 量 的离均 差积和 L 。 m k 和 也可用计算器直接求出相应的方差后再乘
以相应的样本例数减 1 来求得 , L 即 =s(x ) n 一1。
式中 、x n 分别为 自变量 x的方差和样本例数, 的求法亦然 。
表 1 Ⅱ型 加嗽s灭活单价疫苗的免疫持久性 图 3 1型 m s灭活单价癌 苗接种后的 免疫持久性 散 1 t 点 图
其 自然对数的形式为:l l —k =I a bX 令 | ( ) n + , Y =l( 一k , na n )a=I 。则 方程 可简 写 为 : Y =a+
而距线性趋势较近的观察点 和 所对 应的 Y
值 。 为 =( )2求 指 数 曲线 用 ) X + /( 和 =
( × ) 求幂曲线用 ) ( 所对应的 Y值。
( ) 方程 : - 求 1 对 自变量 x及 应变 量 Y或 ( . Y—K 分 别 或单 )
小来确定。实际应用时可根据实测数据所绘制的图 形确 定所要 拟台 的 曲线 方程 。 ( ) - 直线化 : 将实测数据在双对数坐标纸( 幂曲 线) 或半对数坐标纸( 指数曲线 ) 上再次绘制散点图。 若散点已呈直线趋势, 可直接对应变量 Y取对数后 求 其 方程 ; 散 点不 呈 直 线 趋 势 时 , 对 x或 Y加 若 可 减不同的 k 值后反复尝试 , 直到散点呈直线趋势为 止, 所得 k 值即为所拟 曲线方程的常数项 k 值也 。k 可 以通 过公式 k Y xY 一 )( 。 2 Y ) =( 。 /Y +Y —2 来
在疫苗 动 力学 研 究 中 , 常需 用 数年 随访 观 察 的
化学反应器的数学模型及其控制

化学反应器的数学模型及其控制序言化学反应器是化学工业生产的核心设备,其鲁棒性和可控性是影响生产质量和效益的重要因素。
本文将介绍化学反应器的数学模型及其控制策略,旨在为化学工业生产和控制系统的优化提供参考。
一、化学反应器的数学模型化学反应器的数学模型是基于质量守恒、能量守恒和化学反应动力学等理论进行建立的。
其中,最常用的模型是连续拟合模型和分布参数模型。
1. 连续拟合模型连续拟合模型采用宏观平衡方程和动力学方程对反应器系统进行描述。
宏观平衡方程包括质量平衡和能量平衡两部分。
动力学方程则描述了物料在反应过程中的转化速率。
该模型通常采用微分方程组进行求解。
以催化剂颗粒床反应器为例,其数学模型如下:(1)质量平衡方程:$$\frac{\partial(\rho C W)}{\partial t}+\frac{\partial(\rho C W u)}{\partial x}=0$$(2)能量平衡方程:$$\frac{\partial(\rho C_p W T)}{\partial t}+\frac{\partial(\rho C_p W T u)}{\partial x}=\frac{\partial}{\partial x}(\lambda\frac{\partialT}{\partial x})+r\Delta H_R$$(3)物料转化速率方程:$$r=k(C_{A,f}-C_A)^n$$其中,$\rho$ 为颗粒床密度,$C$ 为反应物质浓度,$W$ 为颗粒床体积,$u$ 为颗粒床内流速,$x$ 为颗粒床内径向坐标,$T$ 为颗粒床内温度,$C_p$ 为热容,$\lambda$ 为导热系数,$r$ 为反应速率,$k$ 为反应速率常数,$n$ 为阶数,$\DeltaH_R$ 为反应焓变,$C_{A,f}$ 为反应物质浓度。
2. 分布参数模型分布参数模型则是采用微小体积元方法对反应器系统进行离散化,将反应器分为若干个微小体积,分别进行建模。
化学反应过程的计量学分析和反应动力学参数拟合方法

化学反应过程的计量学分析和反应动力学参数拟合方法化学反应过程是化学学科的核心领域之一,对于了解反应的本质和改进反应工艺具有重要意义。
在研究化学反应过程中,计量学分析和反应动力学参数拟合方法是两个关键概念。
计量学分析是指通过实验测定反应物和生成物的量,推导出化学方程式的反应系数。
反应动力学参数拟合方法则旨在研究反应速率与反应条件之间的关系。
计量学分析在化学反应过程中具有重要意义。
通过仔细测量反应物和生成物的物质量,可以确定化学方程式中的反应系数。
例如,对于涉及氧化还原反应的反应物A和B生成产物C和D的反应:aA + bB → cC + dD通过实验,我们可以测量反应物A和B的摩尔量,以及产物C和D的摩尔量。
根据质量守恒定律和摩尔量比例,我们可以计算出反应系数a、b、c和d的数值。
计量学分析提供了确定化学反应过程中物质转化的定量信息,为研究反应机制和改进反应工艺提供了基础。
而反应动力学参数拟合方法则关注反应速率与反应条件之间的关系。
反应速率是指单位时间内发生反应的物质转化率。
反应速率通常与反应物浓度、温度和催化剂等因素有关。
在研究反应动力学时,常用的方法是测量在不同反应条件下的反应速率,并将实验数据拟合到适当的数学模型中。
最常用的反应动力学模型是速率方程模型。
速率方程关联反应速率与反应物浓度的关系,其形式可由实验数据拟合得出。
例如,对于一级反应,其速率方程可以表示为:r = k[A]其中,r是反应速率,k是反应速率常数,[A]是反应物A的浓度。
通过实验测量不同浓度下的反应速率,可以求解出反应速率常数k的数值。
除了速率方程模型外,还有一些更复杂的模型可用于描述特殊类型的化学反应。
例如,对于涉及催化剂的反应,常用的模型是麦尔金-韦特模型。
该模型考虑反应物在催化剂表面上的吸附和解离过程,能更准确地描述反应动力学过程。
拟合实验数据到适当的数学模型中是确定反应动力学参数的关键一步。
常用的拟合方法包括最小二乘法和非线性回归分析。
matlab拟合动力学方程

matlab拟合动力学方程
MATLAB可以用于拟合动力学方程。
在MATLAB中,我们可以使用curve fitting工具箱来实现这个目标。
首先,我们需要收集我们的数据,并确定我们要拟合的动力学方程的类型。
例如,我们可以选择一阶动力学方程:dy/dt = -k*y,其中y是我们的输出变量,t是时间,k是动力学常数。
然后,我们可以使用MATLAB的curve fitting工具箱来拟合这个方程。
以下是一些步骤:
1. 导入数据:将我们收集的数据导入MATLAB环境。
确保数据已经存储为一个列向量,例如y和t。
2. 建立起始参数:根据我们的动力学方程,我们需要为k提供一个初始猜测值。
这个值可以根据我们的应用和经验来确定。
3. 建立模型:使用fittype函数创建一个模型对象,该对象表示我们要拟合的动力学方程。
4. 进行拟合:使用fit函数拟合我们的数据。
该函数将数据和模型作为参数,并返回包含拟合结果的对象。
5. 分析结果:我们可以通过访问拟合对象的属性来分析拟合结果,例如拟合参数的值和置信区间。
6. 可视化结果:使用plot函数绘制原始数据和拟合结果的图像,以便我们可以直观地评估拟合的质量。
通过这些步骤,我们可以使用MATLAB拟合动力学方程,并从拟合结果中获得我们感兴趣的参数值。
准一级和准二级动力学模型拟合参数

准一级和准二级动力学模型拟合参数
准一级动力学模型是指反应速率与反应物浓度的一次方成正比,其微分方程可以表示为:dy/dt=k[A],其中y为反应物的浓度,t为反应时间,k为反应速率常数,[A]为反应物的浓度。
该模型适用于反应物浓度较低、反应机理为单分子解离或反应中心为稀有物质的情况。
准二级动力学模型是指反应速率与反应物浓度的二次方成正比,其微分方程可以表示为:dy/dt=k[A]^2,其中y为反应物的浓度,t为反应时间,k为反应速率常数,[A]为反应物的浓度。
该模型适用于反应物浓度较高、反应机理为双分子解离或反应中心为富集物质的情况。
关于准一级和准二级动力学模型拟合参数,涉及到复杂的数学模型和计算,建议您请教专业人士。
一级动力学拟合

一级动力学拟合
一级动力学拟合是探究某一系统行为方式的一种方式,它可以被用于解释这种行为方式的根本原因。
下面我们来一步步了解一级动力学拟合的具体内容和应用场景。
一、什么是一级动力学拟合?
一级动力学拟合是通过对某个系统所受到的外部刺激进行实验,并记录下系统响应的变化情况,然后将所得到的数据用一级动力学模型进行拟合并进行分析,以确定实验结果的相关特性与其所受到的刺激之间的关系。
二、一级动力学拟合的基本原理
一级动力学拟合是建立在对科学实验的基本原理上的,其具体的原理包括对输入与输出变量之间的关系进行建模,使用线性方程或非线性方程来拟合所得实验数据,以及选择适当的参数来解释实验结果。
三、一级动力学拟合的应用场景
1.经济学:一级动力学拟合可以被用于研究市场和货币政策对于经济系统的影响。
2.环境学:一级动力学拟合可以被用于预测和控制环境变化的影响,尤其是在探究气候变化的场景下。
3.生物学:一级动力学拟合可以帮助研究生物体的组织生长和代谢过
程以及受到外部环境变化的影响,用于预测疾病的发生和治疗效果。
四、一级动力学拟合的注意事项
1.对数据质量较低的实验, 一级动力学拟合可能会得到错误的解释。
2.适当的模型选择可以更好地解释实验数据和研究结果。
3.一级动力学拟合需要注意实验数据的采集和实验条件的准确性。
五、汇总
一级动力学拟合是一种探究系统行为方式的方法,其原理是通过对输入输出变量之间的关系建立线性方程或非线性方程,在实验中查看所得数据并进行适当的参数选择,从而解释实验结果。
它在经济学、环境学和生物学等领域有广泛的应用,但需要注意数据质量、模型选择和实验条件的准确性等问题。
origin拟合准二级动力学方程

origin拟合准二级动力学方程
Origin是一款科学绘图软件,可以用于数据分析和拟合。
准二级动力学方程是描述快速反应动力学的方程之一,其形式为:
d[A]/dt = k([A]0 - [A])^2
其中,[A]是反应物的浓度,t是时间,k是反应速率常数,[A]0是反应物的初始浓度。
在Origin中,拟合准二级动力学方程可以通过以下步骤完成:
1. 打开Origin软件,并导入数据文件。
2. 选择数据,并打开拟合窗口。
3. 在拟合窗口中选择“非线性拟合”选项。
4. 在拟合函数列表中选择准二级动力学方程。
5. 进行参数设置,包括起始参数、参数界限等。
6. 进行拟合,并查看拟合结果和拟合曲线。
7. 分析拟合结果,包括参数值、相关系数、拟合优度等。
需要注意的是,拟合准二级动力学方程需要有足够的数据点和反应速率常数的估计值,否则拟合结果可能不准确。
同时,拟合结果也需要进行统计分析和验证,
以确保其可靠性和可重复性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动力学方程拟合模型
动力学方程拟合模型主要分为幂函数型模型和双曲线型模型。
在幂函数型动力学方程中,温度和浓度被认为是独立地影响反应速率的,可以表示为:
在双曲线型动力方程中强调模型方程中的吸附常数不能靠单独测定吸附性质来确定,而必须和反应速率常数一起由反应动力学实验确定。
这说明模型方程中的吸附平衡常数并不是真正的吸附平衡常数,模型假设的反应机理和实际反应机理也会有相当的距离。
双曲线型动力学方程的一般表达形式为
上述两类动力学模型都具有很强的拟合实验数据的能力,都既可用于均相反应体系,也可用于非均相反应体系。
对气固相催化反应过程,幂函数型动力学方程可由捷姆金的非均匀表面吸附理论导出,但更常见的是将它作为一种纯经验的关联方式去拟合反应动力学的实验数据。
虽然,在这种情况中幂函数型动力学方程不能提供关于反应机理的任何信息,但因为这种方程形式简单、参数数目少,通常也能足够精确地拟合实验数据,所以在非均相反应过程开发和工业反应器设计中还是得到了广泛的应用。
1.幂函数拟合
刘晓青[1]等人研究了HNO3介质中TiAP萃取Th(Ⅳ)的动力学模式和萃取动力学反应速率方程。
对于本萃取体系,由反应速率方程的一般形式可知:
可用孤立变量法求得各反应物的分反应级数a、b与c,从而确立萃取动力学方程。
第一步:分级数的求算
1.求a
固定反应物中TiAP和HNO3的浓度,
当TiAP的浓度远远大于体系中Th的初始浓
度时,可以认为体系中TiAP浓度在整个萃
取过程中没有变化而为一定値,则速率方程
可以简化为
两边取对数后得:
ln{-d[Th-]/dt}=aln[Th]+ln1,用ln{-d[Th-]/dt}
对ln[Th]作图得到一条直线(r=0.9973),其斜率即为a。
结果如图1所示,从图中可知斜率为1.05,即此动力学速率方程中Th(Ⅳ)的分反应级数a=1.05。
2.求b和c
同求Th(Ⅳ)分反应级数类似,固定反应物中Th(Ⅳ)和HNO3的浓度,则速率方程可以简化为
固定反应物中Th(Ⅳ)和TiAP的浓度,则速率方程可以简化为
画图可得:
TiAP的分反应级数为1.77,HNO3的分反应级数为0.38。
第二步:写出反应反应速率方程
则293K时,该反应的平均速率常数k为1.6*10-2(mol/L)-2.2·s-1。
2.双曲线拟合
双曲线型反应动力学方程是由Hinshelwood在研究气固相催化反应动力学时,根据Langmuir的均匀表面吸附理论导出的,其后Hougen和Watson用此模型成功地处理了许多气固相催化反应,使它成为一种广泛应用的方法。
因此,双曲线型动力学方程又被称为Langmuir-Hin-shelwood方程或Hougen-Watson方程。
王志良[2]等人用半连续式无梯度反应器在130~210 ℃范围内研究了苯与乙烯在FX-02沸石催化剂上烷基化反应的本征动力学。
应用改进的Gauss-Newton 法对常微分形式的动力学模型进行了参数估值,得到了双曲函数形式的本征动力学方程。
体系的反应情况如下:
乙烯( E)、苯( B)、乙苯( EB)、二乙苯( DEB)
根据Langmuir-Hinshelwood 机理, 对上述两个反应用如下的动力学模型来表示:
序贯试验设计选用最小体积判别式( MVD ):
对ks1、ks- 1、ks2、ks- 2、KE、KB、KEB、KDEB八个参数采用改进的Gauss-Newton 法,直接对常微分形式的动力学模型进行参数估值,目标函数由最小二乘估值准则确定:
经过动力学的预试验和序贯试验后,下图给出了参数估值的相对置信区间大小与试验次数的关系。
可以看出,当进行5次序贯试验后,Δ-1/2的值迅速下降, 表
明试验点的安排较合理,在有效的试验次数内使参数的估值达到了相当高的置信度。
参数估计是在序贯试验下进行的,对参数的联合置信区间检验结果证明,参数具有很高的精度。
模型检验其方差分析结果表明,计算值与试验数据的相符性良好, 残差分析进一步证明模型无缺陷。
3.其他算法在动力学方程中的应用
在查找文献的时候,找到多篇与动力学有关的文献采用了不同的算法对动力学参数进行拟合估算。
3.1遗传算法
遗传算法(Genetic Algorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
黄晓峰[3]等用改进的实数编码遗传算法进行了估计反应动力学参数的研究,提出了一种优化分布线性交叉操作策略,使子代个体在搜索空间内达到均匀分布,从而提高了搜索的效率。
作者用这种改进的实数编码遗传算法进行了正丁烷选择氧化反应动力学参数的估计。
正丁烷在VPO催化剂上选择氧化制顺酐,是催化晶格氧参与催化循环、按照氧化还原( RE-DOX) 机理进行的重要烃类选择氧化反应,其简化后的基元反应序列为:
R 和X 分别代表还原态和氧化态催化剂,B 为正丁烷,MA 为顺酐。
主要操作策略和控制参数为:适应度线性调整、带最优个体保存的期望值选
择, 优化分布的线性交叉操作和连续变异操作。
种群数目N =50 , 交叉概率Pc =0.8 , 变异概率Pm =0.05 , 交叉系数α=2.0 。
优化问题描述为估计反应速率常数K 1 、K 2 或活化能E 1 、E 2 与指前因子k01 、k 02 , 以使反应速率的估计值rBE 与测量值rBM 的偏差平方和RSS 极小化:
最后结果如下,表现出较高的精度。
3.2蒙特卡罗法
詹晓力[4]等利用蒙特卡罗方法模拟计算了化学反应动力学参数,由基元反应确定蒙特卡罗模拟的具体做法,将蒙特卡罗方法的模拟结果与动力学实验结果进行比较,根据比较结果自动调整和优化动力学参数,从而无需事先确定动力学方程,即可有效地估算各种化学反应的动力学参数。
用该方法模拟Mo-Bi 系丙烯氨氧化催化剂上的氨分解基元反应。
无丙烯存在下的氨分解基元反应如下:
下图给出了用蒙特卡罗方法对该问题进行模拟的结果,m 为催化剂质量,nA0为初始氨物质的量,c R为转化率,r 为速率。
从图中可见,按估算的动力学参数所计算的转化率-时间和反应速率-时间曲线与实验数据吻合得较好。
总结
化学反应的机理通常是十分复杂的。
一些看起来相当简单的反应的机理至今也没有完全搞清。
因此,不论是双曲线型模型还是幂函数型模型,都只是可以用来拟合反应动力学实验数据的一种函数形式。
由于这两种方程在数学上的适应性极强,对同一组实验数据可同时用这两种方程拟合的例子也是屡见不鲜的。
从这个意义上讲,目前工程上应用的绝大多数动力学模型都不是机理模型,在原实验范围之外作大幅度的外推都是有风险的。
参考文献
[1]刘晓青等.HNO3介质中TiAP萃取Th(Ⅳ)的动力学研究[J].四川大学学报,2014,51(6):1249-1254.
[2]王志良等.FX-02沸石催化剂上苯与乙烯烷基化的反应动力学[J].石油炼制与化工,1999,30(2):52-55.
[3]黄晓峰,潘立登,陈标华,等.用改进的实数编码遗传算法估计反应动力学参数[J].高校化学工程学报,1999,13( 1) : 50-55.
[4]詹晓力,罗正鸿,陈丰秋,等.基于Monte Carlo 模拟的化学反应动力学参数估算[J].高
等学校化学学报,2003,24( 8) : 1511-1514.。
