勾股定理的应用1
勾股定理的应用(1)

S3
S2
S1
心,在森林公园附近有 B、C 两个村庄,现要在 B、C两
村庄之间修一条长为 1000 m 的笔直公路将两村连通,
经测得 ∠B=60°,∠C=30°,问此公路是否会穿过该森
林公园?请通过计算说明.
解: ∵∠B=60°,∠C=30°,
400
A
∴∠BAC=90°
∴AB=½ BC=500m,
由AC勾股定10理00,2 得5002 500 3 60° ┐
l h
┐
b
解:10 1.52 32 33.5(m2 )
5. 如图,在甲村到乙村的公路旁有一块山地正在开发, 现有A处需要爆破.已知点A与公路上的停靠站B,C的距离 分别为400m和300m,且AC⊥AB.为了安全起见,如果爆 破点A周围半径250m的区域内不能有车辆和行人,问在 进行爆破时,公路BC段是否需要暂时封闭?为什么?
解:由勾股定理,得 A
BC AB2 AC 2 l 2 h2 122 82
4 5 8.9(m)
lh
B
C
答:点B离电线杆底部点C的距离
约为8.9米.
4. 如图要修一条塑料蔬菜大棚,棚宽 b=3m,高 h=1.5m, 长 l=10m.求覆盖在顶上的长方形塑料薄膜需要多少平方 米?(精确到 0.1m²)
解:过A作AD⊥BC,垂足为D.
甲
由勾股定理,得
B
BC²=AB²+AC²=400²+300²=250000
∴BC=500
D
勾股定理的应用一(蚂蚁爬行最短路线问题)
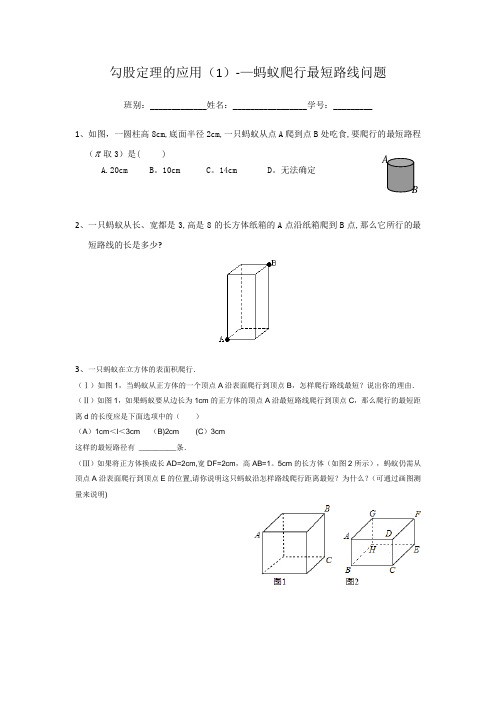
勾股定理的应用(1)-—蚂蚁爬行最短路线问题班别:_____________姓名:_________________学号:_________1、如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( )A.20cm B。
10cm C。
14cm D。
无法确定2、一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是多少?3、一只蚂蚁在立方体的表面积爬行.(Ⅰ)如图1,当蚂蚁从正方体的一个顶点A沿表面爬行到顶点B,怎样爬行路线最短?说出你的理由.(Ⅱ)如图1,如果蚂蚁要从边长为1cm的正方体的顶点A沿最短路线爬行到顶点C,那么爬行的最短距离d的长度应是下面选项中的()(A)1cm<l<3cm (B)2cm (C)3cm这样的最短路径有_________条.(Ⅲ)如果将正方体换成长AD=2cm,宽DF=2cm,高AB=1。
5cm的长方体(如图2所示),蚂蚁仍需从顶点A沿表面爬行到顶点E的位置,请你说明这只蚂蚁沿怎样路线爬行距离最短?为什么?(可通过画图测量来说明)AB4、如图所示:有一个长为3米,宽为1米,高为6米的长方体纸盒,一只小蚂蚁要沿着长方体的表面从A 点开始经过4个侧面绕一圈到达爬到B 点,则这只蚂蚁爬行的最短路径的长为__________。
若从A 点开始绕4个侧面两圈爬到B 点,最短路径长为____________。
5、一个圆柱体元件,底面半径为3,现要在其侧面绕线圈。
(1)若从A 点出发,绕侧面1圈到达B 点,线圈的长度最小为____________。
(结果保留π)(2)若从A 点出发,绕侧面5圈到达B 点,线圈的长度最小为____________。
(结果保留π)B A 6m 3m 1m。
2.7勾股定理的应用1

A B
C
解:在Rt△ABC中,由勾股定理,得 AC2 BA2 2.952 1.362 BC= =
≈2.62(km)
BA+AC≈1.36+2.95=4.31(km),
(BA+AC)-BC≈4.31-2.62=1.69≈1.7(km). 答:直接走湖底隧道比绕道BA和AC减少行程约1.7km.
一架长为10m的梯子AB斜靠在墙上.
8m
C
B
2m 8m
3. 一种盛饮料的圆柱形杯(如图),测得内 部底面半径为2.5㎝,高为12㎝,吸管放进杯 里,杯口外面至少要露出4.6㎝,问吸管要做 多长?
A
B
C
ห้องสมุดไป่ตู้
D
A A
B C
如图是一个正方体盒子,在正方体 下底部的A点有一只蚂蚁,它想吃到上 底面B点的食物(BC=3cm),需爬行的最 短路程是多少?
A’
C
B
B’
A 1.如图,太阳能热水器 的支架AB长为90cm, 与AB垂直的BC长 120cm.太阳能真空管 AC有多长?
C
B
2. 如图,有两棵树,一棵高8m,另一棵 高2m,两树相距8m,一只小鸟从一棵树的 树梢飞到另一棵树的树梢,至少飞了 ( ) A.7m B.8m C.9m D.10m
A
初中数学八年级下册 (苏科版)
2.7勾股定理的应用(1)
A
G
B C D E F
如果知道桥面以上的索塔AB的高, 怎样计算拉索AC、AD、AE、AF、 AG的长?
复习回忆
直角三角形两直角边的平方 和等于斜边的平方
A
a2+b2=c2 AC2+BC2=AB2
勾股定理在生活中的应用

勾股定理在生活中的应用
勾股定理又称勾股论,即毕达哥拉斯设计的一个无理定理:“任意三角形的两边之积等于另外一边的平方之和”。
这个定理具有广泛的应用:
1、勾股定理在日常生活中可以用来确定三角形各边之间的关系:例如可以判断其中一边是不是一个倍数关系或者一个反比例关系。
通过建立对应方程,容易得到三角形三边的数值,作为三角形的参数。
2、也可以依据勾股定理来测量距离。
例如,构建一个直角三角形,让其一条边固定为一个值,我们使用两个斜边长度表示其他边的长度。
可以用i中国的三角测量法来求得某个距离的长度。
3、另外可以用勾股定理判断特殊的三角形。
例如可以判断一个三角形是不是等腰三角形、等边三角形或是直角三角形,只需要判断两边之积是否等于另外一边的平方之和。
4、勾股定理在空间中也有极大的作用,尤其是研究四面体或是更高维度的几何图形时。
例如可以用它来判断四面体的面面角是否都相等,以及求出该四面体的各个角。
另外还可以用它来求棱锥的体积、双曲线的起始点和极点等。
5 、另外勾股定理在物理学中也有广泛的应用,比如可以分析绳子长度或梯形长宽间的关系等。
总之,勾股定理由其卓越的简洁得到广泛应用,从日常生活到飞空实验都能发挥着无穷的作用,它被越来越多的人向科学家们赞美。
勾股定理的应用1
C
B
A
1,你能从点A到点B沿圆柱侧面 画出几条路线,你觉得哪条线路 最短呢?
C
B
A
2,将圆柱侧面开展成一个长方形, 从点A到点B的最短路线是什么?
C
B
C
B
A
A
3.蚂蚁从点A出发,想吃到点B处的食物,它沿 圆柱侧面爬行的最短路程是多少? (圆柱体的底面周长为18cm, 高AC为12cm)
C
B
C
B
3.有一圆形油罐底面圆的周长为24m,高为6m,一 只老鼠从距底面1m的A处爬行到对角B处 吃食物,它爬行的最短路线长为多少?
B
C A
B
A
分析:由于老鼠是沿着圆柱的 表面爬行的,故需把圆柱展开 成平面图形.根据两点之间线段 最短,可以发现A、B分别在 圆柱侧面展开图的宽1m处和长 24m的中点处,即AB长为最短 路线.(如图)
A
A
4,若蚂蚁先从点A 直接向上爬到点C, 然后再从点C沿底 C 面直径爬到点B, 这样爬的总路程与 沿圆柱侧面爬行的 A 最短路程比较,哪 条最短?
B
李叔叔想要检测雕塑底座正面的边AD 和边BC是否分别垂直于底边AB,但 他随身只带了卷尺, 1.你能替他想办法完成任务吗?
D C
A B
2,李叔叔量得边AD长是30cm,边AB 长是40cm,点B,D之间的距离是 50cm,边AD垂直于边AB吗? 3,小明随身只有一个长度 为20cm的刻度尺,他能有办法 检验边AD是否垂直于边AB吗? 边BC与边AB呢?
这是测量 B
3 勾股定理的应用举例 (一 )
A
B
C
B 勾a C 弦c 股b
一、 勾股定理: 字母表示:
如果在Rt∆ABC中,
14.2勾股定理的应用1

14.2章勾股定理的应用(1)教学目标:1、能够灵活运用勾股定理的性质和判定。
2、能用勾股定理解决直角三角形的一些问题。
3、把几何体适当展开成平面图形,再利用“两点之间线段最短”性质来解决最短路程问题。
复习导学:1、如果在Rt∆ABC中,∠C=90°那么直角三角形的两条直角边的等于它斜边的。
2、如果三角形的三边长a 、b 、c满足那么这个三角形是直角三角形。
课堂研讨:问题1:甲船以每小时30海里的速度,从A处向正北方向航行,同时乙船从A处以每小时40海里的速度向正西方向航行,两小时后,甲、乙两艘轮船相距多少海里?解:如图,在Rt∆ABC中,BC2=BC=(海里)答:甲乙两船相距海里。
问题2:甲船在港口A正南方向60海里的B处向港口行进,同时,在甲船正东方向80海里的C处有乙船也向港口行进,甲船的速度为30海里/时,乙船的速度为40海里/时.问: 1.甲、乙两船谁先到达港口?2.先到的船比后到的船提前几小时?挑战“试一试”:一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?说明理由。
最短路程问题:1、一只蚂蚁从点A出发,沿着圆柱的侧面爬行到CD的中点O,试求出爬行的最短路程。
(精确到0.1)2、在一个棱柱形的石凳子上,一位小朋友吃东西时留下一点食物在B处,恰好一只机灵而勇敢的蚂蚁路过A处(A在B的对面),它的触角准确的捕捉到了这个信息,并迅速的传给它的小脑袋,于是它迫不急待的想从A处爬向B处。
聪明的同学们,你们想一想:蚂蚁怎样走最近?练一练:如图,在棱长为10厘米的正方体的一个顶点A处有一只蚂蚁,现要向顶点B处爬行,已知蚂蚁爬行的速度是1厘米/秒,且速度保持不变,问蚂蚁能否在20秒内从A爬到B?课堂小结:1.要记住勾股定理及逆定理的内容。
2.把几何体适当展开成平面图形,再利用“两点之间线段最短”性质来解决最短路程问题。
课堂作业:课本58页,练习题第1、2题课本60页,习题第3、6题课后反思:。
勾股定理的应用1

总结: 运用勾股定理解决实际问题,关键在于 “找”到合适的直角三角形.
例2.一辆卡车装满货物后,能否通过如图所示的 工厂厂门?卡车高2.5m,宽1.6m,说明你的理由.
C
A
o
Q
2m
B
D
分析:由于厂门宽度足够,所以卡车 能否通过,只要看当卡车位于厂门正 中间时其高度是否小于CH,如图所 示,点D在离厂门中线 0.8米处,且CD⊥AB,与地面 交与H,又知DH=2.3m,只需 求CD,在直角△COD中即可求得 已知OC=1m,OD=0.8m.
(一) 直接运用勾股定理求边
1.已知:直角△ABC中,∠C=90°,
a=2, b=6 c 的值 若若 a=3, b=4, 求,求 c 的值。
2、若直角三角形的三边长分别为 12或 20 . 2、 4、 x,则x=_____
勾股定理的综合应用
例1.如图,一圆柱体的底面周长为20㎝,高AB为4 ㎝,BC是上底面的直径。一只蚂蚁从点A出发, 沿着圆柱的侧面爬行到点C,试求出爬行的最短路 程。(精确到0.01 ㎝)
2
(该题是2006年广东省中考题)
2、如图有两颗树,一棵高8m,另一棵高2m, 两树相距8m,一只小鸟从一棵树的树梢飞到 另一棵树的树梢,至少飞了多少米?
A
8m
E
C
2m
B
8m
D
3.在一棵树的20米的B处有两只猴子,其中一 只猴子爬下树走到离树40米的A处,另一只爬 到树顶D后直接跳向A处,且测得AD为50米,求 BD的长.
勾股定理的应用
学习目标:
• 1.学会利用勾股定理解决实际问题; • 2.会在图形中寻找勾股定理的切入点; • 3.培养自己的计算能力。
回顾:勾股定理
勾股定理的应用

勾股定理的应用(一)【知识梳理】1.勾股定理:如果直角三角形的两直角边分别为a,b,斜边为c,则有2.勾股定理逆定理(直角三角形判定定理):如果三角形的三边长a,b,c 满足 ,那么这个三角形是直角三角形.3.常用勾股数:① a=3 b=4 c=5② a=5 b=12 c=13③ a=7 b=24 c=25④ a=9 b=40 c=414.勾股定理实际应用:①已知直角三角形的两边,求第三边;②利用三边关系来判定直角;③用于证明含有平方关系的式子;④借助勾股定理来构造方程,解决实际问题【典例精讲】一、利用勾股定理求边长已知一个直角三角形的两边长分别为3和4,则第三边长是( )A .5B .25C .7D .5或7举一反三:△ABC 中,若AB=15,AC=13,高AD=12,则△ABC 的周长是( )A.42B.32C.42或32D.37或33二、利用勾股定理判断三角形形状已知a ,b ,c 为△ABC 三边,且满足a 2c 2-b 2c 2=a 4-b 4,则它的形状为( )A .直角三角形B .等腰三角形C .等腰直角三角形D .等腰三角形或直角三角形举一反三:△ABC 的三边a,b,c 满足ac bc ab c b a ++=++222则△ABC 是( )A .等边三角形B .等腰三角形C . 直角三角形D .等腰直角三角形三、勾股定理与折叠问题如图,在△ABC 中,∠C=900,AC=3,BC=4,AB 的垂直平分线交AB 于E ,交BC 于D ,求BD的长。
举一反三:把一张矩形纸片(矩形ABCD )按如图方式折叠,使顶点B 和点D 重合,折痕为EF . 若AB = 3 cm ,BC = 5 cm ,(1)重叠部分△DEF 的面积是多少cm 2?(2)求EF 的长。
四、勾股定理与面积问题如图,分别以直角三角形三边向外作三个半圆,若S 1=30,S 2=40,则S 3=_______.举一反三:有一块土地形状如图所示,︒=∠=∠90D B ,AB=20米,BC=15米,CD=7米,请计算这块土地的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最短路线问题:请同学们阅读120页例1,动手操作并思 考下列问题:(1)自制一个圆柱,尝试从A点到C点 沿圆柱侧面画出几条路线,你认为能画多少条路线? (2)如图,将圆柱侧面剪开展成一个长方形,从A点 到C点的最短路程是什么?为什么?如何求线段AC 的长度?
我怎 么走 会最 近呢?
B
C
B
C
A
A
B
C
10cm B 高 4cm A
C
A
长20cm
解:将圆柱如图侧面展开.在Rt△ABC中, ∵ ∠ABC=900 AB =4cm BC=10cm 根据勾股定理可知 AC2=AB2+BC2 AC2=42+102=16+100=116 ∴ AC≈10.77(cm) 答:蚂蚁爬行的最短路程约是10.77cm.
§14.2 勾股定理的应用(1)
内乡初中数学组 庞玖贤
【学习目标】
1、能熟练利用勾股定理求出线段 的长; 2、树立数形结合思想; 3、能将实际问题转化为数学问题, 建立数学模型。
1.勾股定理: (1)直角三角形两直角边 平方 和等于 斜边 的______ ______ 的平方.就是说, 对于任意的直角三角形,如果它的两条 直角边分别为a、b,斜边为c,那么一 2+b2=c2 a 定有: .这就是勾股定理. 三边之间 (2)勾股定理揭示了直角三角形 ______ 的数量关系,是解决有关线段计算问题 的重要依据。
B
五、当堂达标检测
3.如图,是一个三级台阶,它的每一级的长、宽、 高分别为20dm、3dm、2dm,A和B是这个台阶 两个相对的端点,A点有一只蚂蚁,想到B点去 吃可口的食物,则蚂蚁沿着台阶面爬到B点的最 20 短路程是_________ 25dm A
3
A
20 2 3
2 3 2 3
2
B
B
六、反思与评价
4
D
3
C
图①
C
5
3
.B
B
3
. A
C
4
Dห้องสมุดไป่ตู้
2
C
5
4 8 80
2
D A 4 图②
C
5
4
.B
B
4
.A
D
3C
C
5
3 9 90
2 2
D
3
A
图③
五、当堂达标检测
1.如图一个圆柱,底圆周长6cm,高4cm, 一只蚂蚁沿外壁爬行,要从A点爬到B 点,则最少要爬行 cm 5。 2.一只蚂蚁从长、宽都是3,高是8的长 A 方体纸箱的A点沿纸箱爬到B点,那么 它所爬行的最短路线的长是 _________ 10
B
C 1
2
B
A
A
三、小组交流 :
如图,在长是4cm、宽是3cm,高是5cm 的长方体纸箱的外部,一只蚂蚁从顶点A沿 纸箱表面爬到顶点B处,求它所行的最短路 线的长。 (分小组讨论点沿长方体侧面画出几条路线, 你认为哪条路线最短呢?)
. .A
4 3C
四、学生展示与教师指导:
B
B
5
5
A
D
2 2
7 5 84
二、当堂检测:
1、有一圆柱形油罐,底面周长是12米, 高是5米,现从油罐底部A点环绕油罐建 梯子,正好到A点的正上方B点,问梯子 最短需多少米? C B B
A
A
二、当堂检测:
2、如图,边长为1的正方体中,一只 蚂蚁从顶点A出发沿着正方体的外表 面爬到顶点B的最短距离是( B ). (A)3(B ) 5 (C)2(D)1
谈谈你本节课学到了哪些 知识?有什么收获?这节课你 最大的体会是什么?
七、作业
作业课本P123习题5, P126-127复习题4、5 《学导》110页12 117页2
