最短路问题实验
最短路问题案例(short-path problem)
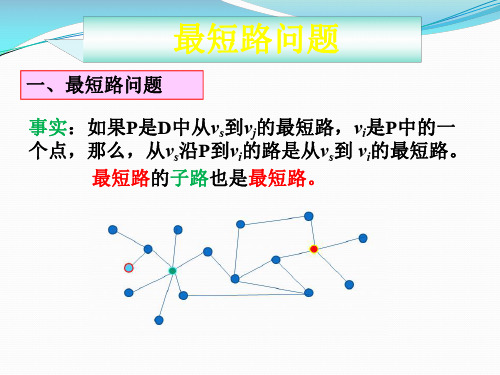
三、Dijkstra算法演示：
5.选取顶点
U=V\S={A(22), B (13)}
l(B)=13, l(B)=l(C)+W(C,B)
6.选取顶点
U=V\S={A(22)}
l(A)=22, l(A)=l(F)+W(F,A)
三、Dijkstra算法演示：
1. 初始时， S只包含起点s ； U包含除s外的其他顶 点，且U中顶点的距离为“起点s到该顶点的距离”[例. U中顶点v的距离为d(s,v)，然而s与v不相邻，故为inf]。
2. 从U中选出“距离最短的顶点w”，并将顶点w 加入到S 中；同时，从U中移除顶点w 。
3. 更新U中各个顶点到起点s的距离。 由于上一步中 确定了w是求出最短路径的顶点，从而可以利用w来更新 其他顶点的距离。[例. (s,v)的距离大于(s,w) + (w,v)]。
l(E)=4, l(E)<l(C)+W(C,E); l(F)=9, l(F)=l(C)+W(C,F)
三、Dijkstra算法演示：
3.选取顶点 U=V\S={A(inf), B (13), F(6), G (12)}
l( )=6, l(F)=l(E)+W(E,F)
4.选取顶点 U=V\S={A(22), B (13), G(12)}
4. 重复步骤2和3，直到遍历完所有顶点。
三、Dijkstra算法演示：
1.选取顶点 U=V\S={A(inf), B (inf), C (3), E (4), F (inf), G (inf)}
2.选取顶点 U=V\S={A(inf), B (13), E (4), F (9), G (inf)}
3第三章最短路问题
现在我们就来构造一个图G，它的顶点就是这10 种情况，G中的边是按照下述原则来连的；如果情况 甲经过一次渡河可以变成情况乙，那么就在情况甲与 乙之间连一条边.
MWSV MWS MWV WSV MS
WV
W
S
V
Ø
例如，MWSV经过一次渡河可以变成WV(人带着羊 过河，左岸留下狼和白菜)，又例如MWV经过一次渡河 可以变为W(人带着白菜过河，留下狼)，或变为V.当 然反过来，W也可以变为MWV(人带着白菜从右岸返回 左岸).
§3.2 求最短有向路的标号法
这一节介绍一种求有向图上最短有向路的方法 ，叫做标号法。
所谓标号,我们是指与图的每一个顶点对应的一个 数(或几个数)．例如设G=(V,A)的顶点集合是V={v1,v2, …,vn}，如果我们能使v1对应一个数b(1)，v2对应数 b(2)，…，vn对应数b(n)，那么，这些数b(i)就称为vi的 标号，当然，在不同的问题中，标号b(i)一般代表不同 的意义.
从上面的简单比较久可以看出，为什么说计算 次数是n的多项式的方法是有效的，而计算次数是 n的指数函数的方法是无效的.另外，也可以看出， 单靠提高计算机的速度还不够，还必须从数学上寻 求有效的计算方法.
现在再回过头来看看标号法好不好.回想一下标 号法的各轮计算，可以看出，它只包含两种运算： 加法与比较大小(比较大小也需要花费时间，所以 也要考虑).加法用于计算k(i,j)，每计算一个k(i,j)进 行一次加法，而且每一条弧最多只计算一次.因此, 如果图中有m条弧，那么至多进行m次加法.对于一 个有n个顶点的简单有向图来说，最多有n(n-1)条 弧(假设从每一个顶点vi出发，都有n-1条弧指向其 他的n-1个顶点)，因此，最多进行n(n-1)次加法， 放宽一点，也可以说，至多进行n2次加法.
最短路问题(整理版)
最短路问题(short-path problem)若网络中的每条边都有一个权值值(长度、成本、时间等)，则找出两节点(通常是源节点与结束点)之间总权和最小的路径就是最短路问题。
最短路问题是网络理论解决的典型问题之一，可用来解决管路铺设、线路安装、厂区布局和设备更新等实际问题。
最短路问题，我们通常归属为三类：单源最短路径问题（确定起点或确定终点的最短路径问题）、确定起点终点的最短路径问题（两节点之间的最短路径）1、Dijkstra算法：用邻接矩阵a表示带权有向图，d为从v0出发到图上其余各顶点可能达到的最短路径长度值，以v0为起点做一次dijkstra，便可以求出从结点v0到其他结点的最短路径长度代码：procedure dijkstra（v0：longint）；//v0为起点做一次dijkstrabegin//a数组是邻接矩阵，a[i,j]表示i到j的距离，无边就为maxlongintfor i:=1 to n do d[i]:=a[v0,i];//初始化d数组（用于记录从v0到结点i的最短路径）， fillchar(visit,sizeof(visit),false);//每个结点都未被连接到路径里visit[v0]:=true;//已经连接v0结点for i:=1 to n-1 do//剩下n-1个节点未加入路径里；beginmin:=maxlongint;//初始化minfor j:=1 to n do//找从v0开始到目前为止，哪个结点作为下一个连接起点（*可优化） if (not visit[j]) and (min>d[j]) then//结点k要未被连接进去且最小begin min:=d[j];k:=j;end;visit[k]:=true;//连接进去for j:=1 to n do//刷新数组d，通过k来更新到达未连接进去的节点最小值，if (not visit[j]) and (d[j]>d[k]+a[k,j]) then d[j]:=a[k,j]+d[k];end;writeln(d[n]);//结点v0到结点n的最短路。
数学网络分析最短路和最大流问题
得到网络上一个新的可行流f’。
(5) 擦除图上所有标号，重复(1)-(4)步，直到图中找不到任何 增广链，计算结束。
网络的最大流
例6.10 用标号算法求下图中s→t的最大流量，并找出最小割。
v1 8(7)
5(4)
s
9(3) 2(0)
v3 5(4)
6(1)
t●
7(5) v2
10(8)
9(9)
v4
网络的最大流
8 ⑥ 16 24
⑧ 18
2
13 3
6
2
④
8 10
2
6 12
⑦
6
18 24
所有点都已标号，点上的标号就是v1到该点的最短距离，最短
路线就是红色的链。
最短距离的矩阵算法
网络图的矩阵表示
v1 d11 d1i d1n
v2
d
21
B
vi
d
i1
d 2i
d ii
d
2
n
d in
dij表示i点到j点 两相邻点间的 距离，若i和j点 不相邻，则
从s点出发，找出与s点相邻的所有的点，记为点集V1，取vr， s.t.， L sr=mvii V n 1{sL s+ ，ds则} i 将r点标注，并将Lsr的值标注在 r点旁的小方框内。
从已标注的点出发，找出与这些点相邻的所有未标注的点 记为点集V2，取vt ，s.t.，L s= t m v i V i 2 { n sL + sd s;i L s+ rd r} i ，则 将t点标注，并将Lst的值标注在t点旁的小方框内。
f ( v i,v j) f ( v j,v i) 0 ( i s ,t )
管理运筹学 第7章 最短路实例
8
§4 最大流问题
• 最大流问题：给一个带收发点的网络，其每条弧的赋权称之为容量， 在不超过每条弧的容量的前提下，求出从发点到收点的最大流量。 一、最大流的数学模型 例6 某石油公司拥有一个管道网络，使用这个网络可以把石油从采地 运送到一些销售点，这个网络的一部分如下图所示。由于管道的直径 的变化，它的各段管道（vi,vj）的流量cij（容量）也是不一样的。cij的 单位为万加仑/小时。如果使用这个网络系统从采地 v1向销地 v7运送石 油，问每小时能运送多少加仑石油？
2 0 0
2 0 2 1
3 v6 4
3 01
2
v7
3 5
3 1 v4
第五次迭代：选择路为v1 v2 v3 v5 v7 。弧（ v2 , v3 ）的顺流容 量为2，决定了pf=2，改进的网络流量图如下图：
1 v2 0 5 2 3 0 0 2 3 v5 2 0 0 0
管 理 运 筹 学
15
20
v1 1
3
(a)
图11-12
管 理 运
(b)
筹 学
(c)
5
§3 最小生成树问题
一、求解最小生成树的破圈算法 算法的步骤：
1、在给定的赋权的连通图上任找一个圈。
2、在所找的圈中去掉一个权数最大的边（如果有两条或两条 以上的边都是权数最大的边，则任意去掉其中一条）。
3、如果所余下的图已不包含圈，则计算结束，所余下的图即 为最小生成树，否则返回第1步。
§2 最短路问题
例 设备更新问题。某公司使用一台设备，在每年年初，公司就要 决定是购买新的设备还是继续使用旧设备。如果购置新设备，就要支 付一定的购置费，当然新设备的维修费用就低。如果继续使用旧设备， 可以省去购置费，但维修费用就高了。请设计一个五年之内的更新设 备的计划，使得五年内购置费用和维修费用总的支付费用最小。 已知：设备每年年初的价格表
最短路问题实际案例
最短路问题实际案例最短路问题是指在图中找出两个顶点之间的最短路径的问题，其中图可以是有向图或无向图，并且每条边可以有权重。
这个问题是在许多实际案例中都会遇到的。
以下是几个实际案例，其中涉及到最短路问题：1. 导航系统：导航系统是最常见的利用最短路问题的实例。
当用户输入起点和终点时，导航系统会计算出最短路径，并显示给用户。
这个过程中，导航系统需要考虑路程的时间或距离，同时还需要考虑道路的限速和交通情况等因素。
2. 物流配送：物流配送涉及到从一个地点到另一个地点的最短路径。
物流公司需要计算出从货物的起始点到目标点的最短路径，以最快速度将货物送达目的地。
在这个问题中，可能还会有其他限制条件，如运输工具的载重量、路段的通行能力等。
3. 电信网络：电信网络是一个复杂的网络，其中存在着许多节点和边，每个节点代表一个通信设备，边代表设备之间的通信连接。
在设计电信网络时，需要考虑到从一个节点到另一个节点的最短路径，以最小化通信的时延。
这个问题中，还会有其他因素，如网络拓扑的复杂性、网络流量的负载均衡等。
4. 交通规划：交通规划涉及到城市道路网络的设计和优化。
在设计城市交通规划时，需要考虑到不同节点之间的最短路径，以便在城市中建设高效的道路系统。
这个问题中，需要考虑到人口分布、交通流量、环境因素等复杂变量。
5. 谷歌地图：谷歌地图是一种广泛使用最短路径算法的应用。
当用户在谷歌地图上搜索起点和终点时，谷歌地图会计算出最短路径，并给出导航指引。
这个过程中，谷歌地图需要考虑到道路的限速、交通情况和实时路况等因素。
综上所述，最短路问题在许多实际案例中都有应用。
无论是导航系统、物流配送、电信网络、交通规划还是谷歌地图等，都需要计算出最短路径以满足需求。
因此，研究和解决最短路问题在实际应用中具有重要意义。
最短路问题(第一次作业)史晓康 29
作业：1、某公司在六个城市621,,,c c c 中有分公司，从i c 到j c 的直接航程票价记在下述矩阵的),(j i 位置上。
（∞表示无直接航路），请帮助该公司设计一张城市1c 到其它城市间的票价最便宜的路线图。
⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡∞∞∞∞∞∞055252510550102025251001020402010015252015050102540500 解：clear,clcw=[ 0 50 inf 40 25 10 50 0 15 20 inf 25 inf 15 0 10 20 inf 40 20 10 0 10 25 25 inf 20 10 0 55 10 25 inf 25 55 0 ]; v0=1;dijkstra(w,v0)起点为第1个顶点，终点为第1个顶点的最短路径为1; 路径长度为0起点为第1个顶点，终点为第2个顶点的最短路径为1 6 2; 路径长度为35起点为第1个顶点，终点为第3个顶点的最短路径为1 5 3; 路径长度为45起点为第1个顶点，终点为第4个顶点的最短路径为1 6 4; 路径长度为35起点为第1个顶点，终点为第5个顶点的最短路径为1 5; 路径长度为25起点为第1个顶点，终点为第6个顶点的最短路径为1 6; 路径长度为10>>2、求下图中第一节点到其它节点的最短距离，并用矩阵表示。
------------------------------------------------------------------------ 参考例题：求v1到其余各点的最短路径。
vvv v24783 10946解：赋权矩阵为：调用附件中dijkstra算法程序，可以得到如下结果：计算过程为：建立一个main1.m文件，输入一下matlab语句：clear,clcw=[0 3 inf inf inf inf inf3 0 2 inf 18 2.5 infinf 2 0 6 2 inf infinf inf 6 0 3 inf infinf 18 2 3 0 4 infinf 2.5 inf inf 4 0 1.5inf inf inf inf inf 1.5 0 ]v0=1;dijkstra(w,v0)然后保存并运行。
短路的原理和应用实验
短路的原理和应用实验1. 短路的原理短路是指电路中两个节点之间的电阻变为零，导致电流在这两个节点之间完全短接的现象。
在理想情况下，短路将导致电流无限增大，电压下降到零。
短路可以是意外发生的，也可以是故意制造的，我们将通过实验来探讨短路的原理和应用。
短路的原理可以简单地解释为以下几点：•在一个电路中，电流会流经电阻最小的路径，当存在短路时，电流会选择通过短路路径，而不会通过其他电阻较大的路径。
•短路会导致电路中电阻的电压降为零，因为短路的存在使得电流不经过该电阻。
•短路会导致电流增大，因为电流只能通过电阻较小的路径，电路总电阻变小，根据欧姆定律，电流增大。
2. 短路的应用实验2.1 实验材料和器材准备为了进行短路的应用实验，我们需要准备以下材料和器材：•直流电源•电阻（多个不同阻值的电阻）•导线•电流表•电压表•万用表2.2 实验步骤以下是短路的应用实验的步骤：1.将直流电源连接好，并打开电源开关。
2.将电阻按照一定的顺序连接在电路中，可以选择不同阻值的电阻。
3.使用导线连接电路的节点。
4.使用电流表和电压表测量电路中的电流和电压。
5.记录测量结果，并观察短路对电路的影响。
2.3 实验结果和观察通过实验可以得到以下结果和观察：•当电路中存在短路时，电流表的读数急剧增大，电压表的读数降为零。
•电路中其他电阻的电流减小，因为电流更多地通过短路路径流过。
•短路使得电路中的电阻总阻值变小，根据欧姆定律，电流增大。
2.4 实验讨论通过对实验结果的观察和分析，我们可以得出以下结论：•短路会导致电路中电流的变化，其影响与电路的拓扑结构和电阻的阻值有关。
•短路可以用来测试电路的稳定性和安全性，当电路设计存在缺陷或短路时，可能会导致电路过负荷、短路、发热等问题。
•短路可以用来观察电路中电流和电压的变化，以进一步理解电路的工作原理和特性。
3. 总结短路是指电路中两个节点之间的电阻变为零，导致电流在这两个节点之间完全短接的现象。
短路试验资料
短路试验在电工领域，短路试验是一种常用的测试方法，用来评估电路中的短路情况以及相关的安全性。
通过模拟电路中发生短路的情况，可以识别潜在的风险并采取相应的措施来防范可能的事故。
短路试验的意义短路试验旨在检测电路中可能存在的短路问题，以确保设备和电路的正常运行。
在实际的电气系统中，短路是一种常见的故障形式，可能导致设备损坏、电路无法正常工作甚至造成安全事故。
通过进行短路试验，可以及早发现潜在问题并及时修复，保障设备的可靠性和安全性。
短路试验的方法短路试验可以采用多种方法来进行，其中常见的包括直流短路试验和交流短路试验。
在直流短路试验中，通过连接正负极来模拟短路情况，检测电路中的电流和电压变化。
而在交流短路试验中，则会使用专门的测试仪器来模拟不同频率下的短路情况，以评估电路的稳定性和安全性。
短路试验的步骤进行短路试验时，需要按照一定的步骤进行，以确保测试的准确性和可靠性。
首先需要对电路进行彻底的检查，确认电路中不存在其他故障或问题。
然后在实验室或专门的测试场地中设置测试设备，并根据所选用的试验方法进行相应的连接和操作。
在测试过程中要及时记录测试数据，并根据测试结果来评估电路的实际情况。
短路试验的注意事项在进行短路试验时，需要特别注意安全问题，避免因操作不当而造成意外伤害或设备损坏。
在测试前应对测试设备和环境进行全面检查，确保测试条件符合要求。
另外，在测试过程中应严格按照操作规程进行，避免误操作或操作失误导致不良后果。
总的来说，短路试验是一种重要的电路测试方法，可帮助我们及早发现潜在问题并做出相应的处理，确保电路和设备的正常运行和安全性。
通过合理的测试方法和注意事项，我们可以更好地保障电气系统的可靠性和耐久性。
电池短路实验报告模板
电池短路实验报告模板实验目的本实验的主要目的是通过对电池短路实验的进行，了解电池的内部原理以及对电池短路的影响。
实验原理电池是一种能量转换装置，能将化学能转化为电能。
一般电池由正极、负极和电解质三部分组成。
其中，正极为正极材料，负极为负极材料，电解质则使得正极、负极之间形成离子传导通道。
当电池正常工作时，正负极之间的电位差将驱动电子从负极流向正极，从而实现电流的流动。
然而，当电池短路时，正负极之间电阻降为零，使得电流大幅度增加，电流密度超过电池设计范围。
这种短路现象会导致电池内部产生大量热量，进而引发电池的过热甚至爆炸。
实验步骤1. 准备工作：将实验器材准备齐全，包括电池、导线、导线夹等。
2. 连接电路：将电池的正极和负极分别与导线夹头连接，确保连接牢固。
3. 开始实验：将导线夹头的另一端分别与电流表和电压表相连。
4. 记录数据：打开电流表和电压表，记录电流和电压的数值。
5. 短路实验：小心将导线夹头的两端直接连接，使电路发生短路。
6. 观察结果：观察短路瞬间电流和电压的变化，并记录相应的数据。
7. 恢复正常：断开短路连接，实验结束。
实验结果在进行短路实验期间，我们观察到了如下结果：1. 瞬间电流大幅度增加，显示数值迅速攀升。
2. 瞬间电压下降，显示数值急剧减少。
3. 实验过程中产生热量，导线和夹头出现灼伤痕迹。
结果分析根据实验结果，我们可以得出以下结论：1. 由于短路导致正负极之间的电阻降为零，电流大幅度增加。
2. 电池内部短路会导致电压下降，电流密度急剧增大。
3. 短路现象会使电池内部发生大量能量转为热能，导致电池过热。
实验总结通过本次电池短路实验，我们对电池的内部原理和短路对电池的影响有了更加深入的了解。
电池的正负极之间的短路会引起电流的大幅度增加，导致电池过热甚至爆炸。
因此，在日常使用电池时应特别注意避免短路现象的发生，确保使用电池的安全性。
参考资料[1] 电池短路实验报告指导书[2] 电池短路实验原理解析,。
最短路问题(课堂PPT)
5
0
5
V2
3
6 5 5 V6
V1 4
7 2
V4 7
1
6
8
V5 4
V3
V7
4
6
(4)找出所有与v1,v2,v3相邻的未标记的点v4,v5,v6，求出
从v1直接到这些点的距离(v1->v4:7)以及经过v2到这些点 的距离(v1->v2->v4:11;v1->v2->v5:10;v1->v2->v6:8)以及 经过v3到这些点的距离(v1->v3->v4:6;v1->v3->v5:12)找出 这些距离中最短的路径为v1->v3->v4，最短距离为L14=6， 将v4标记为6
3 2 4 1
时间
2 3 3 2
25
0
5
V2
3
6 5 5 V6
V1 4
7 2
V4 7
1
6
8
V5 4
V3
V7
4
(2)找出同v1相邻的未标号的点有v2,v3,v4，求出从
v1到其所有相邻点的距离(v1->v2:5;v1->v3:4;v1>v4:7)，距离最短路径为v1->v3，最短距离为L13=4， 将v3标记为4
0
5
V2
3
6 5 5 V6
5
0
5
V2
3
6 6 5 5 V6
V1 4
7 2
V4 7
1
6
8
V5 4
V3
V7
4
7
(5)找出所有与v1,v2,v3,v4相邻的未标记的点v5,v6，求出
5-2最短路问题
9 3 0 1
3
1
0
v1 v2 v3 v4 v5 v6
v1 0 2 5 10 9
v2
2
0
3
8
6
10
D(1) v3 5 3 0 5 3 4
v4 10 8
5
0
4
3
v5 v6
9
6 10
3 4
4 3
0 1
5-2. 最 短 路 问 题
一、问题的提法及应用背景
（1）问题的提法——寻求网络中两点间 的最短路就是寻求连接这两个点的边的 总权数为最小的通路。（注意：在有向 图中，通路——开的初等链中所有的弧 应是首尾相连的。）
（2）应用背景——管道铺设、线路安排、 厂区布局、设备更新等。
二、最短路算法：
1． D氏标号法（Dijkstra） （1）求解思路——从始点出发，逐步顺序
-2
-1 1
v2 3
1
6
vt
2
v3
vs v1 v2 vs 0 4 1 v1 --- 0 -2 v2 -1 --- 0 v3 --- --- --vt --- -1 ---
v3
vt
d
(1) j
d
(2) j
d
(3) j
--- --- 0 0 0
61444
3 --- 1 1 1
0 2 --- 4 4
--- 0 --- 5 5
9 取自第3列
d (1) 16
mkin{d1(k0)
d
} (0)
k6
（第1行+第6列）
运筹学上机报告最短路问题的计算机求解
2014－2015学年第2学期
实验名称最短路问题的计算机求解日期：2015年5月26日
班级
姓名
学号
实验
目的
掌握最短路问题的计算机求解方法。
实验
内容
（1）最短路问题的lingo编程与计算机求解步骤。
（2）最短路问题计算机求解的输出结果分析。
操作
步骤
（1）进入运筹学软件。
（2）利用相应例题（P143例5-1）熟悉网络最短路问题的计算机求解步骤。
实验
总结
用LINGO求解最短路问题简单，方便，明了。在有负权的问题中，应对路线的范围着重说明，本题中u的范围为free.
（3）对求解中出现问题所进行内容在同学间相互交流，并进行总结。
（4）完成上机作业（P162习题3），并记录步骤与结果。
结果
显示
与
分析
习题3结果：
Variable ValueU( 1) 0.000000
U( 2) -5.000000
U( 3) -2.000000
U( 4)3.0000U( 5) 2.000000
16 0.000000
17 0.000000
18 0.000000
19 0.000000但在整体从v1到
用计算机求解得出了v1到各点的最短路结果，有负权值得最短路问题的求解过程与无负权值得一致但在整体从v1到v7的最短路无法用狄克斯拉算法求解，W（x,y）表示x到y的距离，底下的row代表剩余变量，结果显示只有v1到各点的最短距离
P( 2, 6) 0.000000
P( 3, 2) 0.000000 P( 3, 7) 1.000000
P( 4, 5) 1.000000
最短路问题-2
S (vi ) = max{d ij } i = 1,2, Lν 1≤ j ≤ν (3)求出顶点 v k ,使 S (v k ) = min{S (vi )}
1≤i ≤ν
则 v k 就是要求的建立消防站的地点.此点称为图的中心点 中心点. 中心点
TO MATLAB (road3(floyd))
0 3 5 D = 10 7 5 .5 7
返回
选址问题--重心问题 选址问题--重心问题 -例 2 某矿区有七个矿点,如图所示.已知各矿点每天的产矿量 q (v j ) (标在图的各顶点上) 现要从这七个矿点选一个来建造矿厂. . 问 应选在哪个矿点,才能使各矿点所产的矿运到选矿厂所在地的总运力 (千吨公里)最小.
(1)求距离阵 D= ( d ij )ν ×ν .
�
返回
选址问题--中心问题 选址问题--中心问题 -例 1 某城市要建立一个消防站,为该市所属的七个区服务, 如图所示.问应设在那个区,才能使它至最远区的路径最短.
(1)用 Floyd 算法求出距离矩阵 D= ( d ij )ν ×ν .
(2) 计算在各点 vi 设立服务设施的最大 服务距离 S (vi ) .
数学建模与数学实验 最短路问题
实验目的
1,了解最短路的算法及其应用 , 2,会用Matlab软件求最短路 ,会用 软件求最短路
实验内容
3,最 短 路 的 应 用 , 4,建模案例:最优截断切割问题 ,建模案例: 5,实验作业 ,
最 短 路 的 应 用
一, 选 址 问 题 1, 中心问题 , 2, 重心问题 , 二,建模案例:最优截断切割问题 建模案例:
3 0 2 7 4 2 .5 4
5 2 0 5 2 4 .5 6
[管理学]最短路问题
![[管理学]最短路问题](https://img.taocdn.com/s3/m/53ce6a346c175f0e7cd1376c.png)
最短路的子路也是最短路。
思想：将D=（V，A，W）中vs到所有其它顶点的最短
路按其路长从小到大排列为： u0≤ u1 ≤ u2 ≤…≤ un
u0表示vs到自身的长度，相应最短路记为： P0，P1，P2，…，Pn，P1一定只有一条弧。 记X 0 v s , X 0 V \ X 0 , 则
例 用Dijkstra算法求前面例子中从v1到各点的最短路。
v2
6
1 2 6
v5
4 3 10 2
2
v9
6
4
3
v1
1
3
v3
2
v8
v4
10
v6
v7
解：u1=0，u2=6，u3=3，u4=1，u5=u6=u7=u8=u9=+ ，
j=1 （j=2，3，…，9）
X0={v1} ，X0={v2，v3，…，v9}
。设
步骤2 若m+1=n-1，结束。若m+1<n-1，置m=m+1，转步骤1
v2
1
2 5 3 -4
v3
2 3 l(v1)=0, l(vj)=1 (j=2,3,4,5)
v4
u1
(1)
v1
u2 u3
( 2) (1) ( 2) (1)
v5
u 2 w22 1, u 2 w23 3, u5 w54 6, u3 w35 1, u 2 w22 1, u3
uj(m) =
算法步骤：
步骤0 令 l(v1)=0,l(vj)=1(2 j n); m=1,u1(m)=0，uj(m)=w1j (2 j n)。
uk (m) + wkj 步骤1 对于一切2 j n，计算 min 1 k n
判断短路的实验报告
一、实验目的通过本次实验，掌握短路的判断方法，加深对电路中短路现象的理解，提高电路故障排查能力。
二、实验原理短路是指电路中电流不流经用电器，直接连接电源两极的现象。
短路会导致电路中电流增大，电源损坏，甚至引发火灾等安全事故。
判断短路的方法主要有以下几种：1. 观察法：通过观察电路中的导线、元件等是否有明显的烧焦、熔断等现象，初步判断是否存在短路。
2. 测量法：使用电压表、电流表等测量工具，测量电路中的电压、电流值，判断电路是否短路。
3. 欧姆定律法：根据欧姆定律，计算电路中的理论电流值，与实际测量值进行对比，判断电路是否短路。
4. 电阻法：使用万用表等工具，测量电路中元件的电阻值，判断是否存在短路。
三、实验器材1. 电源：直流电源，电压可调。
2. 电阻：若干个不同阻值的电阻。
3. 电容：若干个不同容值的电容。
4. 电感：若干个不同感值的电感。
5. 开关：若干个。
6. 导线：若干根。
7. 电压表、电流表：各一个。
8. 万用表：一个。
四、实验步骤1. 搭建实验电路：按照电路图连接电源、电阻、电容、电感等元件，并接入开关。
2. 测量正常情况下的电路参数：使用电压表、电流表测量电路中的电压、电流值，记录数据。
3. 故意制造短路：将电阻、电容、电感等元件中的某个元件用导线直接连接，制造短路。
4. 测量短路情况下的电路参数：使用电压表、电流表测量电路中的电压、电流值，记录数据。
5. 使用欧姆定律计算短路电流：根据欧姆定律，计算短路电流值，与实际测量值进行对比。
6. 使用电阻法测量短路电阻：使用万用表测量短路电阻值，判断是否存在短路。
五、实验结果与分析1. 正常情况下，电路中的电压、电流值符合理论计算值。
2. 制造短路后，电路中的电压、电流值明显增大，与正常情况下相比，电流值增大数倍。
3. 使用欧姆定律计算短路电流，与实际测量值基本一致。
4. 使用电阻法测量短路电阻，发现短路电阻值非常小，接近于零。
六、实验结论通过本次实验，我们掌握了以下判断短路的几种方法：1. 观察法：通过观察电路中的导线、元件等是否有明显的烧焦、熔断等现象，初步判断是否存在短路。
短路试验方案
短路试验方案一. 引言短路试验是电力系统中常用的一种试验手段，用于评估电气设备在短路条件下的运行性能。
通过模拟短路故障可以检测设备的短路电流容量、温升和电流分布等重要参数，以建立设备的可靠性和稳定性。
二. 实验目的本文将介绍短路试验的基本流程、试验设备和注意事项，以帮助工程技术人员正确进行短路试验并获取可靠的试验结果。
三. 试验流程1. 选择合适的试验装置：根据待测设备的额定电流和额定短路电流，选择相应的短路试验装置。
常用的装置包括电流互感器、电流互感器和电源装置等。
2. 建立试验电路：根据试验设备的接线图，按照正确的接线顺序搭建试验电路。
确保试验电路的连接准确可靠。
3. 测量试验参数：在试验过程中，需要实时监测和记录一些关键参数，如短路电流、电流分布和温升等。
常用的测量工具包括电流表、温度计和数字记录仪等。
4. 施加试验负载：根据设备的额定电流，逐步增加试验负载，测量不同负载下的短路电流，并记录相应的试验数据。
5. 分析试验结果：根据实验数据，计算设备的短路电流容量、温升和电流分布等参数。
将试验结果与设备额定参数进行比较，评估设备的可靠性和稳定性。
四. 试验设备1. 电流互感器：用于测量设备的短路电流，通常采用电子式或传统式电流互感器。
2. 电源装置：用于提供短路试验时所需的电源，可分为直流电源和交流电源两种。
3. 电流表：用于测量试验过程中的电流，常用的电流表包括电子式电流表和传统式电流表。
4. 测温仪：用于测量设备在试验过程中的温升情况，常用的测温仪有接触式和非接触式两种。
五. 注意事项1. 安全保护措施：在进行短路试验时，必须加强安全意识，正确使用试验装置和工具。
遵守相关安全规定，确保试验过程的安全。
2. 试验环境：试验应在合适的环境条件下进行，如温度、湿度和空气流动等。
试验环境的稳定和准确性对于获取可靠的试验结果至关重要。
3. 仪器校准：在进行短路试验前，应确保试验设备的准确度和稳定性。
电器短路实验方法
电器短路实验方法引言:电器短路是指电器设备内部的电路出现异常，导致电流异常增大，造成电器设备无法正常工作甚至损坏的现象。
为了研究电器短路的原因和特性，我们可以进行一些实验来模拟和观察电器短路的发生过程。
本文将介绍一种常用的电器短路实验方法。
材料与仪器:1. 电源：提供实验所需的电能；2. 电线：连接电源和电器设备，搭建电路；3. 电器设备：如灯泡、电风扇等；4. 安全开关：用于控制电路的通断；5. 电流表：测量电路中的电流；6. 电压表：测量电路中的电压；7. 电阻器：调节电路中的电阻。
实验步骤:1. 搭建电路：首先将电源与电器设备连接起来。
使用电线将电源的正极与电器设备的正极相连，负极与负极相连，形成一个闭合的电路。
确保电路连接牢固。
2. 接入安全开关：将安全开关与电路连接，使电路处于断开状态。
3. 接入电流表和电压表：将电流表和电压表分别连接到电路中，以便测量电流和电压的数值。
4. 打开电源：将安全开关打开，使电流可以流动。
此时，电器设备应该工作正常，灯泡应该亮起，电风扇应该转动。
5. 引入电阻器：在电路中加入适当的电阻器，调节电路中的电阻。
观察电器设备的工作状态是否发生变化。
6. 模拟短路：将安全开关再次断开，然后将电阻器调整到最小值，即电路中的电阻接近零。
再次打开安全开关，观察电器设备的反应。
实验结果与讨论:1. 当电路中的电阻较大时，电流的数值较小，电器设备正常工作。
2. 当电路中的电阻减小，电阻接近零时，电流的数值急剧增大，电器设备可能出现异常，如灯泡短暂发光后熄灭，电风扇停止转动等。
3. 通过引入适当的电阻器，可以调节电路中的电阻，从而控制电流的大小，保护电器设备的正常工作。
实验注意事项:1. 在进行实验前，确保实验环境安全，避免发生触电等危险。
2. 使用合适的电压和电流进行实验，不要超过电器设备的额定电压和电流。
3. 实验中的电阻器要选用合适的规格和阻值，以满足实验需求。
4. 实验过程中要随时观察电器设备的工作状态，确保实验安全。