(完整word版)2008-2017年安徽省中考数学压轴题集
2008年全国中考数学压轴题分类解析

并求 为何值时, Y的值最大, 最大值是多少?
解 () B 1 略.c的解析式为Y=÷ + ÷.
-t 二
B
C B Q D
C
Q
() 2 略.A B A C的面积是÷.
二
() 3 过点 Ⅳ作 上MB于点 P 因为 E , , O上 所以
图2
图3
图4
4 7
维普资讯
分 析 ( ) 1 根据 MN/ BC 由相 似三角形 的相似 比可 / ,
用 的代数式 表示 出圆的直径 MN; ( )过 圆心 D作直线 Jc的垂线 O 当 O = 卅J 2 B D, D 1 、 r
维普资讯
20 0 8年 全 国 中 考 数 学 压 轴 题 分 类 解 析
安徽省岳西县城关 中学
从 今年 的 中考数 学 压轴 题 中 , 们 可 以 看 到 在 考察 我 学 生基本 运算 能 力 、 维能 力 的 同时 , 优生 还 要 着重 考 思 对
4,S 一 ( 2 1 )即 :÷t ) 2 一 了 .
因为此抛 物线 开 口向下 , 以当 t=2时 ,量 = , 所 S大 所 以 当点 运动 2 时 , 秒 AMN B的 面积达 到最 大 , 大值 最
为 . 点 评 本题 是 一 道综 合 性 很 强也 是 传 统 型 的压 轴
=
9 。A =4, C = 3 是 A 0 ,B A , B上 的动 点 ( 与 A, 不 B重
令 抛物线 解析式 Y=0 解 二次方程 求得 A B的坐标 , , 、 从而
1
2008年全国中考数学压轴题精选[2]
![2008年全国中考数学压轴题精选[2]](https://img.taocdn.com/s3/m/089b5ca5dd3383c4ba4cd200.png)
2008年全国中考数学压轴题精选1.(08福建莆田)如图:抛物线经过A (-3,0)、B (0,4)、C (4,0)三点. (1) 求抛物线的解析式.(2)已知AD = AB (D 在线段AC 上),有一动点P 从点A 沿线段AC 以每秒1个单位长度的速度移动;同时另一个动点Q 以某一速度从点B 沿线段BC 移动,经过t 秒的移动,线段PQ 被BD 垂直平分,求t 的值;(3)在(2)的情况下,抛物线的对称轴上是否存在一点M ,使MQ+MC 的值最小?若存在,请求出点M 的坐标;若不存在,请说明理由。
(注:抛物线2y ax bx c =++的对称轴为2b x a=-)2.(08甘肃白银等9市)如图,在平面直角坐标系中,四边形OABC 是矩形,点B 的坐标为(4,3).平行于对角线AC 的直线m 从原点O 出发,沿x 轴正方向以每秒1个单位长度的速度运动,设直线m 与矩形OABC 的两边..分别交于点M 、N ,直线m 运动的时间为t (秒). (1) 点A 的坐标是__________,点C 的坐标是__________; (2) 当t= 秒或 秒时,MN=21AC ; (3) 设△OMN 的面积为S ,求S 与t 的函数关系式; (4) 探求(3)中得到的函数S 有没有最大值?若有,求出最大值;若没有,要说明理由.3.(08广东广州)如图,在梯形ABCD 中,AD ∥BC ,AB=AD=DC=2cm ,BC=4cm ,在等腰△PQR 中,∠QPR=120°,底边QR=6cm ,点B 、C 、Q 、R 在同一直线l 上,且C 、Q 两点重合,如果等腰△PQR 以1cm/秒的速度沿直线l 箭头所示方向匀速运动,t 秒时梯形ABCD 与等腰△PQR 重合部分的面积记为S 平方厘米 (1)当t=4时,求S 的值(2)当4t ≤≤10,求S 与t 的函数关系式,并求出S 的最大值4.(08广东深圳)如图9,在平面直角坐标系中,二次函数)0(2>++=a c bx ax y 的图象的顶点为D 点,与y 轴交于C 点,与x 轴交于A 、B 两点, A 点在原点的左侧,B 点的坐标为(3,0),OB =OC ,tan∠ACO=31. (1)求这个二次函数的表达式.(2)经过C 、D 两点的直线,与x 轴交于点E ,在该抛物线上是否存在这样的点F ,使以点A 、C 、E 、F 为顶点的四边形为平行四边形?若存在,请求出点F 的坐标;若不存在,请说明理由.(3)若平行于x 轴的直线与该抛物线交于M 、N 两点,且以MN 为直径的圆与x 轴相切,求该圆半径的长度.(4)如图10,若点G (2,y )是该抛物线上一点,点P 是直线AG 下方的抛物线上一动点,当点P 运动到什么位置时,△APG 的面积最大?求出此时P 点的坐标和△APG 的最5.(08贵州贵阳)某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.设每个房间每天的定价增加x元.求:(1)房间每天的入住量y(间)关于x(元)的函数关系式.(2)该宾馆每天的房间收费z(元)关于x(元)的函数关系式.(3)该宾馆客房部每天的利润w(元)关于x(元)的函数关系式;当每个房间的定价为每天多少元时,w有最大值?最大值是多少?6.(08湖北恩施)如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若∆ABC固定不动,∆AFG 绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.(1)请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明.(2)求m与n的函数关系式,直接写出自变量n的取值范围.(3)以∆ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图2).在边BC上找一点D,使BD=CE,求出D点的坐标,并通过计算验证BD2+CE2=DE2.(4)在旋转过程中,(3)中的等量关系BD2+CE2=DE2是否始终成立,若成立,请证明,若不成立,7.(08湖北荆门)已知抛物线y =ax 2+bx +c 的顶点A 在x 轴上,与y 轴的交点为B (0,1),且b =-4ac . (1) 求抛物线的解析式;(2) 在抛物线上是否存在一点C ,使以BC 为直径的圆经过抛物线的顶点A ?若不存在说明理由;若存在,求出点C 的坐标,并求出此时圆的圆心点P 的坐标;(3) 根据(2)小题的结论,你发现B 、P 、C 三点的横坐标之间、纵坐标之间分别有何关系?8.(08湖北荆州)如图,等腰直角三角形纸片ABC 中,AC =BC =4,∠ACB =90º,直角边AC在x 轴上,B 点在第二象限,A (1,0),AB 交y 轴于E ,将纸片过E 点折叠使BE 与EA 所在直线重合,得到折痕EF (F 在x 轴上),再展开还原沿EF 剪开得到四边形BCFE ,然后把四边形BCFE 从E 点开始沿射线EA 平移,至B 点到达A 点停止.设平移时间为t (s ),移动速度为每秒1个单位长度,平移中四边形BCFE 与△AEF 重叠的面积为S. (1)求折痕EF 的长;(2)是否存在某一时刻t 使平移中直角顶点C经过抛物线243y x x =++的顶点?若存在,求出t 值;若不存在,请说明理由;(3)直接写出....S 与t 的函数关系式及自变量t 的取值范围.BC B P P9.(08湖北天门)如图①,在平面直角坐标系中,A点坐标为(3,0),B点坐标为(0,4).动点M从点O出发,沿OA方向以每秒1个单位长度的速度向终点A运动;同时,动点N 从点A出发沿AB方向以每秒35个单位长度的速度向终点B运动.设运动了x秒.(1)点N的坐标为(________________,________________);(用含x的代数式表示)(2)当x为何值时,△AMN为等腰三角形?(3)如图②,连结ON得△OMN,△OMN可能为正三角形吗?若不能,点M的运动速度不变,试改变点N的运动速度,使△OMN为正三角形,并求出点N的运动速度和此时x的值.10.(08湖北武汉)如图 1,抛物线y=ax2-3ax+b经过A(-1,0),C(3,2)两点,与y轴交于点D,与x轴交于另一点B.(1)求此抛物线的解析式;(2)若直线y=kx-1(k≠0)将四边形ABCD面积二等分,求k的值;(3)如图2,过点 E(1,-1)作EF⊥x轴于点F,将△AEF绕平面内某点旋转180°后得△MNQ(点M,N,Q分别与点 A,E,F 对应),使点M,N在抛物线上,求点M,N的坐标.11.(08湖北咸宁)如图①,正方形 ABCD 中,点A 、B 的坐标分别为(0,10),(8,4),点C 在第一象限.动点P 在正方形 ABCD 的边上,从点A 出发沿A →B →C →D 匀速运动,同时动点Q 以相同速度在x 轴上运动,当P 点到D 点时,两点同时停止运动,设运动的时间为t 秒.(1) 当P 点在边AB 上运动时,点Q 的横坐标x (长度单位)关于运动时间t (秒)的函数图象如图②所示,请写出点Q 开始运动时的坐标及点P 运动速度; (2) 求正方形边长及顶点C 的坐标;(3) 在(1)中当t 为何值时,△OPQ 的面积最大,并求此时P 点的坐标. (1) 附加题:(如果有时间,还可以继续 解答下面问题,祝你成功!)如果点P 、Q 保持原速度速度不变,当点P 沿A →B →C →D 匀速运动时,OP 与PQ 能否相等,若能,写出所有符合条件的t 的 值;若不能,请说明理由.12.(08湖南长沙)如图,六边形ABCDEF 内接于半径为r (常数)的⊙O ,其中AD 为直径,且AB=CD=DE=FA.(1)当∠BAD=75 时,求BC ⌒的长; (2)求证:BC ∥AD ∥FE ;(3)设AB=x ,求六边形ABCDEF 的周长L 关于x 的函数关系式,并指出x 为何值时,L 取得最大值.(第24题图①) 图②D13(08湖南益阳)我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A 、B 、C 、D 分别是“蛋圆”与坐标轴的交点,已知点D 的坐标为(0,-3),AB 为半圆的直径,半圆圆心M 的坐标为(1,0),半圆半径为2.(1) 请你求出“蛋圆”抛物线部分的解析式,并写出自变量的取值范围; (2)你能求出经过点C 的“蛋圆”切线的解析式吗?试试看;(3)开动脑筋想一想,相信你能求出经过点D 的“蛋圆”切线的解析式.14.(08江苏常州)如图,抛物线24y x x =+与x 轴分别相交于点B 、O ,它的顶点为A ,连接AB,把AB 所的直线沿y 轴向上平移,使它经过原点O,得到直线l ,设P 是直线l 上一动点.(1) 求点A 的坐标;(2) 以点A 、B 、O 、P 为顶点的四边形中,有菱形、等腰梯形、直角梯形,请分别直接写出这些特殊四边形的顶点P 的坐标;(3) 设以点A 、B 、O 、P 为顶点的四边形的面积为S,点P 的横坐标为x,当46S +≤≤+,求x 的取值范围.15、(08江苏淮安)如图所示,在平面直角坐标系中.二次函数y=a(x-2)2-1图象的顶点为P ,与x 轴交点为 A 、B ,与y 轴交点为C .连结BP 并延长交y 轴于点D. (1)写出点P 的坐标;(2)连结AP ,如果△APB 为等腰直角三角形,求a 的值及点C 、D 的坐标; (3)在(2)的条件下,连结BC 、AC 、AD ,点E(0,b)在线段CD(端点C 、D 除外)上,将△BCD 绕点E 逆时针方向旋转90°,得到一个新三角形.设该三角形与△ACD 重叠部分的面积为S ,根据不同情况,分别用含b 的代数式表示S .选择其中一种情况给出解答过程,其它情况直接写出结果;判断当b 为何值时,重叠部分的面积最大?写出最大值.16.(08江苏连云港)如图,现有两块全等的直角三角形纸板Ⅰ,Ⅱ,它们两直角边的长分别为1和2.将它们分别放置于平面直角坐标系中的AOB △,COD △处,直角边OB OD ,在x 轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至PEF △处时,设PE PF ,与OC 分别交于点M N ,,与x 轴分别交于点G H ,. (1)求直线AC 所对应的函数关系式;(2)当点P 是线段AC (端点除外)上的动点时,试探究:①点M 到x 轴的距离h 与线段BH 的长是否总相等?请说明理由;②两块纸板重叠部分(图中的阴影部分)的面积S 是否存在最大值?若存在,求出这个最大值及S 取最大值时点P 的坐标;若不存在,请说明理由.17.(08江苏连云港)我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段AB 的最小覆盖圆就是以线段AB 为直径的圆.(1)请分别作出图1中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);(2)探究三角形的最小覆盖圆有何规律?请写出你所得到的结论(不要求证明); (3)某地有四个村庄E F G H ,,,(其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.18、(08江苏南京)一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为(h)x ,两车之间的距离.......为(km)y ,图中的折线表示y 与x 之间的函数关系.根据图象进行以下探究: 信息读取(1)甲、乙两地之间的距离为 km ; (2)请解释图中点B 的实际意义; 图象理解(3)求慢车和快车的速度;(4)求线段BC 所表示的y 与x 之间的函数关系式,并写出自变量x 的取值范围; 问题解决(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?A AB B CC 80100 (图1)GF(图2) y19、(08江苏南通)已知双曲线k y x=与直线14y x =相交于A 、B 两点.第一象限上的点M(m ,n )(在A 点左侧)是双曲线ky x=上的动点.过点B 作BD ∥y 轴交x 轴于点D .过N (0,-n )作NC ∥x 轴交双曲线ky x=于点E ,交BD 于点C . (1)若点D 坐标是(-8,0),求A 、B 两点坐标及k 的值.(2)若B 是CD 的中点,四边形OBCE 的面积为4,求直线CM 的解析式.(3)设直线AM 、BM 分别与y 轴相交于P 、Q 两点,且MA =pMP ,MB =qMQ ,求p -q 的值.20、(08江苏宿迁)如图,⊙O 的半径为1,正方形ABCD 顶点B 坐标为)0,5(,顶点D 在⊙O 上运动.(1)当点D 运动到与点A 、O 在同一条直线上时,试证明直线CD 与⊙O 相切;(2)当直线CD 与⊙O 相切时,求CD 所在直线对应的函数关系式;(3)设点D 的横坐标为x ,正方形ABCD 的面积为S ,求S 与x 之间的函数关系式,并求出S 的最大值与最小值.21、(08江苏泰州)已知二次函数)0(21≠++=a c bx ax y 的图象经过三点(1,0),(-3,0),(0,23-)。
全国中考数学压轴题精选十二题目

2008年中考数学分类汇编 压轴题(12)1、(2008黑龙江、鸡西、佳木斯、齐齐哈尔)如图,在,点(30)C -,,点A B ,分别在x 轴,y 轴的正半轴10OA -=.(1)求点A ,点B 的坐标.(2)若点P 从C 点出发,以每秒1个单位的速度沿射线CB 运动,连结AP .设ABP △的面积为S ,点P 的运动时间为t 秒,求S 与t 的函数关系式,并写出自变量的取值范围.(3)在(2)的条件下,是否存在点P ,使以点A B P ,,为顶点的三角形与AOB △相似?若存在,请直接写出点P 的坐标;若不存在,请说明理由.2、(2008 湖北 天门)如图①,在平面直角坐标系中,A 点坐标为(3,0),B 点坐标为(0,4).动点M 从点O 出发,沿OA 方向以每秒1个单位长度的速度向终点A 运动;同时,动点N 从点A 出发沿AB 方向以每秒35个单位长度的速度向终点B 运动.设运动了x 秒.(1)点N 的坐标为(________________,________________);(用含x 的代数式表示) (2)当x 为何值时,△AMN 为等腰三角形?(3)如图②,连结ON 得△OMN ,△OMN 可能为正三角形吗?若不能,点M 的运动速度不变,试改变点N 的运动速度,使△OMN 为正三角形,并求出点N 的运动速度和此时x 的值.x3、(2008江苏常州)如图,抛物线24y x x =+与x 轴分别相交于点B 、O,它的顶点为A,连接AB,把AB 所的直线沿y 轴向上平移,使它经过原点O,得到直线l,设P 是直线l 上一动点. (1)求点A 的坐标;(2)以点A 、B 、O 、P 为顶点的四边形中,有菱形、等腰梯形、直角梯形,请分别直接写出这些特殊四边形的顶点P 的坐标;(3)设以点A 、B 、O 、P 为顶点的四边形的面积为S,点P 的横坐标为x,当46S +≤≤+,求x 的取值范围.4、(2008广西南宁)随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高。
2008年数学中考试题分类汇编(压轴题)

2008年数学中考试题分类汇编压轴题(2008年芜湖市)如图,已知 (4,0)A ,(0,4)B ,现以A 点为位似中心,相似比为9:4,将OB 向右侧放大,B 点的对应点为C . (1) 求C 点坐标及直线BC 的解析式;(2) 一抛物线经过B 、C 两点,且顶点落在x 轴正半轴上,求该抛物线的解析式并画出函数图象;(3) 现将直线BC 绕B 点旋转与抛物线相交与另一点P ,请找出抛物线上所有满足到直线AB距离为P .河北 周建杰 分类(2008年泰州市)29.已知二次函数y 1=ax 2+bx +c (a ≠0)的图像经过三点(1,0),(-3,0),(0,-23). (1)求二次函数的解析式,并在给定的直角坐标系中作出这个函数的图像;(5分) (2)若反比例函数y 2=x2(x >0)的图像与二次函数y 1=ax 2+bx +c (a ≠0)的图像在第一象限内交于点A (x 0,y 0),x 0落在两个相邻的正整数之间,请你观察图像,写出这两个相邻的正整数;(4分) (3)若反比例函数y 2=xk(x >0,k >0)的图像与二次函数y 1=ax 2+bx +c (a ≠0)的图像在第一象限内的交点A ,点A 的横坐标x 0满足2<x 0<3,试求实数k 的取值范围.(5分)(2008年南京市)28.(10分)一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为(h)x ,两车之间的距离.......为(km)y ,图中的折线表示y 与x 之间的函数关系.根据图象进行以下探究: 信息读取(1)甲、乙两地之间的距离为 km ; (2)请解释图中点B 的实际意义; 图象理解(3)求慢车和快车的速度;(4)求线段BC 所表示的y 与x 之间的函数关系式,并写出自变量x 的取值范围; 问题解决(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?(2008年巴中市)已知:如图14,抛物线2334y x =-+与x 轴交于点A ,点B ,与直线34y x b =-+相交于点B ,点C ,直线34y x b =-+与y 轴交于点E .(1)写出直线BC 的解析式. (2)求ABC △的面积.(3)若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动(不与A B ,重合),同时,点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动.设运动时间为t 秒,请写出MNB △的面积S 与t 的函数关系式,并求出点M 运动多少时间时,MNB △的面积最大,最大面积是多少?第29题图(第28题)y(2008年自贡市)抛物线)0(2≠++=a c bx ax y 的顶点为M ,与x 轴的交点为A 、B (点B 在点A 的右侧),△ABM 的三个内角∠M 、∠A 、∠B 所对的边分别为m 、a 、b 。
2008年安徽省中考数学试卷含答案
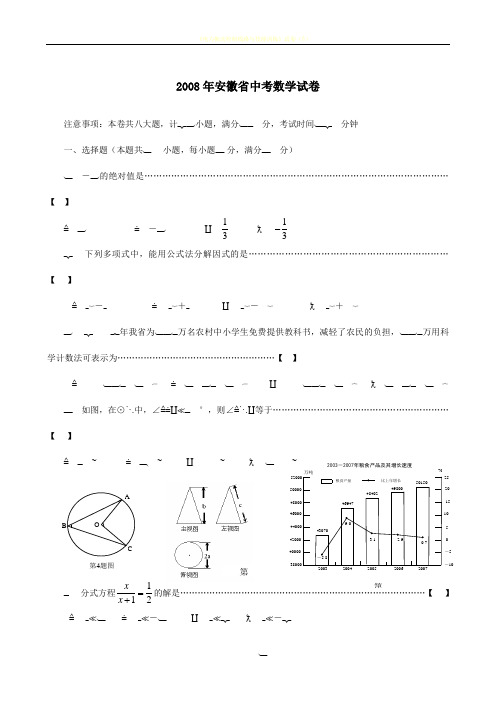
2008年安徽省中考数学试卷注意事项:本卷共八大题,计 小题,满分 分,考试时间 分钟 一、选择题(本题共 小题,每小题 分,满分 分)- 的绝对值是…………………………………………………………………………………………【 】-13 13- 下列多项式中,能用公式法分解因式的是…………………………………………………………【 】- + -+年我省为 万名农村中小学生免费提供教科书,减轻了农民的负担, 万用科学计数法可表示为………………………………………………【 】如图,在⊙ 中,∠ °,则∠ 等于……………………………………………………【 】分式方程112x x =+的解是…………………………………………………………………………【 】 - -第第2003-2007年粮食产品及其增长速度 比上年增长粮食产量0.72.93.19.0-5.85015049800484024694743070%万吨42000400002520151050-5-10第4题图OACB如图是某几何体的三视图及相关数据,则判断正确的是…………………………………………【 】 > >函数ky x=的图象经过点( ,- ),则 的值为…………………………………………………【 】 12 12- -某火车站的显示屏,每隔 分钟显示一次火车班次的信息,显示时间持续 分钟,某人到达该车站时,显示屏上正好显示火车班次信息的概率是……………………………………………………………【 】16 15 1413 如图是我国 ~ 年粮食产量及其增长速度的统计图,下列说法不正确...的是…………【 】.这 年中,我国粮食产量先增后减 .后 年中,我国粮食产量逐年增加 .这 年中,我国粮食产量年增长率最大 .这 年中,我国粮食产量年增长率最小如图,在△ 中, , ,点 为 中点, ⊥ 于点 ,则 等于…………………【 】65 95 125 165二、填空题(本题共 小题,每小题 分,满分 分)化简()24-如图,已知 ∥ ,∠ ,∠ ,则∠ 。
近12年安徽省中考数学压轴题集
2008--2020年安徽省初中学业水平考试数学压轴题集(本卷收录近12年安徽省中考的第10、14、22、23等题)一、选择题每小题都给出A 、B 、C 、D 四个选项,其中只有一个是正确的. 1.如图,在矩形ABCD 中,AB =5,AD =3.动点P 满足13PABABCD S S =矩形 .则点P 到A ,B 两点距离之和P A +PB 的最小值为( )A.29B.34C.52D.412.如图,Rt △ABC ,AB ⊥BC ,AB =6,BC =4,P 是△ABC 内部的一个动点,且满足∠P AB =∠PBC ,则线段CP 长的最小值为( ) 32 B.2 C.81313 D.121313A.第1题图 第2题图3.如图,一次函数1y x =和二次函数22+y ax bx c =+图象相交于P ,Q 两点,则函数2(1)y ax b x c=+-+的图象可能是( )A. B. C. D.第3题图4.如图,正方形ABCD 的对角线BD 长为22,若直线l 满足: ①点D 到直线l 的距离为3;②A ,C 两点到直线l 距离相等.则符合题意的直线l 的条数是( ) A.1 B.2 C.3 D.45.如图,点P 是等边三角形ABC 外接圆⊙O 上点,在以下判断中,不正确的是( ) A.当弦PB 最长时,△APC 是等腰三角形 B.当△APC 是等腰三角形时,PO ⊥AC C.当PO ⊥AC 时,∠ACP =30° D.当∠ACP =30°时,△BPC 是直角三角形第4题图第5题图6.在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是()A.10B.45C.10或45D.10或217第6题图7.如图所示,P是菱形ABCD的对角线AC上一点,过P垂直于AC的直线交菱形ABCD的边于M、N两点,设AC=2,BD=1,AP=x,△AMN的面积为y,则y关于x的函数图象的大致形状是A. B.第7题图C. D.8.甲、乙两个准备在一段长为1200米的笔直公路上进行跑步,甲、乙跑步的速度分别为4m/s和6m/s,起跑前乙在起点,甲在乙前面100米处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙两之间的距离y(m)与时间t(s)的函数图象是()A. B. C. D.9.△ABC中,AB=AC,∠A为锐角,CD为AB边上的高,I为△ACD的内切圆圆心,则∠AIB的度数是A.120°B.125°C.135°D.150°10.如图,在△ABC中,AB=AC=5,BC=6,点M为BC中点,MN⊥AC于点N,则MN等于A.65B.95C.125D.125第10题图的边长为,对角线AC在直线l上,且点C位于点M处.将正方形ABCD沿l向右平移,直到点A 与点N重合为止.记点C平移的距离为x,正方形ABCD的边位于l1,l2之间部分的长度和为y,则y 关于x的函数图象大致为()A.B.C.D.12、如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12,点P正方形的边上,则满足PE+PF=9的点P个数是()A、0B、4C、6D、813、已知三个实数a,b,c满足a-2b+c=0,a+2b+c<0,则()A、b>0,b2-ac≤0B、b<0,b2-ac≤0C、b>0,b2-ac≥0D、b<0,b2-ac≥014、如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12,点P正方形的边上,则满足PE+PF=9的点P个数是()A、0B、4C、6D、815.已知点A,B,C在⊙O上,则下列命题为真命题的是()A.若半径OB平分弦AC,则四边形OABC是平行四边形B.若四边形OABC是平行四边形,则∠ABC=120°C.若∠ABC=120°,则弦AC平分半径OBD.若弦AC平分半径OB,则半径OB平分弦AC16.如图,△ABC和△DEF都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,点C,E重合.现将△ABC在直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为()A .B .C .D .17.一段笔直的公路AC 长20千米,途中有一处休息点B ,AB 长15千米,甲、乙两名长 跑爱好者同时从点A 出发,甲以15千米/时的速度匀速跑至点B ,原地休息半小时后,再 以10千米/时的速度匀速跑至终点C ;乙以12千米/时的速度匀速跑至终点C ,下列选项 能正确反映甲、乙两人出发后2小时内运动路程y (千米)与时间x (时)函数关系的图像 是( )A B C D二、填空题18. 在三角形纸片ABC 中,∠A =90°,∠C =30°,AC =30cm ,将该纸片沿过点B 的直线折叠,使点A 落在斜边BC 上的一点E 处,折痕记为BD (如图1),剪去△CDE 后得到双层△BDE (如图2),再沿着过△BDE 某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为__________cm.19. 如图,在矩形纸片ABCD 中,AB =6,BC =10,点E 在CD 上,将△BCE 沿BE 折叠,点C 恰落在边AD 上的点F 处;点G 在AF 上,将△ABG 沿BG 折叠,点A 恰落在线段BF 上的点H 处,有下列结论:①∠EBG =45°;②△DEF ∽△ABG ;③3=2ABG FGH S S △△;④AG +DF =FG .其中正确的是 .(把所有正确结论的序号都选上)第19题图 第21题图20.已知实数a 、b 、c 满足a b ab c +==,有下列结论:①若c ≠0,则111+=;②若a =3,则b +c =9;③若a =b =c ,则abc =0;④若a 、b 、c 中只有两个数相等,则a +b +c =8.其中正确的是 .(把所有正确结论的序号都选上)21. 如图,在▱ABCD 中,AD =2AB ,F 是AD 的中点,作CE ⊥AB ,垂足E 在线段AB 上,连接EF 、CF ,则下列结论中一定成立的是 .(把所有正确结论的序号都填在横线上) ①12DCF BCD ∠=∠;②EF =CF ;③=2BEC CEF S S △△;④∠DFE =3∠AEF .22.已知矩形纸片ABCD 中,AB =1,BC =2,将该纸片折叠成一个平面图形,折痕EF 不经过A 点(E ,F 是该矩形边界上的点),折叠后点A 落在点A ’处,给出以下判断: ①当四边形A’CDF 为正方形时,EF =2;②当EF =2时,四边形A’CDF 为正方形; ③当EF =5时,四边BA’CD 为等腰梯形;④当四边形BA’CD 为等腰梯形时,EF =5. 其中正确的是 .(把所有正确结论的序号都填在横线上) 23.如图,P 是矩形ABCD 内的任意一点,连接P A 、PB 、PC 、PD ,得到△P AB 、△PBC 、△PCD 、△PDA ,设它们的面积分别是S 1、S 2、S 3、S 4,给出如下结论:①S 1+S 2=S 3+S 4;②S 2+S 4= S 1+S 3;③若S 3=2S 1,则S 4=2S 2 ④若S 1=S 2,则P 点在矩形的对角线上.其中正确的结论的序号是 .(把所有正确结论的序号都填在横线上)第22题图 第23题图 第25题图 24.定义运算(1)a b a b ⊗=-,下面给出了关于这种运算的几个结论:①2(2)6⊗-=;②a b b a ⊗=⊗;③若0a b +=,则()()2a a b b ab ⊗+⊗=;④若0a b ⊗=,则a=0.其中正确结论的序号是__________ .(填上你认为所有正确结论的序号)25.如图,AD 是△ABC 的边BC 上的高,由下列条件中的某一个就能推出△ABC 是等腰三角形的是 ________ _.(把所有正确答案的序号都填写在横线上)①∠BAD=∠ACD ;②∠BAD=∠CAD ;③AB+BD=AC+CD ;④AB -BD=AC -CD .26.已知二次函数的图象经过原点及点11(,)24--,且图象与x 轴的另一交点到原点的距离为1,则该二次函数的解析式为________________________ .27.如图为二次函数2y ax bx c =++的图象,在下列说法中:①ac <0;②方程20ax bx c ++=的根是11x =-,23x =;③0a b c ++>;④当x >1时,y 随x 的增大而增大.正确的说法有__________.(把正确的答案的序号都填在横线上)28.(5分)(2018•安徽)如图,正比例函数y=kx与反比例函数y=的图象有一个交点A(2,m),AB⊥x轴于点B.平移直线y=kx,使其经过点B,得到直线l,则直线l对应的函数表是____.22.(5分)(2018•安徽)矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC 上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为_____________.29、如图,△ABC内接于⊙O,∠CAB=30O,∠CBA=45O,CD⊥AB于点D,若⊙O的半径为2,则CD的长为_______. .30、在平面直角坐标系中,垂直于x轴的直线l分别与函数y=x-a+1和y=x2-2ax的图像交于P,Q两点,若平移直线l,可以使P,Q都在x轴的下方,则实数a的取值范围是________ . 31.如图,一次函数y=x+k(k>0)的图象与x轴和y轴分别交于点A和点B.与反比例函数y=的图象在第一象限内交于点C,CD⊥x轴,CE⊥y轴.垂足分别为点D,E.当矩形ODCE与△OAB的面积相等时,k的值为_____________.32.在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片ABCD沿过点A的直线折叠,使得点B落在CD上的点Q处.折痕为AP;再将△PCQ,△ADQ分别沿PQ,AQ折叠,此时点C,D落在AP上的同一点R处.请完成下列探究:(1)∠PAQ的大小为________________°;(2)当四边形APCD是平行四边形时,的值为_______________________.三、解答题33.某超市销售一种商品,成本每千克40元,规定每千克不低于成本,且不高于80元.经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:售价x(元/千克)506070销售量y(千克)1008060(1)求y与x之间的函数表达式;(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入-成本);(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?34.已知正方形ABCD,点M为AB的中点.(1)如图1,点G为线段CM上的一点,且∠AGB=90°,延长AG、BG分别与边BC、CD交于点E、F.①求证:BE=CF;②求证:2=⋅.BE BC CE(2)如图2,在边BC上取一点E,满足2=⋅,连接AE交CM于点G,连接BG并延长BE BC CE交CD于点F,求tan∠CBF的值.第22题图 1 第22题图235.如图,二次函数2+y ax bx 的图象经过点(2,4)A 与(6,0)B .(1)求a ,b 的值; (2)点C 是该二次函数图象上A ,B 两点之间的一动点,横坐标为x (2<x <6),写出四边形OACB 的面积S 关于点C 的横坐标x 的函数表达式,并求S 的最大值.36.如图,A ,B 分别在射线OA ,ON 上,且∠MON 为钝角,现以线段OA ,OB 为斜边向∠MON 的外侧作等腰直角三角形,分别是△OAP ,△OBQ ,点C ,D ,E 分别是OA ,OB ,AB 的中点. (1)求证:△PCE ≌△EDQ ; (2)延长PC ,QD 交于点R .①如图1,若∠MON =150°,求证:△ABR 为等边三角形;②如图3,若△ARB ∽△PEQ ,求∠MON 大小和ABPQ的值.37.为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为x m,矩形区域ABCD的面积为y m2.(1)求y与x之间的函数关系式,并注明自变量x的取值范围;(2)x为何值时,y有最大值?最大值是多少?第25题图38.如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.(1)求证:AD=BC;(2)求证:△AGD∽△EGF;(3)如图2,若AD、BC所在直线互相垂直,求AD的值.EF第26题图1 第26题图239.若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”. (1)请写出两个为“同簇二次函数”的函数;(2)已知关于x 的二次函数2212421y x mx m =-++和225y ax bx =++,其中1y 的图象经过点(1,1)A ,若12y y +与1y 为“同簇二次函数”,求函数2y 的表达式,并求出当0≤x ≤3时,2y 的最大值.40.如图1,正六边形ABCDEF 的边长为a ,P 是BC 边上一动点,过P 作PM ∥AB 交AF 于M ,作PN ∥CD 交DE 于N .(1)①∠MPN = ;②求证:PM +PN =3a ;(2)如图2,点O 是AD 的中点,连接OM 、ON ,求证:OM =ON ;(3)如图3,点O 是AD 的中点,OG 平分∠MON ,判断四边形OMGN 是否为特殊四边形?并说明理由.第28题图1 第28题图2 第28题图3学习必备 欢迎下载41.某大学生利用暑假40天社会实践参与了一家网店的经营,了解到一种成本为20元/件的新型商品在第x 天销售的相关信息如下表所示.销售量p (件)50p x =- 销售单价q (元/件) 当1≤x ≤20时,1302q x =+;当21≤x ≤40时,52520q x =+ (1)请计算第几天该商品的销售单价为35元/件;(2)求该网店第x 天获得的利润y 关于x 的函数关系式;(3)这40天中该网店第几天获得的利润最大?最大利润是多少?42.我们把由不平行于底边的直线截等腰三角形的两腰所得的四边形称为“准等腰梯形”;如图1,四边形ABCD 即为“准等腰梯形”;其中∠B =∠C .(1)在图1所示的“准等腰梯形”ABCD 中,选择合适的一个顶点引一条直线将四边形ABCD 分割成一个等腰梯形和一个三角形或分割成一个等腰三角形和一个梯形;(画出一种示意图即可)(2)如图2,在“准等腰梯形”ABCD 中∠B =∠C .E 为边BC 上一点,若AB ∥DE ,AE ∥DC ,求证:AB BE DC EC=; (3)在由不平行于BC 的直线AD 截△PBC 所得的四边形ABCD 中,∠BAD 与∠ADC 的平分线交于点E .若EB =EC ,请问当点E 在四边形ABCD 内部时(即图3所示情形),四边形ABCD 是不是“准等腰梯形”,为什么?若点E 不在四边形ABCD 内部时,情况又将如何?写出你的结论.(不必说明理由)学习必备 欢迎下载第30题图1 第30题图2 第30题图343.如图1,在△ABC 中,D 、E 、F 分别为三边的中点,G 点在边AB 上,△BDG 与四边形ACDG 的周长相等,设BC =a 、AC =b 、AB =c .(1)求线段BG 的长;(2)求证:DG 平分∠EDF ;(3)连接CG ,如图2,若△BDG 与△DFG 相似,求证:BG ⊥CG .第31题图1 第31题图244.如图,排球运动员站在点O 处练习发球,将球从O 点正上方2m 的A 处发出,把球看成点,其运行的高度y (m )与运行的水平距离x (m )满足关系式2(6)y a x h =-+.已知球网与O 点的水平距离为9m ,高度为2.43m ,球场的边界距O 点的水平距离为18m.(1)当h =2.6时,求y 与x 的关系式;(不要求写出自变量x 的取值范围)(2)当h =2.6时,球能否越过球网?球会不会出界?请说明理由;(3)若球一定能越过球网,又不出边界,求h 的取值范围.第32题图45.在△ABC 中,∠ACB =90°,∠ABC =30°,将△ABC 绕顶点C 顺时针旋转,旋转角为(0180)θθ︒︒<<,得到△A’B’C’..第33题图1 第33题图2 第33题图3(1)如图(1),当AB ∥BC 时,设BA 与CD 相交于点D ,证明:△CDA 是等边三角形;(2)如图(2),连接A’A 、B’B ,设△ACA’和△BCB’的面积分别为'ACA S 和'BCB S .求证:'':1:3ACA BCB S S =.(3)如图(3),设AC 中点为E ,B’A’中点为P ,AC =a ,连接EP ,当θ= °时,E P 长度最大,最大值为 .46.如图,正方形ABCD 的四个顶点分别在四条平行线l 1、l 2、l 3、l 4上,这四条直线中相邻两条之间的距离依次为h 1、h 2、h 3(h 1>0,h 2>0,h 3>0).(1)求证h 1=h 3;(2)设正方形ABCD 的面积为S .求证22231()S h h h =++;(3)若12312h h +=,当h 1变化时,说明正方形ABCD 的面积S 随h 1的变化情况.第34题图47.春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少 捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第x 天(1≤x ≤20且x 为整数)的捕捞与销售的相关信息如下:鲜鱼销售单价(元/kg ) 20单位捕捞成本(元/kg ) 55x - 捕捞量(kg )950x - (1)在此期间该养殖场每天的捕捞量与前一天的捕劳量相比是如何变化的?(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x 天的收入y (元)与x (天)之间的函数关系式;(当天收入=日销售额-日捕捞成本)(3)试说明(2)中的函数y 随x 的变化情况,并指出在第几天y 取得最大值,最大值是多少?48.如图,已知△ABC ∽△A 1B 1C 1,相似比为k (k >1),且△ABC 的三边长分别为a 、b 、c (a >b >c ),△A 1B 1C 1的三边长分别为a 1、b 1、c 1.(1)若c =a 1,求证:a =kc(2)若c =a 1,试给出符合条件的一对△ABC 和△A 1B 1C 1,使得a 、b 、c 和a 1、b 1、c 1都是正整数,并加以说明;(3)若b =a 1,c =b 1,是否存在△ABC 和△A 1B 1C 1,使得k =2?请说明理由.第36题图49.如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.(1)写出图中三对相似三角形,并证明其中的一对;(2)连结FG,如果α=45°,AB=42,AF=3,求FG的长.50.已知某种水果的批发单价与批发量的函数关系如图(1)所示.(1)请说明图中①、②两段函数图象的实际意义.(2)写出批发该种水果的资金金额w(元)与批发量m(kg)之间的函数关系式;在下图的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果.(3)经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系如图(2)所示,该经销商拟每日售出60kg以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日获得的利润最大.第38题图1 第38题图251.已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.(1)如图1,若点O在BC上,求证:AB=AC;(2)如图2,若点O在△ABC的内部,求证:AB=AC;(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.第39题图1 第39题图252.刚回营地的两个抢险分队又接到救灾命令:一分队立即出发往30千米的A镇;二分队因疲劳可在营地休息a(0≤a≤3)小时再往A镇参加救灾.一分队了发后得知,唯一通往A镇的道路在离营地10千米处发生塌方,塌方地形复杂,必须由一分队用1小时打通道路,已知一分队的行进速度为5千米/时,二分队的行进速度为(4+a)千米/时.(1)若二分队在营地不休息,问二分队几小时能赶到A镇?(2)若二分队和一分队同时赶到A镇,二分队应在营地休息几小时?(3)下列图象中,①②分别描述一分队和二分队离A镇的距离y(千米)和时间x(小时)的函数关系,请写出你认为所有可能合理的代号,并说明它们的实际意义.(a)(b)(c)(d)第40题图53.(10分)(2018•安徽)如图,⊙O为锐角△ABC的外接圆,半径为5.(1)用尺规作图作出∠BAC的平分线,并标出它与劣弧的交点E(保留作图痕迹,不写作法);(2)若(1)中的点E到弦BC的距离为3,求弦CE的长.54.(12分)(2018•安徽)小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆.售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元.调研发现:①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元).(1)用含x的代数式分别表示W1,W2;(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?55.(14分)(2018•安徽)如图1,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E.点M为BD中点,CM的延长线交AB于点F.(1)求证:CM=EM;(2)若∠BAC=50°,求∠EMF的大小;(3)如图2,若△DAE≌△CEM,点N为CM的中点,求证:AN∥EM.56、如图,点E在□ABCD内部,AF∥BE,DF∥CE。
(完整word版)2017安徽中考数学试卷(含答案).docx
2017 年安徽省初中学业水平考试数学(试题卷)一、选择题(本题共 10 个小题 , 每小题 4 分,满分 40 分)每小题都给出 A 、 B 、 C 、 D 四个选项,其中只有一个是正确的.1.1的相反数是()21 1A .C. 2D . -22B .22. 计算 ( a 2 )2的结果是()A . a 6B . a 6C . a 5D . a 53. 如图,一个放置在水平实验台上的锥形瓶,它的俯视图为( )A. B. C. D .4. 截至 2016 年底,国家开发银行对“一带一路”沿线国家累积发放贷款超过 1600 亿美元 . 其中 1600 亿用科学计数法表示为( )A. 16 1010 B. 1.6 1010C.1.6 1011D . 0.16 10125. 不等式 3 2x0 的解集在数轴上表示为()A .B . C. D .6. 直角三角板和直尺如图放置. 若 1 20 ,则 2 的度数为()A. 60B.50 C.40 D.307. 为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100 名学生进行统计,并绘成如图所示的频数直方图. 已知该校共有1000 名学生,据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是()A. 280B.240C.300D.2608. 一种药品原价每盒25 元,经过两次降价后每盒16 元. 设两次降价的百分率都为x ,则 x 满足()A.16(12x) 25B.25(12x) 16 C.16(1 x) 225D.25(1x)2169. 已知抛物线y ax 2bx c 与反比例函数y b的图象在第一象限有一个公共点,其横坐标为 1. 则一次x函数 y bx ac 的图象可能是()A.B. C.D.10. 如图,在矩形ABCD 中, AB 5 , AD 3.动点 P 满足S PAB 1 S矩形ABCD.则点P到A,B两点距3离之和 PA PB 的最小值为()A.29B.34 C. 5 2D.41二、填空题(本大题共 4 小题,每小题 5 分,满分 20 分)11.27 的立方根是.12. 因式分解:a2b 4ab 4b =.13.如图,已知等边 ABC 的边长为6,以 AB 为直径的⊙ O 与边 AC , BC 分别交于 D , E 两点,则劣弧DE 的长为.14. 在三角形纸片ABC 中, A 90 , C 30 , AC 30cm.将该纸片沿过点 B 的直线折叠,使点A 落在斜边 BC 上的一点 E 处,折痕记为BD (如图1),剪去CDE 后得到双层BDE (如图2),再沿着边BDE 某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形.则所得平行四边形的周长为cm.三、(本大题共 2 小题,每小题 8 分,满分 16 分)1115. 计算:| 2 | cos60( ).16.《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四 . 问人数,物价各几何?译文为:现有一些人共同买一个物品,每人出 8 元,还盈余 3 元;每人出 7 元,则还差 4 元 . 问共有多少人?这个物品的价格是多少?请解答上述问题 .四、(本大题共 2 小题,每小题 8 分,满分 16 分)17. 如图,游客在点 A 处坐缆车出发,沿 A B D 的路线可至山顶 D 处.假设 AB 和 BD 都是直线段,且AB BD 600m ,75 ,45 ,求DE的长.(参考数据:sin750.97 , cos75 0.26 ,2 1.41 )18.如图,在边长为 1 个单位长度的小正方形组成的网格中,给出了格点ABC 和DEF (顶点为网格线的交点),以及过格点的直线l .( 1)将ABC 向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形;( 2)画出DEF 关于直线 l 对称的三角形;( 3)填空:C E.五、(本大题共 2 小题,每小题 10 分,满分 20 分)19.【理解】我知道, 123n n( n1),那么 122232n2果等于多少呢?2在 1 所示三角形数中,第 1 行圈中的数1,即12;第 2 行两个圈中数的和 2 2 ,即 22;⋯⋯;第 n 行 n 个圈中数的和n n n ,即n2.,三角形数中共有n(n 1)个圈,所有圈中n个n2数的和 122232n2.【律探究】将桑拿教学数两次旋可得如所示的三角形数,察三个三角形数各行同一位置圈中的数(如第 n1行的第一个圈中的数分n 1 ,2,n),每个位置上三个圈中数的和均.由此可得,三个三角形数所有圈中数的和:3(122232n2 ).因此,122232n2=.【解决】根据以上,算12223220172的果.123201720. 如图,在四边形ABCD 中, AD BC ,B D , AD 不平行于 BC ,过点 C 作 CE / / AD 交ABC 的外接圆 O 于点 E ,连接 AE .(1)求证:四边形AECD为平行四边形;(2)连接CO,求证:CO平分BCE .六、(本题满分 12 分)21.甲、乙、丙三位运动员在相同条件下各射靶10 次,每次射靶的成绩如下:甲: 9, 10, 8, 5,7, 8, 10, 8, 8,7;乙: 5, 7,8, 7, 8, 9, 7, 9, 10, 10;丙: 7, 6,8, 5, 4, 7, 6, 3, 9, 5.( 1)根据以上数据完成下表:平均数中位数方差甲88乙88 2.2丙63(2)依据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;(3)比赛时三人依次出场,顺序由抽签方式决定. 求甲、乙相邻出场的概率 .七、(本题满分 12 分)22. 某超市销售一种商品,成本每千克40 元,规定每千克售价不低于成本,且不高于80 元 . 经市场调查,每天的销售量y (千克)与每千克售价x (元)满足一次函数关系,部分数据如下表:售价 x (元/千克)506070销售量 y (千克)1008060( 1)求y与x之间的函数表达式;( 2)设商品每天的总利润为W (元),求 W 与x之间的函数表达式(利润=收入 - 成本);(3)试说明( 2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?八、(本题满分 14 分)23.已知正方形 ABCD ,点 M 为边 AB 的中点.( 1)如图 1,点G为线段CM上的一点,且AGB90 ,延长 AG , BG 分别与边 BC ,CD 交于点 E ,F.①求证: BE CF ;②求证: BE 2BC CE .( 2)如图 2,在边BC上取一点E,满足BE2BC CE ,连接AE交CM于点G,连接BG延长交CD 于点 F ,求 tan CBF 的值.2017 年中考数学参考答案一、 1-5: BABCD 6-10: CADBD14、 40或80 3二、 11、 312、 b (a - 2) 13、 p23三、 15、解:原式1 3 = -2 .= 2?216、解:设共有 x 人,根据题意,得 8x - 3 = 7x + 4 ,解得 x = 7 ,所以物品价格为 8? 7 3 = 53 (元 ).答:共有7 人,物品的价格为 53 元 .四、 17、解:在 Rt △BDF 中,由 sin b =DF得,BDDF = BD ?sin b2 300 2 ≈ 423 (m).600? sin 45° 600 ?2在 Rt △ ABC 中,由 cos a =BC可得,ABBC = AB ?cosa 600? cos75° 600? 0.26 156(m).所以 DE = DF + EF = DF + BC = 423+156 = 579 (m). 18、 (1)如图所示; (2)如图所示; (3)45五、 19、2n +1(2 n +1)?n (n +1)1n (n +1)( 2n +1)134526 20、 (1)证明:∵ ∠B =∠ D , ∠B = ∠E ,∴ ∠D = ∠E ,∵ CE ∥ AD , ∴∠ E +∠DAE = 180°.∴ ∠D +∠ DAE = 180°,∴ AE ∥ CD . ∴四边形 AECD 是平行四边形 .(2) 证明:过点 O 作 OM ^ EC , ON ^ BC ,垂足分别为 M 、 N .∵四边形 AECD 是平行四边形,∴AD = EC .又 AD = BC ,∴ EC = BC ,∴ OM = ON ,∴ CO 平分 ∠BCE .六、 21、解: (1)平均数中位数 方差甲 2乙丙6(2) 因为 2 < 2.2 < 3 ,所以 s 甲2 < s 乙2 < s 丙2 ,这说明甲运动员的成绩最稳定.(3) 三人的出场顺序有 (甲乙丙 ), ( 甲丙乙 ), (乙甲丙 ) ,(乙丙甲 ), (丙甲乙 ) , (丙乙甲 )共 6 种,且每一种结果 出现的可能性相等,其中,甲、乙相邻出场的结果有(甲乙丙 ),(乙甲丙 ),( 丙甲乙 ), (丙乙甲 )共 4 种,所以 甲、乙相邻出场的概率 P = 4 = 2 .6 3ììy = - 2x + 200 .七、 22.解: (1) 设 y = kx + b ,由题意,得 í,解得 í,∴所求函数表达式为?60k + b = 80?b = 200(2) W = (x - 40)(- 2 x + 200) = - 2 x 2+ 280 x - 8000 .2(3) W = - 2x 2 + 280x - 8000 = - 2( x - 70)+1800 ,其中 40 #x80 ,∵ - 2 < 0,∴当 40 ? x70 时, W 随 x 的增大而增大,当70 < x ? 80 时, W 随 x 的增大而减小,当售价为 70 元时,获得最大利润,这时最大利润为 1800 元.八、 23、 (1)①证明:∵四边形ABCD 为正方形,∴AB = BC ,,∠ABC = ∠BCF = 90°又,∴,又,∴ ∠BAE =∠CBF ,∠AGB = 90° ∠BAE +∠ABG = 90°∠ABG +∠CBF = 90°∴ △ ABE ≌△ BCF (ASA) ,∴ BE = CF .②证明:∵ ,点 M 为 AB 中点,∴ MG = MA = MB ,∴ ∠GAM = ∠AGM ,∠AGB = 90°又∵ ∠CGE = ∠AGM ,从而 ∠CGE = ∠CGB ,又 ∠ECG = ∠GCB ,∴ △CGE ∽△ CBG , ∴CE = CG,即 CG 2 = BC ?CE ,由 ∠CFG = ∠GBM = ∠CGF ,得 CF = CG . CG CB由①知, BE = CF ,∴ BE = CG ,∴ BE 2 = BC ?CE . (2) 解: ( 方法一 )延长 AE , DC 交于点 N ( 如图 1) ,由于四边形ABCD 是正方形,所以 AB ∥ CD ,∴ ∠N = ∠EAB ,又 ∠CEN = ∠BEA ,∴ △CEN ∽△ BEA , 故 CE =CN,即 BE ?CN AB?CE , BE BA∵ AB = BC , BE 2 = BC ?CE ,∴ CN = BE ,由 AB ∥ DN 知, CN = CG =CF,AM GM MB又 AM = MB ,∴ FC = CN = BE ,不妨假设正方形边长为1,设 BE = x ,则由 BE 2= BC ?CE ,得 x 2 =1?(1 x ),解得 x 1 =5 - 1, x 2 =-5 - 1( 舍去 ) ,∴ BE=5 - 1 ,22 BC2FCBE 5 - 1于是 tan ∠CBF ===,BCBC2( 方法二 )不妨假设正方形边长为 1,设 BE = x ,则由 BE 2= BC ?CE ,得 x 2= 1?(1 x ),解得 x 1 =5 - 1, x 2 =-5 - 1( 舍去 ) ,即 BE = 5 - 1 ,222作 GN ∥ BC 交 AB 于 N ( 如图 2) ,则 △ MNG ∽△ MBC ,∴MN=MB= 1,NGBC 25 y ,∵GN =AN,即2 y y +1设 MN = y ,则 GN = 2 y , GM =2 ,=BE AB 5 - 1 12解得 y =1 ,∴ GM = 1,从而 GM = MA = MB ,此时点 G 在以 AB 为直径的圆上, 2 5 2∴ △ AGB 是直角三角形,且 ,∠AGB = 90° 由 (1) 知 BE = CF ,于是 tan ∠CBF =FC = BE= 5 - 1 .BC BC 2。
2008-2017年安徽省中考数学压轴题集(可打印修改)
2008-2017年安徽省初中学业水平考试数学压轴题集(本卷收录近10年安徽省中考的第10、14、22、23题)一、选择题每小题都给出A 、B 、C 、D 四个选项,其中只有一个是正确的.1.如图,在矩形ABCD 中,AB =5,AD =3.动点P 满足 .则点P 到A ,B 两点距离之和13PAB ABCD S S =V 矩形PA +PB 的最小值为()C.2.如图,Rt △ABC ,AB ⊥BC ,AB =6,BC =4,P 是△ABC 内部的一个动点,且满足∠PAB =∠PBC ,则线段CP 长的最小值为( )A.B.2 D.32第1题图第2题图3.如图,一次函数和二次函数图象相交于P ,Q 两点,则函数1y x =22+y ax bx c =+2(1)y ax b x c =+-+的图象可能是( )A. B. C.D.第3题图4.如图,正方形ABCD 的对角线BD 长为l 满足:①点D 到直线l ;②A ,C 两点到直线l 距离相等.则符合题意的直线l 的条数是( )A.1B.2C.3D.45.如图,点P 是等边三角形ABC 外接圆⊙O 上点,在以下判断中,不正确的是()A.当弦PB 最长时,△APC 是等腰三角形B.当△APC 是等腰三角形时,PO ⊥ACC.当PO ⊥AC 时,∠ACP =30°D.当∠ACP =30°时,△BPC 是直角三角形第4题图 第5题图6.在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是( )A.10B.C.10或D.10或 第6题图7. 如图所示,P 是菱形ABCD 的对角线AC 上一点,过P 垂直于AC 的直线交菱形ABCD 的边于M 、N 两点,设AC =2,BD =1,AP =x ,△AMN 的面积为y ,则y 关于x 的函数图象的大致形状是A. B.第7题图 C. D.8.甲、乙两个准备在一段长为1200米的笔直公路上进行跑步,甲、乙跑步的速度分别为4m/s 和6m/s ,起跑前乙在起点,甲在乙前面100米处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙两之间的距离y (m )与时间t (s )的函数图象是( )A. B. C. D.9.△ABC 中,AB =AC ,∠A 为锐角,CD 为AB 边上的高,I 为△ACD 的内切圆圆心,则∠AIB 的度数是A.120°B.125°C.135°D.150°10.如图,在△ABC 中,AB =AC =5,BC =6,点M 为BC 中点,MN ⊥AC 于点N ,则MN 等于 A. B. C. D.6595125125第10题图 第11题图二、填空题11. 在三角形纸片ABC 中,∠A =90°,∠C =30°,AC =30cm ,将该纸片沿过点B 的直线折叠,使点A 落在斜边BC 上的一点E 处,折痕记为BD (如图1),剪去△CDE 后得到双层△BDE (如图2),再沿着过△BDE 某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为__________cm.12. 如图,在矩形纸片ABCD 中,AB =6,BC =10,点E 在CD 上,将△BCE 沿BE 折叠,点C 恰落在边AD 上的点F 处;点G 在AF 上,将△ABG 沿BG 折叠,点A 恰落在线段BF 上的点H 处,有下列结论:①∠EBG =45°;②△DEF ∽△ABG ;③;④AG +DF =FG .其中正确的是3=2ABG FGH S S △△.(把所有正确结论的序号都选上)第12题图 第14题图13.已知实数a 、b 、c 满足,有下列结论:①若c ≠0,则;②若a =3,则a b ab c +==111a b +=b +c =9;③若a =b =c ,则abc =0;④若a 、b 、c 中只有两个数相等,则a +b +c =8.其中正确的是 .(把所有正确结论的序号都选上)14. 如图,在▱ABCD 中,AD =2AB ,F 是AD 的中点,作CE ⊥AB ,垂足E 在线段AB 上,连接EF 、CF ,则下列结论中一定成立的是 .(把所有正确结论的序号都填在横线上) ①;②EF =CF ;③;④∠DFE =3∠AEF .12DCF BCD ∠=∠=2BEC CEF S S △△15.已知矩形纸片ABCD 中,AB =1,BC =2,将该纸片折叠成一个平面图形,折痕EF 不经过A 点(E ,F 是该矩形边界上的点),折叠后点A 落在点A ’处,给出以下判断: ①当四边形A’CDF 为正方形时,EF =2;②当EF =2时,四边形A’CDF 为正方形; ③当EF =5时,四边BA’CD 为等腰梯形;④当四边形BA’CD 为等腰梯形时,EF =5. 其中正确的是 .(把所有正确结论的序号都填在横线上)16.如图,P 是矩形ABCD 内的任意一点,连接PA 、PB 、PC 、PD ,得到△PAB 、△PBC 、△PCD 、△PDA ,设它们的面积分别是S 1、S 2、S 3、S 4,给出如下结论:①S 1+S 2=S 3+S 4;②S 2+S 4= S 1+S 3;③若S 3=2S 1,则S 4=2S 2 ④若S 1=S 2,则P 点在矩形的对角线上.其中正确的结论的序号是 .(把所有正确结论的序号都填在横线上)第15题图 第16题图第18题图17.定义运算,下面给出了关于这种运算的几个结论:(1)a b a b ⊗=-①;②;③若,则;④若,则a =0.其中2(2)6⊗-=a b b a ⊗=⊗0a b +=()()2a a b b ab ⊗+⊗=0a b ⊗=正确结论的序号是 .(填上你认为所有正确结论的序号)18.如图,AD 是△ABC 的边BC 上的高,由下列条件中的某一个就能推出△ABC 是等腰三角形的是 ________ _.(把所有正确答案的序号都填写在横线上)①∠BAD =∠ACD ;②∠BAD =∠CAD ;③AB +BD =AC +CD ;④AB -BD =AC -CD .19.已知二次函数的图象经过原点及点,且图象与x 轴的另一交点到原点的距离为1,则该11(,24--二次函数的解析式为 .20.如图为二次函数的图象,在下列说法中:①a c <0;②方程的根是2y ax bx c =++20ax bx c ++=,;③;④当x >1时,y 随x 的增大而增大.正确的说法有__________.(把正11x =-23x =0a b c ++>确的答案的序号都填在横线上)第20题图三、解答题21. 某超市销售一种商品,成本每千克40元,规定每千克不低于成本,且不高于80元.经市场调查,每天的销售量y (千克)与每千克售价x (元)满足一次函数关系,部分数据如下表:售价x (元/千克)506070销售量y (千克)1008060(1)求y 与x 之间的函数表达式;(2)设商品每天的总利润为W (元),求W 与x 之间的函数表达式(利润=收入-成本);(3)试说明(2)中总利润W 随售价x 的变化而变化的情况,并指出售价为多少元时获得最大 利润, 最大利润是多少?22.已知正方形ABCD ,点M 为AB 的中点.(1)如图1,点G 为线段CM 上的一点,且∠AGB =90°,延长AG 、BG 分别与边BC 、CD 交于点E 、F.①求证:BE =CF ;②求证:.2BE BC CE =⋅(2)如图2,在边BC 上取一点E ,满足,连接AE 交CM 于点G ,连接BG 并延2BE BC CE =⋅长交CD 于点F ,求tan ∠CBF 的值.第22题图1 第22题图223.如图,二次函数的图象经过点与.2+y ax bx =(2,4)A (6,0)B (1)求a ,b 的值;(2)点C 是该二次函数图象上A ,B 两点之间的一动点,横坐标为x (2<x <6),写出四边形OACB 的面积S 关于点C 的横坐标x 的函数表达式,并求S 的最大值.24.如图,A ,B 分别在射线OA ,ON 上,且∠MON 为钝角,现以线段OA ,OB 为斜边向∠MON 的外侧作等腰直角三角形,分别是△OAP ,△OBQ ,点C ,D ,E 分别是OA ,OB ,AB 的中点.(1)求证:△PCE ≌△EDQ ;(2)延长PC ,QD 交于点R .①如图1,若∠MON =150°,求证:△ABR 为等边三角形;②如图3,若△ARB ∽△PEQ ,求∠MON 大小和的值.AB PQ第24题图1第24题图2 第24题图325.为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m 的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC 的长度为x m ,矩形区域ABCD 的面积为y m 2.(1)求y 与x 之间的函数关系式,并注明自变量x 的取值范围;(2)x 为何值时,y 有最大值?最大值是多少?第25题图26.如图1,在四边形ABCD 中,点E 、F 分别是AB 、CD 的中点,过点E 作AB 的垂线,过点F 作CD 的垂线,两垂线交于点G ,连接AG 、BG 、CG 、DG ,且∠AGD =∠BGC .(1)求证:AD =BC ;(2)求证:△AGD ∽△EGF ;(3)如图2,若AD 、BC 所在直线互相垂直,求 的值. AD EF第26题图1 第26题图227.若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.(1)请写出两个为“同簇二次函数”的函数;(2)已知关于x 的二次函数和,其中 的图象经过点2212421y x mx m =-++225y ax bx =++1y ,若与 为“同簇二次函数”,求函数的表达式,并求出当0≤x ≤3时,的最大值.(1,1)A 12y y +1y 2y 2y 28.如图1,正六边形ABCDEF 的边长为a ,P 是BC 边上一动点,过P 作PM ∥AB 交AF 于M ,作PN ∥CD 交DE 于N .(1)①∠MPN = ;②求证:PM +PN =3a ;(2)如图2,点O 是AD 的中点,连接OM 、ON ,求证:OM =ON ;(3)如图3,点O 是AD 的中点,OG 平分∠MON ,判断四边形OMGN 是否为特殊四边形?并说明理由.第28题图1 第28题图2 第28题图329.某大学生利用暑假40天社会实践参与了一家网店的经营,了解到一种成本为20元/件的新型商品在第x 天销售的相关信息如下表所示.销售量p (件)50p x =-销售单价q (元/件)当1≤x ≤20时,;1302q x =+当21≤x ≤40时,52520q x =+(1)请计算第几天该商品的销售单价为35元/件;(2)求该网店第x 天获得的利润y 关于x 的函数关系式;(3)这40天中该网店第几天获得的利润最大?最大利润是多少?30.我们把由不平行于底边的直线截等腰三角形的两腰所得的四边形称为“准等腰梯形”;如图1,四边形ABCD 即为“准等腰梯形”;其中∠B =∠C .(1)在图1所示的“准等腰梯形”ABCD 中,选择合适的一个顶点引一条直线将四边形ABCD 分割成一个等腰梯形和一个三角形或分割成一个等腰三角形和一个梯形;(画出一种示意图即可)(2)如图2,在“准等腰梯形”ABCD 中∠B =∠C .E 为边BC 上一点,若AB ∥DE ,AE ∥DC ,求证:; AB BE DC EC(3)在由不平行于BC 的直线AD 截△PBC 所得的四边形ABCD 中,∠BAD 与∠ADC 的平分线交于点E .若EB =EC ,请问当点E 在四边形ABCD 内部时(即图3所示情形),四边形ABCD 是不是“准等腰梯形”,为什么?若点E 不在四边形ABCD 内部时,情况又将如何?写出你的结论.(不必说明理由)第30题图1 第30题图2 第30题图331.如图1,在△ABC 中,D 、E 、F 分别为三边的中点,G 点在边AB 上,△BDG 与四边形ACDG 的周长相等,设BC =a 、AC =b 、AB =c .(1)求线段BG 的长;(2)求证:DG 平分∠EDF ;(3)连接CG ,如图2,若△BDG 与△DFG 相似,求证:BG ⊥CG .第31题图1 第31题图232.如图,排球运动员站在点O 处练习发球,将球从O 点正上方2m 的A 处发出,把球看成点,其运行的高度y (m )与运行的水平距离x (m )满足关系式.已知球网与O 点的水平距离2(6)y a x h =-+为9m ,高度为2.43m ,球场的边界距O 点的水平距离为18m.(1)当h =2.6时,求y 与x 的关系式;(不要求写出自变量x 的取值范围)(2)当h =2.6时,球能否越过球网?球会不会出界?请说明理由;(3)若球一定能越过球网,又不出边界,求h 的取值范围.第32题图33.在△ABC 中,∠ACB =90°,∠ABC =30°,将△ABC 绕顶点C 顺时针旋转,旋转角为,得到△A’B’C’.(0180)θθ︒︒<<.第33题图1 第33题图2 第33题图3(1)如图(1),当AB ∥BC 时,设BA 与CD 相交于点D ,证明:△CDA 是等边三角形;(2)如图(2),连接A’A 、B’B ,设△ACA’和△BCB’的面积分别为和.求证:'ACA S V 'BCB S V .'':1:3ACA BCB S S =V V (3)如图(3),设AC 中点为E ,B’A’中点为P ,AC =a ,连接EP ,当θ=°时,E P 长度最大,最大值为 .34.如图,正方形ABCD 的四个顶点分别在四条平行线l 1、l 2、l 3、l 4上,这四条直线中相邻两条之间的距离依次为h 1、h 2、h 3(h 1>0,h 2>0,h 3>0).(1)求证h 1=h 3;(2)设正方形ABCD 的面积为S .求证;22231()S h h h =++(3)若,当h 1变化时,说明正方形ABCD 的面积S 随h 1的变化情况.12312h h +=第34题图35.春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少 捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第x 天(1≤x ≤20且x 为整数)的捕捞与销售的相关信息如下:鲜鱼销售单价(元/kg )20单位捕捞成本(元/kg )55x-捕捞量(kg )950x -(1)在此期间该养殖场每天的捕捞量与前一天的捕劳量相比是如何变化的?(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x 天的收入y (元)与x (天)之间的函数关系式;(当天收入=日销售额-日捕捞成本)(3)试说明(2)中的函数y 随x 的变化情况,并指出在第几天y 取得最大值,最大值是多少?36.如图,已知△ABC ∽△A 1B 1C 1,相似比为k (k >1),且△ABC 的三边长分别为a 、b 、c (a >b >c ),△A 1B 1C 1的三边长分别为a 1、b 1、c 1.(1)若c=a1,求证:a=kc(2)若c=a1,试给出符合条件的一对△ABC和△A1B1C1,使得a、b、c和a1、b1、c1都是正整数,并加以说明;(3)若b=a1,c=b1,是否存在△ABC和△A1B1C1,使得k=2?请说明理由.第36题图37.如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F ,ME交BC于G.(1)写出图中三对相似三角形,并证明其中的一对;(2)连结FG,如果α=45°,AB=,AF=3,求FG的长.第37题图38.已知某种水果的批发单价与批发量的函数关系如图(1)所示.(1)请说明图中①、②两段函数图象的实际意义.(2)写出批发该种水果的资金金额w(元)与批发量m(kg)之间的函数关系式;在下图的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果.(3)经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系如图(2)所示,该经销商拟每日售出60kg以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日获得的利润最大.第38题图1 第38题图239.已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.(1)如图1,若点O在BC上,求证:AB=AC;(2)如图2,若点O在△ABC的内部,求证:AB=AC;(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.第39题图1 第39题图240.刚回营地的两个抢险分队又接到救灾命令:一分队立即出发往30千米的A镇;二分队因疲劳可在营地休息a(0≤a≤3)小时再往A镇参加救灾.一分队了发后得知,唯一通往A镇的道路在离营地10千米处发生塌方,塌方地形复杂,必须由一分队用1小时打通道路,已知一分队的行进速度为5千米/时,二分队的行进速度为(4+a)千米/时.(1)若二分队在营地不休息,问二分队几小时能赶到A镇?(2)若二分队和一分队同时赶到A镇,二分队应在营地休息几小时?(3)下列图象中,①②分别描述一分队和二分队离A镇的距离y(千米)和时间x(小时)的函数关系,请写出你认为所有可能合理的代号,并说明它们的实际意义.(a)(b)(c)(d)第40题图。
2008-2017年历届安徽省中考数学试卷(附答案)
2017年安徽省初中学业水平考试数学一、选择题(本大题共10小题,每小题4分,共40分)1.12的相反数是【 】 A .12; B .12-; C .2; D .-2 2.计算()23a -的结果是【 】A .6a ;B .6a -;C .5a -;D .5a3.如图,一个放置在水平试验台上的锥形瓶,它的俯视图为【 】4.截止2016年底,国家开发银行对“一带一路”沿线国家累计发放贷款超过1600亿美元,其中1600亿用科学计数法表示为【 】A .101610⨯;B .101.610⨯;C .111.610⨯;D .120.1610⨯;5.不等式420x ->的解集在数轴上表示为【 】6.直角三角板和直尺如图放置,若120∠=︒,则2∠的度数为【 】A .60︒;B .50︒;C .40︒;D .30︒7.为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘制成如图所示的频数直方图,已知该校共有1000名学生,据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是【 】A .280;B .240;C .300;D .2608一种药品原价每盒25元,经过两次降价后每盒16元,设两次降价的百分率都为x ,则x 满足【 】A .()161225x +=;B .()251216x -=;C .()216125x +=;D .()225116x -=9.已知抛物线2y ax bx c =++与反比例函数b y x=的图像在第一象限有一个公共点,其横坐标为1,则一次函数y bx ac =+的图像可能是【 】10.如图,在矩形ABCD 中,AB =5,AD =3,动点P 满足13PAB ABCD S S =V 矩形,则点P 到A ,B 两点距离之和PA +PB 的最小值为【 】A B C . D 二、填空题(本大题共4小题,每小题5分,满分20分)11.27的立方根是_____________.12.因式分解:244a b ab b -+=_________________.13.如图,已知等边△ABC 的边长为6,以AB 为直径的⊙O 与边AC ,BC 分别交于D ,E 两点,则劣弧DE 的长为___________.14、在三角形纸片ABC 中,90A ∠=︒,30C ∠=︒,AC =30cm ,将该纸片沿过点B 的直线折叠,使点A 落在斜边BC 上的一点E 处,折痕记为BD (如图1),剪去△CDE 后得到双层△BDE (如图2),再沿着过△BDE 某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为___________cm 。
历届中考数学压轴(安徽考生试用)(含答案详解)
中考数学压轴题大集合(一)一、函数与几何综合的压轴题1.(2004安徽芜湖)如图①,在平面直角坐标系中,AB 、CD 都垂直于x 轴,垂足分别为B 、D 且AD 与B 相交于E 点.已知:A (-2,-6),C (1,-3) (1) 求证:E 点在y 轴上;(2) 如果有一抛物线经过A ,E ,C 三点,求此抛物线方程. (3) 如果AB 位置不变,再将DC 水平向右移动k (k >0)个单位,此时AD 与BC 相交于E ′点,如图②,求△AE ′C 的面积S 关于k 的函数解析式.[解] (1)(本小题介绍二种方法,供参考)方法一:过E 作EO ′⊥x 轴,垂足O ′∴AB ∥EO ′∥DC ∴,EO DO EO BO AB DB CD DB ''''==又∵DO ′+BO ′=DB ∴1EO EO AB DC''+=∵AB =6,DC =3,∴EO ′=2 又∵DO EO DB AB ''=,∴2316EO DO DB AB ''=⨯=⨯=∴DO ′=DO ,即O ′与O 重合,E 在y 轴上方法二:由D (1,0),A (-2,-6),得DA 直线方程:y =2x -2① 再由B (-2,0),C (1,-3),得BC 直线方程:y =-x -2 ②联立①②得02x y =⎧⎨=-⎩∴E 点坐标(0,-2),即E 点在y 轴上(2)设抛物线的方程y =ax 2+bx +c (a ≠0)过A (-2,-6),C (1,-3)图①图②E (0,-2)三点,得方程组42632a b c a b c c -+=-⎧⎪++=-⎨⎪=-⎩●解得a =-1,b =0,c =-2 ∴抛物线方程y =-x 2-2(3)(本小题给出三种方法,供参考)由(1)当DC 水平向右平移k 后,过AD 与BC 的交点E ′作E ′F ⊥x 轴垂足为F 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008-2017年安徽省初中学业水平考试数学压轴题集(本卷收录近10年安徽省中考的第10、14、22、23题)一、选择题每小题都给出A 、B 、C 、D 四个选项,其中只有一个是正确的. 1.如图,在矩形ABCD 中,AB =5,AD =3.动点P 满足13PABABCDS S=矩形 .则点P 到A ,B 两点距离之和P A +PB 的最小值为( )A.29B.34C.52D.412.如图,Rt △ABC ,AB ⊥BC ,AB =6,BC =4,P 是△ABC 内部的一个动点,且满足∠P AB =∠PBC ,则线段CP 长的最小值为( ) 32 B.2 C.81313D.121313A.第1题图 第2题图3.如图,一次函数1y x =和二次函数22+y ax bx c =+图象相交于P ,Q 两点,则函数2(1)y ax b x c=+-+的图象可能是( )A. B. C. D.第3题图4.如图,正方形ABCD 的对角线BD 长为22,若直线l 满足: ①点D 到直线l 的距离为3;②A ,C 两点到直线l 距离相等.则符合题意的直线l 的条数是( ) A.1 B.2 C.3 D.45.如图,点P 是等边三角形ABC 外接圆⊙O 上点,在以下判断中,不正确的是( ) A.当弦PB 最长时,△APC 是等腰三角形 B.当△APC 是等腰三角形时,PO ⊥AC C.当PO ⊥AC 时,∠ACP =30°D.当∠ACP =30°时,△BPC 是直角三角形第4题图第5题图6.在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是()A.10B.45C.10或45D.10或217第6题图7.如图所示,P是菱形ABCD的对角线AC上一点,过P垂直于AC的直线交菱形ABCD的边于M、N两点,设AC=2,BD=1,AP=x,△AMN的面积为y,则y关于x的函数图象的大致形状是A. B.第7题图C. D.8.甲、乙两个准备在一段长为1200米的笔直公路上进行跑步,甲、乙跑步的速度分别为4m/s和6m/s,起跑前乙在起点,甲在乙前面100米处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙两之间的距离y(m)与时间t(s)的函数图象是()A. B. C. D.9.△ABC中,AB=AC,∠A为锐角,CD为AB边上的高,I为△ACD的内切圆圆心,则∠AIB的度数是A.120°B.125°C.135°D.150°10.如图,在△ABC中,AB=AC=5,BC=6,点M为BC中点,MN⊥AC于点N,则MN等于A.65B.95C.125D.125第10题图第11题图二、填空题11. 在三角形纸片ABC 中,∠A =90°,∠C =30°,AC =30cm ,将该纸片沿过点B 的直线折叠,使点A 落在斜边BC 上的一点E 处,折痕记为BD (如图1),剪去△CDE 后得到双层△BDE (如图2),再沿着过△BDE 某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为__________cm.12. 如图,在矩形纸片ABCD 中,AB =6,BC =10,点E 在CD 上,将△BCE 沿BE 折叠,点C 恰落在边AD 上的点F 处;点G 在AF 上,将△ABG 沿BG 折叠,点A 恰落在线段BF 上的点H 处,有下列结论:①∠EBG =45°;②△DEF ∽△ABG ;③3=2ABG FGH S S △△;④AG +DF =FG .其中正确的是 .(把所有正确结论的序号都选上)第12题图 第14题图13.已知实数a 、b 、c 满足a b ab c +==,有下列结论:①若c ≠0,则111ab+=;②若a =3,则b +c =9;③若a =b =c ,则abc =0;④若a 、b 、c 中只有两个数相等,则a +b +c =8.其中正确的是 .(把所有正确结论的序号都选上)14. 如图,在▱ABCD 中,AD =2AB ,F 是AD 的中点,作CE ⊥AB ,垂足E 在线段AB 上,连接EF 、CF ,则下列结论中一定成立的是 .(把所有正确结论的序号都填在横线上) ①12DCF BCD ∠=∠;②EF =CF ;③=2BEC CEF S S △△;④∠DFE =3∠AEF .15.已知矩形纸片ABCD 中,AB =1,BC =2,将该纸片折叠成一个平面图形,折痕EF 不经过A 点(E ,F 是该矩形边界上的点),折叠后点A 落在点A ’处,给出以下判断: ①当四边形A’CDF 为正方形时,EF =2;②当EF =2时,四边形A’CDF 为正方形; ③当EF =5时,四边BA’CD 为等腰梯形;④当四边形BA’CD 为等腰梯形时,EF =5. 其中正确的是 .(把所有正确结论的序号都填在横线上) 16.如图,P 是矩形ABCD 内的任意一点,连接P A 、PB 、PC 、PD ,得到△P AB 、△PBC 、△PCD 、△PDA ,设它们的面积分别是S 1、S 2、S 3、S 4,给出如下结论:①S 1+S 2=S 3+S 4;②S 2+S 4= S 1+S 3;③若S 3=2S 1,则S 4=2S 2 ④若S 1=S 2,则P 点在矩形的对角线上.其中正确的结论的序号是 .(把所有正确结论的序号都填在横线上)第15题图 第16题图 第18题图 17.定义运算(1)a b a b ⊗=-,下面给出了关于这种运算的几个结论:①2(2)6⊗-=;②a b b a ⊗=⊗;③若0a b +=,则()()2a a b b ab ⊗+⊗=;④若0a b ⊗=,则a =0.其中正确结论的序号是 .(填上你认为所有正确结论的序号)18.如图,AD 是△ABC 的边BC 上的高,由下列条件中的某一个就能推出△ABC 是等腰三角形的是 ________ _.(把所有正确答案的序号都填写在横线上)①∠BAD =∠ACD ;②∠BAD =∠CAD ;③AB +BD =AC +CD ;④AB -BD =AC -CD .19.已知二次函数的图象经过原点及点11(,)24--,且图象与x 轴的另一交点到原点的距离为1,则该二次函数的解析式为 .20.如图为二次函数2y ax bx c =++的图象,在下列说法中:①a c <0;②方程20ax bx c ++=的根是11x =-,23x =;③0a b c ++>;④当x >1时,y 随x 的增大而增大.正确的说法有__________.(把正确的答案的序号都填在横线上)第20题图三、解答题21. 某超市销售一种商品,成本每千克40元,规定每千克不低于成本,且不高于80元.经市场调查,每天的销售量y (千克)与每千克售价x (元)满足一次函数关系,部分数据如下表:售价x (元/千克) 50 60 70 销售量y (千克) 100 80 60(1)求y 与x 之间的函数表达式; (2)设商品每天的总利润为W (元),求W 与x 之间的函数表达式(利润=收入-成本); (3)试说明(2)中总利润W 随售价x 的变化而变化的情况,并指出售价为多少元时获得最大 利润, 最大利润是多少?22.已知正方形ABCD ,点M 为AB 的中点.(1)如图1,点G 为线段CM 上的一点,且∠AGB =90°,延长AG 、BG 分别与边BC 、CD 交于点E 、F .①求证:BE =CF ;②求证:2BE BC CE =⋅.(2)如图2,在边BC 上取一点E ,满足2BE BC CE =⋅,连接AE 交CM 于点G ,连接BG 并延长交CD 于点F ,求tan ∠CBF 的值.第22题图 1 第22题图223.如图,二次函数2+y ax bx =的图象经过点(2,4)A 与(6,0)B .(1)求a ,b 的值; (2)点C 是该二次函数图象上A ,B 两点之间的一动点,横坐标为x (2<x <6),写出四边形OACB 的面积S 关于点C 的横坐标x 的函数表达式,并求S 的最大值.24.如图,A ,B 分别在射线OA ,ON 上,且∠MON 为钝角,现以线段OA ,OB 为斜边向∠MON 的外侧作等腰直角三角形,分别是△OAP ,△OBQ ,点C ,D ,E 分别是OA ,OB ,AB 的中点.(1)求证:△PCE≌△EDQ;(2)延长PC,QD交于点R.①如图1,若∠MON=150°,求证:△ABR为等边三角形;②如图3,若△ARB∽△PEQ,求∠MON大小和ABPQ的值.第24题图1 第24题图2 第24题图325.为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为x m,矩形区域ABCD的面积为y m2.(1)求y与x之间的函数关系式,并注明自变量x的取值范围;(2)x为何值时,y有最大值?最大值是多少?第25题图26.如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD 的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.(1)求证:AD =BC ;(2)求证:△AGD ∽△EGF ;(3)如图2,若AD 、BC 所在直线互相垂直,求ADEF的值.第26题图1 第26题图227.若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”. (1)请写出两个为“同簇二次函数”的函数;(2)已知关于x 的二次函数2212421y x mx m =-++和225y ax bx =++,其中1y 的图象经过点(1,1)A ,若12y y +与1y 为“同簇二次函数”,求函数2y 的表达式,并求出当0≤x ≤3时,2y 的最大值.28.如图1,正六边形ABCDEF 的边长为a ,P 是BC 边上一动点,过P 作PM ∥AB 交AF 于M ,作PN ∥CD 交DE 于N .(1)①∠MPN = ;②求证:PM +PN =3a ;(2)如图2,点O 是AD 的中点,连接OM 、ON ,求证:OM =ON ;(3)如图3,点O 是AD 的中点,OG 平分∠MON ,判断四边形OMGN 是否为特殊四边形?并说明理由.第28题图1 第28题图2 第28题图329.某大学生利用暑假40天社会实践参与了一家网店的经营,了解到一种成本为20元/件的新型商品在第x 天销售的相关信息如下表所示.销售量p (件)50p x =- 销售单价q (元/件)当1≤x ≤20时,1302q x =+;当21≤x ≤40时,52520q x=+(1)请计算第几天该商品的销售单价为35元/件;(2)求该网店第x 天获得的利润y 关于x 的函数关系式;(3)这40天中该网店第几天获得的利润最大?最大利润是多少?30.我们把由不平行于底边的直线截等腰三角形的两腰所得的四边形称为“准等腰梯形”;如图1,四边形ABCD 即为“准等腰梯形”;其中∠B =∠C .(1)在图1所示的“准等腰梯形”ABCD 中,选择合适的一个顶点引一条直线将四边形ABCD 分割成一个等腰梯形和一个三角形或分割成一个等腰三角形和一个梯形;(画出一种示意图即可) (2)如图2,在“准等腰梯形”ABCD 中∠B =∠C .E 为边BC 上一点,若AB ∥DE ,AE ∥DC ,求证:AB BEDC EC=; (3)在由不平行于BC 的直线AD 截△PBC 所得的四边形ABCD 中,∠BAD 与∠ADC 的平分线交于点E .若EB =EC ,请问当点E 在四边形ABCD 内部时(即图3所示情形),四边形ABCD 是不是“准等腰梯形”,为什么?若点E 不在四边形ABCD 内部时,情况又将如何?写出你的结论.(不必说明理由)第30题图1 第30题图2 第30题图331.如图1,在△ABC 中,D 、E 、F 分别为三边的中点,G 点在边AB 上,△BDG 与四边形ACDG 的周长相等,设BC =a 、AC =b 、AB =c . (1)求线段BG 的长;(2)求证:DG 平分∠EDF ;(3)连接CG ,如图2,若△BDG 与△DFG 相似,求证:BG ⊥CG .第31题图1 第31题图232.如图,排球运动员站在点O 处练习发球,将球从O 点正上方2m 的A 处发出,把球看成点,其运行的高度y (m )与运行的水平距离x (m )满足关系式2(6)y a x h =-+.已知球网与O 点的水平距离为9m ,高度为2.43m ,球场的边界距O 点的水平距离为18m. (1)当h =2.6时,求y 与x 的关系式;(不要求写出自变量x 的取值范围) (2)当h =2.6时,球能否越过球网?球会不会出界?请说明理由; (3)若球一定能越过球网,又不出边界,求h 的取值范围.第32题图33.在△ABC 中,∠ACB =90°,∠ABC =30°,将△ABC 绕顶点C 顺时针旋转,旋转角为(0180)θθ︒︒<<,得到△A’B’C’..第33题图1 第33题图2 第33题图3 (1)如图(1),当AB ∥BC 时,设BA 与CD 相交于点D ,证明:△CDA 是等边三角形; (2)如图(2),连接A’A 、B’B ,设△ACA’和△BCB’的面积分别为'ACA S和'BCB S.求证:'':1:3ACA BCB SS=.(3)如图(3),设AC 中点为E ,B’A’中点为P ,AC =a ,连接EP ,当θ= °时,E P 长度最大,最大值为 .34.如图,正方形ABCD 的四个顶点分别在四条平行线l 1、l 2、l 3、l 4上,这四条直线中相邻两条之间的距离依次为h 1、h 2、h 3(h 1>0,h 2>0,h 3>0). (1)求证h 1=h 3;(2)设正方形ABCD 的面积为S .求证22231()S h h h =++;(3)若12312h h +=,当h 1变化时,说明正方形ABCD 的面积S 随h 1的变化情况.第34题图35.春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少 捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第x 天(1≤x ≤20且x 为整数)的捕捞与销售的相关信息如下:鲜鱼销售单价(元/kg ) 20单位捕捞成本(元/kg ) 55x - 捕捞量(kg )950x - (1)在此期间该养殖场每天的捕捞量与前一天的捕劳量相比是如何变化的?(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x 天的收入y (元)与x (天)之间的函数关系式;(当天收入=日销售额-日捕捞成本)(3)试说明(2)中的函数y 随x 的变化情况,并指出在第几天y 取得最大值,最大值是多少?36.如图,已知△ABC ∽△A 1B 1C 1,相似比为k (k >1),且△ABC 的三边长分别为a 、b 、c (a >b >c ),△A 1B 1C 1的三边长分别为a 1、b 1、c 1.(1)若c =a 1,求证:a =kc(2)若c=a1,试给出符合条件的一对△ABC和△A1B1C1,使得a、b、c和a1、b1、c1都是正整数,并加以说明;(3)若b=a1,c=b1,是否存在△ABC和△A1B1C1,使得k=2?请说明理由.第36题图37.如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.(1)写出图中三对相似三角形,并证明其中的一对;(2)连结FG,如果α=45°,AB=42,AF=3,求FG的长.第37题图38.已知某种水果的批发单价与批发量的函数关系如图(1)所示.(1)请说明图中①、②两段函数图象的实际意义.(2)写出批发该种水果的资金金额w(元)与批发量m(kg)之间的函数关系式;在下图的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果.(3)经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系如图(2)所示,该经销商拟每日售出60kg以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日获得的利润最大.第38题图1 第38题图239.已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.(1)如图1,若点O在BC上,求证:AB=AC;(2)如图2,若点O在△ABC的内部,求证:AB=AC;(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.第39题图1 第39题图240.刚回营地的两个抢险分队又接到救灾命令:一分队立即出发往30千米的A镇;二分队因疲劳可在营地休息a(0≤a≤3)小时再往A镇参加救灾.一分队了发后得知,唯一通往A镇的道路在离营地10千米处发生塌方,塌方地形复杂,必须由一分队用1小时打通道路,已知一分队的行进速度为5千米/时,二分队的行进速度为(4+a)千米/时.(1)若二分队在营地不休息,问二分队几小时能赶到A镇?(2)若二分队和一分队同时赶到A镇,二分队应在营地休息几小时?(3)下列图象中,①②分别描述一分队和二分队离A镇的距离y(千米)和时间x(小时)的函数关系,请写出你认为所有可能合理的代号,并说明它们的实际意义.(a)(b)(c)(d)第40题图。
