华理大物第三章
华东理工大学化工原理(上下册合集

化工原理(上册)小结第一章 流体流动管路计算 伯努利方程 流动阻力(直管阻力、局部阻力)Vs=Vs 1+Vs 2 连续性方程 静力学方程 流量计 λ~Re压强p (绝对压强、表压、真空度)、流速u 雷诺数Re 、粘度μ、流动类型(滞流、湍流、过渡流)、摩擦系数λ、流动阻力(∑h f 、H f 、∆p f )、有效功We 、有效压头He 、有效功率Ne第二章 流体输送设备工作原理和主要部件(气缚现象)基本方程式(H ∞~Q 、β、n 、D )性能参数(Q 、H 、η、N )和特性曲线(H~Q 、η~Q 、N~Q )离心泵 性能改变和换算(ρ、μ、n 、D )气蚀现象和允许吸上高度(允许吸上真空度、汽蚀余量)液体输送设备 工作点与调节(流量调节、并联组合、串联组合)类型和选择其他泵(往复泵、计量泵、旋转泵、旋涡泵)气体输送设备和压缩设备第三章 非均相物系的分离沉降速度u t重力沉降降尘室(V s ≤blu t )沉降离心沉降速度、分离因素 临界直径f (D,Vs )离心沉降 原理 分离效果旋风分离器 性能 分离效率(总效率、粒级效率)型式 压降恒压过滤方程式及应用(K 、q e 、θe 、k 、s 、υ)过滤 过滤设备:板框过滤机、叶滤机、转筒真空过滤机(原理、操作、生产能力)滤饼洗涤(横穿法、置换法、θw 、w d dV ⎪⎭⎫⎝⎛θ、Ed dV ⎪⎭⎫ ⎝⎛θ)第四章 传热传热计算 ()()c c pc c h h ph h mr W t t c W Q r W T T c W Q t KS Q 1221−=−=∆=放吸i o si so m o i i o o o d d R R d bd d d K ++++=λαα11 1212ln t t t t t m ∆∆∆−∆=∆n e i i R d Pr 023.08.0λα=傅立叶定律、牛顿冷却定律导热系数、对流传热系数、总传热系数、平均温度差、传热效率、传热单元数夹套间壁 蛇管类型 混合 套管 固定管板蓄热 列管 U 型管换热器 新型换热器 浮头式间壁式换热器传热的强化途径第五章 蒸 发蒸发器:生产能力Q 、生产强度U (强化途径)、结构单效蒸发:Δ、W 、D 、D/W多效蒸发:操作流程(优点、缺点、应用场合)多效蒸发和单效蒸发的比较(多效:Δ大、D/W 小、Q 小、U 小)化工原理(下册)小结蒸馏:平衡蒸馏、简单蒸馏、间歇蒸馏、相对挥发度、理论板、恒摩尔流、回收率、回流比、进料热状况参数、全回流、最小回流比、板效率、理论板当量高度吸收:亨利系数、溶解度系数、相平衡常数、分子扩散、菲克定律、漂流因素、扩散系数、双膜理论、溶质渗透理论、表面更新理论、吸收速率方程式、吸收系数、气膜控制、液膜控制、回收率、液气比、脱吸因素、等板高度、传质单元高度、施伍德准数、施密特准数、伽利略准数蒸馏及吸收塔设备:板式塔1.塔板类型:泡罩塔板、筛板、浮阀塔板的特点2.流体力学性能: 塔板压降、液泛、雾沫夹带、漏液、液面落差影响因素、负荷性能图3.浮阀塔设计:理解4.塔板效率的表示法及影响因素填料塔1.填料特性:比表面积、空隙率、填料因子(干填料因子,湿填料因子)2.填料塔的流体力学性能:压强降(恒持液区、载液区、液泛区、载点、泛点)、液泛(影响因素:填料特性、流体的物理性质、液气比)、润湿性能3.填料塔的计算、附件、与板式塔的比较:了解干燥:干燥系统的热效率、等焓干燥、非等焓干燥、平衡水分、自由水分、结合水分、非结合水分、恒定干燥条件、干燥速率曲线、干燥速率、临界含水量、恒速干燥阶段、降速干燥阶段。
华东理工大学《物理化学》课件2.11 热力学第三定律

c 106 / J K 3 mol 1
CO(g)
-110.525 197.674 29.16 30.46 32.59 28.70
0.14 4.64
H2O(g)
-241.818 188.825 33.60 36.32 39.96 31.80
4.47 5.10
CO 2(g)
-393.509 213.74 37.20 47.32 52.97 22.59 56.15 -24.85
298.15K和1000K时的
、
r
H
om
r Smo-
和
。 rGmo-
解:由附录查得f源自Hom/kJ
mol
1
Smo- / J K 1 mol 1
C
op,m
(300K
)
/
J
K
1
mol
1
C
op,m
(600K
)
/
J
K
1
mol
1
C
op,m
(900K
)
/
J
K
1
mol
1
a / J K 1 mol 1
b 103 / J K 2 mol 1
r
H
om
T r Smo-
标准摩尔生成吉氏函数
定义:由最稳定单质生成某物质B的标摩 尔反应吉氏函数,符号用 fGmo- (B) 。
CO
O 1
rGmo
22
CO 2
1 2
O2+
O
+
2
C
CO 2
f Gmo
rGmo
CO
f Gmo
C
基准
化学反应工程原理(华东理工大学版)第三章答案

华东版3-1 解:01AA Ax c kt x =- 把数据代入得100.2min A c k -= 当x A =0.75时解得t=15min所以,增加的时间为15-5=10min 3-2 解:()()110111nn A A x n c kt ---=+- (式A )把x A =0.75和t=10min 代入解得100.1n A c k -= 再把t=30min 代入(式A )解得x A =1.25所以,转化率应为1 3-3解:设反应动力学方程为:nA Adc kc dt-= 则()()110111nn A A x n c kt ---=+-,且c A0=1因此有()()()()1110.811810.91118nnn k n k ---=+--=+-解得:n=2;k=0.5L/mo l ·min -13-41)计算进料中酸、醇和水的摩尔浓度c A0、c B0、c S0(注意进料中水的浓度c S0不为0)。
2)列出当酸的转化率为x A 时,各组分浓度的表示式:()0000001A A A B B A A R A A S S A Ac c x c c c x c c x c c c x =-=-==+3)将上列各式及各组分初浓度代入反应速率式,整理得()627.931010.220.1 2.58A A A dx x x dt-=-⨯-+ 4)计算转化率达35%所需的时间为()0.35627.931010.220.1 2.58AA A dx t x x -=⨯-+⎰上述积分可查积分表用公式计算,也可用MA TLAB 语言的quad 解算子计算,结果为 71532t s h =≈5)计算所需反应器体积。
先计算每天的反应批数,再计算每m 3反应体积每天的生产量,然后再计算达到要求产量所需反应器体积。
答案为 V R =51.9m 3 3-51)设酯的平衡转化率为x Ae ,将平衡时各组分浓度代入化学平衡方程得:()()221.1510.2191.151148.76 1.151AeAe Ae x x x =--化简整理上述方程并求解得90.8%Ae x =2)此题解法与3-4中的步骤2~4相同,答案为t=276min 3)此时各组分的浓度为酯:0.207mol/L ;水:47.816 mol/L ;醇、酸:0.910 mol/L ; 反应物系的组成为酯:0.414%;水:95.80%;醇、酸:1.82%; 3-6对可逆放热反应,当反应温度过低时,因反应速率过低转化率偏低,当反应温度过高时,转化率又会受化学平衡的限制。
华东理工大学物理化学第三章2-2

X i 1 ni X i
K
X dT dp p p,n j T ,n j
K i 1
X i dni
一定温度、压力下并保持各物质相 对数量不变,积分得:
X dX
0 K
X
ni
0
K i 1
X i dni i 1 X i dni i 1 X i dni
V nAVA nBVB
VA (V nBVB ) / nA {(18.0152/ 1000)[1002.935 51.832nB / mol 0.1394( nB / mol) 2 ( nB / mol)(51.832 0.2788nB / mol)]}cm 3 mol1 [(18.0152/ 1000)(1002.935 0.1394( nB / mol) 2 ]cm 3 mol1 [18.0681 0.00251 ( nB / mol) 2 ]cm 3 T , p
Xi 和Xi* 都是1mol物质 i 对 X 的贡献
1mol 物 质 i 对 混合物系统 X
1mol 物 质 i 对
纯组分系统 X
的贡献。
的贡献
以体积V 代替X 进行说明 (1)在20℃、101325Pa下, H2O(A)与
C2H5OH(B)混合
Xi 是在系统恒定 T, p 和其它物质的量时,改 变1mol i 物质引起的系统广延性质 X 的变化。
X X i n i
def
T , p , n j i
Xi 是一个状态函数,强度性质
X X (T , p, n1 , n2 , , nK )
X X (T , p, x1 , x2 , , x K 1 , n)
华南理工大学大学物理各章节习题及答案汇编
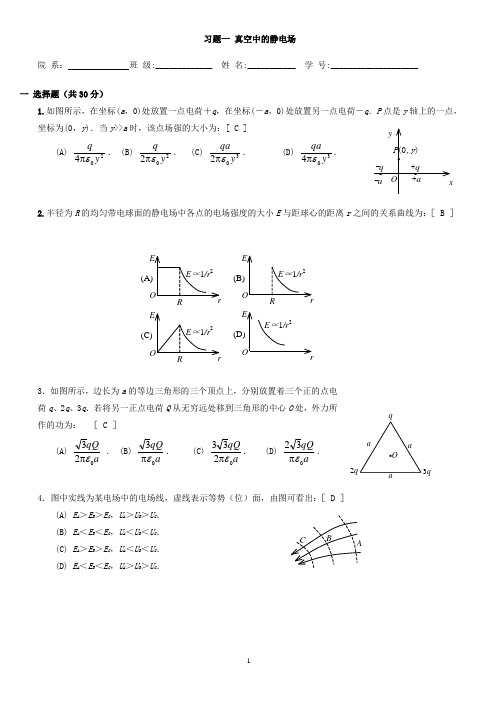
习题一 真空中的静电场院 系: 班 级:_____________ 姓 名:___________ 学 号:____________________一 选择题(共30分)1.如图所示,在坐标(a ,0)处放置一点电荷+q ,在坐标(-a ,0)处放置另一点电荷-q .P 点是y 轴上的一点,坐标为(0,y ).当y >>a 时,该点场强的大小为:[ C ] (A)204y q επ. (B)202y q επ. (C)302y qa επ. (D) 304yqa επ.2.半径为R 的均匀带电球面的静电场中各点的电场强度的大小E 与距球心的距离r 之间的关系曲线为:[ B ]3.如图所示,边长为a 的等边三角形的三个顶点上,分别放置着三个正的点电荷q 、2q 、3q .若将另一正点电荷Q 从无穷远处移到三角形的中心O 处,外力所作的功为: [ C ](A) a qQ 023επ . (B) a qQ 03επ. (C) a qQ 0233επ. (D) aqQ 032επ.4.图中实线为某电场中的电场线,虚线表示等势(位)面,由图可看出:[ D ] (A) E A >E B >E C ,U A >U B >U C . (B) E A <E B <E C ,U A <U B <U C . (C) E A >E B >E C ,U A <U B <U C . (D) E A <E B <E C ,U A >U B >U C .E Or(D) E ∝1/r 23q2q5.半径为R 的“无限长”均匀带电圆柱面的静电场中各点的电场强度的大小E 与距轴线的距离r 的关系曲线为: [ B ]6.在边长为a 的正方体中心处放置一电荷为Q 的点电荷,则正方体顶角处的电场强度的大小为: (A)2012a Q επ. (B) 206a Q επ. (C) 203a Q επ. (D) 20aQεπ. [C ]7.图示为一具有球对称性分布的静电场的E ~r 关系曲线.请指出该静电场是由下列哪种带电体产生的. (A) 半径为R 的均匀带电球面. [ B ](B) 半径为R 的均匀带电球体.(C) 半径为R 的、电荷体密度为=A r (A 为常数)的非均匀带电球体. (D) 半径为R 的、电荷体密度为=A/r (A 为常数)的非均匀带电球体.8.选无穷远处为电势零点,半径为R 的导体球带电后,其电势为U 0,则球外离球心距离为r 处的电场强度的大小为(A) 302r U R . (B) R U 0. (C) 20r RU . (D) r U 0. [ C ]9. 设有一“无限大”均匀带正电荷的平面.取x 轴垂直带电平面,坐标原点在带电平面上,则其周围空间各点的电场强度E随距平面的位置坐标x 变化的关系曲线为(规定场强方向沿x 轴正向为正、反之为负):[C ]10. 一个静止的氢离子(H +)在电场中被加速而获得的速率为一静止的氧离子(O +2)在同一电场中且通过相同的路径被加速所获速率的:(A) 2倍. (B) 22倍. (C) 4倍. (D) 42倍. [ B ]E O rE ∝1/rE Or(D) E ∝1/rR E Or(C) E ∝1/rE Or(A) E ∝1/rO R rE E ∝1/r 2OxE (A)OxE (C)OxE (B)OxE (D)E ∝1/|x|E ∝x11.如图所示,一个电荷为q 的点电荷位于立方体的A 角上,则通过侧面abcd的电场强度通量等于:(A) 06εq . (B) 012εq . (C) 024εq . (D) 048εq. [ C ]二 填空题1.电荷分别为q 1,q 2,q 3的三个点电荷分别位于同一圆周的三个点上,如图所示.设无穷远处为电势零点,圆半径为R ,则b 点处的电势U =___________ . ()32102281q q q R++πε2.图中所示以O 为心的各圆弧为静电场的等势(位)线图,已知U 1<U 2<U 3,在图上画出a 、b 两点的电场强度的方向,并比较它们的大小.E a = E b (填<、=、>).3.两根相互平行的“无限长”均匀带正电直线1、2,相距为d ,其电荷线密度分别为λ1和λ2如图所示,则场强等于零的点与直线1的距离a 为_____________ .d 211λλλ+4.如图所示,两同心带电球面,内球面半径为r 1=5 cm ,带电荷q 1=3×10-8C ;外球面半径为r 2=20 cm , 带电荷q 2=-6×108C ,设无穷远处电势为零,则空间另一电势为零的球面半径r = __________________.10 cm5.已知某静电场的电势函数U =a ( x 2+ y ),式中a 为一常量,则电场中任意点的电场强度分量E x =-2ax ,E y = -a ,E z = 0.6.如图所示.试验电荷q ,在点电荷+Q 产生的电场中,沿半径为R 的整个圆弧的3/4圆弧轨道由a 点移到d 点的过程中电场力作功为 0 ;从d 点移到无穷远处的过程中,电场力作功为qQ / (4πε0R ).7.一个带电荷q 、半径为R 的金属球壳,壳内是真空,壳外是介电常量为ε 的无限大各向同性均匀电介质,则此球壳的电势U =________________.Rqεπ48.在点电荷q 的电场中,把一个-1.0×10-9C 的电荷,从无限远处(设无限远处电势为零)移到离该点电荷距离 0.1 m 处,克服电场力作功 1.8×10-5 J ,则该点电荷q =-2×10-7库伦.(真空介电常量0=8.85×10-12C 2·N -1·m -2)A b caq2 q 1 q 3OOU 1U 2U 3abλ2a d 12q 1 q 2 r 1r 2+Q R q d∞三 计算题1.厚度为d 的“无限大”均匀带电导体板两表面单位面积上电荷之和为σ.试求图示离左板面距离为a 的一点与离右板面距离为b 的一点之间的电势差.解:选坐标如图.由高斯定理,平板内、外的场强分布为:E = 0 (板内) )2/(0εσ±=x E (板外)1、2两点间电势差⎰=-2121d x E U U x x x d b d d d a d 2d 22/2/02/)2/(0⎰⎰+-+-+-=εσεσ )(20a b -=εσ 2.一环形薄片由细绳悬吊着,环的外半径为R ,内半径为R /2,并有电荷Q 均匀分布在环面上.细绳长3R ,也有电荷Q 均匀分布在绳上,如图所示,试求圆环中心O 处的电场强度(圆环中心在细绳延长线上).解:先计算细绳上的电荷在O 点产生的场强.选细绳顶端作坐标原点O ,x 轴向下为正.在x 处取一电荷元 d q = d x = Q d x /(3R ) 它在环心处的场强为 ()20144d d x R qE -π=ε ()20412d x R R xQ -π=ε 整个细绳上的电荷在环心处的场强()203020116412RQx R dx R Q E R εεπ=-π=⎰ 圆环上的电荷分布对环心对称,它在环心处的场强E 2=0由此,合场强 i R Qi E E20116επ== 方向竖直向下.3.电荷Q (Q >0)均匀分布在长为L 的细棒上,在细棒的延长线上距细棒中心O 距离为a 的P 点处放一电荷为q (q >0 )的点电荷,求带电细棒对该点电荷的静电力. 解:沿棒方向取坐标Ox ,原点O 在棒中心处.求P 点场强: ()()20204d 4d d x a xx a q E -π=-π=ελε 3分 ()⎰--π=2/2/204d L L x a xE ελ()2202/2/0414L a Qx a L L -π=-⋅π=-εελ 4分 方向沿x 轴正向. 点电荷受力:==qE F ()2204πL a qQ-ε 方向沿x 轴正方向. 3分1σda1σd abxOO R 3RR /2E 1xR3R x xOPL+Q OaP O L/2L/2d x d q a。
大物1课件——第03章刚体和流体的运动(1)

定理表述:刚体绕平行于质心轴的转动惯量 J,等于
绕质心轴的转动惯量 JC 加上刚体质量与两轴间的距离
平方的乘积: J J C md 2
如:
JC
1 2
mR2
J
JC
J JC mR 2
m
1的转动惯量最小
大学物理(I)教学组
普通物理学
第六版
第三章 刚体和流体的运动
方向是水平向右,则OP与极轴之间的夹角为。
角称为角坐标(或角位置)。
Px
o
角坐标为标量。但可有正负。
大学物理(I)教学组
普通物理学
第六版
2.角位移
角坐标的增量:
称为刚体的角位移
3.角速度 lim
t0 t
d
dt
第三章 刚体和流体的运动
y v2 p v1
P
R
x
方向:满足右手定则,沿刚体转动方向右旋大拇指指向。
始后 t = 6s 时飞轮的角速度;(3)t = 6s
时飞轮边缘上一点的线速度、切向加速
度和法向加速度.
大学物理(I)教学24组
普通物理学
第六版
第三章 刚体和流体的运动
三、刚体定轴转动定律 O’
对刚体中任一质量元 mi
ω
应用牛顿第二定律,可得:
Fi fi miai
上式切向分量式为:
O
ri
mi
fi
i
Fii
Fi sini fi sini miai miri
用ri 乘以上式左右两端:
Firi sini firi sini miri2
大学物理(I)教学组
普通物理学
第六版
第三章 刚体和流体的运动
华东理工大学线性代数习题答案-第三章

第三章 线性方程组一、习题解答3.1解:否,例如121250,()2,363A r A -⎡⎤⎢⎥==⎢⎥⎢⎥--⎣⎦却有12036=-- 3.2(1)解:利用初等行变换化成行阶梯形矩阵来求矩阵的秩。
由12311231015401540154000001540000A--⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥-⎣⎦⎣⎦知()2r A =,最高阶非零子式可取0112(2)由112112013013013000026000B--⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦知()2r B =,且最高阶非零子式可取1112-- 3.3(1)解:由()()r A r A T =,故可转化为求()r A T , 由211211222240112(1)33360112(1)k k A k k k k k k k k k T ----⎡⎤⎡⎤⎢⎥⎢⎥=-----⎢⎥⎢⎥⎢⎥⎢⎥-----⎣⎦⎣⎦1120112(1)00(2)(1)0k k k k k k -⎡⎤⎢⎥---⎢⎥⎢⎥+-⎣⎦,知①当 1k =时,()()1;r A r A T== ②当2k =-时,()()2;r A r A T== ③当1k ≠且2k ≠-时,()()3r A r A T==(2)解:由112301123001221012210162100800024400002Ba ab b --⎡⎤⎡⎤⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥⎢⎥-+--+⎢⎥⎢⎥---+⎣⎦⎣⎦知①当8a =-且2b =-时,()2;r B =②当8a =-且2b ≠-,或8a ≠-且2b =-时,()3;r B =③当8a ≠-且2b ≠-时,()4r B = 3.4解:因为[]A β比A 多了一列,但行数相同,假设()r A k =,那么[]A β也有k 阶子式非零,所以()();r Ar A β≥而假如()()1,r A r A β>+那么,删去增广列及某一行后的1k +阶子式中必有某个非零,与()r A k =矛盾。
2022年华东理工大学化工原理简答题模拟真题汇总

第一章流体流动1.何谓轨线?何谓流线?为什么流线互不相交?99答:轨线是同一流体质点在不同步刻所占空间位置旳连线;流线是采用欧拉法考察旳成果,流线上各点旳切线表达该点旳速度方向;由于同一点只有一种速度,由此可知,流线互不相交。
2.动能校正系数α为什么总是大于、等于1旳?试阐明理由?003.简述数学模型法规划实验旳重要环节。
00、03、06、10答:数学模型实验研究措施立足于对所研究过程旳深刻理解,按如下重要环节进行工作:①将复杂旳真实过程自身化简成易于用数学方程式描述旳物理模型;②将所得到旳物理模型进行数学描述即建立数学模型;③通过实验对数学模型旳合理性进行检查并测定模型参数。
4.流体流动过程中,稳定性是指什么?定态性是指什么?015.简述因次论指引下旳实验研究措施旳重要环节。
01、04答:因次分析法旳具体环节:①找出影响过程旳独立变量;②拟定独立变量所波及旳基本因次;③构造因变量和自变量旳函数式,一般以指数方程旳形式表达;④用基本因次表达所有独立变量旳因次,并出各独立变量旳因次式;⑤根据物理方程旳因次一致性原则和π定理得到准数方程;⑥通过实验归纳总结准数方程旳具体函数式。
6.层流与湍流旳本质区别是什么?02答:湍流旳最基本特性是浮现了径向旳速度脉动。
当流体在管内层流时,只有轴向速度而无径向速度,牛顿型流体服从牛顿粘性定律;然而在湍流时,流体质点沿管道流动旳同步还浮现了径向旳随机脉动,这种脉动加速了径向旳动量、热量和质量旳传质,动量旳传递不仅起因于分子运动,而来源于流体质点旳横向脉动速度。
7.非牛顿流体中,塑性流体旳特点是什么?02、05、06、10答:含固体量较多旳悬浮体常体现出塑性旳力学特性,即只有当施加旳剪应力大于某一临界值(屈服应力)之后才开始流动,流动发生后,一般具有剪切稀化性质,也也许在某一剪切率范畴内有剪切增稠现象。
8.什么是流体流动旳边界层?边界层分离旳条件是什么?03答:由于流体粘性旳作用,接近壁面旳流体将相继受阻而降速,随着流体沿壁面前流动,流体受影响旳区域逐渐扩大,而流速降为未受边壁影响流速旳99%以内旳区域即为边界层。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
若系统的合外力矩为零,则系统的角动量守恒
讨论:1. J、ω均不变, J ω=常数 2. J、ω都改变, 但 J ω不变 注意: 1).运用角动量守恒时,系统中各物体均绕同一转轴转动 2).角动量定理、角动量守恒定律中各角速度或速度均需 相对同一惯性参照系。
X. J. Feng
花样滑冰运动员通过改变 身体姿态即改变转动惯量 来改变转速
aB R (4) a人 a人绳 a绳地 aB (5) 2 aB g 由上五个方程可得: 7
T2
2
A M
Mg
M g 2
X. J. Feng
质点直线运动: F ma 1 2 1 2 Fdx m vb m va 2 2 a
b
2
刚体定轴转动 M J
1 1 2 2 Md J 2 J1 2 2 1
2 r i i mi 质量非连续分布 r为质元到转轴距离 J 2 r m dm 质量连续分布
质量元dm
线分布:dm dx 面分布:dm ds
体分布:dm dV 2.2 转动惯量的计算示例
•均匀细棒m,l (1).绕过中心与棒轴的转动惯量 解: dJ x 2 dm x 2dx
2
平行轴定理:
1 J 2O J 2O M ( R l ) MR 2 M ( R l ) 2 J 2 2 1 2 1 2 2 J J1 J 2 ml MR M ( R l ) 3 2
X. J. Feng
哪种握法转动惯量大?
3.转动定律应用举例 已知: M ,R ,m 例1: 求:m的加速度
讨论: 两不同轴轮子的角加速度
求:两轮子的角加速度 判断:
m , R 1 1 已知: A轮上有一外力矩M,方向如图
A
m2 , R2
B
X. J. Feng
解(一): 1 1 2 2 ( m1 R1 m2 R2 ) M 2 2 两轮不同轴,不能取为同一体系 解(二): 1 R1 2M 1 2 2 ( m1 R1 ) 1 M 1 2 R2 2 m1R1 A轮不只受一个外力矩
mg T ma 1 TR ( MR 2 ) 2 a R
m
T mg
(2)
1 2 0 t t 2
0 t 0
h R
2
mgR mR 2 MR 2 / 2
81.7rad / s
2
h 6.12102 m
(3)从静止态回到原位置
0 2 2 10 rad / s
2
3.3 定轴转动中的功能关系 1. 转动动能: 1 1 2 刚体定轴转动时每 E m v m r 2 2 Ki i i i i 2 2 个质点的动能: 1 2 2 1 2 E E ( m r ) J 刚体转动动能: K Ki i i 2 i i 2 1 与质点Ek mv 2相似 2.力矩的功 2 dA FdS cos F d
1. 转动定律
刚体的定轴转动:?
切向方程: F
v O r
F sin ma t
rF sin rm(r )
ψ
M mr
2
X. J. Feng
刚体定轴转动时:各点均作圆周运动
任一点的方程:
M i (mi ri )
2
M i外 M i内 mi ri
2
对所有质点求和:
定轴O
·
X. J. Feng
M ,R
绳
解:
N
T
m
对 m: mg T ma
对轮: TR
R
T
a
m
J
G
mg
a R
a
例2:
已知:m1 = m2 M1 R1 M2 R2 求:、 T1 、T2 解: 受力分析如图所示 列方程 T1 m1 g m1a1 (1) m2 g T2 m2 a2 (2)
第三章 刚体的转动
X. J. Feng
刚体(rigid body):特殊的质点系,运动过程中形状和 体积变化,理想化的模型。 基本方法:间距不变的质点系----刚体 质点系的牛顿定律----刚体的运动规律 3.1 刚体运动学 平动:与质点处理方法相同
1. 刚体的运动
转动:定轴或定点
复合运动:平动转动的叠加
1
--刚体定轴转动动能定理
合外力矩对定轴转动刚体所作的功等于刚体转动动能的增量 4.刚体重力势能: E m gh
Δ mi
P
C× hc hi Ep=0
m h mg m
i
i
i i
m gh c 重力的力矩可认为重力
作用在质心处
5.机械能守恒定律: 若W外+ W内非=0 则Ek +Ep =常量
l 2
l
A
1 2 1 l 2 2 J A J O ml ml m( ) md 2 3 12 2
l O轴与 A轴间距 d ,且二轴平行 2
x dm=dx
o
x
平行轴定理:
J A J O md
2
其中:
JO: 过质心轴的转动惯量
JA: 平行于过质心轴的轴的转动惯量
d: 两平行轴间的距离
t1
1
1
冲量矩
---角动量定理(积分式)
作用于刚体上冲量矩等于刚体角动量的增量 3.角动量守恒定律
t2
t1
Mdt J2 J1 M 0时,J2 J1
若转动物体的合外力矩为零,则系统的角动量守恒
X. J. Feng
转动系统由两个或两个以上物体组成时:
M合 0时
J 常数
M
i
i外
M i内 ( mi ri )
2 i i
内力矩成对出现:
M
i
2
i内
0
转动惯量
M i外 ( mi ri )
i i
M 合 J
注意:
---刚体定轴转动定律 M , J , 都是对同一轴的
X. J. Feng 2.转动惯量(J)rotational inertia : 描述物体转动惯性的物理量 2.1定义式:
l/2
x x o dm=dx
1 l 3 1 ml 2 1 J O x dx x 3 12 12 l / 2 3 l / 2
l /2
2
(2).绕过棒端与棒轴的转动惯量
X. J. Feng
1 x 3 1 3 1 2 J A x dx l ml 0 3 3 0 3
J
R 0
问题: 球体:
1 2r dr r 4 2
3
R 0
1 mR2 2
柱体:
dr dm=2rdr
r
ω
ω
讨论: 钟摆对O的转动惯量 对同一轴的转动惯量满足叠加ห้องสมุดไป่ตู้理 O
X. J. Feng
m, l
O M , R
J J1 J 2 1 1 2 2 J MR J1 ml 2 O 2 3
X. J. Feng
m, v0
子弹, 杆, 地球为系统: 机械能守恒 1 l 2 J O mg (1 cos ) mgl (1 cos ) 2 2
•均匀园环m,R 绕过中心与环面轴的转动惯量
解: dJ R dm R
2
2R 2
X. J. Feng
R
2
dl
2
dl dm=dl
m 2 J R dl R 2R mR 0 2R •均匀盘m,R 绕过中心与环面轴转动惯量
dJ r 2 dm r 2ds r 2 2rdr
2
方向:沿Z轴正向
即刚体绕定轴转动的角动量为绕该轴 转动惯量与角速度矢量之积
2.刚体定轴转动的角动量定理
X. J. Feng
dL d (r mv ) 质点: M dt dt 定轴转动:M dL d(J) dt dt t2 2 2 Mdt d ( J) J d J2 J1
X. J. Feng
ω
x
F (rd ) cos
A dA Md
r z · 轴
r
F (rd ) sin Md
0 力矩对空间的累积效应
3.刚体定轴转动的动能定理
2
2
X. J. Feng
d d A dA Md J dt 1 1 2 1 1 2 2 J J J d 2 1 2 2
2
z
刚体转动的 各质元:
r P
角量相同
线量不同
转动平面
角速度矢量
X. J. Feng
o
v
p
v r v r
r o
对定轴转动, 角速度只有两个方向. (+, -)
3.2 刚体的定轴转动定律---刚体动力学
X. J. Feng
质点:F ma
2. 刚体的定轴转动 运动的特点:
*各质元均作角速度相同的圆周运动, 且各圆心在同一直线上 — 转轴 *各质元相对位置不变. 运动的描述: 作转动平面: 用P点的圆周运动----刚体转动 用P点的
X. J. Feng
v r v an 2r r dv at r dt
M
正确解: 对A轮:
对B轮:
1 2 M T1 R1 T2 R1 ( m1 R1 )1 2
m1 , R1
