利用matlab实现齿轮滚刀快速设计
MATLAB在齿轮优化设计中的应用

MATLAB在齿轮优化设计中的应用任建华;刘艳层;梁振刚【摘要】Considering the volume of two gears and the related axle in the cylindrical gear reducer, it uses the optimization toolbox of MATLAB to establish objection functions,select the design variables,detemine the constraints and functions and optimize. It turned out that the arithmetic is effective and reliable, the programming is simple and the design efficiency is to be improved to use the MATLAB arithmetic. It provides a good reference value for the optimal design of gear reducer.%在圆柱齿轮减速器中,考虑到对两齿轮及相关轴体积的减小,利用MATLAB优化工具箱,建立优化目标函数、选取设计变量、确定约束条件及函数。
编程最终结果表明采用MATLAB算法求解优化问题,算法有效可靠、程序编写简单快捷,设计效率得以提高,从而为减速器的优化设计提供了良好的参考价值。
【期刊名称】《机电工程技术》【年(卷),期】2014(000)011【总页数】3页(P76-78)【关键词】减速器;优化设计;MATLAB【作者】任建华;刘艳层;梁振刚【作者单位】河北工程大学机电工程学院,河北邯郸 056038;河北工程大学机电工程学院,河北邯郸 056038;河北工程大学机电工程学院,河北邯郸 056038【正文语种】中文【中图分类】TH122优化设计是现代设计法中的一个重要领域,它是从众多的可行设计方案中寻找出最佳设计方案,极大地促进了现代工程设计理论方法的发展。
齿轮范成程序MATLAB代码
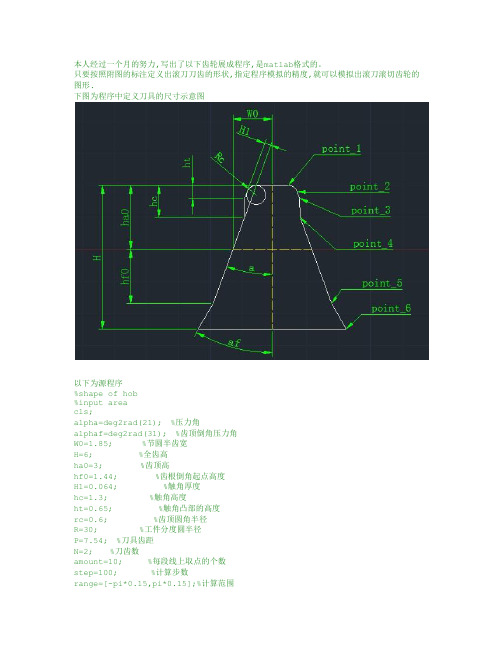
本人经过一个月的努力,写出了以下齿轮展成程序,是matlab格式的。
只要按照附图的标注定义出滚刀刀齿的形状,指定程序模拟的精度,就可以模拟出滚刀滚切齿轮的图形.下图为程序中定义刀具的尺寸示意图以下为源程序%shape of hob%input areacls;alpha=deg2rad(21); %压力角alphaf=deg2rad(31); %齿顶倒角压力角W0=1.85; %节圆半齿宽H=6; %全齿高ha0=3; %齿顶高hf0=1.44; %齿根倒角起点高度H1=0.064; %触角厚度hc=1.3; %触角高度ht=0.65; %触角凸部的高度rc=0.6; %齿顶圆角半径R=30; %工件分度圆半径P=7.54; %刀具齿距N=2; %刀齿数amount=10; %每段线上取点的个数step=100; %计算步数range=[-pi*0.15,pi*0.15];%计算范围%location of key-pointyr=ha0-rc; %齿顶圆角圆心xr=W0+(H1-rc)/cos(alpha)-yr*tan(alpha);point=zeros(6,2);point(1,2)=ha0;point(1,1)=xr;point(2,2)=ha0-rc*(1-sin(alpha));point(2,1)=xr+rc*cos(alpha);point(3,2)=ha0-ht;point(3,1)=(W0+H1/cos(alpha))-(ha0-ht)./cot(alpha);point(4,2)=ha0-hc;point(4,1)=W0-point(4,2)*tan(alpha);point(5,2)=-hf0;point(5,1)=W0-tan(alpha)*point(5,2);point(6,2)=ha0-H;point(6,1)=point(5,1)-tan(alphaf)*(point(6,2)-point(5,2));%-------------直线部分-------------theta=linspace(range(1),range(2),step);w11=linspace(point(4,1),point(5,1),amount)';h11=linspace(point(4,2),point(5,2),amount)';w12=repmat(w11,1,step);h12=repmat(h11,1,step);theta2=repmat(theta,amount,1);x12=(h12-R).*sin(theta2)+(R.*theta2-w12).*cos(theta2);y12=(R.*theta2-w12).*sin(theta2)+(R-h12).*cos(theta2);theta13=(w11-h11/tan(alpha))/R;x13=sin(theta13).*(h11-R)+cos(theta13).*(R.*theta13-w11);y13=sin(theta13).*(R*theta13-w11)+cos(theta13).*(R-h11);%-----------圆角部分--------gama=linspace(pi/2,alpha,amount);w21=(xr+rc.*cos(gama))';h21=(yr+rc.*sin(gama))';w22=repmat(w21,1,step);h22=repmat(h21,1,step);x22=(h22-R).*sin(theta2)+(R.*theta2-w22).*cos(theta2);y22=(R.*theta2-w22).*sin(theta2)+(R-h22).*cos(theta2);theta23=((xr-yr.*cot(gama))/R)';x23=sin(theta23).*(h21-R)+cos(theta23).*(R.*theta23-w21);y23=sin(theta23).*(R*theta23-w21)+cos(theta23).*(R-h21);rmin=R;for i=1:(length(x23)-2)[XX,YY,RR]=threepointcircle(x23(i),y23(i),x23(i+1),y23(i+1),x23(i+2),y2 3(i+2));if RR<rminrmin=RR;endend%---------凸角部分------------------w31=linspace(point(2,1),point(3,1),amount)';h31=linspace(point(2,2),point(3,2),amount)';w32=repmat(w31,1,step);h32=repmat(h31,1,step);theta2=repmat(theta,amount,1);x32=(h32-R).*sin(theta2)+(R.*theta2-w32).*cos(theta2);y32=(R.*theta2-w32).*sin(theta2)+(R-h32).*cos(theta2);theta33=(w31-h31/tan(alpha))/R;x33=sin(theta33).*(h31-R)+cos(theta33).*(R.*theta33-w31);y33=sin(theta33).*(R*theta33-w31)+cos(theta33).*(R-h31);%-------连接部分---------------alpha2=atan(point(4,1)-point(3,1))/(point(3,2)-point(4,2)); w41=linspace(point(3,1),point(4,1),amount)';h41=linspace(point(3,2),point(4,2),amount)';w42=repmat(w41,1,step);h42=repmat(h41,1,step);theta2=repmat(theta,amount,1);x42=(h42-R).*sin(theta2)+(R.*theta2-w42).*cos(theta2);y42=(R.*theta2-w42).*sin(theta2)+(R-h42).*cos(theta2);theta43=(w41-h41/tan(alpha2))/R;x43=sin(theta43).*(h41-R)+cos(theta43).*(R.*theta43-w41);y43=sin(theta43).*(R*theta43-w41)+cos(theta43).*(R-h41);%-------倒角部分---------------alpha3=atan(point(6,1)-point(5,1))/(point(5,2)-point(6,2)); w51=linspace(point(5,1),point(6,1),amount)';h51=linspace(point(5,2),point(6,2),amount)';w52=repmat(w51,1,step);h52=repmat(h51,1,step);theta2=repmat(theta,amount,1);x52=(h52-R).*sin(theta2)+(R.*theta2-w52).*cos(theta2);y52=(R.*theta2-w52).*sin(theta2)+(R-h52).*cos(theta2);theta53=(w51-h51/tan(alpha3))/R;x53=sin(theta53).*(h51-R)+cos(theta53).*(R.*theta53-w51);y53=sin(theta53).*(R*theta53-w51)+cos(theta53).*(R-h51);%----------全刀齿-----------w6=[w21;w31;w41;w11;w51];h6=[h21;h31;h41;h11;h51];w6=flipud(w6);h6=flipud(h6);w6=[w6;-flipud(w6)];h6=[h6;flipud(h6)];w62=w6;h62=h6;for i=2:Nw62=[w6+(i-1)*P;w62];h62=[h6;h62];endtheta6=repmat(theta,5*amount*2*N,1);w62=repmat(w62,1,step);h62=repmat(h62,1,step);x62=(h62-R).*sin(theta6)+(R.*theta6-w62).*cos(theta6);y62=(R.*theta6-w62).*sin(theta6)+(R-h62).*cos(theta6);%---------------------figure;plot(x12,y12);hold on;grid on;axis equal;plot(x22,y22);plot(x32,y32);plot(x42,y42);plot(x52,y52);figure;plot(x12',y12');hold on;grid on;axis equal;plot(x22',y22');plot(x32',y32');plot(x42',y42');plot(x52',y52');figure;plot(x13,y13);hold on;grid on;axis equal;plot(x23,y23,'o');plot(x33,y33,'*');plot(x43,y43,'.');plot(x53,y53,'+');figureplot(x12',y12');hold on;grid on;axis equal;plot(x22',y22');plot(x32',y32');plot(x42',y42');plot(x52',y52');plot(x13,y13,'*');plot(x23,y23,'*');plot(x33,y33,'*');plot(x43,y43,'*');plot(x53,y53,'*');figureplot(w62,h62);hold on;grid on;axis equal;figureplot(x62,y62);hold on;grid on;axis equal;以下为角度转化为弧度的子程序function rad=deg2rad(deg)rad=deg./180.*pi;以下为计算最小圆弧半径的子程序function [x,y,r]=threepointcircle(x1,y1,x2,y2,x3,y3)k12=(x2-x1)/(y1-y2);k23=(x3-x2)/(y2-y3);x=((y2+y3-y1-y2)/2+k12*(x1+x2)/2-k23*(x2+x3)/2)/(k12-k23); y=k12*(x-(x1+x2)/2)+(y1+y2)/2;r=((x-x1)^2+(y-y1)^2)^0.5;以下为程序运行输出的图形1,一个刀刃的展成过程2,一个刀刃上各个点的运动轨迹3,刀刃上各段切削刃分别所展成的齿形段4,两图合二为一5,刀齿的形状6,多个刀齿展成的情形7,将6图放大观察,也许是渐开线起始点的位置吧以上就是程序代码及输出的结果欢迎批评指正分享经验,交流心得,共同进步有意交流的+Q 252320995并说明来意李某人2013/6/30于重庆璧山。
基于AutoCADVBA的齿轮滚刀CAD系统开发

张春雨 ! 俞宗嘉 ! 孙 旭"
( !安徽科技学院工学院, 安徽 凤阳 $""!%% ; 安徽 宣城 $&$%%% ) "安徽宣城职业技术学院, 摘 要: 应用开发工具 !"#$%!& ’(!、 )*% 的对话框以及数据库管理技术, 开发了齿轮滚刀 %!& 系统。 该系统可实现滚刀几何尺寸自动设计、 滚刀零件图的自动化绘制, 实现齿轮滚刀快速可靠的设计。 关键词: ’(! %!& 齿轮滚刀
!
齿轮滚刀的设计计算
齿轮滚刀加工齿轮的过程, 犹如一对相错轴渐开
线圆柱齿轮的啮合过程。为了能切出正确的渐开线齿 轮, 滚刀刀齿的左右两侧刃口应完全符合理论切削刃 口之形状。或者说, 不管滚刀容屑槽的形状如何, 其刀 齿左右两侧刃口应准确地分布在渐开线基本蜗杆的螺 旋面上。无论是新制滚刀或是重磨后的旧滚刀, 其刀 齿刃口均应符合这一原则。 齿轮滚刀的设计计算程序由子模块管理模块、 原 始参数输入模块、 滚刀结构参数计算模块、 滚刀齿形参 数计算模块和滚刀设计结果输出模块等组成。如图 , 所示。
(!) 原始参数的输入
齿轮滚刀设计的原始参数
的绘图程序是在 $%&’($) 环境下运行的, 可以将设计 计算结果和标准参数等绘图数据提取。 (,) 图形绘制程序 主要包括绘制滚刀产品图中 的主视图、 轴向齿形和法向齿形。由于滚刀齿形参数 的计算程序中包含有零前角直槽、 正前角直槽和零前 角螺旋槽以及区分左、 右旋螺旋槽等程序分支。因此, 该模块编制了 0 个功能子程序。 (-) 尺寸、 形状公差和表面粗糙度标注程序 在 滚刀产品图的生成过程中, 要进行尺寸、 形位公’(! ’ ()*+, -./0$1#)#1$2 $3 %!& 45*#+6 3$7 8+)7 9$:
基于MATLAB的两级直齿圆柱 齿轮减速器优化设计

专业:机械设计制造及其自动化学号:0412070117Hebei Normal University of Science & Technology本科毕业设计题目:基于MATLAB的两级直齿圆柱齿轮减速器优化设计院(系、部):机电工程学院学生姓名:孙小亮指导教师:张小芹职称讲师2011年 6月9 日河北科技师范学院教务处制资料目录1. 学术声明 (1)2. 河北科技师范学院本科毕业论文(设计) (61)3. 河北科技师范学院本科毕业论文(设计)任务书 (2)4. 河北科技师范学院本科毕业论文(设计)开题报告 (3)5. 河北科技师范学院本科毕业论文(设计)中期检查表 (1)6. 河北科技师范学院本科毕业论文(设计)答辩记录表 (1)7. 河北科技师范学院本科毕业论文(设计)成绩评定汇总表 (2)8 河北科技师范学院本科毕业论文(设计)工作总结 (2)9 其他反映研究成果的资料(如公开发表的论文复印件、效益证明等)……………………………………………………………共页河北科技师范学院本科毕业设计基于MATLAB的两级直齿圆柱齿轮减速器优化设计院(系、部)名称:机电工程学院专业名称:机械设计制造及其自动化学生姓名:孙小亮学生学号: 0412070117指导教师:张小芹2011年 5月 26 日河北科技师范学院教务处制学术声明本人呈交的学位论文,是在导师的指导下,独立进行研究工作所取得的成果,所有数据、图片资料真实可靠。
尽我所知,除文中已经注明引用的内容外,本学位论文的研究成果不包含他人享有著作权的内容。
对本论文所涉及的研究工作做出贡献的其他个人和集体,均已在文中以明确的方式标明。
本学位论文的知识产权归属于河北科技师范学院。
本人签名:日期:指导教师签名:日期:减速器中直齿圆柱齿轮承载能力计算涉及齿轮的设计、制造工艺、材料和检验等各方面的因素,是一个十分复杂的问题,在减速器设计中齿轮参数的计算繁琐,且手工计算容易出错,在机械传动设计的工作量中占用了较大比重。
齿轮故障动力学仿真matlab-概述说明以及解释

齿轮故障动力学仿真matlab-概述说明以及解释1.引言1.1 概述齿轮是机械传动中常用的零部件,其在各种机械设备中起着至关重要的作用。
然而,由于工作环境的恶劣以及长期使用的磨损,齿轮可能出现故障,导致机械设备的性能下降甚至损坏。
为了更好地理解齿轮故障的动力学特性,可以通过仿真技术来模拟和分析齿轮系统的运行状态,并及时发现潜在的故障点。
本文将介绍齿轮故障动力学仿真在MATLAB中的应用,通过分析齿轮系统的动态特性,探讨不同故障模式对系统性能的影响,从而为齿轮故障诊断和预防提供有益的参考。
通过本文的研究,我们希望能够加深对齿轮故障动力学的理解,提高齿轮系统的可靠性和安全性。
1.2 文章结构文章结构部分的内容如下:文章结构包括以下几个部分:1. 引言:介绍文章的背景和研究意义,引出文章的主题和研究内容。
2. 正文:分为两个部分,分别是齿轮故障动力学简介和MATLAB在齿轮故障动力学仿真中的应用。
在齿轮故障动力学简介部分,将介绍齿轮故障动力学的基本概念和原理,为读者提供必要的背景知识。
在MATLAB 在齿轮故障动力学仿真中的应用部分,将详细介绍MATLAB在该领域的具体应用及其优势。
3. 结论:总结文章的主要内容和研究成果,对研究进行评价和展望未来的研究方向。
通过以上部分的内容安排,读者可以清晰地了解整篇文章的主要结构和内容安排,帮助他们更好地理解和阅读文章。
1.3 目的本文的主要目的在于探讨利用MATLAB进行齿轮故障动力学仿真的方法和技术。
通过对齿轮系统中可能出现的不同故障情况进行建模和仿真,我们可以更好地理解齿轮系统的运行机理,并且能够快速有效地诊断和解决齿轮故障问题。
同时,本文也旨在为工程师和研究人员提供一个基于MATLAB的齿轮故障动力学仿真平台,帮助他们更好地分析和优化齿轮系统的性能,推动齿轮传动技术的发展和应用。
通过本文的研究,我们希望能够为齿轮系统的设计、运行和维护提供更加有效的工程解决方案,提高齿轮系统的可靠性和稳定性。
齿轮传动优化设计及MATLAB实现

第 34 卷
33 2006 年 第 1 期
设计计算
林业机械与木工设备
4.1 建立设计变量及目标函数
要求齿轮传动体积为最小进行优化, 齿轮体积 V
是 mn、z1、!、"d 的函数, 传动比 u 一般作为已知条件给
出, 故其设计变量为:
x=[ x1, x2, x3, x4] T=[ z1, !d, mn, "] T
( ZheJiang Shuren University, Zhejiang Hangzhou 310015, China)
Abstr act: Optimal gear-driven design is greatly important in modern machine design, the article researched into a new method of optimal gear-driven design based on MATLAB for the purpose of finding a convenient and practical measure. The optimal gear-driven design model was established, using MATLAB method how to solve gear parameter optimization was introduced. After an example calculating, the result showed that this method is convenient and effective, and can simplify computer programming, is especially suitable for engineer.
基于matlab遗传算法工具的同心式磁力齿轮优化设计

基于matlab遗传算法工具的同心式磁力齿轮优
化设计
同心式磁力齿轮是一种利用磁场实现扭矩传递的装置,具有无接触、无磨损、高效率、高扭矩密度等优点。
然而,磁力齿轮的设计和优化是一个复杂的问题,涉及到多个参数的优化,包括齿数、磁极形状、磁场强度等。
在Matlab中,可以利用遗传算法工具箱进行同心式磁力齿轮的优化设计。
以下是一个基本的步骤:
1.定义目标函数:首先,你需要定义一个目标函数,用于评估设计的优劣。
目标函数可以根据实际应用场景来确定,例如,你可能希望最小化扭矩损失、最大化扭矩密度等。
2.定义设计变量:定义你想要优化的设计变量。
对于同心式磁力齿轮,设计变量可能包括齿数、磁极形状、磁场强度等。
3.初始化种群:在遗传算法中,种群是所有可能解的集合。
你需要根据设计变量的范围初始化一个种群。
4.适应度评估:使用目标函数评估种群中每个解的适应度。
适应度较高的解被选中的概率较高。
5.选择:根据适应度评估结果,选择用于生成下一代的解。
6.交叉和变异:在遗传算法中,通过交叉和变异操作产
生新的解。
交叉是随机选择两个解的一部分并交换它们,以产生新的解;变异是随机改变解的一部分。
7.终止条件:当达到终止条件(例如,达到最大迭代次数或找到满足要求的最优解)时,停止遗传算法的运行。
8.结果分析:分析遗传算法的结果,查看最优解以及其适应度值。
请注意,以上步骤只是一个基本的概述,实际应用中可能需要进行更多的细节调整和优化。
另外,使用遗传算法进行优化设计时,可能需要考虑一些特殊的问题,例如防止早熟收敛、处理多峰问题等。
基于MATLAB编程软的齿轮设计

摘要齿轮机构是现代机械中最重要的传动机构,应用十分广泛。
它是依靠轮齿齿廓直接接触来传递运动和动力的,具有传动比恒定,传动效率高,使用寿命长,适用范围广及承载能力高等特点,但也存在对制造和安装精度要求较高以及成本较高等缺点。
使用MATLAB编程软件可以简化齿轮设计中的计算过程,只需将参数输入就可以计算出正确的结果。
此设计编写了三个程序,分别为绘制标准直齿圆柱齿轮渐开线曲面,直齿轮几何尺寸设计,以及两齿轮相对滑动系数相等时的变位系数的选择。
在编写程序的过程中需用到一些特殊曲线公式,例如绘制渐开线曲面轮廓时就用到了此曲线在直角坐标系中的表达式。
另外,程序在运行中可能需要在程序代码中设置初始值,以便计算出正确的结果,所选初始值的大小应尽量接近正确的结果,在计算中有可能会出现输入值相同而计算结果不同,这可能是软件本身的问题,还需要弥补。
本次设计一对齿轮,根据给定的参数,使用Matlab计算出齿轮的其他参数及几何尺寸。
关键词:齿轮机构,Matlab计算,初始值,几何尺寸ABTRACTGears of modern machinery are the most important transmission mechanism, a wide range of applications. It is to rely on direct contact with gear tooth profile and the power to transfer the exercise. MATLAB programming software used to simplify the calculation of gear design process, simply enter the parameters you can calculate the correct results. The preparation of this design, three procedures, respectively, rendering the standard spur gear involute surfaces, the design of spur gear geometry, as well as the coefficient of relative sliding between gear changes when the same selection coefficient. In the preparation of the procedures required to process some special curve formula, such as drawing involute surface contours on the use of this curve in the Cartesian coordinate system of expression. In addition, the procedures in the operation code may need to set the initial value for the purpose of calculating the correct result, the size of the initial value selected should be as close as possible to correct the results of the calculation in the input value may be calculated the same the result is different, this may be the software itself, but also need to be filled. The design of a pair of gears, according to the given parameters, the use of Matlab to calculate the other parameters and gear geometry.This is the design of a pair of gear. In accordance with the given parameters, the use of Matlab to calculate the other parameters and gear geometry.KEY WORDS:gears,Matlab programming,Initial value,gear geometry dimension目录目录 (3)第一章前言 (5)1.1 MATLAB简介 (5)1.2 变量、函数与表达式 (6)1.2.1 MATLAB变量名的定义规则 (6)1.2.2 数学运算符号以及标点符号 (7)1.2.3 数学函数 (7)1.2.4 数组与矩阵 (7)1.2.5 MATLAB有两种常用的工作方式 (7)第二章渐开线齿轮机构 (8)2.1 渐开线齿轮的简介 (8)2.1.1 渐开线齿廓曲线 (8)2.1.2 渐开线的极坐标方程式 (9)2.1.3 渐开线齿廓曲线的计算 (10)2.2 渐开线直齿轮变位系数的选择 (10)2.2.1 关于渐开线直齿轮变位系数 (10)2.2.2 最小变位系数的求法 (11)2.2.3 齿轮干涉对变位系数的限制 (11)2.2.4 变位齿轮的啮合传动及几何尺寸 (11)2.3 按两齿轮相对滑动系数相等时的变位系数选择 (13)第三章使用MATLAB编写简单程序 (15)3.1Matlab编程绘制标准直齿圆柱齿轮渐开线曲面 (15)3.1.1 制作MATLAB界面 (15)3.2Matlab编程计算直齿轮的几何尺寸 (18)3.2.1 设计MATLAB界面的过程 (18)3.3 按等滑动系数原则选择变位系数 (20)结论 (21)致谢 (22)参考文献 (23)附录一 (24)附录二 (27)附录三 (37)第一章前言本次设计的目的是使用Matlab编一个程序,实现齿轮参数及几何尺寸的计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
利用matlab实现齿轮滚刀齿形快速设计
随着齿轮行业发展近几十年,人们对齿轮的研究越来越
深入,其中涉及到很多高等数学的运算,在早期,工程师们
用纸笔的方式,进行大量的计算,计算过程非常复杂,工作
量非常大,所以也很辛苦。
目前很多公司研发出专门针对高
等数学运算的软件,非常好用,也节省了大量的计算工作量,
不得不佩服当今科学发展的飞跃性速度。
现在我们借助matlab设计一款标准齿轮滚刀齿形:
齿轮1:m=2,z=37,α=20°,d a1=φ78,r1=37,r b1=34.77
齿轮2:z=41,d a2=φ86
这里我们借用公式
dnf=
√[d−2(h∗an−x n−x f)m n]2+4[(h∗an−x n−x f)m n /tanαt]2 (因为标准齿轮,此处x n=0,x f=0,m n=m,αt=α)
计算渐开线起始圆d nf=φ70.86,r nf=35.43
起始圆压力角α0=arccos(r b1/r nf)=11.076°,转换成弧度为
0.1933
起始圆展角(及该点渐开线函数)θ0=tanα0-α0=0.0024;
同样利用d a1=φ78, r b1=34.77计算出终止圆展角θa=0.038
我们先看齿廓部分渐开线方程组:
x=R b cosθ+R bθsinθ
y=R b sinθ-R bθcosθ
该方程组在齿轮手册中的图形解释如下:
可以看出,当l0=0时,渐开线起点在x轴上,起点在基圆,而我们一般研究时以y轴为纵坐标,且渐开线偏离y轴半个基圆弧齿厚。
所以,我们先旋转90°,即将x轴和y轴切换:
x=R b sinθ-R bθcosθ
y=R b cosθ+R bθsinθ
基圆弧齿厚计算公式:
S b=[s+mzinv(α)]cosα
此处s为分度圆齿厚s=πm/2,
由以上两公式计算出s b=3.99
基圆半弧齿厚s b/2=1.995
基圆周长l=πd b=218.47
故我们可以计算出齿形实际渐开线起点在基圆上偏离y轴的角度为s b/2/l×360°=3.29°
于是,我们将渐开线方程组绕齿轮中心作旋转,旋转变换如
下:
Aφ1=[cos3.29°,sin3.29°,0]
[-sin3.29°,cos3.29°,0]
[0 , 0 , 1]
渐开线方程组写成矩阵形式:
A=[ R b sinθ-R bθcosθ]
[R b cosθ+R bθsinθ ]
[ 0 ]
经过变换的齿廓曲线方程组如下:
B= Aφ1*A,我们将这两个矩阵及变换输入matlab中,计算结
果如下:
B =
[rb*sin(θ) - (57*rb*cos(θ))/10000 - (57*a*rb*sin(θ))/10000 -θ*rb*cos(θ)]
[ rb*cos(θ) + (57*rb*sin(θ))/10000 +θ*rb*sin(θ) - (57*θ*rb*cos(θ))/10000 ] [ 0 ]
即x= rb*sin(θ) - (57*rb*cos(θ))/10000 - (57*a*rb*sin(θ))/10000 -θ*rb*cos(θ)
Y= rb*cos(θ) + (57*rb*sin(θ))/10000 +θ*rb*sin(θ) - (57*θ*rb*cos(θ))/10000 当然该式中数字显示和我们平时习惯有点不一样,可以不理
会它,这就是我们齿轮1齿廓曲线的实际方程组。
在滚齿运动中,齿轮和刀具实际运动变换如下:
从o0到o1的变换为:从O1到O的变换为:
A2=[cosθ,-sinθ,0] A3=[ 0 ]
[sinθ,cosθ,0 ] [-r1]
[0, 0, 1] [ 0]
从O到O2的变换为:
A4=[r1*θ]
[ 0 ]
[ 0 ]
根据滚齿展成原理,最终滚刀齿形的方程组矩阵为:
D= A2*(Aφ1*A)+ A3+ A4
我们将以上变换矩阵及公式输入matlab中,经过计算,得出滚刀齿形方程组的矩阵:
D =
[θ*r1 - cos(θ)*((57*rb*cos(θ))/10000 - rb*sin(θ) + (57*θ*rb*sin(θ))/10000
+θ*rb*cos(θ)) - sin(θ)*(rb*cos(θ) + (57*rb*sin(θ))/10000 +θ*rb*sin(θ) - (57*θ*rb*cos(θ))/10000)]
[cos(θ)*(rb*cos(θ) + (57*rb*sin(θ))/10000 +θ*rb*sin(θ) - (57*θ
*rb*cos(θ))/10000) - r1 - sin(θ)*((57*rb*cos(θ))/10000 - rb*sin(θ) + (57*θ*rb*sin(θ))/10000 +θ*rb*cos(θ))]
[0 ]
即:
x=θ*r1 - cos(θ)*((57*rb*cos(θ))/10000 - rb*sin(θ) + (57*θ*rb*sin(θ))/10000
+θ*rb*cos(θ)) - sin(θ)*(rb*cos(θ) + (57*rb*sin(θ))/10000 +θ*rb*sin(θ) - (57*θ*rb*cos(θ))/10000)
y= cos(θ)*(rb*cos(θ) + (57*rb*sin(θ))/10000 +θ*rb*sin(θ) - (57*θ
*rb*cos(θ))/10000) - r1 - sin(θ)*((57*rb*cos(θ))/10000 - rb*sin(θ) + (57*θ*rb*sin(θ))/10000 +θ*rb*cos(θ))
其中:
r1=37,rb=34.77,θ=[0.0024:0.0001:0.038]
我们将其在matlab中代入D式中,即可出来一系列x,y数
值,即刀具齿形的坐标点。
将matlab中的x,y数值用xlswrite命令导出到excel中并
进行整合后,就可以得到一个关于x,y的坐标数据列,将其
复制。
然后打开autocad,输入spline命令,并粘贴excel中的数
据列后,就在cad中绘出了我们滚刀的刀具齿形,按照前面
给出的齿轮1参数,最终得到的刀具齿形如下:
总结:我们在齿轮计算及微积分,微分几何等学习和研究过
程中,可以尽量借用matlab等数学计算软件,把它们当作
一种高级的计算器来使用,可以大大的节省我们计算的工作量及计算时间,使技术及科学研究变得简单和轻松很多。
何顺洪于2023年10月。
